人教新课标版数学高一- 人教数学必修2能力提升 4-2-3 直线与圆的方程的应用
人教版高中数学必修二4.2.3直线与圆的方程的应用(一)1

复习引入
1. 直线方程有几种情势? 分别是什么? 2. 圆的方程有几种情势?分别是哪些? 3. 求圆的方程时,什么条件下用标准方程?
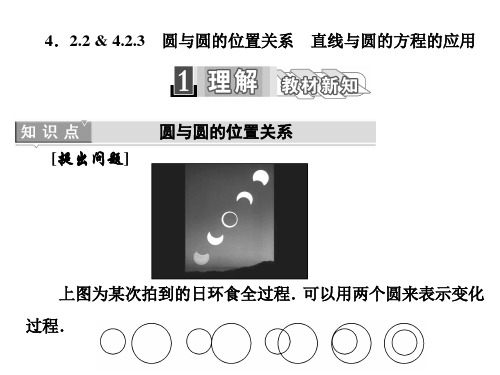
什么条件下用一般方程? 4. 直线与圆的方程在生产生活实践中有广
泛的应用,想想身边有哪些呢?
复习引入
5. 如何用直线和圆的方程判断它们之间的 位置关系?
4. 对称问题 圆关于点对称,圆关于直线对称.
例4.求圆(x-1)2 +(y+1)2=4关于点(2,2) 对称的圆的方程.
练习.求圆(x-1)2 +(y-1)2=4关于直线 l:x-2y-2=0对称的圆的方程.
作业讲评
《习案》P.182第4、5题; 《习案》 P.183第6题.
课后作业
1. 阅读教材P.130到P.132; 2. 《课后限时检测》二十七 .
4.2.3直线与圆 的方程的应用
复习引入
1. 直线方程有几种情势? 分别是什么?
复习引入
1. 直线方程有几种情势? 分别是什么? 2. 圆的方程有几种情势?分别是哪些?
复习引入
1. 直线方程有几种情势? 分别是什么? 2. 圆的方程有几种情势?分别是哪些? 3. 求圆的方程时,什么条件下用标准方程?
复习引入
5. 如何用直线和圆的方程判断它们之间的 位置关系?
6. 如何根据圆的方程,判断它们之间的位 置关系?
讲授新课
1. 标准方程问题 例1. 求圆(x-2)2 +(y+3)2=4上的点到 x-y+2=0的最远、最近的距离.
2. 轨迹问题
充分利用几何图形的性质,熟练 掌握两点间的距离公式、点到直线的 距离公式.
2. 轨迹问题
例2.过点A(4,0)作直线l交圆O: x2+y2=4 于B、C两点,求线段BC的中点P的轨迹 方程.
高一数学人教A版必修2:4-2-3 直线与圆的方程的应用

A点出发射到x轴上后,沿圆的切线方向反射,求这条光线从
A点到切点所经过的路程.
第四章 4.2 4.2.3
第三十四页,编辑于星期日:二十二点 三分。
[解析] 已知点A关于x轴的对称点为A′(0,-2),所求
的路程即为|A′D|. 在Rt△A′CD中,|A′D|2=|A′C|2-|CD|2.
∴|A′D|= |A′C|2-|CD|2=185 5, 光线从A点到切点所经过的路程:
[证明] 如图所示,以边长为a的正方形ABCD的边AB为x 轴,A为原点,建立平面直角坐标系,
则A(0,0),B(a,0),C(a,a),D(0,a), 则kAC=aa--00=1,kBD=a0--0a=-1, ∴kACkBD=-1.∴AC⊥BD. 即正方形的对角线互相垂直.
第四章 4.2 4.2.3
第四章 4.2 4.2.3
第十六页,编辑于星期日:二十二点 三分。
[解析] 以直线AB为x轴,线段AB的垂直平分线为y轴, 建立直角坐标系,如右图所示.设A(-5,0),则B(5,0).在坐 标平面内任取一点P(x,y),设从A地运货到P地的运费为2a元 /km,则从B地运货到P地的运费为a元/km.
设P是圆上不同于A、B的任一点,其坐标为(x0,y0).则x
2 0
+y02=r2.
∴kPA·kPB=yx00-+0r·x0y-0 r
=x20-y20 r2=xr202--xr202=-1.
∴PA⊥PB,
∴∠APB=90°,故在圆中,直径所对的圆周角等于90°.
第四章 4.2 4.2.3
第二十九页,编辑于星期日:二十二点 三分。
第四章 4.2 4.2.3
第十八页,编辑于星期日:二十二点 三分。
数学必修Ⅱ人教新课标A版4-2-2-3直线与圆的方程的应用课件(35张)
=a-4.则有 a+12+a-4-32= a+62+a-4+22,
解得 a=12,故圆心为12,-72,
半径为
12+12+-72-32=
829.
故圆的方程为x-122+y+722=829,
即 x2+y2-x+7y-32=0.
法二: ∵圆 x2+y2+6y-28=0 的圆心(0,-3)不在直线 x-y
[活学活用]
1.两圆 C1:x2+y2-2x-3=0,C2:x2+y2-4x+2y+3=0 的位置
关系是
()
A.相离
B.相切
C.相交
D.内含
答案:C
2.(湖南高考)若圆 C1:x2+y2=1 与圆 C2:x2+y2-6x-8y+m=0
外切,则 m=
()
A.21
B.19
C.9
D.-11
答案:C
与两圆相交有关的问题
[例 2] 求经过两圆 x2+y2+6x-4=0 和 x2+y2+6y-28=0
的交点且圆心在直线 x-y-4=0 上的圆的方程.
[解]
法
一
:
解
方
程
组
x2+y2+6x-4=0, x2+y2+6y-28=0,
得两圆的交点
A(-1,3),B(-6,-2).
设所求圆的圆心为(a,b),因圆心在直线 x-y-4=0 上,故 b
3.公共弦长的求法 (1)代数法:将两圆的方程联立,解出交点坐标,利用两点间 的距离公式求出弦长. (2)几何法:求出公共弦所在直线的方程,利用圆的半径、半 弦长、弦心距构成的直角三角形,根据勾股定理求解.
[活学活用] 已知圆 C1:x2+y2+2x-6y+1=0,与圆 C2:x2+y2-4x+2y-11 =0 相交于 A,B 两点,求 AB 所在的直线方程和公共弦 AB 的长. 解:由圆 C1 的方程减去圆 C2 的方程,整理,得方程 3x-4y+6 =0,又由于方程 3x-4y+6=0 是由两圆相减得到的,即两圆交 点的坐标一定是方程 3x-4y+6=0 的解.因为两点确定一条直 线,所以 3x-4y+6=0 是两圆公共弦 AB 所在的直线方程. ∵圆 C1:x2+y2+2x-6y+1=0,∴圆心为 C1(-1,3),半径 r=3, ∴圆心 C1 到直线 AB 的距离 d=│-3-2152+6│=95,
高一数学(人教A版)必修2能力强化提升:4-2-3 直线与圆的方程的应用

一、选择题1.一辆卡车宽1.6m ,要经过一个半圆形隧道(半径为3.6m)则这辆卡车的平顶车篷篷顶距地面高度不得超过( )A .1.4mB .3.5mC .3.6mD .2.0m[答案] B[解析] 圆半径OA =3.6,卡车宽1.6,∴AB =0.8,∴弦心距OB = 3.62-0.82≈3.5.2.与圆x 2+y 2-ax -2y +1=0关于直线x -y -1=0对称的圆的方程是x 2+y 2-4x +3=0,则a =( )A .0B .1C .2D .3[答案] C[解析] x 2+y 2-4x +3=0化为标准形式为(x -2)2+y 2=1,圆心为(2,0), ∵(2,0)关于直线x -y -1=0对称的点为(1,1), ∴x 2+y 2-ax -2y +1=0的圆心为(1,1).∵x 2+y 2-ax -2y +1=0,即为(x -a 2)2+(y -1)2=a 24,圆心为(a 2,1),∴a2=1,即a =2.3.直线2x -y =0与圆C :(x -2)2+(y +1)2=9交于A 、B 两点,则△ABC (C 为圆心)的面积等于( )A .2 5B .2 3C .4 3D .4 5[答案] A[解析] ∵圆心到直线的距离d =|4+1|5=5,∴|AB |=29-d 2=4,∴S △ABC =12×4×5=2 5..4.点P 是直线2x +y +10=0上的动点,直线P A 、PB 分别与圆x 2+y 2=4相切于A 、B 两点,则四边形P AOB (O 为坐标原点)的面积的最小值等于( )A .24B .16C .8D .4[答案] C[解析] ∵四边形P AOB 的面积S =2×12|P A |×|OA |=2OP 2-OA 2=2OP 2-4,∴当直线OP 垂直直线2x +y +10=0时,其面积S 最小.5.若直线ax +by =1与圆x 2+y 2=1相交,则点P (a ,b )的位置是( ) A .在圆上 B .在圆外 C .在圆内 D .以上都不对[答案] B[解析] 由|0+0-1|a 2+b2<1,∴a 2+b 2>1. 6.(2008年山东高考题)已知圆的方程为x 2+y 2-6x -8y =0.设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为( )A .10 6B .20 6C .30 6D .40 6[答案] B[解析] 圆心坐标是(3,4),半径是5,圆心到点(3,5)的距离为1,根据题意最短弦BD 和最长弦(即圆的直径)AC 垂直,故最短弦的长为252-12=46,所以四边形ABCD 的面积为12×AC ×BD =12×10×46=20 6.7.方程1-x 2=kx +2有唯一解,则实数k 的范围是( ) A .k =±3 B .k ∈(-2,2) C .k <-2或k >2D .k <-2或k >2或k =±3 [答案] D[解析] 由题意知,直线y =kx +2与半圆x 2+y 2=1(y ≥0只有一个交点.结合图形易得k <-2或k >2或k =±3.8.(拔高题)台风中心从A 地以每小时20 km 的速度向东北方向移动,离台风中心30 km 内的地区为危险地区,城市B 在A 的正东40 km 外,B 城市处于危险区内的时间为( )A .0.5 hB .1 hC .1.5 hD .2 h[答案] B[解析] 建系后写出直线和圆的方程,求得弦长为20千米,故处于危险区内的时间为2020=1(h).二、填空题9.已知实数x ,y 满足x 2+y 2-4x +1=0.则x -y 的最大值和最小值分别是________和________.yx 的最大值和最小值分别是________和________. x 2+y 2的最大值和最小值分别是______和______. [答案] 2+6,2-6;1,-1;7+43,7-4 3[解析] (1)设x -y =b 则y =x -b 与圆x 2+y 2-4x +1=0有公共点, 即|2-b |12+12≤3,∴2-6≤b ≤2+ 6故x -y 最大值为2+6,最小值为2- 6 (2)设yx =k ,则y =kx 与x 2+y 2-4x +1=0 有公共点,即|2k |1+k2≤ 3 ∴3≤k ≤3,故yx 最大值为3,最小值为- 3 (3)圆心(2,0)到原点距离为2,半径r = 3 故(2-3)2≤x 2+y 2≤(2+3)2由此x 2+y 2最大值为7+43,最小值为7-4 3.10.如下图所示,一座圆拱桥,当水面在某位置时,拱顶离水面2 m ,水面宽12 m ,当水面下降1 m 后,水面宽为________m.[答案] 251[解析] 如下图所示,以圆拱拱顶为坐标原点,以过拱顶的竖直直线为y 轴,建立直角坐标系,设圆心为C ,水面所在弦的端点为A ,B ,则由已知得A (6,-2),B (-6,-2).设圆的半径为r ,则C (0,-r ),即圆的方程为x 2+(y +r )2=r 2. ①将点A的坐标(6,-2)代入方程①,解得r=10.∴圆的方程为x2+(y+10)2=100.②当水面下降1 m后,可设点A′的坐标为(x0,-3)(x0>0),将A′的坐标(x0,-3)代入方程②,求得x0=51.所以,水面下降1 m后,水面宽为2x0=251.11.已知直线x-2y-3=0与圆(x-2)2+(y+3)2=9相交于E,F两点,圆心为点C,则△CEF的面积等于________.[答案]2 5[解析]∵圆心C(2,-3)到直线的距离为d=|2+6-3|1+(-2)2=5,又R=3,∴|EF|=2R2-d2=4.∴S△CEF=12|EF|·d=2 5.12.若点P在直线l1:x+y+3=0上,过点P的直线l2与曲线C:(x-5)2+y2=16相切于点M,则|PM|的最小值________.[答案] 4[解析]曲线C:(x-5)2+y2=16是圆心为C(5,0),半径为4的圆,连接CP,CM,则在△MPC中,CM⊥PM,则|PM|=|CP|2-|CM|2=|CP|2-16,当|PM|取最小值时,|CP|取最小值,又点P在直线l1上,则|CP|的最小值是点C到直线l1的距离,即|CP|的最小值为d=|5+3|1+1=42,则|PM|的最小值为(42)2-16=4.三、解答题13.如图所示,已知直线l 的解析式是y =43x -4,并且与x 轴、y 轴分别交于A ,B 两点.一个半径为1.5的圆C ,圆心C 从点(0,1.5)开始以每秒0.5个单位的速度沿着y 轴向下运动,当圆C 与直线l 相切时,求该圆运动的时间.[解析] 设运动的时间为t s ,则t s 后圆心的坐标为(0,1.5-0.5t ).∵圆C 与直线l :y =43x -4,即4x -3y -12=0相切,∴|4×0-3×(1.5-0.5t )-12|32+42=1.5.解得t =6或16.即该圆运动的时间为6 s 或16 s.14.设有一个半径为3 km 的圆形村落,甲、乙两人同时从村落中心出发,甲向东,而乙向北前进,甲出村后不久,改变前进方向.沿着相切于村落边界的方向前进,后来恰好与乙相遇,设甲、乙两人的速度都一定,其比为3:1,此二人在何处相遇?[解析] 如图,以村落中心为坐标原点,以东西方向为x 轴,南北方向为y 轴建立直角坐标系.设甲向东走到D 转向到C 恰好与乙相遇.设D ,C 两点的坐标分别为(a,0),(0,b ),其中a >3,b >3,则CD 方程为x a +yb =1.设乙的速度为v ,则甲的速度为3v .依题意,得⎩⎪⎨⎪⎧aba 2+b 2=3,a 2+b 2+a 3v=bv .解得⎩⎨⎧a =5,b =154.∴乙向北走3.75 km 时两人相遇.15.某圆拱桥的示意图如下图所示,该圆拱的跨度AB 是36 m ,拱高OP 是6 m ,在建造时,每隔3 m 需用一个支柱支撑,求支柱A 2P 2的长.(精确到0.01 m)[分析] 建系→求点的坐标→求圆的方程→求A 2P 2的长[解析] 如图,以线段AB 所在的直线为x 轴,线段AB 的中点O 为坐标原点建立平面直角坐标系,那么点A ,B ,P 的坐标分别为(-18,0),(18,0),(0,6).设圆拱所在的圆的方程是x 2+y 2+Dx +Ey +F =0. 因为A ,B ,P 在此圆上,故有⎩⎪⎨⎪⎧182-18D +F =0,182+18D +F =0,62+6E +F =0,解得⎩⎪⎨⎪⎧D =0,E =48,F =-324.故圆拱所在的圆的方程是x 2+y 2+48y -324=0. 将点P 2的横坐标x =6代入上式,解得 y =-24+12 6.答:支柱A 2P 2的长约为126-24.[点评] 在实际问题中,遇到有关直线和圆的问题,通常建立坐标系,利用坐标法解决.建立适当的直角坐标系应遵循三点:①若曲线是轴对称图形,则可选它的对称轴为坐标轴;②常选特殊点作为直角坐标系的原点;尽量使已知点位于坐标轴上.建立适当的直角坐标系,会简化运算过程.16.如图,直角△ABC 的斜边长为定值2m ,以斜边的中点O 为圆心作半径为n 的圆,直线BC 交圆于P 、Q 两点,求证:|AP |2+|AQ |2+|PQ |2为定值.[证明]如上图,以O为坐标原点,以直线BC为x轴,建立平面直角坐标系,于是有B(-m,0),C(m,0),P(-n,0),Q(n,0).设A(x,y),由已知,点A在圆x2+y2=m2上.|AP|2+|AQ|2+|PQ|2=(x+n)2+y2+(x-n)2+y2+4n2=2x2+2y2+6n2=2m2+6n2(定值).。
数学 必修2 新课标人教A版 第四章 4.2 4.2.3 直线与圆的方程的应用[配套课件]
![数学 必修2 新课标人教A版 第四章 4.2 4.2.3 直线与圆的方程的应用[配套课件]](https://img.taocdn.com/s3/m/ff29c51c4b35eefdc9d33334.png)
【学习目标】 1.正确理解直线与圆的概念,并能解决简单的实际问题. 2.能由直线与圆的位置关系解决简单的实际问题.
用坐标方法解决平面几何问题的“三步曲” (1)建立适当的平__面__直__角__坐__标__系__,用坐标和方程表示问题中 的_几__何__元__素___,将平面几何问题转化为__代__数__问__题___; (2)通过代数运算,解决__代__数__问__题____; (3)把代数运算结果___翻__译__成__几__何__结__论_____. 练习:(x-a)2+(y-b)2=r2表示圆心为_(_a_,__b_)__,半径为 ___|r_| __的圆.
【变式与拓展】 3.已知实数 x,y 满足 x2+y2+4x+3=0,求yx- -21的值域.
解:方程 x2+y2+4x+3=0 可化为(x+2)2+y2=1,其表示 以 C(-2,0)为圆心,1 为半径的圆.
设yx- -21=k,其几何意义为:圆 C 上的点 P(x,y)与点 Q(1,2) 连线的斜率.
2ax+2 r2-a2y=r2+a2.
令 x=a,得 y=12 r2-a2.
∴Ha,12
r2-aEF 平分 CD.
【变式与拓展】 2.如图 4-2-3,Rt△ABC 的斜边长为定值 2m,以斜边的中 点 O 为圆心作半径为 n 的圆,BC 的延长线交圆于 P,Q 两点, 求证:|AP|2+|AQ|2+|PQ|2 为定值.
∴|BC|=150 3-200,则该市受台风影响的起始时间 t1= 150 430-200×60≈90(min),即约 90 min 后台风影响该市,台 风影响的持续时间 t2=200+ 40200=10(h),即台风对该市的影响 持续时间为 10 h.
高中数学教案之高一数学人教版必修二4.2.3直线与圆的方程的应用

高一数学必修二教案
科目:数学
课题
课型
直线与圆的方程的应用
( 1)会用“数形结合”的数学思想解决问题 .
教学
目标
( 2)理解掌握,直线与圆的方程在实际生活中的应用
.
新课
( 3)让学生通过观察图形,理解并掌握直线与圆的方程的应用,培养学生分析问
题与解决问题的能力教学教ຫໍສະໝຸດ 内容备过程注
一、 自主 学习
二、 质疑 提问
高中数学教案之高一数学人教版必修二 4.2.3 直线与圆的方程的应用
高中数学教案之高一数学人教版必修二 4.2.3 直线与圆的方程的应用
高中数学教案之高一数学人教版必修二 4.2.3 直线与圆的方程的应用
三、 问题 探究
高中数学教案之高一数学人教版必修二 4.2.3 直线与圆的方程的应用
高中数学教案之高一数学人教版必修二 4.2.3 直线与圆的方程的应用
四、 课堂 检测
五、 小结 评价
人教版高中数学必修二:4-2-3直线与圆的方程的应用(2)

故圆的方程为 x2+ (y- 2)2= 2,切点为 O, 所以观景点应设在 B 景点在小路的投影处 .
要点二 直线与圆的方程在平面几何中的应 用 利用坐标方法解决平面几何问题时,要充分 利用直线方程、圆的方程,直线与圆、圆与 圆的位置关系等有关性质.建立适当的平面 直角坐标系,正确使用坐标法,使几何问题 转化为代数问题,用代数运算求得结果以后, 再解释代数结果的实际含义,也就是将代数 问题再转化到几何问题中,对几何问题作出 合理解释.
(对应学生用书94页)
用坐标法解决几何问题 先用坐标和方程表示相应的几何元素: 点、 直线、 圆,将几何问题转化为代数问题;然后通过代数运算 解决代数问题;最后解释代数运算结果的几何意义, 得出几何问题的结论.这就是用坐标方法解决平面几 何问题的“三步曲”.
建立适当的平面直角坐标系,用坐标和
第一步: 方程表示问题中的几何元素,将几何问题转化为
; 通过代数运算,解决代数问题 :
代数问题
(对应学生用书94页)
探究:利用坐标法与一般方法解决几何问题 有何不同? 提示:一般方法是在几何图形中,利用图形 的几何性质直接推出结果,较简洁,但思路 难想.坐标法是在几何图形所在平面直角坐 标系中,将几何问题转化为代数问题,用代 数方法解决,思路明显,但过程较繁.
例2 如图,Rt△ABC的斜边长为定值 2m,以斜 边的中点O为圆心作半径为 n的圆,BC的延长线 交圆于 P, Q两点,求证: |AP|2+ |AQ|2 + |PQ|2 为 定值. 【分析】 建立平面直角坐标系,用字母或数 值表示A,P,Q的坐标,代入式子化简推证.
【证明】 如上图,以 O 为坐标原点,以直线 BC 为 x 轴,建立平面直角坐标系,于是有 B( - m,0),C(m,0),P(-n,0),Q(n,0). 设A(x,y),由已知,点A在圆x2+y2=m2上, |AP|2+|AQ|2+|PQ|2 =(x+n)2+y2+(x-n)2+y2+4n2=2x2+2y2+6n2 =2m2+6n2(定值).
人教新课标版数学高一-人教A版必修2 课时提升 4.2.3 直线与圆的方程的应用2

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时提升作业(二十八)直线与圆的方程的应用一、选择题(每小题3分,共18分)1.若直线y=ax+b通过第一、二、四象限,则圆(x-a)2+(y-b)2=r2(r>0)的圆心位于( ) A.第一象限 B.第二象限C.第三象限D.第四象限【解析】选B.由于直线通过第一、二、四象限,所以a<0,b>0,故圆心位于第二象限.2.(2014·济宁高一检测)直线2x-y=0与圆C:(x-2)2+(y+1)2=9交于A,B两点,则△ABC(C为圆心)的面积等于( )A.2B.2C.4D.4【解析】选A.因为圆心到直线的距离d==,所以=2=4,所以△ABC的面积为×4×=2.3.点P(x0,y0)在圆x2+y2=r2内,则直线x0x+y0y=r2和已知圆的公共点个数为( ) A.0 B.1 C.2 D.无法确定【解析】选A.因为+<r 2,圆心到直线x0x+y0y=r2的距离d=>r,故直线与圆相离,选A.【举一反三】若将本题改为“点P(x0,y0)在圆x2+y2=r2外”,其余条件不变,又如何求解?【解析】选C.因为+> r 2,圆心到直线x0x+y0y=r2的距离d =< r,故直线与圆相交,选C.4.(2013·江西高考)过点(,0)引直线l与曲线y=相交于A,B 两点,O为坐标原点,当△AOB的面积取最大值时,直线l的斜率等于( )A. B.- C.± D.-【解题指南】圆心到直线的距离与直线的斜率有关,△AOB为等腰三角形,所以AB的长度也可用圆心到直线的距离表示,进而△AOB的面积可表示为圆心到直线的距离d的函数,借助二次函数思想可以求解出当△AOB的面积取最大值时的d,进而可以求出直线的斜率. 【解析】选B.曲线y=表示以(0,0)为圆心,以1为半径的上半圆.设直线l的方程为y=k(x-),即kx-y-k=0.若直线与半圆相交,则k≤0,圆心到直线的距离为d=(d<1),弦长为|AB|=2,△AOB的面积为S=|AB|d=d=,易知当d2=时S 最大,解=得k2=,故k=-.5.若直线l1:2x-5y+20=0和直线l2:mx+2y-10=0与两坐标轴围成的四边形有一个外接圆,则实数m的值为( )A.5B.-5C.±5D.以上都不对【解析】选A.圆的内接四边形对角互补,因为x轴与y轴垂直,所以直线l1与直线l2垂直,直线A1x+B1y+C1=0与直线A2x+B2y+C2=0垂直的充要条件是A1A2+B1B2=0,所以2×m+(-5)×2=0,解得m=5.6.(2014·昆明高一检测)已知两点A(-2,0),B(1,0),如果动点P满足=2,则点P的轨迹所包围的图形的面积等于( )A.9πB.8πC.4πD.π【解析】选 C.设P(x,y),由=2得,=2,化简得x2+y2-4x=0,即(x-2)2+y2=4,所以P的轨迹是半径为2的圆,其面积为4π.二、填空题(每小题4分,共12分)7.设村庄外围所在曲线的方程可用(x-2)2+(y+3)2=4表示,村外一小路方程可用x-y+2=0表示,则从村庄外围到小路的最短距离为.【解析】因为圆心到直线的距离为,从村庄外围到小路的最短距离为-2.答案:-2【变式训练】(2013·保定高一检测)已知实数x,y满足2x+y+5=0,那么的最小值为( )A. B. C.2 D.2【解析】选A.表示点(x,y)与原点的距离,所以其最小值为原点到2x+y+5=0的距离,故d==.8.(2014·大同高一检测)如图所示,一座圆拱桥,当水面在某位置时,拱顶离水面2m,水面宽12m,当水面下降1m后,水面宽为m.【解析】如图所示,以圆拱拱顶为坐标原点,以过拱顶的竖直直线为y轴,建立直角坐标系,设圆心为C,水面所在弦的端点为A,B,则由已知得A(6,-2),B(-6,-2).设圆的半径为r,则C(0,-r),即圆的方程为x2+(y+r)2=r2.①将点A的坐标(6,-2)代入方程①,解得r=10.所以圆的方程为x2+(y+10)2=100.②当水面下降1m后,可设点A′的坐标为A′(a,-3)(a>0),将A′(a,-3)代入方程②,求得a=.所以,水面下降1m后,水面宽为2a=2(m).答案:29.(2013·蚌埠高一检测)设有一个半径为3km的圆形村落,甲、乙两人同时从村落中心出发,甲向东,而乙向北前进,甲出村后不久,改变前进方向.沿着相切于村落边界的方向前进,后来恰好与乙相遇,设甲、乙两人的速度都一定,其比为3∶1,二人相遇时乙向北走了km.【解析】如图,以村落中心为坐标原点,以东西方向为x轴,南北方向为y轴建立直角坐标系.设甲向东走到D转向到C恰好与乙相遇.设D,C两点的坐标分别为(a,0),(0,b),其中a>3,b>3,则CD方程为+=1.设乙的速度为v,则甲的速度为3v.依题意,得=3且=,解得a=5,b=,所以乙向北走km时两人相遇.答案:三、解答题(每小题10分,共20分)10.等边△ABC中,点D,E分别在边BC,AC上且=,=,AD,BE相交于点P.求证:AP⊥CP.【解题指南】要证AP⊥CP,可转化为直线AP,CP的斜率之积等于-1即可,由此以B为原点,BC边所在直线为x轴,线段BC长的为单位长,建立平面直角坐标系.【证明】以B为原点,BC边所在直线为x轴,线段BC长的为单位长,建立平面直角坐标系.则A(3,3),B(0,0),C(6,0).由已知,得D(2,0),E(5,).直线AD的方程为y=3(x-2).直线BE的方程为y=(x-5)+.解以上两方程联立成的方程组,得x=,y=.所以,点P的坐标是.直线PC的斜率k PC=-,因为k AP·k PC=3×=-1,所以,AP⊥CP.11.(2014·徐州高一检测)已知圆C:(x-3)2+(y-4)2=4和直线l:x+2y+2=0,直线n经过圆C外定点A(1,0).若直线n与圆C相交于P,Q两点,与l交于N点,且线段PQ的中点为M,求证:|AM|·|AN|为定值.【解析】方法一:设P(x1,y1),Q(x2,y2),又由题意知直线与圆相交,斜率必定存在,且不为0,可设直线n的方程为kx-y-k=0,由得N.再由得(1+k2)x2-(2k2+8k+6)x+k2+8k+21=0,所以x1+x2=得M.所以|AM|·|AN|=·=·=6为定值.方法二:由题意知直线与圆相交,斜率必定存在,且不为0,可设直线n的方程为kx-y-k=0,由得N,又直线CM与n垂直,由得M.所以|AM|·|AN|=|y M-0|·|y N-0|=|y M·y N|==6,为定值.一、选择题(每小题4分,共16分)1.由y=和圆x2+y2=4所围成的较小扇形的面积是( )A. B.π C. D.【解析】选B.由题意知围成的较小扇形的面积为圆面积的,所以S=πr2=π,故选B.2.(2014·汕头高一检测)过直线x=2上一点M向圆+=1作切线,则M到切点的最小距离为( ) A.4 B.4 C.6 D.3【解析】选A.因为切线长、直线上的点与圆心连线长及半径构成直角三角形的三边长,所以直线上的点与圆心的距离最小时,切线长最小,先求圆心到直线的距离d=2+5=7,再求M到切点的最小距离为=4.3.(2014·襄阳高一检测)如图所示,已知直线l的解析式是y=x-4,并且与x轴、y轴分别交于A,B两点.一个半径为1.5的圆C,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着y轴向下运动,当圆C与直线l相切时,该圆运动的时间为( )A.6sB.6s或16sC.16sD.8s或16s【解析】选B.设运动的时间为ts,则ts后圆心的坐标为(0,1.5-0.5t).因为圆C与直线l:y=x-4相切,所以=1.5.解得t=6或16.即该圆运动的时间为6s或16s.4.(2014·潍坊高一检测)与圆x2+y2-ax-2y+1=0关于直线x-y-1=0对称的圆的方程是x2+y2-4x+3=0,则a= ( )A.0B.1C.2D.3【解题指南】两圆关于直线对称,则圆的半径不变,已知圆与对称圆的圆心坐标关于直线对称.【解析】选C.x2+y2-4x+3=0化为标准形式为(x-2)2+y2=1,圆心为(2,0),因为(2,0)关于直线x-y-1=0对称的点为(1,1),所以x2+y2-ax-2y+1=0的圆心为(1,1).故=1,a=2.二、填空题(每小题5分,共10分)5.若点P(x,y)满足x2+y2=25,则x+y的最大值是.【解析】令x+y=z,则=5,所以z=±5,即-5≤x+y≤5,所以x+y的最大值是5.答案:5【拓展延伸】数形结合思想在解题中的运用利用数形结合求解问题时,关键是抓住“数”中的某些结构特征,联想到解析几何中的某些方程、公式,从而挖掘出“数”的几何意义,实现“数”向“形”的转化,如本题由x+y联想直线的截距.6.已知圆的方程为x2+y2-6x-8y=0.设该圆过点(3,5)的最长弦和最短弦分别为AC,BD,则四边形ABCD的面积为.【解析】圆心坐标是(3,4),半径是5,圆心到点(3,5)的距离为1,根据题意最短弦BD和最长弦(即圆的直径)AC垂直,故最短弦的长为2=4,所以四边形ABCD的面积为×AC×BD=×10×4=20.答案:20三、解答题(每小题12分,共24分)7.(2014·南昌高一检测)中国南海某岛驻岛部队的地面雷达搜索半径为200海里,外国一海洋测量船正在在该海岛正东250海里处以每小时20海里的速度沿西北方向航行,问该海岛雷达能否发现该外国测量船,如能,求能观测到该测量船的时间长.【解析】以该岛为原点,正东、正北方向分别为x,y轴,建立直角坐标系.则雷达最大观测范围是一个圆,其方程为:x2+y2=2002,外国测量船的航行路线所在的直线方程为:x+y=250,海岛到外国测量船的航行路线距离为:d==125≈176.77<200,故能被观测到.航行路线被圆截得的弦|BC|=2=50≈187.1所以能观测到的时间为t==9.355(小时).【变式训练】如图,某海面上有O,A,B三个小岛(面积大小忽略不计),A岛在O岛的东北方向20km处,B岛在O岛的正东方向10km处.(1)以O为坐标原点,O的正东方向为x轴正方向,1km为单位长度,建立平面直角坐标系,试写出A,B的坐标,并求A,B两岛之间的距离.(2)已知在经过O,A,B三个点的圆形区域内有未知暗礁,现有一船在O 岛的南偏西30°方向距O岛20km处,正沿东北方向行驶,若不改变方向,试问该船有没有触礁的危险?【解析】(1)因为A在O的东北方向20km,B在O的正东方向10km,所以A(20,20),B(10,0),由两点间的距离公式知|AB|==10(km).(2)设过O,A,B三点所在圆的方程为x2+y2+Dx+Ey+F=0,将O(0,0),A(20,20),B(10,0)代入上式得解得: D=-10,E=-30,F=0,所以圆的方程为x2+y2-10x-30y=0,圆心坐标为(5,15),r=5.设船起初所在的点为C,则C(-10,-10),且该船航线所在直线的斜率为1,由点斜式方程知:l船:y+10=x+10,即:x-y+10-10=0,因为==5<5,所以有触礁的危险.8.(2013·四川高考)已知圆C的方程为x2+(y-4)2=4,点O是坐标原点.直线l:y=kx与圆C交于M,N两点.(1)求k的取值范围.(2)设Q(m,n)是线段MN上的点,且=+.请将n表示为m 的函数.【解题指南】(1)求解时要抓住直线与圆有两个交点,所以在求解k的取值范围时可以利用判别式进行求解.(2)利用=+找到m,n的关系.【解析】(1)将y=kx代入x2+(y-4)2=4中,得(1+k2)x2-8kx+12=0.(*) 由Δ=(-8k)2-4(1+k2)×12>0,得k2>3.所以,k的取值范围是(-∞,-)∪(,+∞).(2)因为M,N在直线l上,可设点M,N的坐标分别为(x1,kx1),(x2,kx2),则|OM|2=(1+k2),|ON|2=(1+k2),又|OQ|2=m2+n2=(1+k2)m2.由=+,得=+,即=+=.由(*)式可知,x1+x2=,x1x2=,所以m2=.因为点Q在直线y=kx上,所以k=,代入m2=中并化简,得5n2-3m2=36.由m2=及k2>3,可知0<m2<3,即m∈(-,0)∪(0,).根据题意,点Q在圆C内,则n>0,所以n==.于是,n与m的函数关系为n=(m∈(-,0)∪(0,)).关闭Word文档返回原板块。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题1.一辆卡车宽1.6m,要经过一个半圆形隧道(半径为3.6m)则这辆卡车的平顶车篷篷顶距地面高度不得超过()A.1.4m B.3.5mC.3.6m D.2.0m[答案] B[解析]圆半径OA=3.6,卡车宽1.6,∴AB=0.8,∴弦心距OB= 3.62-0.82≈3.5.2.与圆x2+y2-ax-2y+1=0关于直线x-y-1=0对称的圆的方程是x2+y2-4x+3=0,则a=()A.0 B.1C.2 D.3[答案] C[解析]x2+y2-4x+3=0化为标准形式为(x-2)2+y2=1,圆心为(2,0),∵(2,0)关于直线x-y-1=0对称的点为(1,1),∴x2+y2-ax-2y+1=0的圆心为(1,1).∵x 2+y 2-ax -2y +1=0,即为(x -a 2)2+(y -1)2=a 24,圆心为(a 2,1),∴a 2=1,即a =2.3.直线2x -y =0与圆C :(x -2)2+(y +1)2=9交于A 、B 两点,则△ABC (C 为圆心)的面积等于( )A .2 5B .2 3C .4 3D .4 5[答案] A[解析] ∵圆心到直线的距离d =|4+1|5=5, ∴|AB |=29-d 2=4,∴S △ABC =12×4×5=2 5.. 4.点P 是直线2x +y +10=0上的动点,直线PA 、PB 分别与圆x 2+y 2=4相切于A 、B 两点,则四边形PAOB (O 为坐标原点)的面积的最小值等于( )A .24B .16C .8D .4 [答案] C[解析] ∵四边形PAOB 的面积S =2×12|PA |×|OA |=2OP 2-OA 2=2OP 2-4,∴当直线OP 垂直直线2x +y +10=0时,其面积S 最小.5.若直线ax +by =1与圆x 2+y 2=1相交,则点P (a ,b )的位置是( )A .在圆上B .在圆外C .在圆内D .以上都不对[答案] B [解析] 由|0+0-1|a 2+b 2<1,∴a 2+b 2>1. 6.(2008年山东高考题)已知圆的方程为x 2+y 2-6x -8y =0.设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为( )A .10 6B .20 6C .30 6D .40 6 [答案] B[解析] 圆心坐标是(3,4),半径是5,圆心到点(3,5)的距离为1,根据题意最短弦BD 和最长弦(即圆的直径)AC 垂直,故最短弦的长为252-12=46,所以四边形ABCD 的面积为12×AC ×BD =12×10×46=20 6.7.方程1-x 2=kx +2有唯一解,则实数k 的范围是( )A .k =±3B .k ∈(-2,2)C .k <-2或k >2D .k <-2或k >2或k =±3[答案] D[解析] 由题意知,直线y =kx +2与半圆x 2+y 2=1(y ≥0只有一个交点.结合图形易得k <-2或k >2或k =±3.8.(拔高题)台风中心从A 地以每小时20 km 的速度向东北方向移动,离台风中心30 km 内的地区为危险地区,城市B 在A 的正东40 km 外,B 城市处于危险区内的时间为( )A .0.5 hB .1 hC .1.5 hD .2 h [答案] B[解析] 建系后写出直线和圆的方程,求得弦长为20千米,故处于危险区内的时间为2020=1(h).二、填空题9.已知实数x ,y 满足x 2+y 2-4x +1=0.则x -y 的最大值和最小值分别是________和________.y x 的最大值和最小值分别是________和________.x 2+y 2的最大值和最小值分别是______和______.[答案] 2+6,2-6;1,-1;7+43,7-4 3[解析] (1)设x -y =b 则y =x -b 与圆x 2+y 2-4x +1=0有公共点, 即|2-b |12+12≤3,∴2-6≤b ≤2+ 6故x -y 最大值为2+6,最小值为2- 6(2)设y x =k ,则y =kx 与x 2+y 2-4x +1=0有公共点,即|2k|≤ 31+k2最大值为3,最小值为- 3∴3≤k≤3,故yx(3)圆心(2,0)到原点距离为2,半径r= 3故(2-3)2≤x2+y2≤(2+3)2由此x2+y2最大值为7+43,最小值为7-4 3.10.如下图所示,一座圆拱桥,当水面在某位置时,拱顶离水面2 m,水面宽12 m,当水面下降1 m后,水面宽为________m.[答案]251[解析]如下图所示,以圆拱拱顶为坐标原点,以过拱顶的竖直直线为y轴,建立直角坐标系,设圆心为C,水面所在弦的端点为A,B,则由已知得A(6,-2),B(-6,-2).设圆的半径为r,则C(0,-r),即圆的方程为x2+(y+r)2=r2.①将点A的坐标(6,-2)代入方程①,解得r=10.∴圆的方程为x2+(y+10)2=100.②当水面下降1 m后,可设点A′的坐标为(x0,-3)(x0>0),将A′的坐标(x0,-3)代入方程②,求得x0=51.所以,水面下降1 m后,水面宽为2x0=251.11.已知直线x-2y-3=0与圆(x-2)2+(y+3)2=9相交于E,F 两点,圆心为点C,则△CEF的面积等于________.[答案]2 5[解析]∵圆心C(2,-3)到直线的距离为d=|2+6-3|1+(-2)2=5,又R=3,∴|EF|=2R2-d2=4.∴S△CEF=12|EF|·d=2 5.12.若点P在直线l1:x+y+3=0上,过点P的直线l2与曲线C:(x-5)2+y2=16相切于点M,则|PM|的最小值________.[答案] 4[解析] 曲线C :(x -5)2+y 2=16是圆心为C (5,0),半径为4的圆,连接CP ,CM ,则在△MPC 中,CM ⊥PM ,则|PM |=|CP |2-|CM |2=|CP |2-16,当|PM |取最小值时,|CP |取最小值,又点P 在直线l 1上,则|CP |的最小值是点C 到直线l 1的距离,即|CP |的最小值为d =|5+3|1+1=42,则|PM |的最小值为(42)2-16=4. 三、解答题13.如图所示,已知直线l 的解析式是y =43x -4,并且与x 轴、y 轴分别交于A ,B 两点.一个半径为1.5的圆C ,圆心C 从点(0,1.5)开始以每秒0.5个单位的速度沿着y 轴向下运动,当圆C 与直线l 相切时,求该圆运动的时间.[解析] 设运动的时间为t s ,则t s 后圆心的坐标为(0,1.5-0.5t ).∵圆C 与直线l :y =43x -4,即4x -3y -12=0相切,∴|4×0-3×(1.5-0.5t )-12|32+42=1.5.解得t=6或16.即该圆运动的时间为6 s或16 s.14.设有一个半径为3 km的圆形村落,甲、乙两人同时从村落中心出发,甲向东,而乙向北前进,甲出村后不久,改变前进方向.沿着相切于村落边界的方向前进,后来恰好与乙相遇,设甲、乙两人的速度都一定,其比为3:1,此二人在何处相遇?[解析]如图,以村落中心为坐标原点,以东西方向为x轴,南北方向为y轴建立直角坐标系.设甲向东走到D转向到C恰好与乙相遇.设D,C两点的坐标分别为(a,0),(0,b),其中a>3,b>3,则CD方程为xa+yb=1.设乙的速度为v,则甲的速度为3v.依题意,得⎩⎪⎨⎪⎧aba2+b2=3,a2+b2+a3v=b v.解得⎩⎪⎨⎪⎧a=5,b=154.∴乙向北走3.75 km时两人相遇.15.某圆拱桥的示意图如下图所示,该圆拱的跨度AB是36 m,拱高OP是6 m,在建造时,每隔3 m需用一个支柱支撑,求支柱A2P2的长.(精确到0.01 m)[分析]建系→求点的坐标→求圆的方程→求A2P2的长[解析]如图,以线段AB所在的直线为x轴,线段AB的中点O 为坐标原点建立平面直角坐标系,那么点A,B,P的坐标分别为(-18,0),(18,0),(0,6).设圆拱所在的圆的方程是x2+y2+Dx+Ey+F=0.因为A,B,P在此圆上,故有⎩⎪⎨⎪⎧182-18D+F=0,182+18D+F=0,62+6E+F=0,解得⎩⎪⎨⎪⎧D=0,E=48,F=-324.故圆拱所在的圆的方程是x2+y2+48y-324=0.将点P2的横坐标x=6代入上式,解得y=-24+12 6.答:支柱A2P2的长约为126-24.[点评]在实际问题中,遇到有关直线和圆的问题,通常建立坐标系,利用坐标法解决.建立适当的直角坐标系应遵循三点:①若曲线是轴对称图形,则可选它的对称轴为坐标轴;②常选特殊点作为直角坐标系的原点;尽量使已知点位于坐标轴上.建立适当的直角坐标系,会简化运算过程.16.如图,直角△ABC的斜边长为定值2m,以斜边的中点O为圆心作半径为n的圆,直线BC交圆于P、Q两点,求证:|AP|2+|AQ|2+|PQ|2为定值.[证明]如上图,以O为坐标原点,以直线BC为x轴,建立平面直角坐标系,于是有B(-m,0),C(m,0),P(-n,0),Q(n,0).设A(x,y),由已知,点A在圆x2+y2=m2上.打印版|AP|2+|AQ|2+|PQ|2=(x+n)2+y2+(x-n)2+y2+4n2=2x2+2y2+6n2=2m2+6n2(定值).高中数学。
