数学方程式。符号。以及读法
计算公式符号读法

计算公式符号读法在数学和物理学中,我们经常会遇到各种各样的计算公式。
这些公式往往包含了许多符号和符号组合,这些符号的读法对于理解和运用公式至关重要。
在本文中,我们将介绍一些常见的计算公式符号的读法,帮助大家更好地理解和运用这些公式。
1. 加号(+)。
加号是最基本的运算符号之一,表示两个数相加。
在口语中,我们通常称之为“加”,比如“三加四等于七”。
在书面语中,我们也可以称之为“加”,比如“3 + 4 = 7”。
2. 减号(-)。
减号表示两个数相减。
在口语中,我们通常称之为“减”,比如“五减二等于三”。
在书面语中,我们也可以称之为“减”,比如“5 2 = 3”。
3. 乘号(×)。
乘号表示两个数相乘。
在口语中,我们通常称之为“乘”,比如“六乘以九等于五十四”。
在书面语中,我们也可以称之为“乘”,比如“6 × 9 = 54”。
4. 除号(÷)。
除号表示一个数除以另一个数。
在口语中,我们通常称之为“除”,比如“十除以二等于五”。
在书面语中,我们也可以称之为“除”,比如“10 ÷ 2 = 5”。
5. 等于号(=)。
等于号表示两个数相等。
在口语和书面语中,我们都可以称之为“等于”,比如“三加四等于七”或“3 + 4 = 7”。
6. 开方号(√)。
开方号表示一个数的平方根。
在口语中,我们通常称之为“根号”,比如“九的平方根等于三”。
在书面语中,我们也可以称之为“根号”,比如“√9 = 3”。
7. 指数符号(^)。
指数符号表示一个数的幂。
在口语中,我们通常称之为“的几次方”,比如“二的三次方等于八”。
在书面语中,我们也可以称之为“的几次方”,比如“2^3 = 8”。
8. 积分符号(∫)。
积分符号表示对一个函数进行积分运算。
在口语和书面语中,我们都可以称之为“积分”,比如“对函数f(x)进行积分”。
9. 微分符号(d)。
微分符号表示对一个函数进行微分运算。
在口语和书面语中,我们都可以称之为“微分”,比如“对函数f(x)进行微分”。
数学符号及读法大全(详细)

1数学符号及读法大全符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值,常被写作e xa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数a x同 a^xlogb a 以b为底a的对数; b logba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值,其值等于 1/cos xcsc x 余割函数的值,其值等于 1/sin xasin x y,正弦函数反函数在x处的值,即 x = sin yacos x y,余弦函数反函数在x处的值,即 x = cos yatan x y,正切函数反函数在x处的值,即 x = tan yacot x y,余切函数反函数在x处的值,即 x = cot yasec x y,正割函数反函数在x处的值,即 x = sec yacsc x y,余割函数反函数在x处的值,即 x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和,通常是某项指数。
下边界值写在其下部,上边界值写在其上部。
如j从1到100 的和可以表示成:。
这表示 1 + 2 + … + nM 表示一个矩阵或数列或其它|v> 列向量,即元素被写成列或可被看成k×1阶矩阵的向量<v| 被写成行或可被看成从1×k阶矩阵的向量dx 变量x的一个无穷小变化,dy, dz, dr等类似ds 长度的微小变化ρ变量 (x2 + y2 + z2)1/2或球面坐标系中到原点的距离r 变量 (x2 + y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式,其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值,为一个面积、体积或超体积det M M的行列式M-1矩阵M的逆矩阵v×w向量v和w的向量积或叉积2 符号含义θvw向量v和w之间的夹角A•B×C标量三重积,以A、B、C为列的矩阵的行列式uw在向量w方向上的单位向量,即 w/|w|df 函数f的微小变化,足够小以至适合于所有相关函数的线性近似df/dx f关于x的导数,同时也是f的线性近似斜率f ' 函数f关于相应自变量的导数,自变量通常为x∂f/∂x y、z固定时f关于x的偏导数。
数学符号及读法大全(详细)

数学符号及读法大全符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值,常被写作e xa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数a x同 a^xlogb a 以b为底a的对数; b logba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值,其值等于 1/cos xcsc x 余割函数的值,其值等于 1/sin xasin x y,正弦函数反函数在x处的值,即 x = sin yacos x y,余弦函数反函数在x处的值,即 x = cos yatan x y,正切函数反函数在x处的值,即 x = tan yacot x y,余切函数反函数在x处的值,即 x = cot yasec x y,正割函数反函数在x处的值,即 x = sec yacsc x y,余割函数反函数在x处的值,即 x = csc yθ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b)a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和,通常是某项指数。
下边界值写在其下部,上边界值写在其上部。
如j从1到100 的和可以表示成:。
这表示 1 + 2 + … + nM 表示一个矩阵或数列或其它|v> 列向量,即元素被写成列或可被看成k×1阶矩阵的向量<v| 被写成行或可被看成从1×k阶矩阵的向量dx 变量x的一个无穷小变化,dy, dz, dr等类似ds 长度的微小变化ρ变量 (x2 + y2 + z2)1/2或球面坐标系中到原点的距离r 变量 (x2 + y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式,其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值,为一个面积、体积或超体积det M M的行列式M-1矩阵M的逆矩阵v×w向量v和w的向量积或叉积符号含义θvw向量v和w之间的夹角A•B×C标量三重积,以A、B、C为列的矩阵的行列式uw在向量w方向上的单位向量,即 w/|w|df 函数f的微小变化,足够小以至适合于所有相关函数的线性近似df/dx f关于x的导数,同时也是f的线性近似斜率f ' 函数f关于相应自变量的导数,自变量通常为x∂f/∂x y、z固定时f关于x的偏导数。
常用的数学符号和公式的读法

y : partial derivative of y respect to x x
d2y dx2 : second derivative of y respect to x
n
Xi : summation of x sub i, where i goes from 1 to n
i1
n
Xi : product of x sub i, where i goes from 1 to n
精品资料
x x over y
y
x>y
x≥y x< y
xy 0<x<1 0x1
|x| x2 x3 x4
xn
x-n
x is greater than y
x is greater than or equal to y x is less than y
x is less than or equal to y zero is less an x is less than 1
精品资料
b
a f (x)dx : integral of the function of x,between the limits a and b : double integral of
: triple integral of
: n fold integral of
dy : derivative of y respect to x dx
f(x)
fx / f of x / the function f of x
f : S→T
a function f from S to T
x y
f(x)
x maps to y f prime x
(完整版)数学符号及读法大全
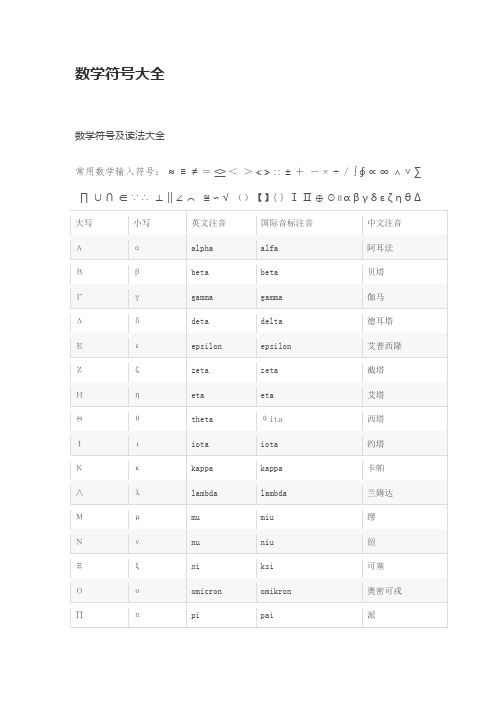
数学符号大全数学符号及读法大全常用数学输入符号:≈≡≠=≤≥<>≮≯∷±+-×÷/∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒≌∽√()【】{}ⅠⅡ⊕⊙∥αβγδεζηθΔ公式输入符号≈≡≠=≤≥<>≮≯∷±+-×÷/∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒⊙≌∽√+:plus(positive正的)-:minus(negative负的)*:multiplied by÷:divided by=:be equal to≈:be approximately equal to():round brackets(parenthess)[]:square brackets{}:braces∵:because∴:therefore≤:less than or equal to≥:greater than or equal to∞:infinityLOGnX:logx to the base nxn:the nth power of xf(x):the function of xdx:diffrencial of xx+y:x plus y(a+b):bracket a plus b bracket closeda=b: a equals ba≠b: a isn't equal to ba>b : a is greater than ba>>b: a is much greater than ba≥b: a is greater than or equal to bx→∞:approches infinityx2:x squarex3:x cube√ ̄x:the square root of x3√ ̄x:the cube root of x3‰:three peimilln∑i=1xi:the summation of x where x goes from 1to nn∏i=1xi:the product of x sub i where igoes from 1to n ∫ab:integral betweens a and b数学符号(理科符号)——运算符号1.基本符号:+- × ÷(/)2.分数号:/3.正负号:±4.相似全等:∽≌5.因为所以:∵∴6.判断类:=≠<≮(不小于)>≯(不大于)7.集合类:∈(属于)∪(并集)∩(交集)8.求和符号:∑9.n次方符号:¹(一次方) ²(平方) ³(立方)⁴(4次方)ⁿ(n次方)10.下角标:₁₂₃₄(如:A₁B₂C₃D₄效果如何?)11.或与非的"非":¬12.导数符号(备注符号):′〃13.度:°℃14.任意:∀15.推出号:⇒16.等价号:⇔17.包含被包含:⊆⊇⊂⊃18.导数:∫∬19.箭头类:↗↙↖↘↑↓↔↕↑↓→←20.绝对值:|21.弧:⌒22.圆:⊙11.或与非的"非":¬12.导数符号(备注符号):′〃13.度:°℃14.任意:∀15.推出号:⇒16.等价号:⇔17.包含被包含:⊆⊇⊂⊃18.导数:∫∬19.箭头类:↗↙↖↘↑↓↔↕↑↓→←20.绝对值:|21.弧:⌒22.圆:⊙αβγδεζηθικλμνξοπρστυφχψωΑΒΓΔΕΖΗΘΙΚ∧ΜΝΞΟ∏Ρ∑ΤΥΦΧΨΩабвгдеёжзийклмнопрстуфхцчшщъыьэюяАБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯΔ。
各种数学符号和表达式的英文读法

各种数学符号和表达式的英文读法.txt52每个人都一条抛物线,天赋决定其开口,而最高点则需后天的努力。
没有秋日落叶的飘零,何来新春绿芽的饿明丽?只有懂得失去,才会重新拥有。
各种数学符号和表达式的英文读法一、一般符号对应的英文单词.period 句号,comma 逗号:colon 冒号;semicolon 分号!exclamation 惊叹号?question mark 问号 ̄hyphen 连字符'apostrophe 省略号;所有格符号—dash 破折号‘ ’single quotat ion marks 单引号“ ”double quotation marks 双引号( )parentheses 圆括号[ ]square brackets 方括号《》French quotes 法文引号;书名号...ellipsis 省略号¨tandem colon 双点号"ditto 同上‖parallel 平行/virgule 斜线号&ampersand = and~swung dash 代字号§section; division 分节号→arrow 箭号;参见号+plus 加号;正号-minus 减号;负号ªplus or minus 正负号×is multiplied by or cross 叉乘÷is divided by 除号=is equal to 等于号≠is not equal to 不等于号≡is equivalent to 全等于号≌is equal to or approximately equal to 等于或约等于号≈is approximately equal to 约等于号<is less than 小于号>is more than (is greater than在数学中更常用)大于号≤is not less than 不小于号≥is not more than 不大于号≢is less than or equal to 小于或等于号≣is more than or equal to 大于或等于号%per cent 百分之…‟per mill 千分之…∞infinity 无限大号∝varies as 与…成比例√(square) root 平方根∵since; because 因为∴hence 所以∷equals, as (proportion) 等于,成比例∟angle 角≨semicircle 半圆≦circle 圆○circumference 圆周πpi 圆周率△triangle 三角形≧perpendicular to 垂直于;另外normal to,right to也都有垂直的意思。
数学符号、公式的英语读法

数学符号和公式的英语读法如下:1.加号"+" 读作"plus"。
2.减号"-" 读作"minus"。
3.乘号"×" 读作"times"。
4.除号"÷" 读作"divided by"。
5.等号"=" 读作"equals"。
6.大于号">" 读作"greater than"。
7.小于号"<" 读作"less than"。
8.不等号"≠" 读作"not equal to"。
9.大于等于号"≥" 读作"greater than or equal to"。
10.小于等于号"≤" 读作"less than or equal to"。
11.约等于号"≈" 读作"approximately equals"。
12.百分号"%" 读作"percent"。
13.度数符号"°" 读作"degree"。
14.开方号"√" 读作"square root"。
15.正负号"±" 读作"plus or minus"。
16.正负平方根号"∛" 读作"cubed root"。
17.正负立方根号"∛" 读作"cubed root"。
高中数学符号读法大全及意义

高中数学符号读法大全及意义一、基本数学符号1. +:加号,表示加法运算。
2. -:减号,表示减法运算。
3. ×:乘号,表示乘法运算。
4. ÷:除号,表示除法运算。
5. =:等于号,表示相等关系。
6. ≠:不等号,表示不相等关系。
7. <:小于号,表示小于关系。
8. >:大于号,表示大于关系。
9. ≤:小于等于号,表示小于等于关系。
10. ≥:大于等于号,表示大于等于关系。
二、集合符号1. ∈:属于,表示一个元素属于某个集合。
2. ∉:不属于,表示一个元素不属于某个集合。
3. ∪:并集,表示所有在某一个以上的集合中出现的元素的新集合。
4. ∩:交集,表示属于所有给定集合的元素的新集合。
5. ⊆:包含关系(子集),表示一个集合包含于另一个集合。
6. ⊇:包含关系(超集),表示一个集合包含另一个集合。
7. ∅:空集,表示没有任何元素的集合。
三、数学函数符号1. f(x):函数符号,表示自变量为x时,函数的值。
2. g(x):函数符号,表示自变量为x时,函数的值。
3. h(x):函数符号,表示自变量为x时,函数的值。
4. lim:极限符号,表示函数在逼近某个数值时的极限。
5. sin:正弦函数符号,表示角度的正弦值。
6. cos:余弦函数符号,表示角度的余弦值。
7. tan:正切函数符号,表示角度的正切值。
8. log:对数函数符号,表示以某个底数为底的对数函数。
四、微积分符号1. dy/dx:导数符号,表示某个函数在某点的导数。
2. ∫:积分符号,表示函数在某个区间上的积分值。
3. dx:微分符号,表示微分变量。
4. Δx:增量符号,表示微分变量的增量。
五、几何图形符号1. ∆ABC:三角形符号,表示三条边分别为AB、BC和CA的三角形。
2. △DEF:三角形符号,表示三条边分别为DE、EF和FD的三角形。
3. ∠:角符号,表示两条射线之间的角度。
4. ⊥:垂直符号,表示两条直线垂直。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学方程式满意回答2013-04-05 14:04三角不等式|a+b|≤|a|+|b| |a-b|≤|a|+|b| |a|≤b<=>-b≤a≤b |a-b|≥|a|-|b| -|a|≤a≤|a| 一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a 根与系数的关系X1+X2=-b/a X1*X2=c/a 注:韦达定理判别式b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosA cos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinB tan(A+B)=(tanA+tanB)/(1-tanAtanB) tan (A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctg ActgB+1)/(ctgB-ctgA) 倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctga co s2a=cos2a-sin2a=2cos2a-1=1-2sin2a 半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2) cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2) tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA)) ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA)) 和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB =sin(A+B)-sin(A-B) 2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B) sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA +tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosB ctgA+ctgBsin(A+B)/sin AsinB -ctgA+ctgBsin(A+B)/sinAsinB 某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/2 1+3+5+7+9+11+13+15+…+(2n-1)=n*2 2+4+6+8+10+12+14+…+(2n) =n(n+1) 12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+ 63+…n3=n2(n+1)2/4 1*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R 注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB 注:角B是边a和边c的夹角圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0 抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py 直棱柱侧面积S=c*h 斜棱柱侧面积S=c'*h 正棱锥侧面积S=1/2c*h' 正棱台侧面积S=1/2(c+c')h' 圆台侧面积S=1/ 2(c+c')l=pi(R+r)l 球的表面积S=4pi*r2 圆柱侧面积S=c*h=2pi*h 圆锥侧面积S=1/ 2*c*l=pi*r*l 弧长公式l=a*r a是圆心角的弧度数r >0 扇形面积公式s=1/2*l*r 锥体体积公式V=1/3*S*H 圆锥体体积公式V=1/3*pi*r2h 斜棱柱体积V=S'L 注:其中, S'是直截面面积,L是侧棱长柱体体积公式;V=s*h 圆柱体V=pi*r2hα——阿尔法β——贝塔γ——伽马Δ——德尔塔ξ——可sei ψ——可赛ω——奥秘噶μ——米哟λ——南木打σ——西格玛τ——套υ——fai2、数学运算符:∑—连加号∏—连乘号↟—并∩—补↔—属于↣—因为↢—所以√—根号‖—平行≧—垂直↚—角≨—弧≦—圆↘—正比于∞—无穷∫—积分≈—约等≡—恒等3、三角函数:sin—赛因cos—考赛因tan—叹近体cot—考叹近体sec—赛看近体csc —考赛看近体大写小写英文注音国际音标注音中文注音Αα alpha alfa 阿耳法Ββ beta beta 贝塔Γγ gamma gamma 伽马Γδ deta delta 德耳塔Δε epsilon epsilon 艾普西隆Εδ zeta zeta 截塔Ζε eta eta 艾塔Θζ theta ζita 西塔Ηη iota iota 约塔Κθ kappa kappa 卡帕↜ ι lambda lambda 兰姆达Μκ mu miu 缪Νλ nu niu 纽Ξμ xi ksi 可塞Ον omicron omikron 奥密可戎↕ π pi pai 派Ρξ rho rou 柔↖ ζ sigma sigma 西格马Τη tau tau 套Υυ upsilon jupsilon 衣普西隆Φθ phi fai 斐Φχ chi khai 喜Χψ psi psai 普西Ψω omega omiga 欧米伽常用数学输入符号:≈ ≡ ≠ =≢≣ <>≤ ≥ ∷ ± +-× ÷ /↠ ↡ ↘ ↙ ↜ ↝ ↖ ↕ ↟ ↞ ↔ ↣ ↢ ≧ ‖ ↚ ≨ ≌ ∽ ↗ ()【】{}Ⅰ Ⅱ ⊕ ≦↛αβγδεδεζΓ大写小写英文国际音标中文注音Αα alpha alfa 阿耳法Ββ beta beta 贝塔Γγ gamma gamma 伽马Γδ deta delta 德耳塔Δε epsilon epsilon 艾普西隆Εδ zeta zeta 截塔Ζε eta eta 艾塔Θζ theta ζita 西塔Ηη iota iota 约塔Κθ kappa kappa 卡帕↜ ι lambda lambda 兰姆达Μκ mu miu 缪Νλ nu niu 纽Ξμ xi ksi 可塞Ον omicron omikron 奥密可戎↕ π pi pai 派Ρξ rho rou 柔↖ ζ sigma sigma 西格马Τη tau tau 套Υυ upsilon jupsilon 衣普西隆Φθ phi fai 斐Φχ chi khai 喜Χψ psi psai 普西Ψω omega omiga 欧米符号含义i -1的平方根f(x) 函数f在自变量x处的值sin(x) 在自变量x处的正弦函数值exp(x) 在自变量x处的指数函数值,常被写作exa^x a的x次方;有理数x由反函数定义ln x exp x 的反函数ax 同 a^xlogba 以b为底a的对数; blogba = acos x 在自变量x处余弦函数的值tan x 其值等于 sin x/cos xcot x 余切函数的值或 cos x/sin xsec x 正割含数的值,其值等于 1/cos xcsc x 余割函数的值,其值等于 1/sin xasin x y,正弦函数反函数在x处的值,即 x = sin yacos x y,余弦函数反函数在x处的值,即 x = cos yatan x y,正切函数反函数在x处的值,即 x = tan yacot x y,余切函数反函数在x处的值,即 x = cot yasec x y,正割函数反函数在x处的值,即 x = sec yacsc x y,余割函数反函数在x处的值,即 x = csc yζ角度的一个标准符号,不注明均指弧度,尤其用于表示atan x/y,当x、y、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c) 以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a•b a、b向量的点积(a•b) a、b向量的点积|v| 向量v的模|x| 数x的绝对值Σ表示求和,通常是某项指数。
下边界值写在其下部,上边界值写在其上部。
如j从1到100 的和可以表示成:。
这表示1 + 2 + … + nM 表示一个矩阵或数列或其它|v> 列向量,即元素被写成列或可被看成k×1阶矩阵的向量<v| 被写成行或可被看成从1×k阶矩阵的向量dx 变量x的一个无穷小变化,dy, dz, dr等类似ds 长度的微小变化ξ变量 (x2 + y2 + z2)1/2 或球面坐标系中到原点的距离r 变量 (x2 + y2)1/2 或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式,其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值,为一个面积、体积或超体积det M M的行列式M-1 矩阵M的逆矩阵v×w 向量v和w的向量积或叉积ζvw 向量v和w之间的夹角A•B×C 标量三重积,以A、B、C为列的矩阵的行列式uw 在向量w方向上的单位向量,即 w/|w|df 函数f的微小变化,足够小以至适合于所有相关函数的线性近似df/dx f关于x的导数,同时也是f的线性近似斜率f ' 函数f关于相应自变量的导数,自变量通常为x∂f/∂x y、z固定时f关于x的偏导数。
通常f关于某变量q的偏导数为当其它几个变量固定时df 与dq的比值。
任何可能导致变量混淆的地方都应明确地表述(∂f/∂x)|r,z 保持r和z不变时,f关于x的偏导数grad f 元素分别为f关于x、y、z偏导数 [(∂f/∂x), (∂f/∂y), (∂f/∂z)] 或 (∂f/∂x)i + (∂f/∂y)j + (∂f/∂z)k; 的向量场,称为f的梯度∇向量算子(∂/∂x)i + (∂/∂x)j + (∂/∂x)k, 读作 "del"∇f f的梯度;它和 uw 的点积为f在w方向上的方向导数∇•w 向量场w的散度,为向量算子∇同向量 w的点积, 或 (∂wx /∂x) + (∂wy /∂y) + (∂wz /∂z)curl w 向量算子∇同向量 w 的叉积∇×w w的旋度,其元素为[(∂fz /∂y) - (∂fy /∂z), (∂fx /∂z) - (∂fz /∂x), (∂fy /∂x) - (∂fx /∂y)]∇•∇拉普拉斯微分算子: (∂2/∂x2) + (∂/∂y2) + (∂/∂z2)f "(x) f关于x的二阶导数,f '(x)的导数d2f/dx2 f关于x的二阶导数f(2)(x) 同样也是f关于x的二阶导数f(k)(x) f关于x的第k阶导数,f(k-1) (x)的导数T 曲线切线方向上的单位向量,如果曲线可以描述成 r(t), 则T = (dr/dt)/|dr/dt|ds 沿曲线方向距离的导数θ曲线的曲率,单位切线向量相对曲线距离的导数的值:|dT/ds|N dT/ds投影方向单位向量,垂直于TB 平面T和N的单位法向量,即曲率的平面η曲线的扭率: |dB/ds|g 重力常数F 力学中力的标准符号k 弹簧的弹簧常数pi 第i个物体的动量H 物理系统的哈密尔敦函数,即位置和动量表示的能量{Q, H} Q, H的泊松括号以一个关于x的函数的形式表达的f(x)的积分函数f 从a到b的定积分。
