【大学物理必备】量子霍耳效应
量子霍尔效应

* zz* nm const z * z e z z z ( x iy) 2lc , z* ( x iy) 2lc lc eB
1/ 2
m
n
在xy平面内单位面积态之数目为 nB eB h 对于某一个Landau能级, 在y方向的平衡位置数目也由n B 决定, 故能级的简并度是 n B .
怎么来解释实验中 H 出现的平台呢?(见上 图)。平台的存在说明有电子的态仅对电子密度 H n有贡献,但对 无贡献。这就表明有局域态, 为解释这一点必须考虑杂质的存在。杂质使朗 道能级变宽而成了能带,并且互相重叠起来。 理论计算表明大部分电子状态局域化了,即被 杂质所束缚,只有那些处在能带中心的状态仍 然是扩展态。改变电子浓度就改变了费米能级。 当费米能级处在局域态区时霍尔电导取量子数 值,而当费米能级跨过一个扩展态时,霍尔电 导率就改变一个量子数。
然而,考虑了局域态后,又为什么霍尔电导 仍是量子化了的呢?对此,普拉格(Prange)认为 局域态的存在并不影响霍尔电流。当电子费米能 级位于局域态时,扩展态的电子会补偿应由局域 态贡献的霍尔电流。后来,劳甫林(Laughlin)又 提出了规范不变的观点。所谓规范不变实质即电 荷守恒。从这一点来说劳甫林的这一观点是普拉 格观点的另一种更实质化、一般化的说法。然而 作为物理的机理来说,哈伯林(Halperin)的“边 界流”观点是十分重要的。边界流是一种拓扑元 激发流。正是边界流的存在,才得以使量子化在 有局域态存在时仍成立。不过,对此也有人持反 对意见。应该说,即使在今天,整数量子霍尔效 应(IQHE)的解释还是不完全清楚的。
电导率与电阻率的关系为
x x x x 2 x x
量子霍尔效应

量子霍尔效应霍尔效应,它实际上一种电磁效应的。
我们给一块半导体通电,在导体外面外加一个与电流方面垂直的磁场,磁场会使半导体中的电子与空穴(可以视为正电荷)受到不同方向的洛伦兹力而在不同方面上聚集,聚集起来的电子和空穴之间会产生电场,此时在半导体两侧产生了垂直于磁场和电流方向的电压,而且在此电压生成的电场力和磁场的洛伦兹力平衡以后,后来的电子和空穴就不在聚集,顺利通过不发生偏移。
这种现象是由美国物理学家霍尔于1879年研究金属导电机制的时候发现的,所以命名为“霍尔效应”,且在实际生活中产生了广泛的应用,根据霍尔效应做成的霍尔器件,就是以磁场为工作媒介,将物体的运动参数转变为数字电压的形式输出,使之具备传感和开关功能。
如:汽车的点火系统,设计人员将霍尔传感器放在分电器内取代机械断电器,用作机械断电器,用作点火脉冲发生器。
这种霍尔点火发生器随着转速变化的磁场在带电半导体内产生脉冲电压,控制电控单元的初级电流。
相对于机械断电器而言,霍尔式点火脉冲发生器无磨损免维护,能够适应恶劣的环境,同时能够精确的控制点火,具有明显的优势。
什么是量子霍尔效应(二维)我们上面所说的霍尔效应是在三维的导体中实现的,其中的电子可以在导体中自由运动。
现在科学家通过某些手段将电子限制在一个二维平面内,之后添加一个垂直于该平面的磁场,同时沿着二维电子平面一个方向通以电流,此时在二维平面的另一个方向上测量到电压。
这种现象称为量子霍尔效应,属于量子力学版的霍尔效应。
该现象是由德国物理学家冯•克利青发现,并因此获得1985年的诺贝尔物理学奖。
但是为何在霍尔效应提出100年后才有人发现量子霍尔效应。
主要原因是理想的二维电子气难以实现,在半导体技术高速发展之后,人们才能在“金属-氧化物-半导体场效应晶体管”中实现比较理想的二维电子气,而且想要观测到这种现象还需要提供极低温和强磁场环境。
量子霍尔效应与上一节提到的霍尔效应最大不同之处在于横向电压对磁场的响应不同。
量子霍尔效应

量子霍尔效应量子霍尔效应是一种在二维材料中观察到的量子输运现象,具有诸多重要的物理和应用意义。
本文将介绍量子霍尔效应的基本原理、实验观测以及相关应用领域。
一、量子霍尔效应的基本原理量子霍尔效应是指当在二维电子气体中施加一弱的磁场时,电子在垂直于磁场方向的平面内沿着边界形成准连续的态,而趋于不散射。
这种不散射的现象可以通过霍尔电阻测量,即电子在横向电场下的电流在垂直方向的电压降。
量子霍尔效应的本质是由于二维系统中的电子受到磁场的束缚,导致电子只能运动在垂直磁场方向的能级上,形成了称为“朗道能级”的能带结构。
在这个结构中,电子的态密度非常紧凑且高度定域,导致电子不易发生散射,从而实现了量子霍尔效应。
二、量子霍尔效应的实验观测量子霍尔效应最早由物理学家冯·克莱因在量子霍尔材料中实验观测到,并因此获得了诺贝尔物理学奖。
他们使用了非常低温以及超高纯度的半导体材料,以观察到这一现象。
实验观测量子霍尔效应的关键在于霍尔电阻的测量。
在二维电子气体中,施加横向电场后,由于电子发生霍尔效应,沿垂直方向会产生电压差。
通过测量这个电压差和施加电场的比值,即得到了霍尔电阻。
当温度趋近于绝对零度时,霍尔电阻呈现出量子化的特征,即呈现为离散的平台。
这种离散的霍尔电阻是量子霍尔效应的直接证据。
三、量子霍尔效应的应用领域量子霍尔效应在凝聚态物理学以及纳米电子学领域具有重要的应用。
其中最重要的应用之一是准粒子和拓扑能带的研究。
在量子霍尔系统中,由于存在较强的相互作用效应以及拓扑性质,准粒子如磁极子、准粒子夸克等得以在这个平面上实现。
这种拓扑态准粒子的研究对于理解凝聚态物理和发展新的量子计算技术具有重要的意义。
另外,量子霍尔效应还在纳米电子器件中有广泛的应用。
由于量子霍尔效应使得电子传输在边界上趋于无散射,因此可以用于构建更加稳定和可控的纳米电子器件。
例如,在量子霍尔体系中可以实现高精度的电流标准以及高灵敏度的传感器,这对于电子技术的发展具有重要的作用。
量子霍尔效应解析

量子霍尔效应解析量子霍尔效应是一种奇特的量子现象,它在凝聚态物理领域中具有重要的地位。
本文将对量子霍尔效应进行解析,从基本概念、实验观测到理论解释等方面进行详细阐述。
量子霍尔效应是指在低温和强磁场下,二维电子气体在横向电场作用下出现的电导率量子化现象。
这一现象首次由德国物理学家冯·克尔门于1980年观测到,他发现在非常低温下,当二维电子气体受到强磁场垂直作用时,电导率会出现突变,而且其值只能取整数或分数。
这种奇特的现象引起了科学界的广泛关注。
实验观测方面,量子霍尔效应可以通过霍尔电阻的测量来进行。
霍尔电阻是指在二维电子气体受到垂直磁场作用时,横向电场和电流之间的关系。
实验中,通过在样品上施加横向电场和测量横向电流,可以得到霍尔电阻的数值。
当样品温度较低且强磁场作用下,霍尔电阻会出现明显的量子化现象,即只能取整数或分数值。
理论解释方面,量子霍尔效应可以通过拓扑物理的概念来解释。
拓扑物理是一门研究物质的几何结构和拓扑性质之间关系的学科。
在量子霍尔效应中,二维电子气体的能带结构具有非平凡的拓扑性质,即存在能隙和不同的拓扑不变量。
这些拓扑不变量决定了电子在强磁场下的行为,使得电导率只能取整数或分数值。
量子霍尔效应的深入研究不仅推动了凝聚态物理的发展,也对新型电子器件的设计和制备具有重要意义。
例如,基于量子霍尔效应的量子阻挡器可以在电子输运中实现无能量损耗的传输,这对于未来低功耗电子器件的发展具有巨大潜力。
另外,量子霍尔效应还可以用于研究拓扑绝缘体和拓扑超导体等新颖物态,这些物态在量子计算和量子通信等领域具有广阔的应用前景。
总结起来,量子霍尔效应是一种重要的量子现象,它在凝聚态物理中具有广泛的应用和研究价值。
通过实验观测和理论解释,我们可以更好地理解量子霍尔效应的本质和特性。
未来随着技术的进步和研究的深入,相信量子霍尔效应将会在更多领域发挥作用,为人类带来更多的科学和技术进步。
量子霍尔效应详解

量子霍尔效应是过去二十年中,凝体物理研究里最重要的成就之一。
要解释这个效应,需要用上许多量子物理中最微妙的概念。
1998年的诺贝尔物理奖,由美国普林斯顿大学的崔琦(Daniel C. Tsui)、哥伦比亚大学的史特莫(Horst L. Stormer)及史丹佛大学的劳夫林(Robert B. Laughlin)三人获得。
得奖理由是“他们发现了一种新形态的量子流体,其中有带分数电荷的激发态”。
在他们三位的新发现之前,物理学者认为除了夸克一类的粒子之外,宇宙中的基本粒子所带的电荷皆为一个电子所带的电荷-e(e=1.6×10-19库伦)的整数倍。
而夸克依其类别可带有±1e/3或±2e/3电荷。
夸克在一般状况下,只能存在于原子核中,它们不像电子可以自由流动。
所以物理学者并不期待在普通凝体系统中,可以看到如夸克般带有分数电子电荷的粒子或激发态。
这个想法在1982年崔琦和史特莫在二维电子系统中,发现分数霍尔效应后受到挑战。
一年后劳夫林提出一新颖的理论,认为二维电子系统在强磁场下由于电子之间的电力库伦交互作用,可以形成一种不可压缩的量子液体(incompressible quantum fluid),会展现出分数电荷。
分数电荷的出现可说是非常神秘,而且出人意表,其实却可以从已知的量子规则中推导出来。
劳夫林还曾想利用他的理论,解释夸克为什么会带分数电子电荷,虽然这样的想法还没有成功。
劳夫林的理论出现后,马上被理论高手判定是正确的想法。
不过对很多人而言,他的理论仍很难懂。
在那之后五、六年间,许多重要的论文陆续出现,把劳夫林理论中较隐晦的观念阐释得更清楚,也进一步推广他的理论到许多不同的物理状况,使整个理论更为完备。
以下扼要说明什么是分数量子霍尔效应,以及其理论解释。
霍尔电导系数编辑我们研究的对象是二维电子系统。
假设电子仅能活动于x-y平面上,而在z轴方向有一均匀磁场B,如图一所示。
霍尔效应就是当x轴方向有电流I时,在y轴方向就会有电位差VH。
量子霍尔效应

量子霍尔效应
量子霍尔效应是一种特殊的量子现象,它发生在二维电子气体中的霍尔系统中。
在强磁场作用下,电子在垂直于磁场方向的空间上形成二维层状结构(即量子阱),并且在此结构中存在禁闭的能级。
当外加一定的电场时,电子会产生沿着磁场方向的漂移,而垂直于磁场方向的速度分量仍然受到限制。
在量子霍尔效应中,当电子填满最低的能级(称为填满能级)时,存在一种特殊的电导现象,称为整数量子霍尔效应。
在这种情况下,电导随着外加电场的增加而逐渐增加,直到达到一个固定的整数倍(即平台),然后保持恒定,直到下一个填满能级被占据。
整数量子霍尔效应的发现是1980年代中期的一项重大科学突破,这一发现奠定了凝聚态物理学中拓扑材料研究的基础,并带动了其他许多有关量子物理的研究。
量子霍尔效应在现代电子学和量子计算中具有重要的应用潜力。
量子霍尔效应
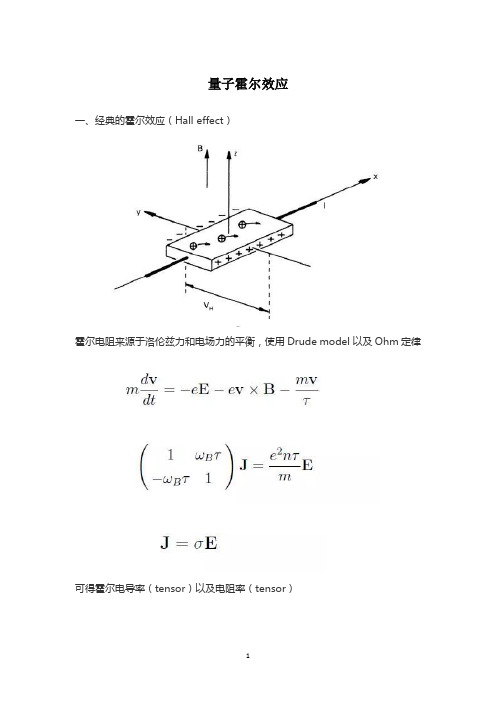
量子霍尔效应一、经典的霍尔效应(Hall effect)霍尔电阻来源于洛伦兹力和电场力的平衡,使用Drude model以及Ohm定律可得霍尔电导率(tensor)以及电阻率(tensor)二、(整数)量子霍尔效应弱磁场的情况下,非对角的霍尔电导和磁场强度满足经典的线性关系,强磁场作用下出现了很多量子化的平台量子化的起源-朗道能级这里使用Landau gauge,Hamiltonian可转化为谐振子模型从而求解其能级波函数代入current operator此时若在y方向加个电场ε,破坏其对称性得到的current依然是不变的(shift Gaussian wave packet center)。
对电流积分可得量子化的霍尔电导率,其中n对应了朗道能级的占据数目Laughlin’s gauge argument将IQHE解释为quantum pump,增加一个量子磁通的test flux的就对应着Gaussian wave packet移动一个单位。
Landauer's approach (Edge modes)Drift velocity 直接由化学电势差决定拓扑的引入(Kubo Formula,Chern number or TKNN number,Berry curvature...)Kubo Formula 是通过linear response得到的电导率上式红色部分是纯虚数,Berry curvature是纯实数所以第n个band的霍尔电导率是上式括号里面的积分是一个整数,即Chern number (first Chern number)=TKNN number。
证明略。
复旦大学物理学系教授修发贤课题组通过对量子霍尔效应的研究,实现了从二维迈向三维的新突破。
他们的科研成果于2018年12月18日在线发表于《自然》期刊上。
早在1879年,美国物理学家霍尔在研究金属的导电机制时发现,如果对通电的导体加上垂直于电流方向的磁场,电子的运动轨迹将发生偏转,在与导体纵向垂直的方向产生电压。
大学物理实验报告霍尔效应

大学物理实验报告霍尔效应霍尔效应是一种基于磁场作用的物理现象,在大学物理实验中经常被用来研究材料的电导性质和载流子的性质。
在本文中,我们将探讨霍尔效应的原理、实验方法以及实验结果的分析。
首先,让我们来了解一下霍尔效应的原理。
霍尔效应是由美国物理学家爱德华·霍尔于1879年发现的,他发现当电流通过一块导体时,如果在导体上施加一个垂直于电流方向的磁场,就会在导体的侧边产生一种电势差。
这个电势差被称为霍尔电压,它与电流、磁场以及导体材料的性质有关。
为了观察和测量霍尔电压,我们需要进行一系列的实验。
首先,我们需要准备一块导体样品,通常是一个长方形的薄片。
然后,在样品的两侧分别接上一个电源,以产生电流。
接下来,我们需要在样品上方放置一个磁场,可以使用一个恒定磁场产生器或者一个电磁铁。
在实验过程中,我们可以通过改变电流和磁场的大小来观察霍尔电压的变化。
在实验中,我们通常使用一个霍尔探头来测量霍尔电压。
霍尔探头由一个细长的导线和一个敏感的电压测量器组成。
将探头放置在导体样品的侧边,使导线与电流方向垂直,并将电压测量器连接到导线的两端。
当磁场施加到样品上时,导线中就会产生霍尔电压。
通过测量电压测量器的读数,我们可以得到霍尔电压的大小。
通过实验测量得到的霍尔电压与电流和磁场的关系可以用下面的公式表示:VH = RHBIL其中,VH是霍尔电压,RH是霍尔系数,B是磁场的大小,I是电流的大小,L是导体样品的长度。
从这个公式可以看出,霍尔电压与电流和磁场成正比,与导体样品的长度成正比。
通过实验测量得到的数据,我们可以绘制出霍尔电压与电流和磁场的关系曲线。
通过分析曲线的斜率,我们可以得到材料的霍尔系数。
霍尔系数是一个描述材料载流子性质的重要参数,它可以告诉我们材料中载流子的类型(正电荷还是负电荷)、密度以及迁移率等信息。
除了测量霍尔电压,我们还可以通过实验测量样品的电阻和磁阻。
通过测量电阻和磁阻的变化,我们可以进一步了解材料的导电性质和载流子的性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
告。为此,冯克里青获得了 1985 年诺贝尔物理奖。
什么是 QHE,简单地说,在一定条件下,处在强磁场中的二维电子系统,
其电导率张量为
0
ie
2
h
ie2
h
0
(5.9)
这里 i 是整数。换句话讲,电流密度 j 严格地与电场 E 垂直,且电流值是量子化
的。
从(5.9)式可知,当 Ex=0 时
jx xy E y , jy 0
vL
(ev
B
/
c) 0 m
(5.3) (5.4)
于是产生 y 方向的电流,为
jL
ne2 0 m
1 nec
j
B
0 nec
j
B
所以总电流为
j
0E
0 nec
j
B
(5.5)
一 个 二 维 导 体 置 于 xOy 平 面 内 , 取 B 沿 z 方 向 , 则 ( 5.5) 式 可 以 写 成 矩 阵
1982 年 , Daniel. Tsui( 丹 尼 尔 · 崔 )、
C
L
图 5-2 Hall 电阻测量
Stormer(斯托美)和 Gossard(戈沙德)发 现,在极低温下,理想样品的 i 值能被一系
列分数值 f 代替,特别有趣的是,这些分数的分母必须是奇数,即 f=1/3,2/3,
2/5,8/5,3/7,4/7…。这一现象称为反常量子 Hall 效应或分数量子 Hall 效应,
记为 FQHE。
在实际的实验过程中,电导率张量和电阻率张量都是非直接测量量,只有电
阻或电导才是直接测量样品到漏极 D。触点 A、B、C 用来测量电压 VL 和 HH。基本的关系
式为
j I W
EL
VL L
EH
VH W
L 是样品长度,W 是样品宽度。于是,纵向电阻和横向电阻分别为
外电场 E 沿 x 方向作用的情况下,电子有一平均速度增量,为
v eE 0
m
(5.1)
电流密度与电子运动的关系为
j
nev
ne 2
0
E
m
(5.2)
式中,n 是电子的数密度,m 是电子的有效质量。将(5.2)式与欧姆定律 j
0 E 作比较,得到电导率 0为
0
ne2 0 m
电 子 因 洛 伦 兹 力 f L eV B 而 引 起 的 速 度 增 量 为
第五章 量子霍耳效应
量子霍耳效应现象
一、霍耳效应
在介绍量子霍耳效应(缩写为 QHE)之前,有必要回顾一下普通的霍耳效
应 。 取 一 块 长 方 体 金 属 样 品 ( a× b× d), 让 电 流
e+ VH ΔV
yI b
- fL xa
z d
图 5-1 霍耳效应
I 沿 x 方向通过,在 z 方向加一均匀磁场 B。由 于电子受洛兹力 fL 的作用,故样品沿 y 方向将 产生一电压 VH,称为霍耳电压,这就是通常 所讲的霍耳效应。半经典半量子的理论认为, 金属中只有费密能级附近的电子可以自由运
形式
1 0
B nec
B 1
nec
0
j j
x y
E E
x y
(5.6)
实际上,对(5.5)式分别取 x 和 y 方向上的分量,则有
jx
0Ex
0
B nec
jy
jy
0Ey
0
B nec
jx
(5.7)
式中的电流项移到左边,并除以 0 ,即为(5.6)式。记电阻率为
0
B
nec
B
nec
,
(5.10)
将(5.10)式记为
j
HE
ie 2 h
E
由此得到 QHE 的主要特点是:
(5.11)
1. jE 。
2. 电导率张量的非对角项 H 由基本常数 e、h 构成,即
H
ie 2 h
(i 是整数)
而对角项为零,表明电流是无耗散的。
QHE 与超导、超流似乎有某种联系。
A VL B
I
S VH W
D
由于 i 取整数,故也称 QHE 为整数量子 霍耳效应,记为 IQHE。
在其上沿 x 方向分布,它们集中在 y=常量 Δ
中 虚 直 线 ), 但 实 际 测 量 结 果 却 出 现 了 一 些 台 阶 ( 见 图 5-3 中 实 线 )。
台阶高度处在 h (e2 RH ) 为整数的地方,
h/e2RH 3
2
1
1 2 3 nhc/eB 图 5-3 Hall 电阻台阶
台阶中心十分平直。此刻尽管磁场 B 有变化,也并不影响 RH 值。对应台阶的
RL VL I LE L jW 11 L W RH VH I WE H jW 12
(5.12) (5.13)
(5.12)式是通常的电阻率定律。式(5.13)表明 Hall 电阻与样品的几何尺寸无
关。
按照通常的 Hall 效应理论,应有
I RH j E H nec B 则 I RH 与 I B 应呈直线关系(见图 5-3
1、一般情况下,电阻率和电导率是张量,而非标量。
2、霍耳电阻率即电阻率的非对角项,它们不是独立的,而是互为相反数,
12 21 而 对 角 项 0 0 。
二、量子霍耳效应
Hall 效应发现后,大约经过了 100 年,Klaus. Von Klitzing(克劳斯·冯克里
青 )、 Dorda( 多 达 ) 和 Pepper( 波 普 ) 在 1980 年 发 表 了 关 于 QHE 的 实 验 工 作 报
RL=0,这时,有电流而无沿电流方向的电压。在低温下,好的样品一般有较宽
的台阶。
上面,介绍了 QHE 的基本特点、实验测量原理和结果。如何解释 QHE,特
别是 FQHE,至今仍是一个引起人们极大兴趣的理论研究课题。下面将简要说明
QHE 的物理机制。
强磁场中的二维电子系统
y 设想有一个二维长方形的样品,电子
0
0
1 0
则(5.6)式简记为
E j
(5.8)
这里电阻率不再是标量,而是一个张量。
电 导 率 是 的 逆 矩 阵 : I0 容 易 求 出
u
0
/(1
c2
2 0
)
12 nec / B 11 / c 0
这 里 c eB mc 是 电 子 在 磁 场 中 的 回 旋 率 。 综 上 所 述 , 得 出 以 下 结 论 :
动。因为泡利原理限制了其它低于费密能级电子的活动性。假定费密电子在连续
的 两 次 碰 撞 之 间 自 由 行 走 的 平 均 时 间 和 平 均 路 程 分 别 为 0 和 l0 , 并 称 0 为 平 均
自 由 时 间 , l0 为 平 均 自 由 程 。 显 然 有 l0 VF 0 , VF 是 费 密 运 动 电 子 的 速 度 。 在
