人教版数学高一-集合的概念 学案二
高中数学人教版必修1(教案与导学案)1_1_1-2集合的含义及其表示[来源:学优高考网148480]
![高中数学人教版必修1(教案与导学案)1_1_1-2集合的含义及其表示[来源:学优高考网148480]](https://img.taocdn.com/s3/m/ac437a43650e52ea55189864.png)
1. 1.1 集合的含义及其表示方法(2)教案【教学目标】1、集合和元素的表示法;2、掌握一些常用的数集及其记法3、掌握集合两种表示法:列举法、描述法。
【教学重难点】集合的两种表示法:列举法和描述法。
【教学过程】一、导入新课复习提问:集合元素的特征有哪些?怎样理解,试举例说明,集合与元素关系是什么?如何用数不符号表示?那么给定一个具体的集合,我们如何表示它呢?这就是今天我们学习的内容—集合的表示 (板书课题)我们可以用自然语言来描述一个集合,但这将给我们带来很多不便,除此之外还常用列举法和描述法来表示集合二、新课讲授(1)、列举法:把集合中的元素一一列举出来,写在大括号内表示集合的方法。
例:“中国的直辖市”构成的集合,写成{北京,天津,上海,重庆}由“maths 中的字母” 构成的集合,写成{m,a,t,h,s}由“book 中的字母” 构成的集合,写成{b,o,k}注:(1) 有些集合亦可如下表示:从51到100的所有整数组成的集合:{51,52,53,…,100}所有正奇数组成的集合:{1,3,5,7,…}(2) a 与{a}不同:a 表示一个元素,{a}表示一个集合,该集合只有一个元素。
(3) 集合中的元素具有无序性,所以用列举法表示集合时不必考虑元素的顺序。
学生自主完成P4 例题1(2)、描述法:用确定的条件表示某些对象是否属于这个集合,并把这个条件写在大括号内表示集合的方法。
格式:{x ∈A| P (x )}含义:在集合A 中满足条件P (x )的x 的集合。
例:不等式12x +<-的解集可以表示为:{|12}x R x ∈+<-或{|3,}x x x R <-∈“中国的直辖市”构成的集合,写成{x x 为中国的直辖市}; “方程x 2+5x-6=0的实数解” {x ∈R| x 2+5x-6=0}={-6,1}学生自主完成P5例题2三、例题讲解例题1.用列举法表示下列集合:(1)小于5的正奇数组成的集合;(2)能被3整除且大于4小于15的自然数组成的集合;(3)方程x 2-9=0的解组成的集合;(4){15以内的质数}; (5){x|x36∈Z ,x ∈Z }. 分析:教师指导学生思考列举法的书写格式,并讨论各个集合中的元素,明确各个集合中的元素,写在大括号内即可提示学生注意:(2)中满足条件的数按从小到大排列时,从第二个数起,每个数比前一个数大3;(4)中除去1和本身外没有其他的约数的正整数是质数;(5)中3-x 是6的约数,6的约数有±1, ±2, ±3, ±6.解: (1)满足题设条件小于5的正奇数有1,3,故用列举法表示为{1,3};(2)能被3整除且大于4小于15的自然数有6,9,12,故用列举法表示为{6,9,12};(3)方程x 2-9=0的解为-3,3,故用列举法表示为{-3,3};(4)15以内的质数有2,3,5,7,11,13,故该集合用列举法表示为{2,3,5,7,11,13}(5)满足的x 有3-x=±1, ±2, ±3, ±6.解之,得x=2,4,1,5,0,6,-3,9,故用列举法表示为{2,4,1,5,0,6,-3,9}变式训练1用列举法表示下列集合:(1)x 2-4的一次因式组成的集合;(2){y|y=-x 2-2x+3,x ∈R ,y ∈N };(3)方程x 2+6x+9=0的解集;(4){20以内的质数};(5){(x,y)|x 2+y 2=1,x ∈Z ,y ∈Z };(6){大于0小于3的整数};(7){x ∈R |x 2+5x-14=0};(8){(x,y)|x ∈N 且1≤x<4,y -2x=0};(9){(x,y)|x+y=6,x ∈N ,y ∈N }.分析:让学生思考用描述法的形式如何表示平面直角坐标系中的点?如何表示数轴上的点?如何表示不等式的解?学生板书,教师在其他学生中间巡视,及时帮助思维遇到障碍的同学.必要时,教师可提示学生:(1)集合中的元素是点,它是坐标平面内的点,集合元素代表符号用有序实数对(x,y)来表示,其特征是满足y=x 2;(2)集合中元素是点,而数轴上的点可以用其坐标表示,其坐标是一个实数,集合元素代表符号用x 来表示,其特征是对应的实数绝对值大于6;(3)集合中的元素是实数,集合元素代表符号用x 来表示,把不等式化为x<a 的形式,则这些实数的特征是满足x<a.解:(1)二次函数y=x 2上的点(x,y)的坐标满足y=x 2,则二次函数y=x 2图象上的点组成的集合表示为{(x,y)|y=x 2};(2)数轴上离原点的距离大于6的点组成的集合等于绝对值大于6的实数组成的集合,则 数轴上离原点的距离大于6的点组成的集合表示为{x ∈R ||x|>6};(3)不等式x-7<3的解是x<10,则不等式x-7<3的解集表示为{x|x<10}.点评:本题主要考查集合的描述法表示.描述法适用于元素个数是有限个并且较多或无限个的集合.用描述法表示集合时,集合元素的代表符号不能随便设,点集的元素代表符号是(x,y),数集的元素代表符号常用x.集合中元素的公共特征属性可以用文字直接表述,最好用数学符号表示,必须抓住其实质.变式训练2用描述法表示下列集合:(1)方程2x+y=5的解集;(2)小于10的所有非负整数的集合;(3)方程ax+by=0(ab≠0)的解;(4)数轴上离开原点的距离大于3的点的集合;(5)平面直角坐标系中第Ⅱ、Ⅳ象限点的集合;(6)方程组⎩⎨⎧==+1y -x 1,y x 的解的集合; (7){1,3,5,7,…};(8)x 轴上所有点的集合;(9)非负偶数;(10)能被3整除的整数.答案:(1)、{(x,y)|2x+y=5};(2)、{x|0≤x<10,x ∈Z };(3)、{(x,y)|ax+by=0(ab≠0)};(4)、{x||x|>3};(5)、{(x,y)|xy<0};(6)、{(x,y)|⎩⎨⎧==+1y -x 1y x }; (7)、{x|x=2k-1,k ∈N *};(8)、{(x,y)|x ∈R ,y=0};(9)、{x|x=2k,k ∈N };(10)、{x|x=3k,k ∈Z }.四、课堂小结1.描述法表示集合应注意集合的代表元素{(x,y)|y= x 2+3x+2}与 {y|y= x 2+3x+2}不同,只要不引起误解,集合的代表元素也可省略,例如:{整数},即代表整数集Z 。
新人教版高中数学必修一《集合的含义与表示》导学案

1.1.1集合的含义与表示一.学习目标:l.知识与技能(1)通过三张图片,了解集合的含义,理解元素与集合之间的属于关系;(2)掌握集合中元素的三要素:确定性.互异性.无序性;(3)熟练应用常用数集及其专用记号;会用集合语言表示有关数学对象.二. 学习重点、难点:重点:集合的含义与表示方法.难点:集合的三要素:确定性、互异性、无序性.三.自学指导:(一)创设情景,揭示课题1.教师首先提出问题:通过PPT 图片,启发引导学生找到三张图片的共同特征,并引导学生举出一些集合的例子。
通过举例说明和互相交流.做好教师对学生的活动的梳理引导,并给予积极评价.2.用6分钟时间预习教材P2~P5,完成下列内容:(1)、集合:一般地,我们把 统称为元素,把一些元素组成的 叫做集合,简称为: 。
(2)、集合元素的三要素(三特征): 、 、 ;若两个集合相等,那么必须有: 。
(3)、元素与集合的关系:若a 是集合A 的元素,则记作:a A ;若a 不是集合A 的元素,则记作:a A 。
(4)、常用数集的记法:自然数集: ; 有理数集: ; 整数集: ;实数集: ; 正实数集: ; 正整数集: .(5)集合的表示方法列举法:把集合中的元素 ,并用 括起来表示集合的方法叫列举法描述法:用集合所含元素的 表示集合的方法称为描述法,具体方法是: 在 内写上表示这个集合元素的 及取值(或变化)范围,再画 , 最后在 后写出这个集合中元素所具有的共同特征。
四.教学过程:(一)、问题导学:检查自学指导内容,并分组探讨一下问题:a.如何判断所给对象是否组成集合?b.集合中元素的特征性质有哪些?如何判断两个集合是相等的? 判断集合A={-2,2}与集合2{|40}B x R x =∈-=一样吗?c.试着总结集合的表示方法有哪些?并试比较各自的特点和适用的对象。
(二).自学检测:完成以下练习:1.下面给出的四类对象中,能组成集合的是( )A.高一某班个子较高的同学B.比较著名的科学家C.无限接近于4的实数D.到一个定点的距离等于定长的点的全体2.用符号∈或∉填空:(1)0 *N ;(2;(3)23 Q ;(4)π Q 。
高中数学人教版(新教材)必修1学案2:1.3 集合的基本运算

1.3 集合的基本运算学习目标1. 理解两个集合的并集与交集的含义,能求两个集合的并集与交集;2. 理解全集和补集的含义,能求给定集合的补集;3. 能使用Venn图表达集合的基本关系与基本运算.核心素养1.数学抽象:并集、交集、全集、补集含义的理解;2.逻辑推理:并集、交集及补集的性质的推导;3.数学运算:求两个集合的并集、交集及补集,已知并集、交集及补集的性质求参数(参数的范围);4.数据分析:通过并集、交集及补集的性质列不等式组,此过程中重点关注端点是否含“=”及∅问题;5.数学建模:用集合思想对实际生活中的对象进行判断与归类.学习重点:1.交集、并集定义的三种语言的表达方式及交集、并集的区别与联系;2全集与补集的定义.学习难点:利用交集并集补集含义和Venn图解决一些与集合的运算有关的问题.学习过程预习导入阅读课本,填写.1.并集一般地,由____________集合A__________集合B的元素所组成的集合,称为集合A与B 的并集,记作:_________(读作:“________”)即:A∪B=________________.Venn图表示:2.交集一般地,由____________集合A____________集合B的元素所组成的集合,叫做集合A与B 的交集,记作:___________(读作:__________)即:A∩B=_______________.Venn图表示:3.全集一般地,如果一个集合含有我们所研究问题中所涉及的____________,那么就称这个集合为全集,通常记作_______.4.补集:对于全集U的一个子集A,由全集U中所有____________的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,记作:____________,即:C U A=____________. 补集的Venn图表示5.常用结论:(1)A∩B___A,A∩B___B,A∩A=___,A∩∅=___,A∩B___B∩A;(2)A___A∪B,B___A∪B,A∪A=___,A∪∅=___,A∪B___B∪A;(3)(C U A)∪A=___,(C U A)∩A=___;(4)若A∩B=A,则A___B,反之也成立;(5)若A∪B=B,则A___B,反之也成立.小试牛刀1.判断(正确的打“√”,错误的打“×”)(1)集合A∪B中的元素个数就是集合A和集合B中所有元素的个数和. ()(2)当集合A与集合B没有公共元素时,集合A与集合B就没有交集. ()(3)若A∪B=⌀,则A=B=⌀. ()(4)若A∩B=⌀,则A=B=⌀. ()(5)若A∪B=A∪C,则B=C. ()(6)∁A⌀=A. ()(7)∁U(A∪B)=(∁U A)∪(∁U B). ()2.设集合M={-1,0,1},N={0,1,2},则M∪N等于()A.{0,1}B.{-1,0,1}C.{0,1,2} D.{-1,0,1,2}3.若集合A={x|-5<x<2},B={x|-3<x<3},则A∩B=()A.{x|-3<x<2} B.{x|-5<x<2}C.{x|-3<x<3} D.{x|-5<x<3}4.全集U={x|0<x<10},A={x|0<x<5},则∁U A=________.自主探究例1(单一运算)1.求下列两个集合的并集和交集:(1) A={1,2,3,4,5},B={-1,0,1,2,3};(2) A={x|x+1>0},B={x|-2<x<2};2.设集合U={1,2,3,4,5,6},M={1,2,4},则∁U M=()A.U B.{1,3,5} C.{3,5,6} D.{2,4,6}例2(混合运算)(1)设集合A={1,2,6},B={2,4},C={x∈R|-1≤x≤5},则(A∪B)∩C=() A.{2}B.{1,2,4}C.{1,2,4,6} D.{x∈R|-1≤x≤5}(2)设全集为R,A={x|3≤x<7},B={x|2<x<10},则∁R(A∪B)=________,(∁R A)∩B=________.例3(由并集、交集求参数的值)已知M={1,2,a2−3a−1},N={-1,a,3},M∩N={3},求实数a的值.例4(由并集、交集的定义求参数的范围)设集合A={x|-1<x<a},B={x|1<x<3}且A∪B={x|-1<x<3},求a的取值范围.例5(由交集、并集的性质求参数的范围)已知集合A={x|-3<x≤4},集合B={x|k+1≤x≤2k-1},且A∪B=A,试求k的取值范围.变式.『变条件』把例5题中的条件“A∪B=A”换为“A∩B=A”,求k的取值范围.当堂检测1.已知集合P={x|-1<x<1},Q={x|0<x<2},那么P∪Q=()A.{x|-1<x<2} B.{x|0<x<1}C.{x|-1<x<0} D.{x|1<x<2}2.设集合U={1,2,3,4,5},A={1,2,3},B={2,3,4},则∁U(A∩B)等于()A.{2,3}B.{1,4,5}C.{4,5} D.{1,5}3.已知集合M={(x,y)|x+y=2},N={(x,y)|x-y=4},那么集合M∩N为()A.x=3,y=-1 B.(3,-1)C.{3,-1} D.{(3,-1)}4.A={x∈N|1≤x≤10},B={x∈R|x2+x-6=0},则下图中阴影部分表示的集合为()A.{2} B.{3}C.{-3,2} D.{-2,3}5.设集合A={a,b},B={a+1,5},若A∩B={2},则A∪B等于()A.{1,2} B.{1,5}C.{2,5} D.{1,2,5}6.设集合A={x|-1≤x<2},B={x|x<a},若A∩B≠∅,则a的取值范围是()A.a<2 B.a>-2C.a>-1 D.-1<a≤27.已知A={x|a<x≤a+8},B={x|x<-1,或x>5},若A∪B=R,则a的取值范围为________.8.已知非空集合A={x|2a+1≤x≤3a-5},B={x|3≤x≤22}.(1)当a=10时,求A∩B,A∪B;(2)求能使A⊆(A∩B)成立的a的取值范围.——★参*考*答*案★——学习过程一、预习导入1.所有属于集合或属于集合A∪B A并B {x|x∈A,或x∈B}2.属于且属于A∩B A交B {x|∈A,且x∈B}3.所有元素U4.不属于集合A C U A {x|x∈U,且x∉A}5.(1)⊆⊆A ∅=(2)⊆⊆A A=(3)U ∅(4)⊆(5)⊆小试牛刀1.(1) ×(2) ×(3) √ (4)×(5) ×(6) √(7) ×2.D3.A4.{x|5≤x<10}自主探究例1『答案』见解析『解析』 1.(1)如图所示,A∪B={-1,0,1,2,3,4,5},A∩B={1,2,3}.(2)由题意知A={x|x>-1},用数轴表示集合A和B,如图所示,则数轴上方所有“线”下面的实数组成了A∪B,故A∪B={x|x>-2},数轴上方“双线”(即公共部分)下面的实数组成了A∩B,故A∩B={x|-1<x<2}.2.因为U={1,2,3,4,5,6},M={1,2,4},由补集的定义,可知∁U M={3,5,6}.故选C.例2『答案』(1)B(2){x|x≤2,或x≥10}{x|2<x<3,或7≤x<10}『解析』(1)A ∪B ={1,2,4,6},又C ={x ∈R |-1≤x ≤5},则(A ∪B )∩C ={1,2,4}.(2)把全集R 和集合A 、B 在数轴上表示如下:由图知,A ∪B ={x |2<x <10}, ∴∁R (A ∪B )={x |x ≤2,或x ≥10}. ∵∁RA ={x |x <3,或x ≥7},∴(∁RA )∩B ={x |2<x <3,或7≤x <10}. 例3『答案』见解析『解析』∵M ∩N ={3},∴3∈M ;∴a 2−3a −1=3,即a 2−3a −4=0,,解得a =-1或4. 当a =-1时,与集合中元素的互异性矛盾,舍去; 当a =4时,M ={1,2,3},N ={-1,3,4},符合题意. ∴a =4.例4『答案』见解析『解析』如图所示,由A ∪B ={x |-1<x <3}知,1<a ≤3. 例5『答案』见解析『解析』∵A ∪B =A ,∴B ⊆A ,①当B =Ø时,k +1>2k -1,∴k <2. ②当B ≠Ø,则根据题意如图所示:根据数轴可得⎩⎪⎨⎪⎧k +1≤2k -1,-3<k +1,2k -1≤4,解得2≤k ≤52.综合①②可得k 的取值范围为⎩⎨⎧⎭⎬⎫k ⎪⎪k ≤52. 变式.『答案』见解析『解析』∵A ∩B =A ,∴A ⊆B .又A ={x |-3<x ≤4},B ={x |k +1≤x ≤2k -1},可知B ≠Ø.由数轴可知⎩⎪⎨⎪⎧k +1≤-3,2k -1≥4,解得k ∈Ø,即当A ∩B =A 时,k 不存在. 当堂检测1-6.ABDADC 7.-3≤a <-18.解:(1)当a =10时,A ={x |21≤x ≤25}. 又B ={x |3≤x ≤22},所以A ∩B ={x |21≤x ≤22},A ∪B ={x |3≤x ≤25}. (2)由A ⊆(A ∩B ),可知A ⊆B , 又因为A 为非空集合, 所以⎩⎪⎨⎪⎧2a +1≥3,3a -5≤22,2a +1≤3a -5,解得6≤a ≤9.。
人教A版必修1 数学:1.1.1 集合的含义与表示 学案2

集合的含义与表示【学习目标】一、知识与技能:(1)初步理解集合的含义,知道常用的数集及其记法。
(2)初步了解“属于”关系的意义。
(3)初步了解有限集、无限集、空集的意义。
二、过程与方法:(1)通过实例,初步体会元素与集合的“属于”关系,从观察分析集合的元素入手,正确地理解集合。
(2)观察关于集合的几组实例,并举出各种集合的例子,初步感受集合语言在描述客观现实和数学对象中的意义。
(3)学会借助实例分析,探究数学问题(如集合中元素的确定性、互异性和无序性)。
三、情感、态度与价值观:(1)在学习运用集合语言过程中,增强认识事件的能力,初步培养实事求是,扎实严谨的科学态度。
(2)探索利用直观图示理解抽象概念,体会数形结合的思想。
【学习重难点】1.学习重点:集合的含义与表示方法,用集合语言表达数学对象或数学内容。
2.学习难点:区别元素与集合等概念及其符号表示。
【学习过程】一、集合的概念一般地,把一些__________不同的对象看成一个整体,就说这个__________是由这些对象的全体构成的集合。
1.集合是现代数学中不加定义的基本概念,学习这个概念应注意以下两点:(1)集合是一个“整体”(2)构成集合的对象必须是“确定”的且“不同”的。
“确定”是指构成集合的对象具有非常明确的特征,这个特征不是模棱两可的。
一般地,判定一组对象a1,a2,a3,…,an能否构成集合,就是要看判定的对象a1,a2,a3,…,an是否具有一个确定的特性,如果有,能构成集合;如果没有,就不能构成集合。
“不同”是指构成集合的各个对象互不相同,即相同的对象归入一个集合时,该对象只能出现一次。
例1:下列各组对象中,哪些能组成集合?哪些不能组成集合? (1)参加2010年全国高考的山东考生。
(2)所有数学难题。
(3)数组2,2,4,6.(4)参加2010年广州亚运会的运动员。
(5)全国所有大湖。
2.元素的概念构成集合的每个对象叫做这个集合的元素。
高一数学必修一:集合的概念(学案)

集合的概念一、课前导入1.集合的故事:一位鱼民非常喜欢数学,但他怎么也想不明白集合的意义。
于是他请教数学家:“尊敬的先生,请你告诉我,集合是什么?”集合是不定义的概念,数学家很难回答那位渔民。
有一天,他来到渔民的船上,看到渔民洒下渔网一拉,许多鱼虾在网中跳动。
数学家非常激动并告诉渔民:“这就是集合!”2.说一说初中阶段遇到的集合:二、新课讲授1.集合:某些指定的对象集在一起成为集合。
(1)集合中的对象称元素,若a是集合A的元素,记作Aa∈;若b不是集合A的元素,记作Ab∉;元素对于集合的隶属关系1)属于:如果a是集合A的元素,就说a属于A,记作a∈A2)不属于:如果a不是集合A的元素,就说a不属于A,记作Aa∉2、集合元素性质确定性:设A是一个给定的集合,x是某一个具体对象,则或者是A的元素,或者不是A的元素,两种情况必有一种且只有一种成立;互异性:一个给定集合中的元素,指属于这个集合的互不相同的个体(对象),因此,同一集合中不应重复出现同一元素;无序性:集合中不同的元素之间没有地位差异,集合不同于元素的排列顺序无关;3、集合表示方法1、列举法:把集合中的元素一一列举出来,写在大括号内;2、描述法:把集合中的元素的公共属性描述出来,写在大括号{}内。
具体方法:在大括号内先写上表示这个集合元素的一般符号及取值(或变化)范围,再画一条竖线,在竖线后写出这个集合中元素所具有的共同特征。
4、韦恩图:用一条封闭的曲线的内部来表示一个集合的方法注意: 何时用列举法?何时用描述法?(1)集合的公共属性不明显,难以概括,不便用描述法表示,只能用列举法如:集合},5,23,{2232y x x y x x +-+ (2)集合的元素不能一一列举出来,或者不便于、不需要一一列举出来,常用描述法5、常用数集及其记法:非负整数集(或自然数集),记作N ;正整数集,记作N *或N +;整数集,记作Z ;有理数集,记作Q ;实数集,记作R 。
集合的概念学案

集合的概念【学习目标】1.掌握集合的表示方法,能在具体问题中选择适当的方法表示集合。
2.通过实例和阅读自学体会用列举法和描述法表示集合的方法和特点,培养自主探究意识和自学能力。
【学习重点】集合的含义与表示方法,用集合语言表达数学对象或数学内容。
【学习难点】区别元素与集合等概念及其符号表示。
【自学导引】1.把集合的元素一一列举出来,并用花括号“{}”括起来表示集合的方法叫做列举法。
2.用集合所含元素的共同特征表示集合的方法称为描述法。
3.写出不等式73x -<的解集:{}0|1x x <。
4.所有偶数的集合可表示为:2{,|}x x k k ∈=∈Z Z 。
5.方程(1)(3)0x x +-=的所有实数根组成的集合为:{}1,3-。
【学习过程】一、用列举法表示集合例1用列举法表示下列集合:(1)15的正约数组成的集合;(2)平方后仍为原数的数组成的集合。
解:(1)15135=⨯⨯,故集合为{1,3,5,15}。
(2)平方后仍为原数的数构成的集合是{}0,1。
点评用列举法表示集合时,里面元素与顺序无关,该法表示集合直观明了。
变式迁移1用列举法表示下列集合:(1)不大于10的非负偶数集;(2)由||(,)||a b a b a b +∈R 所确定的实数集合。
解:(1){0,2,4,6,8,10}(2){2,0,2}-二、用描述法表示集合例2用描述法表示下列集合:(1)正偶数集;(2)被3除余2的正整数集;(3)不等式2x +5<3的解集;(4)第一、三象限点的集合。
分析:(1)中的正偶数都能被2整除,所以正偶数可以表示为()x 2n n =∈*N 的形式;(2)中被3除余2的正整数满足()23x n n -=∈*N ,则()32x n n =+∈*N ;(4)中的点(),x y 满足0xy >.解:(1)2,{|}x x n n =∈N*。
(2){|}32,x x n n =∈N*+。
(3)5{}3|2x x ∈<R +或{|}1x x ∈R <-。
高一数学学案——集合的概念

B组:
6. 已知由 这三个实数构成一个集合,求 应满足的条件.
C组
7.已知集合 ,若集合A中至多有一个元素,求实数 的取值范围.
自我反思:
1.你觉得你本节课的效率怎样?
2.本节课你从知识,方法方面学到了什么?
第 4 页
高一数学课时学案
课 题
集合的概念
编制人
审核人
目标
导学
1.了解集合的含义,知道常用数集及其表示方法。
2.会使用符号 表示元素与集合之间的关系。
自 学 质 疑 学 案
重点难点
重点:明确集合的含义,知道常用数集的概念及其表示方法;
难点:集合中元素的性质及对空集概念的理解.
阅以下两种学习方式:
1
集合中元素的性质
2
3、4、5
6、7
学生笔记(教师点拨)
学 案 内 容
A组:
1. 下列关系是否正确?
(1) (2) (3)
(4) (5) (6)
(7) (8)
2. 用符号 填空:
(1) N (2)3.14Q (3) Z
(4) Q (5) R (6)1
(7) R
3.已知集合 中的三个元素是 的三边长,那么 一定不是( )
一、阅读完教材后,可以先做学案再看微课,亦可以先看微课再完成学案
二、先根据学案上的问题有目的的阅读课本,然后可以先做学案再看微课,亦可以先看微课再完成学案
一、自主学习:
1.集合的概念
(1)对象:
(2)集合及表示:
(3)元素及表示:
2.元素与集合的关系:
注:应区分 , , , 等符号的含义.
集合的概念(第二课时)教学设计 高一上学期数学人教A版(2019)必修第一册
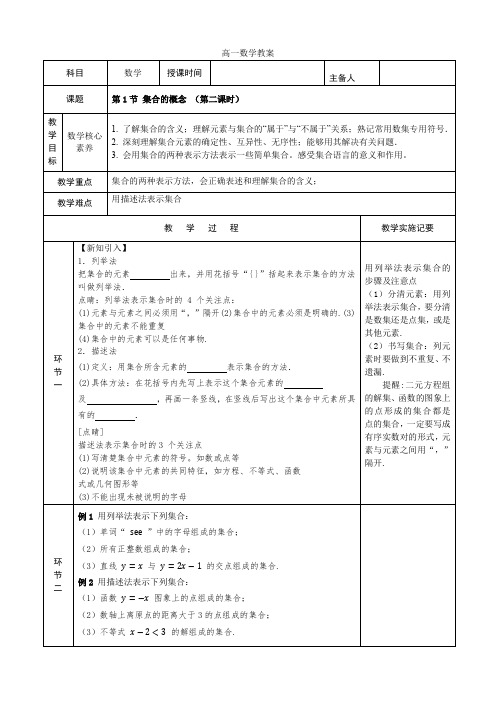
高一数学教案科目数学授课时间主备人课题第1节集合的概念(第二课时)教学目标数学核心素养1. 了解集合的含义;理解元素与集合的“属于”与“不属于”关系;熟记常用数集专用符号.2. 深刻理解集合元素的确定性、互异性、无序性;能够用其解决有关问题.3. 会用集合的两种表示方法表示一些简单集合。
感受集合语言的意义和作用。
教学重点集合的两种表示方法,会正确表述和理解集合的含义;教学难点用描述法表示集合教学过程教学实施记要环节一【新知引入】1.列举法把集合的元素出来,并用花括号“{ }”括起来表示集合的方法叫做列举法.点睛:列举法表示集合时的 4 个关注点:(1)元素与元素之间必须用“,”隔开(2)集合中的元素必须是明确的.(3)集合中的元素不能重复(4)集合中的元素可以是任何事物.2.描述法(1)定义:用集合所含元素的表示集合的方法.(2)具体方法:在花括号内先写上表示这个集合元素的及,再画一条竖线,在竖线后写出这个集合中元素所具有的.[点睛]描述法表示集合时的3 个关注点(1)写清楚集合中元素的符号。
如数或点等(2)说明该集合中元素的共同特征,如方程、不等式、函数式或几何图形等(3)不能出现未被说明的字母用列举法表示集合的步骤及注意点(1)分清元素:用列举法表示集合,要分清是数集还是点集,或是其他元素.(2)书写集合:列元素时要做到不重复、不遗漏.提醒:二元方程组的解集、函数的图象上的点形成的集合都是点的集合,一定要写成有序实数对的形式,元素与元素之间用“,”隔开.环节二例1 用列举法表示下列集合:(1)单词“<m>s ee</m>”中的字母组成的集合;(2)所有正整数组成的集合;(3)直线<m>y=x</m>与<m>y=2x−1</m>的交点组成的集合. 例2 用描述法表示下列集合:(1)函数<m>y=−x</m>图象上的点组成的集合;(2)数轴上离原点的距离大于3的点组成的集合;(3)不等式<m>x−2<3</m>的解组成的集合.环节三【小组合作与展示】1.集合{x|x2−4x+3=0}用列举法表示为( @54 ).A. {1,3}B. {(1,3)}C. {x2−4x+3=0}D. {x=1,x=3}2.方程组{x+y=3,x−y=−1的解集不能表示为( @56 ).A. {(x,y)∣{x+y=3,x−y=−1} B. {(x,y)∣{x=1,y=2}C. {1,2}D. {(x,y)|x=1,y=2}3、用列举法表示下列集合.(1)不大于10的非负偶数组成的集合;(2)方程x3=x的所有实数解组成的集合;(3)直线y=2x+1与y轴的交点所组成的集合.课堂小结1、列举法2、描述法3、例举法和描述法需要注意的问题板书设计1、元素与集合的关系符号书写2、集合的表示方法:列举法和描述法3、注意事项作业布置1、用描述法表示抛物线y=x2+1上的点构成的集合.变式1.[变条件,变设问]本题中点的集合若改为“{x|y=x2+1}”,则集合中的元素是什么?变式2.[变条件,变设问]本题中点的集合若改为“{y|y=x2+1}”,则集合中的元素是什么?2、用描述法表示下列集合:(1)被3除余1的正整数的集合;(2)坐标平面内第一象限的点的集合;(3)大于4的所有偶数.教学反思。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学案
学科 数学 编制人
审核人
教学案编号
1
课型 新授课 课题
1.1.1 集合的概念
课标要求 初步理解集合的含义,了解属于关系的意义,知道常用数集及其记法。
重点难点 集合的概念与集合中元素的性质
教学过程设计
一、 知识要点
1. 集合:一般地,把一些能够 对象的全体构成的
(或
)。
(或
对象看成一个整体,就说这个整体是由这些 )。构成集合的每个对象叫做这个集合的
变式训练:教材第 4 页练习 A 第 1 题Biblioteka 例 2. 用符号或 填空:
(1) -3
(5) 3
N; (2)3.14
Q; (6) 1 2
Q; (3) 1 3
R; (7)1
Q; (4)0 Φ ;
N+; (8) R。
变式训练:教材第 5 页练习 A 第 3 题
三、 课后作业
教材第 5 页练习 B 第 2 题、第 9 页习题 1-1B 第 3 题
2.集合中元素的性质:
、
、
。
3.集合与元素的表示:集合通常用
用
来表示。
来表示,它们的元素通常
4.元素与集合的关系: 如果 a 是集合 A 的元素,就说 如果 a 不是集合 A 的元素,就说
5.空集:
,记作 ,记作
,记作
,读作 ,读作
。
。 。
6.集合的分类:含有有限个元素的集合叫做
,含有无限个元素的集合叫做
。
7.常用的数集及其记号: (1)自然数集: (2)正整数集: (3)整数集: (4)有理数集: (5)实数集:
,记作 ,记作 ,记作 ,记作 ,记作
。 。
。 。
。
高中数学
打印版
二、 典例解析
例1. 你能否确定,你所在班级中,高个子同学构成的集合?并说明理由。 你能否确定,你所在班级中,最高的 3 位同学构成的集合?
四、 思考与讨论
已知由 1, x, x 2 三个实数构成一个集合,求 x 应满足的条件。
五、归纳小结
高中数学
打印版 高中数学
打印版 高中数学
