2008年高考递推数列题型分类归纳解析
2008年全国各地高考试题归类评析——排列、组合、二项式定理

() 1 落实基础. 学生由于求导公式 没记 住 , 忽视定义域 , 没落实导数应用于求单 调性 、 最值 问题 等而导 致 了本题 的
失分 , 因此要继续 落实“ 三基 ” 动摇 , 不 重视高 三课堂 教学 、 复习 的有效性. 住主干知识 的支撑作用 , 抓 体会 基础知识 中
力之所在 , 有数学思维就失去 了数学味. 没 每一个数学 问题
4 教学启示 作为新课程改革高考 方案实施 前 的最后 一年 高考 , 进
一
步 向一线数学教师传递 了这样 一个信 息 : 师一定 要在 教
钻研教学 内容上下功夫 , 最重要 的是对数学精 神 的理解 , 对 数学本质的认 识. 优质 的教学不是盲 目地让学 生多做题 , 而 在于使学生领悟数学知识 的本质. 当我们静 下 心来好 好反 思时 , 发现 2 0 年 浙江省 数学高 考理科 试题 的第 2 08 1题其 实无非是 由 3个部分构成 的 : 1部分 以导数为工具 , 第 求含 参数 函数的单调区间 ; 2部 分是考 查导 数的应 用之 求含 第 参数 函数 的最值问题 ; 3部 分是解 有关 分段 函数 的不等 第 式 问题. 而这 3个部分 所代表 的题 目学生 肯定 也重 点训练
学生思维严谨性 的有效载体
●蒋 荣清
2 0 高考 刚 落下 帏幕 , 0 8年 数学 中排 列 、 组合 与 二项 式
定理又考了哪些内容?需要 哪些解题 策略?有 哪些 新的特 点?给 2 0 09年高考复 习又有何 启示 ?本文就 这几 个 问题
作一简单分析.
纵观近几年高考试 题 , 排列 、 组合 与二项式定 理这部分
20 全 国 各 地 高 考 试 题 归 类 评 析 8年 0
2008年高考数学考试试题分类汇编——数列

2008年高考数学试题分类汇编数列一. 选择题:1.(全国一5)已知等差数列{}n a 满足244a a +=,3510a a +=,则它的前10项的和10S =( C )A .138B .135C .95D .232.(上海卷14) 若数列{a n }是首项为1,公比为a -32的无穷等比数列,且{a n }各项的和为a ,则a 的值是(B )A .1B .2C .12D .543.(北京卷6)已知数列{}n a 对任意的*p q ∈N ,满足p q p q a a a +=+,且26a =-,那么10a 等于( C )A .165-B .33-C .30-D .21-4.(四川卷7)已知等比数列()n a 中21a =,则其前3项的和3S 的取值范围是(D ) (A)(],1-∞- (B)()(),01,-∞+∞(C)[)3,+∞ (D)(][),13,-∞-+∞5.(天津卷4)若等差数列{}n a 的前5项和525S =,且23a =,则7a =B (A )12 (B )13 (C )14 (D )156.(江西卷5)在数列{}n a 中,12a =, 11ln(1)n n a a n+=++,则n a = AA .2ln n +B .2(1)ln n n +-C .2ln n n +D .1ln n n ++ 7.(陕西卷4)已知{}n a 是等差数列,124a a +=,7828a a +=,则该数列前10项和10S 等于( B )A .64B .100C .110D .1208.(福建卷3)设{a n }是公比为正数的等比数列,若n 1=7,a 5=16,则数列{a n}前7项的和为CA.63B.64C.127D.1289.(广东卷2)记等差数列{}n a 的前n 项和为n S ,若112a =,420S =,则6S =( D ) A .16B .24C .36D .4810.(浙江卷6)已知{}n a 是等比数列,41252==a a ,,则13221++++n n a a a a a a =C (A )16(n --41) (B )16(n --21) (C )332(n --41) (D )332(n --21) 11.(海南卷4)设等比数列{}n a 的公比2q =,前n 项和为n S ,则42S a =( C ) A. 2B. 4C.152D.172二. 填空题:1.(四川卷16)设等差数列{}n a 的前n 项和为n S ,若4510,15S S ≥≤,则4a 的最大值为______4_____。
2008届高考数学概念方法题型易误点技巧总结(三)数列

2008届高考数学概念方法题型易误点技巧总结(三)数列1、数列的概念:数列是一个定义域为正整数集N*(或它的有限子集{1,2,3,…,n })的特殊函数,数列的通项公式也就是相应函数的解析式。
如A B C D 2.等差数列的有关概念:(1)等差数列的判断方法:定义法1(n n a a d d +-=为常数)或11(2)n n n n a a a a n +--=-≥。
如(2)等差数列的通项:1(1)n a a n d =+-或()n m a a n m d =+-。
如(3)等差数列的前n 和:1()2n n n a a S +=,1(1)2n n n S na d -=+。
如(4)等差中项:若,,a A b 成等差数列,则A 叫做a 与b 的等差中项,且2a bA +=。
提醒:(1)等差数列的通项公式及前n 和公式中,涉及到5个元素:1a 、d 、n 、n a 及n S ,其中1a 、d 称作为基本元素。
只要已知这5个元素中的任意3个,便可求出其余2个,即知3求2。
(2)为减少运算量,要注意设元的技巧,如奇数个数成等差,可设为…,2,,,,2a d a d a a d a d --++…(公差为d );偶数个数成等差,可设为…,3,,,3a d a d a d a d --++,…(公差为2d )3.等差数列的性质:(1)当公差0d ≠时,等差数列的通项公式11(1)n a a n d dn a d =+-=+-是关于n 的一次函数,且斜率为公差d ;前n 和211(1)()222n n n d dS na d n a n -=+=+-是关于n 的二次函数且常数项为0. (2)若公差0d >,则为递增等差数列,若公差0d <,则为递减等差数列,若公差0d =,则为常数列。
(3)当m n p q +=+时,则有q p n m a a a a +=+,特别地,当2m n p +=时,则有2m n p a a a +=.如 (4) 若{}n a 、{}n b 是等差数列,则{}n ka 、{}n n ka pb + (k 、p 是非零常数)、*{}(,)p nq a p q N +∈、232,,n n n n n S S S S S -- ,…也成等差数列,而{}n a a 成等比数列;若{}n a 是等比数列,且0n a >,则{lg }n a 是等差数列. 如(5)在等差数列{}n a 中,当项数为偶数2n 时,S S nd =偶奇-;项数为奇数21n -时,S S a -=奇偶中,21(21)n S n a -=-⋅中(这里a 中即n a );:(1):奇偶S S k k =+。
分式递推

第十讲:分式递推分式递推数列特指数列{a n }:a 1=t,a n+1=.其通项求解有如下四种类型.1.基本类型(Ⅰ)例1:(2008年陕西高考试题)(理)己知数列{a n }的首项a 1=53,a n+1=123+n na a ,n=1,2,…. (Ⅰ)求{a n }的通项公式; (Ⅱ)证明:对任意的x>0,a n ≥)32()1(1112x x x n -+-+,n=1,2,…; (Ⅲ)证明:a 1+a 2+…+a n >12+n n . 解析:(Ⅰ)由a n+1=123+n n a a ⇒3213111+⋅=+n n a a ⇒)11(31111-=-+n n a a ⇒n a 1-1=2(31)n ⇒a n =233+n n ; (Ⅱ)令f(x)=)32()1(1112x x x n -+-+⇒f '(x)=-2422)1()32(2)1()1(2)32()1()1(1x x x x x x x n n +-=++⋅--+--+⇒f(x)的最大值=f(n 32)=a n ; (Ⅲ)令{b n }的前n 项和为12+n n ,则b n =)1(1)1(+-+n n n n =1-)1(1+n n ,因a n =233+n n =1-232+n ,所以,a n >b n ⇔)1(1+n n >232+n⇔3n+2>2n(n+1),令g(x)=3x+2-2(x 2+x)(x ≥3)⇒g '(x)=3xln3-2(2x+1)⇒g ''(x)=3xln 23-4>0⇒g '(x)≥g '(3)>0⇒g(x)≥g(3)>0⇒当n ≥3时,a n >b n 且g(1)+g(2)>0⇒a 1+a 2>b 1+b 2,所以,a 1+a 2+…+a n >12+n n . [思想方法]:数列{a n }:a 1=x,a n+1=c ba aa n n +的通项,可由a n+1=c ba aa n n +两边取倒数得:11+n a =c n a 1+ab,通过换元x n =n a 1得:x n+2=cx n +a b ,由此求解.一般地,如果x n =n a 1,则x n+2=px n +f(n)⇔a n+1=pa n f a n n+)(.类题:1.(2008年陕西高考试题)(文)己知数列{a n }的首项a 1=32,a n+1=12+n n a a ,n=1,2,….(Ⅰ)证明:数列{n a 1-1}是等比数列; (Ⅱ)求数列{na n}的前n 项和S n . 2.(2006年江西高考试题)己知数列{a n }满足:a 1=23,且a n =12311-+--n a na n n (n ≥2,n ∈N*).(Ⅰ)求数列{a n }的通项公式;(Ⅱ)证明:对一切正整数n,不等式a 1a 2…a n <2×n!恒成立.2.基本类型(Ⅱ)例2:(原创题)己知数列{a n }:a 1=2,a n+1=1223--n n a a .(Ⅰ)求{a n }的通项公式; (Ⅱ)证明:a 1a 2…a n >12+n .解析:(Ⅰ)因数列{a n }的特征方程x=1223--x x 只有一根x=1.故由a n+1=1223--n n a a ⇒111-+n a =112231---n n a a ⇒111-+n a =112--n n a a⇒111-+n a =11-n a +2.令b n =11-n a ⇒⎪⎪⎩⎪⎪⎨⎧-==-=++111111111n n a b a b ⇒b n+1=b n +2⇒{b n }是以b 1=1为首项公差为2的等差数列⇒b n = 2n-1⇒11-n a =2n-1⇒a n =1+121-n ;(Ⅱ)令数列{x n }的前n 项的积为12+n ⇒x 1=3,x n+1=1232++n n ⇒x n =1212-+n n .而a n >x n ⇔1+121-n >1212-+n n ⇔122-n n>1212-+n n ⇔122-n n >12+n ⇔2n>1)2(2-n ,这是显然成立的,故a n >x n >0⇒a 1a 2…a n >x 1x 2…x n =12+n .[思想方法]:若数列{a n }:a 1=x,a n+1=c ba aa n n+的特征方程=x 只有一根α,则数列{}是以α-t 1为首项,公差为的等差数列,特别地,当α=1时,a n =1+ban +1. 类题:1.(原创题)数列{a n }满足:a 1=2,a n+1=2334--n n a a .(Ⅰ)求数列{a n }的通项公式; (Ⅱ)求证:a 1a 2…a n >313+n . 2.(2008年佛山第一次质检试题)数列{a n }满足:a 1=21,a n+1=n a -21.(Ⅰ)求数列{a n }的通项公式; (Ⅱ)设数列{a n }的前n 项和为S n ,证明:S n <n-ln(22+n ). 3.基本类型(Ⅲ)例3:(2007年全国I 高考试题)己知数列{a n }中,a 1=2,a n+1=(2-1)(a n +2),n=1,2,3,….(Ⅰ)求{a n }的通项公式; (Ⅱ)若数列{b n }中,b 1=2,b n+1=3243++n nb b,n=1,2,3,….证明:2<b n ≤a 4n-3,n=1,2,3,….解析:(Ⅰ)a n+1=(2-1)(a n +2)⇒a n+1-2=(2-1)(a n -2),所以,数列{a n -2}是以a 1-2=2-2=2(2-1)为首项,以2-1为公比的等比数列⇒a n -2=2(2-1)(2-1)n-1=2(2-1)n ⇒a n =2(2-1)n+2;(Ⅱ)令f(x)=3243++x x ,由f(x)=x 得x=±2,所以22223223)234()223()234()223(23243232432211+-⋅+-=+++-+-=+++-++=+-++n n n n n n n n n n b b b b b b b b b b =(2-1)422+-⋅n n b b , 所以,数列{22+-n n b b }是以为(2-1)2首项,公比为(2-1)4的等比数列⇒22+-n n b b =(2-1)4n-2⇒b n =22424)12(1)12(1-----+n n . 首先,2<b n ⇔2<22424)12(1)12(1-----+n n ⇔1-(2-1)4n-2<1+(2-1)4n-2⇔2(2-1)4n-2>0;其次,b n ≤a 4n-3⇔22424)12(1)12(1-----+n n≤2(2-1)4n-3+2⇔2424)12(1)12(1-----+n n ≤(2-1)4n-3+1(令(2-1)4n-2=t,则t ∈(0,1))⇔tt-+11≤(2+1)t+1⇔0≤t ≤ (2-1)2.[思想方法]:数列{a n }满足:a 1=t,a n+1=,若特征方程=x 有两根α,β,则数列{}是以βα--t t 为首项,公比为βαb t b t --的等比数列. 类题:1.(2005年重庆高考试题)数列{a n }满足:a 1=1,且8a n+1a n -16a n+1+2a n +5=0(n ≥1).记b n =211-n a (n ≥1).(Ⅰ)求b 1,b 2,b 3,b 4的值; (Ⅱ)求数列{b n }的通项公式及数列{a n b n }的前n 项和S n . 2.(2006年江西高考试题)己知各项均为正数的数列{a n }满足:a 1=3,且1122++--n n nn a a a a =a n a n+1,n ∈N*.(Ⅰ)求数列{a n }的通项公式;(Ⅱ)设S n =a 12+a 22+…+a n 2,T n =211a +221a +…+21n a ,求S n +T n ,并确定最小正整数n,使S n +T n 为整数.4.基本类型(Ⅳ)例4:(2010年全国高中数学联赛江苏初赛试题)设复数列{x n }满足x n ≠a-1,0,且x n+1=1+n nx ax .若对任意n ∈N +都有x n+3=x n , 则a 的值是 .解析:由x n+1=1+n n x ax ⇒x n+3=122+++n n x ax =1)1(112++++n n x a x a =1)1(23+++n n x a a x a =x n 恒成立,即a 3=(a 2+a+1)x n +1⇒因为x n ≠a-1,或0,故a 2+a+1=0⇒a=231i ±-.[思想方法]:数列{a n }满足:a 1=t,a n+1=,若特征方程=x 无实根,则数列{a n }是周期数列. 类题:1.①(2011年第22届希望杯全国数学邀请赛高一试题)已知数列{a n }满足a 1=2,a n+1=-11+n a ,则a 2010的值为______. ②(2005年全国高中数学联赛河南初赛试题)数列{a n }中,a 1=2,a n+1=nna a -+11,则a 2005的值为____________. ③(2004年第15届希望杯全国数学邀请赛高二试题)数列{a n }中,a 1=1,a n+1=313+-n n a a (其中n ∈N*),a 2004= .2.(2009年全国高中数学联赛四川初赛试题)设数列{a n }满足:a 1=2,a n+1=1-na 1.记数列{a n }的前n 项之积为P n ,则P 2009的值为 .5.换元技巧例5:(2005年重庆高考试题)数列{a n }满足:a 1=1,且8a n+1a n -16a n+1+2a n +5=0(n ≥1).记b n =211-n a (n ≥1).(Ⅰ)求b 1,b 2,b 3,b 4的值;(Ⅱ)求数列{b n }的通项公式及数列{a n b n }的前n 项和S n .解析:(Ⅰ)由8a n+1a n -16a n+1+2a n +5=0⇒a n+1=16852+-+n n a a ,令16852+-+x x =x 得x=21,45.所以,452111--++n n a a =45168522116852-+-+-+-+a a a a n n = ⋅214521--nn a a ⇒4521--n n a a =-2(21)n-1⇒a n =1)21(221)21(51++-n n =n n 24251++-⇒b n =211-n a =32(2n-1+2)⇒b 1=2,b 2=38,b 3=4,b 4=320; (Ⅱ)由b n =211-n a ⇒b n (a n -21)=1⇒a n b n =21b n +1=31×2n-1+35⇒S n =31(2n -1)+35n. 另解:由b n =211-n a ⇒b 1=2,且a n =n b 1+21⇒a n+1=11+n b +21,代入8a n+1a n -16a n+1+2a n +5=0得:8(11+n b +21)(n b 1+21)-16(11+n b +21)+2(n b 1+21)+5=0⇒4+3b n+1=6b n ⇒b n+1-34=2(b n -34)⇒数列{b n -34}是以32为首项,公比为2的等比数列⇒b n -34=32×2n-1⇒b n =32(2n-1+2)⇒b 1=2,b 2=38,b 3=4,b 4=320.[思想方法]:数列{a n }满足:a 1=t,a n+1=,若特征方程=x 有两个实根α,β⇒α+β=cd a -,αβ=-cb .40 第十讲:分式递推令b n =α-n a 1⇒b n+1=α-+11n a ⇒11+n b +α=d b c b b a nn ++++)1()1(αα⇒(c α-a)b n+1+(c α+d)b n +c=0,从而转化为线性递推数列. 类题:1.(原创题)己知数列{a n }满足:a 1=1,a n+1=122++n n a a .记b n =11+n a . (Ⅰ)求数列{b n }的通项公式b n ; (Ⅱ)求数列{nb n }的前n 项和S n .2.(2009年全国高中数学联赛陕西初赛试题)数列{a n }满足:a 1=4,a n+1a n +6a n+1-4a n -8=0,记b n =26-n a ,n ∈N *.(Ⅰ)求数列{b n }的通项公式; (Ⅱ)求数列{a n b n }的前n 项和S n .6.通项不等式例6:(2005年辽宁高考试题)己知函数f(x)=13++x x (x ≠-1).设数列{a n }满足:a 1=1,a n+1=f(a n ),数列{b n }满足:b n =|a n - 3|,S n =b 1+b 2+…+b n (n ∈N*).(Ⅰ)证明:b n ≤12)13(--n n; (Ⅱ)证明:S n <332. 解析:(Ⅰ)令f(x)=x ⇒x=3±,由3331313133133)(3)(3311+-⋅+-=+++-++=+-=+-++n n n n n n n n n n a a a a a a a f a f a a =-(2-3)33+-n n a a ⇒33+-n n a a =(3-2)n⇒a n =3nn )23(1)23(1---+⇒b n =|a n -3|=3|nn )23(1)23(2---|,所以,b n ≤12)13(--n n⇔3|nn )23(1)23(2---|≤12)13(--n n⇔3×2n (2-3)n≤(3-1)n|1-(3-2)n|⇔3(3-1)2n≤(3-1)n|1-(3-2)n|⇔3(3-1)n≤|1-(3-2)n|⇔3(3-1)n≤1-(2-3)n(n 为偶数)⇔3(3-1)n+(2-3)n≤1⇔3(3-1)2+(2-3)2≤1;(Ⅱ)由(I)知b n ≤12)13(--n n=21n )213(-⇒S n <21[213-+(213-)2+…+(213-)n ]=21[2131)213(1213-----n]<332. 另解:由a n+1=f(a n )=13++n n a a ⇒a n+1=1+12+n a ≥1,b n+1=|a n+1-3|=|13++n n a a -3|=113+-n a |a n -3|≤213-b n ⇒b n ≤ 213-b n-1≤(213-)2b n-2≤…≤(213-)n-1b 1=12)13(--n n. [思想方法]:数列{a n }满足:a 1=t,a n+1=,特征方程=x.若特征方程有两个实根α,β⇒α+β=c d a -,αβ=-cb.令b n =|a n -α|⇒b n+1=|a n+1-α|=|-α|=||||d ca d c n ++β|a n -α|=||||d ca d c n ++βb n .若||||d ca d c n ++β≤M,则b n ≤M n-1b 1.类题:1.(原创题)己知数列{a n }满足:a 1=2,a n+1=3243++n n a a ,数列{b n }满足:b n =|a n -2|,S n =b 1+b 2+…+b n (n ∈N*).(Ⅰ)证明:b n ≤2(2-1)4n-3; (Ⅱ)证明:S n <412+. 2.(原创题)己知数列{a n }满足:a 1=2,a n+1=124+-n n a a ,数列{b n }满足:b n =|a n -1|,S n =b 1+b 2+…+b n (n ∈N*). (Ⅰ)证明:b n ≤3n-1(2-1)n; (Ⅱ)证明:S n ≤22×3n ×(2-1)n-1.。
高考数列试题解析

前台后库2008年数列大题难易排序数列是高考解答题必考的,看看2008年的各地高考试卷,数列占据着重要的位置,有多份试卷用数列作为试卷的压轴大题,算是“镇卷之宝”吧!总体看来,数列在高考试卷解 答题中算是居后的位置,起着区分、选拔考生的功能1. (江西卷19)(本小题满分12分) 数列{a n }为等差数列, a n 为正整数,其前n 项和为S n ,数列{b n }为等比数列,且a ! 3力 1,数列{b a n}是公比为64的等比数列,b ?S 2 64.(1)求 a n ,b n ;1 1 13 (2)求证—LS S 2S n4【说明】 只要静下心来做,相信一般的学生都可以做出来,考查了等差、等比数列的基础 知识.第一问相比而言,比第二问还要复杂一些,求数列{ b n }时拐了一道弯,但只要按步骤来, 问题会迎刃而解.这对占在三号位置的解答题来说,可以稳定学生的情绪.这也算是江西学生{b n }的公比为q ,则d 为正整数,a n 3(n n 11)d , b n qb a n13 ndq dq依题意有 b a n3 (n 1)dqS 2&2 (6 d)q 由(6 d)q 64知q 为正有理数解①得 d 2,q 8故a n 3 2(n 1) 2n 1,b n (2)S n3 5 L (2n1) .1 1 L1 1SS 2S n 1 321 1 1 1 1 1L (12 3 2 4 3 51 “ 1 1 1 、 3 (1)2 2 n 1 n 2 4 6464,故 8n1 n(n 26①d 为6的因子1,2,3,6之一,2)1n(n 2)解:(1) 设{a n }的公差为d ,又 a ? a 1 3 a i . 的幸运哦.2. (全国二20).(本小题满分12分) 设数列a n 的前n 项和为S n .已知a 1a , a n 1 S n 3n , n N(I )设b n S n 3n ,求数列b n 的通项公式;因此,所求通项公式为于是,当n > 2时,综上,所求的a 的取值范围是 9,(n)若 a n 1》a n , n 求a 的取值范围.解:(I )依题意,S n 1 S n a n 1 S n 3,即 S n 1 2S n 3,由此得 S n 1 3“ ’ 2(S n 3n)b n S n 3n (a 3)2n 1.①(n)由①知S n 3n(an 13)2a n S nS n 13n (a 3) (a 3)2na n 12n3n1(a3)2n 2, a n3n1n 2(a 3)2a n 1》a n12gf2a 3> 012分【说明】本题主要考查数列通项公式的求法、等比数列前n项和公式以及数列单调性的应用作为倒数第三题,在大题中算是占据了中等的地位,起到过渡的作用•比起其他试卷的数列解答题,算是容易题了3.(四川卷20).(本小题满分12分)设数列a n的前n项和为S n ,已知ba n 2n b 1 S n(i)证明:当b 2时,a n n 2n 1是等比数列;(n)求a n的通项公式.解:由题意知a12,且ba n2n byn 1ba n 1 2 b 1 S n 1两式相减得b a n 1 a n 2n b 1 a n 1即a n 1 ba n 2n①(i)当b 2时,由①知a n 1 2a n 2n于是a n 1n 1 2n2a n2n n 1 2n2 a n n 2n 1又a1 1 2n 1 1 0,所以a n n 2n 1是首项为1,公比为2的等比数列。
2008年全国各地高考数学试题及解答分类汇编大全(06数列)

an
4n
5 2
, a1
a2
an
an2
bn
,n
N*
,其
中 a, b 为常数,则 ab -1
2.(2008
安徽理)在数列 {an } 在中,
an
4n
5 2
, a1
a2
an
an2
bn
,n
N*
,其
an bn
中
a,
b
为常数,则
lim
n
an
bn
的值是
1
3.(2008 海南、宁夏文)已知{an}为等差数列,a3 + a8 = 22,a6 = 7,则 a5 = ___15__
∴0 c 1
2.(2008 安徽理)设数列an 满足 a0 0, an1 can3 1 c, c N *, 中 中 c 为实数
(Ⅰ)证明: an [0,1] 对任意 n N * 成立的充分必要条件是 c [0,1];
(Ⅱ)设 0
c
1 3
,证明: an
1 (3c)n1, n
N* ;
(Ⅲ)设
3.解:(Ⅰ)由于 an1 (n2 n )an (n 1, 2,), 且 a1=1, 所以当 a2=-1 时,得 1 2 , 故 3.
从而 a3 (22 2 3) (1) 3.
(Ⅱ)数列{an}不可能为等差数列.证明如下:
由 a1=1, an1 (n2 n )an 得
1 2
Sn
(1)2 2
2(1 )3 2
n( 1 )n1 2
∴1 2
Sn
1 2
(1)2 2
(1)n 2
n( 1 )n1 2
∴ Sn
2008年数学高考题分类总汇编详解(下)【超全超详细】【强烈推荐】
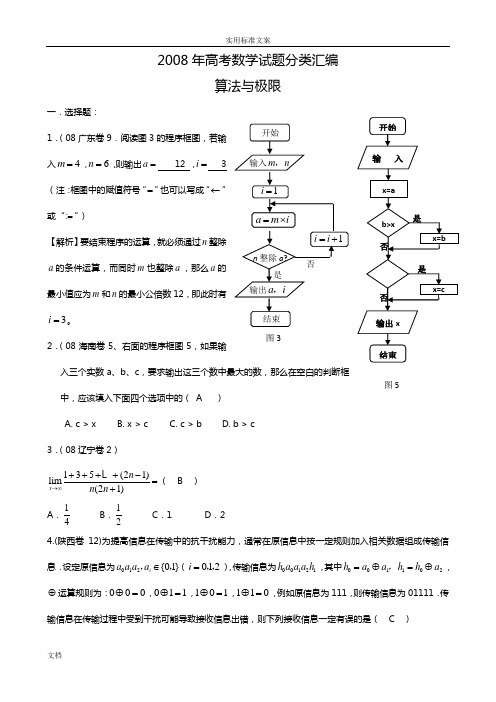
开始 1i =n 整除a ?是 输入m n ,结束 a m i =⨯输出a i ,1i i =+图3否2008年高考数学试题分类汇编算法与极限一.选择题:1.(08广东卷9.阅读图3的程序框图,若输入4m =,6n =,则输出a = 12 ,i = 3(注:框图中的赋值符号“=”也可以写成“←”或“:=”)【解析】要结束程序的运算,就必须通过n 整除a 的条件运算,而同时m 也整除a ,那么a 的最小值应为m 和n 的最小公倍数12,即此时有3i =。
2.(08海南卷5、右面的程序框图5,如果输入三个实数a 、b 、c ,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的( A ) A. c > xB. x > cC. c > bD. b > c3.(08辽宁卷2)135(21)lim(21)x n n n →∞++++-=+L ( B )A .14B .12C .1D .24.(陕西卷12)为提高信息在传输中的抗干扰能力,通常在原信息中按一定规则加入相关数据组成传输信息.设定原信息为012i a a a a ,{01}∈,(012i =,,),传输信息为00121h a a a h ,其中001102h a a h h a =⊕=⊕,,⊕运算规则为:000⊕=,011⊕=,101⊕=,110⊕=,例如原信息为111,则传输信息为01111.传输信息在传输过程中受到干扰可能导致接收信息出错,则下列接收信息一定有误的是( C )是否 开始输入x=ab>x 输出x结束 x=b x=c否 是图5A .11010B .01100C .10111D .00011二.填空题:1.(08湖南卷11)211lim ______34x x x x →-=+-.15 2.(08江西卷11)211lim ______34x x x x →-=+-.153.(08山东卷13)执行右边的程序框图6,若p =0.8,则输出的n = 4 .4.(08陕西卷13)(1)1lim2n a n n a∞++=+→,则a = .15.(08重庆卷12)已知函数f(x)=(当x ≠0时) ,点在x =0处连续,则2221lim x an a n n →∞+=+ . 13图62008年高考数学试题分类汇编直线与圆一.选择题:1.(08上海卷15)如图,在平面直角坐标系中,Ω是一个与x 轴的正半轴、y 轴的正半轴分别相切于点C 、D 的定圆所围成的区域(含边界),A 、B 、C 、D 是该圆的四等分点.若点()P x y ,、点()P x y ''',满足x x '≤且y y '≥,则称P 优于P '.如果Ω中的点Q 满足:不存在Ω中的其它点优于Q ,那么所有这样的点Q 组成的集合是劣弧( D )A.弧AB B .弧BC C .弧CD D .弧DA2.(08全国一10)若直线1x ya b+=通过点(cos sin )M αα,,则( D ) A .221a b +≤ B .221a b +≥ C .22111a b +≤ D .22111a b +≥3.(08全国二5)设变量x y ,满足约束条件:222y x x y x ⎧⎪+⎨⎪-⎩,,.≥≤≥,则y x z 3-=的最小值( D )A .2-B .4-C .6-D .8-4.(08全国二11)等腰三角形两腰所在直线的方程分别为20x y +-=与740x y --=,原点在等腰三角形的底边上,则底边所在直线的斜率为( A )A .3B .2C .13-D .12- 5.(08北京卷5)若实数x y ,满足1000x y x y x ⎧-+⎪+⎨⎪⎩,,,≥≥≤则23x yz +=的最小值是( B )AB CD O xyΩA .0B .1C .3D .96.(08北京卷7)过直线y x =上的一点作圆22(5)(1)2x y -+-=的两条切线12l l ,,当直线12l l ,关于y x =对称时,它们之间的夹角为( C )A .30oB .45oC .60oD .90o7.(08四川卷4)直线3y x =绕原点逆时针旋转090,再向右平移1个单位,所得到的直线为( A ) (A)1133y x =-+ (B)113y x =-+ (C)33y x =- (D)113y x =+ 8.(08天津卷2)设变量y x ,满足约束条件⎪⎩⎪⎨⎧≥+≤+≥-1210y x y x y x ,则目标函数y x z +=5的最大值为D(A )2 (B )3 (C )4 (D )59.(08安徽卷8).若过点(4,0)A 的直线l 与曲线22(2)1x y -+=有公共点,则直线l 的斜率的取值范围为( C )A .[3,3]-B .(3,3)-C .33[,]33-D .33(,)33-10.(08山东卷11)已知圆的方程为08622=--+y x y x .设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为B(A )106 (B )206 (C )306 (D )40611.(08山东卷12)设二元一次不等式组⎪⎩⎪⎨⎧≤-+≥+-≥-+0142,080192y x y x y x ,所表示的平面区域为M ,使函数y =a x (a >0,a ≠1)的图象过区域M 的a 的取值范围是C(A )[1,3] (B)[2,10] (C)[2,9] (D)[10,9]12.(08湖北卷9)过点(11,2)A 作圆22241640x y x y ++--=的弦,其中弦长为整数的共有CA.16条B. 17条C. 32条D. 34条13.(08湖南卷3)已知变量x 、y 满足条件1,0,290,x x y x y ≥⎧⎪-≤⎨⎪+-≤⎩则x y +的最大值是( C )A.2B.5C.6D.814.(08陕西卷5)直线30x y m -+=与圆22220x y x +--=相切,则实数m 等于( C )A .3或3-B .3-或33C .33-或3D .33-或3315.(08陕西卷10)已知实数x y ,满足121y y x x y m ⎧⎪-⎨⎪+⎩≥,≤,≤.如果目标函数z x y =-的最小值为1-,则实数m 等于( B ) A .7B .5C .4D .316.(08重庆卷3)圆O 1:0222=-x y x +和圆O 2: 0422=-y y x +的位置关系是B(A)相离(B)相交(C)外切 (D)内切17.(08辽宁卷3)圆221x y +=与直线2y kx =+没有..公共点的充要条件是( C ) A .(22)k ∈-, B .(2)(2)k ∈--+U ∞,,∞ C .(33)k ∈-,D .(3)(3)k ∈--+U ∞,,∞ 二.填空题:1.(08天津卷15)已知圆C 的圆心与点(2,1)P -关于直线1y x =+对称.直线34110x y +-=与圆C 相交于B A ,两点,且6=AB ,则圆C 的方程为__________________.22(1)18x y ++=2.(08全国一13)若x y ,满足约束条件03003x y x y x ⎧+⎪-+⎨⎪⎩,,,≥≥≤≤则2z x y =-的最大值为 .93.(08四川卷14)已知直线:40l x y -+=与圆()()22:112C x y -+-=,则C 上各点到l 的距离的最小值为_______。
对2008年高考数列题的评析

文科卷 中数列题分值最少 , 9分 , 为 选择题 、 填空题 各一个. 数列题分值最多 的则 是湖北 理科 卷 , 2个填 空题 , 个 解答 1 题, 分值为 2 4分. 在文 、 科各 1 份试 卷中 , 理 8 理科卷 中数列 题 压轴 的有 1 , 0份 文科 卷 中为 5份. 可见数 列题 是考查 考 生数学 能力 和数学 素养 的重要 载体 , 但对文 、 理科考生 在掌
题 量还是分值总体保 持稳定. 份试 卷 中数列 题大 多 以一 一
道小题加一道解答题 的形 式 出现 , 值在 1 左右. 分 7分 宁夏
归为新数列 { 一 ・
} { 一 ・ 一 } 重庆市数学高 和 ,;
考理 科 试 题 第 2 2题 化 为 新 数 列 { 醛 +2o ̄ 和 l 0 1 "} g
在参考 答案中虽未提 出特 征根 的概念 , 因直 接求 解难 度 但
大, 参加过数 学竞 赛训 练 的同学 得 益 明显 , 题 背 景不 公 试
平. 北京市数学高考理科试题第 2 题 , 冗长 而抽象 , O 试题 其
中的第 ( ) 3 小题颇有高等数学味. 这对教 师如何把握数列复 习中的宽度与难度带来了不小 的冲击.
fx 4 , Y ) ? =I
0 <^; < 4 z - 一 二
【 一 芋 2 譬) < ( , <
从 中可 以选 出答 案 B .
复 习建议 这类创新题要 求学生能对所学的知识 融会 贯通 , 因此一方面应扎实掌握立体几何 的知识和 方法 , 另一方 面 . 也应训练学生对 知识 的整合 和迁移. 尤其要注意常与立体几何结合 的那些知识点 , 更应重点复习. 复 习, 同时也应注意 向量在解决立 体几何 问题上 的工具性作用. 在夯 实学生基 础的同时 , 更要注重对能力的训练 和培养.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由递推数列求通项公式分类归纳解析
于泳
各种数列问题在很多情形下,就是对数列通项公式的求解。
特别是在一些综合性比较强的数列问题中,数列通项公式的求解问题往往是解决数列难题的瓶颈。
下面总结出几种求解数列通项公式的方法,希望能对大家有帮助。
类型1 )(1n f a a n n +=+
例: 数列{}n a 中满足1n n a a --=4(2)n n ≥且1a =1。
求{}n a 的通项公式。
变式: 已知数列{}n a 满足211=a ,n
n a a n n ++=+211,求n a 。
类型2 n n a n f a )(1=+ 例:已知数列{}n a 满足321=a ,n n a n n
a 1
1+=
+,求n a 。
变式:已知31=a ,n n a n n a 2
31
31+-=+ )1(≥n ,求n a 。
类型3 q pa a n n +=+1(其中p ,q 均为常数,)0)1((≠-p pq )。
例: (2006,重庆,文,14)已知数列{}n a 中,11=a ,321+=+n n a a ,求n a .
变式:(2006. 福建.理22.本小题满分14分)
已知数列{}n a 满足*111,21().n n a a a n N +==+∈(I )求数列{}n a 的通项公式;
类型4 ()n f pa a n n +=+1
(1) n n n q pa a +=+1(其中p ,q 均为常数,)0)1)(1((≠--q p pq )。
(或1n n n a pa rq +=+,
其中p ,q, r 均为常数) 。
例:已知数列{}n a 中,651=a ,1
1)2
1(31+++=n n n a a ,求n a 。
变式:(2006,全国I,理22,本小题满分12分) 设数列{}n a 的前n 项的和1412
2333
n n n S a +=-⨯+,1,2,3,n = (Ⅰ)求首项1a 与通项n a ;
(2) b an pa a n n ++=+1)001
(≠≠,a 、p 例:设数列{}n a :)2(,123,411≥-+==-n n a a a n n ,求n a .
变式:(2006,山东,文,22,本小题满分14分) 已知数列{n a }中,111
22
n n a n a a +=-、点(、)在直线y=x 上,其中n=1,2,3… 求数列{}的通项;n a
(3)21n+c n n a pa an b +=++
类型5 递推公式为n n n qa pa a +=++12(其中p ,q 均为常数)。
例:数列{}n a :),0(025312N n n a a a n n n ∈≥=+-++, b a a a ==21,,求数列{}n a 的通项公式。
变式:已知数列{}n a 中,11=a ,22=a ,n n n a a a 3
1
3212+=++,求n a 。
变式:(2006,福建,文,22,本小题满分14分)
已知数列{}n a 满足*12211,3,32().n n n a a a a a n N ++===-∈ (1)求数列{}n a 的通项公式;
类型6 递推公式为n S 与n a 的关系式。
(或()n n S f a =) 例:已知数列{}n a 前n 项和2
2
14--
-=n n n a S .
(1)求1+n a 与n a 的关系;(2)求通项公式n a .
变式:(2006,陕西,理,20本小题满分12分) 已知正项数列{a n },其前n 项和S n 满足10S n =a n 2+5a n +6且a 1,a 3,a 15成等比数列,求数列{a n }的通项a n
类型8 r
n n pa a =+1)0,0(>>n a p
例:已知数列{n a }中,2
111,1n n a a
a a ⋅=
=+)0(>a ,求数列{}.的通项公式n a
变式:(2005,江西,理,21.本小题满分12分) 已知数列:,}{且满足的各项都是正数n a .),4(2
1
,110N n a a a a n n n ∈-==+ 求数列}{n a 的通项公式a n .
类型9 1
1n n n pa a qa r
--=
+(2)n p q r ≥且、、为常数
例:已知数列{a n }满足:1,1
3111
=+⋅=--a a a a n n n ,求数列{a n }的通项公式。
变式:数列{}n a 中满足1
1
626n n n a a a --=
+ (2)n ≥,1a =1。
求{}n a 的通项公式。
变式:(2006,江西,理,22,本大题满分14分) 已知数列{a n }满足:a 1=
32,且a n =n 1n 13na n 2n N 2a n 1
*≥∈--(,)+- (1) 求数列{a n }的通项公式;
求解通项公式专题训练 1数列{}n a 中满足11(2)1
n n a n n a n -+=≥- ,1a =1。
求{}n a 的通项公式。
2数列{}n a 中满足134n n a a --= (2)n ≥,1a =1。
求{}n a 的通项公式
3数列{}n a 中满足12n n a a n -+= (2)n ≥,1a =1 。
求{}n a 的通项公式。
5数列{}n a 中满足134n n n a a --= (2)n ≥,1a =1。
求{}n a 的通项公式。
6数列{}n a 中满足1364n n a a n --=- (2)n ≥,1a =3。
求{}n a 的通项公式。
7数列{}n a 中满足1
1
224n n n a a a --=+ (2)n ≥,1a =1。
求{}n a 的通项公式。
8数列{}n a 中满足1134n n n a a a +-=+ (2)n ≥,1a =1,2a =3。
求{}n a 的通项公式。
复习巩固
1)数列{}n a 中满足1n n a a --=
1
(2)(1)
n n n ≥+且1a =1。
求{}n a 的通项公式。
2)数列{}n a 中满足1
3(2)n n
n a n a -=≥ ,1a =1。
求{}n a 的通项公式。
3)数列{}n a 中满足1236n n a a --= (2)n ≥,1a =1。
求{}n a 的通项公式;
4)数列{}n a 中满足121n n a a n -+=+ (2)n ≥,1a =1 。
求{}n a 的通项公式。
6)数列{}n a 中满足1434n n n a a --=⨯ (2)n ≥,1a =1。
求{}n a 的通项公式。
7)数列{}n a 中满足1323n n a a n --=- (2)n ≥,1a =1。
求{}n a 的通项公式。
8)数列{}n a 中满足1
1
343n n n a a a --=+ (2)n ≥,1a =1。
求{}n a 的通项公式。
9)数列{}n a 中满足1123n n n a a a +-=+ (2)n ≥,1a =1,2a =3。
求{}n a 的通项公式。
