2013-2014学年八年级数学上册期末测试题(2)

合集下载

2013-2014学年北师大版八年级数学上册期中检测题(含答案)

八年级数学上册期中检测题本检测题满分：120分，时间：120分钟一、选择题（每小题3分，共30分）1.下列说法正确的是( )①0是绝对值最小的有理数； ②相反数大于本身的数是负数；③数轴上原点两侧的数互为相反数； ④2是有理数.A.①②B.①③C.①②③D.①②③④2.下列四个实数中，绝对值最小的数是（）A ．-5B ．-2C ．1D ．43.估计6+1的值在（）A ．2到3之间B ．3到4之间C ．4到5之间D ．5到6之间4.文文设计了一个关于实数运算的程序，按此程序，输入一个数后，输出的数比输入的数的平方小1，若输入7，则输出的结果为（）A ．5B ．6C ．7D ．85.满足下列条件的三角形中，不是直角三角形的是（）A.三内角之比为1∶2∶3B.三边长的平方之比为1∶2∶3C.三边长之比为3∶4∶5D.三内角之比为3∶4∶56.已知直角三角形两边的长分别为3和4，则此三角形的周长为（）A ．12B ．7＋7C ．12或7＋7D ．以上都不对7.如图，梯子AB 靠在墙上，梯子的底端A 到墙根O 的距离为2 m ，梯子的顶端B 到地面的距离为7 m ，现将梯子的底端A 向外移动到A ′，使梯子的底端A ′到墙根O 的距离等于3m ，同时梯子的顶端B 下降至B ′，那么BB ′（）A ．小于1 mB ．大于1 mC ．等于1 mD ．小于或等于1 m第7题图第8题图8.将一根24 cm 的筷子置于底面直径为15 cm ，高为8 cm 的圆柱形水杯中，如图所示，设筷子露在杯子外面的长度为h cm ，则h 的取值范围是（）A ．h ≤17B ．h ≥8C ．15≤h ≤16D ．7≤h ≤169.若点)3,(x A 与点),2(y B 关于x 轴对称,则( )A. x = -2, y =-3B.x =2, y =3C.x =-2, y =3D. x =2, y =-310.在平面直角坐标系中，△A BC 的三个顶点坐标分别为A （4，5），B （1，2），C （4，2），将△ABC 向左平移5个单位长度后，A 的对应点A 1的坐标是（）A ．（0，5）B ．（-1，5）C ．（9，5）D ．（-1，0）二、填空题（每小题3分，共24分）11.如果将电影票上“6排3号”简记为，那么“10排10号”可表示为；表示的含义是 .12.（2013·宁夏中考）点 P （a ，a －3）在第四象限，则a 的取值范围是 .13.（2013·贵州遵义中考）已知点P （3，－1）关于y 轴的对称点Q 的坐标是（a +b ，1－b ），则a b 的值为__________.14.已知在灯塔的北偏东的方向上，则灯塔在小岛的________的方向上.15.在△ABC 中，，，，则△ABC 是_________.16.已知直角三角形的两直角边长分别为和，则斜边上的高为 .17.若),(b a A 在第二、四象限的角平分线上, a 与b 的关系是_________.18.若10的整数部分为a ，小数部分为b ，则a ＝________，b ＝_______. 三、解答题（共66分）19.(8分)如图，已知等腰△的周长是，底边上的高的长是，求这个三角形各边的长.20.（8分）计算：（1）44.1-21.1；（2）2328-+；（3（4）0)31(33122-++；（5）2)75)(75(++-；（6）2224145-. 21.（8分）某个图形上各点的横坐标不变,纵坐标变为原来的相反数,•此时图形却未发生任何改变,你认为可能吗?22.（8分）在平面直角坐标系中,顺次连接A (-2,1),B (-2,-1),C (2,-2),D (2,3)各点,你会得到一个什么图形?试求出该图形的面积.23．（8分）已知a 31-和︱8b －3︱互为相反数，求()2-ab －27 的值.24.（8分）阅读下列解题过程：已知为△的三边长，且满足，试判断△的形状．解：因为， ① 所以. ② 所以． ③ 所以△是直角三角形. ④回答下列问题：（1）上述解题过程，从哪一步开始出现错误?该步的序号为；（2）错误的原因为；（3）请你将正确的解答过程写下来.25.（8分）观察下列勾股数：C第19题图根据你发现的规律，请写出：（1）当时，求的值；（2）当时，求的值；（3）用（2）的结论判断是否为一组勾股数，并说明理由．26.（10分）一架云梯长25 m，如图所示斜靠在一面墙上，梯子底端C离墙7 m.（1）这个梯子的顶端A距地面有多高？（2）如果梯子的顶端下滑了4 m，那么梯子的底部在水平方向也是滑动了4 m吗？第26题图。

2013-2014学年北京市八年级上学期期末经典题汇编数学试题(含答案)

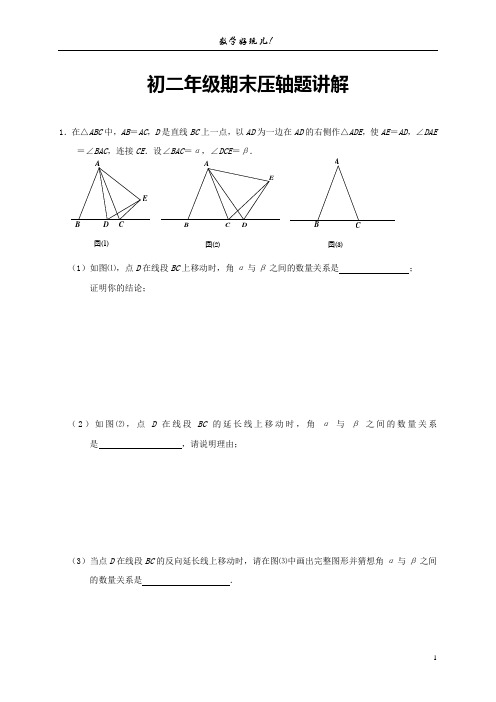
初二年级期末压轴题讲解1．在△ABC 中，AB ＝AC ，D 是直线BC 上一点，以AD 为一边在AD 的右侧作△ADE ，使AE ＝AD ，∠DAE＝∠BAC ，连接CE ．设∠BAC ＝α，∠DCE ＝β．（1）如图⑴，点D 在线段BC 上移动时，角α与β之间的数量关系是；证明你的结论；（2）如图⑵，点D 在线段BC 的延长线上移动时，角α与β之间的数量关系是，请说明理由；（3）当点D 在线段BC 的反向延长线上移动时，请在图⑶中画出完整图形并猜想角α与β之间的数量关系是．图⑴图⑵图⑶AD C EBBCAAD C EB2．已知：如图，在平面直角坐标系xOy 中，(2,0)A -，(0,4)B ，点C 在第四象限，AC ⊥AB ， AC=AB ．（1）求点C 的坐标及∠COA 的度数；（2）若直线BC 与x 轴的交点为M ，点P 在经过点C 与x 轴平行的直线上，直接写出BOM POM S S ∆∆+的值．解：（1）（2）BOM POM S S ∆∆+的值为．3．已知：如图，Rt △ABC 中，∠BAC=90︒．（1）按要求作图：（保留作图痕迹）①延长BC 到点D ，使CD=BC ； ②延长CA 到点E ，使AE=2CA ；③连接AD ，BE 并猜想线段 AD 与BE 的大小关系；（2）证明（1）中你对线段AD 与BE 大小关系的猜想．解：（1）AD 与BE 的大小关系是．（2）证明：4．（7分）已知：如图，△ABC 是等腰直角三角形，∠BAC =90°，过点C 作BC 的垂线l ，把一个足够大的三角板的直角顶点放到点A 处（三角板和△ABC 在同一平面内），绕着点A 旋转三角板，使三角板的直角边AM 与直线BC 交于点D ，另一条直角边AN 与直线l 交于点E . （1）当三角板旋转到图1位置时，若AC =2，求四边形ADCE 的面积；（2）在三角板旋转的过程中，请探究∠EDC 与∠BAD 的数量关系，并证明.lBAC备用图EDCBA图1lNM5．如图1，在△ABC 中，∠ACB =2∠B ，∠BAC 的平分线AO 交BC 于点D ，点H 为AO 上一动点，过点H 作直线l ⊥AO 于H ，分别交直线AB 、AC 、BC 、于点N 、E 、M . （1）当直线l 经过点C 时（如图2），求证：BN =CD ；（2）当M 是BC 中点时，写出CE 和CD 之间的等量关系，并加以证明；（3）请直接写出BN 、CE 、CD 之间的等量关系．D NEMAB CHlDN(E)(M)ABC Hl（1）证明：（2）当M 是BC 中点时,CE 和CD 之间的等量关系为_________________________. 证明：（3）请你探究线段BN 、CE 、CD 之间的等量关系, 并直接写出结论.6. 如图，在△ABC 中，AB =AC ，108A ∠=°，请你在图中，分别用两种不同方法，将△ABC 分割成四个小三角形，使得其中两个是全等．．的不等边三角形．．．．．．(不等边三角形指除等腰三角形以外)，而另外两个是不全等．．．的等腰三角形．请画出分割线段，并在两个全等三角形中标出一对相等的内角的度数，在每个等腰三角形中标出相等两底角度数（画图工具不限，不要求证明，不要求写出画法，但要保留作图痕迹，若经过图形变换后两个图形重合，则视为同一种方法）．备用图DABCO备用图DABCOA B C AB C7．阅读下列材料：通过小学的学习我们知道，分数可分为“真分数”和“假分数”．而假分数都可化为带分数，如：86222223333+==+=．我们定义：在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”．如：11x x -+，21x x -这样的分式就是假分式；再如：31x +，221xx +这样的分式就是真分式．类似的，假分式也可以化为带分式（即：整式与真分式的和的形式）．如：()12121111x x x x x +--==-+++；再如：22111(1)1111x x x )x x x x -++-+==---（111x x =++-．解决下列问题：（1）分式2x是分式（填“真分式”或“假分式”）；（2）假分式12x x -+可化为带分式的形式；（3）如果分式211x x -+的值为整数，那么x 的整数值为．8．在△ABC 中，AB=AC ，点D 是射线CB 上的一动点（不与点B 、C 重合），以AD 为一边在AD 的右侧作△ADE ，使AD=AE ，∠DAE =∠BAC ，连接CE ．（1）如图1，当点D 在线段CB 上，且∠BAC =90°时，那么∠DCE = ▲ 度；（2）设∠BAC =α，∠DCE =β．① 如图2，当点D 在线段CB 上，∠B AC ≠90°时，请你探究α与β之间的数量关系，并证明你的结论；② 如图3，当点D 在线段CB 的延长线上，∠BAC ≠90°时，请将图3补充完整，并直接．．写出此时α与β之间的数量关系（不需证明）．解：（1）∠DCE = 度；（2）结论：α与β之间的数量关系是；证明：BD CAED ED AB C C B A图1图2图3（3）结论：α与β之间的数量关系是．9．已知：四边形ABED 中，AD ⊥DE 、BE ⊥DE .(1) 如图1，点C 是边DE 的中点，且AB=2AD=2BE ．判断△ABC 的形状：（不必说明理由）；(2) 保持图1中△ABC 固定不变，将直线DE 绕点C 旋转到图2中所在的MN 的位置（垂线段AD 、BE 在直线MN 的同侧）．试探究．．．线段AD 、BE 、DE 长度之间有什么关系？并给予证明； (3) 保持图2中△ABC 固定不变，继续绕点C 旋转DE 所在的直线MN 到图3中的位置（垂线段AD 、BE 在直线MN 的异侧）．⑵中结论是否依然成立，若成立请证明；若不成立，请写出新的结论，并给予证明．10．阅读材料1：对于两个正实数,a b ，由于()02≥-ba ，所以()()0222≥+⋅-b b a a ，即02≥+-b ab a ，所以得到ab b a 2≥+，并且当a b =时，2a b ab +=．阅读材料2：若0x >，则22111x x x x x x x+=+=+，因为10,0x x >>，所以由阅读材料1可得，ABCDEABC DEMNMNABCDE 图1图2图32121=⋅≥+xx x x ，即21x x +的最小值是2，只有1x x =时，即1x =时取得最小值．根据以上阅读材料，请回答以下问题：（1）比较大小：21x + 2x （其中1x ≥）； 1x x+2-（其中1x <-）（2）已知代数式2331x x x +++变形为11x n x +++，求常数n 的值；（3）当x = 时，133+++x xx 有最小值，最小值为 . （直接写出答案）11．在四边形ABDE 中，C 是BD 边的中点．（1）如图(1)，若AC 平分BAE ∠，ACE ∠=90°, 则线段AE 、AB 、DE 的长度满足的数量关系为；（直接写出答案）（2）如图（2），AC 平分BAE ∠， EC 平分AED ∠，若120ACE ∠=︒，则线段AB 、BD 、DE 、AE 的长度满足怎样的数量关系？写出结论并证明；12．已知：如图，在△ABC 中，AD 平分∠BAC ，CD ⊥AD 于点D ，∠DCB=∠B ，若AC=10，AB=26，求AD 的长．EDC BA图（2）EDC BA图（1）ABCD13. 已知：如图，△AOB 的顶点O 在直线l 上，且AO ＝AB .（1）画出△AOB 关于直线l 成轴对称的图形△COD ，且使点A 的对称点为点C ；（2）在（1）的条件下， AC 与BD 的位置关系是；（3）在（1）、（2）的条件下，联结AD ，如果∠ABD =2∠ADB ，求∠AOC 的度数.14. 我们知道，假分数可以化为整数与真分数的和的形式.例如：32=112+. 在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”.例如：像11x x +-，22x x -，…这样的分式是假分式；像42x - ，221x x +，…这样的分式是真分式.类似的，假分式也可以化为整式与真分式的和的形式. 例如：112122111111x x x x x x x x +-==+=+-----（-）+；22442(2)4422222x x x )x x x x x x -++-+===++----（. （1）将分式12x x -+化为整式与真分式的和的形式；（2）如果分式2211x x --的值为整数，求x 的整数值.BAOl15. 请阅读下列材料：问题：如图1，△ABC中，∠ACB=90°，AC=BC，MN是过点A的直线，DB⊥MN于点D，联结CD.求证：BD+ AD =2CD.小明的思考过程如下：要证BD+ AD =2CD，需要将BD，AD转化到同一条直线上，可以在MN上截取AE=BD，并联结EC，可证△ACE和△BCD全等，得到CE=CD，且∠ACE=∠BCD，由此推出△CDE为等腰直角三角形，可知DE =2CD，于是结论得证.小聪的思考过程如下：要证BD+ AD =2CD，需要构造以CD为腰的等腰直角三角形，可以过点C作CE⊥CD交MN于点E，可证△ACE和△BCD全等，得到CE=CD，且AE=BD，由此推出△CDE为等腰直角三角形，可知DE =2CD，于是结论得证.请你参考小明或小聪的思考过程解决下面的问题：(1) 将图1中的直线MN绕点A旋转到图2和图3的两种位置时，其它条件不变，猜想BD，AD，CD之间的数量关系，并选择其中一个图形加以证明；(2) 在直线MN绕点A旋转的过程中，当∠BCD=30°，BD =2时，CD=__________．MDNBCA图2BCNMDA图3AC BNDM E图116.（本题5分）如图，在△ABC 中，∠BAC=60°,∠ACB=40°,P 、Q 分别在BC 、CA 上，并且AP 、BQ 分别是∠BAC 、∠ABC 的角平分线. 求证：（1）BQ = CQ ； (2) BQ+AQ=AB+BP. 证明: (1) (2)17.（本题7分）在△ABC 中，∠BAC=90°，AB=AC ，点D 是线段BC 上的一个动点（不与点B 重合）．DE ⊥BE 于E ，∠EBA=21∠ACB ，DE 与AB 相交于点F ．（1）当点D 与点C 重合时（如图1），探究线段BE 与FD 的数量关系，并加以证明；（2）当点D 与点C 不重合时（如图2），试判断（1）中的猜想是否仍然成立，请说明理由．PQBCA18.如图,在直角△ABC 中, ∠ACB=90,CD ⊥AB,垂足为D,点E 在AC 上,BE 交CD 于点G,EF ⊥BE交AB 于点F,若AC=BC,CE=EA.试探究线段EF 与EG 的数量关系，并加以证明.答：EF 与EG 的数量关系是 . 证明:19．在平面直角坐标系xoy 中，等腰三角形ABC 的三个顶点A (0，1)，点B 在x 轴的正半轴上，∠ABO =30°，点C 在y 轴上．（1）直接写出点C 的坐标为；（2）点P 关于直线AB 的对称点P ′在x 轴上，AP =1，在图中标出点P 的位置并说明理由；（3）在（2）的条件下，在y 轴上找到一点M ，使PM +BM 的值最小，则这个最小值为．20．解决下面问题：如图，在△ABC 中，∠A 是锐角，点D ，E 分别在AB ， AC 上，且12DCB EBC A ∠=∠=∠，BE 与CD 相交于点O ，探究BD 与CE 之间的数量关系，并证明你的结论．小新同学是这样思考的：在平时的学习中，有这样的经验：假如△ABC 是等腰三角形，那么在给定一组对应条件，如图a ，BE ，CD 分别是两底角的平分线（或者如图b ，BE ，CD 分别是两条腰的高线，或者如图c ，BE ，CD 分别是两条腰的中线）时，依据图形的轴对称性，利用全等三角形和等腰三角形的有关知识就可证得更多相等的线段或相等的角.这个问题也许可以通过添加辅助线构造轴对称图形来解决．xy O-3-1-2-3123-1-2-4123GF EDCBA OEDCA B图a 图b21．已知A (-1，0)，B (0，-3)，点C 与点A 关于坐标原点对称，经过点C 的直线与y 轴交于点D ，与直线AB 交于点E ．（1）若点D ( 0，1)，过点B 作BF ⊥CD 于F ，求∠DBF 的度数及四边形ABFD 的面积；（2）若点G （G 不与C 重合）是动直线CD 上一点，点D 在点（0，1）的上方，且BG =BA ，试探究∠ABG 与∠ECA 之间的等量关系.DED E CC DEC AA ABB BD ECC ABD EC C AB备用图xOyxOy数学试卷参考答案及评分标准 2014．121．（1）α＋β＝180°； ……………………1分证明：∵∠DAE ＝∠BAC ，∴∠DAE －∠DAC ＝∠BAC －∠DAC ， ∴∠CAE ＝∠BAD ． ∵在△ABD 和△ACE 中，AB ＝AC ，∠BAD ＝∠CAE ，AD ＝AE ，∴△ABD ≌△ACE （SAS ）， ……………………2分 ∴∠ABD ＝∠ACE ，∵∠BAC ＋∠ABD ＋∠ACB ＝180°， ∴∠BAC ＋∠ACE ＋∠ACB ＝180°，∴∠BAC ＋∠BCE ＝180°，即α＋β＝180°． ………………3分（2）α＝β； ………………4分理由如下：∵∠DAE ＝∠BAC ， ∴∠DAE ＋∠CAD ＝∠BAC ＋∠CAD ， ∴∠BAD ＝∠CAE ．在△BAD 和△CAE 中，∵AB ＝AC ，∠BAD ＝∠CAE ，AD ＝AE ，∴△ABD ≌△ACE （SAS ）， ……………………5分 ∴∠ABD ＝∠ACE ，∵∠ACD ＝∠ABD ＋∠BAC ＝∠ACE ＋∠DCE ，∴∠BAC ＝∠DCE ，即α＝β． ……………………6分（3）如图，α＝β． …………7分BECDA4. （7分）（1）解：∵AB=AC，∠BAC=90°，∴∠ABC=∠ACB=45°.∵BC⊥l，∴∠BCE=90°，12ED CBAlN M∴∠ACE =45°， ∴∠ACE =∠B . ∵∠DAE=90°， ∴∠2+∠CAD =90°. 又∵∠1+∠CAD =90°， ∴∠1=∠2，∴△BAD ≌△CAE （ASA ）.………………….2分 ∵S 四边形ADCE = S △CAE + S △ADC ， ∴S四边形ADCE= S △BAD + S △ADC = S △ABC .又∵AC =2， ∴AB =2， ∴S △ABC =1， ∴S四边形ADCE=1.. ……………………………….3分（2）解：分以下两类讨论：①当点D 在线段BC 上或在线段CB 的延长线上时，∠EDC=∠BAD ，如图1、图2所示.如图1∵△BAD ≌△CAE （ASA ），（已证） ∴AD =AE . 又∵∠MAN =90°， ∴∠AED =45°. ∴∠AED =∠ACB .在△AOE 和△DOC 中，∠AO E =∠DO C ， ∴∠EDC =∠2. 又∵∠1=∠2，∴∠EDC =∠1.………………………………………....5分如图2中同理可证NMl图3ABCD E12O12MN NMOll图2图1EDC BAABCD E②当点D 在线段BC 的延长线上时，∠EDC +∠BAD=180°，如图3所示.…………..…….6分同理可证△BAD ≌△CAE （ASA ）， ∴AD =AE .∴∠A DE =∠AED =45°. ∵∠EDC=45°+∠A DC ， ∠BAD=180°-45°-∠A DC ，∴∠EDC +∠BAD=180°.. …………………………….7分5. （1）证明：连结ND∵AO 平分BAC ∠, ∴12∠=∠ ∵直线l ⊥AO 于H , ∴4590∠=∠=︒ ∴67∠=∠ ∴AN AC =∴NH CH =∴AH 是线段NC 的中垂线 ∴DC DN = ∴98∠=∠∴AND ACB ∠=∠∵3AND B ∠=∠+∠,2ACB B ∠=∠, ∴3∠=∠B∴DN BN =∴BN DC = ……………………………………………………………………2分（2）当M BC 是中点时,CE 和CD 之间的等量关系为2CD CE =证明：过点C 作'CN AO ⊥交AB 于'N由（1）可得'BN CD =,',AN AC AN AE == ∴43∠=∠,'NN CE =过点C 作CG ∥AB 交直线l 于点G ∴42∠=∠,1B ∠=∠ ∴23∠=∠∴CG CE = ∵M BC 是中点, ∴BM CM =在△BNM 和△CGM 中，1,,,B BM CM NMB GMC ∠=∠⎧⎪=⎨⎪∠=∠⎩987654321ENMDABC H l4321EN'GN MDABCH Ol∴△BNM ≌△CG M ∴BN CG =∴BN CE =∴''2CD BN NN BN CE ==+= …………………………………………4分（3）BN 、CE 、CD 之间的等量关系：当点M 在线段BC 上时，CD BN CE =+；当点M 在BC 的延长线上时，CD BN CE =-；当点M 在CB 的延长线上时，CD CE BN =-………………………………6分 (阅卷说明：三种情况写对一个给1分，全对给2分)67．解：（1）真分式；…………………………………………………………………1分（2）13122x x x -=-++；……………………………………………………3分（3）x 的可能整数值为 0，－2，2，－4 . …………………………………5分8．解：（1） 90 度.…………………………………………………………1分图3E DCBA图1图2ED ED ABCCBA（2）① 180αβ+=︒．………………………………………………………2分理由：∵∠BAC =∠DAE ，∴∠BAC －∠DAC =∠DAE －∠DAC ．即∠B A D =∠CA E ．………………………………………………………3分又AB =AC ，AD =AE ，∴△A B D ≌△A C E ．…………………………………………………4分 ∴∠B =∠ACE ．∴∠B +∠ACB =∠ACE +∠ACB ．36°36°72°72°72°72°FEDABC36°36°72°72°72°72°E DA CB∴B ACB DCE β∠+∠=∠=．∵180B ACB α+∠+∠=︒，∴180αβ+=︒．…………………………………………………5分（3）图形正确．………………………………………………………………6分 αβ=．……………………………………………………………………7分9．解(1) 等腰直角三角形 ………………………………………………1分(2) DE =AD +BE ；………………………………………………2分证明：如图2，在Rt △ADC 和Rt △CEB 中，∵∠1+∠CAD =90︒，∠1+∠2=90︒，∴∠CAD =∠2又∵AC =CB ，∠ADC =∠CEB =90︒， ∴Rt △ADC ≅Rt △CEB∴DC =BE ，CE =AD ，∴DC +CE =BE +AD ， ………………………………………3分即DE =AD +BE(3) DE =BE -AD …………………………………………………4分如图3，Rt △ADC 和Rt △CEB 中，∵∠1+∠CAD =90︒，∠1+∠2=90︒，∴∠CAD =∠2，又∵∠ADC =∠CEB =90︒，AC =CB ，∴Rt △ADC ≅Rt △CEB ，∴DC =BE ，CE =AD ，∴DC -CE =BE -AD ， ……………………………………………5分即DE =BE -AD.1 A BCDE图12MN ABCDE 图212ABC DEMN 图31 2<10．（1）比较大小：21x + ≥ 2x （其中1x ≥）； 1x x +____2-（其中1x <-）---------2分（2）解： 111332+++=+++x n x x x x()()1111121+++=+++++x n x x x x x 11112+++=+++x n x x x ∴2=n --------------------------------------------4分（3）当x = 0 时，133+++x xx 有最小值，最小值为 3 . （直接写出答案）---6分11．（1） AE=AB+DE ； ------------1分（2）解：猜想：AE =AB+DE +BD 21．------------2分证明：在AE 上取点F ，使AF =AB ，连结CF ，在AE 上取点G ，使EG =ED ，连结CG ．∵C 是BD 边的中点，∴CB =CD=BD 21．∵AC 平分BAE ∠，∴∠BAC =∠FAC ．∵AF =AB ，AC =AC ，∴△ABC ≌△AFC .∴CF =CB ，∴∠BCA =∠FCA ．----------------------------4分同理可证：CD =CG ，∴∠DCE =∠GCE ． ∵CB =CD ，∴CG =CF ∵120ACE ∠=︒，∴∠BCA +∠DCE=180°-120°=60°．图（2） ∴∠FCA +∠GCE=60°．∴∠FCG=60°． ∴△FGC 是等边三角形．-------------------------5分 ∴FG =FC=BD 21． ∵AE =AF+EG+FG ．∴AE =AB+DE +BD 21．-----------------------6分（3）2410+． ----------------7分EDCBA图（3）EDC BA图（1）GFEDCBA12．解：如图，延长CD 交AB 于点E . ……………… 1分∵ AD 平分∠BAC ，CD ⊥AD 于点D ， ∴ ∠EAD = ∠CAD ，∠ADE=∠ADC =90°. ∴ ∠AED=∠ACD . ……………… 2分 ∴ AE=AC . ∵ AC=10，AB=26，∴ AE=10，BE=16. ……………… 3分 ∵ ∠DCB=∠B ， ∴ EB= EC=16. ∵ AE= AC ，CD ⊥AD ，∴ ED= CD=8. ……………………………………………… 4分在Rt △ADC 中，∠ADC =90°，∴22AD AC CD =-=22108-=6． ……………………………………… 5分13．（1）如图1．……1分（2）平行． ……2分（3）解：如图2，由（1）可知，△AOB 与△COD 关于直线l 对称， ∴△AOB ≌△COD ．……3分∴AO =CO ，AB = CD ，OB = OD ，∠ABO ＝∠CDO ．图1 图2 ∴∠OBD ＝∠ODB ． ……4分∴∠ABO+∠OBD ＝∠CDO+∠ODB ，即∠ABD ＝∠CDB ． ∵∠ABD =2∠ADB ，∴∠CDB =2∠ADB ．∴∠CDA =∠ADB ．……5分由（2）可知，AC ∥BD ，∴∠CAD ＝∠ADB ．∴∠CAD =∠CDA ，∴CA = CD ．……6分 ∵AO = AB ，∴AO = OC = AC ，即△AOC 为等边三角形． ∴∠AOC = 60°． ……7分 14．解：（1）12x x -+()232x x +-=+……1分DCBAElODCBAABCDOl2232x x x +=+-+ ……2分312x+=-. ……3分（2）2211x x --22211x x -+=- ()()21111x x x +-+=-()1211x x =++-. ……5分 ∵分式的值为整数，且x 为整数， ∴11x -=±，∴x =2或0．……7分15．解：（1）如图2，BD －AD =2CD . ……1分如图3，AD －BD =2CD . ……2分证明图2：（法一）在直线MN 上截取AE =BD ，联结CE ．设AC 与BD 相交于点F ，∵BD ⊥MN ，∴∠ADB =90°，∴∠CAE+∠AFD =90°． ∵∠ACB =90°，∴∠1+∠BFC =90°． ∵∠AFD =∠BFC ，∴∠CAE =∠1．∵AC =BC ，∴△ACE ≌△BCD （SAS ）． ……3分 ∴CE =CD ，∠ACE =∠BCD ．∴∠ACE －∠ACD =∠BCD －∠ACD ，即∠2=∠ACB =90°．在Rt △CDE 中，∵222CD CE DE +=，∴222CD DE = ，即DE =2CD ．……4分 ∵DE = AE －AD = BD －AD ，∴BD －AD =2CD ． ……5分（法二）过点C 作CE ⊥CD 交MN 于点E ，则∠2=90°． ∵∠ACB =90°，∴∠2+∠ACD =∠ACB+∠ACD ，即∠ACE =∠BCD ．设AC 与BD 相交于点F ，∵DB ⊥MN ，∴∠ADB =90°．F12图2A C BNDME FM DA∴∠CAE+∠AFD =90°，∠1+∠BFC =90°． ∵∠AFD =∠BFC ，∴∠CAE =∠1．∵AC =BC ，∴△ACE ≌△BCD （ASA ）． ……3分 ∴CE =CD ，AE =BD ．在Rt △CDE 中，∵222CD CE DE +=，∴222CD DE = ，即DE =2CD ．……4分 ∵DE = AE －AD = BD －AD ，∴BD －AD =2CD ． ……5分证明图3：（法一）在直线MN 上截取AE =BD ，联结CE ．设AD 与BC 相交于点F ，∵∠ACB =90°，∴∠2+∠AFC =90°． ∵BD ⊥MN ，∴∠ADB =90°，∠3+∠BFD =90°． ∵∠AFC =∠BFD ，∴∠2=∠3．∵AC =BC ，∴△ACE ≌△BCD （SAS ）． ……3分 ∴CE =CD ，∠1=∠4．∴∠1+∠BCE =∠4+∠BCE ，即∠ECD =∠ACB =90°．在Rt △CDE 中，∵222CD CE DE +=，∴222CD DE = ，即DE =2CD ．……4分 ∵DE = AD －AE = AD －BD ，∴AD －BD =2CD ． ……5分（法二）过点C 作CE ⊥CD 交MN 于点E ，则∠DCE =90°． ∵∠ACB =90°，∴∠ACB －∠ECB = ∠DCE －∠ECB ，即∠1=∠4．设AD 与BC 相交于点F ，∵DB ⊥MN ，∴∠ADB =90°． ∴∠2+∠AFC =90°，∠3+∠BFD =90°． ∵∠AFC =∠BFD ，∴∠2=∠3．∵AC =BC ，∴△ACE ≌△BCD （ASA ）． ……3分 ∴CE =CD ，AE =BD ．在Rt △CDE 中，∵222CD CE DE +=， ∴222CD DE = ，即DE =2CD ．……4分∵DE = AD －AE = AD －BD ，∴AD －BD =2CD ． ……5分（2）31± ． ……7分4F 321 图3A DM N CBE E BCN M DA 图3123F 416. 证明：延长AB 至M, 使得BM = BP ，联结MP 。

2013-2014学年上学期期末考试(含答案)八年级数学

八年级（上）数学期末测试题第1卷（选择题）一、选择题（本题20小题，每小题3分，在每小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来，并把答题卡上对应题目的正确答案标号涂黑）1．下列各组数中不能作为直角三角形的三条边长的是( )A.6,8,10B.9,12, 15C.1.5,2,3D.7,24, 252．一三，27t，等，o，0.23 2233 2233 2233…中，有理数的个数是( ) A.l B.2 C.3 D.43．下列扑克牌中，绕着某一点旋转1800后可以与原来的完全重合的是( )4．点P(-5，6)关于原点对称的点的坐标是( )A.(-5, -6)B.(5,6)C.(6,.5)D.(5,.6)5.估算24的算术平方根在( )A.2和3之间B.3和4之间C.4和5之间D.5和6之间中，一次函数的有( )A.4个B.3个C.2个D.l个7．为了筹备班级初中毕业联欢会，班长对全班同学爱吃哪几种水果作了民意调查，那么最终买什么水果，下面的调查数据中最值得关注的是( )A.平均数 B．力口权平均数 C．中位数 D．众数8.-次函数y= -x-l不经过的象限是( )A.t第一象限 B．第二象限 C．第三象限 D.第四象限A. 20 B．15 C．10 D．510.w边形ABCD中，AC、BD相交于点D，能判别这个四边形是正方形的条件是( )11.点彳的坐标为(6，3)，D为原点，将OA绕点0按顺时针方向旋转90度得到OA1，则点A1的坐标为 ( )么．（3.-6) B.(-3,6) C．（一3，．6) D.(3,6)12.下列说法正确的有____个．( )①有两个底角相等的梯形是等腰梯形②有两边相等的梯形是等腰梯形③有两条对角线相等的梯形是等腰梯形④等腰梯形上下底中点连线把梯形分成面积相等的两部分A.l个 B．2个 C．3个 n 4个13.如果直线y=3x+6 y=2x-4交点坐标为（a，b），的解( )14.某同学使用计算器求30个数据的平均数时，错将其中一个数据105输为 15，那么与实际平均数的差为( )A.3B.．3C.j 0.5D.3.515.把一张正方形纸片按如图所示的方法对折两次后剪去两个角，那么打开以后的形状是( )么．六边形 B．八边形 C．十二边形D.十六边形16.如图，在四边形ABCD中，动点P从点A开始沿A→_B→C→D的路径匀速前进到D为止。

(中学教材全解)2013-2014学年八年级数学上学期期末检测题冀教版

期末检测题（时间：120分钟，满分：120分）一、选择题（每小题3分，共36分）1.若y x 3=则222272)(yxy x y xy y x ++-+-的值为（） A.0 B.21C. 319D.12.下列二次根式中，化简后能与2合并的是( ) A.21B. C. D. 3.如图，每个小正方形的边长为1，那么△的三边长的大小关系为（） A. B. C. D.4.如图，在△中，，∠∠∠∠∠则∠（）A. B. C. D.5.下列计算正确的是（） A.822-=B.27129413-=-=C.(25)(25)1-+=D.62322-= 6.若，则的立方根是（） A B. C. D. 7.16的算术平方根和25的平方根的和是（） A. B. C. D.8.下列说法：①任何数都有算术平方根；②一个数的算术平方根一定是正数；③的算术平方根是；④的算术平方根是；⑤算术平方根不可能是负数.其中，不正确的有（）A.2个B.3个C.4个D.5个 9.设－1，在两个相邻整数之间，则这两个整数是（）A.1和2B.2和3C.3和4D.4和510.将△的三个顶点的横坐标都乘，纵坐标不变，则所得图形（）A.与原图形关于轴对称B.与原图形关于轴对称C.与原图形关于原点对称D.向轴的负方向平移了一个单位11.如图所示，点B 、C 、E 在同一条直线上，△ABC 与△CDE 都是等边三角形，则下列结论不一定成立的是（）A.△ACE ≌△BCDB.△BGC ≌△AFCC.△DCG ≌△ECFD.△ADB ≌△CEA12.直角三角形两直角边的和为7，面积为6，则斜边长为（） A. B. C. D.二、填空题（每小题3分，共24分）13.1)(2________. 14.若分式2102a a a -=+-，则____________．15.如图，在△中，，是∠的平分线，，∠，则 ∠______.16.如图是一个艺术窗的一部分，所有的四边形都是正方形，三角形是直角三角形，其中最大正方形的边长为，则正方形A ，B 的面积和是_________． 17.如果一个正数的平方根是与,则这个正数是______. 18.当时，=___________.19.已知0113=-++b a ，则________.20.若实数y x ,2(0y =,则xy 的值为 . 三、解答题（共60分） 21.（5分）如图，在△中，垂直平分线段，，△的周长为，求△的周长.22.(5分)如图，已知等腰△的周长是，底边上的高的长是，求这个三角形各边的长.23.（5分）用反证法证明：等腰三角形两底角必为锐角． 24.(5分）比较与的大小． 25.（8分）计算：（1） E A C DB第21题图第22题图第11题图（2）.26.（8分）阅读下面问题：12)12)(12()12(1211-=-+-⨯=+；();23)23)(23(231231-=-+-⨯=+()25)25)(25(251251-=-+-⨯=+.试求：（1）671+的值；（2）n n ++11（n 为正整数）的值.（3⋅⋅⋅+27.（8分）已知,a b 为等腰三角形的两条边长，且,a b 满足4b =，求此三角形的周长.28.（6分）如图所示，已知AE ⊥AB ，AF ⊥AC ，AE =AB ，AF =AC . 求证：（1）EC =BF ；（2）EC ⊥BF.29.（10分）如图所示，在△ABC 中，∠C =90°， AD 是∠BAC 的平分线，DE ⊥AB 交AB 于E ，F 在AC 上，BD =DF . 求证：（1）CF =EB ；（2）AB =AF +2EB．第29题图第28题图期末检测题参考答案1.C 解析：()().31931937332372)(2222222222==+⋅⨯+-⋅⨯+-=++-+-y y yy y y y y y y y y xy x y xy y x 2.A 解析：因为，55512.0，5220不能再化简，22，2221====所以只有A 项化简后能与2合并.故选A. 3.C 解析：因为，，，所以．故选C ． 4.D 解析：因为，∠所以，所以所以因为∠∠所以所以，所以所以∠，故选D.5. 解析：，故正确；错误；，故B 333323331227=-=-()()()错误；，故C 15452525222-=-=-=+-.D 1232226226错误，故-=-=- 6.A 解析：负数的立方根是负数,任意一个数的立方根都可表示成,故选A.7.C 解析：因为16的算术平方根是4,25的平方根是±5,所以16的算术平方根和25的平方根的和为.8.C 解析：负数没有算术平方根，故①不正确；0的算术平方根是0，故②不正确；可能是负数，如果是负数，则不成立，故③不正确；是负数，一个非负数的算术平方根是非负数，故④不正确；⑤正确.9.C 解析：∵∴故选C. 10.A 解析：根据轴对称的性质，知将△的三个顶点的横坐标都乘，就是把横坐标变成其相反数，纵坐标不变，因而是把三角形的三个顶点以轴为对称轴进行轴对称变换．所得图形与原图形关于轴对称.故选A ．11. D 解析：∵ △ABC 和△CDE 都是等边三角形， ∴ BC =AC ，CE =CD ，∠BCA =∠ECD =60°，∴ ∠BCA +∠ACD =∠ECD +∠ACD ，即∠BCD =∠ACE ， ∴ 在△BCD 和△ACE 中，∴ △BCD ≌△ACE （SAS ），故A 成立. ∵ △BCD ≌△ACE ，∴ ∠DBC =∠CAE . ∵ ∠BCA =∠ECD =60°，∴ ∠ACD =60°. 在△BGC 和△AFC 中，∴ △BGC ≌△AFC ，故B 成立.∵ △BCD ≌△ACE ，∴ ∠CDB =∠CEA ，在△DCG和△ECF中，∴△DCG≌△ECF，故C成立.故选D．12.A 解析：设直角三角形的两条直角边的长分别为斜边长为，则，所以，所以13.2解析：14.1 解析：由题意，得所以当时，分式无意义，舍去；当时，所以所以15.解析：因为，∠，所以∠.因为是∠的平分线，所以∠因为，所以∠所以∠16.25解析：设正方形A的边长为正方形B的边长为则，所以.17.49 解析：由一个正数的两个平方根互为相反数，知，解得，所以这个正数的平方根是,这个正数是.18.解析：当时，19.解析:由，得，所以.20.23解析：由题意知21.解：因为垂直平分线段，所以，.因为，所以，所以.因为△的周长为，所以，所以，故△的周长为.22.解：设，由等腰三角形的性质，知.由勾股定理，得，即，解得，所以，．23.证明：①设等腰三角形底角∠B，∠C都是直角，则∠B+∠C=180°，而∠A+∠B+∠C=180°+∠A＞180°，这与三角形内角和等于180°矛盾．②设等腰三角形的底角∠B，∠C都是钝角，则∠B+∠C＞180°，而∠A+∠B+∠C＞180°，这与三角形内角和等于180°矛盾．综上所述，假设①，②错误，所以∠B，∠C只能为锐角．故等腰三角形两底角必为锐角24.解：因为所以. 所以，所以.25.解：（1）224525292145051183-+=-+2822229=-+=. （2）1217125134519169161=+=⨯+=⨯++=.26.解：（1）671+1(76)(76)(76)⨯-=+-=76-.（2）1(1)11(1)(1)n n n n n n n n n n ⨯+-==+-+++++-.（3）122334989999100+++⋅⋅⋅+++++++27.解：由题意可得即所以3a =，332364b =-⨯-4=. 当腰长为3时，三角形的三边长为，周长为10；当腰长为4时，三角形的三边长为，周长为11.28. 证明：(1)∵ AE ⊥AB ，AF ⊥AC ，∴ ∠EAB =90°=∠FAC ， ∴∠EAB +∠BAC =∠FAC +∠BAC .又∵ ∠EAC =∠EAB +∠BAC ，∠BAF =∠FAC +∠BAC .∴ ∠EAC =∠BAF . 在△EAC 与△BAF 中，∴ △EAC ≌△BAF. ∴ EC =BF.(2)∵ ∠AEB +∠ABE =90°，又由△EAC ≌△BAF 可知∠AEC =∠ABF ，∴ ∠CEB +∠ABF +∠EBA =90°，即∠MEB +∠EBM =90°，即∠EMB =90°，∴ EC ⊥BF . 29. 证明：（1）∵ AD 是∠BAC 的平分线，DE ⊥AB ，DC ⊥AC ，∴ DE =DC ．又∵ BD =DF ，∴ Rt△CDF ≌Rt△EDB （HL ），∴ CF =EB . （2）∵ AD 是∠BAC 的平分线，DE ⊥AB ，DC ⊥AC ， ∴ △ADC ≌△ADE ，∴ AC =AE ，∴ AB =AE +BE =AC +EB =AF +CF +EB =AF +2EB ．。

2013-2014学年八年级数学上学期期末考试试题 (新人教版第12套)

广西北海市合浦县教育局教研室2013-2014学年八年级上学期期末考试数学试题新人教版第一卷客观题一、选择题（每小题3分，共36分） 1．下列说法错误的是（）A. 三角形的中线、高、角平分线都是线段B. 任意三角形内角和都是180°C. 三角形按角可分为锐角三角形、直角三角形和等腰三角形D. 直角三角形两锐角互余 2．下列各式①πx 6、②x x 1-、③(2a－1)÷(2b－5)、④213+x 中，是分式的有: （） A. ②③ B. ②③④ C. ①②③ D. ③3．若两个直角三角形的两直角边对应相等,则这两个三角形全等的依据是（） A. HL B. SSS C. AAS D. SAS4．小明在镜子里看到自己的像在用右手拿着梳子向左梳头，那么他实际是（） A.用右手向左梳头 B.用左手向右梳头 C.用右手向右梳头 D.用左手向左梳头5．等腰三角形ABC 在直角坐标系中,底边的两点坐标是(－2,0)、(6,0),则可以确定其顶点的（）A.横坐标B.纵坐标C.横坐标及纵坐标D.横坐标或纵坐标 6．如图所示，四边形OABC 为正方形，边长为3，点A ，C 分别在x 轴，y 轴的正半轴上，点D 在 OA 上，且D 的坐标为（1，0），P 是OB 上的一动点，则“求PD+PA 和的最小值”要用到的数理依据是（） A. “两点之间，线段最短” B. “轴对称的性质”C. “两点之间，线段最短”以及“轴对称的性质”D. 以上答案都不正确7．今天数学课上，老师讲了单项式乘以多项式，放学回到家，小明拿出课堂笔记复习，发现一道题：+-=---y x xy x y xy 22612)124.(3空格的地方被钢笔水弄污了，你认为空格内上应填写（）A. xy 3B. xy 3-C. －1D. 1 8．下列多项式乘法中,能用平方差公式计算的是（） A. (x ＋1)(－1－x ) B. )21)(21(b a b a -+ C. (3b ＋2a)(2a －3b) D. (x 2－y )(x ＋y 2)9．已知)2311)(1713()1713)(3119(-----x x x x 可因式分解成(a x +b)(8x +c)，其中a 、b 、c 均为整数，则a+b+c=（）A. 72B. 38C. －32D. －12第6题图10．93122--÷--y a a y a 化简结果为（） A. a y 3- B. a y 3+ C. )3()3()1(22+--y y a a D. )3)(3()1(2-+-y y a a 11．已知△ABC 与△DEF 全等,∠A=∠D=90°,∠B=25°,则∠E 的度数是（） A.25° B.65° C.25°或55° D.25°或65°12．甲乙两工程队共同参与一项筑路工程，规定x 天内完成任务。

2013-2014学年上学期期末考试八年级数学(上册)测试卷

2013-2014学年上学期期末考试八年级数学（上册）测试卷（满分：120分时间：100分）一、选择题（每小题3分，共30分）1、下列说法不正确的是（）A. －1的立方根是－1B. －1的平方是1C. －1的平方根是－1D. 1的平方根是1±2、平行四边形的周长为50，设它的长为x ，宽为y ，则y 与x 的函数关系为（）A. y=25－xB. y=25+xC. y=50－xD. y=50+x3、下列四点中，在函数y=3x+2的图象上的点是（）A.（－1，1）B.（－1，－1）C.（2，0）D.（0，－1.5）4、下列各式估算正确的是（） A. 4.602536≈ B. 38.62603≈ C. 066.043.0≈ D. 969003≈5、某工厂10名工人生产同一种零件，生产的件数分别是15，17，14，10，15， 17， 17， 16， 14， 12，设其平均数为a ，中位数为b ，众数为c ，则有。

A. c b a >>B. a c b >>C. b a c >>D. a b c >>6、在函数x x k y 2)1(--=中，y 随x 的增大而增大，则k 的值可能是（）A . 1 B. 2 C. 2 D. 227、下列命题正确的是（）① 对角线互相垂直且相等的平行四边形是正方形。

② 平行四边形、矩形、等边三角形、正方形既是中心对称图形也是轴对称图形。

③ 两组对角分别相等的四边形是平行四边形。

④ 底角是︒45的等腰梯形，高是h ，则腰长是h 2。

A. 全对B. ①②④C. ①②③D. ①③④8、甲、乙两人练习赛跑，若甲先跑半小时，则乙出发后40分钟可追上甲，设甲、乙每小时分别跑x 千米、y 千米，则可列方程（）A.y x 405.0=B. y x )325.0(5.0+=C. y x 40)405.0(=+D.y x 32)325.0(=+ 9、方程2x+y=7在正整数范围内的解有（）对。

怀文中学初二数学上学期期末模拟试题2

怀文中学2013-2014学年度第一学期期末模拟测试题二初二数学总分：150分时间：120分钟日期：2013-12-28命题人：陈秀珍审核人：郁胜军考试时间：2014-1-8 班级学号姓名得分一、选择题（3分×8＝24分）1.下列标志既是轴对称图形又是中心对称图形的是（）2.下列各组数分别是三角形的三边长，不是直角三角形的一组是（） A.3，4，5B.6，8，10C.5，12，13D.8, 9, 153.等腰三角形的周长为cm 13，其中一边长为3cm ，则该等腰三角形的底边为（） A.cm 3 B.cm 7 C.cm 7或3cm D.cm 84.在101001.0-, 7, 41 , 2π-0，722等数中，无理数的个数是（）A.1个B.2个C.3个D.4个5.明天数学课要学“勾股定理”，小颖在“百度”搜索引擎中输入“勾股定理”，能搜到与之相关的结果个数约为12 500 000，这个数用科学记数法表示为（） A.51.2510⨯ B.61.2510⨯ C.71.2510⨯ D.81.2510⨯6.下列说法，正确的是（） A.125.0的立方根是5.0± B.如果2))((b a c a c =-+，那么△ABC 是直角三角形 C.无限小数是无理数，无理数也是无限小数 D.一个无理数和一个有理数之积为无理数7. 如图，直线y kx b =+经过(21)A ，，(12)B --，两点，则不等式122x kx b >+>-的解集为．8. 父亲节，学校“文苑”专栏登出了某同学叫忆父亲的小诗：“同辞家门赴车站，别时叮咛语千万，学子满载信心去，老父怀抱希望还．”如果用纵轴y 表示父亲和学子在行进中离家的距离，横轴t 表示离家的时间，那么下面与上述诗意大致相吻的图象是 ( ) 第7题A B CD55 二、填空题（3分×14空＝42分）9. 81的算术平方根是 ___，-27的立方根是；94的算术平方根是。

2013-2014学年青岛版八年级上数学期末测试题二

图12013-2014学年青岛版八年级上数学期末检测题二一、选择题：1.下列六个图形中是轴对称图形的有（）A 、1个B 、2个C 、3个D 、4个 2.可判定两个直角三角形全等的条件是( )A 、斜边相等B 、两直角边对应相等C 、一锐角对应相等D 、两锐角对应相等 3.下列各式中，无论字母取何实数时，分式都有意义的是（）A 、225x x+B 、211y y -+C 、213x x+D 、21ba + 4.在实施“中小学生蛋奶工程”中，某配送公司按上级要求，每周向学校配送鸡蛋10000个，鸡蛋用甲乙两种不同规格的包装箱进行包装，若单独使用甲型包装箱比单独使用乙型包装箱可少用10个，每个甲型包装箱比每个乙型包装箱可多装50个鸡蛋，设每个甲型包装箱可装x 个鸡蛋，下列方程正确的是（） A 、10 00010 0001050x x -=+ B 、10 00010 0001050x x -=- C 、10 00010 0001050x x -=- D 、10 00010 0001050x x-=+ 5.如果方程x333-=-mx x 有增根，那么m 的值为（）A 、0 B 、-1 C 、3 D 、1 6.某校把学生的纸笔测试、实践能力、成长纪录三项成绩分别按50%、20%、30%的比例计入学期总评成绩，90分以上为优秀．甲、乙、丙三人的各项成绩如下表（单位：分），学期总评成绩优秀的是（） A 、甲 B 、乙丙 C 、甲乙 D 、甲丙7.如图1，点P 在∠AOB 的内部，点M 、N 分别是点P 关于直线OA 、OB 的对称点，线段MN 交OA 、OB 于点E 、F ，若△PEF 的周长是20cm ，则线段MN 的长是( )A 、10cmB 、20cmC 、在10cm 和20cm 之间D 、不能确定8.针对甲、乙两组数据：甲组：20，21，23，25，26；乙组：l00，101，103，105，106．下列说法正确的是（）A 、乙组比甲组稳定B 、甲组比乙组稳定C 、甲乙两组的稳定程度相同D 、无法比较两组数据的稳定程度 9.等腰三角形的一个角是50︒，则它的底角是（） A 、50︒ B 、50︒或65︒ C 、80︒ D 、65︒ 10.和点P （2，-5）关于x 轴对称的点是（） A 、（-2，-5） B 、（2，-5） C 、（2，5） D 、（-2，5）11.将一张长方形纸片按如图3所示的方式折叠，BC ，BD 为折痕，则∠CBD 的度数为（） A 、60° B 、75° C 、90° D 、95°12.如图2，从下列四个条件：①BC＝B′C， ②AC＝A′C，③∠A′C A ＝∠B′CB，④AB＝A′B′中，任取三个为条件，余下的一个为结论，则最多可以构成正确的结论的个数是（） A ．1个 B ．2个 C ．3个 D ．4个图2图3二、填空题（每小题3分，共24分） 13.化简262393m m m m +÷+--的结果是； 14.如图1，PM=PN ，∠BOC=30°，则∠AOB= ；15.如图3，在△ABC 和△FED， AD=FC ，AB=FE ，当添加条件时，就可得到△ABC≌△FED ； (只需填写一个你认为正确的条件)16.如图4, 已知AB=AC, ∠A=40°, AB 的垂直平分线MN 交AC 于点D,则∠DBC= 度； 17.观察给定的分式：,16,8,4,2,15432xx x x x --，猜想并探索规律，第10个分式是__________； 18.已知118x y x +=，xy = ，已知x:y=2:3,y:z=4:7,x:y:z= 。

四川省自贡市2013-2014学年度八年级上期末测试数学试题及答案(WORD版)【新课标人教版】

2013-2014学年四川省自贡市八年级（上）期末数学试卷一、选择题（本题有8个小题，每小题3分，满分24分.每小题只有一个选项符合题意）．．+y3．已知，则的值是（）5．在分式中，若将x、y都扩大为原来的2倍，则所得分式的值（）三角形，则符合条件的点P共有（）二、填空题（本题有6个小题，每小题3分，共18分）9．要使分式有意义，x需满足的条件是_________．10．已知一个多边形的内角和等于900°，则这个多边形的边数是_________．11．汉字“王、中、田”等都是轴对称图形，请再写出一个这样的汉字_________．12．若x2﹣kxy+25y2是一个完全平方式，则k的值是_________．13．三角形周长是奇数，其中两边的长是2和5，则第三边长是_________．14．如图，在ABC中，AP=DP，DE=DF，DE⊥AB于E，DF⊥AC于F，则下列结论：①AD平分∠BAC；②△BED≌△FPD；③DP∥AB；④DF是PC的垂直平分线．其中正确的是_________．三、（本大题有5小题，每小题5分，共25分）15．因式分解：x3+2x2y+xy2．16．解方程：．17．如图，在△ABC中，D是AB上一点，DF交AC于点E，DE=FE，AE=CE，AB与CF有什么位置关系？证明你的结论．18．先化简：÷（a﹣2+），然后任选一个你喜欢的a的值代入求值．19．已知（a+2b）（2a+b）=2a2+5ab+2b2，如图是正方形和长方形卡片（各有若干张），你能用拼图的方法说明上式吗？四、（本大题有3小题，每小题6分，共18分）20．（6分）作图题（不写作法）已知：如下图所示，①作出△ABC关于y轴对称的△A1B1C1，并写出△A1B1C1三个顶点的坐标．②在x轴上确定点P，使PA+PC最小．21．（6分）仔细阅读下面例题，解答问题：例题：已知二次三项式x2﹣4x+m有一个因式是（x+3），求另一个因式以及m的值．解：设另一个因式为（x+n），得x2﹣4x+m=（x+3）（x+n）则x2﹣4x+m=x2+（n+3）x+3n∴．解得：n=﹣7，m=﹣21∴另一个因式为（x﹣7），m的值为﹣21问题：仿照以上方法解答下面问题：已知二次三项式2x2+3x﹣k有一个因式是（2x﹣5），求另一个因式以及k的值．22．（6分）D是等边三角形内一点，DB=DA，BP=AB，∠DBP=∠DBC，求∠BPD的度数．五、（本大题有2小题，23小题7分.24小题8分.共15分）23．（7分）在长江某处一座桥的维修工程中，拟由甲、乙两个工程队共同完成某项目．从两个工程队的资料可以知道：若两个工程队合作24天恰好完成；若两个工程队合作18天后，甲工程队再单独做10天，也恰好完成，请问：（1）甲、乙两个工程队单独完成该项目各需多少天？（2）又已知甲工程队每天的施工费为0.6万元，乙工程队每天的施工费为0.35万元．要使该项目总的施工费不超过22万元，则乙工程队最少施工多少天？24．（8分）数学课上，李老师出示了如下的题目：“在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED=EC，如图，试确定线段AE与DB的大小关系，并说明理由”．小敏与同桌小聪讨论后，进行了如下解答：（1）特殊情况，探索结论当点E为AB的中点时，如图1，确定线段AE与DB的大小关系，请你直接写出结论：AE_________ DB（填“＞”，“＜”或“=”）．（2）特例启发，解答题目解：题目中，AE与DB的大小关系是：AE_________DB（填“＞”，“＜”或“=”）．理由如下：如图2，过点E作EF∥BC，交AC于点F．（请你完成以下解答过程）（3）拓展结论，设计新题在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且ED=EC．若△ABC的边长为1，AE=2，求CD的长（请你直接写出结果）．2013－2014学年八年级上学期期末考试数学参考答案一、选择题：本大题共8个小题，每小题3分，共24分．1．C 2．D 3．B 4．D 5．A 6．C 7．A 8．D 二、填空题：本大题共6个小题，每小题3分，共18分．9． 10．7；11．干； 12．；13．4或6 ； 14．①③⑤.三、解答题（每小题5分，共25分）15．解：原式=22(2)x x xy y ++ ……（3分） =2()x x y + ……（5分） 16．解：方程两边同乘以24x -得 ……（2分）2(2)14x x x +-=- 22214x x x +-=- ∴ 32x =- ……（4分）经检验32x =-是原方程的解 ∴ 方程的解是32x =- ……（5分） 17． FC 与AB 是平行关系 ……（1分）证明：∵ AC 、DF 交于E ， ∴ ∠1=∠2 ……（2分）∵12AE CEDE FE =⎧⎪∠=∠⎨⎪=⎩∴ A E D C E F ∆≅∆ ……（3分）∴ A D E C F E ∠=∠ ……（4分） ∴ FC ∥AB ……（5分）18．解：原式= 2121()a a a a a--+÷……（1分） = 21(1)a a a a -⋅- ……（3分）= 11a - ……（4分） 2a =时，原式值为1. ……（5分）当19．解：……（4分）由图知22(2)(2)252a b a b a ab b ++=++ …（5分）3;x ≠10;k =±ABC ··· B 1C 1A 1P · ·A ′四、解答题（每小题6分，共18分） 20．解：(1)1(1,2)A -，1(3,1)B -，1(4,4)C -…（3分） (2)点P 是CA ′与x 轴的交点.…（6分） 21．解：设另一个因式为()x n + …（1分） 223(25)()x x k x x n --=-+则 22232(52)5x x k x n x n --=--- ……（2分）∴ 5235n k n-=⎧⎨=⎩ 解得1n = 5k = ……（4分）∴ 另一个因式是(1)x + k 的值是5. ……（6分）22．解： ∵ △ABC 为等边三角形∴ AC=BC=AB ∠ACB ＝60︒又DB =DA DC=DC ∴ △DCA ≌△DCB (SSS) ……（2分） ∴∠DCB=∠DCA=12∠ACB=30︒ ……（3分）又 BP=AB ∴ BP=BC ∴ ∠DBP=∠DBC BD=BD △DBP ≌△DBC （SAS ） …（5分） ∴ ∠BPD=∠BCD=30︒ ……（6分）五、解答题（23题7分，24题8分，共15分）23．解：（1）设甲、乙两工程队单独完成此项工程各需x 天，y 天， …（0.5分）由题得 11(2411110(181x y x yx ⎧+⨯=⎪⎪⎨⎪+⨯+=⎪⎩ 解得4060x y =⎧⎨=⎩……（2.5分）经检验4060x y =⎧⎨=⎩是原方程组的解且符合题意 …（3.5分）答：甲、乙单独完成各需40天和60天. ……（4分）（2）甲队工程队施工a 天，乙工程队施工b 天时总的施工费不超过22万元…（4.5分）由题意有 140600.60.3522a b a b ⎧+=⎪⎨⎪+≤⎩ 解得 40b ≥ ……（6.5分）答：乙工程至少施工40天. ……（7分）24．解：（1）AE=DB …（1分）(2) AE与DB的大小关系是AE=DB理由如下：如图10，过点E作EF∥AC交AC于F∵△ABC为正△∴△AEF为正△，AE=EF BE=CF …（2分）图10 ∵ED=EC ∴∠D= ∠ECD又∠DEB=60︒－∠D∠ECF=60︒－∠ECD∴∠DEB=∠ECF又DE=CE , BE=CF ∴△DBE≌△EFC (SAS)∴DB=EF ∴DB=AE ……（4分）(3)图①图②①如图①点E在AB的延长线上时，可证得△DBE≌△EFCDB=EF=2 BC=1 ∴CD=3 ……（6分）②如图②当E在BA的延长线上时，可证得△DBE≌△EFCDB=EF=2 BC=1 ∴CD=1 ……（8分）。

2013-2014学年八年级数学上学期期中试题 (新人教版第2套)

AB DCM N甸南一中2013—2014年八年级数学(上）期中试卷一．选择题：（本大题共8小题，每小题3分，共24分．）1．国旗是一个国家的象征，下面的国旗是轴对称图形的是（） A.加拿大、哥斯达黎加、乌拉圭 B.加拿大、瑞典、澳大利亚 C.加拿大、瑞典、瑞士 D.乌拉圭、瑞典、瑞士加拿大哥斯达黎加澳大利亚乌拉圭瑞典瑞士 2.△ABC 中，AB=AC,AB 的垂直平分线与直线AC 相交所成锐角为 40°则此等腰三角形的顶角为( )A. 50°B. 60°C. 150°D. 50°或150°3.小明在镜子里看到自己的像在用右手拿着梳子向左梳头，那么他实际是（） A.用右手向左梳头 B.用左手向右梳头C.用右手向右梳头D.用左手向左梳头4.点 P(a+b,2a-b)与点Q （-2，-3）关于X 轴对称，则 a+b=( )A. B. C. -2 D. 25．如图，已知MB=ND,∠MBA=∠NDC ，下列条件中不能判定△ABM ≌△CDN 的是（） A.∠M=∠N B.AM=CN C.AB=CD D.AM ∥CN 6. 下列说法中正确的是（）① 角平分线上任意一点到角的两边的线段长相等 ② 角是轴对称图形 ③线段不是轴对称图形 ④ 线段垂直平分线上的点到这条线段两个端点的距离相等 A.①②③④ B.①②③ C.②③④ D.②④7. 等腰三角形的周长为13cm ，其中一边长为3cm ，则该等腰三角形的底边长为（） A 、7cm B 、3cm C 、7cm 或3cm D 、5cm 8.如图，AB ∥CD ，∠ABE =60°，∠D =50°，则∠E 的度数为( )A .10°B .20°C .30°D .40°二．填空题：（本大题共6小题，每小题3910. 已知⊿ABC 为等边三角形，BD为中线，延长BC 至E ，使CE=CD=1，连接DE ，则∠E= .学校班级姓考号订线313211.△ABC 中，AB=AC ，∠BAC=120°,AC 的垂直平分线EF 交AC 于E, 交BC 于F.若 FC=3㎝,则AF= ．12. 如图,在△ABC 中，∠C=90°，BC=16cm ，∠BAC 的平分线交BC 于D ，且BD ：DC=5：3，则D 到AB 的距离为_____________. 13. 如图所示，∠B=∠D=90°，要证明△ABC•与△ADC•全等，还需要补充的条件是________。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 / 5
2013-2014八年级数学上册期末测试题(2) 姓名
一．选择题( 3 ×10=30分)
1．下列各式由左边到右边的变形中，是分解因式的为（）。

A 、a (x + y) =a x + a y B 、x ²－4x+4=x(x －4)+4
C 、10x ²－5x=5x(2x －1)
D 、x ²－16+3x=(x －4)(x+4)+3x 2．下列运算中，正确的是（）。

A 、 x x =x 336
⋅ B 、3x ²÷2x=x
C 、x =x 235
（） D 、x+y =x y 2224+（）
3．下列图形中，不是轴对称图形的是（）。

4．已知△ABC 的周长是24，且AB=AC ，又AD ⊥BC ，D 为垂足，若△ABD 的周长是
20，则AD 的长为（）。

A 、6
B 、8
C 、10
D 、12
5．8．已知m 6x =，3n x =，则
2m n x -的值为（）。

A 、9
B 、34
C 、12
D 、4
3 6. 当分式3
x 1-有意义时，字母x 应满足（）
A. 0=x
B. 0≠x
C. 1=x
D. 1≠x
7．已知等腰三角形一边长为4，一边的长为6，则等腰三角形的周长为（）。

A 、14 B 、16 C 、10 D 、14或16
8．已知m 6x =，3n
x =，则
2m n x -的值为（）。

A 、9
B 、34
C 、12
D 、4
3
B C D
A
9.若分式22
x 9x 4x 3--+的值为0，则x 的值为（）
A ．3 B.3或－3 C.－3 D.0
10. 如果把分式y x xy
+中的x 和y 都扩大2倍，则分式的值（）
A 、扩大4倍；
B 、扩大2倍；
C 、不变；
D 缩小2倍
二．填空题 ( 3 ×10=30分)
11．已知a 1－b
1
＝５，则b ab a b ab a ---+2232的值是
12．一个汽车牌在水中的倒影为，则该车牌照号码____________。

13．若分式方程x-3
=m x+31+有增根，则这个增根的值为___________ 。

14. 已知点A （l ，－2），若A 、B 两点关于x 轴对称，则B 点的坐标为________。

15．分解因式
3322x 2-+y x y xy ＝ ________________________。

16.1纳米=0.000000001米，7.5纳米用科学记数法表示为_______________________。

17．若等腰三角形腰上的高是腰长的一半,则这个等腰三角形的底角是____________。

18. 多项式
24a 1+加上一个单项式后，使它能成为一个整式的完全平方，那么加上的单项式可以是____________________________。

（填上一个你认为正
确的即可）
19.已知x ＋y ＝1，则2211
22
++x xy y ＝ _______________________。

20．如图EB 交AC 于M ，交FC 于D ，AB 交FC 于N ，∠E ＝∠F ＝
90°，
∠B ＝∠C ，AE ＝AF 。

给出下列结论：①∠1＝∠2；②BE ＝CF ；
③△ACN ≌△ABM ；④CD=DN 。

其中正确的结论有____________(填序号)
三、简答题：（共60分）
M
N A
B
C
D
E F
1 2
3 /
21．化简: (2×10分)
（1）22(5a 2a)4(22a )+-+；（2）2
5x (x 1)(x 1)+-
22. 分解因式(2×10分)
(1) 416-a (2) 2229-+-x xy y
23．（5分）作图题（不写作图步骤，保留作图痕迹）．已知：如图，求作点P ，使点P 到A 、B 两点的距离相等，且P 到∠MON 两边的距离也相等
24．（10分）△ABC 为正三角形，点M 是射线BC 上任意一点，点N 是射线CA 上任意一点，且BM=CN ，BN 与AM 相交于Q 点，∠AQN 等于多少度．
25．（5分）先化简，再求值：11
222
3+----x x x
x x x ，其中x=2
26．（5分）先化简，再求值：8m ²－5m(－m ＋3n) ＋4m(－4m －5
2n)，其中m ＝2，n ＝－
1
27. （5分）解方程
222 716
1
+=
+--x x x x x
28. （10分）某工厂现在平均每天比原计划多生产50台机器，现在生产600台机器所需时间与原计划生产450台机器所需时间相同，现在平均每天生产多少台机器？
5 / 5。