湖南大学数值计算教材课后习题答案
数值计算课后答案2
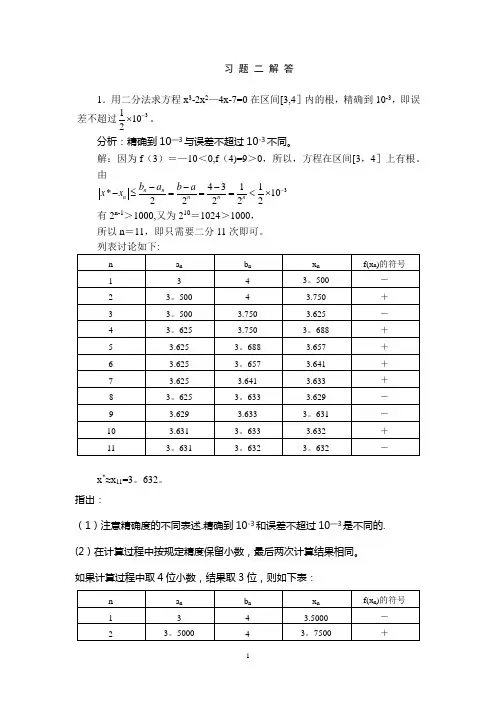
习 题 二 解 答1．用二分法求方程x 3-2x 2—4x-7=0在区间[3,4］内的根，精确到10-3，即误差不超过31102-⨯。
分析：精确到10—3与误差不超过10-3不同。
解：因为f （3）＝—10＜0,f （4)=9＞0，所以，方程在区间[3，4］上有根。
由34311*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1＞1000,又为210＝1024＞1000， 所以n ＝11，即只需要二分11次即可。
x *≈x 11=3。
632。
指出：（1）注意精确度的不同表述.精确到10-3和误差不超过10—3是不同的. (2）在计算过程中按规定精度保留小数，最后两次计算结果相同。
如果计算过程中取4位小数，结果取3位，则如下表：（3）用秦九韶算法计算f （x n )比较简单。
1＊．求方程x 3-2x 2-4x-7=0的隔根区间。
解:令32247y x x x =---， 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时，有12223,x x =-=。
因为214902150327(),()y y -=-<=-<，所以方程在区间223(,)-上无根； 因为21490327()y -=-<，而函数在23(,)-∞-上单调增,函数值不可能变号，所以方程在该区间上无根；因为2150()y =-<，函数在（2,+∞）上单调增，所以方程在该区间上最多有一个根,而（3）=-10〈0，y(4）=9>0,所以方程在区间（3，4）有一个根。
所以，该方程有一个根，隔根区间是（3。
4）。
2．证明1sin 0x x --=在［0,1]内有一个根,使用二分法求误差不大于41102-⨯的根,需要迭代多少次？分析:证明方程在指定区间内有一个根，就是证明相应的函数在指定区间有至少一个零点.解：令()1sin f x x x =--，因为(0)10sin 010,(1)11sin1sin10f f =--=>=--=-<， 则(0)(1)0f f <，由零点定理，函数f （x)在［0,1]区间有一个根。
数值计算课后答案3
习 题 三 解 答1、用高斯消元法解下列方程组。
（1）12312312231425427x x x x x x x x -+=⎧⎪++=⎨⎪+=⎩①②③解：⨯4②＋(-)①2，12⨯③＋(-)①消去第二、三个方程的1x ，得：1232323231425313222x x x x x x x ⎧⎪-+=⎪-=⎨⎪⎪-=⎩④⑤⑥ 再由52)4⨯⑥＋(-⑤消去此方程组的第三个方程的2x ，得到三角方程组：1232332314272184x x x x x x ⎧⎪-+=⎪-=⎨⎪⎪-=⎩回代，得：36x =-，21x =-，19x = 所以方程组的解为(9,1,6)T x =--注意：①算法要求，不能化简。
化简则不是严格意义上的消元法，在算法设计上就多出了步骤。
实际上，由于数值计算时用小数进行的，化简既是不必要的也是不能实现的。
无论是顺序消元法还是选主元素消元法都是这样。
②消元法要求采用一般形式,或者说是分量形式，不能用矩阵，以展示消元过程。
要通过练习熟悉消元的过程而不是矩阵变换的技术。
矩阵形式错一点就是全错，也不利于检查。
一般形式或分量形式： 12312312231425427x x x x x x x x -+=⎧⎪++=⎨⎪+=⎩①②③ 矩阵形式123213142541207x x x -⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭向量形式 123213142541207x x x -⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪++= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭③必须是方程组到方程组的变形。
三元方程组的消元过程要有三个方程组，不能变形出单一的方程。
④消元顺序12x x →→L ，不能颠倒。
按为支援在方程组中的排列顺序消元也是存储算法的要求。
实际上，不按顺序消元是不规范的选主元素。
⑤不能化简方程，否则系数矩阵会变化，也不利于算法设计。
（2）1231231231132323110221x x x x x x x x x --=⎧⎪-++=⎨⎪++=-⎩①②③解：⨯23②＋()①11，111⨯③＋(-)①消去第二、三个方程的1x ，得： 123232311323523569111111252414111111x x x x x x x ⎧--=⎪⎪⎪-=⎨⎪⎪+=-⎪⎩④⑤⑥ 再由2511)5211⨯⑥＋(-⑤消去此方程组的第三个方程的2x ，得到三角方程组：123233113235235691111111932235252x x x x x x ⎧⎪--=⎪⎪-=⎨⎪⎪=-⎪⎩回代，得：32122310641,,193193193x x x =-==， 所以方程组的解为 41106223(,,)193193193Tx =-2、将矩阵1020011120110011A ⎛⎫ ⎪⎪= ⎪- ⎪⎝⎭作LU 分解。
数值计算方法课后习题答案(李庆扬等)
第一章 绪论（12）1、设0>x ，x 的相对误差为δ，求x ln 的误差。
[解]设0*>x 为x 的近似值，则有相对误差为δε=)(*x r ，绝对误差为**)(x x δε=，从而x ln 的误差为δδεε=='=*****1)()(ln )(ln x x x x x ， 相对误差为****ln ln )(ln )(ln x x x x rδεε==。
2、设x 的相对误差为2%，求n x 的相对误差。
[解]设*x 为x 的近似值，则有相对误差为%2)(*=x r ε，绝对误差为**%2)(x x =ε，从而nx 的误差为nn x x nxn x x n x x x **1***%2%2)()()()(ln *⋅=='=-=εε，相对误差为%2)()(ln )(ln ***n x x x nr==εε。
3、下列各数都是经过四舍五入得到的近似数，即误差不超过最后一位的半个单位，试指出它们是几位有效数字：1021.1*1=x ，031.0*2=x ，6.385*3=x ，430.56*4=x ，0.17*5⨯=x 。
[解]1021.1*1=x 有5位有效数字；0031.0*2=x 有2位有效数字；6.385*3=x 有4位有效数字；430.56*4=x 有5位有效数字；0.17*5⨯=x 有2位有效数字。
4、利用公式（3.3）求下列各近似值的误差限，其中*4*3*2*1,,,x x x x 均为第3题所给的数。
（1）*4*2*1x x x ++； [解]3334*4*2*11***4*2*1*1005.1102110211021)()()()()(----=⨯=⨯+⨯+⨯=++=⎪⎪⎭⎫ ⎝⎛∂∂=++∑x x x x x f x x x e nk k k εεεε；（2）*3*2*1x x x ；[解]52130996425.010********.2131001708255.01048488.2121059768.01021)031.01021.1(1021)6.3851021.1(1021)6.385031.0()()()()()()()()(3333334*3*2*1*2*3*1*1*3*21***3*2*1*=⨯=⨯+⨯+⨯=⨯⨯+⨯⨯+⨯⨯=++=⎪⎪⎭⎫⎝⎛∂∂=-------=∑x x x x x x x x x x x f x x x e n k k kεεεε；（3）*4*2/x x 。
数值计算课后答案5
习 题 五 解 答1、用矩形公式、梯形公式、抛物线公式计算下列积分，并比较结果。
(1)120(8)4xdx n x =+⎰，(2)20sin (8)x xdx n π=⎰(3)1(4)n =⎰，(4)1(4)x e dxn -=⎰1*、用矩形公式、梯形公式、抛物线公式计算下列积分，并比较结果。
(1)120(4)4xdx n x =+⎰ 解：解：将区间［0，1］4等分，5个分点上的被积函数值列表如下（取2位小数）(1)矩形法。
用矩形法公式计算（取2位小数） 011()()1(00.060.120.16)0.094b n ab a f x dx y y y n--≈+++=+++≈⎰或者12()()1(0.060.120.160.20)0.144bn ab af x dx y y y n-≈+++=+++≈⎰(2)梯形法用梯形法公式计算（取2位小数）： 01211()[())]21[(00.20)0.060.120.16]0.114b n n ab a f x dx y y y y y n --≈+++++=++++≈⎰(3)抛物线法用抛物线法公式计算（取2位小数）： 2413b-a ()2(4(]3n1[(00.2)20.124(0.060.16)]0.1112b n af x dx y y y y y ≈+++++=++⨯+⨯+≈⎰ 0n-2n-1[(y )++y )++y )2、用复化梯形公式计算积分841dx x⎰，由此计算ln2（注：841ln 2dx x =⎰），精度要求为410-。
解：8418ln 8ln 4ln ln 24dx x =-==⎰，要求精度为410-，即误差不超过41102ε-=⨯。
将积分区间［4，8］n 等份，则步长844h n n -== 在本题中，复化梯形公式的余项为2228484416()()()()12123r h f f f n n ηηη--''''''=-=-=-注意到 231(),(),()2f x f x x f x x x--'''==-=，所以在［4，8］区间上3()24f x -''≤⨯，则32232161621283346r n n n -⨯≤⨯⨯==⨯， 要使42111062n -≤⨯，需有42421110310577.36757862n n n n n -≤⨯⇒≥⇒≥⇒≥⇒=。
数值计算方法课后习题答案
习题一1．设x >0相对误差为2%4x 的相对误差。
解：由自变量的误差对函数值引起误差的公式：(())(())'()()()()f x xf x f x x f x f x δδ∆=≈得 （1）()f x =11()()*2%1%22x x δδδ≈===；（2）4()f x x =时444()()'()4()4*2%8%x x x x x x δδδ≈===4．计算正方形面积时，若要求面积的允许相对误差为1%，测量边长所允许的相对误差限为多少？解：设该正方形的边长为x ，面积为2()f x x =，由(())(())'()()()()f x xf x f x x f x f x δδ∆=≈ 解得(())()()'()f x f x x xf x δδ≈=2(())(())22f x x f x x xδδ= =0.5%5．下面计算y 的公式哪个算得准确些？为什么？（1）已知1x <<，（A ）11121x y x x -=-++，（B ）22(12)(1)x y x x =++； （2）已知1x >>，（A）y =，（B）y =（3）已知1x <<，（A ）22sin x y x=，（B ）1cos 2xy x -=；（4）（A）9y =（B）y =解：当两个同（异）号相近数相减（加）时，相对误差可能很大，会严重丧失有效数字；当两个数相乘（除）时，大因子（小除数）可能使积（商）的绝对值误差增大许多。
故在设计算法时应尽量避免上述情况发生。
（1）（A ）中两个相近数相减，而（B ）中避免了这种情况。
故（B ）算得准确些。
（2）（B ）中两个相近数相减，而（A ）中避免了这种情况。
故（A ）算得准确些。
（3）（A ）中2sin x 使得误差增大，而（B ）中避免了这种情况发生。
故（B ）算得准确些。
（4）（A ）中两个相近数相减，而（B ）中避免了这种情况。
数值计算课后答案3
习 题 三 解 答1、用高斯消元法解下列方程组。
（1）12312312231425427x x x x x x x x -+=⎧⎪++=⎨⎪+=⎩①②③解：⨯4②＋(-)①2，12⨯③＋(-)①消去第二、三个方程的1x ，得：1232323231425313222x x x x x x x ⎧⎪-+=⎪-=⎨⎪⎪-=⎩④⑤⑥ 再由52)4⨯⑥＋(-⑤消去此方程组的第三个方程的2x ，得到三角方程组：1232332314272184x x x x x x ⎧⎪-+=⎪-=⎨⎪⎪-=⎩回代，得：36x =-，21x =-，19x = 所以方程组的解为(9,1,6)T x =--注意：①算法要求，不能化简。
化简则不是严格意义上的消元法，在算法设计上就多出了步骤。
实际上，由于数值计算时用小数进行的，化简既是不必要的也是不能实现的。
无论是顺序消元法还是选主元素消元法都是这样。
②消元法要求采用一般形式,或者说是分量形式，不能用矩阵，以展示消元过程。
要通过练习熟悉消元的过程而不是矩阵变换的技术。
矩阵形式错一点就是全错，也不利于检查。
一般形式或分量形式： 12312312231425427x x x x x x x x -+=⎧⎪++=⎨⎪+=⎩①②③ 矩阵形式123213142541207x x x -⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪= ⎪⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭向量形式 123213142541207x x x -⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪++= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭③必须是方程组到方程组的变形。
三元方程组的消元过程要有三个方程组，不能变形出单一的方程。
④消元顺序12x x →→L ，不能颠倒。
按为支援在方程组中的排列顺序消元也是存储算法的要求。
实际上，不按顺序消元是不规范的选主元素。
⑤不能化简方程，否则系数矩阵会变化，也不利于算法设计。
（2）1231231231132323110221x x x x x x x x x --=⎧⎪-++=⎨⎪++=-⎩①②③解：⨯23②＋()①11，111⨯③＋(-)①消去第二、三个方程的1x ，得： 123232311323523569111111252414111111x x x x x x x ⎧--=⎪⎪⎪-=⎨⎪⎪+=-⎪⎩④⑤⑥ 再由2511)5211⨯⑥＋(-⑤消去此方程组的第三个方程的2x ，得到三角方程组：123233113235235691111111932235252x x x x x x ⎧⎪--=⎪⎪-=⎨⎪⎪=-⎪⎩回代，得：32122310641,,193193193x x x =-==， 所以方程组的解为 41106223(,,)193193193Tx =-2、将矩阵1020011120110011A ⎛⎫ ⎪⎪= ⎪- ⎪⎝⎭作LU 分解。
数值计算课后习题答案
习 题 一 解 答1．取3.14，3.15，227，355113作为π的近似值，求各自的绝对误差，相对误差和有效数字的位数。
分析：求绝对误差的方法是按定义直接计算。
求相对误差的一般方法是先求出绝对误差再按定义式计算。
注意，不应先求相对误差再求绝对误差。
有效数字位数可以根据定义来求，即先由绝对误差确定近似数的绝对误差不超过那一位的半个单位，再确定有效数的末位是哪一位，进一步确定有效数字和有效数位。
有了定理2后，可以根据定理2更规范地解答。
根据定理2，首先要将数值转化为科学记数形式，然后解答。
解：（1）绝对误差:e(x)=π－3.14＝3.14159265…－3.14＝0.00159…≈0.0016。
相对误差：3()0.0016()0.51103.14r e x e x x-==≈⨯有效数字：因为π＝3.14159265…=0.314159265…×10，3.14＝0.314×10，m=1。
而π－3.14＝3.14159265…－3.14＝0.00159…所以│π－3.14│＝0.00159…≤0.005=0.5×10－2＝21311101022--⨯=⨯所以，3.14作为π的近似值有3个有效数字。
（2）绝对误差:e(x)=π－3.15＝3.14159265…－3.14＝－0.008407…≈－0.0085。
相对误差：2()0.0085()0.27103.15r e x e x x--==≈-⨯有效数字：因为π＝3.14159265…=0.314159265…×10，3.15＝0.315×10，m=1。
而π－3.15＝3.14159265…－3.15＝－0.008407…所以│π－3.15│＝0.008407……≤0.05=0.5×10－1＝11211101022--⨯=⨯所以，3.15作为π的近似值有2个有效数字。
（3）绝对误差:22() 3.14159265 3.1428571430.0012644930.00137e x π=-=-=-≈-相对误差：3()0.0013()0.4110227r e x e x x--==≈-⨯有效数字：因为π＝3.14159265...=0.314159265 (10)22 3.1428571430.3142857143107==⨯，m=1。
《数值计算方法》课后题答案(湖南大学曾金平)
习题一1．设x >0相对误差为2%，4x 的相对误差。
解：由自变量的误差对函数值引起误差的公式：(())(())'()()()()f x xf x f x x f x f x δδ∆=≈得（1）()f x =11()()*2%1%22x x δδδ≈===；（2）4()f x x =时444()()'()4()4*2%8%x x x x x xδδδ≈===2．设下面各数都是经过四舍五入得到的近似数，即误差不超过最后一位的半个单位，试指出他们各有几位有效数字。
（1）12.1x =；（2）12.10x =；（3）12.100x =。
解：由教材9P 关于1212.m nx a a a bb b =±型数的有效数字的结论，易得上面三个数的有效数字位数分别为：3，4，53．用十进制四位浮点数计算 （1）31.97+2.456+0.1352； （2）31.97+（2.456+0.1352）哪个较精确？解：（1）31.97+2.456+0.1352 ≈21((0.3197100.245610)0.1352)fl fl ⨯+⨯+ =2(0.3443100.1352)fl ⨯+=0.3457210⨯（2）31.97+（2.456+0.1352）21(0.319710(0.245610))fl fl ≈⨯+⨯ = 21(0.3197100.259110)fl ⨯+⨯ =0.3456210⨯易见31.97+2.456+0.1352=0.345612210⨯，故（2）的计算结果较精确。
4．计算正方形面积时，若要求面积的允许相对误差为1%，测量边长所允许的相对误差限为多少？解：设该正方形的边长为x ，面积为2()f x x =，由(())(())'()()()()f x xf x f x x f x f x δδ∆=≈解得(())()()'()f x f x x xf x δδ≈=2(())(())22f x x f x x xδδ==0.5%5．下面计算y 的公式哪个算得准确些？为什么？（1）已知1x <<，（A ）11121xy x x-=-++，（B ）22(12)(1)x y x x =++； （2）已知1x >>，（A）y =，（B）y =； （3）已知1x <<，（A ）22sin x y x =，（B ）1cos 2xy x-=；（4）（A）9y =（B）y =解：当两个同（异）号相近数相减（加）时，相对误差可能很大，会严重丧失有效数字；当两个数相乘（除）时，大因子（小除数）可能使积（商）的绝对值误差增大许多。