广西贵港市2019年中考数学总复习试题 题型专项(八)类型1 探究图形面积数量关系及最值等问题
2019年广西贵港市中考数学试卷附分析答案

2019 年广西贵港市中考数学试卷
参考答案与试题解析
一、选择题(本大题共 12 小题,每小题 3 分,共 36 分)每小题都给出标号为 A、B、C、
D 的四个选项,其中只有一个是正确的、请考生用 2B 铅笔在答题卡上将选定的答案标号涂
黑.
1.(3 分)计算(﹣1)3 的结果是( )
,
t
∴
,
C.2
∴DE=4,
,
∵∠ACD=∠B,
∠ADE=∠B,
∴∠ADE=∠ACD,
∵∠A=∠A,
∴△ADE∽△ACD,
t ∴
t ,
tt
第 10页(共 24页)
D.5
设 AE=2y,AC=3y,
t
∴
,
t
∴AD y,
∴
,
t
∴CD=2 ,
故选:C.
12.(3 分)如图,E 是正方形 ABCD 的边 AB 的中点,点 H 与 B 关于 CE 对称,EH 的延长
(图中阴影部分),若∠ACB=45°,则重叠部分的面积为( )
A.2 cm2
B.2 cm2
C.4cm2
【解答】解:如图,过 B 作 BD⊥AC 于 D,则∠BDC=90°,
∵∠ACB=45°,
∴∠CBD=45°,
第 9页(共 24页)
D.4 cm2
∴BD=CD=2cm, ∴Rt△BCD 中,BC ∴重叠部分的面积为 2 故选:A.
是( )
A.40°
B.50°
C.60°
【解答】解:∵
t,∠AOB=40°,
∴∠COD=∠AOB=40°,
∵∠AOB+∠BOC+∠COD=180°,
广西贵港市2019年届中考数学复习专项(一)计算求值题试题

题型专项(一) 计算求值题类型1 实数的运算1.(2019·钦州)计算:|-8|+(-2)3+tan45°- 4.解:原式=8-8+1-2=-1.2.(2019·河池模拟)计算:(π-3)0-|3-2|+(-13)-2-tan60°. 解:原式=1+3-2+9-3=8.3.(2019·昆明)计算:2 0160-|-2|+(13)-1+2sin45°. 解:原式=1-2+(3-1)-1+2×22=1-2+3+2=4. 类型2 分式的化简求值1.(2019·盐城)先化简,再求值:(x x -2+2x -4x 2-4x +4)·1x +2的值,其中x =3. 解:原式=x (x -2)+2x -4(x -2)2·1x +2=(x +2)(x -2)(x -2)2·1x +2 =1x -2. 当x =3时,原式=1.2.先化简,再求值:a 2-b 2a 2-2ab +b 2·a -b a +b -a a -b,其中a =1+3,b =1- 3. 解:原式=(a +b )(a -b )(a -b )2·a -b a +b -a a -b=a +b a -b ·a -b a +b -a a -b=1-a a -b =-b a -b . 当a =1+3,b =1-3时, 原式=-1-31+3-1+3=-1-323=3-36. 类型3 解分式方程1.(2019·龙岩)解方程:2x x -2+1=32-x. 解:方程两边都乘以(x -2),得2x +(x -2)=-3,解得x =-13.经检验,x =-13是原分式方程的解. 2.解方程:x +2x -2-1x +2=16x 2-4. 解:方程两边同乘(x 2-4),得(x +2)2-(x -2)=16,解得x 1=2,x 2=-5.检验:把x 1=2代入(x 2-4),得x 2-4=0,∴x =2是原方程的增根.把x 2=-5代入(x 2-4),得x 2-4=21≠0,∴原方程的解为x =-5.类型4 不等式(组)的解法1.(2019·南京)解不等式组:⎩⎪⎨⎪⎧3x +1≤2(x +1),①-x<5x +12,②并写出它的整数解. 解:解不等式①,得x≤1.解不等式②,得x>-2.∴不等式组的解集是-2<x≤1.∴该不等式组的整数解是-1、0、1.2.(2019·威海)解不等式组:⎩⎪⎨⎪⎧2x +5≤3(x +2),①1-2x 3+15>0,②并把解集表示在数轴上.解:解不等式①,得x≥-1.解不等式②,得x<45. ∴原不等式组的解集为-1≤x<45. ∴原不等式组的解集在数轴上表示为2019-2020学年数学中考模拟试卷一、选择题1.下列运算正确的是()A.3a3+a3=4a6B.(a+b)2=a2+b2C.5a﹣3a=2a D.(﹣a)2•a3=﹣a62.《九章算术》是中国传统数学最重要的著作之一,其中记载:“今有共买物人出八,盈三;人出七,不足四问人数、物价各几何?”译文:“几个人去购买物品,如果每人出8钱,则剩余3钱;如果每人出7钱,则差4钱问有多少人,物品的价格是多少”?设有m人,物品价格是n钱,下列四个等式:①8m+3=7m﹣4;②=;③=;④8m﹣3=7m+4,其中正确的是()A.①②B.②④C.②③D.③④3.如图,一个平行四边形被分成面积为S1、S2、S3、S4四个小平行四边形,当CD沿AB自左向右在平行四边形内平行滑动时,S1S4与S2S3的大小关系为()A.S1S4>S2S3B.S1S4<S2S3C.S1S4=S2S3D.无法确定4.若关于x的不等式组无解,且关于y的分式方程有非正整数解,则符合条件的所有整数k的值之和为()A.﹣7B.﹣12C.﹣20D.﹣345.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,点D是AC的中点,连接BD,按以下步骤作图:①分别以B,D为圆心,大于12BD的长为半径作弧,两弧相交于点P和点Q;②作直线PQ交AB于点E,交BC于点F,则BF=()A .56B .1C .136D .526.国家统计局统计资料显示,2018年第一季度我国国内生产总值为31355.55亿元,用科学记数法表示为( )元.(用四舍五入法保留3个有效数字)A .831355.510⨯B .133.1410⨯C .123.1410⨯D .123.1310⨯7.不等式组222x x >⎧⎨-≥-⎩的解集在数轴上表示为( )A .B .C .D .8.若两个连续整数x ,y 满足x <19﹣1<y ,则这两个整数是( )A .1和2B .2和3C .3和4D .4和59.如图,反比例函数y=k x的图象经过▱ABCD 对角线的交点P ,已知点A ,C ,D 在坐标轴上,BD ⊥DC ,▱ABCD 的面积为6,则k 的值为( )A .6-B .5-C .4-D .3-10.如图,A 是半径为1的⊙O 上两点,且OA ⊥OB .点P 从A 点出发,在⊙O 上以每秒一个的速度匀速单位运动:回A 点运动结束.设运动时间为x ,弦BP 长为y ,那么图象中可能表示数关y 与x 的函数关系的是( )A .①B .②C .①或④D .③或④11.《庄子》一书里有:“一尺之棰(木棍),日取其半,万世不竭(尽,完)”这句话可以用数学符号表示:1=23111++222+…+12n +…;也可以用图形表示.上述研究问题的过程中体现的主要数学思想是( )A .函数思想B .数形结合思想C .公理化思想D .分类讨论思想 12.二次函数y =ax 2+bx+c (a≠0)的图象如图所示,给出下列四个结论:①abc >0;3b+2c <0;③4a+c<2b ;④当y >0时,﹣52<x <12.其中结论正确的个数是( )A .2B .3C .4D .1二、填空题 13.正方形ABCD 中,F 是AB 上一点,H 是BC 延长线上一点,连接FH ,将△FBH 沿FH 翻折,使点B 的对应点E 落在AD 上,EH 与CD 交于点G ,连接BG 交FH 于点M ,当GB 平分∠CGE 时,BM=226,AE=8,则ED=_____.14.在矩形ABCD 中,AB=3cm ,BC=4cm ,则点A 到对角线BD 的距离为___________15.“任意打开一本100页的书,正好是第30页”,这是__事件(选填“随机”或“必然”或“不可能”).16.如图,直角ABC ∆中,090∠=A ,030B ∠=,4AC =,以A 为圆心,AC 长为半径画四分之一圆,则图中阴影部分的面积是________.(结果保留π)17.分解因式(x -1)2-4的结果是______.18.如图,在平面直角坐标系xOy 中,点A ,P 分别在x 轴、y 轴上,∠APO =30°.先将线段PA 沿y 轴翻折得到线段PB ,再将线段PA 绕点P 顺时针旋转30°得到线段PC ,连接BC .若点A 的坐标为(﹣1,0),则线段BC 的长为_____.三、解答题19.如图,在平面直角坐标系中,A(0,1),B(4,2),C(2,0).(1)将△ABC沿y轴翻折得到△A1B1C1,画出△A1B1C1;(2)将△ABC绕着点(﹣1,﹣1)旋转180°得到△A2B2C2,画出△A2B2C2;(3)线段B2C2可以看成是线段B1C1绕着平面直角坐标系中某一点逆时针旋转得到,直接写出旋转中心的坐标为.20.如图,在▱ABCD中,过A、B、C三点的⊙O交AD于点E,连接BE、CE,BE=BC.(1)求证:△BEC∽△CED;(2)若BC=10,DE=3.6,求⊙O的半径.21.某单位需要购买一些钢笔和笔记本.若购买2支钢笔和1本笔记本需42元,购买3支钢笔和2本笔记本需68元.(1)求买一支钢笔要多少钱?(2)若购买了钢笔和笔记本共50件,付款可能是810元吗?说明理由.22.3(1)5 5(1)3(5)x yy x-=+⎧⎨-=+⎩23.如图,直线m:y=kx(k>0)与直线n:3233y x=-+相交于点C,点A、B为直线n与坐标轴的交点,∠COA=60°,点P从O点出发沿线段OC向点C匀速运动,速度为每秒1个单位,同时点Q从点A出发沿线段AO向点O匀速运动,速度为每秒2个单位,设运动时间为t秒.(1)k=;(2)记△POQ的面积为S,求t为何值时S取得最大值;(3)当△POQ的面积最大时,以PQ为直径的圆与直线n有怎样的位置关系,请说明理由.24.甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中不超过200元的不打折,超过200元后的价格部分打7折.设商品原价为x元,顾客购物金额为y元.(I).根据题意,填写下表:商品原价100 150 250 …甲商场购物金额(元) 80 …乙商场购物金额(元) 100 …(Ⅱ).分别就两家商场的让利方式写出y关于x的函数关系式;(Ⅲ).若x≥500时,选择哪家商场去购物更省钱?并说明理由.25.如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.(1)求证:PB是⊙O的切线;(2)若OC=3,AC=4,求sin∠PAB的值.【参考答案】***一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12答案 C D C B C C C C D C B A二、填空题13.414.125cm15.随机16.4 433π-17.(x-3)( x+1)18.2三、解答题19.(1)详见解析;(2)详见解析;(3)(﹣2,﹣2).【解析】【分析】(1)利用关于y轴对称的点坐标特征写出点A1、B1、C1的坐标,然后描点即可;(2)利用网格特点和旋转的性质画出点A1、B1、C1的对应点A2、B2、C2,从而得到△A2B2C2;(3)作B1B2和C1C2的垂直平分线,它们相交于点P,则点P为旋转中心,然后写出P点坐标即可.【详解】解:(1)如图,△A1B1C1为所作;(2)如图,△A2B2C2为所作;(3)如图,线段B2C2可以看成是线段B1C1绕着点P逆时针旋转90°得到,此时P点的坐标为(﹣2,﹣2).故答案为(﹣2,﹣2).【点睛】本题考查了作图﹣旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.20.(1)见解析;(2)5091 91【解析】【分析】(1)证明两个等腰三角形相似,证明一个底角对应相等即可;(2)利用直径构造直角三角形,从而涉及到半径(直径),再利用垂径定理即可解决问题.【详解】(1)证明:∵BE=BC,∴∠BEC=∠BCE∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD.∴∠BCE=∠DEC,∠A+∠D=180°.∴∠BEC=∠DEC∵四边形ABCD内接于⊙O,∴∠A+∠BCE=180°.∴∠BCE=∠D∴△BEC∽△CED即得证.(2)过点O作OF⊥CE,垂足为F,连接OC,如下图.∴CF=12 CE,∴直线OF垂直平分CE,∵BE=BC,∴直线OF经过点B,∵△BEC∽△CED,又由(1)可知CE=CD,∴BC CE CE DE=,∵BC=10,DE=3.6,∴CE=CD=6∴CF=12CE=3,设⊙O的半径为r,可得BF=2291BC CF-=,OF=91﹣r,在Rt△OCF中,OF2+CF2=OC2,∴(91﹣r)2+9=r2∴r=5091 91,即圆的半径为5091 91.【点睛】本题考查的是相似三角形的判定与性质,尤其是对两个等腰三角形的判定更为特殊,利用直径构造直角三角形是相关问题中的常用思路.21.(1)16;(2)不可能,理由见解析.【解析】【分析】(1)设一支钢笔x 元,一本笔记本y 元,根据“购买2支钢笔和1本笔记本需42元,购买3支钢笔和2本笔记本需68元.”,即可得出关于x 、y 的二元一次方程组,解之即可得出结论;(2)设学校购买m 支钢笔,则购买(50﹣m )本笔记本,根据总价=单价×数量结合购买的费用为810元,即可得出关于m 的一元一次方程,解得m 的值为不大于50的正整数即可.【详解】解:(1)设一支钢笔x 元,一本笔记本y 元,根据题意得:2423268x y x y +=⎧⎨+=⎩, 解得:1610x y =⎧⎨=⎩. 答:一支钢笔16元,一本笔记本10元.(2)设学校购买m 支钢笔,则购买(50﹣m )本笔记本,根据题意得:16m+10(50﹣m )=810,解得:m =52>50,不符合题意.答:若购买了钢笔和笔记本共50件,付款不可能是810元.【点睛】本题考查了二元一次方程组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次方程.22.57x y =⎧⎨=⎩ 【解析】【分析】先将原方程组中的每个方程整理后利用加减消元法即可解答.【详解】原方程组可整理为:383520x y x y -=⎧⎨-+=⎩①② ①+②得:4y=28y=7把y=7代入①得:3x-7=8x=5∴原方程组的解为:57x y =⎧⎨=⎩ 【点睛】 本题考查解一元一次方程组,对于较复杂的方程组要先整理成一般形式再解方程组.掌握解一元一次方程组的方法:代入消元法、加减消元法是关键.23.(1)k =3;(2)当t =32时,S 有最大值;(3)直线AB 与以PQ 为直径的圆O 相离,理由详见解析. 【解析】【分析】(1)依据k =tan ∠COA 进行求解即可;(2)如图1所示:过点P 作PD ⊥OA ,垂足为D .由锐角三角函数的定义和特殊锐角三角函数值可求得PD =32t ,然后利用三角形的面积公式列出关系式,最后利用配方法求得三角形面积最大时t 的值即可; (3)如图2所示:过点P 作PD ⊥OA 垂足为D ,过圆心O 作OE ⊥AB ,垂足为E .首先证明四边形,四边形OPCE 为矩形,然后求得d 和r 的值即可.【详解】(1)k =tan ∠COA =tan60°=3.(2)如图1所示:过点P 作PD ⊥OA ,垂足为D .令直线n :y =﹣33 x+23的y =0得:﹣33x+23=0,解得x =6, ∴OA =6. ∵∠COA =60°,PD ⊥OA , ∴32PD OP = ,即32PD t =. ∴PD =32t . 2222133333393(62)(3()())()22222228OPQ S t t t t t =⨯-⨯=--+-=--+△ ∴当t =32时,S 有最大值. (3)如图2所示:过点P 作PD ⊥OA 垂足为D ,过圆心O 作OE ⊥AB ,垂足为E .令直线n:y =﹣33x+23的x=0得:y=23.∴OB=23.∵tan∠BAO =23363OBOA==,∴∠BAO=30°.∴∠ABO=60°.∴OC=OBsin60°=2332⨯=3.∵∠COA=60°,∴∠BOC=30°.∴∠BOC+∠OBC=90°.∴∠OCA=90°.当t=32时,OD=3122⨯=34,PD =3333=224⨯.DQ=3﹣34=94.∴tan∠PQO =3334=934.∴∠PQO=30°.∴∠BAO=∠PQO.∴PQ∥AB,∴∠CPQ+∠PCA=180°.∴∠CPQ=180°﹣90°=90°.∴∠ECP=∠CPO=∠OEC=90°.∴四边形OPCE为矩形.∴d=OE=PC=OC﹣OP=3﹣32=32.PQ=OQsin 60°=3×333=22.∴r=PO =13333=224⨯.∵d>r.∴直线AB与以PQ为直径的圆O相离.本题主要考查的是直线和圆的位置关系、一次函数、矩形的性质和判定、二次函数的最值、锐角三角函数的综合应用,求得d 和r 的值是解题的关键.24.(Ⅰ)120,150,200,235;(Ⅱ)甲商场0.8y x =(0)x ≥;乙商场y=(0200)0.760(200)x x x x ≤≤⎧⎨+>⎩;(Ⅲ)当600x =时,选择这两家商场一样合算;当x 600>时,选择乙商场更省钱;当500x<600≤时,选择甲商场更省钱【解析】【分析】(Ⅰ)根据题意分别求出购物金额即可;(Ⅱ)根据题意可得y 1的解析式,分别讨论0200x ≤≤时和x>200时,根据题意可得y 2的解析式;(Ⅲ)设顾客甲商场与乙商场的购物金额的差为y 元,得出x≥500时y 关于x 的解析式,根据一次函数的性质解答即可.【详解】(Ⅰ)150×80%=120(元),150×100%=150(元),250×80%=200(元),200+(250-200)×70%=235(元),故答案为:120,150,200,235(Ⅱ)甲商场()0.80y x x =≥;乙商场:当0≤x≤200时,y=x ,当x>200时,y=200+(x-200)×70%=0.7x+60,∴y=()02000.760(200)x x x x ⎧≤≤⎨+>⎩(Ⅲ)设顾客甲商场与乙商场的购物金额的差为y 元.∵x 500≥,()y 0.8x 0.7x 60∴=-+,即y 0.1x 60=-.当y=0时,即0.1x 600-=,得600x =.∴当600x =时,选择这两家商场一样合算.∵0.10>,∴y 随x 的增大而增大.∴当600x >时,有0y >,选择乙商场更省钱;当500x<600≤时,有0y <,选择甲商场更省钱【点睛】本题考查一次函数的实际应用,熟练掌握一次函数的性质是解题关键.25.(1)详见解析;(2)45【解析】(1)要证明是圆的切线,须证明过切点的半径垂直,所以连接OBB ,证明OB ⊥PE 即可;(2)证明∠PAB =∠AOC 即可得到结论.【详解】(1)证明:连接OB ,∵PA 为⊙O 相切于点A ,∴∠OAP =90°∵PO ⊥AB ,∴AC =BC ,∴PA =PB ,在△PAO 和△PBO 中PA PB AO B0PO P0=⎧⎪=⎨⎪=⎩,∴△PAO ≌△PBO (SSS ),∴∠OBP =∠OAP =90°,即PB ⊥OB ,∵OB 为⊙O 的半径,∴PB 是⊙O 的切线;(2)在Rt △ACO 中,OC =3,AC =4,∴AO =5,∵∠PAB+∠CAO =90°,∠AOC+∠CAO =90°∴∠PAB =∠AOC ,∴sin ∠PAB =AC AO =45. 【点睛】本题考查了切线的判定以及求三角函数值.能够通过角转移到相应的直角三角形中,是解答此题的关键.2019-2020学年数学中考模拟试卷一、选择题1.如图,在正方形ABCD 中,E 为AB 的中点,G ,F 分别为AD 、BC 边上的点,若AG=1,BF=2,∠GEF=90°,则GF 的长为( )A.2B.3C.4D.52.下列四个图案中,不是中心对称图案的是( )A. B. C. D.3.某地今年计划栽插这种超级杂交水稻3000亩,预计该地今年收获这种超级杂交水稻的总产量是2460000千克.用科学记数法表示是( )A.62.510⨯千克B.52.510⨯千克C.62.4610⨯千克D.52.4610⨯千克4.已知:1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52,…,根据前面各式的规律可猜测:101+103+105+…+199=( )A .7500B .10000C .12500D .25005.从甲,乙,丙三人中任选一名代表,甲被选中的可能性是 A.12 B.1 C.23 D.136.如图,在菱形ABOC 中,∠ABO =120°,它的一个顶点C 在反比例函数k y x=的图象上,若将菱形向下平移2个单位,点A 恰好落在函数图象上,则该反比函数的表达式为( )A .3y x =-B .33y x =-C .3y x =-D .23y x=- 7.若5-m m-3()>0,则( )A .m <5B .3≤m<5C .3≤m≤5D .3<m <5 8.计算11x -- 1x x -的结果为( )A .1B .2C .﹣1D .﹣29.如图,在△ABC 中,BD 平分∠ABC ,DE ∥BC ,且交AB 于点E ,∠A =60°,∠BDC =86°,则∠BDE 的度数为( )A .26°B .30°C .34°D .52°10.下列图形中,可以看作是中心对称图形的是( )A .B .C .D .11.实数a ,b ,c ,d 在数轴上的对应点的位置如图所示,则下列结论正确的是( )A.|a|>|b|B.a >﹣3C.a >﹣dD.11c< 12.如图,已知等腰梯形ABCD 中,AD ∥BC ,AB =DC ,AC 与BD 相交于点O ,则下列判断不正确的是( )A .△ABC ≌△DCBB .△AOD ≌△COBC .△ABO ≌△DCOD .△ADB ≌△DAC二、填空题 13.若关于x 的一元二次方程(k ﹣1)x 2+4x+1=0有实数根,则k 的取值范围是_____.14.已知△ABC 与△DEF 相似且周长比为2:5,则△ABC 与△DEF 的相似比为________15.正方形ABCD 的边长为10,点M 在AD 上,8AM =,过M 作MN AB ∥,分别交AC 、BC 于H 、N 两点,若E 、F 分别为(3)(2)x x f f ≤、BM 的中点,则EF 的长为_________________16.如图,在等腰Rt ABC 中,90ACB ︒∠=,4AC =,以边AC 为直径的半圆交AB 于点D ,则图中阴影部分的面积是__________(结果保留π).17.一次函数y x b =-+,当0b <时,这个一次函数的图象不经过的象限是________.18.据统计,2018年哈尔滨冰雪大世界接待中外游客突破45000000人次,请将45000000人用科学记数法表示为__________人.三、解答题19.云峰中学为了了解学生上学的交通方式,提高学生交通安全意识,开展了以“我上学的主要交通方式”为主题的调查活动,围绕“在乘公交车、城私家车、乘送子车、步行、骑自行车共五种方式中,你上学的主要交通方式是哪种?(必选且只选一种)”的问题,在全校范围内随机抽取部分学生进行问卷调查,将调查结果整理后绘制成如图所示的不完整的统计图.请你根据统计图中的信息回答下列问题:()1本次调查共抽取了多少名学生?()2通过计算补全条形统计图;()3若云峰中学共有1200名学生,请你估计该中学步行上学的学生有多少名.20.我市某高科技公司生产一种矩形新型材料板,其长宽之比为 3∶2,每张材料板的成本 c 与它的面积成正比例。
广西贵港市2019年中考数学真题试题(含解析)
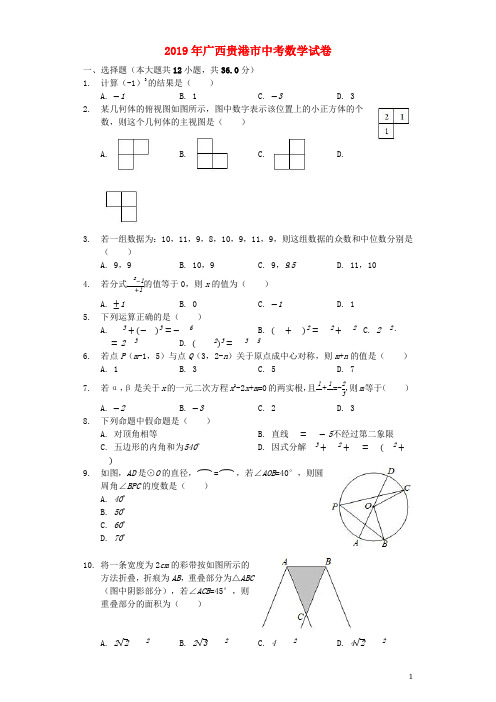
2019年广西贵港市中考数学试卷一、选择题(本大题共12小题,共36.0分)1. 计算(-1)3的结果是( )A. −1B. 1C. −3D. 32. 某几何体的俯视图如图所示,图中数字表示该位置上的小正方体的个数,则这个几何体的主视图是( ) A. B. C. D.3. 若一组数据为:10,11,9,8,10,9,11,9,则这组数据的众数和中位数分别是( )A. 9,9B. 10,9C. 9,9.5D. 11,104. 若分式x 2−1x +1的值等于0,则x 的值为( )A. ±1B. 0C. −1D. 15. 下列运算正确的是( )A. x 3+(−x )3=−x 6B. (x +x )2=x 2+x 2C. 2x 2⋅x =2x 3D. (xx 2)3=x 3x 5 6. 若点P (m -1,5)与点Q (3,2-n )关于原点成中心对称,则m +n 的值是( )A. 1B. 3C. 5D. 77. 若α,β是关于x 的一元二次方程x 2-2x +m =0的两实根,且1x +1x =-23,则m 等于( )A. −2B. −3C. 2D. 38. 下列命题中假命题是( )A. 对顶角相等B. 直线x =x −5不经过第二象限C. 五边形的内角和为540∘D. 因式分解x 3+x 2+x =x (x 2+x )9. 如图,AD 是⊙O 的直径,xx⏜=xx ⏜,若∠AOB =40°,则圆周角∠BPC 的度数是( )A. 40∘B. 50∘C. 60∘D. 70∘10. 将一条宽度为2cm 的彩带按如图所示的方法折叠,折痕为AB ,重叠部分为△ABC(图中阴影部分),若∠ACB =45°,则重叠部分的面积为( )A. 2√2xx 2B. 2√3xx 2C. 4xx 2D. 4√2xx 211. 如图,在△ABC 中,点D ,E 分别在AB ,AC 边上,DE ∥BC ,∠ACD =∠B ,若AD =2BD ,BC =6,则线段CD 的长为( ) A. 2√3B. 3√2C. 2√6D. 512. 如图,E 是正方形ABCD 的边AB 的中点,点H 与B 关于CE对称,EH 的延长线与AD 交于点F ,与CD 的延长线交于点N ,点P 在AD 的延长线上,作正方形DPMN ,连接CP ,记正方形ABCD ,DPMN 的面积分别为S 1,S 2,则下列结论错误的是( )A. x 1+x 2=xx 2B. 4x =2xxC. xx =4xxD. cos ∠xxx =35 二、填空题(本大题共6小题,共18.0分)13. 有理数9的相反数是______.14. 将实数3.18×10-5用小数表示为______.15. 如图,直线a ∥b ,直线m 与a ,b 均相交,若∠1=38°,则∠2=______.16. 若随机掷一枚均匀的骰子,骰子的6个面上分别刻有1,2,3,4,5,6点,则点数不小于3的概率是______.17. 如图,在扇形OAB 中,半径OA 与OB 的夹角为120°,点A 与点B 的距离为2√3,若扇形OAB 恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为______.18. 我们定义一种新函数:形如y =|ax 2+bx +c |(a ≠0,且b 2-4a >0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y =|x 2-2x -3|的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为(-1,0),(3,0)和(0,3);②图象具有对称性,对称轴是直线x =1;③当-1≤x ≤1或x ≥3时,函数值y 随x 值的增大而增大;④当x =-1或x =3时,函数的最小值是0;⑤当x =1时,函数的最大值是4.其中正确结论的个数是______.三、解答题(本大题共8小题,共66.0分)19. (1)计算:√4-(√3-3)0+(12)-2-4sin30°;(2)解不等式组:{6x −2>2(x −4)23−3−x 2≤−x 3,并在数轴上表示该不等式组的解集.20. 尺规作图(只保留作图痕迹,不要求写出作法):如图,已知△ABC ,请根据“SAS ”基本事实作出△DEF ,使△DEF ≌△ABC .21. 如图,菱形ABCD 的边AB 在x 轴上,点A 的坐标为(1,0),点D (4,4)在反比例函数y =x x (x >0)的图象上,直线y =23x +b 经过点C ,与y 轴交于点E ,连接AC ,AE .(1)求k ,b 的值;(2)求△ACE 的面积.22. 为了增强学生的安全意识,某校组织了一次全校2500名学生都参加的“安全知识”考试.阅卷后,学校团委随机抽取了100份考卷进行分析统计,发现考试成绩(x 分)的最低分为51分,最高分为满分100分,并绘制了如下尚不完整的统计图表.请根据图表提供的信息,解答下列问题:分数段(分) 频数(人) 频率51≤x <61a 0.1 61≤x <7118 0.18 71≤x <81b n91≤x<101 12 0.12合计100 1(1)填空:=______,=______,=______;(2)将频数分布直方图补充完整;(3)该校对考试成绩为91≤x≤100的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为1:3:6,请你估算全校获得二等奖的学生人数.23.为了满足师生的阅读需求,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.(1)求这两年藏书的年均增长率;(2)经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的5.6%,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到2018年底中外古典名著的册数占藏书总量的百分之几?24.如图,在矩形ABCD中,以BC边为直径作半圆O,OE⊥OA交CD边于点E,对角线AC与半圆O的另一个交点为P,连接AE.(1)求证:AE是半圆O的切线;(2)若PA=2,PC=4,求AE的长.25.如图,已知抛物线y=ax2+bx+c的顶点为A(4,3),与y轴相交于点B(0,-5),对称轴为直线l,点M是线段AB的中点.(1)求抛物线的表达式;(3)设动点P,Q分别在抛物线和对称轴l上,当以A,P,Q,M为顶点的四边形是平行四边形时,求P,Q两点的坐标.26.已知:△ABC是等腰直角三角形,∠BAC=90°,将△ABC绕点C顺时针方向旋转得到△A′B′C,记旋转角为α,当90°<α<180°时,作A′D⊥AC,垂足为D,A′D 与B′C交于点E.(1)如图1,当∠CA′D=15°时,作∠A′EC的平分线EF交BC于点F.①写出旋转角α的度数;②求证:EA′+EC=EF;(2)如图2,在(1)的条件下,设P是直线A′D上的一个动点,连接PA,PF,若AB=√2,求线段PA+PF的最小值.(结果保留根号)答案和解析1.【答案】A【解析】解:(-1)3表示3个(-1)的乘积,所以(-1)3=-1.故选:A.本题考查有理数的乘方运算.乘方是乘法的特例,乘方的运算可以利用乘法的运算来进行.负数的奇数次幂是负数,负数的偶数次幂是正数;-1的奇数次幂是-1,-1的偶数次幂是1.2.【答案】B【解析】解:从正面看去,一共两列,左边有2竖列,右边是1竖列.故选:B.先细心观察原立体图形中正方体的位置关系,从正面看去,一共两列,左边有2竖列,右边是1竖列,结合四个选项选出答案.本题考查了由三视图判断几何体,解题的关键是具有几何体的三视图及空间想象能力.3.【答案】C【解析】解:将数据重新排列为8,9,9,9,10,10,11,11,∴这组数据的众数为9,中位数为=9.5,故选:C.根据众数和中位数的概念求解可得.本题为统计题,考查众数与中位数的意义.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.4.【答案】D【解析】解:==x-1=0,∴x=1;故选:D.化简分式==x-1=0即可求解;本题考查解分式方程;熟练掌握因式分解的方法,分式方程的解法是解题的关键.5.【答案】C【解析】解:a3+(-a3)=0,A错误;(a+b)2=a2+2ab+b2,B错误;(ab2)3=a3b5,D错误;故选:C.利用完全平方公式,合并同类项法则,幂的乘方与积的乘方法则运算即可;本题考查整式的运算;熟练掌握完全平方公式,合并同类项法则,幂的乘方与积的乘方法则是解题的关键.6.【答案】C【解析】解:∵点P(m-1,5)与点Q(3,2-n)关于原点对称,∴m-1=-3,2-n=-5,解得:m=-2,n=7,则m+n=-2+7=5.故选:C.根据关于原点对称的点的横坐标互为相反数,纵坐标互为相反数,可得答案.本题考查了关于原点对称的点的坐标,关于原点对称的点的横坐标互为相反数,纵坐标互为相反数.7.【答案】B【解析】解:α,β是关于x的一元二次方程x2-2x+m=0的两实根,∴α+β=2,αβ=m,∵+===-,∴m=-3;故选:B.利用一元二次方程根与系数的关系得到α+β=2,αβ=m,再化简+=,代入即可求解;本题考查一元二次方程;熟练掌握一元二次方程根与系数的关系是解题的关键.8.【答案】D【解析】解:A.对顶角相等;真命题;B.直线y=x-5不经过第二象限;真命题;C.五边形的内角和为540°;真命题;D.因式分解x3+x2+x=x(x2+x);假命题;故选:D.由对顶角相等得出A是真命题;由直线y=x-5的图象得出B是真命题;由五边形的内角和为540°得出C是真命题;由因式分解的定义得出D是假命题;即可得出答案.本题考查了命题与定理、真命题和假命题的定义:正确的命题是真命题,错误的命题是假命题;属于基础题.9.【答案】B【解析】解:∵=,∠AOB=40°,∴∠COD=∠AOB=40°,∵∠AOB+∠BOC+∠COD=180°,∴∠BOC=100°,∴∠BPC=∠BOC=50°,故选:B.根据圆周角定理即可求出答案.本题考查了圆周角定理,熟练掌握圆周角定理是解题的关键.10.【答案】A【解析】解:如图,过B作BD⊥AC于D,则∠BDC=90°,∵∠ACB=45°,∴BD=CD=2cm,∴Rt△BCD中,BC==2(cm),∴重叠部分的面积为×2×2=2(cm),故选:A.过B作BD⊥AC于D,则∠BDC=90°,依据勾股定理即可得出BC的长,进而得到重叠部分的面积.本题主要考查了折叠问题,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.11.【答案】C【解析】解:设AD=2x,BD=x,∴AB=3x,∵DE∥BC,∴△ADE∽△ABC,∴=,∴=,∴DE=4,=,∵∠ACD=∠B,∠ADE=∠B,∴∠ADE=∠ACD,∵∠A=∠A,∴△ADE∽△ACD,∴=,设AE=2y,AC=3y,∴=,∴AD=y,∴=,∴CD=2,故选:C.设AD=2x,BD=x,所以AB=3x,易证△ADE∽△ABC,利用相似三角形的性质可求出DE的长度,以及,再证明△ADE∽△ACD,利用相似三角形的性质即可求出得出=,从而可求出CD的长度.本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于中等题型.12.【答案】D【解析】解:∵正方形ABCD,DPMN的面积分别为S1,S2,在Rt△PCD中,PC2=CD2+PD2,∴S1+S2=CP2,故A结论正确;连接CF,∵点H与B关于CE对称,∴CH=CB,∠BCE=∠ECH,在△BCE和△HCE中,∴△BCE≌△HCE(SAS),∴BE=EH,∠EHC=∠B=90°,∠BEC=∠HEC,∴CH=CD,在Rt△FCH和Rt△FCD中∴Rt△FCH≌Rt△FCD(HL),∴∠FCH=∠FCD,FH=FD,∴∠ECH+∠ECH=∠BCD=45°,即∠ECF=45°,作FG⊥EC于G,∴△CFG是等腰直角三角形,∴FG=CG,∵∠BEC=∠HEC,∠B=∠FGE=90°,∴△FEG∽△CEB,∴==,∴FG=2EG,设EG=x,则FG=2x,∴CG=2x,CF=2x,∴EC=3x,∵EB2+BC2=EC2,∴BC2=9x2,∴BC2=x2,∴BC=x,在Rt△FDC中,FD===x,∴3FD=AD,∴AF=2FD,故B结论正确;∵AB∥CN,∴=,∵PD=ND,AE=CD,∴CD=4PD,故C结论正确;∴EF=x,∵FH=FD=x,∵BC=x,∴AE=x,作HQ⊥AD于Q,∴HQ∥AB,∴=,即=,∴HQ=x,∴CD-HQ=x-x=x,∴cos∠HCD===,故结论D错误,故选:D.根据勾股定理可判断A;连接CF,作FG⊥EC,易证得△FGC是等腰直角三角形,设EG=x,则FG=2x,利用三角形相似的性质以及勾股定理得到CG=2x,CF=2x,EC=3x,BC=x,FD=x,即可证得3FD=AD,可判断B;根据平行线分线段成比例定理可判断C;求得cos∠HCD 可判断D.本题考查了正方形的性质,三角形全等的判定和性质三角形相似的判定和性质,勾股定理的应用以及平行线分线段成比例定理,作出辅助线构建等腰直角三角形是解题的关键.13.【答案】-9【解析】解:9的相反数是-9;故答案为-9;根据相反数的求法即可得解;本题考查相反数;熟练掌握相反数的意义与求法是解题的关键.14.【答案】0.0000318【解析】解:3.18×10-5=0.0000318;故答案为0.0000318;根据科学记数法的表示方法a×10n(1≤a<9)即可求解;本题考查科学记数法;熟练掌握科学记数法的表示方法是解题的关键.15.【答案】142°【解析】解:如图,∵a∥b,∴∠2=∠3,∵∠1+∠3=180°,∴∠2=180°-38°=142°.如图,利用平行线的性质得到∠2=∠3,利用互补求出∠3,从而得到∠2的度数.本题考查了平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.16.【答案】23【解析】解:随机掷一枚均匀的骰子有6种等可能结果,其中点数不小于3的有4种结果,所以点数不小于3的概率为=,故答案为:.骰子六个面出现的机会相同,求出骰子向上的一面点数不小于3的情况有几种,直接应用求概率的公式求解即可.此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.17.【答案】23【解析】解:连接AB,过O作OM⊥AB于M,∵∠AOB=120°,OA=OB,∴∠BAO=30°,AM=,∴OA=2,∵=2πr,∴r=故答案是:利用弧长=圆锥的周长这一等量关系可求解.本题运用了弧长公式和圆的周长公式,建立准确的等量关系是解题的关键.18.【答案】4【解析】(3,0)和(0,3)坐标都满足函数y=|x2-2x-3|,解:①∵(-1,0),∴①是正确的;②从图象可知图象具有对称性,对称轴可用对称轴公式求得是直线x=1,因此②也是正确的;③根据函数的图象和性质,发现当-1≤x≤1或x≥3时,函数值y随x值的增大而增大,因此③也是正确的;④函数图象的最低点就是与x轴的两个交点,根据y=0,求出相应的x的值为x=-1或x=3,因此④也是正确的;⑤从图象上看,当x<-1或x>3,函数值要大于当x=1时的y=|x2-2x-3|=4,因此⑤时不正确的;故答案是:4由(-1,0),(3,0)和(0,3)坐标都满足函数y=|x 2-2x-3|,∴①是正确的;从图象可以看出图象具有对称性,对称轴可用对称轴公式求得是直线x=1,②也是正确的; 根据函数的图象和性质,发现当-1≤x≤1或x≥3时,函数值y 随x 值的增大而增大,因此③也是正确的;函数图象的最低点就是与x 轴的两个交点,根据y=0,求出相应的x 的值为x=-1或x=3,因此④也是正确的;从图象上看,当x <-1或x >3,函数值要大于当x=1时的y=|x 2-2x-3|=4,因此⑤时不正确的;逐个判断之后,可得出答案. 理解“鹊桥”函数y=|ax 2+bx+c|的意义,掌握“鹊桥”函数与y=|ax 2+bx+c|与二次函数y=ax 2+bx+c 之间的关系;两个函数性质之间的联系和区别是解决问题的关键;二次函数y=ax 2+bx+c 与x 轴的交点、对称性、对称轴及最值的求法以及增减性应熟练掌握.19.【答案】解:(1)原式=2-1+4-4×12 =2-1+4-2 =3;(2)解不等式6x -2>2(x -4),得:x >-32, 解不等式23-3−x 2≤-x 3,得:x ≤1, 则不等式组的解集为-32<x ≤1,将不等式组的解集表示在数轴上如下:【解析】(1)先计算算术平方根、零指数幂、负整数指数幂、代入三角函数值,再计算乘法,最后计算加减可得;(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.20.【答案】解:如图,△DEF 即为所求.【解析】先作一个∠D=∠A ,然后在∠D 的两边分别截取ED=BA ,DF=AC ,连接EF 即可得到△DEF ; 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了全等三角形的判定.21.【答案】解:(1)由已知可得AD =5,∵菱形ABCD ,∴B (6,0),C (9,4), ∵点D (4,4)在反比例函数y =x x (x >0)的图象上,∴k =16,将点C (9,4)代入y =23x +b ,∴b =-2;(2)E (0,-2),直线y =23x -2与x 轴交点为(3,0),∴S △AEC =12×2×(2+4)=6;【解析】(1)由菱形的性质可知B (6,0),C (9,4),点D (4,4)代入反比例函数y=,求出k ;将点C (9,4)代入y=x+b ,求出b ;(2)求出直线y=x-2与x 轴和y 轴的交点,即可求△AEC 的面积;本题考查反比例函数、一次函数的图象及性质,菱形的性质;能够将借助菱形的边长和菱形边的平行求点的坐标是解题的关键.22.【答案】10 25 0.25【解析】解:(1)a=100×0.1=10,b=100-10-18-35-12=25,n==0.25;故答案为:10,25,0.25;(2)补全频数分布直方图如图所示;(3)2500××=90(人), 答:全校获得二等奖的学生人数90人.(1)利用×这组的频率即可得到结论;(2)根据(1)求出的数据补全频数分布直方图即可;(3)利用全校2500名学生数×考试成绩为91≤x≤100考卷占抽取了的考卷数×获得二等奖学生人数占获奖学生数即可得到结论.本题考查的是频数分布直方图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.直方图能清楚地表示出每个项目的数据,也考查了利用样本估计总体的思想.23.【答案】解:(1)设这两年藏书的年均增长率是x ,5(1+x )2=7.2,解得,x 1=0.2,x 2=-2.2(舍去),答:这两年藏书的年均增长率是20%;(2)在这两年新增加的图书中,中外古典名著有(7.2-5)×20%=0.44(万册), 到2018年底中外古典名著的册数占藏书总量的百分比是:5×5.6%+0.447.2×100%=10%,答:到2018年底中外古典名著的册数占藏书总量的10%.【解析】(1)根据题意可以列出相应的一元二次方程,从而可以得到这两年藏书的年均增长率;(2)根据题意可以求出这两年新增加的中外古典名著,从而可以求得到2018年底中外古典名著的册数占藏书总量的百分之几.本题考查一元二次方程的应用,解答本题的关键是明确题意,列出相应的方程,利用方程的知识解答,这是一道典型的增长率问题.24.【答案】(1)证明:∵在矩形ABCD 中,∠ABO =∠OCE =90°,∵OE ⊥OA ,∴∠AOE =90°,∴∠BAO +∠AOB =∠AOB +∠COE =90°,∴∠BAO =∠COE ,∴△ABO ∽△OCE , ∴xx xx =xx xx , ∵OB =OC , ∴xx xx =xx xx ,∵∠ABO =∠AOE =90°,∴△ABO ∽△AOE ,∴∠BAO =∠OAE ,过O 作OF ⊥AE 于F ,∴∠ABO =∠AFO =90°,在△ABO 与△AFO 中,{∠xxx =∠xxx∠xxx =∠xxx xx =xx,∴△ABO ≌△AFO (AAS ),∴OF =OB ,∴AE 是半圆O 的切线;(2)解:∵AF 是⊙O 的切线,AC 是⊙O 的割线,∴AF 2=AP •AC ,∴AF =√2(2+4)=2√3,∴AB =AF =2√3,∵AC =6,∴BC =√xx 2−xx 2=2√6,∴AO =√xx 2+xx 2=3,∵△ABO ∽△AOE , ∴xx xx =xx xx ,∴3xx =2√33, ∴AE =3√32. 【解析】(1)根据已知条件推出△ABO ∽△OCE ,根据相似三角形的性质得到∠BAO=∠OAE ,过O 作OF ⊥AE 于F ,根据全等三角形的性质得到OF=OB ,于是得到AE 是半圆O 的切线;(2)根据切割线定理得到AF==2,求得AB=AF=2,根据勾股定理得到BC==2,AO==3,根据相似三角形的性质即可得到结论.本题考查了切线的判定和性质,矩形的性质,相似三角形的判定和性质,全等三角形的判定和性质,正确的作出辅助线是解题的关键.25.【答案】解:(1)函数表达式为:y=a(x=4)2+3,将点B坐标代入上式并解得:a=-1,2x2+4x-5;故抛物线的表达式为:y=-12(2)A(4,3)、B(0,-5),则点M(2,-1),设直线AB的表达式为:y=kx-5,将点A坐标代入上式得:3=4k-5,解得:k=2,故直线AB的表达式为:y=2x-5;m2+4m-5),(3)设点Q(4,s)、点P(m,-12①当AM是平行四边形的一条边时,点A向左平移2个单位、向下平移4个单位得到M,m2+4m-5)向左平移2个单位、向下平移4个单位得到Q(4,s),同样点P(m,-12m2+4m-5-4=s,即:m-2=4,-12解得:m=6,s=-3,故点P、Q的坐标分别为(6,1)、(4,-3);②当AM是平行四边形的对角线时,m2+4m-5+s,由中点定理得:4+2=m+4,3-1=-12解得:m=2,s=1,故点P、Q的坐标分别为(2,1)、(4,1);故点P、Q的坐标分别为(6,1)或(2,1)、(4,-3)或(4,1).【解析】(1)函数表达式为:y=a(x=4)2+3,将点B坐标代入上式,即可求解;(2)A(4,3)、B(0,-5),则点M(2,-1),设直线AB的表达式为:y=kx-5,将点A坐标代入上式,即可求解;(3)分当AM是平行四边形的一条边、AM是平行四边形的对角线两种情况,分别求解即可.本题考查的是二次函数综合运用,涉及到一次函数、平行四边形性质、图象的面积计算等,其中(3),要主要分类求解,避免遗漏.26.【答案】(1)①解:旋转角为105°.理由:如图1中,∵A ′D ⊥AC ,∴∠A ′DC =90°,∵∠CA ′D =15°,∴∠A ′CD =75°,∴∠ACA ′=105°,∴旋转角为105°.②证明:连接A ′F ,设EF 交CA ′于点O .在EF 时截取EM =EC ,连接CM . ∵∠CED =∠A ′CE +∠CA ′E =45°+15°=60°,∴∠CEA ′=120°,∵FE 平分∠CEA ′,∴∠CEF =∠FEA ′=60°,∵∠FCO =180°-45°-75°=60°,∴∠FCO =∠A ′EO ,∵∠FOC =∠A ′OE ,∴△FOC ∽△A ′OE ,∴xx x′x =xx xx ,∴xx xx =x′x xx ,∵∠COE =∠FOA ′,∴△COE ∽△FOA ′,∴∠FA ′O =∠OEC =60°,∴△A ′OF 是等边三角形,∴CF =CA ′=A ′F ,∵EM =EC ,∠CEM =60°,∴△CEM 是等边三角形,∠ECM =60°,CM =CE ,∵∠FCA ′=∠MCE =60°,∴∠FCM =∠A ′CE ,∴△FCM ≌△A ′CE (SAS ),∴FM =A ′E ,∴CE +A ′E =EM +FM =EF .(2)解:如图2中,连接A ′F ,PB ′,AB ′,作B ′M ⊥AC 交AC 的延长线于M .由②可知,∠EA′F=′EA′B′=75°,A′E=A′E,A′F=A′B′,∴△A′EF≌△A′EB′,∴EF=EB′,∴B′,F关于A′E对称,∴PF=PB′,∴PA+PF=PA+PB′≥AB′,在Rt△CB′M中,CB′=BC=√2AB=2,∠MCB′=30°,CB′=1,CM=√3,∴B′M=12∴AB′=√xx2+x′x2=√(√2+√3)2+12=√626.∴PA+PF的最小值为√626.【解析】(1)①解直角三角形求出∠A′CD即可解决问题.②连接A′F,设EF交CA′于点O.在EF时截取EM=EC,连接CM.首先证明△CFA′是等边三角形,再证明△FCM≌△A′CE(SAS),即可解决问题.(2)如图2中,连接A′F,PB′,AB′,作B′M⊥AC交AC的延长线于M.证明△A′EF≌△A′EB′,推出EF=EB′,推出B′,F关于A′E对称,推出PF=PB′,推出PA+PF=PA+PB′≥AB′,求出AB′即可解决问题.本题属于四边形综合题,考查了旋转变换,全等三角形的判定和性质,相似三角形的判定和性质,三角形的三边关系等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用转化的思想思考问题,属于中考压轴题.。
广西贵港市2019年中考数学试题

……○…………装学校:___________姓名……○…………装绝密★启用前广西贵港市2019年中考数学试题试卷副标题注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 一、单选题1.计算(−1)3的结果是( * ). A .-1 B .1C .-3D .3【答案】A 【解析】(−1)3表示3个-1相乘,故选A2.某几何体的俯视图如图所示,图中数字表示该位置上的小正方体的个数,则这个几何体的主视图是( )A .B .C .D .【答案】B 【解析】 【分析】先细心观察原立体图形中正方体的位置关系,从正面看去,一共两列,左边有2竖列,右边是1竖列,结合四个选项选出答案. 【详解】解:从正面看去,一共两列,左边有2竖列,右边是1竖列.试卷第2页,总27页故选:B . 【点睛】本题考查了由三视图判断几何体,解题的关键是具有几何体的三视图及空间想象能力. 3.若一组数据为:10,11,9,8,10,9,11,9,则这组数据的众数和中位数分别是( ) A .9,9 B .10,9C .9,9.5D .11,10【答案】C 【解析】 【分析】根据众数和中位数的概念求解可得. 【详解】解:将数据重新排列为8,9,9,9,10,10,11,11, ∴这组数据的众数为9,中位数为9109.52+=, 故选:C . 【点睛】本题为统计题,考查众数与中位数的意义.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.4.若分式211x x -+的值为0,则x 的值为( )A .0B .1C .﹣1D .±1【答案】B 【解析】【分析】根据分式值为0的条件,分子为0分母不为0列式进行计算即可得.【详解】∵分式2x 1x 1-+的值为零,∴21010x x -=⎧⎨+≠⎩, 解得:x=1, 故选B .【点睛】本题考查了分式值为0的条件,熟知分式值为0的条件是分子为0分母不为0是解题的关键.5.下列运算正确的是( )A .()336a a a +-=- B .()222a b a b +=+ C .2322a a a ⋅= D .()3235ab a b =【答案】C 【解析】 【分析】利用完全平方公式,合并同类项法则,幂的乘方与积的乘方法则运算即可; 【详解】 解:()330a a+-=,A 错误;()2222a b a ab b +=++,B 错误;()3235ab a b =,D 错误;故选:C . 【点睛】本题考查整式的运算;熟练掌握完全平方公式,合并同类项法则,幂的乘方与积的乘方法则是解题的关键.6.若点()1,5P m -与点()3,2Q n -关于原点成中心对称,则m n +的值是( ) A .1 B .3C .5D .7【答案】C 【解析】 【分析】根据关于原点对称的点的横坐标互为相反数,纵坐标互为相反数,可得答案. 【详解】解:∵点()1,5P m -与点()3,2Q n -关于原点对称, ∴13m -=-,25n -=-, 解得:2m =-,7n =, 则275m n +=-+= 故选:C . 【点睛】本题考查了关于原点对称的点的坐标,关于原点对称的点的横坐标互为相反数,纵坐标互为相反数.试卷第4页,总27页7.若α,β是关于x 的一元二次方程2x 2x m 0-+=的两实根,且1123αβ+=-,则m 等于( )A .2-B .3-C .2D .3【答案】B 【解析】 【分析】利用一元二次方程根与系数的关系得到2αβ+=,m =ab ,再化简11αβαβαβ++=,代入即可求解; 【详解】解:α,β是关于x 的一元二次方程2x 2x m 0-+=的两实根, ∴2αβ+=,m =ab ,∵11223m αβαβαβ++===-, ∴3m =-; 故选:B . 【点睛】本题考查一元二次方程;熟练掌握一元二次方程根与系数的关系是解题的关键. 8.下列命题中假命题是( ) A .对顶角相等B .直线5y x =-不经过第二象限C .五边形的内角和为540︒D .因式分解()322x x x x x x ++=+【答案】D 【解析】 【分析】由对顶角相等得出A 是真命题;由直线5y x =-的图象得出B 是真命题;由五边形的内角和为540︒得出C 是真命题;由因式分解的定义得出D 是假命题;即可得出答案. 【详解】解:A .对顶角相等;真命题;B .直线5y x =-不经过第二象限;真命题;…订…………○_____考号:___________…订…………○C .五边形的内角和为540︒;真命题;D .因式分解()322+1++=+x x x x x x ;假命题; 故选:D . 【点睛】本题考查了命题与定理、真命题和假命题的定义:正确的命题是真命题,错误的命题是假命题;属于基础题.9.如图,AD 是O e 的直径,»»AB CD =,若40AOB ∠=︒,则圆周角BPC ∠的度数是( )A .40︒B .50︒C .60︒D .70︒【答案】B 【解析】 【分析】根据圆周角定理即可求出答案. 【详解】解:∵»»AB CD =,40AOB ∠=︒, ∴40COD AOB ∠=∠=︒,∵180AOB BOC COD ∠+∠+∠=︒, ∴100BOC ∠=︒, ∴1502BPC BOC ∠=∠=︒, 故选:B . 【点睛】本题考查了圆周角定理,熟练掌握圆周角定理是解题的关键.10.将一条宽度为2cm 的彩带按如图所示的方法折叠,折痕为AB ,重叠部分为ABC ∆(图中阴影部分),若45ACB ∠=︒,则重叠部分的面积为( )试卷第6页,总27页……○……………………订……………○……订※※线※※内※※答……○……………………订……………○……A .2B .2C .24cmD .2【答案】A 【解析】 【分析】过B 作BD AC ⊥于D ,则90BDC ∠=︒,依据勾股定理即可得出BC 的长,进而得到重叠部分的面积. 【详解】解:如图,过B 作BD AC ⊥于D ,则90BDC ∠=︒, ∵45ACB ∠=︒, ∴45CBD ∠=︒, ∴2BD CD cm ==, ∴Rt BCD ∆中,)BC cm ==,∴重叠部分的面积为)122cm ⨯=, 故选:A . 【点睛】本题主要考查了折叠问题,折叠是一种对称变换,它属于轴对称,折叠前后=图形的形状和大小不变,位置变化,对应边和对应角相等.11.如图,在ABC ∆中,点D ,E 分别在AB ,AC 边上,//DE BC ,ACD B ∠=∠,若2AD BD =,6BC =,则线段CD 的长为( )A .B .C .D .5【答案】C 【解析】 【分析】设2AD x =,BD x =,所以3AB x =,易证ADE ABC ∆∆:,利用相似三角形的性质可求出DE 的长度,以及23AE AC =,再证明ADE ACD ∆∆:,利用相似三角形的性质即可求出得出AD AE DEAC AD CD==,从而可求出CD 的长度. 【详解】解:设2AD x =,BD x =, ∴3AB x =, ∵//DE BC , ∴ADE ABC ∆∆:,∴DE AD AEBC AB AC ==, ∴263DE xx=, ∴4DE =,23AE AC =, ∵ACD B ∠=∠,ADE B ∠=∠,∴ADE ACD ∠=∠, ∵A A ∠=∠, ∴ADE ACD ∆∆:, ∴AD AE DEAC AD CD==, 设2AE y =,3AC y =,∴23AD yy AD=, ∴AD =,4CD=, ∴CD = 故选:C .试卷第8页,总27页………外…………………○……※※答※※题※※………内…………………○……【点睛】本题考查相似三角形,解题的关键是熟练运用相似三角形的性质与判定,本题属于中等题型.12.如图,E 是正方形ABCD 的边AB 的中点,点H 与B 关于CE 对称,EH 的延长线与AD 交于点F ,与CD 的延长线交于点N ,点P 在AD 的延长线上,作正方形DPMN ,连接CP ,记正方形ABCD ,DPMN 的面积分别为1S ,2S ,则下列结论错误的是( )A .212S S CP +=B .2AF FD =C .4CD PD=D .3cos 5HCD ∠=【答案】D 【解析】 【分析】根据勾股定理可判断A ;连接CF ,作FG EC ⊥,易证得FGC ∆是等腰直角三角形,设EG x =,则2FG x =,利用三角形相似的性质以及勾股定理得到2CG x =,CF =,3EC x =,5BC x =,5FD x =,即可证得3FD AD =,可判断B ;根据平行线分线段成比例定理可判断C ;求得cos HCD ∠可判断D . 【详解】解:∵正方形ABCD ,DPMN 的面积分别为1S ,2S ,∴21S CD =,22S PD =,在Rt PCD ∆中,222PC CD PD =+,∴212S S CP +=,故A 结论正确;连接CF ,∵点H 与B 关于CE 对称, ∴CH CB =,BCE ECH ∠=∠, 在BCE ∆和HCE ∆中,CH CB ECH BCE CE CE =⎧⎪∠=∠⎨⎪=⎩∴()BCE HCE SAS ∆≅∆,∴BE EH =,90EHC B ∠=∠=︒,BEC HEC∠=∠, ∴CH CD =,在Rt FCH ∆和Rt FCD ∆中CH CDCF CF=⎧⎨=⎩ ∴()Rt FCH Rt FCD HL ∆≅∆, ∴FCH FCD ∠=∠,FH FD =, ∴1452ECH ECH BCD ∠+∠=∠=︒,即45ECF ∠=︒, 作FG EC ⊥于G ,∴CFG ∆是等腰直角三角形, ∴FG CG =,∵BEC HEC ∠=∠,90B FGE ∠=∠=︒, ∴FEG CEB ∆∆:, ∴12EG EB FG BC ==, ∴2FG EG =,设EG x =,则2FG x =, ∴2CG x =,CF =, ∴3EC x =,∵222EB BC EC +=,试卷第10页,总27页∴22594BC x=,∴22365BC x=,∴BC x=,在Rt FDC∆中,5FD x===,∴3FD AD=,∴2AF FD=,故B结论正确;∵//AB CN,∴12ND FDAE AF==,∵PD ND=,12AE CD=,∴4CD PD=,故C结论正确;∵EG x=,2FGx=,∴EF=,∵5FH FD x==,∵5BC x=,∴AE x=,作HQ AD⊥于Q,∴//HQ AB,∴HQ HFAE EF=x=,∴25HQ x=,∴CD HQ x x x-=-=,∴cos25xCD HQHCDCF-∠===,故结论D错误,故选:D.【点睛】本题考查了正方形的性质,三角形全等的判定和性质三角形相似的判定和性质,勾股定理的应用以及平行线分线段成比例定理,作出辅助线构建等腰直角三角形是解题的关键.试卷第12页,总27页…………外……………内…第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题13.有理数9的相反数是______. 【答案】9- 【解析】 【分析】根据相反数的求法即可得解; 【详解】解:9的相反数是9-; 故答案为9-; 【点睛】本题考查相反数;熟练掌握相反数的意义与求法是解题的关键. 14.将实数53.1810-⨯用小数表示为______. 【答案】0.0000318 【解析】 【分析】根据科学记数法的表示方法()1019na a ⨯≤<即可求解;【详解】解:53.18100.0000318-⨯=; 故答案为:0.0000318; 【点睛】本题考查科学记数法;熟练掌握科学记数法的表示方法是解题的关键.15.如图,直线a ∥b ,直线m 与a ,b 均相交,若∠1=38°,则∠2=______.【答案】142° 【解析】…订…………○____考号:__________…订…………○【分析】根据平行的性质得∠2=∠3,又因为∠1+∠3=180°,即可求出∠2. 【详解】 解:如图, ∵a ∥b , ∴∠2=∠3, ∵∠1+∠3=180°, ∴∠2=180°﹣38°=142°. 故答案为142°.【点睛】本题考查的是平行,熟练掌握平行的性质是解题的关键.16.若随机掷一枚均匀的骰子,骰子的6个面上分别刻有1,2,3,4,5,6点,则点数不小于3的概率是______. 【答案】23【解析】 【分析】骰子六个面出现的机会相同,求出骰子向上的一面点数不小于3的情况有几种,直接应用求概率的公式求解即可. 【详解】解:随机掷一枚均匀的骰子有6种等可能结果,其中点数不小于3的有4种结果, 所以点数不小于3的概率为4263=, 故答案为:23. 【点睛】此题考查概率的求法:如果一个事件有n 种可能,而且这些事件的可能性相同,其中事件A 出现m 种结果,那么事件A 的概率()m P A n=. 17.如图,在扇形OAB 中,半径OA 与OB 的夹角为120︒,点A 与点B 的距离为试卷第14页,总27页……订………………○…线※※内※※答※※……订………………○…若扇形OAB 恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为______.【答案】43【解析】 【分析】利用弧长=圆锥的周长这一等量关系可求解. 【详解】解:连接AB ,过O 作OMAB ⊥于M ,∵120AOB ∠=︒,OA OB =, ∴30BAO ∠=︒,AM = ∴2OA =,∵24022180r ππ⨯=,∴43r =故答案是:43【点睛】本题运用了弧长公式和圆的周长公式,建立准确的等量关系是解题的关键.18.我们定义一种新函数:形如2y ax bx c =++(0a ≠,且240b a ->)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y =|x 2-2x -3|223y x x =--的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为()1,0-,()3,0和()0,3;②图象具有对称性,对称轴是直线1x =;③当11x -≤≤或3x ≥时,函数值y 随x 值的增大而增大;④当1x =-或3x =时,函数的最小值是0;⑤当1x =时,函数的最大值是4.其中正确结论的个数是______.线…………○……线…………○……【答案】4 【解析】 【分析】由()1,0-,()3,0和()0,3坐标都满足函数223y x x =--,∴①是正确的;从图象可以看出图象具有对称性,对称轴可用对称轴公式求得是直线1x =,②也是正确的; 根据函数的图象和性质,发现当11x -≤≤或3x ≥时,函数值y 随x 值的增大而增大,因此③也是正确的;函数图象的最低点就是与x 轴的两个交点,根据0y =,求出相应的x 的值为1x =-或3x =,因此④也是正确的;从图象上看,当1x <-或3x >,函数值要大于当1x =时的2234y x x =--=,因此⑤时不正确的;逐个判断之后,可得出答案. 【详解】解:①∵()1,0-,()3,0和()0,3坐标都满足函数223y x x =--,∴①是正确的;②从图象可知图象具有对称性,对称轴可用对称轴公式求得是直线1x =,因此②也是正确的;③根据函数的图象和性质,发现当11x -≤≤或3x ≥时,函数值y 随x 值的增大而增大,因此③也是正确的;④函数图象的最低点就是与x 轴的两个交点,根据0y =,求出相应的x 的值为1x =-或3x =,因此④也是正确的;⑤从图象上看,当1x <-或3x >,函数值要大于当1x =时的2234y x x =--=,因此⑤时不正确的; 故答案是:4线…………○……线…………○……【点睛】理解“鹊桥”函数2y ax bx c=++的意义,掌握“鹊桥”函数与2y ax bx c=++与二次函数2y ax bx c=++之间的关系;两个函数性质之间的联系和区别是解决问题的关键;二次函数2y ax bx c=++与x轴的交点、对称性、对称轴及最值的求法以及增减性应熟练掌握.三、解答题19.(1))20134sin302-⎛⎫+-︒⎪⎝⎭;(2)解不等式组:()622423323x xx x⎧->-⎪⎨--≤-⎪⎩,并在数轴上表示该不等式组的解集.【答案】(1)3;(2)312-<≤x;见解析.【解析】【分析】(1)先计算算术平方根、零指数幂、负整数指数幂、代入三角函数值,再计算乘法,最后计算加减可得;(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【详解】解:(1)原式121442=-+-⨯2142=-+-3=;(2)解不等式()6224x x->-,得:32x>,解不等式23323x x--≤-,得:1x≤,试卷第16页,总27页…○……………订………线…………学校:________________考号:___…○……………订………线…………则不等式组的解集为312-<≤x , 将不等式组的解集表示在数轴上如下:【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键. 20.尺规作图(只保留作图痕迹,不要求写出作法):如图,已知ABC ∆,请根据“SAS ”基本事实作出DEF ∆,使DEF ABC ∆≅∆.【答案】见解析. 【解析】 【分析】先作一个D A ∠=∠,然后在D ∠的两边分别截取ED BA =,DF AC =,连接EF 即可得到DEF ∆; 【详解】 解:如图,DEF ∆即为所求.【点睛】本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了全等三角形的判定.21.如图,菱形ABCD 的边AB 在x 轴上,点A 的坐标为()1,0,点()44D ,在反比例试卷第18页,总27页………线………………线………函数ky x =(0x >)的图象上,直线23y x b =+经过点C ,与y 轴交于点E ,连接AC ,AE .(1)求k ,b 的值;(2)求ACE ∆的面积. 【答案】(1)16k =,2b =-;(2)6∆=AEC S . 【解析】 【分析】(1)由菱形的性质可知()6,0B ,()9,4C ,点()44D ,代入反比例函数ky x=,求出k ;将点()9,4C 代入23y x b =+,求出b ; (2)求出直线223y x =-与x 轴和y 轴的交点,即可求AEC ∆的面积; 【详解】解:(1)由已知可得5AD =, ∵菱形ABCD , ∴()6,0B ,()9,4C ,∵点()44D ,在反比例函数()0ky x x=>的图象上, ∴16k =, 将点()9,4C 代入23y x b =+, ∴2b =-; (2)()0,2E -, 直线223y x =-与x 轴交点为()3,0, ∴()122462AECS ∆=⨯⨯+=; 【点睛】本题考查反比例函数、一次函数的图象及性质,菱形的性质;能够将借助菱形的边长和菱形边的平行求点的坐标是解题的关键.…○…………线……____…○…………线……22.为了增强学生的安全意识,某校组织了一次全校2500名学生都参加的“安全知识”考试.阅卷后,学校团委随机抽取了100份考卷进行分析统计,发现考试成绩(x 分)的最低分为51分,最高分为满分100分,并绘制了如下尚不完整的统计图表.请根据图表提供的信息,解答下列问题:(1)填空:a =______,b =______,n =______; (2)将频数分布直方图补充完整;(3)该校对考试成绩为91100x ≤≤的学生进行奖励,按成绩从高分到低分设一、二、三等奖,并且一、二、三等奖的人数比例为1:3:6,请你估算全校获得二等奖的学生人数.【答案】(1)10 ,25 , 0.25;见解析;(3)全校获得二等奖的学生人数90人. 【解析】 【分析】(1)利用×这组的频率即可得到结论;(2)根据(1)求出的数据补全频数分布直方图即可;(3)利用全校2500名学生数×考试成绩为91100x ≤≤考卷占抽取了的考卷数×获得二等奖学生人数占获奖学生数即可得到结论.试卷第20页,总27页…○…………线…题※※…○…………线…【详解】解:(1)1000.110a =⨯=,1001018351225b =----=,250.25100n ==; 故答案为:10,25,0.25;(2)补全频数分布直方图如图所示;(3)12325009010010⨯⨯=(人), 答:全校获得二等奖的学生人数90人. 【点睛】本题考查的是频数分布直方图,读懂统计图,从统计图中得到必要的信息是解决问题的关键.直方图能清楚地表示出每个项目的数据,也考查了利用样本估计总体的思想. 23.为了满足师生的阅读需求,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.(1)求这两年藏书的年均增长率;(2)经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的5.6%,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到2018年底中外古典名著的册数占藏书总量的百分之几?【答案】(1)这两年藏书的年均增长率是20%;(2)到2018年底中外古典名著的册数占藏书总量的10%. 【解析】 【分析】(1)根据题意可以列出相应的一元二次方程,从而可以得到这两年藏书的年均增长率; (2)根据题意可以求出这两年新增加的中外古典名著,从而可以求得到2018年底中外古典名著的册数占藏书总量的百分之几. 【详解】解:(1)设这两年藏书的年均增长率是x ,()2517.2x +=,试卷第21页,总27页○…………订…班级:___________考号○…………订…解得,10.2x =,2 2.2x =-(舍去), 答:这两年藏书的年均增长率是20%;(2)在这两年新增加的图书中,中外古典名著有()7.2520%0.44-⨯=(万册), 到2018年底中外古典名著的册数占藏书总量的百分比是:5 5.6%0.44100%10%7.2⨯+⨯=,答:到2018年底中外古典名著的册数占藏书总量的10%. 【点睛】本题考查一元二次方程的应用,解答本题的关键是明确题意,列出相应的方程,利用方程的知识解答,这是一道典型的增长率问题.24.如图,在矩形ABCD 中,以BC 边为直径作半圆O ,OE OA ⊥交CD 边于点E ,对角线AC 与半圆O 的另一个交点为P ,连接AE .(1)求证:AE 是半圆O 的切线;(2)若2PA =,4PC =,求AE 的长. 【答案】(1)见解析;(2)2=AE . 【解析】 【分析】(1)根据已知条件推出ABO COE ∆∆:,根据相似三角形的性质得到BAO OAE ∠=∠,过O 作OF AE ⊥于F ,根据全等三角形的性质得到OF OB =,于是得到AE 是半圆O 的切线; (2)根据切割线定理得到AF ==求得AB AF ==根据勾股定理得到BC ==,3AO =,根据相似三角形的性质即可得到结论. 【详解】(1)证明:∵在矩形ABCD 中,90ABO OCE ∠=∠=︒, ∵OE OA ⊥, ∴90AOE ∠=︒,…………装……※※请※※不※※要※※…………装……∴90BAO AOB AOB COE∠+∠=∠+∠=︒,∴BAO COE∠=∠,∴ABO COE∆∆:,∴AB AOOC OE=,∵OB OC=,∴AB AOOB OE=,∵90ABO AOE∠=∠=︒,∴ABO AOE∆∆:,∴BAO OAE∠=∠,过O作OF AE⊥于F,∴90ABO AFO∠=∠=︒,在ABO∆与AFO∆中,BAO FAOABO AFOAO AO∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()ABO AFO AAS∆≅∆,∴OF OB=,∴AE是半圆O的切线;(2)解:∵AF是Oe的切线,AC是Oe的割线,∴2AF AP AC=⋅,∴AF==∴AB AF==,∵6AC=,∴BC==,∴AO===试卷第22页,总27页试卷第23页,总27页…………订……班级:___________考号:__…………订……∵ABO AOE ∆∆:, ∴AO ABAE AO=, ∴AE =∴AE =【点睛】本题考查了切线的判定和性质,矩形的性质,相似三角形的判定和性质,全等三角形的判定和性质,正确的作出辅助线是解题的关键.25.如图,已知抛物线2y ax bx c =++的顶点为()4,3A ,与y 轴相交于点()0,5B -,对称轴为直线l ,点M 是线段AB 的中点.(1)求抛物线的表达式;(2)写出点M 的坐标并求直线AB 的表达式;(3)设动点P ,Q 分别在抛物线和对称轴l 上,当以A ,P ,Q ,M 为顶点的四边形是平行四边形时,求P ,Q 两点的坐标. 【答案】(1)21452=-+-y x x ;(2)()2,1-M ,25y x =-;(3)点P 、Q 的坐标分别为()6,1或()2,1、()4,3-或()4,1. 【解析】 【分析】(1)函数表达式为:()243y a x ==+,将点B 坐标代入上式,即可求解; (2)()4,3A 、()0,5B -,则点()2,1-M ,设直线AB 的表达式为:5y kx =-,将点A 坐标代入上式,即可求解;(3)分当AM 是平行四边形的一条边、AM 是平行四边形的对角线两种情况,分别求解即可. 【详解】试卷第24页,总27页解:(1)函数表达式为:()243y a x ==+, 将点B 坐标代入上式并解得:12a =-, 故抛物线的表达式为:21452=-+-y x x ; (2)()4,3A 、()0,5B -,则点()2,1-M , 设直线AB 的表达式为:5y kx =-,将点A 坐标代入上式得:345k =-,解得:2k =, 故直线AB 的表达式为:25y x =-; (3)设点()4,Q s 、点21,452P m m m ⎛⎫-+- ⎪⎝⎭, ①当AM 是平行四边形的一条边时,点A 向左平移2个单位、向下平移4个单位得到M ,同样点21,452P m m m ⎛⎫-+-⎪⎝⎭向左平移2个单位、向下平移4个单位得到()4,Q s , 即:24m -=,214542m m s -+--=, 解得:6m =,3s =-,故点P 、Q 的坐标分别为()6,1、()4,3-; ②当AM 是平行四边形的对角线时, 由中点定理得:424m +=+,2131452m m s -=-+-+, 解得:2m =,1s =,故点P 、Q 的坐标分别为()2,1、()4,1;故点P 、Q 的坐标分别为()6,1或()2,1、()4,3-或()4,1. 【点睛】本题考查的是二次函数综合运用,涉及到一次函数、平行四边形性质、图象的面积计算等,其中(3),要主要分类求解,避免遗漏.26.已知:ABC ∆是等腰直角三角形,90BAC ∠=︒,将ABC ∆绕点C 顺时针方向旋转得到A B C ∆'',记旋转角为α,当90180α︒<<︒时,作A D AC '⊥,垂足为D ,A D '与B C '交于点.E试卷第25页,总27页…外…………○………………○……学校:_____…内…………○………………○……(1)如图1,当15CA D '∠=︒时,作A EC '∠的平分线EF 交BC 于点F . ①写出旋转角α的度数;②求证:EA EC EF '+=;(2)如图2,在(1)的条件下,设P 是直线A D '上的一个动点,连接PA ,PF ,若AB =PA PF +的最小值.(结果保留根号)【答案】(1)①旋转角为105︒;②见解析;(2)PA PF +【解析】 【分析】(1)①解直角三角形求出A CD '∠即可解决问题.②连接A F ',设EF 交CA '于点O .在EF 时截取EM EC =,连接CM .首先证明CFA '∆是等边三角形,再证明()FCM A CE SAS '∆≅∆=,即可解决问题.(2)如图2中,连接A F ',PB ',AB ',作B M AC '⊥交AC 的延长线于M .证明A EF A EB '''∆≅∆,推出EF EB '=,推出B ',F 关于A E '对称,推出PF PB '=,推出PA PF PA PB AB ''+=+≥,求出AB '即可解决问题. 【详解】解:(1)①旋转角为105︒. 理由:如图1中,∵A D AC '⊥, ∴90A DC '∠=︒, ∵15CA D '∠=︒, ∴75A CD '∠=︒,试卷第26页,总27页∴105ACA '∠=︒, ∴旋转角为105︒.②证明:连接A F ',设EF 交CA '于点O .在EF 时截取EM EC =,连接CM . ∵451560CED A CE CA E ''∠=∠+∠=︒+︒=︒, ∴120CEA '∠=︒, ∵FE 平分CEA '∠, ∴60CEF FEA '∠=∠=︒, ∵180457560FCO ∠=︒-︒-︒=︒, ∴FCO A EO '∠=∠,∵FOC A OE '∠=∠, ∴FOC A OE '∆∆:,∴OF OCA O OE =', ∴OF A OOC OE'=, ∵COE FOA '∠=∠, ∴COE FOA '∆∆:, ∴60FA O OEC '∠=∠=︒, ∴A OF '∆是等边三角形, ∴CF CA A F ''==,∵EM EC =,60CEM ∠=︒, ∴CEM ∆是等边三角形,60ECM ∠=︒,CM CE =,∵60FCA MCE '∠=∠=︒, ∴FCM A CE '∠=∠, ∴()FCM A CE SAS '∆≅∆, ∴FM A E '=,∴CE A E EM FM EF '+=+=.(2)解:如图2中,连接A F ',PB ',AB ',作B M AC '⊥交AC 的延长线于M .试卷第27页,总27页……线…………○…………线…………○……由②可知,75EAF EA B '''∠=∠=︒,A E A E ''=,A F A B '''=, ∴A EF A EB '''∆≅∆, ∴EF EB '=,∴B ',F 关于A E '对称, ∴PF PB '=,∴PA PF PA PB AB ''+=+≥, 在Rt CB M '∆中,2CB BC '===,30MCB '∠=︒,∴112B M CB ''==,CM =, ∴AB '===∴PA PF +【点睛】本题属于四边形综合题,考查了旋转变换,全等三角形的判定和性质,相似三角形的判定和性质,三角形的三边关系等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用转化的思想思考问题,属于中考压轴题.。
2019年广西贵港市中考数学试卷(附答案与解析)

---------------- 密★启用前数学7.若 α , β 是关于 x 的一元二次方程 x 2 - 2x + m = 0 的两实根,且 1第Ⅰ卷(选择题 共 36 分)__ _ __ __ _号卷 生 __ 考 __ __ ___ __ 上 ____ __ 名__ 姓 __ _ 答 _____4.若分式 x 2 - 1x + 1 的值等于 0,则 x 的值为_--------------------校 学A . ±1B .0C . -1D .1____() ____则这个几何体的主视图是__ _ _ _ _ _ _ _ _ ___ A . 9,9B .10,9C . 9,9.5D .11,10__ __ _ 题业 毕 -------------绝广西贵港市 2019 年初中毕业学业水平考试在--------------------本试卷满分 120 分,考试时间 120 分钟.此--------------------一、选择题(本大题共 12 小题,共 36.0 分)__ 1.计算 (-1)3的结果是A . -1B .1C . -3 D. 3--------------------2.某几何体的俯视图如图所示,图中数字表示该位置上的小正方体的个数,( )--------------------A B C D3. 若一组数据为:10,11,9,8,10,9,11,9,则这组数据的众数和中位数分别是--------------------( )( )5.下列运算正确的是()A . -2B.-3C.2D.312α+β=-3,则m等于()A.-2B.-3C.2D.38.下列命题中假命题是()A.对顶角相等B.直线y=x-5不经过第二象限C.五边形的内角和为540°D.因式分解x3+x2+x=x(x2+x)9如图,AD是O的直径,AB=CD,∠AOC=40°,则圆周角∠BPC的度数是()A.40°B.50°C.60°D.60°10.将一条宽度为2cm的彩带按如图所示的方法折叠,折痕为AB,重叠部分为△ABC(图中阴影部分),若∠AOC=45°,则重叠部分的面积为无()--------------------A.a3+(-a)3=-a6B.(a+b)2=a2+b2()C.2a2a=2a3D.(ab2)3=a3b56.若点P(m-1,5)与点Q(3,2-n)关于原点成中心对称,则m+n的值是A.22cm2B.23cm2效数学试卷第1页(共26页)数学试卷第2页(共26页)(2)解不等式组: ⎨ 2 2 ≤ - x ,并在数轴上表示该不等式组的解集. ⎩C . 4 cm 2D . 4 2 cm 211.如图,在 △ABC 中,点 D , E 分别在 AB , AC 边上, DE ∥BC ,∠ACD = ∠B ,若 AD = 2BD , BC = 6 ,则线段 CD 的长为()A . 2 3B . 3 2C . 2 6D .512.如图, E 是正方形 ABCD 的边 AB 的中点,点 H 与 B 关于 CE对称,EH 的延长线与 AD 交于点 F ,与 CD 的延长线交于点 N ,点 P 在 AD 的延长线上,作正方形 DPMN ,连接 CP ,记正方形 ABCD , DPMN 的面积分别为 S , S ,则下列结论错误的12是()A . S + S = CP 2B . 4F = 2FD 12C . CD = 4PDD . cos ∠HCD =35第Ⅱ卷(非选择题 共 84 分)二、填空题(本大题共 6 小题,共 18.0 分)13.有理数 9 的相反数是.14.将实数 3.18 ⨯10-5 用小数表示为.15.如图,直线 a ∥b ,直线 m 与 a , b 均相交,若∠1 = 38° ,则∠2 =.数学试卷 第 3 页(共 26 页)16.若随机掷一枚均匀的骰子,骰子的 6 个面上分别刻有 1,2,3,4,5,6 点,则点数不小于 3 的概率是 .17.如图,在扇形 OAB 中,半径 OA 与 OB 的夹角为 120 ° ,点 A 与点 B 的距离为 2 3 ,若扇形 OAB 恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为 .18.我们定义一种新函数:形如 y =| ax 2 + bx + c | ( a ≠ 0 ,且b 2 - 4a >0 )的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数 y =| x 2 - 2x - 3 | 的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为 (-1,0) , (3,0) 和(0,3) ;②图象具有对称性,对称轴是直线 x = 1 ;③当-1≤x ≤1 或 x ≥3 时,函数值 y 随 x 值的增大而增大;④当 x = -1 或 x = 3 时,函数的最小值是 0;⑤当 x = 1 时,函数的最大值是 4.其中正确结论的个数是 .三、解答题(本大题共 8 小题,共 66.0 分)119.(1)计算: 4 - ( 3 - 3)0 + ( )2 - 4sin30 ︒2⎧6 x - 2>2( x - 4) ⎪ 3 - x ⎪ 3 - 3数学试卷 第 4 页(共 26 页)基本事实作出 △DEF ,使 △DEF ≌△ABC .D(4,4) 在反比例函数 y = ( x >0) 的图象上,直线 y = 2 ___号 卷生 __ __ __ ___ __ 上__ __ __ 姓 _ 答 ___ 71≤x <81 b n __ __ __题_校 (1)填空: a = , b = , n =; 等奖 -------------20.尺规作图(只保留作图痕迹,不要求写出作法):如图,已知 △ABC ,请根据“ SAS ”----------------在--------------------21.如图,菱形 ABCD 的边 AB 在 x 轴上,点 A 的坐标为 (1,0) ,点此k _-------------------- x 3 x + b__ 经过点 C ,与 y 轴交于点 E ,连接 AC , AE .__(1)求 k , b 的值; __ (2)求 △ACE 的面积. __ __ -------------------- 考 ____22.为了增强学生的安全意识,某校组织了一次全校 2 500 名学生都参加的“安全知识” 考试.阅卷后,学校团委随机抽取了 100 份考卷进行分析统计,发现考试成绩( x 分) _ _的最低分为 51 分,最高分为满分 100 分,并绘制了如下尚不完整的统计图表.请根据 --------------------图表提供的信息,解答下列问题: _ _ 分数段(分) 频数(人) 频率 _ _ _ _ 51≤x <61 a 0.1 名 __ 61≤x <71 18 0.18--------------------___ __ 81≤x <91 35 0.35 __ 91≤x <101 12 0.12-------------------- 合计 100 1学 业万册增加到 7.2 万册.(1)求这两年藏书的年均增长率;(2)经统计知:中外古典名著的册数在 2016 年底仅占当时藏书总量的 5.6% ,在这两 年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到 2018 年底中外古典名著的册数占藏书总量的百分之几?24.如图,在矩形 ABCD 中,以 BC 边为直径作半圆 O ,OE ⊥OA 交 CD 边于点 E ,对角线 AC 与半圆 O 的另一个交点为 P ,连接 AE .(1)求证: AE 是半圆 O 的切线; (2)若 P A = 2 , PC = 4 ,求 AE 的长.25.如图,已知抛物线 y = ax 2 + bx + c 的顶点为 A(4,3) ,与 y 轴相交于点 B(0, -5) ,对称轴为直线 l ,点 M 是线段 AB 的中点.(1)求抛物线的表达式;(2)写出点 M 的坐标并求直线 AB 的表达式;(3)设动点 P ,Q 分别在抛物线和对称轴 l 上,当以 A ,P ,Q , M 为顶点的四边形是平行四边形时,求 P , Q 两点的坐标.26.已知:△ABC 是等腰直角三角形,∠BAC = 90° ,将△ABC 绕点 C 顺时针方向旋转得到 △A 'B 'C ' ,记旋转角为α ,当90°<α <180° 时,作 A 'D ⊥AC ,垂足为 D , A 'D与 B 'C 交于点 E .毕(2)将频数分布直方图补充完整;无(3)该校对考试成绩为 91≤x <100 的学生进行奖励,按成绩从高分到低分设一、二、三 --------------------,并且一、二、三等奖的人数比例为1:3:6 ,请你估算全校获得二等奖的学生人数.23.为了满足师生的阅读需求,某校图书馆的藏书从 2016 年底到 2018 年底两年内由 5(1)如图 1,当∠CA 'D = 15° 时,作∠A 'EC = 15° 的平分线 EF 交 BC 于点 F .效数学试卷 第 5 页(共 26 页)数学试卷 第 6 页(共 26 页)①写出旋转角α的度数;②求证:EA'+EC=EF;(2)如图2,在(1)的条件下,设P是直线A'D上的一个动点,连接P A,PF,若AB=2,求线段P A+PF的最小值.(结果保留根号).数学试卷第7页(共26页)数学试卷第8页(共26页)化简分式 x 2 - 1 2 =9.5 ,故选:C .α + = α +β x + 1 = α + 广西贵港市 2019 年初中毕业学业水平考试数学答案解析第Ⅰ卷一、选择题1.【答案】A【解析】解: (-1)3 表示 3 个 (-1) 的乘积,所以 (-1)3 =3 .故选:A .乘方是乘法的特例,乘方的运算可以利用乘法的运算来进行.负数的奇数次幂是负数,负数的偶数次幂是正数; -1的奇数次幂是 -1, -1的偶数次幂是 1.【考点】有理数的乘方运算.2.【答案】B【解析】解:从正面看去,一共两列,左边有 2 竖列,右边是 1 竖列.故选:B .先细心观察原立体图形中正方体的位置关系,从正面看去,一共两列,左边有 2 竖列,右边是 1 竖列,结合四个选项选出答案.【考点】由三视图判断几何体,解题的关键是具有几何体的三视图及空间想象能力.3.【答案】C【解析】解:将数据重新排列为 8,9,9,9,10,10,11,11,∴这组数据的众数为 9,中位数为 9+10根据众数和中位数的概念求解可得.本题为统计题,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不故选:D .( x + 1)(x - 1)x + 1 = x + 1 = x - 1 = 0 即可求解;【考点】解分式方程;熟练掌握因式分解的方法,分式方程的解法是解题的关键.5.【答案】C【解析】解: a 3 + (-a 3 ) = 0 ,A 错误;(a + b )2 = a 2 + 2ab + b 2 ,B 错误;(ab 2 )3 = a 3b 5 ,D 错误;故选:C .利用完全平方公式,合并同类项法则,幂的乘方与积的乘方法则运算即可;【考点】整式的运算;熟练掌握完全平方公式,合并同类项法则,幂的乘方与积的乘方法则是解题的关键.6.【答案】C【解析】解:∵点 P(m -1,5) 与点 Q(3,2 - n) 关于原点对称,∴ m - 1 = -3 , 2 - n = -5 ,解得: m = -2 , n = 7 ,则 m + n = -2 + 7 = 5 ,故选:C .关于原点对称的点的坐标,关于原点对称的点的横坐标互为相反数,纵坐标互为相反数.【考点】本题考查列方程组解应用题.7.【答案】B【解析】 α , β 是关于 x 的一元二次方程 x 2 - 2x + m = 0 的两实根,∴ α + β = 2 , αβ = m ,好,不把数据按要求重新排列,就会出错. ∵ 1 1 β αβ = 2 2 m =- 3 ,【考点】众数与中位数的意义.4.【答案】D∴ m = -3 ; 【解析】解: x 2 - 1 ( x + 1)(x - 1) x + 1 = x - 1 = 0 ,故选:B .利用一元二次方程根与系数的关系得到α + β = 2 , αβ = m ,再化简11 α +ββ = αβ,代∴ x = 1 ;数学试卷 第 9 页(共 26 页) 数学试卷 第 10 页(共 26 页)BC=∴DEAC=∴∠BPC=∠BOC=50°,∴DE3y=6y =入即可求解;【考点】一元二次方程;熟练掌握一元二次方程根与系数的关系是解题的关键.8.【答案】D【解析】解:A.对顶角相等;真命题;B.直线y=x-5不经过第二象限;真命题;C.五边形的内角和为540°;真命题;D.因式分解x3+x2+x=x(x2+x);假命题;故选:D.由对顶角相等得出A是真命题;由直线y=x-5的图象得出B是真命题;由五边形的内角和为540°得出C是真命题;由因式分解的定义得出D是假命题;即可得出答案.【考点】命题与定理、真命题和假命题的定义:正确的命题是真命题,错误的命题是假过B作BD⊥AC于D,则∠BDC=90°,依据勾股定理即可得出BC的长,进而得到重叠部分的面积.【考点】折叠问题,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.11.【答案】C【解析】设AD=2x,BD=x,∴AB=3x,∵DE∥BC,∴△ADE∽△ABC,命题.∴DE AD DEAB=CD,9.【答案】B【解析】解:∵AB=CD,∠AOB=40°,∴∠COD=∠AOB=40°,2x6=3x,∴DE=4,AE23,∵∠AOB+∠BOC+∠COD=180°,∴∠BOC=100°,12故选:B.根据圆周角定理即可求出答案.【考点】圆周角定理,熟练掌握圆周角定理是解题的关键.10.【答案】A ∵∠ACD=∠B,∠ADE=∠B,∴∠ADE=∠ACD,∵∠A=∠A,∴△ADE∽△ACD,AE DEBC=AD=CD,设AE=2y,AC=3y,【解析】如图,过B作BD⊥AC于D,则∠BDC=90°,∴AD2yAD,∵∠ACB=45°,∴AD=6y,∴∠CBD=45°,∴BD=CD=2cm,∴2y4CD,∴△Rt BCD中,BC=22+22=22(cm),1∴重叠部分的面积为⨯22⨯2=22(cm),2故选:A.数学试卷第11页(共26页)∴CD=2,故选:C.设AD=2x,BD=x,所以AB=3x,易证△ADE∽△ABC,利用相似三角形的性质数学试卷第12页(共26页)⎨∠ECH = ∠BCE ⎪CE = CE ⎩CF = CF 可求出 DE 的长度,以及 AE 3,再证明△ADE ∽△ACD ,利用相似三角形的性 质即可求出得出 DE ∴ EG 5 x ,∴ND 2 CD ,5 x ,5 x ,5 x ,2AC =AE DEBC = AD =CD ,从而可求出 CD 的长度.【考点】相似三角形,解题的关键是熟练运用相似三角形的性质与判定.12.【答案】D【解析】解:∵正方形 ABCD , DPMN 的面积分别为 S , S ,12∴ S = CD , S = PD ,12 2 2在 △Rt PCD 中, PC 2 = CD 2 + PD 2 ,∴ S + S = CP 2 ,故 A 结论正确;12连接 CF ,∵点 H 与 B 关于 CE 对称,∴ CH = CB ,∠BCE = ∠ECH ,在 △BCE 和 △HCE 中, ⎧CH = CB⎪ ⎩∴ △CE ≌△HCE (SAS ) ,∴ BE = EH ,∠ECH = ∠B = 90° ,∠BEC = ∠HEC ,∴ CH = CD ,在 △Rt FCH 和 △Rt FCD 中 ⎧ CH =CD ⎨∴ Rt △FCH ≌Rt △FCD ( H L) ,∴∠FCH = ∠FCD , FH = FD ,∴∠ECH +∠ECH = ∠BCD = 45° ,即∠ECH =45° ,作 FG ⊥EC 于 G ,∴ △CFG 是等腰直角三角形,∴ FG = CG ,∵∠BEC = ∠HEC ,∠B = ∠FGH = 90° ,数学试卷 第 13 页(共 26 页)∴ △FEG ∽△CEB ,EB 1FG = BC = 2 ,∴ FG = 2EG ,设 EG = x ,则 FG = 2 x ,∴ CG = 2x , CF = 2 x ,∴ EC = 3x ,∵ EB 2 + BC 2 = EC 2 ,5∴ BC 2 = 9x 2 ,4∴ BC 2 = x 2 ,∴ BC = x ,在 △Rt FCD 中, FD = CF 2- CD 2= (2 2 x )2- 36∴ 3FD = AD ,∴ AF = 2FD ,故 B 结论正确;∵ AB ∥CN ,FD 1AE = AF = 2 ,∵ PD = ND , AE = 1∴ CD = 4PD ,故 C 结论正确;∵ EG = x , FG = 2 x ,∴ EF = 5x ,∵ FH = FD = 2 5∵ BC = 6 5∴ AE = 3 5作 HQ ⊥ AD 于 Q ,∴ HQ ∥AB ,数学试卷 第 14 页(共 26 页)AE=5 25x,5x-n3.∴HQ HFEF,即25HQ x35=5x5x,【解析】解:3.18⨯10-5=0.0000318;故答案为0.0000318;∴HQ=65∴CD-HQ=656524525x=25x,根据科学记数法的表示方法a⨯10(1≤a<9)即可求解;【考点】科学记数法;熟练掌握科学记数法的表示方法是解题的关键.245∴cos∠HCD=CD-HQ=25=610,故结论D错误,CF22x25故选:D.根据勾股定理可判断A;连接CF,作FG⊥EC,易证得△FGC是等腰直角三角形,设EG=x,则FG=2x,利用三角形相似的性质以及勾股定理得到CG=2x,EC=3x,BC=x,FD=x,即可证得3FD=AD,可判断B;根据平行线分线段成比例定理可判断C;求得cos∠HCD可判断D.【考点】正方形的性质,三角形全等的判定和性质三角形相似的判定和性质,勾股定理的应用以及平行线分线段成比例定理,作出辅助线构建等腰直角三角形是解题的关键.第Ⅱ卷二.填空题13.【答案】-9【解析】解:9的相反数是-9;故答案为-9;根据相反数的求法即可得解;【考点】考查相反数;熟练掌握相反数的意义与求法是解题的关键.14.【答案】0.0000318数学试卷第15页(共26页)15.【答案】142°【解析】解:如图,∵a∥b,∴∠2=∠3,∵∠1+∠3=180°,∴∠2=180°-38°=142°.故答案为142°.如图,利用平行线的性质得到∠2=∠3,利用互补求出∠2,从而得到∠3的度数..【考点】平行线的性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.16.【答案】23【解析】解:随机掷一枚均匀的骰子有6种等可能结果,其中点数不小于3的有4种结果,42所以点数不小于3的概率为=,63故答案为:2骰子六个面出现的机会相同,求出骰子向上的一面点数不小于3的情况有几种,直接应用求概率的公式求解即可.【考点】概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事数学试卷第16页(共26页)∵ ∠AOB = 120, OA = OB , (2)解不等式 6x - 2>2( x - 4) ,得: x >- ,n .180 = 2π r , 解不等式 2 3 - 3 - x件 A 出现 m 种结果,那么事件 A 的概率 P( A ) = m17.【答案】23【解析】解:连接 AB ,过 O 作 OM ⊥ AB 于 M ,°∴ ∠BAO = 30° , AM = 3 ,∴ OA = 2 ,∵ 120π∴ r = 23故答案是:23利用弧长=圆锥的周长这一等量关系可求解.【考点】本题考查了勾股定理、平面直角坐标系内点的坐标弧长公式和圆的周长公式,建立准确的等量关系是解题的关键.18.【答案】4【解析】解:①∵ (-1,0) , (3,0) 和 (0,3) 坐标都满足函数 y =| x 2 - 2x - 3 | ,∴①是正确的;②从图象可知图象具有对称性,对称轴可用对称轴公式求得是直线 x = 1 ,因此②也是正确的;③根据函数的图象和性质,发现当 -1 ≤ x ≤ 1 或 x ≥ 3 时,函数值 y 随 x 值的增大而增大,因此③也是正确的;④函数图象的最低点就是与 x 轴的两个交点,根据 y = 0 ,求出相应的 x 的值为 x = -1 或 x = 3 ,因此④也是正确的;⑤ 从 图 象 上 看 , 当 x < - 1 或 x >3 , 函 数 值 要 大 于 当 x = 1 时 的y =| x 2 - 2x - 3 | =4 ,因此⑤时不正确的;数学试卷 第 17 页(共 26 页)故答案是:4由 (-1,0) ,(3,0) 和 (0,3) 坐标都满足函数 y =| x 2 - 2x - 3 | =4 ,∴①是正确的;从图象可以看出图象具有对称性,对称轴可用对称轴公式求得是直线 x=1,②也是正确的;根据函数的图象和性质,发现当 -1 ≤ x ≤ 1 或 x ≥ 3 时时,函数值 y 随 x 值的增大而增大,因此③也是正确的;函数图象的最低点就是与 x 轴的两个交点,根据 y = 0 ,求出相应的 x 的值为 x = -1 或 x = 3 ,因此④也是正确的;从图象上看,当 x < - 1 或 x >3 , 函数值要大于当 x = 1 时的 y =| x 2 - 2x - 3 | =4 ,因此⑤时不正确的;逐个判断之后,可得出答案.理解“鹊桥”函数 y =| x 2 - 2x - 3 | 的意义,掌握“鹊桥”函数与y =| ax 2 + bx + c | 与二次函数 y = ax 2 + bx + c 之间的关系;两个函数性质之间的联系和区别是解决问题的关键;二次函数 y = ax 2 + bx + c 与 x 轴的交点、对称性、对称轴及最值的求法以及增 减性应熟练掌握.【考点】二次函数轴 y = ax 2 + bx + c 与 x 的交点、对称性、对称轴及最值的求法以及增减性应熟练掌握.三、解答题19.【答案】解:(1)原式 = 2 - 1 + 4 - 4 ⨯12= 2 -1 + 4 - 2 = 3 ;3 2x2 ≤3 ,得: x ≤ 1 ,3则不等式组的解集为 - < x ≤ 1 ,2将不等式组的解集表示在数轴上如下:【解析】(1)先计算算术平方根、零指数幂、负整数指数幂、代入三角函数值,再计算乘法,最后计算加减可得;(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、数学试卷 第 18 页(共 26 页)10010=90(人)100=0.25;x (x>0)的图象上,10010=90(人),3x+b,3x-2与x轴交点为(3,0),=⨯2⨯(2+4)=6;2-x,求出k;将点C(9,4)代入y=大大小小无解了确定不等式组的解集.评分说明第(1)题,与“去括号法则用错”等同的说法均给分.【考点】解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.20.【答案】解:如图,(2)求出直线y=x-2与x轴和y轴的交点,即可求△AEC的面积;.【考点】反比例函数、一次函数的图象及性质,菱形的性质;能够将借助菱形的边长和菱形边的平行求点的坐标是解题的关键.22.【答案】(1)10250.25△DEF即为所求.【解析】先作一个∠D=∠A,然后在∠D的两边分别截取ED=BA,DF=AC,连接EF即可得到△DEF;解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了全等三角形的判定.【考点】作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.21.【答案】解:(1)由已知可得AD=5,∵菱形ABCD,∴B(6,0),C(9,4),∵点D(4,4)在反比例函数y=k∴k=16,将点C(9,4)代入y=2∴b=-2;(2)E(0,2),直线y=21△S AEC∴【解析】(1)由菱形的性质可知B∴B(6,0),C(9,4),(2)(3)2500⨯12⨯3【解析】解:(1)a=100⨯0.1=10,b=100-10-18-35-12=25,n=25故答案为:10,25,0.25;(2)补全频数分布直方图如图所示;(3)2500⨯12⨯3答:全校获得二等奖的学生人数90人.(1)利用×这组的频率即可得到结论;(2)根据(1)求出的数据补全频数分布直方图即可;(3)利用全校2500名学生数×考试成绩为91≤x≤100考卷占抽取了的考卷数×获得二等奖学生人数占获奖学生数即可得到结论.解答本题的关键是明确题意,列出相应的方程,利用方程的知识解答,这是一道典型的增长率问题.【考点】一元二次方程的应用.点D(4,4)代入反比例函数y=k23x+b,求出b;23.【答案】解:(1)设这两年藏书的年均增长率是x,5(1+x)2=7.2,数学试卷第19页(共26页)数学试卷第20页(共26页)在△ABO与△AOE中,⎨∠ABO=∠AFO,⎪AO=AOAE=∴32.∴AB∴AB解得,x=0.2,x=-2.2(舍去),12答:这两年藏书的年均增长率是20%;(2)在这两年新增加的图书中,中外古典名著有(7.2-5)⨯20%=0.44(万册),到2018年底中外古典名著的册数占藏书总量的百分比是:(5⨯5.6%+0.44)7.2⨯100%=10%,答:到2018年底中外古典名著的册数占藏书总量的10%.【解析】(1)根据题意可以列出相应的一元二次方程,从而可以得到这两年藏书的年均增长率;(2)根据题意可以求出这两年新增加的中外古典名著,从而可以求得到2018年底中外古典名著的册数占藏书总量的百分之几.提示:(1)根据题意作出圆弧;(2)根据轴对称图形和中心对称图形的概念进行判断;(3)根据弧长公式求出三条弧的长度的和即可.【考点】本题考查基本作图一一作弧、轴对称图形和中心对称图形的概念、扇形的弧长.24.【答案】(1)证明:∵在矩形ABCD中,∠ABO=∠OCE=90°,过O作OF⊥AE于F,∴∠ABO=∠AFO=90°,⎧∠BAO=∠FAO⎪⎩∴△ABO≌△AFO(AAS),∴OF=OB,∴AE是半圆O的切线;(2)解:∵AF是O的切线,AC是O的割线,∴AF2=AP AC,∴AF=2(2+4)=23,∴AB=AF=23,∵AC=6,∴BC=AC2-AB2=26,∴AO=AB2+OB2=3,∵△ABO∽△AOE,∵OE⊥OA,∴AO ABAO,∴∠AOE=90°,∴∠BAO=∠AOD=∠AOB=∠COE=90°,∴∠BAO=∠COE,∴△ABO∽△OCE,AOOC=OE,∵OB=OC,AOOB=OE,∵∠ABO=∠AOE=90°,∴△ABO∽△AOE,∴∠BAO=∠OAE,数学试卷第21页(共26页)23AE=3,∴AE=33【解析】(1)根据已知条件推出△ABO∽△OCE,根据相似三角形的性质得到∠BAO=∠OAE,过O作OF⊥AE于F,根据全等三角形的性质得到OF=OB,于是得到AE是半圆O的切线;(2)根据切割线定理得到AF=2(2+4)=23,求得AB=AF=23,根据勾股定理得到BC=AC2-AB2=26,AO=AB2+OB2=3,根据相似三角形的性质即可得到结论.【考点】切线的判定和性质,矩形的性质,相似三角形的判定和性质,全等三角形的判定和性质,正确的作出辅助线是解题的关键.25.【答案】解:(1)函数表达式为:y=a(x+4)2+3,数学试卷第22页(共26页)2 ,' A 'O = OC = ' 将点 B 坐标代入上式并解得: a = - 11故抛物线的表达式为: y = - x 2 + 4x - 5 ;2(2) A(4,3) 、 B(0, -5) ,则点 M (2, -1) ,设直线 AB 的表达式为: y = kx - 5 ,将点 A 坐标代入上式得: 3 = 4k - 5 ,解得: k = 2 ,故直线 AB 的表达式为: y = 2 x - 5 ;1(3)设点 Q(4, s) 、点 P(m , - m 2 + 4m - 5) ,2①当 AM 是平行四边形的一条边时,点 A 向左平移 2 个单位、向下平移 4 个单位得到 M ,1同样点 P(m , - m 2 + 4m - 5) 向左平移 2 个单位、向下平移 4 个单位得到 Q (4, s) ,21即: m - 2 = 4 , - m 2 + 4m - 5=s ,2解得: m = 6 , s = -3 ,故点 P 、 Q 的坐标分别为 (6,1) 、 (4, -3) ;②当 AM 是平行四边形的对角线时,1由中点定理得: 4 + 2 = m + 4 , 3 - 1 = - m 2 + 4m - 5+s ,2解得: m = 2 , s = 1 ,故点 P 、 Q 的坐标分别为 (2,1) 、 (4,1) ;故点 P 、 Q 的坐标分别为 (6,1) 或 (2,1) 、 (4, -3) 或 (4,1) .【解析】(1)函数表达式为: y = a( x +4)2 + 3 ,将点 B 坐标代入上式,即可求解;(2) A(4,3) 、 B(0, -5) ,则点 M (2, -1) ,设直线 AB 的表达式为: y = kx - 5 ,将点 A 坐26.【答案】(1)①解:旋转角为105° .理由:如图 1 中,∵ A 'D ⊥ AC ,∴∠A 'DC = 90° ,∵∠CA 'D = 15° ,∴∠A 'CD = 75° ,∴∠ACA ' = 105° ,∴旋转角为105° .②证明:连接 A 'F ,设 EF 交 CA ' 于点 O .在 EF 时截取 EM = EC ,连接 CM .∵∠CED = ∠A 'CE + ∠CA 'E = 45° + 15° = 60° ,∴∠CEA ' = 120° ,∵ FE 平分∠EA 'C ,∴∠CEF = ∠FEA ' = 60° ,∵∠FCO = 180° - 45° - 75° = 60° ,∴∠FCO = ∠A 'EO ,∵∠FOC = ∠AOE ,∴ △FOC ∽ △A 'OE ,标代入上式,即可求解;(3)分当 AM 是平行四边形的一条边 AM 是平行四边形的对角线两种情况,分别求解即可.∴OF∴ OFOCOE , A 'O OE ,【考点】二次函数综合运用,涉及到一次函数、平行四边形性质、图象的面积计算等,其中(3),要主要分类求解,避免遗漏.∵∠COE = ∠FOA ' ,∴ △COE ∽△FOA ,∴∠FA 'O = ∠OEC = 60° ,数学试卷 第 23 页(共 26 页)数学试卷 第 24 页(共 26 页)' '∴△A 'OF 是等边三角形, ∴ CF = CA ' = A 'F ,∵ EM = EC ,∠CEM = 60° ,∴ △CEM 是等边三角形,∠ECM = 60° , CM = CE ,∵∠FCA ' = ∠MCE = 60° ,∴∠FCM = ∠A 'CE ,∴ △FCM ≌△A 'CE (SAS ) ,∴ FM = A 'E ,∴ CE + A 'E = EM + FM = EF .(2)解:如图 2 中,连接 A 'F , PB ' , AB ' ,作 B 'M ⊥ AC 交 AC 的延长线于 M .∴ P A + PF 的最小值为 6 + 2 6 .【解析】①解直角三角形求出∠A 'CD 即可解决问题.②连接 A 'F ,设 EF 交 CA ' 于点 O .在 EF 时截取 EM = EC ,连接 CM .首先证明 △CFA '是等边三角形,再证明△FCM ≌△A 'CE (SAS ) ,即可解决问题.(2) 如图 2 中,连接 A 'F , PB ' , AB ' ,作 B 'M ⊥ AC 交 AC 的延长线于 M .证明△A ' △EF ≌ A EB ,推出 EF = EB ' ,推出 B ' , F 关于 A 'E 对称,推出 PF = PB ' ,推出 P A + PF = P A + PB ' ≥ AB ' ,求出 AB ' 即可解决问题.【考点】四边形综合题,旋转变换,全等三角形的判定和性质,相似三角形的判定和性质,三角形的三边关系等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用转化的思想思考问题.由②可知,∠EA 'F = 'EA 'B ' = 75° , A 'E = A 'E , A 'F = A 'B ' ,∴ △A 'EF ≌△A 'EB ' ,∴ EF = EB ' ,∴ B ' , F 关于 A 'E 对称,∴ PF = PB ' ,∴ P A + PF = P A + PB ' ≥ AB ' ,在 △Rt CB 'M 中, CB ' = BC = 2 AB = 2 ,∠MCB ' = 30° ,1∴ B 'M = CB ' = 1 , CM = 3 ,2∴ AB '= AM 2 + B ' M 2 = ( 2 + 3) 2 + 12 = 6 + 2 6数学试卷 第 25 页(共 26 页)数学试卷 第 26 页(共 26 页)。
广西贵港市2019年中考数学总复习试题 题型专项(八 类型4 探究全等三角形的存在性问题

类型4 探究全等三角形的存在性问题1.如图、抛物线y =ax 2+bx +c 的顶点为D 、与y 轴交于点C 、直线CD 的解析式为y =3x +2 3. (1)求b 、c 的值;(2)过C 作CE∥x 轴交抛物线于点E 、直线DE 交x 轴于点F 、且F(4、0)、求抛物线的解析式;(3)在(2)条件下、抛物线上是否存在点M 、使得△CDM≌△CEM?若存在、请直接写出点M 的坐标;若不存在、请说明理由.解:(1)∵直线CD 的解析式为y =3x +23、∴C(0、23).∴c =2 3.设直线CD 交x 轴于点A 、∴A(-2、0).∴OA OC =223=33. ∴∠OCA =30°.过点D 作DM⊥y 轴于点M 、∴∠DCM =30°. ∴MC =3DM.设抛物线的顶点横坐标为h 、则CM =3h.∴D(h 、23+3h).∴y =a(x -h)2+23+3h.代入C(0、23)、∴23=ah 2+23+3h.∴h 1=0(舍)、h 2=-3a. ∴y =a(x +3a )2+23+(-3a)=ax 2+23x +2 3. ∴b =2 3.(2)作抛物线的对称轴交x 轴于点B(如图)、∵∠ACO =30°、∴∠CDB =30°.由抛物线的对称性、可得△DCE 为等边三角形.∵CE ∥x 轴、∴△DAF 为等边三角形.∴B 为AF 中点、∵A(-2、0)、F(4、0)、∴B(1、0).∵抛物线对称轴为直线x =1.∴-b 2a =1、∴-232a=1. ∴a =-3.∴D(1、33).∴y =-3(x -1)2+33=-3x 2+23x +2 3.(3)存在.点M 的坐标为(53、2339).2.(2015·金华改编)如图、抛物线y =ax 2+c(a≠0)与y 轴交于点A 、与x 轴交于点B 、C 两点(点C 在x 轴正半轴上)、△ABC 为等腰直角三角形、且面积为4.现将抛物线沿BA 方向平移、平移后的抛物线经过点C 时、与x 轴的另一交点为E 、其顶点为F 、对称轴与x 轴的交点为H.(1)求a 、c 的值;(2)连接OF 、试判断△OEF 是否为等腰三角形、并说明理由;(3)现将一足够大的三角板的直角顶点Q 放在射线AF 或射线HF 上、一直角边始终过点E 、另一直角边与y 轴相交于点P 、是否存在这样的点Q 、使以点P 、Q 、E 为顶点的三角形与△POE 全等?若存在、请直接写出点Q 的坐标;若不存在、请说明理由.解:(1)∵△ABC 为等腰直角三角形、∴OA =12BC. 又∵△ABC 的面积=12BC×OA=4、即OA 2=4、 ∴OA =2.∴A(0、2)、B(-2、0)、C(2、0).∴⎩⎪⎨⎪⎧c =2,4a +c =0,解得⎩⎪⎨⎪⎧a =-12,c =2.图1(2)△OEF 是等腰三角形.理由如下:如图1、∵A(0、2)、B(-2、0)、∴直线AB 的函数表达式为y =x +2、又∵平移后的抛物线顶点F 在射线BA 上、∴设顶点F 的坐标为(m 、m +2).∴平移后的抛物线函数表达式为y =-12(x -m)2+m +2. ∵抛物线过点C(2、0)、∴-12(2-m)2+m +2=0、 解得m 1=0(舍去)、m 2=6.∴平移后的抛物线函数表达式为y =-12(x -6)2+8、即y =-12x 2+6x -10. 当y =0时、-12x 2+6x -10=0、 解得x 1=2、x 2=10.∴E(10、0)、OE =10.又∵F(6、8)、OH =6、FH =8.∴OF =OH 2+FH 2=62+82=10、EF =FH 2+HE 2=82+42=45、∴OE =OF 、即△OEF 为等腰三角形.(3)存在.点Q 的坐标为(6、221)或(6、3)或(10、12)或(4+14、6+14)或(4-14、6-14).。
2019年广西贵港市中考数学试卷和答案

2019年广西贵港市中考数学试卷一、选择题(本大题共12小题,每小题3分,共36分)每小题都给出标号为A、B、C、D的四个选项,其中只有一个是正确的、请考生用2B铅笔在答题卡上将选定的答案标号涂黑.1.(3分)计算(﹣1)3的结果是()A.﹣1B.1C.﹣3D.32.(3分)某几何体的俯视图如图所示,图中数字表示该位置上的小正方体的个数,则这个几何体的主视图是()A.B.C.D.3.(3分)若一组数据为:10,11,9,8,10,9,11,9,则这组数据的众数和中位数分别是()A.9,9B.10,9C.9,9.5D.11,10 4.(3分)若分式的值等于0,则x的值为()A.±1B.0C.﹣1D.15.(3分)下列运算正确的是()A.a3+(﹣a)3=﹣a6B.(a+b)2=a2+b2C.2a2•a=2a3D.(ab2)3=a3b56.(3分)若点P(m﹣1,5)与点Q(3,2﹣n)关于原点成中心对称,则m+n的值是()A.1B.3C.5D.77.(3分)若α,β是关于x的一元二次方程x2﹣2x+m=0的两实根,且+=﹣,则m等于()A.﹣2B.﹣3C.2D.38.(3分)下列命题中假命题是()A.对顶角相等B.直线y=x﹣5不经过第二象限C.五边形的内角和为540°D.因式分解x3+x2+x=x(x2+x)9.(3分)如图,AD是⊙O的直径,=,若∠AOB=40°,则圆周角∠BPC的度数是()A.40°B.50°C.60°D.70°10.(3分)将一条宽度为2cm的彩带按如图所示的方法折叠,折痕为AB,重叠部分为△ABC(图中阴影部分),若∠ACB=45°,则重叠部分的面积为()A.2cm2B.2cm2C.4cm2D.4cm211.(3分)如图,在△ABC中,点D,E分别在AB,AC边上,DE ∥BC,∠ACD=∠B,若AD=2BD,BC=6,则线段CD的长为()A.2B.3C.2D.512.(3分)如图,E是正方形ABCD的边AB的中点,点H与B关于CE对称,EH的延长线与AD交于点F,与CD的延长线交于点N,点P在AD的延长线上,作正方形DPMN,连接CP,记正方形ABCD,DPMN的面积分别为S1,S2,则下列结论错误的是()A.S1+S2=CP2B.AF=2FD C.CD=4PD D.cos∠HCD =二、填空题(本大题共6小题,每小题3分,共18分)13.(3分)有理数9的相反数是.14.(3分)将实数3.18×10﹣5用小数表示为.15.(3分)如图,直线a∥b,直线m与a,b均相交,若∠1=38°,则∠2=.16.(3分)若随机掷一枚均匀的骰子,骰子的6个面上分别刻有1,2,3,4,5,6点,则点数不小于3的概率是.17.(3分)如图,在扇形OAB中,半径OA与OB的夹角为120°,点A与点B的距离为2,若扇形OAB恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为.18.(3分)我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,且b2﹣4ac>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为(﹣1,0),(3,0)和(0,3);②图象具有对称性,对称轴是直线x=1;③当﹣1≤x≤1或x≥3时,函数值y随x值的增大而增大;④当x=﹣1或x=3时,函数的最小值是0;⑤当x=1时,函数的最大值是4.其中正确结论的个数是.三、解答题(本大题共8小题,满分66分。
2019年广西贵港市中考数学试卷

2019年广西贵港市中考数学试卷一、选择题(本大题共12小题,每小题3分,共36分)每小题都给出标号为A、B、C、D 的四个选项,其中只有一个是正确的、请考生用2B铅笔在答题卡上将选定的答案标号涂黑. 1.(3 分)计算(﹣1)3 的结果是()A.﹣1 B.1 C.﹣3 D.32.(3 分)某几何体的俯视图如图所示,图中数字表示该位置上的小正方体的个数,则这个几何体的主视图是()A.B.C.D.3.(3 分)若一组数据为:10,11,9,8,10,9,11,9,则这组数据的众数和中位数分别是()A.9,9 B.10,9 C.9,9.5 D.11,104.(3 分)若分式的值等于0,则x的值为()A.±1 B.0 C.﹣1 D.15.(3 分)下列运算正确的是()A.a3+(﹣a)3=﹣a6 B.(a+b)2=a2+b2C.2a2•a=2a3 D.(ab2)3=a3b56.(3 分)若点P(m﹣1,5)与点Q(3,2﹣n)关于原点成中心对称,则m+n的值是()A.1 B.3 C.5 D.77.(3 分)若α,β是关于x的一元二次方程x2﹣2x+m=0 的两实根,且+ =﹣,则m等于()A.﹣2 B.﹣3 C.2 D.38.(3 分)下列命题中假命题是()A.对顶角相等B.直线y=x﹣5 不经过第二象限第1页(共29页)C.五边形的内角和为540°D.因式分解x3+x2+x=x(x2+x)9.(3 分)如图,AD是⊙O的直径,=,若∠AOB=40°,则圆周角∠BPC的度数是()A.40°B.50°C.60°D.70°10.(3 分)将一条宽度为2cm的彩带按如图所示的方法折叠,折痕为AB,重叠部分为△ABC (图中阴影部分),若∠ACB=45°,则重叠部分的面积为()A.2 cm2 B.2 cm2 C.4cm2 D.4 cm2 11.(3 分)如图,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6,则线段CD的长为()A.2 B.3 C.2 D.512.(3 分)如图,E是正方形ABCD的边AB的中点,点H与B关于CE对称,EH的延长线与AD交于点F,与CD的延长线交于点N,点P在AD的延长线上,作正方形DPMN,连接CP,记正方形ABCD,DPMN的面积分别为S1,S2,则下列结论错误的是()第2页(共29页)A.S1+S2=CP2 B.4F=2FD C.CD=4PD D.cos∠HCD=二、填空题(本大题共6小题,每小题3分,共18分)13.(3 分)有理数9 的相反数是.14.(3 分)将实数3.18×10﹣5 用小数表示为.15.(3 分)如图,直线a∥b,直线m与a,b均相交,若∠1=38°,则∠2=.16.(3 分)若随机掷一枚均匀的骰子,骰子的6 个面上分别刻有1,2,3,4,5,6 点,则点数不小于3 的概率是.17.(3 分)如图,在扇形OAB中,半径OA与OB的夹角为120°,点A与点B的距离为2 ,若扇形OAB恰好是一个圆锥的侧面展开图,则该圆锥的底面半径为.18.(3 分)我们定义一种新函数:形如y=|ax2+bx+c|(a≠0,且b2﹣4a>0)的函数叫做“鹊桥”函数.小丽同学画出了“鹊桥”函数y=|x2﹣2x﹣3|的图象(如图所示),并写出下列五个结论:①图象与坐标轴的交点为(﹣1,0),(3,0)和(0,3);②图象具有对称性,对称轴是直线x=1;③当﹣1≤x≤1 或x≥3 时,函数值y随x值的增大而增大;④当x=﹣1 或x=3 时,函数的最小值是0;⑤当x=1 时,函数的最大值是4.其中正确结论的个数是.第3页(共29页)三、解答题(本大题共8小题,满分66分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题型专项(八)二次函数与几何图形综合题
类型1 探究图形面积数量关系及最值等问题
1.(2016·贵港模拟)如图甲、四边形OABC 的边OA 、OC 分别在x 轴、y 轴的正半轴上、顶点在B 点的抛物线交x 轴于点A 、D 、交y 轴于点C.已知A(3、0)、D(-1、0)、C(0、3).
(1)求抛物线的解析式及顶点B 的坐标;
(2)设△AOC 沿x 轴正方向平移t 个单位长度(0<t≤3)时、△AOC 与△ABC 重叠部分的面积为S 、求S 与t 之间的函数关系式、并指出t 的取值范围;
(3)当0<t≤32
时、求S 的最大值.
解:(1)设抛物线的解析式为y =a(x -3)(x +1).
∵将C(0、3)代入、得-3a =3、解得a =-1.
∴y =-x 2+2x +3.
∵y =-x 2+2x +3=-(x -1)2+4、
∴B(1、4).
(2)设直线AB 的解析式为y =kx +b.
∵将A(3、0)、B(1、4)代入y =kx +b 得⎩⎪⎨⎪⎧3k +b =0,k +b =4,解得⎩
⎪⎨⎪⎧k =-2,b =6, ∴y =-2x +6.
过点C 作射线CF∥x 轴交AB 于点F.
∵将y =3代入直线AB 的解析式得:
-2x +6=3、得x =32、∴F(32
、3).
图1
①当0<t≤32
时、如图1所示. 设△AOC 平移到△PNM 的位置、PM 交AB 于点H 、MN 交AC 于点G.则ON =AP =t 、过点H 作LK⊥x 轴于点K 、交CF 于点L.
由△AHP∽△FHM、得
AP FM =HK HL 、即t 32
-t =HK 3-HK .解得HK =2t. ∴S =S △MNP -S △G NA -S △HAP =12×3×3-12(3-t)2-12t×2t=-32
t 2+3t.
图2
②当32
<t≤3时、如图2所示: 设△AOC 平移到△PQR 的位置、RQ 交AB 于点I 、交AC 于点V.
∵直线AC 的解析式为y =-x +3、直线AB 的解析式为y =-2x +6、
∴V(t 、t +3)、I(t 、-2t +6).
∴IV =-2t +6-(-t +3)=-t +3、AQ =3-t.
∴S =S △IVA =12AQ·IV=12(3-t)2=12t 2-3t +92
. 综上所述、S =⎩⎪⎨⎪⎧-32t 2+3t (0<t≤32),12t 2
-3t +92(32<t≤3). (3)当0<x≤32时、S =-32t 2+3t =-32(t -1)2+32、当t =1时、S 最大=32
.
2.(2016·十堰模拟)如图1、在平面直角坐标系中、抛物线y =ax 2+bx +3(a≠0)经过点A(-1、0)和点B(3、0).
(1)求抛物线的解析式、并写出顶点D 的坐标;
(2)若点P 在直线x =2上运动、当点P 到直线AD 的距离d 等于点P 到x 轴的距离时、求d 的值;
(3)如图2、直线AC :y =-x +m 经过点A 、交y 轴于点C.探究:在x 轴上方的抛物线上是否存在点M 、使得S △CDA =2S △ACM ?若存在、求点M 的坐标;若不存在、请说明理由.
解:(1)∵抛物线y =ax 2
+bx +3(a ≠0)经过点A(-1、0)和点B(3、0)、
∴⎩⎪⎨⎪⎧a -b +3=0,9a +3b +3=0,解得⎩⎪⎨⎪⎧a =-1,b =2. ∴y =-x 2+2x +3=-(x -1)2
+4.∴D(1、4).
(2)设P(2、y P )、过P 作PE⊥AD 于点E 、设直线AD 与直线x =2交于点G 、
则PE =d =|y P |、直线AD 的解析式为y =2x +2、
∴G(2、6).∴PG=6-y P .
∵sin ∠AGP =AN AG =335
、 ∴PE PG =15.∴PG=5|y P |=5d. ①若点P 在第一象限、则PG =6-d 、
②若点P 在第四象限、则PG =6+d 、 ∴5d =6+d 、解得d =35+32
. ∴d 的值为35-32或35+32
. (3)∵直线AC 过点A 、所以可求得直线AC :
y =-x -1.
过点D 作DE∥AC、交y 轴于点E 、可求得直线DE :y =-x +5.
∴E(0、5).∴EC 的中点F(0、2).
∴过点F 平行于AC 的直线为y =-x +2.
∴⎩
⎪⎨⎪⎧y =-x +2,y =-x 2+2x +3. 解得⎩⎪⎨⎪⎧x 1=3-132,y 1=1+132.或⎩⎪⎨⎪⎧x 2=3+132,y 2
=1-132.(舍去) ∴M(3-132、1+132
). 3.(2016·玉林模拟)已知抛物线y =ax 2
+bx +c 与x 轴交于A 、B 两点、与y 轴交于点C.其中点A 在x 轴的负半轴
上、点C 在y 轴的负半轴上、线段OA 、OC 的长(OA <OC)是方程x 2-5x +4=0的两个根、且抛物线的对称轴是直线
x =1.
(1)求A 、B 、C 三点的坐标;
(2)求此抛物线的解析式;
(3)若点D 是线段AB 上的一个动点(与点A 、B 不重合)、过点D 作DE∥BC 交AC 于点E 、连接CD 、设BD 的长为m 、△CDE 的面积为S 、求S 与m 的函数关系式、并写出自变量m 的取值范围.S 是否存在最大值?若存在、求出最大值并求此时D 点坐标;若不存在、请说明理由.
解:(1)∵OA、OC 的长是
x 2-5x +4=0的根、OA <OC 、
∴OA =1、OC =4. ∵点A 在x 轴的负半轴、点C 在y 轴的负半轴、
∴A(-1、0)、C(0、-4).
∵抛物线y =ax 2+bx +c 的对称轴为x =1、
∴由对称性可得B 点坐标为(3、0).
∴A 、B 、C 三点坐标分别是A(-1、0)、B(3、0)、C(0、-4).
(2)∵点C(0、-4)在抛物线y =ax 2+bx +c 图象上、∴c =-4. 将A(-1、0)、B(3、0)代入y =ax 2+bx -4、得
⎩⎪⎨⎪⎧a -b -4=0,9a +3b -4=0.解得⎩⎪⎨⎪⎧a =43
,b =-83.
∴所求抛物线解析式为y =43x 2-83
x -4. (3)根据题意、BD =m 、则AD =4-m.
在Rt △OBC 中、BC =OB 2+OC 2
=5.
∵DE ∥BC 、∴△ADE ∽△ABC.∴DE BC =AD AB
. ∴DE =AD·BC AB =5(4-m )4=20-5m 4
. 过点E 作EF⊥AB 于点F 、则sin ∠EDF =sin ∠CBA =OC BC =45.∴EF DE =45
. ∴EF =45DE =45×20-5m 4
=4-m. ∴S △CDE =S △ADC -S △ADE =12(4-m)×4-12(4-m)(4-m)=-12
m 2+2m(0<m <4). ∵S =-12(m -2)2+2、a =-12
<0、 ∴当m =2时、S 有最大值2.
∴点D 的坐标为(1、0).。
