Finite-Length Soliton Solutions of the Local Homogeneous Nonlinear Schroedinger Equation
非线性发展方程的无网格比高精度有限元方法

非线性发展方程的无网格比高精度有限元方法石东洋;王俊俊【摘要】对于几类非线性的发展型方程——非线性抛物方程、非线性Schr?dinger方程、非线性Sobolev方程、非线性双曲方程,本文从协调有限元方法、非协调有限元方法、混合有限元方法等不同角度,利用不同技巧深入系统地研究了其线性化的全离散格式的构造、无网格比约束下的超逼近和超收敛分析.【期刊名称】《数学杂志》【年(卷),期】2019(039)001【总页数】19页(P1-19)【关键词】非线性发展方程;线性化的全离散格式;无网格比;超逼近及超收敛性【作者】石东洋;王俊俊【作者单位】郑州大学数学与统计学院,河南郑州 450001;平顶山学院数学与统计学院,河南平顶山 467000【正文语种】中文【中图分类】O242.211 前言众所周知,非线性发展方程的解通常无法直接用解析式写出来,或是写出来的表达式非常复杂,所以利用数值方法给出其近似解就显得尤为重要.而对于有限元方法这一主流方向,我们常见的线性化BE(Backward-Euler)方法和CN(Crank-Nicolson)方法凭借可以避免在每一个时间层都要求解非线性方程的劣势且不降低计算精度的优势,成为了该方向的研究热点之一.事实上,研究一个非线性发展方程的线性化有限元方法总会涉及到一个有限元解关于某种模的有界性问题,由于这些模的先验估计不容易直接得到,通常的处理技巧就是利用逆不等式.比如在二维的情况下,考虑有限元解有界时的经典做法是其中un是原始问题的解,Ih是某个插值算子或者投影算子.由于通常有误差估计(m1,m2为某些正数),要使有界就不可避免的要对时间步长τ有一个限制,从而导致空间网格参数h与时间步长τ需要满足某个比值关系(即网格比).在实际计算中,这样的网格比经常会导致时间步长变的非常小,从而引起很长的耗时.因此,怎样甩掉这些限制就成了备受关注的课题.最近,为了克服这一严重缺陷,孙伟伟、李步扬、王冀鲁、高华东等学者都在此方面做出了许多有价值的工作.其主要思想(见文献[1])是通过引入一个时间离散方程系统,并利用其解Un把误差分裂成两部分——时间误差un−Un和空间误差,利用时间误差的结果得到关于时间离散方程解的正则性,再利用空间误差得到有限元解的无网格比有界性事实上,由于空间误差的分析过程中甩掉了经典误差估计中的截断误差项,只要空间上的误差能写成(m3,m4为某些正数)的形式,网格比即可去掉.随后,王冀鲁、高华东、司志勇等又把该思想应用于非线性多孔介质流问题[2,3],非线性的Joule Heating方程[4],非线性Thermistor方程[5,6],非线性Schrdinger方程[7,8]和非线性Navier-Stokes方程[9]等.以上研究都考虑了这些非线性发展方程在协调元下关于无网格比的收敛性,有许多问题需要进行更深层次的研究.首先,为了提高有限元解的逼近精度,超收敛的思想已成为了一个重要的研究途径.事实上,在理论分析和实际计算中,若有好的网格,有限元解与有限元插值的误差在某种范数的意义下比有限元解与真解的误差要小得多,即超逼近现象.从上个世纪80年代开始,以林群院士为代表的众多学者专家都在此方面取得了许多有出色的成果,所以如何将无网格比收敛的结果推广到无网格比超收敛上去是我们感兴趣的话题.但是,为了达到超收敛的结果,如果我们把文献[1–9]中所考虑的区域换成更具一般性的矩形区域(不再满足C2的条件),则由椭圆的正则性可以看到,引入的时间离散方程解的有界性就很难达到H3-模.因此,如何在时间离散方程解的有界性较弱的前提下,探讨无网格比的超逼近结果就显得尤为重要.其次,由于非协调元方法在大多数情况下对方程解的正则性要求比较低,因此人们对非协调元的研究一直保持着较高的热度(见以石钟慈院士为代表的众多学者专家所得到的具有特色的工作).这样就很有必要研究怎样利用自由度少、精度高的低阶非协调单元研究非线性发展方程的无网格比的超收敛性.再次,传统的有限元方法对解的光滑度要求都比较高,这会给实际计算造成很多困难,因此混合有限元方法受到了高度的关注.事实上,混合有限元方法的关键性问题在于如何构造出合适的空间对,使其满足LBB条件,这其实是不容易做到的.因此构造特别的格式来降低LBB条件的难度成为了一个热点,比如:文献[10–13]对二阶椭圆问题提出了一种混合元格式,它具有当两个逼近空间满足一个简单的包含关系时,LBB条件容易满足且能避勉因涉及散度算子带来的麻烦等优点.另一方面,直接绕开LBB稳定性条件(如最小二乘法、稳定化有限元方法等)也成为了大家另一个关注的方面.事实上,1998年,Pani在文献[14]中提出了一种称之为H1-Galerkin混合有限元方法.这种方法不需要所选取的混合元空间满足LBB相容性条件,并被广泛应用在各种方程上.例如,长波方程[15],双曲方程[16],带有记忆项的方程[17],积分微分方程[18–20],抛物方程[21].因此,怎样利用H1-Galerkin方法得到非线性发展方程无网格比的超收敛结果是值得深思的.最后,对于线性化的全离散格式来说,由于当时时刻的时间层分析需要用到上一时刻时间层的结论,我们往往会选择数学归纳法进行证明.但是对于每一个时间层的结果到最后都应该由一个统一的系数来控制这个问题显然就不是一件容易的事了.更进一步地,根据不同非线性问题的具体特点,针对不同方程的逼近格式,设计新的高效的有限元数值算法来验证理论分析的正确性也是必须且困难的.最近,我们在文献[22–34]中,在分裂思想的基础上,博采众家之长,创新性的把无网格比、高精度分析与非协调单元、新的线性化离散格式等特色和优势有机结合起来,形成非线性发展方程在全离散格式上无网格比约束的有限元超收敛分析的一套新理论体系.与此同时,更是尝试着探索、研究一些特殊的方程,考虑绕过分裂的方法也达到无网格比的超收敛结果.近期所做的工作,主要的创新点集中表现在以下几个方面:(1)超收敛结果对方程解的光滑性要求比较高,但构造时间离散辅助问题(即时间离散方程系统)时,在多边形区域(例如矩形)下,就无法保证其解较强模的有界性.因此我们利用了一些特殊的、不同以往的技巧,在其解空间较弱的条件下得到无网格比超收敛的结论;巧用Taylor展开式对非线性项进行处理,以保证对时间步长τ的阶不丢失.(2)由于选择的全离散格式是线性化的形式,在利用数学归纳法分析第n层的结果时需要用到第n−1层的结论,我们用一个统一的系数来控制每一个时间层的结果,这也是其数学归纳法成立的关键所在.(3)构造了非线性双曲方程新的二阶格式,以此得到无网格比超收敛结果.而以往对非线性双曲方程的无网格比研究甚至连收敛性也没有见到报道.(4)对一些特殊的非线性发展方程,抛弃分裂误差思想,采用一些新的技巧也证明了其无网格比超收敛性.本文的目的是在前期我们所做的工作的基础上,挑拣出有特色的创新点给予说明,以期窥探出对非线性发展方程无网格比超收敛分析的重要方法和思路,起到抛砖引玉的作用.2 非线性抛物方程的无网格比超收敛分析非线性抛物方程有着深刻的物理背景,它的有限元方法也越来越受人们关注.例如:文献[35]针对一般的非线性抛物方程建立了两种线性化的格式,当τ≤h时,利用线性三角形元得到了L2-模意义下的收敛结果.文献[36]在限制下利用两层时间离散的方法讨论了非线性抛物方程的最优误差估计.文献[37]采用了一个非线性H1投影,当τ4=O(hq),q≤3时,得到了其解在L2-模和H1-模意义下的最优误差估计.文献[1]利用分裂技巧摆脱了此类限制,给出了一类称之为Joule Heating的非线性抛物型方程的协调元无网格比收敛性分析.我们看到,一方面,一般的非线性抛物方程中的非线性项∇·(a(u)∇u)的处理对于超收敛的分析是很有挑战的,特别是在分析空间误差的时候,怎样处理a(u)才可以在不降阶的情况下使其结果能提出空间网格参数h,才能在使用逆不等式的时候不产生网格比,但同时还得能维持数学归纳法所需要要的系数统一性?另一方面,当非线性抛物方程右端的非线性项是局部Lipschitz连续时,对有限元解的正则性要求可能会更苛刻,如何把这些限制考虑进去且得到无网格比超收敛结果是我们想要研究的方向之一.考虑如下非线性抛物方程其中Ω⊂R2是一个矩形,其边界为∂Ω,0<T<∞,X=(x,y),u0(X)是已知光滑函数.a(u)关于u是二阶可导连续的函数,其中0<a0≤a(u)≤a1,a0,a1是某些正数.利用低阶非协调单元(参见文献[21,38–40]),对(2.1)式开展了无网格比超收敛性质的研究.在矩形区域下,引进了一个时间离散方程,证明了时间离散方程解的H2-模有界.绕过时间离散方程解较弱的正则性,利用Taylor展开,在不降低时间方向阶的前提下,得到其CN格式的无网格比超逼近结果.另一方面,限制(2.1)式右端项为仅满足局部Lipschitzt连续条件,利用数学归纳法,巧妙的使用几个不等式,在每一层都得到数值解L∞-模有界的前提下,保证了结果系数的统一性,采用双线性元(参见文献[13,41]),得到其在BE格式下无网格比超逼近结果.2.1 非协调有限元方法首先,设f(u)是Ω上整体Lipschitz连续的函数,Ω是一个四条边都平行于坐标轴的矩形,Γh是一个拟一致正则矩形剖分.对于给定的K∈Γh,令其四个顶点和四条边分别为ai,i=1∼4和.记.定义非协调有限元空间:其中[vh]表示vh跨过单元边界F的跳度,而当F⊂∂Ω时,[vh]=vh.令Ih:H1(Ω)→Vh 为相对应的插值算子,且Ih=Ih|K满足则文献[21,38–40]证明了下面重要引理.引理1 若,则对于任意的vh∈Vh,有进一步地,若,则有这里∇h表示分片梯度,且是Vh上的一个能量模.文献[40]证明了对于任意正整数m,vh∈Vh,设{tn:tn=nτ;0≤n≤N}是[0,T]上的一个等距剖分,时间步长为τ=T/N,设,且u(X,tn)=un,若为一列函数.记利用这些记号,考虑(2.1)式的线性化Galerkin有限元逼近:寻找,使得对于任意的vh∈Vh0,类似于文献[35],由以下方程求解:其中.可以看到先利用(2.7)式计算出,再利用(2.8)式得到.由于线性化后,(2.6)–(2.8)式是一个线性系统,其解的存在唯一性是显然的.下面分步骤地阐述有创新性的重要过程.第一步建立一个时间离散系统,当n>1时求Un满足当n=1时,利用以下式子计算U1:和其中U1,0(X)|∂Ω =0,U1(X)|∂Ω =0.令e1,0,u1−U1,0,en,un−Un(n=0,1,2,···,N). 通过分析时间误差,给出U1,0,Un(n=0,1,2,···,N) 的正则性. 设u和Um(m=0,1,2,···,N) 分别为 (2.1)和(2.9)–(2.11)式的解,u∈L∞(0,T;H3(Ω)),ut,utt∈L∞(0,T;H2(Ω)),uttt∈L∞(0,T;L2(Ω)),则对于m=1,···,N,存在τ0>0,使得当τ≤τ0 时,有和其中C0是一个与m,h和τ无关的正数.此时,注意到由于Ω是矩形,其边界不属于C1,那么就不容易得到Un的H3-模有界性.因此随后的无网格比超收敛分析需要利用新的方法得到.第二步讨论空间误差,也为最终无网格比超逼近结果kIhun−做好准备.给出记号令分别为 (2.9)–(2.11)和 (2.6)–(2.8)式的解,其中m=1,2,···,N,在前面所做工作的前提下,当τ充分小时,有第三步令设分别为(2.1)和(2.6)–(2.8)式的解,则对n=1,2,···,N,有在这个过程中注意到,将τ从内积的一端转向另一端的恒等变化化简过之后需要估计误差如果按照传统的方法,则有这样最终的结果会降一阶.但是若利用Taylor展开则有其中这样就可以保持到想要的结果.在这里我们还指出本节的结果对于正方形网格上的非协调单元(参见文献[42]),矩形的带约束的非协调单元(参见文献[43])和P1-非协调四边形单元(参见文献[44])也成立,因为这些单元都满足引理1.2.2 协调有限元方法限制f(u)为局部Lipschitz连续的,利用双线性协调单元可研究(2.1)式的无网格比超逼近性质(区域及剖分如前面一样).定义其有限元空间Vh0为其中Ih:H2(Ω)→Vh0是相对应的插值算子,且对于以上双线性元有以下高精度结果[41].引理2 若,则对于任意的vh∈Vh0,有考虑(2.1)式的线性化有限元逼近:寻找,使得其中,显然(2.19)式在每一个时间层只需要解决一个线性问题.引入时间离散方程:当n≥1时求Un满足接下来,我们分别就时间误差和空间误差中的新技巧予以说明.时间误差记,则有注意到在第n−1层中归纳假设(2.21)式成立后,进一步地得到是必需的.主要表现在以下两个方面.1.在第n层估计中,误差方程左端有,右端部分在的前提下有估计项和可以看到,此时当τ充分小时,在第n层误差方程的右端才可以去掉.2.由于f的局部Lipschitz连续,要想估计误差方程右端项,则必须得有做前提,这样就保证了空间误差注意到,由于f的局部Lipschitz连续,在估计下面误差时,利用前面的结论以及协调元的性质,有这样可以估计得到注1更进一步地,我们在文献[34]中将文献[10–12]中的混合元和无网格比的思想有机的结合起来,利用分裂内积等思想,得到了(2.1)式关于原始变量u的H1-模和~p=∇u的L2-模的无网格比超收敛结果.3 非线性Schrdinger方程的无网格比超收敛分析对于非线性Schrdinger方程来说,文献[7,8]利用分裂技巧得到了协调元的无网格比收敛结果.但是怎样能够使得其无网格比的超收敛结果成立呢?首先,要使得时间误差H2-模的阶比文献[7,8]有所提高,这样才能为下面的无网格比超逼近结果做铺垫.其次,可以看到,文献[7,8]是利用投影算子来得到的无网格比的收敛结果的.事实上,对我们而言,仅用投影算子是不能直接利用插值后处理技巧得到整体超收敛的.所以从这个角度考虑,利用插值算子更有优势.但是,若仅仅考虑插值算子得到超逼近的结果,则在tn时刻对时间离散方程解Un的正则性要求就比较高了,而在矩形网格下,要想得到Un的H3-模以上的有界性并不是那么容易的事情.既然单独利用插值算子或者投影算子都不能得到令人满意的效果,那把二者结合在一起是否会有更好的结果?考虑如下 Schrdinger方程其中Ω同(2.1)式,i是虚数单位,u0(X)是已知复值函数.另外,f(s)是一个实值函数,且关于s是二阶可导连续的.在克服非线性Schrdinger方程由于虚数单位i所带来困难的同时,需要采用新的技巧,得到每一层数值解的L∞-模有界性质,保证其每一层解的存在唯一性,并导出其无网格比超逼近性质.一方面,我们利用新的技巧得到了比文献[8]更高阶的时间误差,从而导出了结果更好的时间离散方程解的正则性,这也为下面无网格比的超逼近奠定了基础.另一方面,在证明过程中我们引入了经典的Ritz投影算子,避开了对引入的时间离散方程解的正则性要求过高的麻烦,得到了合适的空间误差结果.同时,结合插值算子和Ritz投影算子相结合的思想达到了超逼近的结果.最后,利用文献[41]中的插值后处理算子得到了整体超收敛性质.选用上一部分的区域,剖分和双线性元单元,且仍定义其有限元空间为Vh0.令Rh:是定义在Vh0上的相对应的Ritz投影算子有且更进一步地,当u∈H3(Ω),又由文献[13]可知其中Ih是定义在Vh0上相对应的插值算子.下面我们仍采用了分裂技巧,分别给出时间误差和空间误差上分析时所遇到的困难和解决方法.时间误差对于CN格式将误差方程相邻两层相减,则就变成至此,得到的结果kenk2=O(τ2)相关估计,可以比文献[8]的结果高二分之一阶,也就是这样的结果导出了,为后面的无网格比超逼近结果奠定了基础.对于BE格式得到结果kenk2=O(τ)比文献[7]中的结果阶高二分之一阶,这也导出了,也为下面的空间误差做出了铺垫.空间误差 1.对误差方程相邻两层相减,对比文献[45]中的结果,可以看到不需要的有界性也得到了无网格比高精度的结果,这就改进了已有结论.2.使用插值算子和投影算子相结合的思想:若仅使用插值算子,为了得到高精度结果,避免不了利用高精度结果(∇(un−Ihun),∇vh)=O(h2)kunk3kvhk1或者(∇(un−Ihun),∇vh)=O(h2)kunk4kvhk0,则对Un和un的正则性要求过于苛刻.然而,在Ω为一个矩形的前提下,目前只能得到kUnk2的有界性,此时选用投影算子Rh是合适的.另一方面,若仅仅使用投影算子Rh,则不能构造相应于Rh的插值后处理算子,也就不能得到整体超收敛结果了.4 非线性Sobolev方程H1-Galerkin混合有限元方法的无网格比超收敛分析Sobolev方程起源于流体通过裂隙岩石的流动、二阶流体的热力学剪切和粘土的固结等物理现象.到目前为止,已有很多文献研究了它的数值方法.例如:文献[46]得到了当τ=O(hd/3)(d≤3)时,在三种情况下关于H1-模最优误差估计结果.而文献[47]利用混合有限元方法,在条件τ=O(h)下得到了最优误差估计.文献[38]控制条件为τ=O(h1+ε)(ε>0)时分别利用协调有限元和非协调有限元讨论了其特征有限元方法,也得到了H1(Ω)-模和L2(Ω)-模的最优误差估计.大家都知道,H1-Galerkin方法是一个不需要满足LBB条件的混合有限元方法,加上一些技巧的应用,还可得到关于流量~p=∇u散度模的误差估计.但是由于H1-Galerkin混合有限元方法需要的时间离散方程解的正则性较高,在矩形区域下不容易得到,所以对于一般的诸如非线性抛物方程利用上述分裂技巧直接处理暂时还不能去掉h和τ的比值.非线性Sobolev方程有着其自身的特点,它比非线性抛物方程多了一个非线性的导数项,正是多了这一项,使得我们考虑在分析的时候可以不用以上的分裂法就得到无网格比超收敛结果.因此我们通过与前面不同的分析,不引进时间离散方程,即在不必考虑所谓的时间误差的前提下,避免由于时间离散方程解的正则性达不到相应的要求而带来的麻烦,给出了无网格比的超逼近结论.考虑如下非线性Sobolev方程:这里对于正数b1,有|b(u)|≤b1,其余同(2.1)式中的假设.首次尝试选择非协调元单元对及零阶Raviart-Thomas(RT)单元)构造H1-Galerkin混合有限元格式去解决(4.1)式的无网格比超逼近问题.给出一个重要引理,完全不同于文献[1–9]的思路,先估计和k∇ξ1k0的结果,再通过不等式k∇ξnk0≤给出k∇ξnk0超收敛性,其中,Ih是相对应的插值算子.采用非协调元,假定所有符号同第二节.设零阶RT单元的空间定义为对于,定义相对应的插值算子Πh为其中是单元边上li的外法线.令,相对应的弱形式是:寻找,使得其中.给出线性化的CN全离散格式:寻找,使得n≥2时,当n=1时,和其中.下面先给出一个新的引理.引理3 对于任意的,则有这里仅给出该引理成立的关键点.事实上,由的定义可知,在K上为常数,利用的插值定义以及空间性质,图1其中l1,l3分别为K的下边和上边,l2,l4分别为K右边和左边,则有注意到,由于该引理的证明利用了的插值定义,若此时将单元对换成协调单元对Q11×Q10×Q01,此结果将不再成立.令由引理3,并利用数学归纳法,可分以下几步分析说明非线性Sobolev方程的无网格比超收敛结果第一步 .第二步利用,得到利用Gronwall引理,当τ充分小时有所以第三步进一步地,将(4.9)式代入(4.10)式,当τ充分小,利用Gronwalls引理有,再利用(4.9)式得到kξnkh≤Ch2+Cτ2.这里强调以下三点(1)如果直接估计kξnkh,对τ和h的比例限制将不可避免;(2)在分析中起到重要的作用;(3)在通常的估计中,的阶低一阶,而在这里保持了一样的阶.5 非线性双曲方程在物理上,双曲方程是一类一直很受关注的偏微分方程,它可以用来描述声波和电磁波的传播等现象,其中也有很多文献关注其非线性问题的有限元方法.例如,文献[48]和[49]分析了非线性双曲方程的全离散格式,其中文献[48]讨论了混合有限元方法,达到了最优误差估计.文献[49]利用Galerkin交替方向法讨论了一类三维非线性双曲方程,利用先验估计的结果得到了误差的H1(Ω)-模和L2(Ω)-模.但上述结果也都没有摆脱h和τ的比值限制,在文献[48]和[49]中分别需要假设条件τ=O(h),hr=O(τ)(1≤r≤k+1,k≥0)和τ=O(h2).因此,如何有效的对非线性双曲方程展开无网格比的研究具有相当重要的科学价值.另一方面,在现有的参考文献中对非线性双曲方程的二阶线性化格式讨论的非常少,怎样构造新的非线性双曲方程的线性化全离散格式,使得其有更好的稳定性以及超收敛结果也值得进行深入的探讨. 考虑如下非线性双曲方程关于方程的一些基本假设如同第二节.我们将对(5.1)式创造性地构造一个新的线性化二阶格式,技巧性地证明其截断误差的二阶性质,给出其相对应的时间离散方程解的正则性,并由此得到在非协调单元下无网格比的超逼近结果.本节仍采用第二节中非协调元的空间.记则有利用这些记号,考虑(5.1)式线性化的逼近方程:寻找,使得当n≥2,有利用如下方程求解:和其中,且utt(0)可以利用utt(0)=∇·(a(u0)∇u0)+f(u0)得到,u0是已知函数.时间误差引入时间离散方程,利用其解Un分裂误差,通过估计时间误差得到Un的正则性.令,则有和注意到,在这一节里针对非线性双曲方程构造了一个新的线性化的二阶格式,可以看到要证明其截断误差为O(τ2)是非常不容易的.另一方面,在得到误差结果时,由于C0在第n层和第n+1层必须统一,则在估计误差时,我们需要利用ēm+1≤τ(m≤n−1),而不是ēm+1≤C0τ2(m≤n−1)来得到结果.空间误差利用以上结果得到超逼近结果,令,则有在此过程中,有以下几点需要特别关注1.如果将本节使用的单元换成协调单元(比如Q11单元),由于没有的和的H2-模的有界性,则结果(5.8)式将不成立.2.(5.8)式的右端不能直接被估计成C1(h2+τ2),否则h和τ的比值将无法避免.事实上,也不能将其估计为C1h,因为利用数学归纳法,我们需要统一n层和n+1层的,所以利用了.进一步地,在误差估计过程中会出现以下项如果利用类似前面的估计方法,将τ从内积的一端转向另一端,则有结果,这时将不可避免的出现网格比.为了克服关键问题,重新分裂内积为则有其中以及rn=Un−IhUn.这样可得到最后可导出以下结果6 总结与展望本文在矩形区域下,对非线性抛物方程、非线性Schrdinger方程、非线性Sobolev方程、非线性双曲方程,讨论了它们线性化的全离散格式的构造以及无网格比超收敛分析.首先,把原来文献中已有的对非线性发展方程无网格比收敛的结果,进一步延伸到对非线性发展方程无网格比的超逼近和超收敛的研究中.由于要想得到高精度的结果,对原始方程解正则性的要求往往都会比较高.那么怎样绕过在矩形区域下,引入的时间离散方程解的有界性达不到H3(Ω)时,有技巧的得到无网格比超逼近结果是之前文献所不曾见过的.其次,对于非线性发展方程,其非线性项中a(u)的处理也是之前很少有的.我们创新性的利用Taylor展开式,保持了最后时间方向上的误差不丢失阶.。
零维锑基有机-无机杂化氯化物的自陷态激子发光及其发光二极管

第43卷㊀第1期2022年1月发㊀光㊀学㊀报CHINESE JOURNAL OF LUMINESCENCEVol.43No.1Jan.,2022文章编号:1000-7032(2022)01-0094-09㊀㊀收稿日期:2021-10-06;修订日期:2021-10-25㊀㊀基金项目:国家自然科学基金(11904345,61905230,52072355,52103241);浙江省自然科学基金(LQ19F040004)资助项目Supported by National Natural Science Foundation of China(11904345,61905230,52072355,52103241);Natural Science Foun-dation of Zhejiang Province(LQ19F040004)零维锑基有机-无机杂化氯化物的自陷态激子发光及其发光二极管蔡培庆1∗,滕嵘驭1,张㊀帝1,王㊀淞1,占宇鑫1,王祥夫2∗,司俊杰1,姚㊀鑫1,艾㊀琦1,刘祖刚1∗(1.中国计量大学光学与电子科技学院,浙江杭州㊀310000;2.南京邮电大学电子与光学工程学院,微电子学院,江苏南京㊀210023)摘要:新兴的零维金属卤化物材料由于其优异的光电性能,近期引起了研究者们的特别关注㊂本文使用反溶剂法和旋涂法分别制备了零维金属卤化物四苯基膦氯化锑[(C 6H 5)4P]2SbCl 5的发光材料和器件,通过稳态激发/发射光谱㊁瞬态光谱对其发光性能进行了研究㊂研究结果表明,在紫外光激发下,[(C 6H 5)4P]2SbCl 5可以发出明亮的橙红光,这种橙红光源于零维限域作用下的自陷态激子三重态发光㊂变温光致发光(PL)和衰减寿命研究表明该物质具有600meV 左右的热激活能,抗热猝灭性能较强㊂通过优化器件结构,引入聚[双(4-苯基)(4-丁基苯基)胺](Poly-TPD )作为空穴传输层,通过混合Poly-TPD 的荧光发射和[(C 6H 5)4P]2SbCl 5的自陷激子发光,获得了在6V 偏压下126cd /m 2的暖白光电致发光器件㊂本工作对溶液法加工无铅金属卤化合物电致发光器件的进程具有一定的推动作用㊂关㊀键㊀词:零维发光材料;自陷态激子;电致发光中图分类号:O482.31;TN383+.1㊀㊀㊀文献标识码:A㊀㊀㊀DOI :10.37188/CJL.20210318Self-trapped Exciton Luminescence and Light-emitting-diodes Based onZero-dimensional Organic-inorganic Hybrid Antimony ChlorideCAI Pei-qing 1∗,TENG Rong-yu 1,ZHANG Di 1,WANG Song 1,ZHAN Yu-xin 1,WANG Xiang-fu 2∗,SI Jun-jie 1,YAO Xin 1,AI Qi 1,LIU Zu-gang 1∗(1.College of Optical and Electronic Technology ,China Jiliang University ,Hangzhou 310000,China ;2.College of Electronic and Optical Engineering and College of Microelectronics ,Nanjing University of Posts and Telecommunications ,Nanjing 210023,China )∗Corresponding Authors ,E-mail :pqcai @ ;xfwang @ ;zgliu 78@Abstract :The emerging of the zero-dimensional metal halide materials has attracted great attention of researchers due to their excellent photoelectric properties.Herein,the luminescent material and device based on zero-dimensional metal halide tetraphenylphosphoniumantimony chloride[(C 6H 5)4P]2SbCl 5were prepared by anti-solvent method and spin-coating method,respectively.The optoelectronic properties of [(C 6H 5)4P]2SbCl 5were investigated by excitation spectra,emis-sion spectra,and time-resolved spectra.The results show that [(C 6H 5)4P]2SbCl 5can emit bright orange-red emission under the ultraviolet excitation.This orange-red emission originates from the triplet self-trapped exciton induced by the zero-dimensional spatial confinement.Temperature. All Rights Reserved.㊀第1期蔡培庆,等:零维锑基有机-无机杂化氯化物的自陷态激子发光及其发光二极管95㊀dependent PL and decay lifetime studies reveal that the material has a thermal activation energy withthe value of~600meV,thus it has favorable anti-thermal quenching effect.By optimizing the de-vice structure and introducing poly[bis(4-phenyl)(4-butylphenyl)amine](Poly-TPD)as a hole transport layer,the warm white emission by mixing the fluorescence emission of Poly-TPD and the self-trapped exciton emission of[(C6H5)4P]2SbCl5was obtained with a brightness of126cd/m2 under a bias of6V.This work provides an alternative approach for the development of the manufac-ture of lead-free metal halide electroluminescent devices by solution method.Key words:zero-dimensional luminescent material;self-trapped exciton;electroluminescence1㊀引㊀㊀言铅基金属卤化物钙钛矿材料由于具有优异的光电性能,近年来引起了广大研究者的关注[1-5]㊂然而,其中存在的可溶性重金属铅元素对人体健康存在隐患,因此无铅金属卤化物材料逐渐成为研究热点㊂目前,人们已经开发出多种具有较高能量转化效率的全无机无铅金属卤化物材料和有机-无机杂化金属卤化物光电材料,并研究了这些材料在紫外光探测[6]㊁X射线成像[7]㊁太阳能电池[8]㊁照明与显示[9]等领域的应用㊂在无铅金属卤化物材料中,零维金属卤化物材料具有多变的空间几何特性和独特的电子结构,因此,关于该类化合物的光致发光研究已有大量的文献见诸报道,华南理工大学夏志国教授近期综述了该领域的进展[10-11]㊂零维金属卤化物发光材料的发光来源主要有两大类㊂一类是孤立发光中心的发光,如掺杂于其中的稀土离子或者过渡金属离子;另一类是由零维金属卤化物的晶格受到光照或者偏压等诱导产生变形和极化,由此产生的束缚自陷态激子(Self-trapped exciton, STE)发光,属于复合发光的范畴㊂近期,该类STE发光现象引起了大量研究者的关注[12-14]㊂零维金属卤化物材料的自陷态激子发光一般有如下特点:(1)由于空间位置的限域特性和三维空间内较强的介电屏蔽作用,激子的扩散距离往往较短,体现出类似于弗兰克尔激子和空间转移激子的特性;(2)激发态下的激子由于受晶格的束缚,电子-晶格耦合作用较强,具有较大的弗兰克-康登因子(Frank-Condon-factor),发光峰型较宽,斯托克斯位移一般较大,光子循环作用较弱,量子产率较高;(3)由于自陷态激子受零维金属卤化物中存在的卤素和金属的重原子效应影响,自旋-轨道耦合作用较为明显,因此一般呈现出微秒级别的三重态自陷激子磷光寿命㊂然而,目前关于自陷态激子电致发光(Electroluminescence,EL)现象的报道较少,主要有CsPbI3体系[15-17]㊁Cs2AgInCl6体系[18]㊁Cs3Cu2I5/CsCu2I3体系[19-22],以及本课题组报道的二维钙钛矿体系[23]等㊂因此,开拓出新型基于自陷态激子发光的电致发光器件对金属卤化物光电器件的无铅化研究非常重要㊂芳香膦(氧)基团由于结构上打破共轭,可以同时调控电子效应和空间效应,因此非常适合用于构建综合性能优异的电致发光材料和器件㊂黑龙江大学许辉教授在该方面有综合性的评述[24]; 2017年,福建物构所陈忠宁研究员报道了基于四苯基膦溴化锰的绿光电致发光器件,最高外量子效率可达10.49%[25];2018年,Ma等报道了光致发光量子效率接近100%的四苯基膦氯化锑橙光材料[26]㊂因此,通过芳香膦基无铅金属配合物获得高效电致发光器件是实现无铅化器件的可行途径之一㊂本文通过反溶剂结晶的方法,合成出具有较高发光强度的零维四苯基膦氯化锑[(C6H5)4P]2SbCl5 (以下缩写为TPP2SbCl5)材料,对其发光性质进行了研究㊂并通过溶液加工和真空镀膜等工艺,成功制备出基于自陷态激子的暖白光电致发光器件㊂2㊀实㊀㊀验2.1㊀样品制备粉末样品的制备:首先将四苯基氯化膦(C6H5)4PCl(阿拉丁,98%)和三氯化锑SbCl3(阿拉丁,99.98%)按2ʒ1的量比称取样品,溶于二甲基亚砜DMSO(阿法埃莎,99.9%)溶液中;然后将装有DMSO溶液的5mL小瓶置于盛有10mL乙. All Rights Reserved.96㊀发㊀㊀光㊀㊀学㊀㊀报第43卷醚(国药,分析纯)的50mL烧杯中,将烧杯的开口塑封;通过乙醚的反溶剂作用,静置一周左右可析出大量白色沉淀,将产生的白色沉淀离心并置于130ħ的真空干燥箱内干燥过夜,所得粉末产物即为最终产物TPP2SbCl5㊂薄膜样品的制备:在充满氮气的手套箱中使用DMSO和N,N-二甲基甲酰胺DMF(阿法埃莎, 99.9%)溶解上述获得的白色产物,然后将溶液旋涂在洁净的石英片上,将石英片置于120ħ的热台上退火,获得薄膜样品㊂2.2㊀器件制备将ITO玻璃基片依次使用洗涤剂Decon90 (英国迪康)㊁丙酮(国药,分析纯)㊁超纯水㊁异丙醇(国药,分析纯)等超声清洗,氮气吹干并用等离子体清洗机处理后备用㊂在空气氛围中,以3000r/min的转速旋涂空穴注入层聚3,4-乙烯二氧噻吩/聚苯乙烯磺酸盐PEDOTʒPSS(西安宝莱特)于ITO玻璃基片上, 110ħ退火10min,然后将基片转移至氮气手套箱内,再次旋涂空穴传输层聚[双(4-苯基)(4-丁基苯基)胺]Poly-TPD(西安宝莱特,M nȡ60000)的氯苯(阿法埃莎,99.9%)溶液,120ħ退火10 min㊂然后在基片上旋涂含有TPP2SbCl5的DMSO 溶液,并经过120ħ退火30min处理㊂将处理后的基片转移至真空蒸镀镀膜机中,在真空度降低至5.33ˑ10-4Pa(4ˑ10-6torr)后,分别蒸镀电子传输层材料1,3,5-三(1-苯基-1H-苯并咪唑-2-基)苯TPBi(西安宝莱特,99.9%)㊁电子注入层LiF(中诺新材,99.99%)和金属Al(中诺新材, 99.999%)电极,最后使用紫外固化胶(乐泰3492)和玻璃盖板完成对器件的封装,用于下一步的器件测试㊂2.3㊀表征手段使用德国Bruker D8型X射线衍射仪测量粉末和薄膜的物相信息;利用爱丁堡稳态瞬态荧光光谱仪FLS1000测量样品的光谱数据;稳态光源选用的是欧司朗除臭氧的450W氙灯,稳态激发光谱(Photoluminescence excitation,PLE)和发射光谱(Photoluminescence emission,PL)数据分别经过爱丁堡FLS1000内置的氙灯谱线参考文件和滨松R928P型光电倍增管(Photomultiplier tube,PMT)矫正文件进行矫正;瞬态光谱测试使用爱丁堡375nm皮秒脉冲激光器作为光源,利用单光子计数技术测量荧光衰减曲线㊂通过东方晨景NCV30-2W-H型液氮低温恒温器控制样品的测试温度㊂使用耐驰STA449F3同步热分析仪进行热重分析,使用台阶仪(美国KLA Alpha-Step D-500)测试器件各功能层的厚度㊂利用Thermo ES-CALAB XI光电子能谱仪测量紫外光电子能谱(Ultroviolet photoelectron spectrometer,UPS)㊂采用Keithley2400电流-电压源表㊁硅光电探头和PR670光度计构成的测试系统测量电流(I)-电压(V)-亮度曲线和外量子效率(External quantum ef-ficiency,EQE)㊂3㊀结果与讨论3.1㊀TPP2SbCl5的室温光致发光和结构性质分析图1(a)是粉末样品的发射光谱和激发光谱㊂激发光谱表明TPP2SbCl5可以在260~410nm左右的紫外区域内被有效激发,光谱在紫外区的强度分布较为平坦,没有明显的锐线激子特征峰出现,激发峰边在370nm左右以后快速变陡,以上特征表明该物质具有基质晶格吸收特性㊂由于本实验中使用的激发光源为除臭氧型氙灯,光源在高于260nm以上的紫外区域内强度较弱,因此无法探测该物质在真空紫外区的激发情况,相关性能后期可以通过真空紫外光谱技术研究㊂另外,已有报道表明有机无机杂化卤化物的自陷态激子可以被X射线等高能射线有效激发[27],因此,该类物质也可能有着良好的闪烁性能,相关性能有待进一步研究㊂发射光谱显示该物质的发射峰值在700nm 左右,为一宽带发射,可以将其归于自陷态激子的发射;发射光谱与激发光谱有着较大的斯托克斯位移,表明该物质的发光可以用强耦合模型的位型坐标图去解释㊂由于滨松R928P型PMT的探测范围限制,800nm以后的发射区域噪声过大,因此超过800nm的光谱区域并未扫谱㊂图1(a)中插图显示,该粉末在日光照射下为一白色物质,表明其在可见光区没有吸收;在365nm的紫外灯激发下,该粉末发射出肉眼可见的明亮的橙红光,但这与实测发射光谱峰值位于700nm是不一致的㊂该现象可以解释如下:由于该物质在500~ 900nm左右均有非常强的宽带发射,但人眼对680nm以上的深红光不敏感,所以人眼观测到该. All Rights Reserved.㊀第1期蔡培庆,等:零维锑基有机-无机杂化氯化物的自陷态激子发光及其发光二极管97㊀图1㊀(a)TPP2SbCl5粉末的激发/发射光谱,激发光谱的监测波长为700nm,发射光谱的激发波长为365nm,插图从左到右分别为粉末样品在日光下㊁在365nm紫外灯激发下以及在365nm紫外灯激发下通过650nm长波通滤波片拍摄的照片;(b)TPP2SbCl5粉末和薄膜的发射光谱对比,插图自上往下分别为在365nm紫外灯激发下,使用DMSO㊁DMF旋涂的TPP2SbCl5薄膜,以及TPP2SbCl5粉末的荧光照片;TPP2SbCl5粉末和薄膜的XRD图谱(c)和结构图(d)㊂Fig.1㊀(a)Excitation and emission spectra of TPP2SbCl5,where the excitation wavelength of PL spectrum is365nm,and the monitoring wavelength of PLE spectrum is700nm,the inserts,from left to right,show the photographs of the powder sample under sun light,365nm UV excitation and365nm UV excitation with650nm long-pass filter,respectively.(b) PL spectra comparation of TPP2SbCl5powder and films,the inserts,from top to bottom,show the photographs under365 nm UV excitation of the TPP2SbCl5films spin-coated by DMSO and DMF solution and the TPP2SbCl5powder,respectively.(c)XRD data of TPP2SbCl5powder and film.(d)Crystal structure of TPP2SbCl5.物质的发光为橙红光㊂另外,如图1(a)中插图所示,通过透过650nm的长波通滤波片观察,我们可以确认该物质存在深红光区域的发射,这也意味着该物质在植物生长补光领域有着潜在的应用[28]㊂如图1(b)所示,TPP2SbCl5的粉末PL谱与使用DMSO㊁DMF溶液旋涂的薄膜PL谱相比,谱线有所不同㊂Ma等在制备该样品时发现了类似的现象㊂他们认为,由于金属卤化物自陷激子的荧光性质强烈依赖于软晶格的结构变化,这种自陷激子荧光发射的差异是由不同的残留有机溶剂分子导致材料热力学稳定相的转变造成的㊂研究发现,快速结晶的小颗粒薄膜样品为热力学不稳定相,薄膜的荧光呈现黄色;而缓慢结晶的大块样品是热力学稳定相,其荧光则红移至红色[26,29]㊂图1(b)插图的薄膜样品图片显示,使用DMSO旋涂而成的薄膜较为光滑,表明晶体颗粒较小;而用DMF旋涂而成的薄膜较为粗糙,表明晶体颗粒较大㊂在365nm紫外光激发下,DMSO和DMF作为溶剂旋涂的TPP2SbCl5薄膜发射峰值分别在635nm和660nm左右,粉末的发射峰值在705nm左右,随着颗粒的增大,光谱逐渐红移㊂因此,我们的实验结果与他们的结论符合得很好㊂如图1(c)所示,粉末和薄膜的XRD衍射测试结果表明,粉末的衍射图谱与已报道的TPP2SbCl5结构计算所得的衍射数据相匹配㊂但是,薄膜样品由于旋涂的厚度较薄(台阶仪测得约60nm),因此X射线衍射峰的强度较弱,图谱. All Rights Reserved.98㊀发㊀㊀光㊀㊀学㊀㊀报第43卷显示的仅为玻璃片的背景峰㊂图1(d)是TPP2SbCl5的结构示意图㊂如图所示,该物质属于三斜晶系的P1空间群,每个SbCl2-5阴离子基团均被四苯基膦大阳离子分隔开,形成具有较大空间位阻的零维结构㊂由于有机组分和无机组分的介电常数差异较大,这样的结构可阻碍激子的有效扩散范围,促进光生载流子自陷在SbCl2-5阴离子基团周围,增强自陷态激子的复合,最终导致高效的激子发射㊂3.2㊀TPP2SbCl5的变温光致发光分析变温荧光性质的分析可以探究TPP2SbCl5激发态的一些性质㊂图2(a)是TPP2SbCl5粉末从80~470K的变温荧光光谱㊂可以看到,荧光强度在室温以下温区的变化不太明显,但随着温度升高至高于室温的温区,荧光强度呈现大幅度下降的趋势,这与有机分子在室温以上的分子振动增强有关㊂图2(c)的热重分析表明,在80~470 K内,样品的重量并没有明显的变化,因此荧光强度的降低不是由于样品受热分解造成的㊂图2(b)是TPP2SbCl5粉末的变温荧光寿命图谱㊂在80~470K的测试温区内,该样品的自陷激子态发光均呈现出单指数衰减,并随着温度升高至室温左右,寿命开始大幅降低㊂上述现象表明,在这种零维限域结构的有机金属卤化物内,自陷态激子复合发光衰减是一个单分子过程,并且该过程受无辐射弛豫的影响较为明显[30-32]㊂另外,无论是在液氮温度或是470K左右的高温下,该物质的发光始终保持在时间较长的微秒量级(5.741~ 0.289μs),说明该物质的发光源于自陷激子的三重态禁阻发射[33]图2㊀TPP2SbCl5粉末的变温荧光光谱(a)和荧光衰减寿命(b);(c)TPP2SbCl5粉末的热重分析图;(d)~(e)荧光积分强度和荧光衰减寿命随着温度变化的计算结果和拟合曲线;(f)强耦合作用下的STE发光位型坐标模型图㊂Fig.2㊀Temperature dependent PL spectra(a)and decay curves of TPP2SbCl5powder(b).(c)TG curve of the TPP2SbCl5pow-der.(d)-(e)Integrated intensity of PL and lifetime values as a function of temperature,respectively.(f)Configuration coordinate diagram of STE luminescence under strong-coupling regime.通过以上荧光光谱和衰减寿命的分析,我们认为该物质的发光特征符合黄昆用于解释F色心发光行为的高温强耦合无辐射跃迁理论[34],可用如图2(f)所示的位型-坐标模型去解释㊂根据该理论的推导结果,不同温度下的荧光积分强度I(T)和荧光衰减寿命τ(T)随着温度T的变化符合如下公式[35]:I(T)=I01+A exp(-ΔE/kT),(1)τ(T)=τr1+(τr/τnr)exp(-ΔE/kT),(2)其中I0是绝对零度时的发光强度积分,A是前因子,τr是辐射跃迁寿命,τnr是非辐射跃迁寿命,ΔE是热激活能,k是玻尔兹曼常数㊂图2(d)㊁(e)是分别对I(T)和τ(T)随着T的变化拟合获得的结果㊂拟合获得的ΔE值分别为608meV和603meV,两种拟合方式获得的ΔE误差值较小,表明实验与理论符合得非常好㊂与室温相对应的热能. All Rights Reserved.㊀第1期蔡培庆,等:零维锑基有机-无机杂化氯化物的自陷态激子发光及其发光二极管99㊀(~26meV)相比,600meV左右的热激活能较大,因此这是零维TPP2SbCl5的自陷态激子在室温下没有热解离并能保持接近100%荧光量子效率的原因之一[26]㊂3.3㊀电致发光器件的构筑和发光分析通过UPS测试和吸收光谱计算,我们确定了如图3(c)所示的器件结构图,并经过逐层和多次的正交参数调控和优化,制备出以TPP2SbCl5为发光层的电致发光EL器件,器件参数为ITO/PEDOTʒPSS(40 nm)/Poly-TPD(30nm)/TPP2SbCl5(60nm)/TPBi(50 nm)/LiF(1.5nm)/Al(100nm)㊂图3(a)是该器件的I-V-L曲线,从图中可以看出器件的启亮电压为3.2V,在6V电压下,器件亮度达到126cd/m2㊂图3(b)展示了该器件外量子效率EQE与器件电流密度的函数曲线㊂数据结果表明,器件的最高EQE为0.39%㊂图3(d)为Poly-TPD/TPP2SbCl5薄膜的归一化PL光谱及器件EL的对比,可以看出器件的蓝光发射来源于空穴传输层的Poly-TPD发光,橙光来源于TPP2SbCl5的自陷态激子发光㊂但是, TPP2SbCl5的EL光谱与PL光谱相比在高能区和低能区均变窄㊂我们经分析认为,影响峰型窄化的因素如下:(1)首先,从能级的角度来看,无论是光致发光还是电致发光,Kasha规则确保光子必须在最低激发态下发射,自陷态激子发生T2ңS0辐射复合造成高能区一侧谱线变宽的可能性很小;(2)振动辅助的辐射跃迁(Vibration assisted radiative transition)几率降低可以导致谱线窄化㊂在PL过程和EL过程中,一些在PL过程中允许的振动辅助跃迁在EL过程中很可能是禁阻的,载流子在STE T1和S0的振动能级上复合的几率存在差异;在偏压作用下,分子的刚性增强也可能会导致振动减弱,导致STE EL光谱窄化㊂图3㊀(a)器件的I-V-L曲线;(b)器件的EQE与电流密度函数曲线;(c)器件的能级结构图;(d)Poly-TPD/TPP2SbCl5薄膜PL谱及器件EL谱比较;(e)不同电压下的器件EL谱;(f)不同电压下的CIE坐标,插图为器件在6V电压下的照片㊂Fig.3㊀(a)I-V-L curves of the prepared device.(b)EQE data of the device as a function of the current density.(c)Energy level structure of the device.(d)Comparation of the PL spectrum of the Poly-TPD/TPP2SbCl5film and the device EL spectrum.(e)EL spectra of the device at different applied bias.(f)CIE coordination at different applied voltages,the insert is the photograph of the device operated at6V.不同电压下的器件EL谱(图3(e))表明,随着电压的增大,蓝光部分逐渐增强,器件运行的视频请见本文的补充文件㊂图3(f)的CommissionInternationale de L Eclairage(CIE)1931图更加明显地显示了不同电压下色坐标的变化㊂从图3(c)的器件结构能级图中可以看出,该器件空穴传输层最低占据轨道(Lowest unoccupied molecu-lar orbital,LUMO)能级与发光层LUMO能级差较小(0.16eV),无法有效阻挡电子,而电子传输层最高占据轨道(Highest occupied molecular orbital,. All Rights Reserved.100㊀发㊀㊀光㊀㊀学㊀㊀报第43卷HOMO)能级和发光层HOMO 能级的能级差较大(0.72eV),阻挡空穴效果较好㊂因此,器件在工作过程中电子与空穴并未达到注入平衡㊂随着电压增大,更多的电子到达空穴传输层Poly-TPD 处,导致Poly-TPD 蓝光增强[36]㊂另外,如图3(f)插图所示,器件在6V 正置偏压下可发出明亮的暖白光,色坐标为(0.36,0.31),表明该器件在无铅金属卤化物白光照明上有着潜在的应用㊂图4为器件在较低电流密度20mA /cm 2下亮度随时间变化的老化测试㊂其在初始亮度110cd /cm 2下的T 90为5min,器件的稳定性能有待进一步改善㊂㊀图4㊀器件在20mA /cm 2电流密度下亮度随时间的变化Fig.4㊀The luminance of the device as a function of time un-der a constant driving current density of 20mA /cm 24㊀结论与展望本文成功制备了TPP 2SbCl 5发光材料和器件,并对其光致发光和电致发光性能进行了研究㊂结果表明,在紫外光激发下,TPP 2SbCl 5可以发出明亮的橙红光,这种橙红光源于零维限域作用下的自陷态激子三重态发光;变温PL 和衰减寿命研究表明该物质具有600meV 左右的热激活能,抗热猝灭性能较强㊂通过优化器件结构,引入Poly-TPD 作为空穴传输层,获得了在6V 偏压下126cd /m 2的暖白光电致发光器件,但是由于TPP 2SbCl 5的成膜性能一般,器件的效率和寿命有待进一步改善㊂在后续有关无铅锑基STE 电致发光的研究中仍需关注如下几点:(1)STE 电致发光无铅材料的溶液法薄膜制备工艺有待进一步优化,双源共蒸发薄膜制备工艺有待研究;(2)STE 发光的斯托克斯位移较大,在电场作用下热损耗不可避免,对器件的寿命影响较大,因此需要降低STE 的斯托克斯位移;(3)STE 结构上类似F 色心,是一种激发态下的暂态局域化激子,存在饱和效应,因此需要调控晶体结构来提高自陷激子态密度,以提高单位电流密度下的复合效率;(4)一般STE 的发光为三重态磷光,衰减寿命较长,对器件的正常工作是不利因素,因此,通过降低STE S 1和T 1能级的能级差,引入热激活延迟荧光机制(Thermally activated delayed fluorescence,TADF),是有效提高STE 电致发光的可能途径㊂本工作是对有机无机杂化零维无铅金属卤化物的自陷态激子发光用于发光二极管的一次有益尝试,有望进一步推动溶液法加工金属卤化合物电致发光器件的无铅化进程㊂本文专家审稿意见㊁作者回复信及补充文件的下载地址: /thesisDetails #10.37188/CJL.20210318.参㊀考㊀文㊀献:[1]DOU L T ,WONG A B ,YU Y ,et al.Atomically thin two-dimensional organic-inorganic hybrid perovskites [J ].Science ,2015,349(6255):1518-1521.[2]TSAI H ,NIE W Y ,BLANCON J C ,et al.High-efficiency two-dimensional Ruddlesden-Popper perovskite solar cells [J ].Nature ,2016,536(7616):312-316.[3]WANG N N ,CHENG L ,GE R ,et al.Perovskite light-emitting diodes based on solution-processed self-organized multiple quantum wells [J ].Nat.Photonics ,2016,10(11):699-704.[4]王娜娜,司俊杰,金一政,等.可溶液加工的有机-无机杂化钙钛矿:超越光伏应用的 梦幻 材料[J].化学学报,2015,73(3):171-178.WANG N N,SI J J,JIN Y Z,et al.Solution-processed organic-inorganic hybrid perovskites:a class of dream materials be-yond photovoltaic applications [J].Acta Chim.Sinica ,2015,73(3):171-178.(in Chinese)[5]姚鑫,丁艳丽,张晓丹,等.钙钛矿太阳电池综述[J].物理学报,2015,64(3):038805-1-8.. All Rights Reserved.㊀第1期蔡培庆,等:零维锑基有机-无机杂化氯化物的自陷态激子发光及其发光二极管101㊀YAO X,DING Y L,ZHANG X D,et al.A review of the perovskite solar cells[J].Acta Phys.Sinica,2015,64(3):038805-1-8.(in Chinese)[6]LI Y,SHI Z F,LIANG W Q,et al.Highly stable and spectrum-selective ultraviolet photodetectors based on lead-free cop-per-based perovskites[J].Mater.Horiz.,2020,7(2):530-540.[7]ZHANG M Y,ZHU J S,YANG B,et al.Oriented-structured CsCu2I3film by close-space sublimation and nanoscale seedscreening for high-resolution X-ray imaging[J].Nano Lett.,2021,21(3):1392-1399.[8]LI P W,LIU X L,ZHANG Y Q,et al.Low-dimensional dion-jacobson-phase lead-free perovskites for high-performancephotovoltaics with improved stability[J].Angew.Chem.Int.Ed.,2020,59(17):6909-6914.[9]YUAN F L,ZHENG X P,JOHNSTON A,et al.Color-pure red light-emitting diodes based on two-dimensional lead-freeperovskites[J].Sci.Adv.,2020,6(42):eabb0253-1-9.[10]LI M Z,XIA Z G.Recent progress of zero-dimensional luminescent metal halides[J].Chem.Soc.Rev.,2021,50(4):2626-2662.[11]苏彬彬,夏志国.新兴零维金属卤化物的光致发光与应用研究进展[J].发光学报,2021,42(6):733-754.SU B B,XIA Z G.Research progresses of photoluminescence and application for emerging zero-dimensional metal halidesluminescence materials[J].C hin.J.Lumin.,2021,42(6):733-754.(in Chinese)[12]SMITH M D,KARUNADASA H I.White-light emission from layered halide perovskites[J].Acc.Chem.Res.,2018,51(3):619-627.[13]LI Z Y,LI Y,LIANG P,et al.Dual-band luminescent lead-free antimony chloride halides with near-unity photolumines-cence quantum efficiency[J].Chem.Mater.,2019,31(22):9363-9371.[14]ZHOU C K,XU L J,LEE S,et al.Recent advances in luminescent zero-dimensional organic metal halide hybrids[J].Adv.Opt.Mater.,2020,9(18):2001766.[15]CHEN J W,WANG J,XU X B,et al.Efficient and bright white light-emitting diodes based on single-layer heterophase hal-ide perovskites[J].Nat.Photonics,2021,15(3):238-244.. All Rights Reserved.[16]XIANG H Y,CHEN J W,WANG R,et al.Perspective on single-emissive-layer white-LED based on perovskites[J].Ap-pl.Phys.Lett.,2021,119(8):080502.[17]XIANG H Y,WANG R,CHEN J W,et al.Research progress of full electroluminescent white light-emitting diodes based ona single emissive layer[J].Light Sci.Appl.,2021,10(1):206-1-16.[18]LUO J J,WANG X M,LI S R,et al.Efficient and stable emission of warm-white light from lead-free halide double perovs-kites[J].Nature,2018,563(7732):541-545.[19]WANG L T,SHI Z F,MA Z Z,et al.Colloidal synthesis of ternary copper halide nanocrystals for high-efficiency deep-bluelight-emitting diodes with a half-lifetime above100h[J].Nano Lett.,2020,20(5):3568-3576.[20]JUN T,SIM K,IIMURA S,et al.Lead-free highly efficient blue-emitting Cs3Cu2I5with0D electronic structure[J].Adv.Mater.,2018,30(43):1804547-1-6.[21]CHEN H,ZHU L,XUE C,et al.Efficient and bright warm-white electroluminescence from lead-free metal halides[J].mun.,2021,12(1):1421-1-7.[22]JIANG X G,SI J J,LIU Z G,et al.Solvent engineering for Cs3Cu2I5based light-emitting diodes[C].Proceedings of SPIE11606,ICOSM2020:Optoelectronic Science and Materials,Hefei,2020:116061A.[23]CAI P Q,WANG X F,SEO H J,et al.Bluish-white-light-emitting diodes based on two-dimensional lead halide perovskite(C6H5C2H4NH3)2PbCl2Br2[J].Appl.Phys.Lett.,2018,112(15):153901-1-5.[24]韩春苗,许辉.膦基电致发光材料及器件的研究进展[J].科学通报,2019,64(7):663-681.HAN C M,XU H.Recent progress of phosphine electroluminescent materials and devices[J].Chin.Sci.Bull.,2019,64(7):663-681.(in Chinese)[25]XU L J,SUN C Z,XIAO H,et al.Green-light-emitting diodes based on tetrabromide manganese(Ⅱ)complex through so-lution process[J].Adv.Mater.,2017,29(10):1605739-1-5.[26]ZHOU C K,WORKU M,NEU J,et al.Facile preparation of light emitting organic metal halide crystals with near-unityquantum efficiency[J].Chem.Mater.,2018,30(7):2374-2378.[27]MORAD V,SHYNKARENKO Y,YAKUNIN S,et al.Disphenoidal zero-dimensional lead,tin,and germanium halides:102㊀发㊀㊀光㊀㊀学㊀㊀报第43卷highly emissive singlet and triplet self-trapped excitons and X-ray scintillation[J].J.Am.Chem.Soc.,2019,141(25):9764-9768.[28]ZHOU Z W,ZHENG J M,SHI R,et al.Ab initio site occupancy and far-red emission of Mn4+in cubic-phase La(MgTi)1/2O3forplant cultivation[J].ACS Appl.Mater.Interfaces,2017,9(7):6177-6185.[29]WANG Z P,XIE D L,ZHANG F,et al.Controlling information duration on rewritable luminescent paper based on hybridantimony(Ⅲ)chloride/small-molecule absorbates[J].Sci.Adv.,2020,6(48):eabc2181-1-9.[30]许少鸿.固体发光[M].北京:清华大学出版社,2011.XU S H.Luminescence of Solids[M].Beijing:Tsinghua University Press,2011.(in Chinese)[31]WILLIAMS R T,SONG K S.The self-trapped exciton[J].J.Phys.Chem.Solids,1990,51(7):679-716.[32]黄桂芹,刘楣,陈凌孚.KMgF3晶体的色心和自陷态激子研究[J].物理学报,2005,54(4):1702-1706.HUANG G Q,LIU M,CHEN L F.The colour centers and self-trapped exciton in KMgF3[J].Acta Phys.Sinica,2005,54(4):1702-1706.(in Chinese)[33]POOLEY D,RUNCIMAN W A.Recombination luminescence in alkali halides[J].J.Phys.C Solid State Phys.,1970,3(8):1815-1824.[34]黄昆.晶格弛豫和多声子跃迁理论[J].物理学进展,1981,1(1):31-85.HUANG ttice relaxation and theory of multiphonon transitions[J].Prog.Phys.,1981,1(1):31-85.(in Chinese)[35]HENDERSON B,IMBUSCH G F.Optical Spectroscopy of Inorganic Solids[M].Oxford:Oxford University Press,2006.[36]刘祖刚,陆慧庆,赵伟明,等.有机薄膜电致发光器件载流子注入和传输性质的研究[J].发光学报,1997,18(1):59-64.LIU Z G,LU H Q,ZHAO W M,et al.Study on the injection and transportion of carrier in organic thin film electrolumines-cent device[J].Chin.J.Lumin.,1997,18(1):59-64.(in Chinese)蔡培庆(1991-),男,江苏盐城人,博士,讲师,2018年于韩国釜庆大学获得博士学位,主要从事过渡金属发光材料与金属卤化物发光器件的研究㊂E-mail:pqcai@.cn 刘祖刚(1961-),男,湖北孝感人,博士,教授,1992年于厦门大学获得博士学位,主要从事印刷OLED㊁QLED㊁CIGS太阳能电池等印刷光电子学的研究㊂E-mail:zgliu78@.cn 王祥夫(1979-),男,山东邹城人,博士,副教授,2012年于南京航空航天大学获得博士学位,主要从事稀土掺杂发光玻璃和柔性电子传感器件的研究㊂E-mail:xfwang@. All Rights Reserved.。
(完整版)基于MATLAB的快速傅里叶的非线性薛定谔方程

GP方程很好的描述BEC的行为
iht
r,t
h2 2m
2
Vext
r
g
r,t
2
r,t
非线性项
G-P方程是非线性薛定谔(Nonlinear Schrödinger)方程的一种, 这类方程大多都只能通过数值办法求解。
2020/2/14
理论物理
7/50
Outline
➢ Matlab程序的实现 ➢ Matlab实例
2020/2/14
理论物理
8/50
III. 算符劈裂算法
Gross-Pitaevskii (G-P)方程:
iht
r,
t
h2 2m
2
Vext
r
g r,t 2
非线性项
r,t
it r,t H Tˆ Vˆextnon r,t
2020/2/14
理论物理
5/50
Outline
➢ 玻色-爱因斯坦凝聚 (BECs) ➢ Gross-Pitaevskii (G-P) 方程 ➢ 算符劈裂算法 (Operator-Splitting methods)
虚时演化 实时演化
➢ 傅里叶变换(离散DFT和快速FFT)
离散傅里叶变换(DFT)算法 快速傅里叶变换(FFT)算法
➢ Matlab程序的实现 ➢ Matlab实例
2020/2/14
理论物理
6/50
II. Gross-Pitaevskii (G-P) 方程
薛定谔(Schrödinger)方程:
关于求解非线性耦合Schrǒdinger方程的Sonnier—Christov格式

(. 1) 4
由( ) 知,只要 一 L和 R足够大 ( 一 L 即 X, R》 0)则问题 (.)(.) ( 1一1 ) , 11~1 与 1 )(. 、 4 3 ( ) 一致的 . 是
收 稿 日期 : 0 7 1 —5 修 订 日期 : 0 90 — 6 2 0 —2 1 ; 2 0 —2 1
、 、
(.) 11
(. 1) 2 (. 1) 3
(半 半)
进行 了数值研 究,提 出T-+ NN- 恒差分格 式 .其 中 、 1 - ,  ̄ F是 已知常数 .非线 性耦合 Sh6 i e 方程在诸如非线性光学、量子物理等物理学的很多领域都有很重要的应 crd gr n 用 [ 9 便于计 算 ,我们取 如下边 界条件 4 ] -. UX ,) ux ,) , VX ,) (n0 =0 (L0 (n 0 =0 (L0 =vx ,) .
文 献 [5 指 出 非守恒 格式 容 易导 致非 线性 的 bo —p 并对 非 线性 ShS igr方 程提 1】 l u, w crdne 出一个 新的 线性化 守恒 差分 格式 . L 和 V — o 也 在文 献 f ] i uQu c 1 中指 出 “ o ra,h 6 i smeaeste n
E— a l m i:wan t n hu g i gc n@nu a e a du. n c
.
基 金 项 目: 国家 自然 科 学基 金 (0 7 0 7 15 2 5 )资 助
N . 王廷 春等 :关 于求 解 非线性耦 合 Sh6igr 程的 S n i — r tv格 式 o1 crdn e 方 one Chio r s 初 边值 问题 (. 1 ) 有两个 重 要的守 恒性 质 .即 电荷守 恒 1 )(. 具 1 4
孤立子解法及其在非线性光学中别具一格

孤立子解法及其在非线性光学中别具一格摘要:孤立子是一种特殊的非线性波动现象,具有较强的稳定性和可移动性,广泛应用于非线性光学中。
本文将介绍孤立子的解法以及在非线性光学中的应用,并重点讨论孤立子的特性和优势。
引言:随着科学技术的进步,非线性光学在各个领域中得到了广泛的应用,其中孤立子作为一种特殊的非线性波动现象,引起了科学家们的极大兴趣。
孤立子是一种具有较强的稳定性和可移动性的波动现象,其在信息传输、光纤通信、光存储等领域中有着重要的应用。
本文将详细介绍孤立子的解法以及其在非线性光学中的独特性。
一、孤立子的基本概念孤立子最早由约翰•斯科特•拉塞尔(John Scott Russell)在19世纪初期的苏格兰運河上观察到。
孤立子是一种在非线性介质中传播的孤立波,其具有以下几个特点:1. 稳定性:孤立子在传播过程中可以保持波形的稳定性,不会扩散或变形。
2. 可移动性:孤立子可以相对稳定地自由传播,不会受到外界扰动的影响。
3. 可变形性:孤立子波形可以改变,同时保持特定的形态。
4. 和谐性:孤立子是和谐振荡的,其波形是周期性的。
二、孤立子的解法孤立子的数学描述常使用非线性薛定谔方程(Nonlinear Schrödinger Equation,简称NLSE)。
NLSE是由非线性项引起的薛定谔方程的一种扩展形式,它描述了非线性介质中的光波传播过程。
常见的NLSE包括标准NLSE、色散NLSE和非线性色散NLSE等。
针对不同类型的NLSE,科学家们提出了多种解法用于描述孤立子。
其中,Hirota方法、贝尔多多方法和逆散射方法是应用较广泛的数学工具。
1. Hirota方法:Hirota方法是一种直接构造孤立子解的方法。
其基本思想是将NLSE转化为一个适合求解的方程,然后通过变换和代数运算求解方程,最后得到孤立子解。
Hirota方法简单明了,适用于各类非线性波动现象的求解。
2. 贝尔多多方法:贝尔多多方法是一种量子力学中常用的方法,用于求解非线性波动现象。
光通信必读优秀书籍

非线性光学部分介质在强激光场作用下产生的极化强度与入射辐射场强之间不再是线性关系,而是与场强的二次、三次以至于更高次项有关,这种关系称为非线性。
凡是与非线性有关的光学现象称为非线性光学现象,属于非线性光学的研究内容。
非线性光学一方面研究光辐射在非线性介质中传播时由于和介质的非线性相互作用自身所受的影响,另一方面则研究介质本身在光场作用下所表现出的特性。
在光通信中,主要是进入高速通信,10g,尤其是40G,随着入纤光功率的增强,非线性效应逐渐显现,系统设计必须加以考虑这方面的影响,于是在40G里面变出现了形形色色的编码。
以下切入正题1、《Nonlinear Fiber Optics》和《Applications of Nonlinear Fiber Optics》Agrawl ,这2本书从书名大家应该也可以看出是偏重于光纤通信应用的,目前第一个已经到第四版,第二个为第二版了,包括中译本,论坛都有,大家可以搜索下就可以都看到了。
/viewthread. ... =nonlinear%2Boptics/viewthread. ... =nonlinear%2Boptics2、Boyd W.R的《nonlinear optics》3rdW. Boyd教授在2002年被任命为Rochester大学M. Parker Givens Professor of Optics,lz发的应该是第二版,该书1992年第一版,第二版在第一版的基础上增加了很多新内容,并对以前的内容做了不少修订,在2008年的4月,该书又出了第三版。
整体来说,该书内容比较深,学校里的高年级研究生和一般研究人员可参考。
W.Boyd今年5月份曾代表美国光学学会来南京开会下载链接:/viewthread. ... =nonlinear%2Boptics3、华裔学者沈元镶的《非线性光学原理》沈是这方面非常牛b的,他的导师算是非线性光学方面的开创者吧,并因此获得了诺贝尔奖。
Sawada-Kotera方程的非局域对称和精确解

第41卷第5期Vol.41No.5丽水学院学报JOURNAL OF LISHUI UNIVERSITY2019年9月Sept.2019 Sawada-Kotera方程的非局域对称和精确解费金喜1,马正义1,许慧2(1.丽水学院工学院,浙江丽水323000;2.浙江理工大学理学院,浙江杭州310018)摘要:在包含五阶偏导数的Lax对的基础上,通过引入两个合适的辅助变量,成功地应用了李对称群方法求得具有非局域对称的Sawada-Kotera方程的精确不变解,并在延拓系统的基础上,导出了与雅可比椭圆函数相关的显式解析的相互作用解。
图显示了椭圆函数波和孤立波之间的物理相互作用。
关键词:Sawada-Kotera方程;Lax对;非局域对称;精确解doi:10.3969/j.issn.2095-3801.2019.05.001中图分类号:0411.1文献标志码:A文章编号:2095-3801(2019)05-0001-06Nonlocal Symmetry and Explicit Solution to the Sawada-KoteraEquationFEI Jinxi1,MA Zhengyi1,XU Hui2(1.Faculty of Engineering,Lishui University,Lishui323000,Zhejiang;2.College of Science,Zhejiang Sci-tec University,Hangzhou310018,Zhejiang)Abstract:Based on the Lax pair which contains the fifth-order partial derivative,the Lie symmetry group method is successfully applied to finding the exact invariant solution to the Sawada-Kotera equation with nonlocal symmetry by introducing two suitable auxiliary variables.Meanwhile,based on the prolonged system,the explicit analytic interaction solutions related to the Jacobi elliptic functions are derived.Figures show the physical interaction between the cnoidal waves and a solitary wave.Keywords:Sawada-Kotera equation;Lax pair;nonlocal symmetry;explicit solution0引言孤子理论是非线性科学中的典型课题之一,广泛应用于非线性介质光学、光子学、等离子体、Bose-E-instein凝聚体的平均场理论、凝聚态物理等许多领域。
【国家自然科学基金】_非局域非线性_基金支持热词逐年推荐_【万方软件创新助手】_20140801
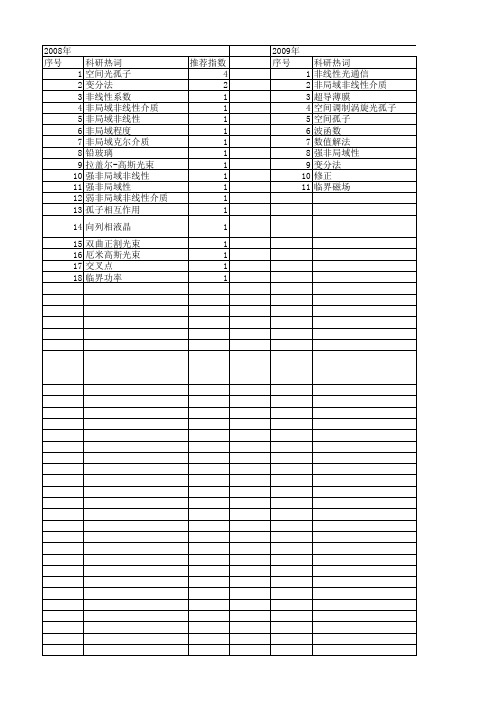
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
科研热词 推荐指数 非局域非线性 2 稳定性 2 高阶光学模式 1 高斯函数 1 非线性非局域介质 1 非线性光学 1 非线性介质 1 非局域自散焦 1 非局域 1 质点振荡模型 1 解析解 1 表面波模 1 表面波 1 稳定区间 1 界面孤子 1 横向结构 1 数值模拟 1 多极表面孤子 1 典雅 1 光格子 1 光暗孤子成丝 1 光学冲击波 1 光呼吸 1 传播常数 1 elegant ince gaussian breathers, 1 nonlocal nonline
2008年 序号 1 2 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
科研热词 空间光孤子 变分法 非线性系数 非局域非线性介质 非局域非线性 非局域程度 非局域克尔介质 铅玻璃 拉盖尔-高斯光束 强非局域非线性 强非局域性 弱非局域非线性介质 孤子相互作用 向列相液晶 双曲正割光束 厄米高斯光束 交叉点 临界功率
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
2011年 科研热词 非线性光学 空间光孤子 非局域介质 非局域 铅玻璃 临界功率 非线性情形 非线性 非局域非线性分界面 非局域非线性介质 非局域非线性 空间暗孤子 空间孤子 束宽节点 指向误差 干涉条纹 多色矢量孤子 厄米-高斯光束 分步傅里叶方法 分数傅里叶变换 光束传输 光束传播 光孤子 互诱导 推荐指数 4 3 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
