2018年高中数学人教A版必修3第1章算法初步1.1.2.3习题含解析
2018秋新版高中数学人教A版必修3习题:第一章算法初步 1.1.1

1.1.1 算法的概念课时过关·能力提升一、基础巩固1.算法的每一步都应该是确定的,能有效执行的,并且得到的结果是确定的,而不是模棱两可的.这是指算法的( )A.确定性B.普遍性C.有限性D.不唯一性2.下列各式中,T的值不能用算法求解的是( )A.T=12+22+32+42+…+1 002B.T=12+13+14+15+…+150C.T=1+2+3+4+5+…D.T=1-2+3-4+5-6+…+99-100C中的求和不符合算法的有限性,∴C中T的值不能用算法求解.3.一个算法的步骤如下,若输入x的值为-3,则输出z的值为( )第一步,输入x的值.第二步,计算x的绝对值y.第三步,计算z=2y-y.第四步,输出z的值.A.4B.5C.6D.8x=-3,∴y=|x|=3.∴z=23-3=5.4.已知直角三角形两直角边长分别为a,b,求斜边长c的一个算法分下列三步:①计算c=a2+b2;②输入直角三角形两直角边长a,b的值;③输出斜边长c的值.其中正确的顺序是( )A.①②③B.②③①C.①③②D.②①③,再计算,最后输出的顺序执行.5.有如下算法:第一步,输入x的值.第二步,若x≥0成立,则y=x;否则,y=x2.第三步,输出y的值.若输入x=-2,则输出y= .x=-2后,x=-2≥0不成立,则计算y=x2=(-2)2=4,输出y=4.6.完成解不等式2x+2<4x-1的算法:第一步,移项并合并同类项,得 .第二步,在不等式的两边同时除以x的系数,得 .2x<-3 x >327.给出算法:第一步,输入n=6.第二步,令i=1,S=0.第三步,判断i≤n是否成立.若不成立,则输出S,结束算法;若成立,则执行下一步.第四步,令S的值加i,仍用S表示,令i的值加1,仍用i表示,返回第三步.该算法的功能是 .:n=6,i=1,S=0,i=1≤6成立;S=0+1=1,i=1+1=2,i=2≤6成立;S=1+2,i=2+1=3,i=3≤6成立;S=1+2+3,i=3+1=4,i=4≤6成立;S=1+2+3+4,i=4+1=5,i=5≤6成立; S=1+2+3+4+5,i=5+1=6,i=6≤6成立;S=1+2+3+4+5+6,i=6+1=7,i=7≤6不成立,输出S=1+2+3+4+5+6.1+2+3+4+5+6的值8.给出下列算法:第一步,输入x的值.第二步,当x>1时,计算y=x+2;否则计算y=4-x.第三步,输出y.当输出y=4时,x= .,y ={x+2,x>1,4-x,x≤1.当x>1时,令x+2=4,得x=2.当x≤1时,x=-12.令4-x=4,解得12或29.试写出判断圆(x-a)2+(y-b)2=r2(r>0)和直线Ax+By+C=0(A2+B2≠0)位置关系的算法.:第一步,输入圆心的坐标(a,b)、直线方程的系数A,B,C和半径r.第二步,计算z1=Aa+Bb+C.第三步,计算z2=A2+B2.第四步,计算d =|z1|z2.第五步,若d>r,则输出“相离”;若d=r,则输出“相切”;若d<r,则输出“相交”.10.有蓝和黑两个墨水瓶,但现在却错把蓝墨水装在了黑墨水瓶中,黑墨水装在了蓝墨水瓶中,要求将其互换,请你设计算法解决这一问题.:第一步,取一只空的墨水瓶,设其为白色.第二步,将黑墨水瓶中的蓝墨水装入白瓶中.第三步,将蓝墨水瓶中的黑墨水装入黑墨水瓶中.第四步,将白瓶中的蓝墨水装入蓝墨水瓶中,交换结束.二、能力提升1.阅读下面的四段话,其中不是算法的是( )A.求1×2×3的值,先计算1×2=2,再计算2×3=6,最终结果为6B.解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1C.今天,我上了8节课,真累D.求1+2+3+4+5的值,先计算1+2=3,再计算3+3=6,6+4=10,10+5=15,最终结果为15项中,都是解决问题的步骤,故A,B,D项中所叙述的是算法;C项中是说明一个事实,不是算法.2.阅读下面的算法:第一步,输入两个实数a,b.第二步,若a<b,则交换a,b的值;否则,不交换a,b的值.第三步,输出a.这个算法输出的是( )A.a,b中较大的数B.a,b中较小的数C.原来的a的值D.原来的b的值,若a<b,则交换a,b的值,那么a是a,b中较大的数;否则a<b不成立,即a≥b,那么a也是a,b中较大的数.3.小明中午放学回家自己煮面条吃,有下面几道工序:①洗锅盛水2分钟;②洗菜6分钟;③准备面条及佐料2分钟;④用锅把水烧开10分钟;⑤煮面条3分钟.以上各道工序,除了④之外,一次只能进行一道工序.小明要将面条煮好,最少要用的分钟数为( )A.13B.14C.15D.23洗锅盛水2分钟、④用锅把水烧开10分钟(同时②洗菜6分钟、③准备面条及佐料2分钟)、⑤煮面条3分钟,共为15分钟.4.给出如下算法:第一步,输入a,b,c的值.第二步,当a>b时,令“最小值”为b;否则,令“最小值”为a.第三步,当“最小值”大于c时,令“最小值”为c;否则,“最小值”不变.第四步,输出“最小值”.若输入a=3,b=1,c=-2,则输出的“最小值”是 .a,b,c的值,输出其中的最小值,由于c<b<a,则输出-2.2★5.一个算法如下:第一步,令S=0,i=1.第二步,若i不大于10,则执行下一步;否则执行第五步.第三步,计算S+i且将结果代替S.第四步,用i+2代替i,返回第二步.第五步,输出S.则运行以上步骤输出的结果为 .1,第二次运算的结果为S=1+3,依此类推,此算法的功能为计算S=1+3+5+7+9的值,故输出S=25.6.已知球的表面积为16π,求球的体积.写出解决该问题的算法.R,再由球的体积公式可求得体积.:第一步,取S=16π.第二步,计算R =S4π.第三步,计算V =43πR3.第四步,输出V的值.★7.某班共有50人,要找出在一次数学测试中及格(60分及60分以上)的成绩.试设计一个算法.:第一步,把计数变量n的初始值设为1.第二步,输入一个成绩r,比较r与60的大小,若r≥60,则输出r,然后执行下一步;若r<60,则直接执行下一步.第三步,使计数变量n的值增加1.第四步,判断计数变量n与学生个数50的大小,若n≤50,则返回第二步;若n>50,则结束算法.。
2018年高中数学人教A版必修3第1章算法初步1.3.2习题含解析

人教版2018-2019学年高中数学必修 3习题第2课时进位制课时过关能力提升13.33 ⑷是( )A.十进制数 C.三进制数2•下列写法正确的是 A.858(8)B.865(7)C.121(3)D.68(6)解析:k 进制中各位上的数字均小于k,故A,B,D 错误•3•已知k 进制数32501 (k ),则k 不可能是( )A.5B.6C.7D.84.101(2)转化为十进制数是( )A.2B.5C.20D.1012105.下列各数中最大的是( )A.110(2)B.18C.16(8)D.20(5)解析:| 110(2)=1 X22+ 1 X21 + 0疋0= 6;16(8)=1 ^81+6X8°= 14;20(5)= 2^51+0X5°= 10.则最大数是 答案:|B6.312⑷化为十进制数后的个位数字是_________ . 2107.把十进制数93化为二进制数为 _______ 解析]以2作为除数相应得出的除法算式为、基础巩固B.四进制数 D.二进制数18.I即93=1011101 (2) 答案:| 1011101 (2)8.二进制数中的最大四位数化为十进制数是_____________解析:最大的四位二进制数是 1111(2),化为十进制数为1怎3+ 1怎2+ 1 >2+1 = 15. 答案:| 159•把98(5)转化为九进制数为 __________ .—鞘---------- 11o解析:98(5)= 9拓 +8拓=53,故 98(5)=58(9). 答案:58(9)10.求将127(8)化为六进制数时,最高数位上的数字• 解:T 127(沪1 X82+2 X8+7=87,「. 127(8)=223(6).解析:3|血殛3] 63 A 21 0 3TT Q 3]T 10 1答案:|D3.已知k 进制数132与十进制数30相等,那么k 等于( )A.-7B.4C.-7 或 4D.7解析:|由题意得1乂2+3 *+2 >°=30,即k 2+ 3k-28=0,解得k=4或k=- 7(舍).故选B. 答案:B 4.计算机中常用的十六进制是逢16进1的数制,采用数字0— 9和字母A — F 共16个记数符号,这些十八进制 0 1 2 3 4 56789 A B C D E F 十进制0 1 2 3 4 5 6 7 8 9101112131415例如,用十六进制表示:E+D = 1B ,则A X B = ( ) A.6EB.72C.5FD.B0•••127( 8)化为六进制数后的最高数位上的数字是 2.二、能力提升11.01(9)化为十进制数为() A.9B.11C.82解析:101(9)=1 X92+0 X91+1 >90= 82. 答案:|C2.把十进制数189化为三进制数,则末位数是(D.1010 25.21(7)+ 個4)= ___ .1010★ 6.古时候,当边境有敌人入侵时,守边的官兵通过在烽火台上点火向国内报告.如图,烽火台上点火表示二进制数1,不点火表示数字0,约定二进制数对应十进制的单位是 1 000,请你计算一下,这组烽火台表示有 ___________________ 名敌人入侵.解析::由题图可知这组烽火台表示的二进制数为11011,它表示的十进制数为11011(2)= 27,因为对应十进制的单位是1000,所以入侵敌人的人数为27000.答案 :|27 0007.已知175(8)=120+r,求正整数r. 解:|175(8)=1 X82+7 X81 + 5 X8°=125,••• 125=120+r. ••• r= 5,即所求正整数r 为5.★ 8.已知44(紆=36把67(k)转化为十进制数. 解:|由题意得36=4>k1 + 4>k0,^ k= 8.故67(k)= 67(8)=6 4+7 X°=55.。
高中数学必修3(人教A版)第一章算法初步1.1知识点总结含同步练习及答案

描述:例题:高中数学必修3(人教A版)知识点总结含同步练习题及答案第一章 算法初步 1.1 算法与程序框图一、学习任务1. 了解算法的含义,了解算法的基本思想,能用自然语言描述解决具体问题的算法.2. 了解设计程序框图表达解决问题的过程,了解算法和程序语言的区别;了解程序框图的三种基本逻辑结构,会用程序框图表示简单的常见问题的算法.二、知识清单算法 程序框图三、知识讲解1.算法算法(algorithm)是指按照一定规则解决某一类问题的明确和有限的步骤 .可以理解为由基本运算及规定的运算顺序所构成的完整的解题步骤,或者看成按照要求设计好的有限的确切的计算序列,并且这样的步骤或序列能够解决一类问题.描述算法可以有不同的方式.例如,可以用自然语言和数学语言加以描述,也可以借助形式语言(算法语言)给出精确的说明,也可以用框图直观地显示算法的全貌.算法的要求:(1)写出的算法,必须能解决一类问题,并且能重复使用;(2)算法过程要能一步一步执行,每一步执行的操作必须确切,不能含混不清,而且经过有限步后能得到结果.下列对算法的理解不正确的是( )A.一个算法应包含有限的步骤,而不能是无限的B.算法中的每一个步骤都应当是确定的,而不应当是含糊的、模棱两可的C.算法中的每一个步骤都应当是有效地执行,并得到确定的结果D.一个问题只能设计出一种算法解:D算法的有限性是指包含的步骤是有限的,故 A 正确;算法的确定性是指每一步都是确定的,故 B正确;算法的每一步都是确定的,且每一步都应有确定的结果,故 C 正确;对于同一个问题可以有不同的算法,故 D 错误.下列叙述能称为算法的的个数为( )描述:2.程序框图程序框图简称框图,是一种用程序框、流程线及文字说明来表示算法的图形.其中,起、止框是任何流程不可少的,表明程序的开始和结束.输入和输出框可用在算法中任何需要输入、输出的位置.算法中间要处理数据或计算,可分别写在不同的处理框内.一个算法步骤到另一个算法步骤用流程线连接.如果一个框图需要分开来画,要在断开处画上连接点,并标出连接的号码.①植树需要运苗、挖坑、栽苗、浇水这些步骤;②依次进行下列运算:,,,,;③从枣庄乘火车到徐州,从徐州乘飞机到广州;④ ;⑤求所有能被 整除的正整数,即 .A. B. C. D.解:B①、②、③为算法.1+1=22+1=33+1=4⋯99+1=1003x >x +133,6,9,12,⋯2345写出解方程组的一个算法.解:方法一:代入消元法. 第一步,由 得 ;第二步,将 代入 ,得 ,解得 ;第三步,将 代入方程 ,得 ;第四步,得到方程组的解为 .方法二:加减消元法.第一步,方程 两边同乘以 ,得 ;第二步,将第一步所得的方程与方程 作差,消去 ,得 ,解得 ;第三步,将 代入方程 ,得 ,解得 ;第四步,得到方程组的解为 .{2x +y =74x +5y =112x +y =7y =7−2x y =7−2x 4x +5y =114x +5(7−2x )=11x =4x =4y =7−2x y =−1{x =4y =−12x +y =7510x +5y =354x +5y =11y 6x =24x =4x =42x +y =72×4+y =7y =−1{x =4y =−1例题:画程序框图的规则(1)使用标准的图形符号.(2)框图一般按从上到下、从左到右的方向画.(3)除判断框外,大多数流程图符号只有一个进入点和一个退出点.判断框是具有超过一个退出点的惟一符号.(4)判断框分两大类,一类判断框是“是”与“否”两分支的判断,而且有且仅有两个结果;另一类是多分支判断,有几种不同的结果.(5)在图形符号内描述的语言要非常简练清楚.算法的三种基本逻辑结构顺序结构:语句与语句之间,框与框之间按从上到下的顺序进行.条件分支结构:在一个算法中,经常会遇到一些条件的判断,算法的流程条件是否成立有不同的流向,条件结构就是处理这种过程的结构.循环结构:在一些算法中,经常会出现从某处开始,按照一定的条件反复执行某些步骤的情况,这就是循环结构.下列程序框图分别是解决什么问题的算法.解:(1)已知圆的半径,求圆的面积的算法.(2)求两个实数加法的算法.执行如图的程序框图,输出的 ______ .解:T =30四、课后作业 (查看更多本章节同步练习题,请到快乐学)某程序框图如图所示,若输出的 ,则判断框内为( )A. B. C. D.解:AS =57k >4?k >5?k >6?k >7?已知函数 ,对每次输入的一个值,都得到相应的函数值,画出程序框图.解:f (x )={2x +3,3−x ,x 2x ⩾0x <0x答案:1. 关于算法的说法中,正确的是 A .算法就是某个问题的解题过程B .算法执行后可以产生不确定的结果C .解决某类问题的算法不是唯一的D .算法可以无限地操作下去不停止C()答案:解析:2. 下列运算不属于我们所讨论算法范畴的是 A .已知圆的半径求圆的面积B .随意抽 张扑克牌算到二十四点的可能性C .已知坐标平面内两点求直线方程D .加减乘除法运算法则B注意算法需按照一定的顺序进行.()4答案:解析:3. 执行如图所示的程序框图,如果输入的 ,则输出的 属于 .A .B .C .D .D取 ,得输出的 ,即可判断.t ∈[−2,2]S ()[−6,−2][−5,−1][−4,5][−3,6]t =−2S =64. 某批发商按客户订单数额的大小分别给予不同的优惠折扣.计算客户应付货款的算法步骤如下: :输入订单数额 (单位:件);输入单价 (单位:元);:若 ,则折扣率 ;若 ,则折扣率 ;若 ,则折扣率 ;若 ,则折扣率 ;:计算应付货款 (单位:元);:输出应付货款 .S 1x A S 2x <250d =0250⩽x <500d =0.05500⩽x <1000d =0.10x ⩾1000d =0.15S 3T =Ax (1−d )S 4T。
2018秋新版高中数学人教A版必修3习题第一章算法初步 1.2.1 Word版含解析

课时过关·能力提升
.下列语句正确的是() “”
一、基础巩固
() ≤ .赋值语句 解析:对,不能输入运算式,故错正确;对,输出语句应为<,故错;对,不能将赋给表达式,故错. 答案 .下列程序运行后的结果是()
解析:该程序的运行过程是
输出. 答案 .执行下列程序后的结果(表示整数除以整数的余数)为() “”
“^” “^”
★.用两根长度均为的细铁丝分别围成一个正方形和一个圆,求所围成的正方形的面积和圆的面积.编 写一个程序,要求输入的值,输出正方形的面积和圆的面积(π 取). 分析:设围成的正方形的边长为,依题意得,若设围成的圆的半径为,则 ππ,采用语句输入的值,利用赋值 语句得到面积,最后输出这两个面积,注意 π 取.
解析:由输出的(),解得或. 答案或 ★.阅读下面两个程序: 程序()程序()
如果两个程序输入的数值相同,并且运行后输出的结果也相同,那么这两个程序输入的数值是,运行后 输出的结果是. 解析:因为两个程序输入的数值相同,并且运行后输出的结果也相同,所以,解得,即输入值是,运行后结 果是. 答案 .编写一个程序,要求输入两个正数和的值,输出与的值. 解:程序如下. “” ^ ^
解:程序如下:
^ ^( )
“正方形的面积为” “圆的面积为”
()
^
“” 解析:该程序的运行过程是:
()
输出. 答案 .以下是一个用基本算法语句编写的程序,根据程序画出其相应的程序框图.
解:程序框图:
.下列语句正确的个数是() ①输入语句 ②赋值语句 ③输出语句
二、能力提升
解析:①中语句不能是表达式,所以①错误;②中表示变量减去后再赋给,即完成后比原来的值小,所以 ②正确;③中不能输出赋值语句,所以③错误. 答案 .下面程序输出的结果是()
高中数学 人教A版 必修3 第一章 算法初步 高考复习习题(解答题1-100)含答案解析

高中数学人教A版必修3 第一章算法初步高考复习习题(解答题1-100)含答案解析学校:___________姓名:___________班级:___________考号:___________一、解答题1.某班共有学生50人,在一次数学测试中,要搜索出测试中及格(60分及以上)的成绩,试设计一个算法,并画出程序框图.2.阅读如图所示的程序框图,运行相应的程序,则程序运行后输出的结果为________.3.如图所示的程序框图,(1)输入x=-1,n=3,则输出的数S是多少?(2)该程序框图是什么型?试把它转化为另一种结构.4.画出计算1+++…+的值的程序框图.5.根据如图算法的程序,画出其相应的算法程序框图,并指明该算法的目的.y 时,输入的x的值. 6.读下列程序,写出此程序表示的函数,并求当输出的67.函数y=试写出给定自变量x,求函数值y的算法.8.写出求任意给出的4个数a,b,c,d的平均数的一个算法.9.下面给出了一个问题的算法:第一步,输入x.第二步,若x≥4,则执行第三步,否则执行第四步.第三步,y=2x-1,输出y.第四步,y=x2-2x+3,输出y.问题:(1)这个算法解决的问题是什么?(2)当输入的x值为多大时,输出的数值最小?10.设计一个算法,找出闭区间上所有能被3整除的整数.11.写出一个算法,求底面边长为,侧棱长为的正四棱锥的体积.12.一队士兵来到一条有鳄鱼的深河的左岸.只有一条小船和两个小孩,这条船只能承载两个小孩或一个士兵.试设计一个算法,将这队士兵渡到对岸.13.写出求过两点的直线与坐标轴围成的图形的面积的一个算法. 14.从某校随机抽取200名学生,获得了他们一周课外阅读时间(单位:h)的数据,整理得到数据的频数分布表和频率分布直方图(如图).编号分组频数1[0,2)122[2,4)163[4,6)344[6,8)44续表编号分组频数5[8,10)506[10,12)247[12,14)128[14,16)49[16,18]4合计200(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12 h的概率;(2)求频率分布直方图中的a,b的值;(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.15.读下列程序,写出此程序表示的函数,并求当输出的时,输入的的值.16.阅读如图所示的程序框图,解答下列问题:(1)求输入的的值分别为,时,输出的的值;(2)根据程序框图,写出函数()的解析式;并求当关于的方程有三个互不相等的实数解时,实数的取值范围.17.某函数的解析式由如图所示的程序框图给出.(1)写出该函数的解析式;(2)若执行该程序框图,输出的结果为9,求输入的实数x 的值.18.(1)用秦九韶算法求多项式()543254323f x x x x x x =++++-当2x =时的值;(2)用辗转相除法或更相减损术求81和135的最大公约数. 19.阅读如图所示的程序框图,解答下列问题:(1)求输入的x 的值分别为1,2-时,输出的()f x 的值;(2)根据程序框图,写出函数()f x (x R ∈)的解析式;并求当关于x 的方程()0f x k -=有三个互不相等的实数解时,实数k 的取值范围.20.已知函数f(x)=x 2-5,写出求方程f(x)=0在[2,3]上的近似解(精确到0.001)的算法并画出程序框图.21.高一(2)班共有54名同学参加数学竞赛,现已有这54名同学的竞赛分数,请设计一个将竞赛成绩优秀同学的平均分输出的程序(规定90分以上为优秀),并画出程序框图. 22.用秦九韶算法计算f(x)=2x 4+3x 3+5x -4在x =2时的值.23.已知函数 ,对每输入的一个x 值,都得到相应的函数值.画出程序框图并写出程序.24.画出计算12+32+52+…+9992的程序框图,并编写相应的程序. 25.25.以下是某次考试中某班15名同学的数学成绩:72,91,58,63,84,88,90,55,61,73,64,77,82,94,60.要求将80分以上的同学的平均分求出来.画出程序框图.26.函数y =1,0{0,0 1,0x x x x x -+>+<=,写出给定自变量x ,求函数值的算法.27.如图,给出了一个程序框图, 其作用是输入 的值, 输出相应的 的值(1) 若视为自变量,为函数值,试写出函数的解析式;(2)若要使输入的的值与输出的的值相等,则输入的值为多少?28.某人带着一只狼和一只羊及一捆青菜过河,只有一条船,船仅可载重此人和狼、羊及青菜中的一种,没有人在的时候,狼会吃羊,羊会吃青菜.设计安全过河的算法.29.写出解方程x2-2x-3=0的一个算法.30.读框图(如图),说明该程序框图所表示的算法功能,并写出与之对应的程序.31.根除如下一个算法:第一步,输入;第二步,若,则,否则执行第三步;第三步,若,则,否则;第四步,输出.(1)画出该算法的程序框图;(2)若输出的值为1,求输入实数的所有可能的取值.32.分别用辗转相除法和更相减损术求1734,816的最大公约数.33.用辗转相除法求294,84的最大公约数.34.“鸡兔同笼”问题是我国古代著名的趣题之一.《孙子算经》中就记载了这个有趣的问题.书中这样描述:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔几何?试设计一个算法,输入鸡兔的总数量和鸡兔的脚的总数量,分别输出鸡、兔的数量,写出程序语句.并画出相应的程序框图.35.对于任意的实数a,b,定义一种运算a*b=a3-a2b+ab2+b3,试设计一个程序,能够验证该运算是否满足交换律.36.以下是一个用基本算法语句编写的程序,根据程序画出其相应的程序框图.INPUT “ ,y=”; ,yx=x/3y=2*y∧2PRINT x,yx=2*x-yy=y-1PRINT x,yEND37.在R1,R2,R3这三个电阻并联的电路中,电压为U,则电流的公式为I=UI的程序.38.某代销点出售《无线电》《计算机》《看世界》三种杂志,它们的定价分别为1.20元、1.55元、2.00元,编写一个程序,求输入杂志的订购数后,立即输出所付金额. 39.已知直线方程为 A +By+C=0(A·B≠0),试编写一个程序,要求输入符合条件的A,B,C的值,输出该直线在x轴、y轴上的截距和直线的斜率.40.已知函数f(x)=x2-2x+1,y1=f(3),编写一个程序计算f(y1)的值.41.已知函数f(x)=x2+3x+1,编写一个程序来计算f(4)的值.42.2015年春节期间,某水果店的三种水果标价分别为香蕉:2元/千克,苹果:3元/千克,梨:2.5元/千克.请你设计一个程序,以方便店主的收款.43.由程序框图写出程序.44.结合图形,说明下列程序的功能.45.汽车托运重量为P(kg)的货物时,托运每千米的费用(单位:元)标准为:y=()0.220{ 0.2200.112020P P kg P P kg≤⨯+⨯-> 当 当试编写一程序求行李托运费.46.给出如下程序(其中x 满足:0<x<12) 程序: INPUT xIF x>0AND x<=4 THEN y=2x ELSEIF 4<x AND x<=8 THEN y=8 ELSE y=24-2x END IF END IF PRINT y END(1)该程序用函数关系式怎样表达? (2)画出这个程序的程序框图.47.已知函数y=3,0,{3,0,x xx x->+≤设计程序,使输入x的值,输出相应的y值.48.读下面所给的程序,依据程序画出程序框图,并说明其功能:INPUT xIF x>1 OR x<-1 THENy=1ELSE y=0END IFPRINE yEND.49.用秦九韶算法求多项式f(x)=x6-5x5+6x4+x2+0.3x+2当x=-2时的值.50.已知函数y.51.(1)用辗转相除法求567与405的最大公约数;(2)用更相减损术求2 004与4 509的最大公约数.52.儿童乘坐火车时,若身高不超过1.1 m,则无须购票;若身高超过1.1 m但不超过1.4 m,可买半票;若超过1.4 m,应买全票.试写出一个购票算法程序.53.给出一个算法的程序框图(如图所示).(1)说明该程序的功能;(2)请用WHILE型循环语句写出程序.54.编写程序,使得任意输入2个整数按从大到小的顺序输出.55.已知函数f (x )=(x+1)2,将区间[1,10]九等分,画出求函数在各等分点及端点处所取得函数值算法的程序框图.56.画出求12-22+32-42+…+992-1002的值的算法的程序框图. 57.(1)将137化为六进制数. (2)将53(8)转化为三进制数.58.用辗转相除法求888与1 147的最大公约数.59.利用秦九韶算法求多项式f(x)=3x 6+12x 5+8x 4-3.5x 3+7.2x 2+5x-13当x=6时的值,写出详细步骤.60.分别用辗转相除法和更相减损术求261与319的最大公约数. 61.把三进制数2101211(3)转化为八进制的数.62.已知()()10175125r =,求在这种进制里的数()76r 应记成十进制的什么数? 63.学习优秀奖的条件如下: (1)五门课的成绩总分不低于500分. (2)每门课成绩都不低于90分.(3)三门主课每门的成绩都不低于100分,其他两门课的成绩都不低于90分. 输入某学生的五门课的成绩,问他是否够优秀条件.画出程序框图. 64.阅读如图程序框图,并根据该框图回答以下问题.(1)分别求f (-1),f (0),f ,f (3)的值. (2)写出函数f (x )的表达式.65.在音乐唱片超市里,每张唱片售价25元,顾客如果购买5张以上(含5张)唱片,则按照九折收费;如果顾客购买10张以上(含10张)唱片,则按照八五折收费.请设计一个完成计费工作的算法,并画出程序框图.66.画出输入一个数x ,求分段函数y .67.设计一个算法计算1×3×5×7×…×99值的算法,画出程序框图,写出程序.68.设计一个算法,求使1+2+3+4+…+n>2 017成立的最小自然数,画出程序框图,并写出程序语句.69.已知f(x)=x2-2x-3,求f(3),f(-5),f(5),并计算f(3)+f(-5)+f(5)的值.设计出解决该问题的一个算法,并画出程框图.70.已知一个直角三角形的两条直角边长为a、b,斜边长为c,写出它的外接圆和内切圆面积的算法,并画出程序框图.71.已知两个单元分别存放了变量x和y,试变换两个变量的值,并输出x和y,请写出算法并画出程序框图.72.已知一个圆柱的底面半径为R,高为h,求圆柱的体积.设计解决该问题的一个算法,并画出相应的程序框图.73.已知x=10,y=2,画出计算w=5x+8y值的程序框图.74.如图,在边长为4的正方形ABCD的边上有一点P,沿着折线BCDA由点B(起点)向点A(终点)运动.设点P运动的路程为x,△APB的面积为y,求y与x之间的函数关系式,并画出程序框图.75.76.求函数()()222y={22x x xx-≥-<的值的程序框图如图所示.(1)指出程序框图中的错误,并写出算法;(2)重新绘制解决该问题的程序框图,并回答下面提出的问题.①要使输出的值为正数,输入的x的值应满足什么条件?②要使输出的值为8,输入的x值应是多少?③要使输出的y值最小,输入的x值应是多少?77.用辗转相除法或者更相减损术求三个数324,243,135的最大公约数.78.如图是为求1~100中所有自然数的平方和而设计的程序框图,将空补上,指明它是循环结构中的哪一种类型,并画出它的另一种循环结构框图.79.在音乐唱片超市里,每张唱片售价25元,顾客购买5张(含5张)以上但不足10张唱片,则按九折收费,顾客购买10张以上(含10张)唱片,则按八五折收费,编写程序,输入顾客购买唱片的数量a,输出顾客要缴纳的金额C.并画出程序框图.80.下列是某个问题的算法程序,将其改为程序语言,并画出程序框图.算法:第一步,令i=1,S=0.第二步,若i≤999成立,则执行第三步;否则,输出S,结束算法.第三步,S=S.第四步,i=i+2,返回第二步.81.分别用辗转相除法和更相减损术求282与470的最大公约数.82.如图所示的程序框图,当输入的x的值为0和4时,输出的值相等,根据该图和下列各小题的条件解答下面的几个问题.(1)该程序框图解决的是一个什么问题?(2)当输入的x的值为3时,求输出的f(x)的值;(3)要想使输出的值最大,求输入的x的值.83.如图所示的程序框图,要使输出的y的值最小,则输入的x的值应为多少?此时输出的y的值为多少?84.已知一个三角形的三边边长分别为2,3,4,设计一个算法,求出它的面积,并画出程序框图.85.给出20个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推,如图所示的程序框图的功能是计算这20个数的和.(1)请在程序框图中填写两个(_______)内缺少的内容;(2)请补充完整该程序框图对应的计算机程序(用WHILE语句编写).86.阅读程序框图,并完成下列问题:(1)若输入x=0,求输出的结果;(2)请将该程序框图改成分段函数解析式;(3)若输出的函数值在区间11,42⎡⎤⎢⎥⎣⎦内,求输入的实数x的取值范围.87.编写一个程序计算12+32+52+…+992,并画出相应的程序框图.88.用辗转相除法和更相减损术求1734和816的最大公约数(写出过程)89.《中国诗词大会》第二季总决赛已于2017年2月初完美收官,来自全国各地的选手们通过答题竞赛的方式传播中国古诗词,从诗经、汉魏六朝诗、唐宋诗词、明清诗词―直到毛泽东诗词,展现了对中国传统文化经典的传承与热爱,比赛采用闯关的形式,能闯过上一关者才能进人下一关测试,否则即被淘汰.已知某选手能闯过笫一、二、三关.(1)求该选手在第3关被淘汰的概率;(2)该选手在测试中闯关的次数记为X,求随机变量X的分布列与数学期塑. 90.根据下面的要求,求13599++++的值.(1)请完成执行该问题的程序框图;(2)请用for语句写出该算法.91.已知175(r)=125(10),求在这种进制里的数76(r)应记成十进制的什么数?92.分别用当型和直到型循环语句编写一个程序,计算2×4×6×…×100的值.93.199100++⨯并画出程序框图及编写程序.94.编写一个程序计算12+32+52+…+992,并画出相应的程序框图.95.读下列各题所给的程序,依据程序画出程序框图,并说明其功能:(1)INPUT “x=”;xIF x>1 OR x<-1 THENy=1ELSE y=0END IFPRINE yEND(2)INPUT “输入三个正数a,b,c=”;a,b,cIF a+b>c AND a+c>b AND b+c>a THENp=(a+b+c)/2S=SQR(p*(p-a)*(p-b)*(p-c))PRINT “三角形的面积S=”SELSEPRINT “构不成三角形”END IFEND96.某商场为迎接店庆举办促销活动,活动规定:购物额在100元及以内不予优惠,在100~300元之间优惠5%,超过300元之后,超过部分优惠8%,原优惠条件仍然有效.写出顾客的购物额与应付金额之间的程序,要求输入购物额能够输出实付货款,并画出程序框图.97.已知函数y=f(x)的程序框图如图所示.(1)求函数y=f(x)的表达式;(2)写出输入x的值计算y的值的程序.98.编写一个程序,求用长度为L的细铁丝分别围成一个正方形和一个圆时所围成的正方形和圆的面积.要求输入L的值,输出正方形和圆的面积,并画出程序框图.(π取3.14)99.中秋节到了,糕点店的售货员很忙,请设计一个程序,帮助售货员算账,已知豆沙馅的月饼每千克25元,蛋黄馅的月饼每千克35元,莲蓉馅的月饼每千克30元,那么依次购买这三种月饼a、b、c千克,应收多少钱?100.“鸡兔同笼”问题是我国古代著名的趣题之一.大约在1500年前,《孙子算经》中就记载了这个有趣的问题.书中这样描述:今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔几何?试设计一个算法,输入鸡兔的总数和鸡兔的脚的总数,分别输出鸡、兔的数量.参考答案1.见解析.【解析】试题分析:由题意,从成绩中搜索出大于等于60的成绩,由此可得选择结构的判断框的条件,再依据搜索数据的个数确定循环的条件,得到算法,即可画出相应框图试题解析:算法如下:第一步:i=1.第二步,输入x.第三步,若x≥60则输出.第四步,i=i+1.第五步,判断i>50,是,结束;否则执行第二步.程序框图如图所示:2.9【解析】试题分析:由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.试题解析:第一次执行循环体后,,不满足退出循环的条件,,再次执行循环体后,,不满足退出循环的条件,,再次执行循环体后,,不满足退出循环的条件,,再次执行循环体后,,不满足退出循环的条件,,再次执行循环体后,,满足退出循环的条件,故输出的值为9,故答案为93.(1);(2)见解析.【解析】试题分析:(1)列出循环过程中与的数值,满足判断框的条件即可结束循环.(2)原图是当型循环,改为直到型试题解析:(1)当n=3时,i=3-1=2,满足i≥0,故S=6×(-1)+2+1=-3;执行i=i-1后i的值为1,满足i≥0,故S=(-3)×(-1)+1+1=5;再执行i=i-1后i的值为0,满足i≥0,故S=5×(-1)+0+1=-4;继续执行i=i-1后i的值为-1,不满足i≥0,故输出S=-4.(2)原图是当型循环,改为直到型(如图):4.见解析.【解析】试题分析: 由已知中程序的功能为用循环结构计算1+++…+的值,为累加运算,且要反复累加10次,可令循环变量的初值为1,终值为10,步长为1,由此确定循环前和循环体中各语句,即可得到相应的程序框图.试题解析:程序框图如下图所示:【点睛】本题考查设计程序框图解决实际问题,其中熟练掌握利用循环进行累加和累乘运算的方法,是解答本题的关键.5.见解析【解析】分析:根据已知中的程序语句可知,该程序是一个直到型循环结构,进而可画出程序的框图,进而根据循环条件及输出项,可判断出程序的功能,进而构造满足条件的不等式,解不等式,可得答案.详解:画出的其相应的算法程序框图如下:该算法的目的:求使1+2+3+…+n>2010成立的最小自然数n.(或1+2+3+…+n≤2010的最大正整数n的值再加1)点睛:该题考查的是有关程序框图的问题,在解题的过程中,需要先从题中所给的程序中判断该程序所要解决的问题,即其运行的目的,之后根据题意求得结果.6.2,0{1,0 2,0x x y x x x <=-=>,或3x =.【解析】试题分析: 分析此程序框图表示的函数是分段函数, 讨论x 的取值范围,求出6y =时x 的值.试题解析:根据程序图,可知此程序框图表示的函数为2,0{1,0 2,0x x y x x x <=-=>, 当0x <时,由26x =当0x >时,由26x = 得, 3x =.; 故当输出的6y =时,输入的或3x =.7.见解析【解析】试题分析:本题考查的知识点是设计程序框图解决实际问题,我们根据题目已知中分段函数的解析式y=,然后根据分类标准,设置两个判断框的并设置出判断框中的条件,再由函数各段的解析式,确定判断框的“是”与“否”分支对应的操作,由此即可写出算法.试题解析:因为函数是分段函数,故要先输入变量值,再进行判断,分别进行不同的计算.算法如下:第一步,输入x.第二步,若x>0,则令y=-x+1后执行第五步;否则执行第三步.第三步,若x=0,则令y=0后执行第五步;否则执行第四步.第四步,令y=x+1.第五步,输出y 的值.点睛:分析题意,解答此类问题,可以依据已知的分段函数,将x 的取值范围作为条件设计算法;联系题设,依据不同x 的取值范围下对应不同的函数式结合算法的概念写出算法过程.8.见解析【解析】试题分析:熟悉并掌握算法的步骤,分解平均数的计算步骤即可作答.试题解析:第一步,输入a,b,c,d的值;第二步,计算S=a+b+c+d;第三步,计算V=;第四步,输出V的值.9.(1)见解析(2)当输入的x的值为1时,输出的数值最小.【解析】试题分析:本题考查了一个条件分支结构的算法,可分为和,执行不同的计算,即可得到结论.试题解析:(1)这个算法解决的问题是求分段函数y的函数值的问题.(2)本问的实质是求分段函数最小值的问题.当x≥4时,y=2x-1≥7;当x<4时,y=x2-2x+3=(x-1)2+2≥2.∴函数最小值为2,当x=1时取到最小值.∴当输入x的值为1时,输出的数值最小.点睛:本题主要考查了一个条件分支结构的算法的应用问题,解答中涉及到分段函数的性质,其中程序填空是重点考查的题型,这种试题考试的重点:①分支条件;②循环的条件;③变量的赋值;④变量的输出,其中前两个是考试的重点,正确理解算法的流程,读懂题意是解答的关键.10.见解析【解析】试题分析:可通过循环结构的算法实现求闭区间上所有能被整除的整数.试题解析:第一步,用20除以3,余数不为0,故20不能被3整除;第二步,用21除以3,余数为0,故21能被3整除;第三步,用22除以3,余数不为0,故22不能被3整除;第四步,用23除以3,余数不为0,故23不能被3整除;第五步,用24除以3,余数为0,故24能被3整除;第六步,用25除以3,余数不为0,故25不能被3整除;第七步,指出在闭区间[20,25]上能被3整除的整数为21和24.11.见解析【解析】试题分析:求解正四棱锥的体积,先求出棱锥的高与底面面积和高,再利用体积公式求出体积.试题解析:第一步,令a=4,l=5.第二步,计算R=.第三步,计算h=.第四步,计算S=a2.第五步,计算V=Sh.第六步,输出运算结果V.12.见解析【解析】试题分析:根据算法的概念和算法的流程为一个循环结构的算法,可把该算法分为五步,即可写出算法.试题解析:第一步,两个小孩将船划到右岸.第二步,他们中一个上岸,另一个划回来.第三步,小孩上岸,一个士兵划过去.第四步,士兵上岸,让小孩划回来.第五步,如果左岸没有士兵,那么结束,否则转第一步点睛:本题考查了算法的一个实际应用问题,解题时要主语熟练掌握循环结构算法的性质和应用是解答的关键,算法时新课标中新增内容,也一直是命题的一个热点,试题比较基础,属于基础题.13.见解析【解析】试题分析:根据算法的概念和算法的流程即可写出该算法.试题解析:第一步,取x1=-2,y1=-1,x2=2,y2=3.第二步:计算y y.y y第三步:在第二步结果中令x=0得到y的值为m,得直线与y轴交点为(0,m).第四步:在第二步结果中令y=0得到x的值为n,得直线与x轴交点为(n,0).第五步:计算S=|m|·|n|.第六步:输出运算结果S.14.(1)0.9(2)0.125(3)4【解析】试题分析:(1)求出对应情况下出现的频数,频数与总数之比为频率;(2)根据频数求出频率,频率乘以组距得出a,b的值;(3)结合频率分布直方图根据题意算出平均数.试题解析:(1)由频率分布表可知该周课外阅读时间不少于12 h的频数为12+4+4=20,故可估计该周课外阅读时间少于12 h的概率为1-=0.9.(2)由频率分布表可知数据在[4,6)的频数为34,故这一组的频率为0.17,即a=0.085,数据在[8,10)的频数为50,故这一组的频率为0.25,即b=0.125.(3)数据的平均数为(12×1+3×16+5×34+7×44+9×50+11×24+13×12+15×4+17×4)=7.68(h),故样本中的200名学生该周课外阅读时间的平均数在第四组.15.【解析】试题分析:阅读程序框图可知,此程序表示的函数为,当时,得.当时,得.试题解析:此程序表示的函数为,当时,得.当时,得.故当输出的时,输入的,故答案为.16.(1),;(2).【解析】试题分析:(1)根据框图中条件语句,判断变量执行哪个函数,计算求解即可;(2)由框图可知,分析分段函数的单调性,进而可得解.试题解析:(1)当输入的 的值为 时,输出的 . 当输入的 的值为2时,输出的 .(2)根据程序框图,可得, 当 时, ,此时 单调递增,且 ;当 时, ;当 时, 在 0 1 上单调递减,在 上单调递增,且 .结合图象,知当关于 的方程 有三个不同的实数解时,实数 的取值范围为 0 1 .17.(1)2,1{ 21,1x x x y x -<=+≥;(2)7x =-或3. 【解析】试题分析:(1)利用条件结构框图得到函数的解析式;(2)分两种情况解得输入的实数x 的值.试题解析:(1)2,1{ 21,1x x x y x -<=+≥.(2)当1x <时, 29x -=, 7x =-; 当1x ≥时, 2+1=9x , 3x =, 所以7x =-或3.18.(1)255;(2)27【解析】试题分析:(1)把所给的函数式变化成都是一次式的形式,逐一求出从里到外的函数值的值,最后得到当2x =时的函数值;(2)用辗转相除法求81与135的最大公约数,写出135=81×1+54=27×2+0,得到两个数字的最大公约数.试题解析:(1)()()()()()543213f x x x x x x =++++-05v =; 152414v =⨯+=; 2142331v =⨯+=; 3312264v =⨯+=46421129v =⨯+=; 512923255v =⨯-=所以,当2x =时,多项式的值为255.(2)13581154=⨯+8154127=⨯+,542720=⨯+,则81与135的最大公约数为27点睛:本题主要考查辗转相除法和更相减损术求最大公约数,属于中档题. 辗转相除法和更相减损术是求两个正整数的最大公约数的方法,辗转相除法是当大数被小数除尽时,结束除法运算,较小的数就是最大公约数;更相减损术是当大数减去小数的差等于小数时停止减法运算.较小的数就是最大公约数.一般情况下,用辗转相除法得到最大公约数的步骤较少,而用更相减相术步骤较多.但运算简易.解题时要灵活运用.19.(1)见解析(2)()0,1.【解析】试题分析:(1)根据输入的x 的值为1-时,输出结果;当输入的x 的值为2时,输出结果;(2)根据程序框图,可得()f x ,结合函数图象及()0f x k -=有三个互不相等的实数解即可求出实数k 的取值范围.试题解析:(1)当输入的x 的值为1-时,输出的 当输入的x 的值为2时,输出的()222211f x =-⨯+= (2)根据程序框图,可得()22,0{2,0 21,0x x f x x x x x <==-+>当0x <时, ()2xf x =,此时()f x 单调递增,且()01f x <<; 当0x =时, ()2f x =;当0x >时, ()()22211f x x x x =-+=-在()0,1上单调递减,在()1,+∞上单调递增,且()0f x ≥.结合图象,知当关于x 的方程()0f x k -=有三个互不相等的实数解时,实数k 的取值范围为()0,1.20.见解析【解析】试题分析:本题可用二分法来解决,设,,算法如下,第一步,,,第二步,第三步,计算,如果,则输出,如果,则,否则第四步,若,则输出,否则返回第二步解析:点睛:本题考查了用二分法求解函数零点的近似解,按照精确条件,设计出循环结构图,通过限制条件做运算,本题在求解的过程中需要很好的理解二分法的做法,以及确定好限制条件。
高中数学 人教A版 必修3 第一章 算法初步 高考复习习题(选择题201-300)含答案解析
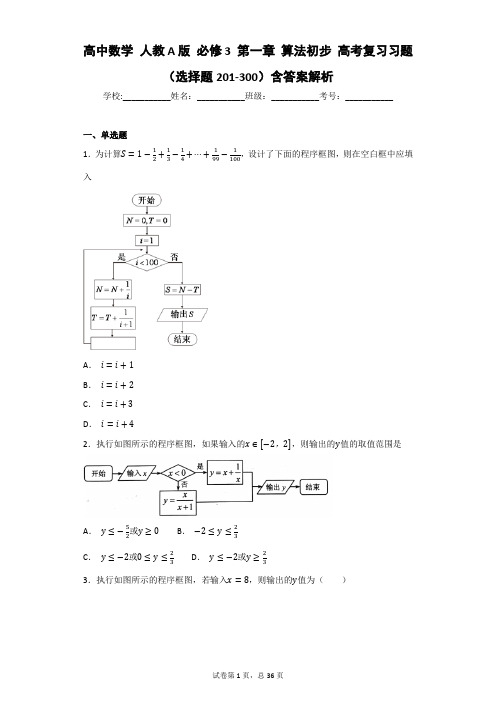
高中数学人教A版必修3 第一章算法初步高考复习习题(选择题201-300)含答案解析学校:___________姓名:___________班级:___________考号:___________一、单选题1.为计算,设计了下面的程序框图,则在空白框中应填入A.B.C.D.2.执行如图所示的程序框图,如果输入的,,则输出的值的取值范围是A.或B.C.或D.或3.执行如图所示的程序框图,若输入,则输出的值为()A.B.C.D.34.执行如图所示的程序框图,若输出,则判断框内应填的内容是A.B.C.D.5.将八进制数135(8)化为二进制数为( )A.1110101(2)B.1011101(2)C.1010101(2)D.1111001(2)6.秦九韶是我国南宋时期的数学家,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入的值为3,则输出v的值为A.B.C.D.7.执行如图所示的程序框图,输出的S的值是A.-1B.2C.D.18.执行如图所示的程序框图,则输出的值为()A.B.C.D.9.利用秦九韶算法计算()A.B.19C.D.10.《九章算术》中盈不足章中有这样一则故事:“今有良马与驽马发长安,至齐. 齐去长安三千里. 良马初日行一百九十三里,日增一十二里;驽马初日行九十七里,日减二里.” 为了计算每天良马和驽马所走的路程之和,设计框图如下图. 若输出的的值为350,则判断框中可填()A.B.C.D.11.如图①,一块黄铜板上插着三根宝石针,在其中一根针上从下到上穿好由大到小的若干金片.若按照下面的法则移动这些金片:每次只能移动一片金片;每次移动的金片必须套在某根针上;大片不能叠在小片上面.设移完片金片总共需要的次数为,可推得.如图②是求移动次数的程序框图模型,则输出的结果是①②A.1022B.1023C.1024D.102512.我国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之剩一,五五数之剩三,七七数之剩六,问物几何?”人们把此类题目称为“中国剩余定理”.若正整数N除以正整数m后的余数为n,则记为N≡n(modm),例如10≡2(mod4).现将该问题以程序框图给出,执行该程序框图,则输出的n等于()A.13B.11C.15D.813.101110(2)转化为等值的八进制数是( ) .A.46(8)B.56(8)C.67(8)D.78(8)14.我们可以用随机模拟的方法估计的值,如下程序框图表示其基本步骤(函数是产生随机数的函数,它能随机产生内的任何一个实数),若输出的结果为527,则由此可估计的近似值( )A.B.C.D.15.元朝著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,遇店添一倍,逢友饮一斗,店友经四处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的,则一开始输入的的值为()A.B.C.D.16.古代著名数学典籍《九章算术》在“商功”篇章中有这样的描述:“今有圆亭,下周三丈,上周二丈,问积几何?”其中“圆亭”指的是正圆台体形建筑物.算法为:“上下底面周长相乘,加上底面周长自乘、下底面周长自乘的和,再乘以高,最后除以36.”可以用程序框图写出它的算法,如图,今有圆亭上底面周长为6,下底面周长为12,高为3,则它的体积为()A.32B.29C.27D.2117.五进制是以5为底的进位制,主因乃人类的一只手有五只手指中国古代的五行学说也是采用的五进制,0代表土,1代表水,2代表火,3代表木,4代表金,依此类推,5又属土,6属水,,减去5即得如图,这是一个把k进制数共有N位化为十进制数b的程序框图,执行该程序框图,若输入的k,a,n分别为5,324,3,则输出的A.45B.89C.113D.44518.下图中的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的值分别为8,10,0,则输出和的值分别为( )A.2,4B.2,5C.0,4D.0,519.如果下面程序框图运行的结果,那么判断框中应填入()A.B.C.D.20.执行如图所示的程序框图,则输出的的值为()A.B.C.D.21.阅读程序框图,运行相应的程序,则输出的的值为()A.72B.90C.101D.11022.执行如图所示的程序框图.如果输入,则输出的()A.B.C.D.23.在如图所示的程序框图中,若输出的,则判断框内可以填入的条件是()A.B.C.D.24.当m=7,n=3时,执行如图所示的程序框图,输出的S值为()A.7B.42C.210D.84025.运行如图所示的程序框图,则输出的等于A.B.C.3D.126.用辗转相除法,计算56和264的最大公约数是( ).A.7B.8C.9D.627.我国古代名著《庄子•天下篇》中有一句名言“一尺之棰,日取其半,万世不竭”,其意思为:一尺的木棍,每天截取一半,永远都截不完.现将该木棍依此规律截取,如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位:尺),则①②③处可分别填入的是A.B.C.D.28.把化为二进制数为( )A.B.C.D.29.《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法.该作中有题为“李白沽酒:李白街上走,提壶去买酒。
【专业资料】新版高中数学人教A版必修3习题:第一章算法初步 1.2.3 含解析

1.2.3循环语句课时过关·能力提升一、基础巩固1.下列说法正确的是()A.当型(WHILE)循环结构不能转化为直到型(UNTIL)循环结构B.当型(WHILE)循环结构先执行循环体,后判断条件C.当型(WHILE)循环结构先判断条件,后执行循环体D.以上说法都不正确,直到型循环是先执行循环体,后判断条件,它们之间可以进行转化,故选C.2.要使下面的程序能运算出“1+2+…+100”的结果,需将语句“i=i+1”加在()A.①处B.②处C.③处D.④处i=i+1”应在循环体中,并且先执行“S=S+i”后执行“i=i+1”,故应加在③处,故选C.3.下面为一个求10个数的平均数的程序,在横线上应填充的语句为()A.i>10B.i<10C.i>=10D.i<=10,在程序一开始,即当i=1时,开始执行循环体,当i=10时,继续执行循环体,题目中求10个数的平均数,所以当i>10时应终止循环.4.下列程序中循环体运行次数是()A.4B.5C.6D.601次运行后,i=50,第2次运行后,i=60,第3次运行后,i=70,第4次运行后,i=80,第5次运行后,i=90,第6次运行后,i=100>90开始成立,循环终止,则共运行了6次.5.下列程序的功能是()A.计算1+3+5+…+2 016B.计算1×3×5×…×2 016C.求方程1×3×5×…×i=2 016中的i值D.求满足1×3×5×…×i>2 016的最小整数iS=1×3×5×…×i,当S≤2016开始不成立,即S>2016开始成立时,输出i,则求满足1×3×5×…×i>2016的最小整数i.6.如图所示的程序运行后输出的第3个数是.:第一次输出的数是1,第二次输出的数是x=1+12=32,第三次输出的数是x=32+12=2.7.下列程序输出的结果是.a=1b=1b=1<5成立c=1+1=2a=1b=2b=2<5成立c=1+2=3a=2b=3b=3<5成立c=2+3=5a=3b=5b=5<5不成立输出b=5.8.下面程序是求1+3+5+…+99的值,阅读程序完成问题.问题:(1)程序中的循环语句是型循环语句;(2)将此程序用另一类型的循环语句来实现.当(WHILE)(2)改成直到型循环语句如下:9.写出求满足1+2+3+…+n>10 000的最小整数n的程序.:二、能力提升1.下面的程序运行后,输出的i值等于()A.6B.7C.8D.9,S=0+0=0,i=0+1;第二次循环,S=0+1=1,i=1+1=2;第三次循环,S=1+2=3,i=2+1=3;第四次循环,S=3+3=6,i=3+1=4;第五次循环,S=6+4=10,i=4+1=5;第六次循环,S=10+5=15,i=5+1=6;第七次循环,S=15+6=21,i=6+1=7,因为S=21>20,所以输出i=7.2.下面两个程序最后输出的“S”分别等于()i=1WHILE i<8i=i+2S=2 i+3WENDPRINT SEND i=1WHILE i<8S=2 i+3i=i+2WENDPRINT SENDA.17,17B.21,21C.21,17D.14,21,i=7时执行循环体i=i+2,此时i为9,S=2×9+3=21,结束循环.第二个程序中,i=7时,S=2×7+3=17,然后执行i=i+2,此时i=9,结束循环.3.下面程序运行后输出的结果为()A.0B.1C.2D.4j=1时,余数a=1;当j=2时,余数a=3;当j=3时,余数a=1;当j=4时,余数a=0;当j=5时,余数a=0;当j=6时,不满足条件,此时退出循环.4.根据下列程序框图,把对应的程序中所缺少的语句补充完整.,对应的语句为直到型循环语句,DO后面执行的语句为循环体,故①②处应分别为S=S+i^2,i=i+1,直到满足条件i>100为止,所以③处应为i>100.S=S+i^2②i=i+1③i>100★5.下列循环体执行的次数是.6.根据下列程序,画出相应的程序框图.DOS=S+1/(k (k+1)):★7.下面程序的功能是输出1~100之间的所有偶数.程序:(1)试将上面的程序补充完整;(2)改写为含WHILE型循环语句的程序.①m=0②i=i+1(2)改写为含WHILE型循环语句的程序如下:。
高中数学人教A版必修三课时习题:第1章算法初步1.1.1含答案
1. 1.1算法的观点课时目标1.认识详细算法的基本过程与主要特色;2.能应用算法思想解决相关的详细问题;3.能按步骤用自然语言写出简单问题的算法过程.识记加强1.算法往常能够编成计算机程序,让计算机履行并解决问题,计算机解决任何问题都要依靠于算法.只有将解决问题的过程分解为若干个明确的步骤,即算法,并用计算机能够接受的“语言”正确地描绘出来,计算机才能够解决问题.2.算法的五个特色为归纳性、逻辑性、有穷性、不独一性、广泛性.课时作业一、选择题1.算法的有穷性是指()A.算法一定包括输出步骤B.算法中每个操作步骤都是可履行的C.算法一定在有穷步内结束D.以上说法均不正确答案: C分析:算法的有穷性是指一个算法的步骤序列是有限的,它应在有限步骤以后停止,而不可以是无穷的.2.以下对于算法的描绘正确的是()..A.算法与求解一个问题的方法同样B.算法只好解决一个问题,不可以重复使用C.算法过程要一步一步履行,每步履行的操作一定切实D.算法要求循规蹈矩做,每一步能够有不一样的结果答案: C分析: A 中算法能够解决一类问题而不是一个问题,同理 B 也不正确, D 中每一步履行的操作,只好有独一的结果,故 D 错误.3.利用计算机进行运算,第一一定()A.编程 B .人机对话C.计算机自动达成 D .没法进行答案: A分析:编程就是设计算法.4.对算法的理解不正确的选项是()A.一个算法应包括有限的操作步骤,而不可以是无穷的B.算法中的每一个步骤都应该是确立的,而不该该是含糊的、含糊其词的C.算法中的每一个步骤都应该有效地履行,并获得确立的结果D.一个问题只好设计出一种算法答案: D分析:算法是不独一的.5.看下边的四段话,此中不是解决问题的算法是()A.方程x2- 100=0 有两个实根± 10B.解一元一次方程的步骤是去分母、去括号、移项、归并同类项、系数化为1C.某人去深圳打工,先步行到县城,再乘火车到省城,最后坐飞机到达D.求 1+2+ 3+ 4+ 5 的值:先计算1+ 2=3,再计算3+ 3= 6,6 + 4= 10,10 + 5=15,最后结果为15答案: A6.对于算法:第一步:输入n第二步:判断n 能否等于2,若 n=2,则 n 知足条件;若n>2,则履行第三步第三步:挨次从 2 到n- 1 查验能不可以整除n,若不可以整除n,则履行第四步;若能整除n,则履行第一步第四步:输出n知足条件的n 是()A.质数 B .奇数C.偶数 D .约数答案: A分析:本题第一要理解质数,除 1 和它自己外没有其余约数的正整数叫做质数, 2 是最小的质数,这个算法经过对 2 到( n- 1) 一一考证,看能否有其余约数来判断其能否为质数.二、填空题7.已知一个学生的语文成绩为98,数学成绩为87,外语成绩为92,以下是他的总分和均匀成绩的一个算法:( 在横线上填入算法中缺的两个步骤)第一步:取A=98, B=87, C=92;第二步: ________;第三步: ________;第四步:输出计算的结果.答案:计算总分D= A+ B+ CD计算均匀成绩E= .38.求 1×3×5×7×9×11 的值的一个算法是:第一步:求1×3获得结果 3.第二步:将第一步所得结果 3 乘 5,获得结果15.第三步: _______________________________________________.第四步:再将105 乘 9 获得 945.第五步:再将945×11,获得10395,即为最后结果.答案:将第二步所得的结果15 乘 7,获得结果 105.9.下边给出一个问题的算法:第一步:输入 x.第二步:假如≥2014,那么y =- 2014,不然y= 2014-.x x x第三步:输出y.则这个算法解决的问题是________________________________ .答案:求 x 与2014的差的绝对值.三、解答题10.下边给出了一个问题的算法:第一步,输入a.第二步,若a≥4,则履行第三步,不然履行第四步.第三步,输出2a- 1.第四步,输出a2-2a+3.: (1) 个算法解决的是什么?(2)当入的 a 多大,出的数最小?解: (1) 个算法解决的是求分段函数f (x) =2x- 1,x≥4,的函数的.x2-2x+3, x<4(2)a=1出的数最小.11.写出求解一元二次方程ax2+ bx+ c=0( a≠0)的根的算法.解:第一步:算=b2-4ac;第二步:若<0;行第三步;否行第四步;第三步:出方程无根;-b± b2-4ac第四步:算并出方程根x1,2=2a.能力提高12.写出求 2+ 4+ 6+⋯+ 200 的一个算法.能够运用公式2+ 4+ 6+⋯+ 2n=n( n+ 1)直接算.第一步__① __;第二步__② __;第三步出运算果.答案:①取 n=100② 算n(n+1)分析:本考算法步.解此第一求出算式中n 的取,而后将 n 的取代入公式 n( n+1)行算,即可得此的一个算法.13.写出求两点M(-2,-1), N(2,3)的直与坐成面的一个算法.解:第一步:取x1=-2,y1=-1, x2=2, y2=3;第二步:算y- y1=x- x1;y2-y2x2- x1第三步:在第二步果中令x = 0获得y的,得直与y交点(0, );m m第四步:在第二步果中令y=0获得 x 的 n,得直与 x 交点( n, 0);第五步:算=1||·||;S2m n第六步:出运算果.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3课时循环结构
课时过关能力提升
、基础巩固
i •下列关于循环结构的说法正确的是 A. 可能不含顺序结构 B. 可能不含条件结构 C.含有顺序结构和条件结构 D.以上说法都不正确 答答案1C
A.i < 19?
B.i > 19? D.i<21?
2.执行如图所示的程序框图,输出的 S 的值为(
)
D.15
C.7 A.1 B.3 解析:开始时k=0,S=0. 第一次循环,k=0<3,S=0+20
=1,k= 0+1 = 1, 第二次循环,k=1<3,S=1 + 21
= 3,k= 1+1 = 2,
第三次循环,k=2<3,S=3+22=7,k= 2+1 = 3.
此时不满足条件k<3,输出结果S,即输出7.故选 答案:|C C. 3•某同学设计的程序框图如图所示 ,用来计算和式12 + 22+ 32+…+ 202的值,则在判断框中应填写(
) C.i>21?
,y= 12 X )= 60,x= 5+1 = 6;
,y= 60 X )= 360,x= 6+1 = 7;
x=7 < 6不成立 输出y=360. 答案:
|D
5•执行如图所示的程序框图,输出的k 的值为( )
A.4
B.5
C.6
D.7
解析]第一次循环得S=0+2°=1,k=1; 第二次循环得S=1 + 21 = 3,k=2; 第三次循环得
S=3+23=11,k=3, 第四次循环得S=11 + 211= 2059,k=4,但此时不满足条件,退出循环,输出k=4. 答案:|A
6•执行如图所示的程序框图,输出的S 的值为 _____________
解析]该程序框图中含有当型循环结构 止循环,则在判断框中应填写i< 21?.
,判断框内的条件不成立时循环终
止
•由于是当
i= 21时开始终
答案:D A.3 4•执行如图所示的程序框图 B.12
解析:x= 3,y= 1; x= 3 < 6成立
,y= 1 X3= 3,x=3+1 =
4; x=4 < 6成立 ,y= 3 X 4= 12,x= 4+1=5;
x= 5 < 6成立 x=6 < 6成立
解析]该程序框图的运行过程是:i= 1,S=1
i= 1+ 1 = 2
S=2 >(1 + 1)= 4
i= 2> 5不成立
i= 2+ 1 = 3
S=2 ><4+1)=10
i= 3> 5不成立
i= 3+ 1 = 4
S=2 ><10 + 1)=22
i= 4> 5不成立
i= 4+ 1 = 5
S=2 <22 + 1)=46
i= 5> 5不成立
i= 5+ 1 = 6
S=2 <46 + 1)=94
i= 6> 5 成立
答案:|94
7•如图是一个算法的程序框图,若此程序运行结果为S=720,则在判断框中应填入关于是 __________ .
解析:k=10,S=1,判断条件成立,S=10X1=10,k=10-1=9;k的判断条件
判断条件成立,S=10X9=90,k=9-1=8; 判断条件成立,S=90X8=720,k= 8-仁7;
判断条件不成立,输出S=720,从而关于k 的条件是k > 8?”. 答案:
k >8?
8•执行如图所示的程序框图 若输入n 的值为4,则输出s 的值为 ______________
解析:由程序框图可知 M 表示及格人数,N 表示不及格人数,所以q
答案:q
!=1¥1
解析]第一步运算结果
第二步运算结果 第三步运算结果 第四步运算结果
:s=1,i= 2(i < 4 成立); :s=2,i= 3(i < 4 成立); :s=4,i= 4(i < 4 成立);
:s=7,i= 5(i < 4不成立),程序结束,故输出s 的值为
9•如图是计算某年级 入 500名学生期末考试(满分为100分)及格率q 的程序框图,则图中空白框内应填 (=1 ]
gfi ■:
10.画出计算1 -- 的值的一个程序框图
人教版2018-2019学年高中数学必修3习题
(方法一)当型循
环结构如图①(方法二)直到型循
环结构如图②
1•执行如图所示的程序框图,则输出S=(
图①
图②
、能力提升
A.2
B.6
C.15
D.31
解析:第一次满足条件,循环,S=1+仁2,k=2;第二次满足条件,循环,S=2+22=6,k=3;第三次满足条件,循
2 环,S=6+
3 =15,k=4;第四次不满足条件,退出循环,输出S=15选C.
2•执行如图所示的程序框图,如果输入a=4,那么输出n的值为()
A.2
B.3
C.4
D.5
解析:若输入a=4,则执行P=0,Q= 1,判断0<1成立,进行第一次循环;
P=1,Q= 3,n=1,判断1<3成立,进行第二次循环;
P=5,Q=7,n=2,判断5<7成立,进行第三次循环;
P=21,Q=15,n=3,判断21<15不成立,故输出n =3.
3•阅读如图的程序框图,若输出S的值为52,则判断框内可填写()
A.i> 10?
B.i<10?
C.i>9?
D.i< 9?
4•阅读如图的程序框图,则输出的S等于()
答案
:B 5•执行两次如图所示的程序框图 ,若第一次输入的a 的值为-1.2,第二次输入的a 的值为 输出a 的值是 _______ ,第二次输出a 的值是 ______ .
解析:|根据输入的a 的值的不同而执行不同的程序 •
由程序框图可知:当 a=-1.2 时,•/ a< 0, ••• a=-1.2+ 1=-0.2,a<0,a=- 0.2+1 = 0.8,a> 0. •/ 0.8<1,二输出 a=0.8.
当 a=1.2 时,•/ a > 1,.・.a= 1.2-1= 0.2. •/ 0.2<1,「.输出 a=0.2. 答案 :|0.8 0.2
★ 6.执行如图所示的程序框图,若输入x=- 5.2,则输出y 的值为 _________ .
A.40
B.38
C.32 1.2,则第一次
/ 辑Ai/
I
n|
/ ttlliy /
解析]输入x=-5.2后,该程序框图的运行过程是:x=- 5.2,
y=0,i=0,
y=|- 5.2-2|=7.2,
i= 0+ 1=1,
x= 7.2,
i= 1 > 5不成立;
y=|7.2-2|=5.2,
i= 1+ 1 = 2,
x= 5.2,
i= 2> 5不成立;
y=|5.2-2|=3.2,
i= 2+ 1 = 3,
x= 3.2,
i= 3>5不成立;
y=|3.2-2|=1.2,
i= 3+ 1 = 4,
x=1.2,
i= 4>5不成立;
y=|1.2-2|=0.8,
i= 4+ 1 = 5,
x= 0.8,
i= 5> 5成立;
输出y=0.8.
7•求使1 + 2+3+4+5+…+n < 100成立的最大自然数n的值,画出程序框图
分析:由题目可获取以下主要信息:
① 1 + 2+3+4+5+…+n < 100为关于n的不等式;
②设计求n的最大自然数的算法.
解答本题可先思考如何设计循环变量及循环体,再关注每一次循环后输出的变量的情况是否符
合题目的要求• 解:|程序框图:
★ 8•相传古代印度国王舍罕要褒赏他聪明能干的宰相达依尔(国际象棋的发明者),问他需要什么,达依
尔说:国王只要在国际象棋的棋盘第一个格子上放一粒麦子,第二个格子上放两粒,第三个格子上放
四粒,以后按此比例每一格加一倍,一直放到第64格(国际象棋8疋=64格),我就感恩不尽,其他什么也不要了•”国王想:这有多少,还不容易!”让人扛来一袋小麦,但不到一会儿就全用没了,再扛来一袋很
快又没有了,结果全印度的粮食用完还不够,国王很奇怪•一个国际象棋棋盘一共能放多少粒小麦?试用程序框图表示其算法• 分析]根据题目可知:
第一格放1粒,1 = 20,第二格放2粒,2=21,
第三格放4粒,4=22,第四格放8粒,8=23,
第六十四格放263粒•
则此题就转化为求1 + 21 + 22+ 23+ 24+…+ 263的和的问题•我们可弓I入一个累加变量S,—个计数变量i,累加64次就能算出一共有多少粒小麦•
解一个国际象棋棋盘一共能放1+21+22+23+24+ - + 263粒小麦•
程序框图:。
