1. 试用拉氏方程建立单摆的运动微分方程(已知摆长,摆球质量为m)重点
机械能守恒定律笔记重点

机械能守恒定律笔记重点一、机械能的概念1. 动能- 定义:物体由于运动而具有的能,表达式为E_{k}=(1)/(2)mv^2,其中m是物体的质量,v是物体的速度。
- 动能是标量,且恒为正值。
2. 重力势能- 定义:物体由于被举高而具有的能,表达式为E_{p}=mgh,其中m是物体的质量,g是重力加速度,h是物体相对于参考平面的高度。
- 重力势能是标量,但有正负之分。
参考平面上方的物体重力势能为正,参考平面下方的物体重力势能为负。
3. 弹性势能- 定义:发生弹性形变的物体的各部分之间,由于有弹力的相互作用而具有的能。
对于弹簧,其弹性势能表达式为E_{p}=(1)/(2)kx^2(k为弹簧的劲度系数,x为弹簧的形变量)。
- 弹性势能也是标量,且恒为正值。
- 机械能:动能和势能(重力势能、弹性势能)统称为机械能,表达式为E = E_{k}+E_{p}(这里E_{p}包括重力势能和弹性势能)。
二、机械能守恒定律1. 内容- 在只有重力或弹力做功的物体系统内,动能与势能可以相互转化,而总的机械能保持不变。
2. 表达式- E_{1}=E_{2},即初状态的机械能等于末状态的机械能。
- Δ E_{k}=-Δ E_{p},动能的增加量等于势能的减少量(或者动能的减少量等于势能的增加量)。
3. 条件- 对单个物体:只有重力做功(如自由落体运动、平抛运动等)。
- 对多个物体组成的系统:- 只有重力或弹力做功。
例如,一个弹簧和一个物体组成的系统,在只有弹簧弹力做功时,系统机械能守恒。
- 其他力不做功或者其他力做功的代数和为零。
如光滑斜面上滑块与弹簧组成的系统,若斜面光滑,滑块下滑过程中,除重力和弹簧弹力外无其他力做功,系统机械能守恒。
三、机械能守恒定律的应用1. 解题步骤- 确定研究对象(单个物体或系统)。
- 分析研究对象的受力情况,判断是否满足机械能守恒定律的条件。
- 选取合适的参考平面(确定重力势能的零点)。
- 确定初状态和末状态的机械能(分别计算动能和势能)。
单摆周期公式及影响单摆周期的因素研究

单摆周期公式及影响单摆周期的因素研究摘要:结合理论知识,基础物理实验,构建线性数学模型。
对单摆运动进行分析。
其中,理论部分主要依据高等数学及数学物理方法的知识,对单摆运动周期公式进行论证;实验部分主要通过改变单摆摆线长度进行实验;观察、分析单摆运动规律。
从而验证单摆周期公式。
并对影响单摆周期的因素展开研究。
最后总结出影响单摆周期的因素。
关键词:数学模型 ; 单摆运动 ; 周期公式单摆运动问题是一个古老的问题,无论是中学物理还是大学物理,我们都在学习研究单摆。
作为一个重要的理想物理模型,单摆的运动周期规律和实验研究在生产生活中意义重大。
单摆问题是物理学中经典问题。
从阅读物理学史并可知道,早在 1583 年,十九岁的伽利略(1564—1642)在比萨教堂祈祷时注意到因被风吹而摆动的大灯,他利用自己的脉搏来测定大灯的摆动周期,发现了摆的等时性。
但现在这个故事的真实性受到怀疑 ,因为比萨大教堂所保留的许多相关历史文献都表明该吊灯是在伽利略二十三岁那年才首次安装的。
专家指出,伽利略是于1602 年注意到单摆运动的等时性,不过伽利略误认为在大摆动条件下等时性也成立,他说:“物体从直立圆环上任一点落到最低位置的时间相同。
”随后吉多彼得做实验发现这个结论与实验不符,伽利略解释说可能是由于摩擦力。
伽利略从实验中得出单摆周期与摆长的平方根成正比。
他还指出周期与摆球质量无关。
他说:“因此我取两个球,一个是铅的而另一个是软木的,前者比后者重 100 多倍,用两根等长细线把它们悬挂起来、把每一个球从铅直位置拉到旁边,我在同一时刻放开它们,它们就沿着以这些等长线为半径的圆周下落,穿过铅垂位置,并且沿同一路径返回。
”最早系统地研究单摆的是惠根斯(ChristiaanH uygens )。
由于当时实验技术条件的落后,重力加速度在惠根斯之前是很难精确测出来的,所以惠更斯不可能从实验中总结出或猜出单摆周期公式的系数π2。
事实上,反过来重力加速度是 1659 年惠更斯根据单摆周期公式首次精确测出来的。
《理论力学》作业

8. 质点系中各质点的惯性力对质心的力矩相互抵消
9.
T
1 2
mrc2
1 2
mi ri 2
10. 主矢和对简化中心的主矩,力偶和合力
11. 1 3 3 6
12. 空间极迹
本体极迹
13. 任意移动,力线平移定理,在平移的同时必须附加一力偶,其力偶矩等于原力对新作用点的力矩。
14. Il I1 2 I 2 2 I3 2 ,刚体对 o 点的三个惯量主轴的转动惯量。
19. a a r ( r) 2 vr
20. F mw2 xi FC 2m v
dv
dm
21.
m dt
F Vr
dt
(或者
d
(e) dm (mv) F u
dm
dt
22. 对力心的动量矩守恒 和 机械能守恒
23. rຫໍສະໝຸດ r r r 2 r 2r24.
H
1 2
mr 2
1 2
L 1 m(r2 r2 2 ) b
24. 已知一运动质点的拉格朗日函数为 2
r ,则哈密顿函数为 H=________(式中b为常
数)。
'
'
1. r r
''
'2
''
''
r r r 2r
2. 质点所在处曲线的切线方向
v ds dt
dv '' az dt S
v2 an
3. d J M dt
O
(3)
T
A
C
x
P
六. 解:由平面运动动力学基本力学方程得
mxc
mg sin
三.试用拉格朗日方程建立弹簧振子的运动微分方程,并求出其振.

三. 试用拉格朗日方程建立弹簧振子的运动微分方程,并求出其振动周期(已知:弹簧的倔强系数为K ,物块的质量为m )。
四. 长l 2,质量为m 的均匀棒,其上端A 靠在光滑的墙上,下端则固联一不能伸长的线BC ,线的上端固结于墙上C 点,C 点与A 点在同一垂直线上,棒与墙所成的角度为α,线与墙所成的角度为β,如果ABC 平面为与墙垂直的铅垂面。
求平衡时αβ与之间的关系。
(用刚体平衡方程求解)。
三. 解:系统自由度1=S ,取q=x,系统的动能2'21x m T = 系统的势能22
1kx V = =-=V T L 2'21x m -22
1kx 代入拉氏方程:0)(=∂∂-∂∂x l x l dt d ,得: 0''=+kx x m 0''=+
∴x m k x 令m
k w =2,则w 为弹簧振子简谐振动的圆频率。
k
m W T ππ22==∴
四. 解:αβ
cos 0(1)
0sin 0(2)0sin 2cos 0(3)()0yi xi
B i
T mg F N T F mgl N l m F ββαα⎧-==⎪-==⎨⎪-==⎩∑∑∑
)
1()2((3)N tg N mg tg mg ββ==得:。
代入式得 sin 2cos 0mgl mg tg l αβα-∙= 即:202tg tg tg tg αβαβ-=∴=。
第三章 两自由度系统振动

d d( tq L j) q L jQ j - q D j (j 1 ,2 , ,n )
式D 中 1 2 C 1 x 1 2 1 2 C 2 (x 1-x 2)2 1 2 C 3 x 2 2
例题: 置于光滑平面的小车质量m1,车上质量为m2的圆柱体可作 无滑动的纯滚动。试建立该系统的运动微分方程。
两自由度与单自由度系统振动特性与分析方法的不同:
①两自由度振动系统具有两阶固有频率; ②两自由度振动系统引入主振型的概念,与系统的固
有频率一样,是系统本身的物理特性与固有特性, 与其初始条件无关。 ③一般情况下系统的振动是两种主振动的叠加,是一 种复杂的非周期运动。当满足一定条件时,系统才 作主振动。
(j1,2, ,n)
或
dd(tqLj)qLj 0 (j1,2, ,n)
(1)
其中,L=T-U称为拉格朗日函数。
2)当作用在系统上的主动力中,部分为有势力,部分 是非有势力,广义力Qj可分为两部分:
Qj Qj Q (j1,2,,n) 其中 Q是对应于非有 义势 力力 Q, j是 的对 广应于有势 广义力。 拉氏方程可写成
1
第三节 两自由度系统振动模型的建立
动力学系统振动模型的建立方法: 牛顿运动定律 定轴转动微分方程 能量法
一、拉氏方程的原理
在理想、完整约束条件下的n个自由度系统,选取广义坐 标为qj(j=1,2, ···,n),其运动可由如下拉格朗日方程来描述:
dT T d( tq j)qj Q j
取静x,平衡位置作为坐标原点,
进行受力分析,建立系统的运 动微分方程:
m1x K1(x r) I0 K1(xr)r K2r2
(必考题)高中物理选修一第二章《机械振动》测试卷(答案解析)(9)
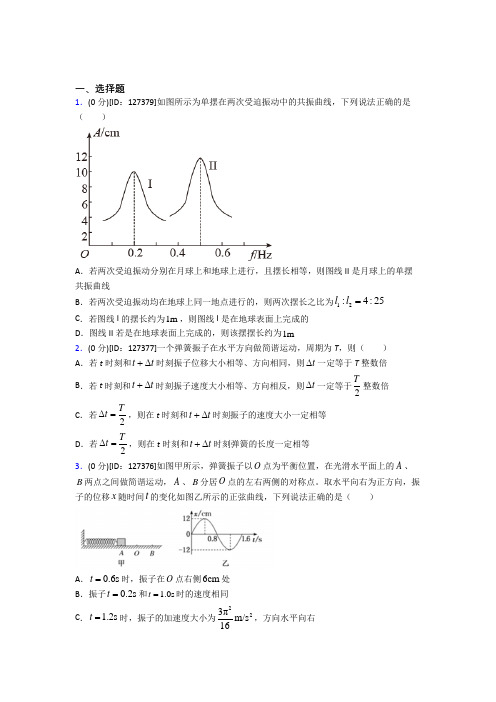
一、选择题1.(0分)[ID :127379]如图所示为单摆在两次受迫振动中的共振曲线,下列说法正确的是( )A .若两次受迫振动分别在月球上和地球上进行,且摆长相等,则图线II 是月球上的单摆共振曲线B .若两次受迫振动均在地球上同一地点进行的,则两次摆长之比为12:4:25l l =C .若图线I 的摆长约为1m ,则图线I 是在地球表面上完成的D .图线II 若是在地球表面上完成的,则该摆摆长约为1m2.(0分)[ID :127377]一个弹簧振子在水平方向做简谐运动,周期为T ,则( ) A .若t 时刻和t t +∆时刻振子位移大小相等、方向相同,则t ∆一定等于T 整数倍 B .若t 时刻和t t +∆时刻振子速度大小相等、方向相反,则t ∆一定等于2T整数倍 C .若2Tt ∆=,则在t 时刻和t t +∆时刻振子的速度大小一定相等 D .若2Tt ∆=,则在t 时刻和t t +∆时刻弹簧的长度一定相等 3.(0分)[ID :127376]如图甲所示,弹簧振子以O 点为平衡位置,在光滑水平面上的A 、B 两点之间做简谐运动,A 、B 分居O 点的左右两侧的对称点。
取水平向右为正方向,振子的位移x 随时间t 的变化如图乙所示的正弦曲线,下列说法正确的是( )A .0.6s t =时,振子在O 点右侧6cm 处B .振子0.2s t =和 1.0s t =时的速度相同C . 1.2s t =时,振子的加速度大小为223πm/s 16,方向水平向右D . 1.0s t =到 1.4s t =的时间内,振子的加速度和速度都逐渐增大4.(0分)[ID :127375]把一个筛子用四根弹簧支起来,筛子上装一个电动偏心轮,它每转一周,给筛子一个驱动力,这就做成了一个共振筛,如图所示。
不开电动机让这个筛子自由振动时,完成20次全振动用15 s ,在某电压下,电动偏心轮的转速是50 r/min 。
已知增大电动偏心轮电压可使其转速提高,而增加筛子的总质量可以增大筛子的固有周期。
单摆的运动微分方程与解

单摆的运动微分方程与解
单摆是一个基本的物理模型,其运动可以用微分方程来描述。
假设单摆的摆长为L,质量为m,角度为θ,角速度为ω。
根据牛顿第二定律,单摆的运动微分方程可以表示为:
m * d²θ/dt² = -mg * sin(θ)
这里,g 是重力加速度。
这个微分方程描述了单摆在受到重力和阻尼力作用下的运动。
解这个微分方程,可以得到单摆的角速度和角度随时间的变化。
解这个微分方程,可以得到单摆的角速度和角度随时间的变化。
角速度ω 的通解为:
ω = ω₀ * (1 - exp(-t / 2L))
其中,ω₀ 是初始角速度。
角度θ 的通解为:
θ = θ₀ * (1 - exp(-t / 2L)) + θ₁ * exp(-t / 2L)
其中,θ₀ 和θ₁ 是初始角度和最终角度。
这些解描述了单摆在受到重力和阻尼力作用下的运动规律。
高中物理波动的应用题解题思路

高中物理波动的应用题解题思路波动是高中物理课程中的一个重要内容,它广泛应用于生活和科学研究中。
在解决波动应用题时,我们需要掌握一些基本的解题思路和技巧。
本文将通过具体的题目举例,分析解题思路,并给出一些解题技巧,帮助高中学生和他们的父母更好地理解和应用波动知识。
题目一:一根长为L的细绳,一端固定,另一端悬挂一个质量为m的小球。
当小球作简谐振动时,细绳上的波动传播速度为v,频率为f。
求小球的振动周期T。
解题思路:首先,我们需要知道简谐振动的周期与频率之间的关系:T = 1/f。
而频率与波动传播速度之间的关系为:v = λf,其中λ为波长。
细绳上的波动传播速度v可以表示为v = √(T/μ),其中μ为细绳的线密度。
细绳上的波动传播速度v与波长λ之间的关系为:v = λf。
将以上两个关系代入,可以得到:λ = √(Tμ)。
将波长λ代入频率与波长之间的关系,可以得到:T = 1/(f√(μ))。
题目二:一束波长为λ的单色光通过一条宽度为d的狭缝,经过衍射后,观察到第一级主极大的角度为θ。
求狭缝的宽度d。
解题思路:根据衍射的基本原理,我们知道主极大的位置满足sinθ = mλ/d,其中m为主极大的级数。
我们可以通过观察第一级主极大的角度θ,以及波长λ,来求解狭缝的宽度d。
将已知条件代入公式,可以得到:d = mλ/sinθ。
题目三:一根长为L的弦上,由一点源产生的波传播到另一端的时间为t。
现将弦剪短为原来的一半,重新产生波,波传播到另一端的时间为多少?解题思路:首先,我们需要知道波传播速度与弦的线密度和张力之间的关系:v = √(T/μ)。
弦的线密度μ与长度L之间的关系为:μ = m/L,其中m为弦的质量。
弦的张力T与长度L之间的关系为:T = kL,其中k为弦的弹性系数。
将以上两个关系代入波传播速度与弦的线密度和张力之间的关系,可以得到:v = √(k/m)。
根据波传播速度与弦的线密度和张力之间的关系,可以得到:v' = √(k/2m)。
