高二数学上学期单元测试(1)新人教版

合集下载

2024-2025学年度上学期高二数学单元测试卷《直线方程》

2024-2025学年度上学期高二数学单元测试卷《直线方程》本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分150分，考试时间120分钟．第Ⅰ卷（选择题）一、单选题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知直线1l ：210x ay -+=，2l ：()10a x y a --+=，则“2a =”是“12//l l ”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2.已知直线的点斜式方程为34)y x -=-，则这条直线经过的定点、倾斜角分别是()A ．(4,3)，60︒B ．(3,4)--，60︒C ．(4,3)，30︒D ．(4,3)--，60︒3.直线10kx y --=与直线220x y +-=的交点在第四象限，则实数k 的取值范围为()A ．11(,)22-B ．1(,0)2-C ．1(,)2+∞D ．1(,)2-∞-4.设点3(2,)A -､(3,2)B --，若直线l 过点(1,1)P 且与线段AB 相交，则直线l 的斜率k 的取值范围是（）A ．34k ≥或4k ≤-B ．34k ≥或14k ≤-C ．344k -≤≤D ．344k -≤≤5.设点3(2,)A -､(3,2)B --，若直线l 过点(1,1)P 且与线段AB 相交，则直线l 的斜率k 的取值范围是（）A ．34k ≥或4k ≤-B ．34k ≥或14k ≤-C ．344k -≤≤D ．344k -≤≤6.已知点(1,1)A --，(1,1)B ．若点C 在函数232y x =-+的图象上，则使得ABC ∆为直角三角形的点C 的个数为()A ．4B ．5C ．6D ．77.当点()2,3M -到直线()()411210m x m y m ---++=的距离取得最大值时，m =（）A ．2B ．47C ．2-D ．4-8.数学家欧拉在1765年提出定理：三角形的外心、重心、垂心依次位于同一直线上，且重心到外心的距离是重心到垂心距离的一半，这条直线被后人称之为三角形的欧拉线.已知ABC △的顶点()2,0A ，()0,4B ，AC BC =，则ABC △的欧拉线方程为（）A ．230x y +-=B ．230x y -+=C ．230x y --=D ．230x y -+=二、多选题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9.在下列四个命题中，正确的是（）A ．坐标平面内的任何一条直线均有倾斜角和斜率B ．若直线12l l ⊥，则这两条直线的斜率的乘积为1-C ．若两条直线的斜率的乘积为1-，则这两条直线垂直D ．两条直线12,l l ，若一条直线的斜率不存在，另一条直线的斜率为零，则12l l ⊥10.对于直线:1l x my =+，下列说法错误的是()A ．直线l 恒过定点(1,0)B ．直线l 斜率必定存在C ．m =时直线l 的倾斜角为60︒D ．2m =时直线l 与两坐标轴围成的三角形面积为1411．三条直线0x y +=，0x y -=，3x ay +=构成三角形，则a 的取值可以是()A ．1-B ．1C ．2D ．5第Ⅱ卷（非选择题）三、填空题：本题共3小题，每小题5分，共15分．12.已知ABC ∆的三个顶点分别为(3,0)A -，(2,1)B ，(2,3)C -，则顶点B 到BC 边上中线AD 所在直线的距离为______.13.已知(1,12)A ，(3,4)B ，过点(1,0)C -且斜率为k 的直线1l 与线段AB 相交，点(0,1)D 到直线2:340l x y k ++=的距离为d ，则实数d 的取值范围是______.14.平面内称横坐标为整数的点为“次整点”．过函数y =直线，则倾斜角大于45︒的直线条数为______.四、解答题:本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15.（本小题满分13分）已知直线l 方程为()2380m x my m +---=，m R ∈.（1）求证：直线l 恒过定点P ，并求出定点P 的坐标；（2）若直线l 在x 轴，y 轴上的截距相等，求直线l 的方程.已知直线l过点1)P-，且其倾斜角是直线1y=+的倾斜角的1 2．（1）求直线l的方程；（2）若直线m与直线l平行，且点P到直线m的距离是3，求直线m的方程．17.（本小题满分15分）已知直线l经过点(2,4)P-．（1）若原点到直线l的距离为2，求直线l的方程；（2）若直线l被两条相交直线1:220l x y--=和2:70l x y+-=所截得的线段恰被点P平分，求直线l的方程．已知直线0132:=+-y x l ，点)2,1(--A ，求(1)点A 关于直线l 的对称点A '的坐标；（2）直线0623:=--y x m 关于直线l 的对称直线m '的方程；（3）直线l 关于点A 对称的直线l '的方程.19.（本小题满分17分）已知一条动直线3(1)(1)620m x m y m ++---=，（1）求证：直线恒过定点，并求出定点P 的坐标；（2）若直线与x 、y 轴的正半轴分别交于A ，B 两点，O 为坐标原点，是否存在直线满足下列条件：①AOB ∆的周长为12；②AOB ∆的面积为6．。

高二数学人教版：第一章解三角形单元检测试卷 Word版含解析

第一章解三角形专项训练试卷(名师精选试题+详细解答过程，值得下载打印练习)一、选择题1．在△ABC 中，角A 、B 、C 所对应的边分别为a 、b 、c ，若A ＋C ＝2B ，有a ＝1，b ＝3，则S △ABC 等于( ) A.2 B.3 C.32D ．2答案 C解析由A ＋C ＝2B ，解得B ＝π3.由余弦定理得(3)2＝1＋c 2－2c cos π3，解得c ＝2或c ＝－1(舍去)．于是，S △ABC ＝12ac sin B ＝12×1×2sin π3＝32.2．在△ABC 中，sin A ＝34，a ＝10，则边长c 的取值范围是( )A.⎝ ⎛⎭⎪⎫152，＋∞ B ．(10，＋∞) C．(0,10) D.⎝⎛⎦⎥⎤0，403答案 D解析 ∵c sin C ＝a sin A ＝403，∴c ＝403sin C ．∴0<c ≤403.3．在△ABC 中，若a ＝52b ，A ＝2B ，则cos B 等于( )A.53 B.54 C.55 D.56答案 B解析由正弦定理得a b ＝sin Asin B ，∴a ＝52b 可化为sin A sin B ＝52.又A ＝2B ，∴sin 2B sin B ＝52，∴cos B ＝54.4．在△ABC 中，角A ，B ，C 所对的边长分别为a ，b ，c .若C ＝120°，c ＝2a ，则( )A ．a ＞bB ．a ＜bC ．a ＝bD ．a 与b 的大小关系不能确定答案 A解析由余弦定理得c 2＝a 2＋b 2－2ab cos C ，又C ＝120°，∴2a 2＝a 2＋b 2＋ab ，∴a 2＝b 2＋ab ＞b 2，∴a ＞b ，故选A.5．已知△ABC 中，sin A ∶sin B ∶sin C ＝k ∶(k ＋1)∶2k ，则k 的取值范围是( ) A ．(2，＋∞) B．(－∞，0) C ．(－12，0) D ．(12，＋∞)答案 D解析由正弦定理得：a ＝mk ，b ＝m (k ＋1)，c ＝2mk (m >0)，∵⎩⎪⎨⎪⎧ a ＋b >c a ＋c >b 即⎩⎪⎨⎪⎧m k ＋mk 3mk >m k ＋，∴k >12.6．△ABC 的两边长分别为2,3，其夹角的余弦值为13，则其外接圆的半径为( )A.922 B.924 C.928D ．92答案 C解析设另一条边为x ，则x 2＝22＋32－2×2×3×13， ∴x 2＝9，∴x ＝3.设cos θ＝13，则sin θ＝223.∴2R ＝3sin θ＝3223＝924，R ＝928.7．在△ABC 中，sin A ＝sin C ，则△ABC 是( ) A ．直角三角形 B ．等腰三角形 C ．锐角三角形 D ．钝角三角形答案 B解析 ∵sin A ＝sin C 且A 、C 是三角形内角， ∴A ＝C 或A ＋C ＝π(舍去)． ∴△ABC 是等腰三角形．8．在锐角△ABC 中，BC ＝1，∠B ＝2∠A ，则AC 的取值范围是( ) A ．[－2,2] B ．[0,2] C ．(0,2] D ．(2，3)答案 D解析由题意得⎩⎪⎨⎪⎧0＜π－3∠A ＜π2，0＜2∠A ＜π2⇒π6＜∠A ＜π4，由正弦定理ACsin B ＝BCsin A得AC ＝2cos A .∵∠A ∈⎝ ⎛⎭⎪⎫π6，π4，∴AC ∈(2，3)．9．根据下列情况，判断三角形解的情况，其中正确的是( ) A ．a ＝8，b ＝16，A ＝30°，有两解 B ．b ＝18，c ＝20，B ＝60°，有一解 C ．a ＝5，c ＝2，A ＝90°，无解 D ．a ＝30，b ＝25，A ＝150°，有一解答案 D解析 A 中，因a sin A ＝bsin B，所以sin B ＝16×sin 30°8＝1，∴B ＝90°，即只有一解；B 中，sinC ＝20sin 60°18＝539，且c >b ，∴C >B ，故有两解；C 中，∵A ＝90°，a ＝5，c ＝2，∴b ＝a 2－c 2＝25－4＝21，即有解；故A 、B 、C 都不正确．用排除法应选D.10．在△ABC 中，AB ＝7，AC ＝6，M 是BC 的中点，AM ＝4，则BC 等于( ) A.21 B.106 C.69 D.154答案 B解析设BC ＝a ，则BM ＝MC ＝a2.在△ABM 中，AB 2＝BM 2＋AM 2－2BM ·AM ·cos∠AMB ，即72＝14a 2＋42－2×a2×4·cos∠AMB ① 在△ACM 中，AC 2＝AM 2＋CM 2－2AM ·CM ·cos∠AMC 即62＝42＋14a 2＋2×4×a2·cos∠AMB ②①＋②得：72＋62＝42＋42＋12a 2，∴a ＝106.二、填空题11．已知△ABC 中，3a 2－2ab ＋3b 2－3c 2＝0，则cos C 的大小是________．答案 13解析由3a 2－2ab ＋3b 2－3c 2＝0，得c 2＝a 2＋b 2－23ab .根据余弦定理，得cos C ＝a 2＋b 2－c 22ab＝a 2＋b 2－a 2－b 2＋23ab2ab＝13，所以cos C ＝13. 12．在△ABC 中，若b ＋c ＝2a,3sin A ＝5sin B ，则角C ＝________. 答案2π3解析由已知3sin A ＝5sin B ，利用正弦定理可得3a ＝5b . 由3a ＝5b ，b ＋c ＝2a ，利用余弦定理得cos C ＝a 2＋b 2－c 22ab ＝－12.C ∈(0，π)，C ＝23π.13．在△ABC 中，已知cos A ＝35，cos B ＝513，b ＝3，则c ＝________.答案145解析在△ABC 中，∵cos A ＝35>0，∴sin A ＝45.∵cos B ＝513>0，∴sin B ＝1213.∴sin C ＝sin[π－(A ＋B )]＝sin(A ＋B )＝sin A cos B ＋cos A sin B ＝45×513＋35×1213＝5665.由正弦定理知b sin B ＝c sin C ，∴c ＝b sin Csin B ＝3×56651213＝145.14．太湖中有一小岛C ，沿太湖有一条正南方向的公路，一辆汽车在公路A 处测得小岛在公路的南偏西15°的方向上，汽车行驶1 km 到达B 处后，又测得小岛在南偏西75°的方向上，则小岛到公路的距离是________ km. 答案36解析如图，∠CAB ＝15°，∠CBA ＝180°－75°＝105°，∠ACB ＝180°－105°－15°＝60°，AB ＝1 (km)．由正弦定理得BC sin∠CAB ＝ABsin∠ACB ，∴BC ＝1sin 60°·sin 15°＝6－223 (km)．设C 到直线AB 的距离为d ，则d ＝BC ·sin 75°＝6－223·6＋24＝36(km)．三、解答题15．已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且a ＝2，cos B ＝35.(1)若b ＝4，求sin A 的值；(2)若△ABC 的面积S △ABC ＝4，求b ，c 的值．解 (1)∵cos B ＝35>0，且0<B <π，∴sin B ＝1－cos 2B ＝45. 由正弦定理得a sin A ＝b sin B ，sin A ＝a sin Bb ＝2×454＝25.(2)∵S △ABC ＝12ac sin B ＝4，∴12×2×c ×45＝4，∴c ＝5.由余弦定理得b 2＝a 2＋c 2－2ac cos B ＝22＋52－2×2×5×35＝17，∴b ＝17.16.如图所示，我艇在A 处发现一走私船在方位角45°且距离为12海里的B 处正以每小时10海里的速度向方位角105°的方向逃窜，我艇立即以14海里/时的速度追击，求我艇追上走私船所需要的时间．解设我艇追上走私船所需时间为t 小时，则BC ＝10t ，AC ＝14t ，在△ABC 中，由∠ABC ＝180°＋45°－105°＝120°，根据余弦定理知(14t )2＝(10t )2＋122－2·12·10t cos 120°， ∴t ＝2(t ＝－34舍去)．答我艇追上走私船所需要的时间为2小时． 17．在△ABC 中，a ＝3，b ＝26，∠B ＝2∠A .(1)求cos A 的值； (2)求c 的值．解 (1)因为a ＝3，b ＝26，∠B ＝2∠A ，所以在△ABC 中，由正弦定理得3sin A ＝26sin 2A.所以2sin A cos A sin A ＝263.故cos A ＝63.(2)由(1)知cos A ＝63，所以sin A ＝1－cos 2A ＝33. 又因为∠B ＝2∠A ，所以cos B ＝2cos 2A －1＝13.所以sin B ＝1－cos 2B ＝223.在△ABC 中，sin C ＝sin(A ＋B ) ＝sin A cos B ＋cos A sin B ＝539.所以c ＝a sin C sin A＝5.18．已知△ABC 的角A 、B 、C 所对的边分别是a 、b 、c ，设向量m ＝(a ，b )，n ＝(sin B ，sin A )，p ＝(b －2，a －2)．(1)若m ∥n ，求证：△ABC 为等腰三角形；(2)若m ⊥p ，边长c ＝2，角C ＝π3，求△ABC 的面积．(1)证明 ∵m ∥n ，∴a sin A ＝b sin B ，即a ·a 2R ＝b ·b2R，其中R 是△ABC 外接圆半径，∴a ＝b . ∴△ABC 为等腰三角形． (2)解由题意知m ·p ＝0，即a (b －2)＋b (a －2)＝0. ∴a ＋b ＝ab .由余弦定理可知，4＝a 2＋b 2－ab ＝(a ＋b )2－3ab ，即(ab )2－3ab －4＝0. ∴ab ＝4(舍去ab ＝－1)， ∴S △ABC ＝12ab sin C ＝12×4×sin π3＝3.。

2021届新人教版高二上学期数学单元测试(1)

2021届新人教版高二上学期数学单元测试(1)●-------------------------题--------------答-------------_-__要_--_-_--_-_--_-_--：---号不考---_-_--_-_--_-_--_--__请_-：---级---班---_-_--_-__内_--_-_--_--_-：---名---姓线--------------封--------------密-------------------------●2021届新人教版高二上学期数学单元测试（1）一、多项选择题（这个大问题有12个子问题，每个子问题是0，总共是0。

每个子问题中只有四个选项中的一个选项是符合题目要求的）1.设a2a1?a21,a2,a3,a4成等比数列，其公比为2，则2a的值是（）3?a4a．14b.12c.18d.1【答案解析】a【解析】略2.以下四个数字中的哪一个是序列{n（n？1）}（a.380b.39c.35d.23）中的项目【答案解析】a【解析】略3.已知系列？一遇到一个？1.2，一个？1.一1.0（n？n），那么这个序列的一般项an等于（）a、氮气？1b.n？1c.1？第三名？N【答案解析】d【解析】略4.系列？一A的通项公式？1n？N1，则序列的前（）项之和等于9。

（）a、 98b.99c.96d.97【答案解析】b【解析】略一5.各项为正数的等比数列?an?的公比q?1，且a2,（）1A的值是多少？Aa3和A1形成一个等差序列，然后是342a4？a55？15? 11? 55? 15? 一a．2B。

2C。

2D。

2或2【答案解析】b【解析】略6.在哪里？ABC，知道吗？30?， C45?， A.2.那么？ABC的面积等于（）答。

2b．3?1c．22d．12(3?1)【答案解析】b【解析】略7.在100和500之间可以被9除的所有数字之和是（a.12699b.13266c.13833d.14400）【答案解析】b【解析】略8.在-1和8之间插入两个数字a和B，使四个数字成为等差序列，然后（）a、 a=2，b=5b.a=-2，b=5c.a=2，b=-5d.a=-2，b=-5【答案解析】a【解析】略9.第一项是什么？如果24的等差序列与第10项为正，则公差D的值范围为（A.D＞） 83b．d＞3c．883≤d＜3d．3＜d≤3【答案分析】d【分析】省略2））10.在等差数列?an?中，已知a1+a4+a7=39，a2+a5+a8=33，则a3+a6+a9=（）a．30b．27c．24d．21【分析】B11.一群羊中，每只羊的重量数均为整千克数，其总重量为65千克，已知最轻的一一只羊重7公斤。

高二数学上学期第一学段模块检测试题文新人教版

—————————— 新学期新成绩新目标新方向 ——————————2019学年第一学期第一学段质量检测试卷高二数学（文科）试卷总分150分完卷时间120分钟一、选择题（本题每小题5分，共60分）1．若a ，b 是任意实数，且a ＞b ，则下列不等式中一定正确的是( ) A.ac ＞bc B.1<abC. a －c ＞b －cD.|a |＞|b |2．在ABC ∆中，若60A ∠=，45B ∠=，BC =AC =（）A. 3.若椭圆x 24＋y 2m2＝1(m >0)的一个焦点坐标为(1,0)，则m 的值为( )A ．5B ．3C ． 5D ． 34.设n S 为等差数列{}n a 的前n 项和，已知15918a a a ++=，则9S 的值为（） A ．54B ．45C ．27D ．185．设集合M={x|x>2},P={x|x<3},那么“x ∈M,或x ∈P ”是“x ∈M ∩P ”的（） A ．必要不充分条件 B ．充分不必要条件 C ．充要条件 D ．既不充分也不必要条件6.对于任意实数x ，不等式210mx mx +-<恒成立，则实数m 的取值范围（）A ．(,4)-∞-B ．(,4]-∞-C ．(4,0)-D ．(4,0]-7．方程222=+ky x 表示焦点在y 轴上的椭圆，则k 的取值范围是（）A ．),0(+∞B ．（0，2）C ．（1，+∞）D ．（0，1）8．下列命题中正确的是（）①“若x 2＋y 2≠0，则x ，y 不全为零”的否命题 ②“正多边形都相似”的逆命题③“若m>0，则x 2＋x －m=0有实根”的逆否命题 ④“若x －123是有理数，则x 是无理数”的逆否命题A 、①②③④B 、①③④C 、②③④D 、①④9．若变量x y ，满足约束条件22024010x y x y x +-≥⎧⎪-+≥⎨⎪-≤⎩，则目标函数32z x y =-的最小值为（）A ． -5B ．-4 C.-2 D ．3 10.下列函数中，最小值为4的是（）A ．4y x x=+B ．4sin sin y x x=+（0x π<<） C ．4xxy e e-=+D ．3log 4log 3x y x =+11.如果一个等差数列前3项的和为34，最后3项的和为146，且所有项的和为390，则这个数列有（）A ．13项B ．12项C ．11项D ．10项12．已知命题p ：∀x ∈[1,2]，x 2－a ≥0，命题q ：∃x 0∈R ，x 20＋2ax 0＋2－a ＝0.若命题 “p ∧q ”是真命题，则实数a 的取值范围是( )A ．a ≤－2或a ＝1B ．a ≤－2或1≤a ≤2C ．a ≥1D ．－2≤a ≤1 二、填空题(本题共4小题，每题4分，共16分）13．已知命题p ：∃x ∈R ，x 2＋2ax ＋a ≤0，则⌝p 为____ ___．14.若数列{}n a 的前n 项和221n S n n =++，则n a = ．15．已知关于x 的不等式20x ax b ++<的解集为(1,2)，则关于x 的不等式210bx ax ++>的解集为_________ __.16．若点P 在椭圆1222=+y x 上，1F 、2F 分别是椭圆的两焦点，且 9021=∠PF F ，则21PF F ∆的面积是 . 三、解答题(本题共6小题，共74分)17．(本小题满分12分)求与椭圆369422=+y x 有相同的焦点,且过点(－3，２)的椭圆方程。

高二数学上学期第一次月考试题新人教版 (新版).doc

2019学年高二数学上学期第一次月考试题一．选择题（共60分） 1. 设全集为R ，集合，，则A.B.C.D.2. 过点P （-1，3）平行直线 x-2y+3=0的直线方程 ( ) A. 2x+y-1=0 B. 2x+y-5=0 C. x+2y-5=0 D. x-2y+7=0 3.已知圆22:40C x y x +-=，过点(3,0)P 的直线l ，则（）A.l 与C 相交B. l 与C 相切C.l 与C 相离D. 以上三个选项均有可能 4.直线2550x y +-+=被圆22240x y x y +--=截得的弦长为（）A ． 1B ．2C ．4D ．465.圆0882:221=-+++y x y x C ，圆0244:222=---+y x y x C ，圆1C 与圆2C 的位置关系. （）（A ）内切（B ）相交（C ）外切（D ）相离 6. 已知，则的大小关系为（）A.B.C.D.7.将函数的图象向右平移个单位长度，所得图象对应的函数（）A. 在区间上单调递增B. 在区间上单调递减C. 在区间上单调递增 D. 在区间上单调递减8.已知,x y 满足约束条件020x y x y y -≥⎧⎪+≤⎨⎪≥⎩，若z ax y =+的最大值为4，则a = （）（A ）3 （B ）-3 （C ）2 （D ）-29.点42P （，-）与圆422=+y x 上任一点连线的中点轨迹方程是（）10.直线20x y ++=分别与x 轴，y 轴交于A ，B 两点，点P 在圆()2222x y -+=上，则ABP △面积的取值范围是（） A ．[]26，B ．[]48，C ．()232，D ．2232⎡⎤⎣⎦，11．（理科）已知正方体的棱长为1，每条棱所在的直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为 ( ) A.435 B.433 C.332 D.423 11.（文科）已知圆O ：x 2＋y 2＝1和点A (－2，0)，若定点B (b ，0)(b ≠－2)和常数λ满足：对圆O 上任意一点M ，都有|MB |＝λ|MA |，则 ( )A ．1,2b λ=-=B ．1,2b λ==C ．11,22b λ==D ．11,22b λ=-=12. 如图，在平面四边形ABCD 中，，，，. 若点E为边CD 上的动点，则 AE BE u u u r u u u rg 的最小值为 ( ) A. B. C.D.二．填空题（共20分）13.在直角坐标系中，直线330x y --=的倾斜角的度数是14. 设,x y 满足约束条件：,013x y x y x y ≥⎧⎪-≥-⎨⎪+≤⎩；则2z x y =-的最小值为 .15.在平面直角坐标系xOy 中,(12,0),(0,6),A B -点P 在圆2250O x y +=：上,若20,PA PB ⋅u u u r u u u r≤则点P 的横坐标的取值范围是 .16.等差数列{}n a 的前n 项和为n S ，33a =，410S =，则1211S S +311nS S +++=L三．解答题(共70分)17.（10分）（1）求过点(1,2)P -且在两个坐标轴上的截距相等的直线方程；（2）求圆心在直线032=--y x 上,且过点)2,3(),2,5(-B A 的圆的方程18、（12分）某化肥厂生产甲、乙两种混合肥料，需要A,B,C 三种主要原料.生产1车皮甲种肥料和生产1车皮乙中肥料所需三种原料的吨数如下表所示：现有A 种原料200吨，B 种原料360吨，C 种原料300吨，在此基础上生产甲乙两种肥料.已知生产1车皮甲种肥料，产生的利润为2万元；生产1车皮乙种肥料，产生的利润为3万元.分别用x,y 表示生产甲、乙两种肥料的车皮数. (Ⅰ)用x,y 列出满足生产条件的数学关系式，并画出相应的平面区域；(Ⅱ)问分别生产甲、乙两种肥料各多少车皮，能够产生最大的利润？并求出此最大利润.19．(12分) 在平面四边形ABCD 中，AB AD ⊥，2721,cos ,73BC B ACB π==∠=. （1）求AC 的长；（2）若21AD =，求CD 的长和四边形ABCD 的面积.20.（理科12分）在四棱锥P ABCD -中,侧面PCD⊥底面ABCD ,PD CD ⊥,E 为PC中点,底面ABCD是直角梯形,//AB CD ,90ADC ∠=o,1AB AD PD ===,2CD =．（1）求证：BC ⊥平面PBD ；（2）在线段PC 上是否存在一点Q ,使得二面角Q BD P --为45o？若存在,求PQPC的值；若不存在,请说明理由．20.文科（12分）如图，在四棱锥P-ABCD 中，平面PAD ⊥平面ABCD ，AB//DC ，△PAD 是等边三角形，BD ＝2AD ＝8，AB ＝2DC ＝45．（1）设M 是PC 上的一点，证明：平面MBD ⊥平面PAD ；（2）求四棱锥P-ABCD 的体积．20．[文科] 如图，三棱柱ABC A 1B 1C 1中，侧面BB 1C 1C 为菱形，B 1C 的中点为O ，且AO ⊥平面BB 1C 1C .(1)证明：B 1C ⊥AB ；(2)若AC ⊥AB 1，∠CBB 1＝60°，BC ＝1，求三棱柱ABC A 1B 1C 1的高．21.（12分）数列}{n a 满足)0(m ,111≠==+m a a a n n ，数列{n b }的前n 项和为=n s 12n 2++n ，（1）求数列}{n a 的前n 项和，及数列{n b }的通项公式；（2）当3=m 时，设n n nb ac ⋅=，求数列{n c }的前n 项和n T ；（3）若12-≤n T k n 对*∈N n 都成立，求k 的取值范围．22. （12分）已知直线l :4x +3y +10=0，半径为2的圆C 与l 相切，圆心C 在x 轴上且在直线l 的右上方.(1) 求圆C 的方程；(2) 过点M (1,0)的直线与圆C 交于A ,B 两点(A 在x 轴上方)，问在x 轴正半轴上是否存在定点N ，使得x 轴平分∠ANB ?若存在，请求出点N 的坐标；若不存在，请说明理由。

人教版高二第一章三角函数单元测试精选(含答案)1

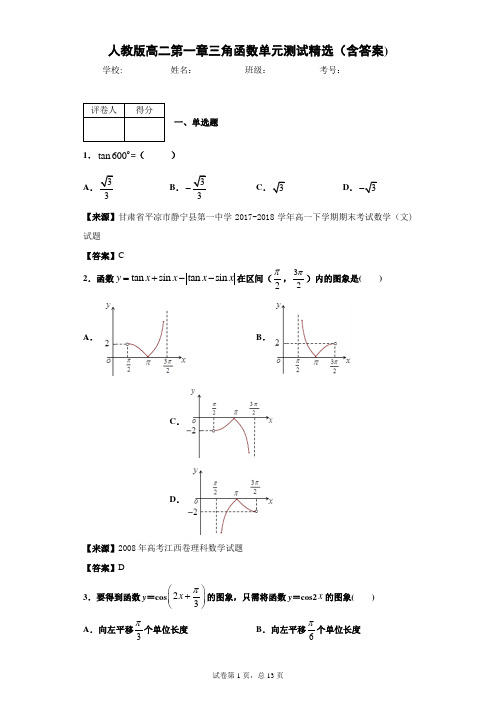
人教版高二第一章三角函数单元测试精选（含答案)学校:___________姓名：___________班级：___________考号：___________一、单选题1．tan 600o =（）A ．B ．-C D ．【来源】甘肃省平凉市静宁县第一中学2017-2018学年高一下学期期末考试数学（文)试题【答案】C2．函数tan sin tan sin y x x x x =+--在区间（2π，32π）内的图象是( )A ．B ．C ．D ．【来源】2008年高考江西卷理科数学试题【答案】D3．要得到函数y ＝cos 23x π⎛⎫+ ⎪⎝⎭的图象，只需将函数y ＝cos2x 的图象( )A ．向左平移π个单位长度 B ．向左平移π个单位长度C ．向右平移6π个单位长度 D ．向右平移3π个单位长度【来源】浙江省金华十校2017-2018学年高一上学期期末调研考试数学试题【答案】B4．已知0>ω，函数()sin()4f x x πω=+在(,)2ππ上单调递减，则ω的取值范围是（） A ．15[,]24B ．13[,]24C ．1(0,]2D ．(0,2]【来源】2012年全国普通高等学校招生统一考试理科数学（课标卷带解析) 【答案】A5．已知cos cos θθ=，tan tan θθ=-|，则2θ的终边在( ) A ．第二、四象限B ．第一、三象限C ．第一、三象限或x 轴上D ．第二、四象限或x 轴上【来源】辽宁省营口市2017-2018学年高一4月月考数学试题【答案】D6．记0cos(80)k -=，那么0tan100=（）A ．B ．C D ．【来源】2010年普通高等学校招生全国统一考试（全国Ⅰ)理科数学全解全析【答案】B7．在ABC ∆中，tan tan tan A B A B ++=，则C 等于（）A ．6π B ．4π C ．3π D ．23π 【来源】广西宾阳县宾阳中学2017-2018学年高一5月月考数学试题【答案】C8．若扇形的面积为38π、半径为1，则扇形的圆心角为（） A ．32π B ．34π C ．38π D ．316π 【来源】浙江省杭州第二中学三角函数单元测试题【答案】B9．如图，在平面直角坐标系xOy 中，质点M N ，间隔3分钟先后从点P ，绕原点按逆时针方向作角速度为6π弧度/分钟的匀速圆周运动，则M 与N 的纵坐标之差第4次达到最大值时，N 运动的时间为（）A ．37.5分钟B ．40.5分钟C ．49.5分钟D ．52.5分钟【来源】福建省福州格致中学2017-2018学年高一下学期第四学段质量检测数学试题【答案】A10．函数sin(2)3y x π=+图象的对称轴方程可能是（）A ．6x π=-B ．12x π=-C ．6x π=D ．12x π=【来源】2008年普通高等学校招生全国统一考试数学文科（安徽卷) 【答案】D11．函数y =的定义域是（）A ．()2,233k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦B ．()22,233k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦C ．()2,266k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦D ．()222,233k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦【来源】2019年一轮复习讲练测 4.3三角函数的图象与性质【答案】D12．设函数2()sin sin f x x b x c =++，则()f x 的最小正周期 A ．与b 有关，且与c 有关 B ．与b 有关，但与c 无关 C ．与b 无关，且与c 无关 D ．与b 无关，但与c 有关【来源】2019高考备考一轮复习精品资料专题十八三角函数的图象和性质教学案【答案】B象关于y 轴对称，则m 的最小值是（） A ．6π B ．3π C ．23π D ．56π 【来源】2011届江西省湖口二中高三第一次统考数学试卷【答案】C14．若tan 3α=,4tan 3β=,则tan()αβ-= A ．3B ．3-C ．13D ．13-【来源】北京市清华附中2017-2018学年高三数学十月月考试题（文) 【答案】C 15．若sin cos 1sin cos 2αααα+=-，则tan 2α等于（）A ．34-B ．34C ．43-D ．43【来源】2012年全国普通高等学校招生统一考试文科数学（江西卷带解析) 【答案】B16．函数()sin()f x x ωϕ=+（其中2πϕ<）的图象如图所示，为了得到()sin g x xω=的图象，则只要将()f x 的图象A ．向右平移个单位长度B ．向右平移个单位长度C ．向左平移个单位长度D ．向左平移个单位长度【来源】2015届福建省八县（市)一中高三上学期半期联考文科数学试卷（带解析) 【答案】A17．曲线sin (0,0)y A x a A ωω=+>>在区间2π0,ω⎡⎤⎢⎥⎣⎦上截直线2y =及1y =-所得的弦长相等且不为0，则下列对A ，a 的描述正确的是（）． A ．12a =，32A >B ．12a =，32A ≤ C ．1a =，1A ≥ D ．1a =，1A ≤【来源】广东省华南师范大学附属中学2016-2017学年高一上学期期末考试数学试题【答案】A价y （单位：元/平方米）与第x 季度之间近似满足关系式：()()500sin 95000y x ωϕω=++>.已知第一、二季度的平均单价如下表所示：则此楼盘在第三季度的平均单价大约是（） A ．10000B ．9500C ．9000D ．8500【来源】第一章全章训练【答案】C19．函数5sin(2)2y x π=+的图象的一条对称轴方程是（） A ．2x π=-B ．4πx =-C ．8x π=D ．54x π=【来源】2012-2013学年黑龙江省集贤县第一中学高一上学期期末考试数学试题（带解析) 【答案】A 20．已知－2π<θ<2π，且sin θ＋cos θ＝a ，其中a ∈(0,1)，则关于tan θ的值，在以下四个答案中，可能正确的是( ) A ．－3B ．3或13C ．－13D ．－3或－13【来源】浙江省温州中学2016-2017学年高一下学期期中考试数学试题【答案】C 21．设5sin 7a π=，2cos 7b π=，2tan 7c π=，则（） A ．a b c <<B ．a c b <<C ．b c a <<D ．b a c <<【来源】2008年高考天津卷文科数学试题【答案】D 22．1cos()2πα+=-，322παπ<<，()sin 2πα-的值为（）A ．B ．12C ．±D ．2【来源】江西省上饶市“山江湖”协作体2018-2019学年高一下学期统招班第一次月考【答案】D23．若0<α<β<π4,sinα+cosα=a,sinβ+cosβ=b,则( ).A ．a <bB ．a >bC ．ab <1D ．ab >2【来源】河北省石家庄市辛集中学2015-2016学年高一下学期综合练习（三)数学试题【答案】A24．在ABC ∆中，内角A ，B ，C 所对的边分别为a ，b ，c ，若3a =，7c =，60C =︒，则b = （） A ．5B ．8C ．5或-8D ．-5或8【来源】正余弦定理滚动习题（三) [ 范围 1 ] 【答案】B25．已知πcos sin 6αα⎛⎫-+= ⎪⎝⎭7sin()6πα+的值是（）A ．5-B ．5C ．45-D ．45【来源】广东省广州市执信中学2018-2019学年度上学期高三测试数学（必修模块)试题【答案】C26．将函数sin 25y x π⎛⎫=+⎪⎝⎭的图象向右平移10π个单位长度，所得图象对应的函数 A ．在区间,44ππ⎡⎤-⎢⎥⎣⎦ 上单调递增 B ．在区间,04π⎡⎤-⎢⎥⎣⎦ 上单调递减 C ．在区间,42ππ⎡⎤⎢⎥⎣⎦上单调递增 D ．在区间,2ππ⎡⎤⎢⎥⎣⎦上单调递减【来源】黑龙江省牡丹江市第一高级中学2017-2018学年高二下学期期末考试数学（文)试题【答案】A27．若α是第三象限的角, 则2απ-是( )A ．第一或第二象限的角B ．第一或第三象限的角C ．第二或第三象限的角D ．第二或第四象限的角【来源】浙江省杭州第二中学三角函数单元测试题28．已知函数()()0,0,2f x Asin x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示，则函数()f x 的解析式为（）A ．()sin()84f x x ππ=+B ．()sin()84f x x ππ=-C ．3()sin()84f x x ππ=+D ．3()sin()84f x x ππ=-【来源】浙江省杭州第二中学三角函数单元测试题【答案】A29．曲线cos 2y x =与直线y =在y轴右侧的交点按横坐标从小到大依次记为1P ,2P ,3P ,4P ,5P ,…,则15PP 等于 ( )A ．πB ．2πC ．3πD ．4π【来源】浙江省杭州第二中学三角函数单元测试题【答案】B二、填空题30．若sin(+θ)=25，则cos2θ= ．【来源】2017届福建福州外国语学校高三文上学期期中数学试卷（带解析) 【答案】31．已知直线l ：mx +y +3m −√3=0与圆x 2+y 2=12交于A ，B 两点，过A ，B 分别作l 的垂线与y 轴交于C ，D 两点，若|AB|=2√3，则|CD|=__________．【来源】2016年全国普通高等学校招生统一考试理科数学（全国3卷参考版) 【答案】432．已知点P(tan α，cos α)在第三象限，则角α的终边在第________象限．【答案】二33．设定义在R 上的函数()()0,122f x sin x ππωϕωϕ⎛⎫=+>-<<⎪⎝⎭,给出以下四个论断：①()f x 的周期为π； ②()f x 在区间,06π⎛⎫-⎪⎝⎭上是增函数；③()f x 的图象关于点,03π⎛⎫⎪⎝⎭对称；④()f x 的图象关于直线12x π=对称.以其中两个论断作为条件，另两个论断作为结论，写出你认为正确的一个命题（写成“p q ⇒”的形式）______________.（其中用到的论断都用序号表示）【来源】浙江省杭州第二中学三角函数单元测试题【答案】①④⇒②③ 或①③⇒②④ 34．关于下列命题：①若,αβ是第一象限角，且αβ>，则sin sin αβ>； ②函数sin()2y x ππ=-是偶函数；③函数sin(2)3y x π=-的一个对称中心是(,0)6π；④函数5sin(2)3y x π=-+在,]1212π5π[-上是增函数，所有正确命题的序号是_____．【来源】2018-2019学年高中数学（人教A 版，必修4)第一章《三角函数》测试题【答案】②③ 35．在ABC ∆中，若B a bsin 2=，则A =______．【来源】正余弦定理滚动习题（三) [ 范围 1 ] 【答案】30o 或150o36．若sin()2cos(2),αππα-=-则sin()5cos(2)3cos()sin()παπαπαα-+----的值为____________.【来源】浙江省杭州第二中学三角函数单元测试题【答案】35-37．若函数f (x )=sin 2x+cos 2x ,且函数y=f 2x ϕ⎛⎫+ ⎪⎝⎭(0<φ<π)是一个偶函数,则φ的值等于_____.【答案】π4三、解答题38．已知函数()3sin(2)3f x x π=-，（1）请用“五点作图法”作出函数()y f x =的图象；（2）()y f x =的图象经过怎样的图象变换，可以得到sin y x =的图象.（请写出具体的变换过程）【来源】浙江省杭州第二中学三角函数单元测试题【答案】（1）见解析；（2）变换过程见解析.39．在△ABC 中，222a c b +=(1)求B 的大小；(2)求cos A ＋cos C 的最大值．【来源】浙江省嘉兴市第一中学2017-2018学年高二10月月考数学试题【答案】（1）π4（2）140．已知A 、B 、C 是△ABC 的三个内角，向量m ＝(－1，n ＝(cos A ，sin A )，且m ·n ＝1. (1)求角A ； (2)若221sin 2cos sin BB B+-＝－3，求tan C ．【来源】2017秋人教A 版高中数学必修四：学业质量标准检测3【答案】(1)3π;(2) . 41．已知函数()()()sin 0,0,02f x A x A ωϕωϕπ=+>><<的部分图象如图所示，且()506f f π⎛⎫=⎪⎝⎭.（1）求函数()f x 的最小正周期；（2）求()f x 的解析式，并写出它的单调递增区间. 【来源】第一章全章训练【答案】（1）π；（2）()22sin 23f x x π⎛⎫=+⎪⎝⎭；单调递增区间为7,,1212k k k ππππ⎡⎤--∈⎢⎥⎣⎦Z .42．已知函数()f x =4tan xsin （2x π-）cos （3x π-）-.（Ⅰ）求f （x ）的定义域与最小正周期；（Ⅱ）讨论f （x ）在区间[,44ππ-]上的单调性.【来源】2017秋人教A 版高中数学必修四：学业质量标准检测3 【答案】（Ⅰ）{|,}2x x k k Z ππ≠+∈，π；（Ⅱ）在区间,124ππ⎡⎤-⎢⎥⎣⎦上单调递增, 在区间412ππ⎡⎤--⎢⎥⎣⎦，上单调递减. 43．已知函数()cos(2)2sin()sin()344f x x x x πππ=-+-+ （Ⅰ）求函数()f x 的最小正周期和图象的对称轴方程（Ⅱ）求函数()f x 在区间[,]122ππ-上的值域【来源】2008年普通高等学校招生全国统一考试数学文科（安徽卷)【答案】（Ⅰ）见解析（Ⅱ）函数()f x 在区间[,]122ππ-上的值域为[ 44．设函数()sin(2)()3f x A x x R π=+∈的图像过点7(,2)12P π-.（2）已知10()21213f απ+=，02πα-<<，求1cos()sin()2sin cos 221sin cos ππαααααα-++-+++的值；（3）若函数()y g x =的图像与()y f x =的图像关于y 轴对称，求函数()y g x =的单调区间.【来源】浙江省杭州第二中学三角函数单元测试题【答案】（1）()223f x sin x π⎛⎫=+ ⎪⎝⎭；（2）713-；（3）单减区间为15(,)()1212k k k z ππππ-+∈，单增区间为511(,)()1212k k k z ππππ++∈. 45．(1)已知角α的终边经过点P (4，－3)，求2sin α＋cos α的值；(2)已知角α的终边经过点P (4a ，－3a )(a ≠0)，求2sin α＋cos α的值；(3)已知角α终边上一点P 与x 轴的距离与y 轴的距离之比为3∶4，求2sin α＋cos α的值．【来源】第3章章末检测-2018-2019版数学创新设计课堂讲义同步系列（湘教版必修2)【答案】（1）－25(2)见解析（3）见解析 46．是否存在实数a ，使得函数y =sin 2x +acosx +5a 8−32在闭区间[0,π2]上的最大值是1？若存在，求出对应的a 值；若不存在，请说明理由．【来源】重庆市万州二中0910年高一下学期期末考试【答案】f max (t)=f(a 2)=a 42+58a −12=1， 47．A,B 是单位圆O 上的点,点A 是单位圆与x 轴正半轴的交点,点B 在第二象限,记∠AOB =θ,且sinθ=45.(1)求点B 的坐标;(2)求sin (π+θ)+2sin(π2−θ)2tan (π−θ)的值.【来源】2015-2016学年广西钦州港开发区中学高二上第一次月考理科数学试卷（带解析)【答案】（1）(−35,45)；（2）−53． 48．已知函数()sin 214f x x π⎛⎫=++ ⎪⎝⎭(1)用“五点法”作出()f x 在7,88x ππ⎡⎤∈-⎢⎥⎣⎦上的简图; (2)写出()f x 的对称中心以及单调递增区间;(3)求()f x 的最大值以及取得最大值时x 的集合.【来源】2018-2019学年高中数学（人教A 版，必修4)第一章《三角函数》测试题【答案】（1）见解析；（2）k ππ,028⎛⎫+ ⎪⎝⎭,k Z ∈，最大值为2,此时,,8x k k ππ=+∈Z . 49．在ABC ∆中，内角A ，B ，C 所对的边分别为a ，b ，c ，已知2a =，5c =，3cos 5B =. （1）求b 的值；（2）求sin C 的值.【来源】正余弦定理滚动习题（三) [ 范围 1 ]【答案】（1；（2.50．已知函数f (x )=4sin π-3x ⎛⎫ ⎪⎝⎭cos . (1)求函数f (x )的最小正周期和单调递增区间;(2)若函数g (x )=f (x )-m 区间在π0,2⎡⎤⎢⎥⎣⎦上有两个不同的零点x 1,x 2,求实数m 的取值范围,并计算tan(x 1+x 2)的值.【来源】人教A 版2018-2019学年高中数学必修4第三章三角恒等变换测评【答案】(1)T=π,递增区间为π5ππ-,π1212k k ⎡⎤+⎢⎥⎣⎦(k ∈Z).(2) m ∈-3.。

安徽省芜湖市高二数学上学期第一学段模块测评(A) 新人教版

芜湖市09—10学年高二第一学期第一学段年纪模块测评数学试卷A一、选择题（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A 、B 、C 、D 的四个答案，其中只有一个是正确的，请将正确答案的代号填在题后的括号中。

1．设α、β是两个不同的平面，l 是一条直线，以下命题正确的是A ．若,l ααβ⊥⊥，则l β⊂B ．若//,//,l ααβ则l β⊂C ．若,//l ααβ⊥，则l β⊥D ．若//,,l ααβ⊥则l β⊥2．若正四棱柱1111ABCD A BC D -的底面边长为1，AB 1与底面ABCD 成60°角，则A 1C 1到底面ABCD 的距离为A B ．1C D 3．直线l 的斜率为1ln2k =，则直线l 的倾斜角的取值范围是 A ．[0,90]︒︒ B ．(0,90)︒︒ C ．[90,180]︒︒ D ．(90,180)︒︒4．对于任意的直线l 与平面α，在平面α内必有直线m ，使m 与lA ．平行B ．相交C ．垂直D ．异面5．在空间四边形ABCD 中，平面ABD ⊥平面BCD ，且DA ⊥平面ABC ，则ABC ∆的形状是A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定6．直线320x y m -+=与直线2(1)3320m x y m -+-+=的位置关系是A ．平行B ．重合C ．相交D ．不能确定7．如图，在半径为3的球面上有A 、B 、C 三点，90ABC ︒∠=，BA BC =，球心O 到平面ABC B 、C 两点的球面距离．．．．．．．（经过这两点的大圆在这两点间的劣弧的长度）是A ．3π B ．π C ．43π D ．2π8．已知点(,2)(0)a a >>到直线:30l x y -+=的距离为1，则a 的值为A B ．2 C 1 D 19．如图，正四面体ABCD 的顶点,,A B C 分别在两两垂直的三条射线,,Ox Oy Oz 上，则在下列命题中，错误的为A ．O ABC -是正三棱锥B ．直线//OB 平面ACDC ．直线AD 与OB 所成的角是45︒D ．二面角D OB A --为45︒10．一个圆柱的侧面积展开图是一个正方形，这个圆柱的全面积与侧面积的比是A ．122ππ+B ．144ππ+C ．12ππ-D ．142ππ+ 二、填空题（本大题4个小题，每小题5分，共20分）在每小题中，请将答案直接填在题后的横线上。

新人教版高中数学选修二第一单元《数列》测试题(包含答案解析)

一、选择题1．若数列{}n a 满足12a =，23a =，12n n n a a a --=（3n ≥且*N n ∈），则2018a 等于（） A ．12B ．2C ．3D ．232．我国古代著名的数学专著《九章算术》里有一段叙述：今有良马和驽马发长安至齐，良马初日行一百零三里，日增十三里；驽马初日行九十七里，日减半里；良马先至齐，复还迎驽马，九日后二马相逢.问：齐去长安多少里？（） A ．1125B ．1250C ．2250D ．25003．已知数列{}n a 的前n 项和为n S ，且11a =，1n n a S +=，若(0,2020)n a ∈，则称项n a 为“和谐项”，则数列{}n a 的所有“和谐项”的平方和为（） A ．1111433⨯- B ．1211433⨯- C ．1012433⨯+D ．1112433⨯+4．已知数列{}n b 满足12122n n b n λ-⎛⎫=-- ⎪⎝⎭，若数列{}n b 是单调递减数列，则实数λ的取值范围是（）A ．101,3B ．110,23⎛⎫- ⎪⎝⎭C ．(-1，1)D ．1,12⎛⎫-⎪⎝⎭5．数列{}n a 的通项公式为12n n a +=，其前n 项和为n T ，若不等式()2log 4(1)73n n T n n λ+-++对任意*n N ∈恒成立，则实数λ的取值范围为（）A ．3λB ．4λC ．23λ D ．34λ6．已知数列{}n a 满足：113a =，1(1)21n n n a na n ++-=+，*n N ∈，则下列说法正确的是（） A ．1n n a a +≥ B ．1n n a a +≤C ．数列{}n a 的最小项为3a 和4aD ．数列{}n a 的最大项为3a 和4a 7．已知函数()()633,7,,7.x a x x f x a x -⎧--≤=⎨>⎩令()()n a f n n *=∈N 得数列{}n a ，若数列{}n a 为递增数列，则实数a 的取值范围为（）A ．()1,3B ．()2,3C ．9,34⎛⎫ ⎪⎝⎭D ．92,4⎛⎫ ⎪⎝⎭8．等差数列{}n a 的前n 项和为n S ，已知1210,a a =为整数，且4n S S ≤，设11n n n b a a +=，则数列{}n b 的前项和n T 为（） A ．310(103)nn -B ．10(103)nn -C ．103nn-D ．10(133)nn -9．已知数列{}n a 的前n 项和为n S ，且21n n S a =-，则66(S a = ) A ．6332B ．3116C ．12364 D ．12712810．在等差数列{}n a 中，若12336a a a ++=，11121384a a a ++=，则59a a +=（） A ．30B ．35C ．40D ．4511．已知数列{}n a 为等差数列，n S 是其前n 项和，25a =，535S =.数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为n T ，若对一切n ∈+N 都有21n m T +>恒成立，则m 能取到的最小整数为（）A ．1-B ．0C ．1D ．212．定义12...nnp p p +++为n 个正数12,,......n p p p 的“均倒数”，若已知正整数数列{}n a 的前n 项的“均倒数”为121n +，又14n n a b +=，则12231920111b b b b b b +++=（） A ．1920 B ．120C ．1011 D ．111二、填空题13．在数列{}n a 中，若121,(1)2nn n a a a +=+-=，记n S 是数列{}n a 的前n 项和，则100S =__________.14．已知等差数列{}n a 的前n 项和n S 满足318S =，3180n S -=，270n S =，则n =________.15．已知数列{}n a 的前n 项和2231n S n n =-+，则n a =__________．16．设等差数列{}n a 的前n 项和为n S ，且10a >，149S S =，则满足0n S >的最大自然数n 的值为_____________.17．已知数列{}n a 中，11a =，()132,n n a a n n N *-=+≥∈，数列{}n b 满足11n n n b a a +=，*n N ∈，则()12lim n n b b b →∞++⋅⋅⋅+=________.18．等比数列{}n a 中，11a =，且2436a a a +=，则5a =________. 19．已知函数()31xf x x =+，对于数列{}n a 有()1n n a f a -=（*n N ∈且2n ≥），如果11a =，那么n a =______.20．数列{}n a 中，n S 为{}n a 的前n 项和，()()*1n n n n a a a n N+-=∈，且3aπ=，则4tan S 等于______.三、解答题21．设等差数列}{n a 的公差为0d >，n *∈N .且满足3616a a +=，4563a a ⋅=. （1）求数列}{n a 的通项公式. （2）记数列11n n n b a a +=，求}{n b 的前n 项和n T . 22．已知定义在R 上的函数()f x ，对任意实数1x ，2x 都有()()()12121f x x f x f x +=++，且()11f =.（1）若对任意正整数n ，有112n n a f ⎛⎫=+⎪⎝⎭，求{}n a 的通项公式；（2）若31n b n =+，求数列{}n n a b 前n 项和n S . 23．在数列{}n a 中，已知114a =，(),m t m t a a a m t +++=⋅∈∈N N ，1423log n nb a +=，（n ∈+N ）（1）求数列{}n a ，{}n b 的通项公式；（2）设数列{}n c 满足n n n c a b =⋅，求{}n c 的前n 项和n S ． 24．设数列{}n a 满足10a =且112n n a a +=-，n *∈N .记11n nb a =-，n *∈N .（1）求证：数列{}n b 为等差数列；（2）设32nna n c ⎛⎫= ⎪⎝⎭，求满足不等式12312311113n n c c c c c c c c ⎛⎫++++>++++ ⎪⎝⎭的正整数n 的集合.25．已知正项数列{}n a 满足2220n n a na n --=，数列(){}12n nn aa -⋅+的前n 项和为n S ．（1）求数列{}n a 的通项公式；（2）求n S ．26．已知{}n a 是各项均为正数的等比数列，且126a a +=，123a a a =.（1）求数列{}n a 的通项公式；（2）数列{}n b 通项公式为21n b n =+，求数列n n b a ⎧⎫⎨⎬⎩⎭的前n 项和n T .【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】先由题设求得数列{}n a 的前几项，然后得到数列{}n a 的周期，进而求得结果. 【详解】因为12a =，23a =，12n n n a a a --=（3n ≥且*N n ∈），所以23132a a a ==，34231232a a a ===， 453112332a a a ===， 564123132a a a ===，67523213a a a ===，7862323a a a ===，，所以数列{}n a 是周期为6的周期数列，所以20183366223a a a ⨯+===，故选：C. 【点睛】思路点睛：该题考查的是有关数列的问题，解题方法如下：（1）根据题中所给的前两项以及递推公式，逐项写出数列的前几项；（2）根据规律判断出数列的周期；（3）根据所求的数列的周期，求得20182a a =，进而求得结果.2．A解析：A 【分析】由题意可知，良马每日行的距离{}n a 以及驽马每日行的距离{}n b 均为等差数列，确定这两个数列的首项和公差，利用等差数列的求和公式可求得结果.【详解】由题意可知，良马每日行的距离成等差数列，记为{}n a ，其中1103a =，公差113d =. 驽马每日行的距离成等差数列，记为{}n b ，其中197b =，公差20.5d =-. 设长安至齐为x 里，则1291292a a a b b b x +++++++=，即9813980.521039979225022x ⨯⨯⨯⨯=⨯++⨯-=，解得1125x =. 故选：A. 【点睛】关键点点睛：解本题的关键在于得出长安至齐的距离等于良马和驽马九日所行的距离之和的 2倍，并结合题意得知两匹马所行的距离成等差数列，解题时要充分抓住题中信息进行分析，将实际问题转化为数学问题来求解.3．D解析：D 【分析】当2n ≥时，1nn a S -=，又由1n n a S +=，两式相减，得到12n n a a +=，求得22,2n n a n -=≥，得到数列{}n a 的所有“和谐项”为101,1,2,4,8,,2，结合等比数列的求和公式，即可求解. 【详解】由11a =，1n n a S +=，可得1211a S a ===，当2n ≥时，1nn a S -=，又由1n n a S +=，两式相减，可得11n n n n n a a S S a +--=-=，即12n n a a +=，即12n na a +=，则数列{}n a 从第二项起是公比为2的等比数列，即22,2n n a n -=≥，又由(0,2020)n a ∈，即222020n -<，可得13,n n N +<∈，所以“和谐项”共有12项，则数列{}n a 的所有“和谐项”为101,1,2,4,8,,2，可得数列{}n a 的所有“和谐项”的平方和为111110(11244)11416413431-+++++=+=⨯+-.故选：D. 【点睛】与数列的新定义有关的问题的求解策略：通过给出一个新的数列的定义，或约定一种新的运算，或给出几个新模型来创设新问题的情景，要求在阅读理解的基础上，依据题目提供的信息，联系所学的知识和方法，实心信息的迁移，达到灵活解题的目的；遇到新定义问题，应耐心读题，分析新定义的特点，弄清新定义的性质，按新定义的要求，“照章办事”，逐条分析、运算、验证，使得问题得以解决.4．A解析：A 【分析】由题1n n b b +>在n *∈N 恒成立，即16212nn λ⎛⎫-<+ ⎪⎝⎭，讨论n 为奇数和偶数时，再利用数列单调性即可求出. 【详解】数列{}n b 是单调递减数列，1n n b b +∴>在n *∈N 恒成立，即()122112+1222nn n n λλ-⎛⎫⎛⎫-->-- ⎪ ⎪⎝⎭⎝⎭恒成立，即16212nn λ⎛⎫-<+ ⎪⎝⎭，当n 为奇数时，则()6212nn λ>-+⋅恒成立，()212n n -+⋅单调递减，1n ∴=时，()212n n -+⋅取得最大值为6-，66λ∴>-，解得1λ>-；当n 为偶数时，则()6212nn λ<+⋅恒成立，()212n n +⋅单调递增，2n ∴=时，()212n n +⋅取得最小值为20，620λ∴<，解得103λ<，综上，1013λ-<<. 故选：A. 【点睛】关键点睛：本题考查已知数列单调性求参数，解题的关键由数列单调性得出16212nn λ⎛⎫-<+ ⎪⎝⎭恒成立，需要讨论n 为奇数和偶数时的情况，这也是容易出错的地方. 5．A解析：A 【分析】将不等式()2log 4(1)73n n T n n λ+-++对任意*n N ∈恒成立，转化为271n n n λ-++对任意*n N ∈恒成立，由2min71n n n λ⎛⎫-+ ⎪+⎝⎭求解.【详解】依题意得，()24122412n n nT +-==--，∴不等式()2log 4(1)73n n T n n λ+-++可化为22log 2(1)73n n n n λ+-++，即27(1)n n n λ-++.又*n N ∈，∴271n n n λ-++对任意*n N ∈恒成立.只需满足2min71n n n λ⎛⎫-+ ⎪+⎝⎭即可.设1n t +=，则*t N ∈，2t ，∴27931n n t n tλ-+=+-+.∵993233t t t t+-⋅-=，当且仅当3t =，即2n =时等号成立， ∴2min731n n n ⎛⎫-+= ⎪+⎝⎭. ∴3λ，故选：A. 【点睛】方法点睛：恒（能）成立问题的解法：若()f x 在区间D 上有最值，则()()min ,00x D f x f x ∀∈>⇔>；()()max ,00x D f x f x ∀∈<⇔<；若能分离常数，即将问题转化为：()a f x >（或()a f x <），则()()max a f x a f x >⇔>；()()min a f x a f x <⇔<. 6．C解析：C 【分析】令n n b na =，由已知得121n n b b n +-=+运用累加法得2+12n b n =，从而可得12+n a n n=，作差得()()()+13+4+1n n a n n a n n -=-，从而可得12345>>n a a a a a a =<<<，由此可得选项. 【详解】令n n b na =，则121n n b b n +-=+，又113a =，所以113b =，213b b -=，325b b -=，，121n n b b n --=-，所以累加得()()213+2113++122nn n b n --==，所以2+1212+n nb n a n n n n===，所以()()()()+13+41212+1+++1+1n n n n a a n n n n n n -⎛⎫-=-= ⎪⎝⎭，所以当3n <时，+1n n a a <，当3n =时，+1n n a a =，即34a a =，当>3n 时，+1>n n a a ，即12345>>n a a a a a a =<<<，所以数列{}n a 的最小项为3a 和4a ，故选：C. 【点睛】本题考查构造新数列，运用累加法求数列的通项，以及运用作差法判断差的正负得出数列的增减性，属于中档题.7．B解析：B 【分析】由()()633,7,,7.x a x x f x ax -⎧--≤=⎨>⎩，()()n a f n n N *=∈得数列{}n a ，根据数列{}n a 为递增数列，联立方程组，即可求得答案. 【详解】()()633,7,,7.x a x x f x a x -⎧--≤=⎨>⎩ 令()()n a f n n N *=∈得数列{}n a∴()633,7,7n n a n n a a n -⎧--≤=⎨>⎩()n N *∈且数列{}na 为递增数列，得()230,1,733,a a a a ⎧->⎪>⎨⎪--<⎩解得23a <<. 即：()2,3a ∈ 故选：B. 【点睛】本题主要考查了根据递增数列求参数范围问题，解题关键是掌握递增数列的定义，考查了分析能力和计算能力，属于中档题.8．B解析：B 【分析】根据已知条件求得{}n a 的通项公式，利用裂项求和法求得n T .依题意等差数列{}n a 的前n 项和为n S ，已知1210,a a =为整数，且4n S S ≤，所以4151030040a a d a a d ≥+≥⎧⎧⇒⎨⎨<+<⎩⎩，即10301040d d +≥⎧⎨+<⎩，解得10532d -≤<-，由于2a 为整数，1a 为整数，所以d 为整数，所以3d =-.所以()11313n a a n d n =+-=-+. 所以()13113310n a n n +=-++=-+，()()1111113133103310313n n n b a a n n n n +⎛⎫===⨯- ⎪-+-+-+-+⎝⎭，所以1111111371047310313n T n n ⎡⎤⎛⎫⎛⎫⎛⎫=-+-++- ⎪ ⎪ ⎪⎢⎥-+-+⎝⎭⎝⎭⎝⎭⎣⎦()()()10310111133101031010310103n n n n n --+⎡⎤=-=⨯=⎢⎥-+--⎣⎦. 故选：B 【点睛】本小题主要考查裂项求和法，属于中档题.9．A解析：A 【分析】利用数列递推关系：1n =时，1121a a =-，解得1a ；2n 时，1n n n a S S -=-．再利用等比数列的通项公式与求和公式即可得出．【详解】21n n S a =-，1n ∴=时，1121a a =-，解得11a =；2n 时，1121(21)n n n n n a S S a a --=-=---，化为：12n n a a -=．∴数列{}n a 是等比数列，公比为2．56232a ∴==，66216321S -==-．则666332S a =．故选：A ．【点睛】本题考查数列递推关系、等比数列的通项公式与求和公式，考查推理能力与计算能力，属于中档题．10．C【分析】利用等差数列性质，若++m n p q ＝，则++m n p q a a a a ＝及等差中项公式可求. 【详解】因为 12336a a a ++=，由等差中项公式，得2336a =，同理11121384a a a ++=，得12384a =，2123+3=81036+42a a ∴=．212+=40a a ∴ 21529+=40a a a a ∴+=故选：C ．【点睛】本题考查等差数列性质与等差中项公式.（1）如果{}n a 为等差数列，若++m n p q ＝，则++m n p q a a a a ＝ ()*m n p q N ∈，，，．（2）{}n a 为等差数列，则有11n n n a a a ＝2-++.11．B解析：B 【分析】根据25a =，535S =求出数列的通项公式，再利用裂项相消法求出数列的和，然后由21n m T +>恒成立求解.【详解】因为数列{}n a 为等差数列，n S 是其前n 项和，25a =，535S =. 设首项为1a ，公差为d ，所以115545352a d a d +=⎧⎪⎨⨯+=⎪⎩，解得132a d =⎧⎨=⎩，故32(1)21n a n n =+-=+，所以111111()·(21)(23)22123n n a a n n n n +==-++++，所以11111111111()()23557212323236n T n n n =-+-+⋯+-=-<+++. 因为对于一切n ∈+N 都有21n m T +>恒成立，所以1216+m ，解得512≥-m ，故m 的最小整数为0.【点睛】本题主要考查数列的通项公式，裂项相消法求数列的和，还考查了运算和求解的能力，属于中档题.12．A解析：A 【分析】首先根据新定义求得()21n S n n =+，再求数列{}n a 的通项公式，以及求得n b n =，最后利用裂项相消法求和. 【详解】由已知可得数列{}n a 的前n 项的“均倒数”为1211..21n n n a a a S n ==++++，可得()21n S n n =+，则2n ≥时，()()212111231n S n n n n -=-+-=-+⎡⎤⎣⎦，∴ 141n n n a S S n -=-=-，当1n =时，113a S ==，满足41n a n =-，41n a n ∴=-，又14n n a b +=，故n b n =， 12231920111111 (12231920)b b b b b b ∴+++=+++⨯⨯⨯ 111111191..122319202020⎛⎫⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选：A 【点睛】本题考查新定义数列的理解，考查裂项相消法求和，以及已知n S 求n a ，属于基础题型，本题的关键是理解新定义.，并能抽象为121n n S n =+. 二、填空题13．【分析】当为奇数时可得数列的奇数项为公差为2的等差数列当为偶数时可得偶数项的特征将所求问题转化为奇数项和偶数项求和即可【详解】∵∴当为奇数时即数列的奇数项为公差为2的等差数列当为偶数时∴∴故答案为：解析：2550【分析】当n 为奇数时，可得数列{}n a 的奇数项为公差为2的等差数列，当n 为偶数时，可得偶数项的特征，将所求问题转化为奇数项和偶数项求和即可.∵121,(1)2nn n a a a +=+-=，∴当n 为奇数时，22n n a a +-=，即数列{}n a 的奇数项为公差为2的等差数列，当n 为偶数时，22n n a a ++=， ∴135995049501225002a a a a ⨯++++=⨯+⨯=， ()()()()24681012485022550a a a a a a a a ++++++++=⨯=，∴1002500502550S =+=，故答案为：2550. 【点睛】关键点点睛：（1）得到数列{}n a 的奇数项为公差是2的等差数列；（2）得到数列{}n a 的偶数项满足22n n a a ++=.14．15【分析】根据等差数列的前项和与等差数列的性质求解【详解】因为所以又所以故解得故答案为：15【点睛】本题考查等差数列的前项和等差数列的性质利用等差数列的性质求解可以减少计算量解析：15 【分析】根据等差数列的前n 项和与等差数列的性质求解，【详解】因为32318S a ==，所以26a =，又2311390n n n n n n a a S S a a ----=++-==，所以130n a -=.故()()12127022n n n n a a n a a S -++===，解得15n =. 故答案为：15．【点睛】本题考查等差数列的前n 项和，等差数列的性质，利用等差数列的性质求解可以减少计算量．15．【解析】分析：当时求得；当时类比写出由求出再将代入检验即可求出答案详解：当时当时由得两式相减将代入上式通项公式为故答案为点睛：本题主要考查已知数列的前项和求数列的通项公式的方法其求解过程分为三步：（解析：0,145,2n n a n n =⎧=⎨-≥⎩【解析】分析：当1n =时，求得11a S =；当2n ≥时，类比写出1n S -，由1n n n a S S -=-求出n a ，再将1n =代入n a 检验，即可求出答案.详解：当1n =时，110a S ==当2n ≥时，由2231n S n n =-+，得212(1)3(1)1n S n n -=---+，两式相减，145n n n a S S n -=-=-，将1n =代入上式，110a =-≠， ∴通项公式为0,145,2n n a n n =⎧=⎨-≥⎩故答案为0,145,2n n a n n =⎧=⎨-≥⎩.点睛：本题主要考查已知数列{}n a 的前n 项和n S ，求数列的通项公式的方法.其求解过程分为三步：（1）当1n =时， 11a S =求出1a ；（2）当2n ≥时，用1n -替换n S 中的n 得到一个新的关系，利用1n n S S -- (2)n ≥便可求出当2n ≥时n a 的表达式；（3）对1n =时的结果进行检验，看是否符合2n ≥时n a 的表达式，如果符合，则可以把数列的通项公式合写；如果不符合，则应该分1n =与2n ≥两段来写．16．22【分析】由等差数列的前项和的公式求解解出､的关系式再求出的临界条件最后得解【详解】解：等差数列的前项和为所以所以其中所以当时解得所以的最大自然数的值为22故答案为：22【点睛】本题应用公式等差数解析：22 【分析】由等差数列{}n a 的前n 项和的公式求解149S S =，解出1a ､d 的关系式，再求出0n S =的临界条件，最后得解. 【详解】解：等差数列{}n a 的前n 项和为n S ，149S S =，所以()114579a a a +=，1117(13)9(4)a a d a d ++=+，111a d =-，所以()12n a n d =-，其中10a >，所以0d <，当0n a =时，解得12n =，()2312312232302S a a a =+==， 1222222()1102a a S d +==->，所以0n S >的最大自然数n 的值为22.故答案为：22．【点睛】本题应用公式()12n n n a a S +=，等差数列的性质：若m n p q +=+，则m n p q a a a a +=+.对数列的公式要灵活应用是快速解题的关键，解出1a ､d 的关系式，再求出0n S =的临界条件，判断满足0n S >的最大自然数n 的值.17．【分析】求出数列的通项公式利用裂项求和法求出利用极限的运算法则可得出所求极限值【详解】且则数列是以为首项以为公差的等差数列所以因此故答案为：【点睛】本题考查数列前项和的极限值的求法是中档题解题时要认解析：13【分析】求出数列{}n a 的通项公式，利用裂项求和法求出12n b b b ++⋅⋅⋅+，利用极限的运算法则可得出所求极限值. 【详解】()132,n n a a n n N *-=+≥∈且11a =，则数列{}n a 是以1为首项，以3为公差的等差数列，所以，()13132n a n n =+-=-，()()111111323133231n n n b a a n n n n +⎛⎫∴===- ⎪-+-+⎝⎭， 1211111111134473231393n b b b n n n ⎛⎫∴++⋅⋅⋅+=-+-++-=- ⎪-++⎝⎭，因此，()12111lim lim 3933n n n b b b n →∞→∞⎛⎫++⋅⋅⋅+=-=⎪+⎝⎭. 故答案为：13. 【点睛】本题考查数列前n 项和的极限值的求法，是中档题，解题时要认真审题，注意等差数列的性质的合理运用．18．4【分析】在等比数列中将已知转化为首项和公比求得再将其带入通项公式中求得答案【详解】因为所以在等比数列中所以或-3（舍）故故答案为：4【点睛】本题考查等比数列中知三求二由已知转化为首项和公比进而表示解析：4 【分析】在等比数列中，将已知转化为首项和公比求得2q ，再将其带入通项公式中，求得答案. 【详解】因为11a =，所以在等比数列中32422431116a a a a q a q a q q q +=⋅+=+=所以22q =或-3（舍），故425124a a q === 故答案为：4 【点睛】本题考查等比数列中知三求二，由已知转化为首项和公比，进而表示所求问题，属于简单题.19．【分析】由已知条件得出变形为可知数列为等差数列确定该数列的首项和公差求出进而可得出【详解】且（且）在等式两边取倒数得且所以数列是以为首项以为公差的等差数列因此故答案为：【点睛】本题考查利用构造法求数解析：132n - 【分析】由已知条件得出()11231n n n a a n a --=≥+，变形为1113n n a a --=，可知数列1n a ⎧⎫⎨⎬⎩⎭为等差数列，确定该数列的首项和公差，求出1na ，进而可得出n a .【详解】()31x f x x =+，且()11131n n n n a a f a a ---==+（*n N ∈且2n ≥），在等式1131n n n a a a --=+两边取倒数得11113113n n n n a a a a ---+==+，1113n n a a -∴-=且111a ，所以，数列1n a ⎧⎫⎨⎬⎩⎭是以1为首项，以3为公差的等差数列，()113132nn n a ∴=+-=-，因此，132n a n =-. 故答案为：132n -. 【点睛】本题考查利用构造法求数列的通项公式，涉及等差数列定义的应用，考查计算能力，属于中等题.20．【分析】将变形为利用累乘法求出数列的通项公式求出的值再利用诱导公式可求出的值【详解】则所以因此故答案为：【点睛】本题考查利用累乘法求数列通项同时也考查了数列求和以及正切值的计算考查计算能力属于中等题【分析】将()1n n n n a a a +-=变形为11n n a n a n++=，利用累乘法求出数列{}n a 的通项公式，求出4S的值，再利用诱导公式可求出4tan S 的值. 【详解】()()*1n n n n a a a n N +-=∈，()11n n na n a +∴=+，11n n a n a n++∴=， 3211112123121n n n a a a na a a na a a a n -∴=⋅⋅⋅⋅=⨯⨯⨯⨯=-，313a a π==，13a π∴=，则3n a nπ=，所以，424103333S πππππ=+++=，因此，410tan tan tan 3tan 333S ππππ⎛⎫==+== ⎪⎝⎭，【点睛】本题考查利用累乘法求数列通项，同时也考查了数列求和以及正切值的计算，考查计算能力，属于中等题.三、解答题21．（1）21n a n =-，n *∈N ；（2）21nn +. 【分析】（1）根据等差数列性质,结合方程解的定义，可知4a ,5a 是方程216630x x -+=的两根.根据公差0d >，即可求得4a ,5a .进而求得公差d .结合等差数列通项公式求法即可得解. （2）由（1）中所得数列{}n a 的通项公式，代入可得数列{}n b 的通项公式，利用裂项求和法即可得数列{}n b 的前n 项和. 【详解】（1）由364516a a a a +=+=，4563a a ⋅=，则4a ，5a 是方程216630x x -+=的两根，由0d >，则47a =，59a =，则542d a a =-=，则)(4421n a a n d n =+-⋅=-，n *∈N .（2）将21n a n =-代入可得)()(1111221212121n b n n n n ⎛⎫==-⎪-+-+⎭⎝，则1211111111112135721212121n n T b b b n n n ⎛⎛⎫⎫=++⋅⋅⋅+=-+-+⋅⋅⋅+-=-⎪⎪ -++⎭⎭⎝⎝ 11122121nn n ⎛⎫=-=⎪++⎭⎝. 【点睛】结论点睛：数列求和的常用方法：（1）公式法：即直接用等差、等比数列的求和公式求和.（2）错位相减法：若{}n a 是等差数列，{}n b 是等比数列，求1122n n a b a b a b ++⋅⋅⋅. （3）裂项相消法：把数列的通项拆成两项之差，相消剩下首尾的若干项.常见的裂顶有()11111n n n n =-++，()1111222n n n n ⎛⎫=- ⎪++⎝⎭，()()1111212122121n n n n ⎛⎫=- ⎪-+-+⎝⎭等.（4）分组求和法：把数列的每一项分成若干项，使其转化为等差或等比数列，再求和. （5）倒序相加法. 22．（1）()*112n n a n -=∈N ；（2）137142n n n S -+=-. 【分析】（1）令1212x x ==，求出102f ⎛⎫= ⎪⎝⎭，从而可得11a =，再有112n n a f ⎛⎫=+ ⎪⎝⎭，求得12n n a a +=，利用等比数列的通项公式即可求解.（2）由1312n n n n a b -+=，利用错位相减法即可求解. 【详解】解：（1）令1212x x ==，则()111122f f ⎛⎫==+ ⎪⎝⎭，∴102f ⎛⎫= ⎪⎝⎭，11112a f ⎛⎫=+= ⎪⎝⎭. ∵1111111111112221222222n n n n n n n a f f f f a +++++⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+=++=+=+=⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦， ∴112n n a a +=，∴{}n a 为以1为首项，12为公比的等比数列，∴()*112n n a n -=∈N . （2）∵1312n n n n a b -+=， ∴21471031S 1222n n n -+=++++①，由①12⨯，得23147103122222n nn S +=++++②，由①-②，得21133331422222n n n n S -+=++++- 1131374317222n n n n n -++⎛⎫=+--=- ⎪⎝⎭，∴137142n n n S -+=-.【点睛】关键点点睛：本题考查了函数与数列的综合，解题的关键是根据关系式求出()*112n n a n -=∈N ，考查了计算能力. 23．（1）14nn a ⎛⎫= ⎪⎝⎭，32n b n =-；（2）232334n n n s +=-⨯.【分析】（1）令,m n =1t =，可得数列{}n a 是等比数列，即可求出通项公式，进而求出n b ；（2）利用错位相减法可求出. 【详解】（1）令,m n =1t =，则11n n a a a +=⋅，114n n a a +∴=，114a =，∴数列{}n a 是首项为14，公比为14的等比数列， ∴1111444n nn a -⎛⎫⎛⎫=⨯= ⎪⎪⎝⎭⎝⎭， ∴1413log 2324nn b n ⎛⎫=-=- ⎪⎝⎭；（2）由（Ⅰ）知，14nn a ⎛⎫= ⎪⎝⎭，()*32nb n n N=-∈，则()1324nn c n ⎛⎫=⋅- ⎪⎝⎭， ()2311111+4+7++324444nn S n ⎛⎫⎛⎫⎛⎫=⨯⨯⨯-⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，则()234+1111111+4+7++3244444n n S n ⎛⎫⎛⎫⎛⎫⎛⎫=⨯⨯⨯-⨯ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，两式相减得()234+13111111+3+3+3++3324444444nn n S n ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=⨯⨯⨯⨯--⨯ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭()1+1+131116411132+321442414n n n n n -⎡⎤⎛⎫⨯-⎢⎥ ⎪⎝⎭+⎢⎥⎛⎫⎣⎦=--⨯=- ⎪⎝⎭-， 232334n nn S +∴=-⨯．【点睛】方法点睛：数列求和的常用方法：（1）对于等差等比数列，利用公式法可直接求解；（2）对于{}n n a b 结构，其中{}n a 是等差数列，{}n b 是等比数列，用错位相减法求和；（3）对于{}+n n a b 结构，利用分组求和法；（4）对于11n n a a +⎧⎫⎨⎬⎩⎭结构，其中{}n a 是等差数列，公差为d ，则111111n n n n a a d a a ++⎛⎫=- ⎪⎝⎭，利用裂项相消法求和. 24．（1）证明见解析；（2）{}1,2,3. 【分析】（1）利用112n na a +=-证明出1n n b b +-是常数，进而可证明出数列{}n b 为等差数列；（2）求得132n n c -⎛⎫= ⎪⎝⎭，利用等比数列的求和公式结合已知条件可得出33291122nn⎛⎫⎛⎫⋅+⋅< ⎪ ⎪⎝⎭⎝⎭，设3322nt ⎛⎫=≥ ⎪⎝⎭，可得出不等式221190t t -+<，解出t 的取值范围，由此可得出符合条件的正整数n 的值.【详解】（1）数列{}n a 满足10a =且112n n a a +=-，则211122a a ==-，321223a a ==-，依次类推可知，对任意的n *∈N ，2n a ≠，()1121111111112111111122n n n n n n n n nn na b b a a a a a a a a ++--∴-=-=-=-==----------，所以，数列{}n b 是等差数列，且首项为11111b a ==-，公差为1， ()11111n n b n n a ∴==+-⨯=-，解得1n n a n-=；（2）132n n c -⎛⎫= ⎪⎝⎭，则1123n n c -⎛⎫= ⎪⎝⎭，所以，11332232nn n n c c +-⎛⎫ ⎪⎝⎭==⎛⎫ ⎪⎝⎭，则数列{}n c 为等比数列，同理可知，数列1n c ⎧⎫⎨⎬⎩⎭也为等比数列，则1233132223212nnn c c c c ⎛⎫- ⎪⎛⎫⎝⎭++++==⋅- ⎪⎝⎭-，12321111123332313nnn c c c c ⎛⎫- ⎪⎛⎫⎝⎭++++==-⋅ ⎪⎝⎭-，由12312311113n n c c c c c c c c ⎛⎫++++>++++ ⎪⎝⎭可得23912232n n⎡⎤⎛⎫⎛⎫⋅->⋅-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦，所以，32291123nn⎛⎫⎛⎫⋅+⋅< ⎪ ⎪⎝⎭⎝⎭，设32nt ⎛⎫= ⎪⎝⎭，n N *∈，则32t ≥，可得9211t t +<，整理可得221190t t -+<，解得912t <<，即39122n⎛⎫<< ⎪⎝⎭，n N *∈，所以，正整数n 的集合为{}1,2,3.【点睛】方法点睛：证明等比数列常用以下几种方法：（1）定义法：证明1n n a a +-为常数；（2）等差中项法：对任意的n *∈N ，证明出122n n n a a a ++=+.25．（1）2n a n =；（2）()()123?216n n S n n n +=-+++. 【分析】（1）由已知得()()20n n a n a n -+=且0n a >，即可得通项公式.（2）由（1）有()()122122nnn n a a n n -⋅+=-⋅+，利用分组、错位相减法求n S .【详解】（1）由2220n n a na n --=得()()20n n a n a n -+=，又{}n a 为正项数列，∴2n a n =．（2）由（1）知()()122122nnn n a a n n -⋅+=-⋅+，令n T 为数列(){}212nn -⋅的前n 项和，则()123123252212n nTn =⨯+⨯+⨯+⋅⋅⋅+-⨯，∴()23412123252212n n T n +=⨯+⨯+⨯+⋅⋅⋅+-⨯，两式相减，得()123112222222212nn n T n +-=⨯+⨯+⨯+⋅⋅⋅+⨯--⨯，所以()()2112212221212n n nT n ++⨯⨯--=+--⨯-，所以()12326n n T n +=-⨯+，令n B 为数列{}2n 的前n 项和，则()()1212n n n B n n +=⨯=+，所以()()123216n n n n S T B n n n +=+=-⨯+++．【点睛】关键点点睛：（1）由已知方程，将n a 作为未知数求正解，即为数列通项公式.（2）将所得数列分为(){}212n n -⋅、{}2n 两组分别求和，应用错位相减、等差数列前n 项和公式求n S .26．（1）2n n a =；（2）2552n n n T +=-. 【分析】（1）设{}n a 的公比为q ，利用基本量运算求出公比，可得数列{}n a 的通项公式；（2）利用错位相减法计算出数列n n b a ⎧⎫⎨⎬⎩⎭的前n 项和n T ．【详解】（1）设{}n a 的公比为q ，由题意知：()116a q +=，2211a q a q =. 又0n a >，解得12a =，2q，所以2n n a =. （2）21n b n =+.令n n n b c a =，则212n n n c +=，因此12231357212122222n n n n n n T c c c --+=+++=+++++，又234113572121222222n n n n n T +-+=+++++，两式相减得12111113111213121525122222222222n n n n n n n n n T --++++++⎛⎫⎛⎫=++++-=+--=- ⎪ ⎪⎝⎭⎝⎭ 所以2552n nn T +=-. 【点睛】方法点睛：本题考查等比数列的通项公式，考查数列的求和，数列求和的方法总结如下：公式法，利用等差数列和等比数列的求和公式进行计算即可；裂项相消法，通过把数列的通项公式拆成两项之差，在求和时中间的一些项可以相互抵消，从而求出数列的和；错位相减法，当数列的通项公式由一个等差数列与一个等比数列的乘积构成时使用此方法；倒序相加法，如果一个数列满足首末两项等距离的两项之和相等，可以使用此方法求和．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

a19 值。
21．（本小题满分 12 分）已知 a 、 b 、 c 分别是 ABC 的三个内角 A 、 B 、 C 所对的边
（1）若 ABC 面积 S ABC
3 , c 2, A 60 , 求 a 、 b 的值； 2
（2）若 a c cos B ，且 b c sin A ，试判断 ABC 的形状．
22．（本小题满分 12 分）在等差数列 an 中， a1 1，前 n 项和 Sn 满足条件
a1 a1q a1q 2 27 a1q a1q 3 30
16．18 324
解得：
a1
1
a1
或
1
q3
q3
（ II） Sn a1 (1 q n ) 1q
a1
当
1 时， S6
q3
1 (1 36 ) 13
1 36 2
364 ．
a1
当
q
1 时， S6
3
( 1) [1 ( 3) 6 ] 13
36 1 182 4
10 9
其和 S 10 25
( 6) 20
2
21．解：（1）
S ABC
1 bc sin A
3，
1 b 2 sin 60
2
2
2
3 ，得 b 1
2
由余弦定理得： a2 b2 c2 2bc cos A 12 22 2 1 2 cos60 3 ，
所以 a 3
（ 2 ）由余弦定理得：
a c a 2 c2 b2 2 ac
2，则 2a1 a2 的值为 2a3 a4
1
A．
4
（）
1
B．
2
1
C．
8
D． 1
2 ．下列四个数中，哪一个是数列 { n(n 1) } 中的一项
A．380
（） B． 39
C． 35
D． 23
3 ．已知数列 an 满足 a1 2 ， an 1 an 1 0 (n N ) ，则此数列的通项 an 等于
19．（本小题满分 12 分）海中有 A岛，已知 A 岛四周 8 海里内有暗礁，现一货轮由西向东航行，在 B 处望见 A 岛在北偏东 75 ，再航行 20 2 海里到 C 后，见 A 岛在北偏东 30 ，如货轮
不改变航向继续航行，有无触礁的危险？
20．（本小题满分 12 分）已知 an 是等差数列，其中 a1 25, a4 16 （ 1）求 an 的通项 ; （ 2）数列 an 从哪一项开始小于 0;（ 3）求 a1 a3 a5
a 2 b 2 c 2 ，所以
C 90
在 Rt ABC 中， sin A
a ，所以 b
a c
a 所以
ABC 是等腰直角三角形；
c
c
22．解：（ 1）设等差数列 an 的公差为 d ,由 S2n Sn
4n 2 得： a1 a2
n1
a1
3 ，所以 a2 2 ，即
d a2 a1 1 ，所以 an n 。
（2）由 bn an pan ，得 bn npn 。所以 Tn p 2p2 3 p3
（ 2） ∵ cosA＝ 2bc ＝
2bc
＝ 2bc ＝ 2bc
∴
6－
2bc ＝
1，∴
bc＝ 2．
2bc 2
19．解：如图所示，
又∵ b＋ c＝3，∴ b＝ 1， c＝ 2 或 b＝ 2， c＝ 1．
可求得 BAC 45 , ABC 15 , ACD 60
北
北
BC sin15
由正弦定理得： AC sin 45
B．（ 2 ， 3 ）
C．（ 2 ， 2）
D ．（ 0， 2）
第 II 卷（非选择题共 90 分）
二、填空题：（共 4 小题，每小题 5 分，共 20 分）请将答案直接添在题中的横线上．
13．在 ABC 中， AC= 2 2 ， A=45°， B=30 °，则 BC=___________ ． 14．在△ ABC 中，已知 (a b c)( b c a) 3bc ，则角 A 的大小为
2
a4 a5
51
A．
2
（）
51
B．
2
15
C．
2
D．
5 1或 2
51 2
6 、在 ABC 中，已知 A 30 ， C
（）
A． 2
B． 3 1
45 ， a 2 ，则
C． 2 2
ABC 的面积等于 1
D． 2 ( 3 1)
7 、在 100 和 500 之间能被 9 整除的所有数之和为
40sin15
A
在
直
角
三
角
形
A C中
AD AC sin60 15 2 5 6 8
从而可知船不改变航向将没有触礁的危险。
B
20．解：（ 1） a4 a1 3d d 3
an 2 8 3n
CD
（2）
1 28 3n 0 n 9
3
∴数列 an 从第 10 项开始小于 0
（3） a1 a3 a5
a19 是首项为 25，公差为 6 的等差数列，共有 10 项
15．已知数列 an 的前 n 项和 Sn 3 2n ，则 an =
16．已知数列的通项公式 an 2n 37 ,则 Sn 取最小值时 n =
,此时 Sn =
．
三、解答题：（共 6 小题，共 70 分）解答应写出文字说明，证明过程或演算步骤。
17．（本小题满分 10 分）在等比数列 an 中， a1 a2 a3 27 ， a2 a4 30
65 千克，已知最轻的一只羊重 7
千克，除去一只 10 千克的羊外，其余各只羊的千克数恰能组成一等差数列，则这群羊共
有（
）
A．6 只
B．5 只
C． 8 只
D．7 只
12．在锐角三角形中，（）
a、b、 c 分别是内角
A 、B、 C 的对边，设
B=2A ，则 b 的取值范围是 a
A ．（ -2， 2）
18．解：（ 1）由题设得
2[1－ cos（B＋ C）
]－（
2
2cos A－
1）＝
72，
∵ cos（ B＋ C）＝－ cosA，∴ 2（ 1＋ cosA）－ 2cos2A＋ 1＝72，
整理得（ 2cosA－ 1） 2＝ 0，∴ cosA＝ 1，∴ A＝ 60°． 2
b2＋ c2－ a2 (b＋ c)2 － 2bc－ a2 9－ 2bc－ 3 6－2bc
S2 n
4n 2 ,n 1,2,
．
Sn n 1
（ 1）求数列 an 的通项公式；（ 2）记 bn an pan ( p 0) ，求数列 bn 的前 n 项和 Tn ．
参考答案
一、 AADBB
BBADB AB
二、 13． 4 14． 60
15． an
三、
5,( n 1)
。
2n 1, (n 2)
17．解：（ I）在等比数列 an 中，由已知可得：
（）
8 A． d ＞
3
B． d ＞ 3
C． 8 ≤ d ＜ 3 3
D． 8 ＜ d ≤3 3
10 ．在等差数列 an 中，已知 a1 + a4 + a7 =39 ， a2 + a5 + a8 =33 ，则 a3 + a6 + a9 =
（）
A ． 30
B． 27
C． 24
D ．21
11．一群羊中，每只羊的重量数均为整千克数，其总重量为
试求：（ I） a1 和公比 q ；
（II ）前 6 项的和 S6 ．
18．（本小题满分 12 分）在 △ ABC 中， a， b， c 分别为角 A， B， C 所对的边，且
2B 4sin
＋ 2
C －
cos2A＝
7 2
．
（ 1）求角 A 的度数；
（ 2）若 a＝ 3， b＋ c＝ 3，求 b 和 c 的值．
( n 1) pn 1 npn ，
当 p 1 时， Tn
n(n 1) 2 ；当 p 1 时， pTn
p2 2 p3 3p4
( n3
pn 1 pn npn 1
p(1 pn ) npn 1 1p
即 Tn
n( n 1)
, p1
2
p(1 pn ) (1 p)2
npn 1 , p 1p
．
1
（）
A．12699
B．13266
C． 13833
D． 14400
8 ．在 -1 和 8 之间插入两个数 a,b ，使这四个数成等差数列，则
（）
A ． a=2，b=5
B． a=-2， b=5
C． a=2， b=-5
D ． a=-2， b=-5
9 ．首项为 24 的等差数列，从第 10 项开始为正数，则公差 d 的取值范围是
2011—2012 学年度上学期单元测试高二数学试题（ 1）【新人教】
命题范围：必修五第一章、第二章
第Ⅰ卷（选择题共 60 分）
一、选择题：（共 12 小题，每小题 5 分，共 60 分）在下列各小题的四个选项中，只有一项是符合题目要求的．请将选项前的字母填入下表相应的空格内．
1．设 a1 ,a2 , a3 , a4 成等比数列，其公比为
A． n 2 1
（）
B． n 1
C． 1 n
D． 3 n