数值分析2-1
西安电子科技大学数值分析
题目要求1. 编制条件如图所示，用差分法求区域内的电压值。
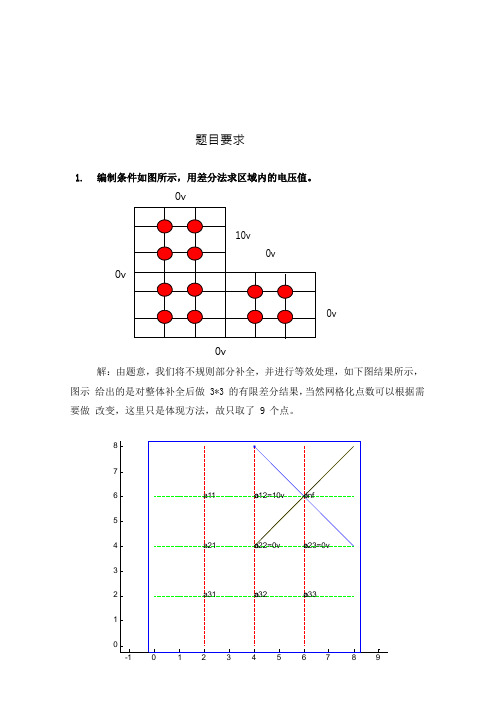
0v10v0v0v0v0v解：由题意，我们将不规则部分补全，并进行等效处理，如下图结果所示，图示给出的是对整体补全后做3*3 的有限差分结果，当然网格化点数可以根据需要做改变，这里只是体现方法，故只取了 9 个点。
876 a11o a12=10v o-inf54 a21o a22=0v o a23=0v32 a31o a32o a331-1 0 1 2 3 4 5 6 7 8 9根据拉普拉斯 5 点差分原理，可知得到关于电压变量 a(i, j 1, 2, 3) 的i , j方程如下：4a 1,1 a 2,110;a 1,1 4a 2,1 a 3,1 0; a 2,1 4a 3,1 a 3,2 0; a 3,1 4a 3,2 a 3,3 0; a 3,2 4a 3,30.4 1 0 0 0 10 1 4 1 00 0 写成矩阵的形式： Ax b ; 其中， A 0 1 4 10 ， b 0 。
0 0 1 41 0编写程序可以求得0 01 4a , a , a , a , a , 2.6790.7180.1920.0513 0.0132. 在区域一边有个源，边界为 PML 边界，用 FDTD 法求所研究区域的场分布。
建模说明：二维 TE 波在空间传播，采用 PML 边界吸收，点辐射源验证。
FDTD 基本差分方程Yee 采用矩形网格进行空间离散，将每个节点进行编号，节点的编号和其空 间坐标位置按照下面的方式对应起来()(),,,,i j k i x j y k z =∆∆∆ (2-1) 而该点的任意函数()x,y,z,F t 在时刻n t ∆的值可以表示为：()(),,,,,n F i j k F i x j y k z n t =∆∆∆∆ (2-2)式中x ∆、y ∆、z ∆分别为沿,,x y z 方向上离散的空间步长，t ∆是时间步长。
数值分析实验报告--实验2--插值法
1 / 21数值分析实验二：插值法1 多项式插值的震荡现象1.1 问题描述考虑一个固定的区间上用插值逼近一个函数。
显然拉格朗日插值中使用的节点越多，插值多项式的次数就越高。
我们自然关心插值多项式的次数增加时， 是否也更加靠近被逼近的函数。
龙格（Runge ）给出一个例子是极著名并富有启发性的。
设区间[-1,1]上函数21()125f x x=+ (1)考虑区间[-1,1]的一个等距划分，分点为n i nix i ,,2,1,0,21 =+-= 则拉格朗日插值多项式为201()()125nn ii iL x l x x ==+∑(2)其中的(),0,1,2,,i l x i n =是n 次拉格朗日插值基函数。
实验要求：(1) 选择不断增大的分点数目n=2, 3 …. ，画出原函数f(x)及插值多项式函数()n L x 在[-1，1]上的图像，比较并分析实验结果。
(2) 选择其他的函数，例如定义在区间[-5，5]上的函数x x g xxx h arctan )(,1)(4=+=重复上述的实验看其结果如何。
(3) 区间[a,b]上切比雪夫点的定义为 (21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+ ⎪+⎝⎭(3)以121,,n x x x +为插值节点构造上述各函数的拉格朗日插值多项式，比较其结果,试分析2 / 21原因。
1.2 算法设计使用Matlab 函数进行实验, 在理解了插值法的基础上，根据拉格朗日插值多项式编写Matlab 脚本，其中把拉格朗日插值部分单独编写为f_lagrange.m 函数，方便调用。
1.3 实验结果1.3.1 f(x)在[-1,1]上的拉格朗日插值函数依次取n=2、3、4、5、6、7、10、15、20，画出原函数和拉格朗日插值函数的图像，如图1所示。
Matlab 脚本文件为Experiment2_1_1fx.m 。
可以看出，当n 较小时，拉格朗日多项式插值的函数图像随着次数n 的增加而更加接近于f(x)，即插值效果越来越好。
数值计算方法第2章2-1节
（2）计算
f
(
a
2
b)
。
（3）若
f
(
a
2
b
)
0
，计算停止；若
f
(
a
2
b
)
f
(a)
0
，用
若
f
(
a
2
b)
f
(b)
0
，以
a
2
b
代替
a
。
a
2
b
代替
b
；
（4）反复执行第二步与第三步，直到区间长缩小到允许误差范围
之内，此时区间中点即可作为所求的近似解。
18
证明方程 x3 3x2 6x 1 0 在区间（0，1）内有唯一的实根，并
在[－1,－0.25]，[0.5，1.25]，[1.25，2]各区间内至少有一个实根。
10
2.1.3 区间二分法
定理 函数f(x)在[a,b]上单调连续，且f(a)f(b)<0， 则方程f(x)=0在区间[a,b]上有且仅有一个实根x*。
二分法的基本思想 将有根的区间二分为两个小区间，然后判断根在那 个小区间，舍去无根的小区间，而把有根的小区间 再一分为二，再判断根属于哪个更小的区间，如此 反复 ，直到求出满足精度要求的近似根。
5
有根区间
介值定理 若函数 f (x) 在[a, b] 连续，且
f (a) f (b) 0 ，则方程 f ( x) 0 在(a,b) 内至
少有一个实根。将[a, b] 称为 f (x) 的有根区间。
6
2.1.2 逐步搜索法
假设f(x)在区间[a,b]内有一
个实根x*,若 b – a较小，则可 在(a,b)上任取一点x0作为初始 近似根。
数值分析习题课
例1-3 已知f(x) 的五组数据(1,0)、(2,2)、(3,12)、(4,42)、 (5,116),求 N4 (x)。如果再增加一个节点(6,282),求出N5(x)， 并计算 N4(1.5)、N5(1.5). 解：先由前五组数据列差商表 1 0 2 2 2 如果，再增加一点(6, 282), 3 12 10 4 就在上表中增加一行计算差商 4 42 30 10 2 5 116 74 22 4 0.5 0.1 6 282 166 46 8 1
结论：通过四舍五入原则求得的近似数，其有效数 字就是从末尾到第一位非零数字之间的所有数字。
1 mn x x 10 2
*
例1-2 下列近似数是通过四舍五入的方法得到的，试 判定它们各有几位有效数字： x1* =87540，x2*=8754×10, x3*=0.00345, x4*= 0.3450 ×10-2 解：我们可以直接根据近似数来判断有效数字的位数， 1 也可以通过绝对误差限来判断。 x x 10
解: 记f(x)以-1，0，1，2为插值节点的三次插值多项式为 L3(x)．由插值余项定理有
所以
例4．证明由下列插值条件 所确定的拉格朗日插值多项式 是一个二次多项式． x0 x2 x4
该例说明了什么问题?( t8) 解: 以x0，x2，x4为插值节点作f(x)的2次插值多项式p(x)，则
容易验证 因而6个点(xi, yi)，i＝0 1,…,5均在二次曲线p(x)＝x2-1 上． 换句话说，满足所给插值条件的拉格朗日插值多项式 为 p(x)＝x2-1.
f ( ) 1 R( x ) ( x x0 )( x x1 )( x x2 ) f ( ) ( x x0 )( x x1 )( x x2 ) 3! 6 1 max f ( ) max ( x x0 )( x x1 )( x x2 ) x0 x x 2 6 x0 x x 2
数值分析第二章答案
∑
n
i=1
ln x i = 0
θ
∧
= −
n
∑ ∑
n
n
i=1
ln x i n
θ
= =
解之得：
i=1
ln x i
（2）母体 X 的期望
E (x) =
∫
+∞ −∞
xf ( x ) d x =
∫
1 0
θ xθ dx =
θ θ +1
而样本均值为：
1 n X = ∑ xi n i =1 令E ( x) = X 得 θ =
x e 2σ 1 n
d x = 2 x ) =
∫
+ ∞ 0
x 2σ
e
−
x σ
d x = − x e ) = 1 ⋅ nσ n
−
x σ
+ ∞
+
0
∫
+ ∞ 0
e
−
x σ
d x =
E (σ ) = E (
∑
n
i=1
i
1 n
∑
n
E ( x
i=1
i
= σ
所以
σ=
∧
1 n ∑ xi σ n i=1 为 的无偏估计量。
∧
X 1− X
5.。解：其似然函数为：
L (σ ) = ∏
i =1
n
1 ⋅e 2σ
−
xi σ
=
1 ⋅e (2σ ) n 1 σ
n i =1
−
1 σ
∑ xi
i =1
n
ln L (σ ) = − n ln(2σ ) − 得： σ =
∧
(完整)数值分析历年考题
数值分析A 试题2007.1第一部分:填空题10⨯51.设3112A ⎛⎫= ⎪⎝⎭,则A ∞=___________ 2()cond A =___________2.将4111A ⎛⎫= ⎪⎝⎭分解成TA LL =，则对角元为正的下三角阵L =___________，请用线性最小二乘拟合方法确定拟合函数()bx f x ae =中的参数:a = ___________ b =___________4.方程13cos 2044x x π--=在[0,1]上有 个根，若初值取00.95x =,迭代方法113cos 244k k x x π+=-的收敛阶是5.解方程2210x x -+=的Newton 迭代方法为___________,其收敛阶为___________6。
设()s x = 3232323,[0,1]31,[1,2]ax x x x x x bx x +-+∈--+∈为三次样条函数，则a = ___________ b =___________ 7。
要想求积公式：1121()(()f x dx A f f x -≈+⎰的代数精度尽可能高，参数1A = ___________ 2x =___________此时其代数精度为：___________8.用线性多步法2121(0.50.5)n n n n n y y h f f f ++++-=-+来求解初值问题00'(,),(),y f x y y x y ==其中(,)n n n f f x y =，该方法的局部截断误差为___________，设,0,f y μμ=〈其绝对稳定性空间是___________9。
用线性多步法2121()n n n n n y ay by h f f ++++-+=-来求解初值问题00'(,),(),y f x y y x y ==其中(,)n n n f f x y =,希望该方法的阶尽可能高，那么a = ___________ b =___________,此时该方法是几阶的：___________10。
2-1数值分析
2 a 当 b 或 | f ( xk ) | 停止计算 k 1
不能保证x 的精度
3 二分法的算法
(1) 取初始有根区间[a,b],和精度要求 ；
ba , 则停止计算； (2) 若 2 ba (3) 取 x ，若 f (a ) f ( x ) 0, 则 b=x； 2
一、 二分法 1 基本概念和定理 定义 若存在x*,使得f(x*)=0,则称x*是方程的根
也称x*为函数f(x)的零点,进一步,若f(x)可以表 * m * 示为 f ( x) ( x x ) g( x), g( x ) 0 其中m是大于1的正整数，则称x*是方程f(x)=0 的m重根. 从几何上看，方程f(x)=0的实根是函数y=f(x) 的图形与横坐标的交点.
否则a=x； (4) 转(2).
例 求 x 3 x 1 0 在[1.0, 1.5]内的一个实根， 要求精确到小数点后的第2位. 解 由有效数字定义可知 | x xk | 0.005
1 ba 所以 k 1 k 2 0.005 k 6 2 2
k ak bk
数 值 分 析
第二章
解非线性方程的数值方法
1 二分法 2 迭代法
3 Newton法
本章主要讨论求解一元非线性方程
f ( x) 0
根的数值方法,其中f(x)是连续的非线性函数.
非线性方程的分两类： 1. 代数方程 n n1 a0 x a1 x an1 x an 0 其中 a0 0, ai R,(i 1, 2,, n) 2. 超越方程 f (x) 含超越函数，如 sin(x), ex, lnx 等
求有根区间和隔根区间的方法
《数值分析》李庆杨,第五版第2章课件PDF
1 第1节引言第2节拉格朗日插值第3节均差与牛顿插值多项式第4节埃尔米特插值第5节分段低次插值第6节三次样条插值2 2.1 引言10niyxPii1.1 设函数在区间上有定义且已知在点上的值若存在一简单函数使xfybabxxxan10nyyy10xP成立就称为的插值函数点称为插值节点包含节点的区间称为插值区间求插值函数的方法称为插值法. xPxfnxxx10baxP 2.1.1 插值问题的提出 3 nnxaxaaxP101.2 若是次数不超过的代数多项式xPn其中为实数就称为插值多项式相应的插值法称为多项式插值. iaxP本章只讨论多项式插值与分段插值.若为分段的多项式就称为分段插值. xP 若为三角多项式就称为三角插值. xP即4 从几何上看插值法就是确定曲线使其通过给定的个点并用它近似已知曲线. xPy1nniyxii10xfy图2-1 见图2-1. 5 由此可以得到关于系数的元线性方程组上的函数值求次数不超过的多项式使 2.1.2 多项式插值10niyxPii1.3 设在区间上给定个点10nixfyiibabxxxan10naaa101n1nnxP6101111000010nnnnnnnnnyxaxaayxaxaayxaxaa1.4 此方程组的系数矩阵为1111100nnnnnxxxxxxA称为范德蒙德Vandermonde矩阵由于互异故10nixi1.5 7 因此线性方程组1.4的解存在且唯一. .0det1njiojijixxAnaaa10 定理1 满足条件1.3的插值多项式是存在唯一的. xP8 2.2.1 线性插值与抛物插值对给定的插值点可以用多种不同的方法求得形如1.2的插值多项式. 先讨论的简单情形. 1n问题给定区间及端点函数值1kkxx11kkkkxfyxfy要求线性插值多项式1xL.1111kkkkyxLyxL2.2 拉格朗日插值使它满足nnxaxaaxP101.2 9 其几何意义就是通过两点的直线.11kkkkyxyx图2-2 如图2-2. 10 由的几何意义可得到表达式1xL111kkkkkkxxxxyyyxL点斜式11111kkkkkkkkyxxxxyxxxxxL两点式2.1 由两点式看出是由两个线性函数1xL11kkkkxxxxxl11kkkkxxxxxl2.2 的线性组合得到其系数分别为及即ky1ky111xlyxlyxLkkkk2.3 11 称及为线性插值基函数xlk1xlk1kkxl01kkxl01kkxl111kkxl显然及也是线性插值多项式在节点及xlk1xlkkx1kx上满足条件图形见图2-3. 12 图2-3 13 下面讨论的情形. 2n 假定插值节点为要求二次插值多项式1kxkx1kx2xL112kkkjyxLjj 几何上是通过三点的抛物线. 2xL1111kkkkkkyxyxyx 可以用基函数的方法求的表达式此时基函数是二次函数且在节点上满足条件2xL101111kkjxlxljkkk1101kkjxlxljkkk2.4 .101111kkjxlxljkkk使它满足1xlkxlk1xlk14 接下来讨论满足2.4的插值基函数的求法以求为例1xlk由插值条件它应有两个零点及kx1kx11kkkxxxxAxl可由插值条件定出111kkxl其中为待定系数A1111kkkkxxxxA于是.11111kkkkkkkxxxxxxxxxl可表示为101111kkjxlxljkkk1101kkjxlxljkkk2.4 .101111kkjxlxljkkk101111kkjxlxljkkk15 同理.1111kkkkkkkxxxxxxxxxl.11111kkkkkkkxxxxxxxxxl 二次插值基函数在区间上的图形见图2-4. 1xlkxlk1xlk11kkxx16 图2-4 17 利用1xlkxlk1xlk11112xlyxlyxlyxLkkkkkk2.5 显然将代入2.51xlkxlk1xlk111112kkkkkkkxxxxxxxxyxL1111kkkkkkkxxxxxxxxy.11111kkkkkkkxxxxx xxxy立即得到二次插值多项式.112kkkjyxLjj它满足条件得18 2.2.2 拉格朗日插值多项式将前面的方法推广到一般情形讨论如何构造通过个节点的次插值多项式. 1nnxxx10nxLn.10njyxLjjn2.6 根据插值的定义应满足xLn先定义次插值基函数. n 为构造xLn19 定义1 若次多项式在个节点上满足条件10.01nkjjkjkxlkj2.7 就称这个次多项式为节点1nn10xlxlxln上的次插值基函数. nxxx10nn10njxlj1nnxxx1020 显然它满足条件2.7. 于是满足条件2.6的插值多项式可表示为xLn.0nkkknxlyxL2.9 110110nkkkkkknkkkxxxxxxxxxxxxxxxxxl.10nk2.8 与前面的推导类似次插值基函数为n10.01nkjjkjkxlkj2.7 .10njyxLjjn2.6 21 由的定义知xlk.100njyxlyxLjnkjkkjn形如2.9的插值多项式称为拉格朗日插值多项式xLn而2.3与2.5是和的特殊情形. 1n2n容易求得1101nkkkkkkknxxxxxxxxx101nnxxxxxxx2.10 若引入记号.0nkkknxlyxL2.9111xlyxlyxLkkkk2.3 11112xlyxlyxlyxLkkkkkk2.5 22 于是公式2.9可改写成.011nkknknknxxxxyxL2.11 注意: 次插值多项式通常是次数为的多项式nxLnn 特殊情况下次数可能小于. n.0nkkknxlyxL2.9 例如通过三点的二次插值多项式如果三点共线则就是一条直线而不是抛物线这时是一次多项式.221100yxyxyx2xL2xLy2xL23 定理2 设在上连续在内存在节点是满足条件2.6 的插值多项式则对任何插值余项2.2.3 插值余项与误差估计xfnba1xfnba10xLbxxxannbax这里且依赖于是2.10所定义的. bax1xn 若在上用近似baxLnxfxLxfxRnn则其截断误差为也称为插值多项式的余项.101nnxxxxxxx2.10 111xnfxLxfxRnnnn2.14 .10njyxLjjn2.6 24 证明由给定条件知在节点上为零即于是xRn10nkxk100nkxRkn其中是与有关的待定函数.xKx110xxKxxxxxxxKxRnnn2.13 现把看成上的一个固定点作函数xba10nnxtxtxtxKtLtft根据的假设可知在上连续在内存在. ftnba1tnba25 根据罗尔定理在的两个零点间至少有一个零点故在内至少有个零点. tttba1n 对再应用罗尔定理可知在内至少有个零点. ttban 依此类推在内至少有一个零点记为使1tnbaba0111xKnfnn根据插值条件及余项定义可知在点及tnxxx10处均为零故在上有个零点tba2nx26 于是将它代入2.13 余项表达式只有在的高阶导数存在时才能应用. xf 但在内的具体位置通常不可能给出ba如果可以求出那么插值多项式逼近的截断误差限是max11nnbxaMxfxLnxf.111xnMxRnnn2.1411banfxKnx且依赖于110xxKxxxxxxxKxRnnn2.13 就得到余项表达式2.12. 27 当时线性插值余项为1n21211021xxxxfxfxR10xx2.15 当时抛物插值余项为2n612102xxxxxxfxR20xx2.16 28 利用余项表达式2.12当时由于于是有nkxxfk01xfn00xlxxxRniikikn由此得.100nkxxlxkniiki2.17 特别当时有0k.10xlnii2.18 29 利用余项表达式2.12还可知若被插函数由于故即它的插值多项式nHxf01xfn0xLxfxRnn.xfxLn30 例1 证明其中是关于点的插值基函数.0502xlxxiiixli510xxx证明利用公式2.17可得.0222222502505025022502xxxxlxxlxxxlxxlxxxxxlxxiiiiiiiiiiiiiii31314567.032.000yx.352274.036.022yx 用线性插值计算取由公式2.1333487.034.0sin314567.032.0sin352274.036.0sin333487.034.011yx例2 已知的值并估计截断误差. 3367.0sin用线性插值及抛物插值计算解由题意取34.032.010xx111kkkkkkxxxxyyyxL点斜式323367.03367.0sin1L0167.002.001892.0314567.03367.000101xxxyyy.330365.033 由2.15其截断误差21021xxxxMxR其中max102xfMxxx于是3367.03367.0sin3367.011LR0033.00167.03335.021xxxxsinmax103335.0sin1x.1092.052 1211021xxxxfxfxR34 用抛物插值计算由公式2.5得3367.0sin21012012010210xxxxxxxxyxxxxxxxxy1202102xxxxxxxxy3367.02L333487.0 0008.0107689.0314567.040008.0105511.0352274.00004.01089.344330374.011112xlyxl yxlyxLkkkkkk2.5 35 由2.14 621032xxxxxxMxR其中max203xfMxxx于是这个结果与6位有效数字的正弦函数表完全一样0cosx9493.0这说明查表时用二次插值精度已相当高了. 截断误差限363367.03367.0sin3367.022LR0233.0033.00167.09493.061.100132.2637 例2 设试证2baCf81max22Mabaxabafbfafxfbxa.max2xfMbxa其中证明通过两点及的线性插值为afabfb1axabafbfafxL于是.81max22maxmaxmax2221MabbxaxMbxaxfxLxfaxabafbfafxfbxabxabxabxa38 2.3 均差与牛顿插值公式2.3.1 插值多项式的逐次生成利用插值基函数很容易得到拉格朗日插值多项式公式结构紧凑在理论分析中甚为方便但当插值节点增减时全部插值基函数均要随之变化整个公式也将发生变化甚为不便.为了计算方便可重新设计一种逐次生成插值多项式的方法. 10nkxlk39 当时记线性插值多项式为插值条件为1n1xP111001xfxPxfxP由点斜式01xxabafbfafxP将看成是零次插值的修正即1xP01xfxP0101xxaxPxP其中是函数的差商. 01011xxxfxfaxf 对于三个节点的二次插值插值条件为2xP222112002xfxPxfxPxfxP40 .10202xxxxaxPxP插值多项式显然112002xfxPxfxP由得222xfxP.1201010202120221222xxxxxfxfxxxfxfxxxxxPxPa 系数是函数的“差商的差商”. 2af41 一般情况已知在插值点上的值为要求次插值多项式满足条件f10nixi10nixfinxPn10nixfxPiin则可表示为xPn10010nnnxxxxaxxaaxP其中为待定系数可由插值条件确定. naaa10 这里的是由基函数逐次递推得到的这一点与拉格朗日插值不同. xPn1100nxxxxxx3.1 3.2 42 称为函数关于点的一阶均差. 000xxxfxfxxfkkkxfkxx0定义2 2.3.2 均差及其性质110010xxxxfxxfxxxfkkk称为的二阶均差. xf43 11102010kkkkkkxxxxxfxxxfxxxf3.3 一般地称为的阶均差kxf均差也称为差商. 44 均差有如下的基本性质.011010kjkjjjjjjjkxxxxxxxxxfxxxf3.4 这个性质可用归纳法证明. 1 阶均差可表为函数值的线性组合10kxfxfxfk 这性质也表明均差与节点的排列次序无关称为均差的对称性. 即45 3 若在上存在阶导数且节点xfban10baxxxn.10banfxxxfnk3.5 这公式可直接用罗尔定理证明. 2 由性质1及3.3可得0120110xxxfxxxxfxxxfkkk即则阶均差与导数关系如下n.010110xxxxfxxfxxxfkkkk3.3’ 11102010kkkkkkxxxxxfxxxfxxxf3.3 46 4321043214324344321032132332102122101100xxxxxfxxxxfxxxfxxfxfxxxxxfxxxfxxfxf xxxxfxxfxfxxxfxfxxfxxfxkk四阶均差三阶均差二阶均差一阶均差1表2 均差计算可列均差表如下表2-1. 47 2.3.3 牛顿插值公式根据均差定义一次插值多项式为010001001xxxxfxfxxxxfxPxP二次插值多项式为.1021001001021012xxxxxxxfxxxxfxfxxxxxxxfxPxP48 根据均差定义把看成上一点xba000xxxxfxfxf110100xxxxxfxxfxxf.101010nnnnxxxxxxfxxxfxxxf可得49 只要把后一式依次代入前一式就得到0100xxxxfxfxf10210xxxxxxxfxRxPnn0100xxxxfxfxPn10210xxxxxxxf其中1010nnxxxxxxxf10xxxxfnn3.6 1010nnxxxxxxxf50 10xxxxfxPxfxRnnnn3.7 是由2.10定义的. 1xn 显然由3.6确定的多项式满足插值条件xPn且次数不超过n.100nkxxfakk称为牛顿Newton均差插值多项式. xPn 系数就是均差表2-1中加横线的各阶均差它比拉格朗日插值计算量省且便于程序设计. ka其系数为它就是形如3.1的多项式101nnxxxxxxx2.10 0100xxxxfxfxPn3.61010nnxxxxxxxf10210xxxxxxxf10nnxxxxa3.1 102010xxxxaxxaaxPn。
计算方法与数值计算(2-1插值与逼近)
800 1:42.58 罗达尔
1000
1500 3:32.07 恩格尼
是否能建立竞赛距离与纪录时间之间的 函数关系，并测算男子1000米纪录。
4
200
150
100
400
600
800
1000
1200
1400
散点图
5
引例2 设f ( x) ln x，并假定已给出下列三 点 处的函数值，试近似计 算 ln11.75的值。
30
f ( n1) ( ) n Rn ( x) (x x j ) (n 1)! j 0
不能确定，实际计算时，
在[a, b]上，若有 f ( n1) ( x) M，则
n f ( n1) ( ) n M Rn ( x) ( x x j ) (n 1)! ( x x j ) (n 1)! j 0 j 0
已知函数f(x)在n+1个互异节点ax0<x1 <……< xn b
处的函数值yi = f(xi) (i=0,1,2,……，n)，
则存在唯一一个次数不超过n次的多项式： Pn(x)=a0+a1x+……+anxn 满足条件Pn (xi) = yi = f(xi) 。
11
证明：设所要构造的插值多项式为：
y1 y=P1(x)
y0
x0
线性插值
18
x1
x
L1(x)= l0(x)y0 + l1(x)y1
其中
x x1 l0 ( x ) x0 x1
x x0 , l1 ( x) x1 x0
l0(x)：点x0的一次插值基函数， l1(x)：点x1的一次插值基函数。
数值分析实验报告2——Runge现象
数值分析课程实验报告——插值逼近题目一.Runge 函数的插值1. Runge 函数Runge 函数的表达式为：21()125R x x =+ 其在[-1,1]区间上的函数图像如图1.1。
在课程学习中我们知道，对Runge 函数进行高次插值时有可能在两端出现不收敛的情况，即Runge 现象。
下面将分别用四种不同的插值方法在[-1,1]区间上对Runge 函数进行插值，并分析是否产生Runge 现象，比较插值效果。
图1.1.Runge 函数在[-1,1]区间的函数图像2.Newton 插值首先根据课本上的Newton 插值算法进行编程（代码略）。
核心思想就是用符号变量进行中间运算，以便将最终的插值函数用符号表达式表示出来，并进一步生成图像。
此处插值节点选择为等距插值节点，即：0.1(0,1,2,,)i x ih i =-+= (20)其中h=0.1。
插值曲线与原曲线的对比如图1.2（蓝色为原曲线，红色为插值曲线）。
从图中看出，在区间中部，二者吻合较好；但在区间两端二者则产生了明显偏差，甚至可以达到一个非常大的数值（e20量级）。
因此，在等距节点的20次Newton 插值下，产生了明显的Runge 现象。
图1.2.Newton 插值曲线与原曲线对比3. Lagrange 插值此处同样是根据Lagrange 插值的具体算法进行编程。
但插值节点不再是等距分布，而是如下形式：21cos()(0,1,2,,)42i i x i π+==…20 插值曲线与原曲线的对比如图1.3（蓝色为原曲线，红色为插值曲线）。
从图中看出，插值曲线与原曲线吻合的很好，没有产生明显的Runge 现象。
对比产生了明显Runge 现象的20次Newton 插值，Lagrange 插值的最高次数虽然也是20，但由于此处的插值节点不是等距分布的（事实上，此处采用的插值节点正是Chebyshev 多项式的零点），而是中间疏两边密，因此两侧较密的节点很好地抑制了Runge 现象。
数值分析(清华大学出版社)第1,2章
2.
x 的相对误差是
x x d x er ( x ) d ln x x x
它是对数函数的微分。
设 u = xy , 则 lnu=lnx+lny , 因而 dlnu = dlnx + dlny
e r ( u ) e r ( x ) e r ( y ) r ( u ) r ( x ) r ( y )
即 m- n = - 2, m=1, n = 3, 所以 x = 3.14 作为 近似值 时, 就有3 位有效数字。
16
四、 相对误差限与有效数字的关系
定理1
设近似值
x 0.a1a2 an 10m
有n 位有效数字， a1 0 。则其相对误差限为 1 n 1 r (x ) 10 2a1 x 0.a1a2 an 10m 故 证明
a1 10
m 1
| x | (a1 1) 10
m 1
r (x )
x x x
0 .5 10m n 1 10 n1 a1 10m 1 2a1
17
定理2 设近似值 x 0.a1a2 an 10 的相对误差限
m
1 10 n1 ,则它至少有n 位有效数字。 不大于 2( a 1) 1
25
对多元函数 y f ( x1 , x2 , , xn ), 自变量的近似值为 x1 , x2 ,, xn , y 的近似值为 y f ( x1 , x2 , , xn ),
y 的运算误差为 函数值
e ( y ) e[ f ( x1 , x2 , , xn )] df ( x1 , x2 , , xn )
(完整版)数值分析每节课的教学重点、难点
计算方法教案新疆医科大学数学教研室张利萍一、课程基本信息1、课程英文名称：Numerical Analysis2、课程类别：专业基础课程3、课程学时：总学时544、学分：45、先修课程：《高等数学》、《线性代数》、《Matlab 语言》二、课程的目的与任务：计算方法是信息管理与信息系统专业的重要理论基础课程，是现代数学的一个重要分支。
其主要任务是介绍进行科学计算的理论方法，即在计算机上对来自科学研究和工程实际中的数学问题进行数值计算和分析的理论和方法。
通过本课程的学习，不仅使学生初步掌握数值分析的基本理论知识，而且使学生具备一定的科学计算的能力、分析问题和解决问题的能力，为学习后继课程以及将来从事科学计算、计算机应用和科学研究等工作奠定必要的数学基础。
三、课程的基本要求：1．掌握计算方法的常用的基本的数值计算方法2．掌握计算方法的基本理论、分析方法和原理3．能利用计算机解决科学和工程中的某些数值计算应用问题，增强学生综合运用知识的能力4．了解科学计算的发展方向和应用前景四、教学内容、要求及学时分配：(一) 理论教学：引论（2学时）第一讲（1-2节）1．教学内容：计算方法(数值分析)这门课程的形成背景及主要研究内容、研究方法、主要特点；算法的有关概念及要求；误差的来源、意义、及其有关概念。
数值计算中应注意的一些问题。
2．重点难点：算法设计及其表达法；误差的基本概念。
数值计算中应注意的一些问题。
3．教学目标：了解数值分析的基本概念；掌握误差的基本概念：误差、相对误差、误差限、相对误差限、有效数字；理解有效数字与误差的关系。
学会选用相对较好的数值计算方法。
A 算法B 误差第二讲典型例题第二章线性方程组的直接法（4学时）第三讲1．教学内容：线性方程组的消去法、Gauss消去法及其Gauss列主元素消去法的计算过程；三种消去法的程序设计。
2．重点难点：约当消去法，Gauss消去法，Gauss列主元素消去法3．教学目标：了解线性方程组的解法；掌握约当消去法、Gauss消去法、Gauss列主元素消去的基本思想；能利用这三种消去法对线性方程组进行求解，并编制相应的应用程序。
应用数值分析(第四版)课后习题答案第2章
第二章习题解答1.（1） R n×n中的子集“上三角阵”和“正交矩阵”对矩阵乘法是封闭的。
（2）R n×n中的子集“正交矩阵”，“非奇异的对称阵”和“单位上（下）三角阵”对矩阵求逆是封闭的。
设A 是ｎ×ｎ的正交矩阵。
证明A -1也是ｎ×ｎ的正交矩阵。
证明：(1),n nA B A B R⨯∈证明：为上三角阵，为上三角阵，10(),0(),0(),,()(()),()()ij ij nij ik kj ij k n n T T T T T T T T T T a i j b i j C AB c a b c i j A B A B R AA A A E BB B B EAB AB ABB A E AB AB B A AB E AB =⨯∴=>=>==∴=>∴∈========∴∑则上三角阵对矩阵乘法封闭。
以下证明：为正交矩阵，为正交矩阵，为正交矩阵,故正交矩阵对矩阵乘法封闭。
（2）A 是ｎ×ｎ的正交矩阵∴A A -1 =A -1A=E 故（A -1）-1=A∴A -1（A -1）-1=（A -1）-1A -1 =E 故A -1也是ｎ×ｎ的正交矩阵。
设A 是非奇异的对称阵，证A -1也是非奇异的对称阵。
A 非奇异 ∴A 可逆且A -1非奇异 又A T =A ∴（A -1）T =（A T ）-1=A-1故A -1也是非奇异的对称阵设A 是单位上（下）三角阵。
证A -1也是单位上（下）三角阵。
证明：A 是单位上三角阵，故|A|=1，∴A 可逆，即A -1存在，记为（b ij ）n×n由A A -1=E ，则∑==nj ik jkij ba 1δ （其中0=ij a j ＞i 时，1=ii a ）故b nn =1, b ni =0 (n≠j)类似可得，b ii =1 (j=1…n) b jk =0 (k ＞j)即A -1是单位上三角阵综上所述可得。
数值分析课后习题答案
x2 6.6667x2 8.205
再解
1
15 56
x31.785,7得 x35.769
1 25069x4 0.47847x4 1.4872
1 x5 5.3718 x5 5.3718
2-10.证明下列不等式:
(1)x-yx-z+z-y; (2)|x-y|x-y;
证明 (1)x-y=(x-z)+(z-y)x-z+z-y
b.用Gauss消元法
102 x y 1 x y 2
回代得解: y=1, x=0.
102 x Байду номын сангаасy 1
100y 100
再用列主元Gauss消元法
102 x y 1 x y 2
回代得解: y=1, x=1.
x y
y 1
2
2-8.用追赶法求解方程组:
4 1
x1 100
1 4 1
x2 0
3-8.判定求解下列方程组的SOR方法的收敛性.
2 1 0 0 x1 1
1
0 0
2 1 0
1 2 1
0 12
x2 x3 x4
0 00
解 直接可验证系数矩阵A是负定矩阵,所以-A是对称
1-3.为了使101/2的相对误差小于0.01%,试问应取几位 有效数字?
解 因为101/2=3.162…=0.3162…10,若具有n位有效 数字,则其绝对误差限为0.5 101-n ,于是有
r=0.5101-n/3.162…<0.5101-n/3<0.01% 因此只需n=5.即取101/2=3.1623
1 2
0
12 1,
1 2
1 2
0
12
数值分析课程第五版课后习题答案(李庆扬等)(OCR)
根是ｘ，，２…，ｘ－，且Ｖ。ｘ，ｘ…·，ｘ）＝Ｖ，Ｃｘ６，ｘ…·）（ｘ－ｘ）…（ｘ－ｘ）。
Ｖ，（ｘｏ，ｘ，…ｘ－ｘ）＝１１】 －ｘ，）用ａ－ｘ，）
［证明］由
可得求证。
＝Ｖ，（Ｃｘ８，ｘ，…，ｘＸ））１１（ｘ－ｘ）
２、当ｘ＝１－１，２时，ｆ（ｘ）＝０，－３．４，求ｆ（ｘ）的二次插值多项式。
Ｌ，（ｘ）＝ｙ％（（ｘｘ６－－ｘｘ，）（（ｘｘ－２ｘ－ｘ２２））
ｙ＝ｆ（ｘ）＝ｆ０．５）＝－０．６９３１４７，ｙ２＝ｆ（ｘ）＝ｆ（０．６）＝－０．５１０８２６，则
Ｌ２（ｘ）＝ｙ。 （ｘ－ｘ）（ｘ－ｘ２）
（ｘ６－ｘ）ｘ－ｘ）
（ｘ－ｘ）（ｘ－ｘ）
（ｘ－ｘ）（ｘ－ｘ２）
（ｘ－ｘｏ）（ｘ－ｘ） （ｘ２－ｘｏ）（ｘ２－ｘ）
＝－０．９１６２９１×．（０（．ｘ４－０－．０５．）５（）ｘ（－００．．６４）－０．６－．
３０—＋２—９．ｘ９５８３ｘ３１￣０２＇＝０．８３３６×１０４
１４、试用消元法解方程ｘ组１＋１０＂ｘ＝１００
ｘ＋ｘ２＝２
，假定只有三位数计算，问结果是否
可靠？
［解］精确解为ｘ１＝０１００－＊１ １０＂－２ ，当使用三位数运 算时，得到
ｘ ＝１，ｘ２＝１，结果可靠。
１５、已知三角形面积ｓ＝ｓ去＝ ａｂｓｉｎｃ，其中ｃ为弧度，０＜ｃ＜ 且测量ａ，ｂ，ｃ
位有效数字；ｘ＝５６．４３０有５位有效数字；ｘ＝７×１０有２位有效数字。 ４、利用公式（３．３）求下列各近似值的误差限，其中ｘ，ｘ；，ｘ，ｘ；均为第３题所给
的数。
（１）ｘ＋ｘ２＋ｘ：
ｅ（ｘ＋ｘ写＋ｘ）＝＞
［解］
Ｅ（ｘ）＝Ｅ（ｘ）＋Ｅ（ｘ）＋Ｅ（ｘ；）
３＋ｔｘ１０＝１．０５×１０３
（２）ｘｘｘ；
数值分析-第二章小结
第二章 线性方程组的数值解法-------学习小结姓名 班级 学号 一、本章学习体会通过本章的学习，我了解了线性方程组的不同解法，切实体会到了不同的计算方法对计算结果的影响。
求解线性方程组的方法可分为两大类：直接方法和迭代方法。
直接方法在解一般的线性方程组的时候比较简便，使用此方法经过有限次运算就可得到方程组的解。
然而迭代法是要构造一个无限的向量序列，其极限是方程组的解向量，它适用于求解大型稀疏线性方程组。
总的来说，直接方法和迭代法各有优点与不足，在解线性方程组的时候，我们要根据具体的线性方程组的特点来选择合适的解法，这样我们才能快速准确的得到方程组的解。
因此，我们要熟悉书中介绍的各类线性方程组的解法，同时要善于思考、总结，在使用各种方法求解的同时尽量提出自己独特的见解，通过不断练习计算，使自己的能力得到提高。
二、本章知识梳理线性方程组的求解方法分为直接法和迭代法两种，Gramer （克莱姆）法是直接法的一种，但由于其计算量比较大，在世界工作中其效率比较低、经济效益差，所以此方法我们很少使用，本章主要介绍其他的计算方法。
2.1 Gauss 消去法Gauss （高斯）消去法由消元和回代两个过程组成。
消元过程就是对方程组的增广矩阵做有限次的初等行变换，使它的系数矩阵部分变换为上三角阵。
所用的初等行变换主要有两种：第一种，交换两行的位置；第二种，用一个数乘某一行加到另一行上。
回代过程就是先由方程组的最后一个方程解出n x ，然后通过逐步回代，依次求出1n x -，2n x -，…，1x 。
这种Gauss 消去法可分为Gauss 消去法和列主元素Gauss 消去法两种。
2.1.1 顺序Gauss 消去法在Gauss 消去法的消元过程中对方程组的增广矩阵只做前述的第二种初等行变换就形成了顺序Gauss 消去法，其算法如下：记(1)ij ij a a = （i ，j=1，2，…，n ）i i 1、 消元过程对于k=1,2，…，n-1执行 （1）如果()0k kka =，则算法失效，停止计算；否则转（2）。
(仅供参考)数值分析课后第二章习题解答
6第二章 习题解答一、习题解答1 用二分法求解下列方程，要求误差不超过10-5 （1）x – ln x=2 在区间[2，4]内的根；（2）x e x– 1 = 0 在区间[0，1]内的根；（3）x 3 + 4x 2– 10 = 0 在区间[1，2]内的根。
解：（1）x 18 = 3.14618。
二分法程序2-1a=2;b=4;k=0;f=inline('x-log(x)-2'); ya=f(a);while (b-a)>0.00001x0=.5*(a+b);y0=f(x0); if ya*y0<0 b=x0; elsea=x0;ya=y0; end k=k+1; endformat long disp([x0,k])（2） x 17 = 0.567146。
（利用上面程序修改前两行） （3） x 17 = 1.365226。
2 证明方程 1 – x – sin x = 0 在区间[0，1]上有一根。
使用二分法求误差不大于41021−×的根需二分多少次？证明 令f (x ) = 1 – x – sin x ，则f (0) = 1，f (1)= – sin 1。
于是 f (0) f (1)< 0，故所给方程在区间[0，1]上必有根。
又因为x x f cos 1)(−−=′ 所以，函数 f (x ) 在区间[0，1]内单减。
故，方程在区间[0，1]内只有一个根。
利用二分法收敛定理，由411021201−+×≤−n 得 2n ≥ 104，所以二分法求根至少需14次二分计算能满足误差要求。
3 比较以下两种方法求 e x+ 10 x – 2 =0 的根到三位小数所需要的计算量。
（1） 在区间[0，1]内用二分法；（2） 用迭代法)2(1011n x n e x −=+，取初值 x 0 = 0。
解：（1）二分法迭代11次，x 11 = 0.090。
（利用第1题程序修改前两行） （2）不动点迭代5次，x 5 = 0.0905。
博士研究生入学考试《数值分析(二)》
博士研究生入学考试《数值分析（二）》
考试大纲
（科目代码：2228）
一、误差分析
1.误差来源
2.误差的基本概念
3.误差分析的若干原则
二、插值法
1. 拉格朗日插值
2. 均差与牛顿插值公式
3．分段线性插值公式
4.三次样条插值
三、函数逼近与计算
1. 最佳一致逼近多项式
2. 切比雪夫多项式
3. 最佳平方逼近
4. 正交多项式
5. 曲线拟合的最小二乘法
6. 离散富氏变换及其快速算法
四、数值积分与数值微分
1. 龙贝格求积算法
2. 高斯求积公式
3. 数值微分
五、常微分方程数值解法
1. 尤拉方法
2. 龙格-库塔方法
3. 单步法的收敛性和稳步性
4. 线性多步法
5. 方程组与高阶方程的情形
六、方程求根
1. 牛顿法
2. 弦截法与抛物线法
3. 代数方程求根
七、解线性方程组的迭代法
1. 雅可比迭代法与高斯-塞德尔迭代法
2. 迭代法的收敛性
3. 解线性方程组的松弛迭代法。
牛顿插值三次插值多项式例题
牛顿插值三次插值多项式例题假设有如下数据点：(1, 1), (2, 8), (4, 64), (5, 125)首先，我们需要计算差商表。
差商表是用来计算牛顿插值多项式的系数的重要工具。
差商表的第一列是给定的数据点的y值，第二列是第一次差商，第三列是第二次差商，以此类推。
x | y |1st Dif.|2nd Dif.|3rd Dif.----------------------------------1 | 1 |2 | 8 | 74 | 64 | 28 75 | 125 | 61 18 11计算第一次差商。
第一次差商可以用以下公式计算：f[x1, x2] = (f(x2) - f(x1)) / (x2 - x1)对于第一行和第二行的数据点，我们可以计算：f[1, 2] = (8 - 1) / (2 - 1) = 7类似地，我们可以计算出其他的差商。
计算第二次差商。
第二次差商可以用以下公式计算：f[x1, x2, x3] = (f[x2, x3] - f[x1, x2]) / (x3 - x1)对于第一行到第三行的数据点，我们可以计算：f[1, 2, 4] = (28 - 7) / (4 - 1) = 7类似地，我们可以计算出其他的差商。
计算第三次差商。
第三次差商可以用以下公式计算：f[x1, x2, x3, x4] = (f[x2, x3, x4] - f[x1, x2, x3]) / (x4 - x1)对于所有数据点，我们可以计算：f[1, 2, 4, 5] = (11 - 7) / (5 - 1) = 1现在，我们可以使用差商表中的第一列和第一行的差商来构建牛顿插值多项式。
多项式的形式为：P(x) = f(x0) + f[x0,x1] * (x - x0) + f[x0,x1,x2] * (x - x0)(x - x1) + f[x0,x1,x2,x3] * (x - x0)(x - x1)(x - x2)代入给定的数据点的值，我们有：P(x) = 1 + 7(x - 1) + 7(x - 1)(x - 2) + 1(x - 1)(x - 2)(x - 4)将多项式展开并化简，得到最终的牛顿插值三次插值多项式。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
我们称这样的问题为插值问题，并称 φ(x)为 f (x)的插值函数，f (x)为被插 函数， x0 , x1, x2, …, xn是插值节(基)点
条件
( xi ) yi ,
i 0,1,, n
是插值原则.
思考题 当数据点(xi, yi)给定后，满 足插值条件的插值函数φ(x)有多少 种类型？
答 有许多种。例如给出平面上两 个点，则过这两个点的曲线有无穷 多种，可以是代数多项式、三角多 项式、有理函数等等，但最简单而 最常用的是代数多项式，它有许多 良好的性质，故本章仅考虑代数多 项式插值问题
2. 代数多项式插值问题 已知条件 设给出关于函数y= f (x)的一组函数值，
x y
x0 y0
数 值 分 析
第二章 插 值 法
§1 引 言
一、实际背景 二、问题的分类 三、插值问题的定义
一、实际背景 飞机、汽车的外形设计制造
基本过程： 测点 插值曲线
插曲面
三角函数表、对数表等
不在表上的函数值如何求？
二、问题的分类 插值问题： 求一条曲线严格通过数据点 曲线拟合问题： 求一条曲线在一定意义下靠近 数据点 注：插值问题和曲线拟合问题统称 函数逼近问题！
三、插值问题的定义
1. 插值问题的有关概念 已知条件 设给出关于函数y= f (x)的一组函数值，
x y x0 y0 x1 y1 x2 … xn y2 … yn
其中x0 , x1, x2, …, xn是区间[a,b]上的 互异点，
求 一个简单函数φ(x)作为f(x)的近似 表达式，以满足
( xi ) yi ,
例如
P ( x) P ( x) p ( x) ( x xi ) n
i 0
n
也是一个插值多项式，其中 p ( x ) 可
以是任意多项式。
称Pn(x)为 f (x)的n次插值多项式
问题：这样的插值多项式是否存在唯 一呢？
定理 在n+1个互异节点处满足插值 原则且次数不超过n的多项式Pn(x)存 在并且唯一。
证明 设Pn(x)为所求多项式，则
a0 a1 x0 a 2 x a n x y0 2 n a0 a1 x1 a 2 x1 a n x1 y1 a a x a x 2 a x n y 0 1 n 2 n n n n
注意 从定理的证明可以看出，只要 通 过 求 解 一 个 线 性 方 程 组 得 出 a0 , a1,…,an 的值，便可以确定Pn(x)了。 然而这样构造多项式不但计算量大， 而且难以得到Pn(x)的简单公式，因 此本章下面几节将介绍几种直接构 造Pn(x)的方法。
注：若不将多项式次数限制为 n ，则 插值多项式不唯一。
x1 y1
x2 … xn y2 … y n
其中x0 , x1, x2, …, xn是区间[a, b]上 的互异点，
求 一个次数不超过n的多项式
Pn ( x ) a0 a1 x a2 x an x
2 n
使满足插值原则(条件)
Pn ( x i ) yi , i 0,1,, n
2 0 n 0
这是未知量a0, a1,…,an的线性方程组， 其系数行列式是范德蒙行列式
1 V ( x 0 , x 1 , , x n ) 1
x0 x1
x0 x0 x1
2
2
n n
x1
1 xn xn xn
2 n
(x
0 j i n
i
xj)
因为x0, x1,…,xn的互不相同，故系数行 列式不等于0，因此方程组有唯一解， 即Pn(x)存在并唯一。