高一数学必修三《算法初步》单元测试题
高一数学必修三《算法初步》单元测试题
)
A.
B.
C.
D.
【答案】 A
【解析】
试题分析：本题考查了选择结构，由程序框图所体现的算法可知判断一个数是奇数还是偶数，
看这个数除以 2 的余数是 1 还是 0，从而得到判断框条件．
解：由程序框图所体现的算法可知判断一个数是奇数还是偶数，看这个数除以
2 的余数是 1
还是 0．
由图可知应该填 m=1．
最基本的是顺序结构，
一个算法一定包含有顺序结构，但是可以含有三种逻辑结构的任意组合
.
故选： D.
点睛：本题考查的知识点是算法的概念及算法的特点，是对概念的直接考查，属基础题，熟
练掌握相关概念是解答本题的关键 .
3.3. 下列给出的赋值语句中正确的是（
）
A.
B.
C.
D.
【答案】 B
【解析】
【分析】
根据赋值语句定义判断选择 .
【答案】 D
【解析】
【分析】
根据进制先换成十进制，再换成五进制 .
【详解】因为
，
所以
，选 D.
【点睛】本题考查不同进制之间转换 , 考查基本求解能力 .
11.11. 假设
，那么在执行
后 的值为（
）
A. 0.5 B. 11.5 C. 10.5 D.
【答案】 B
【解析】
【分析】
将
，代入计算
– 0.5 得结果 .
, 当条件满
足时进入循环，否则结束循环。
5.5. 以下给出的各数中不可能是八进制数的是（
）
A. 312 B. 10 110 C. 82 D. 7 457
【答案】 C
【解析】
(典型题)高中数学必修三第二章《算法初步》测试题(含答案解析)
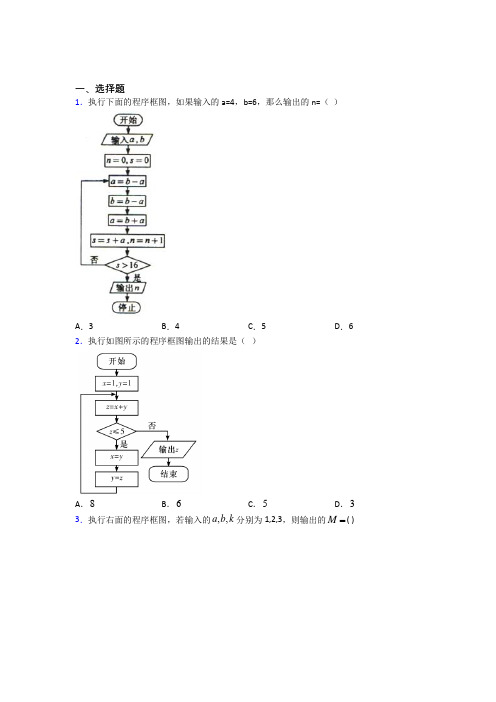
一、选择题1．执行下面的程序框图，如果输入的a=4，b=6，那么输出的n=（）A．3 B．4 C．5 D．6 2．执行如图所示的程序框图输出的结果是（）A．8B．6C．5D．3a b k分别为1,2,3，则输出的M ( ) 3．执行右面的程序框图，若输入的,,A．203B．72C．165D．1584．执行如图所示的程序框图，则输出的a=（）A．-9 B．60 C．71 D．815．执行如图所示的程序框图，若输出S的值为511，则判断框内可填入的条件是（）A ．4i ≤B ．5i ≤C ．5i <D ．6i ≤6．执行如图所示的程序框图，如果输入x ＝5，y ＝1，则输出的结果是（ ）A ．261B ．425C ．179D ．5447．朱世杰是我国元代伟大的数学家，其传世名著《四元玉鉴》中用诗歌的形式记载了下面这样一个问题：我有一壶酒，携着游春走.遇务①添一倍，逢店饮斛九②.店务经四处，没了这壶酒.借问此壶中，当原多少酒？①“务”：旧指收税的关卡所在地；②“斛九”：1.9斛.下图是解决该问题的算法程序框图，若输入的x 值为0，则输出的x 值为（ ）A．5740B．13380C．5732D．5893208．若执行如图所示的程序框图，输出S的值为511，则输入n的值是（）A．7B．6C．5D．4 9．执行如下图的程序框图，如果输入的N的值是7，那么输出的p的值是（）A．3 B．15 C．105 D．94510．如图所示程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入的,a b 分别为10，14，则输出的a =（ ）A ．6B ．4C ．2D ．011．执行如图的程序框图，如果输出a 的值大于100，那么判断框内的条件为()A ．5k <？B ．5k ≥？C ．6k <？D ．6k ≥？12．执行如图所示程序框图，当输入的x 为2019时，输出的y (= )A ．28B ．10C．4D．2二、填空题13．下图所示的算法流程图中，输出的S表达式为__________．14．已知某程序框图如图所示，则该程序运行后输出S的值为__________．15．执行如图所示的程序框图，输出的值为__________．16．如图是一个算法流程图，则输出的S的值为______．17．阅读如图所示的程序框图，运行相应的程序，则输出n的值为___________18．下图程序运行结果是________．19．执行下图所示的程序框图，若输入，则输出的值为_____________.20．执行如图所示的程序框图,输出的T ______．三、解答题21．如图，在边长为4的正方形ABCD的边上有一点P，沿着折线BCDA由点B(起点)向点A(终点)运动．设点P运动的路程为x，APB△的面积为y，求y与x之间的函数关系式，并画出程序框图.22．有关专家建议预测，在未来几年内，中国的通货膨胀率保持在3%左右，这将对我国经济的稳定有利无害．所谓通货膨胀率为3%，指的是每年消费品的价格增长率为3%.在这种情况下，某种品牌的钢琴2015年的价格是10 000元，试分析其算法并用流程图描述这种钢琴今后四年的价格变化情况，并输出四年后的价格．23．写出一个算法，求底面边长为42，侧棱长为5的正四棱锥的体积．24．设计程序求π的近似值可以用公式:2222π1116123=+++…+21n ,用此公式求2π6,即逐项进行累加,直到21n <0.000 01为止(该项不累加),然后求出π的近似值. 25．古希腊杰出的数学家丢番图的墓碑上有这样一首诗:这是一座古墓,里面安葬着丢番图.请你告诉我,丢番图的寿数几何?他的童年占去了一生的六分之一,接着十二分之一是少年时期,又过了七分之一的时光,他找到了自己的终身伴侣.五年之后,婚姻之神赐给他一个儿子,可是儿子不济,只活到父亲寿数的一半,就匆匆离去.这对父亲是一个沉重的打击,整整四年,为失去爱子而悲伤,终于告别了数学,离开了人世.试用循环结构,写出算法分析和算法程序. 26．已知函数2()32,(3)(5)f x x x f f =--+-求的值，设计一个算法并画出算法的程序框图．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【解析】试题分析：模拟执行程序, 可得4,6,0,0a b n s ====,执行循环体,2,4,6,6,1a b a s n =====,不满足条件16s >,执行循环体,2,6,4,10,2a b a s n =-====, 不满足条件16s >,执行循环体,2,4,6,16,3a b a s n =====, 不满足条件16s >,执行循环体,2,6,4,20,4a b a s n =-====,不满足条件16s >,退出循环, 输出n 的值为4,故选B.考点：1、程序框图；2、循环结构.2．A解析：A【分析】根据程序框图循环结构运算，依次代入求解即可．【详解】根据程序框图和循环结构算法原理，计算过程如下：1,1,x y z x y ===+第一次循环2,1,2z x y ===第二次循环3,2,3z x y ===第三次循环5,3,5z x y ===第四次循环8z =，退出循环输一次8z =.所以选A【点睛】本题考查了程序框图的基本结构和运算，主要是掌握循环结构在何时退出循环结构，属于基础题．3．D解析：D【详解】试题分析：根据题意由13≤成立，则循环，即1331,2,,2222M a b n =+====;又由23≤成立，则循环，即28382,,,33323M a b n =+====;又由33≤成立，则循环，即3315815,,,428838M a b n =+====;又由43≤不成立，则出循环，输出158M =． 考点：算法的循环结构4．C解析：C【分析】根据程序框图，模拟运算即可求解.【详解】第一次执行程序后，1a =-，i=2；第二次执行程序后，9a =-，i=3；第三次执行程序后，a=71，i=4>3，跳出循环，输出a=71.故选：C【点睛】本题主要考查了程序框图，循环结构，条件分支结构，属于中档题.5．B【分析】模拟运行程序1i =，满足条件，1013S =+⨯，2i =，满足条件，进入循环体，反复操作，直到输出511S =，核对满足的条件即可. 【详解】 1i =，满足条件，1013S =+⨯； 2i =，满足条件，111335S =+⨯⨯； 3i =，满足条件，111133557S =++⨯⨯⨯； 4i =，满足条件，111113355779S =+++⨯⨯⨯⨯； 5i =，满足条件，11111115(1)1335577991121111S =++++=-=⨯⨯⨯⨯⨯； 6i =，不满足条件，输出511S =. 故选：B.【点睛】 本题考查了对程序框图的理解与应用，由程序运行结果，补充条件，数列求和的裂项相消法，属于中档题.6．B解析：B【分析】根据循环结构的条件，依次运算求解，即得解.【详解】起始值：5,1,0x y n ===，满足1105<⨯，故：5,0,2x y n ===；满足0105<⨯，故：7,4,4x y n ===；满足4107<⨯，故：11,36,6x y n ===；满足361011<⨯，故：17,144,8x y n ===；满足1441017<⨯，故：25,400,10x y n ===；此时：4001025>⨯，满足输出条件：输出425x y +=故选：B【点睛】本题考查了程序框图的循环结构，考查了学生逻辑推理，数学运算的能力，属于中档题. 7．C【分析】本题首先可以根据题意以及程序框图明确输入的数据为“0x =，0i =”和运算的算式为“119210x x 、1i i =+”，然后进行运算并结合条件“4i ”得出结果。
(典型题)高中数学必修三第二章《算法初步》检测卷(含答案解析)
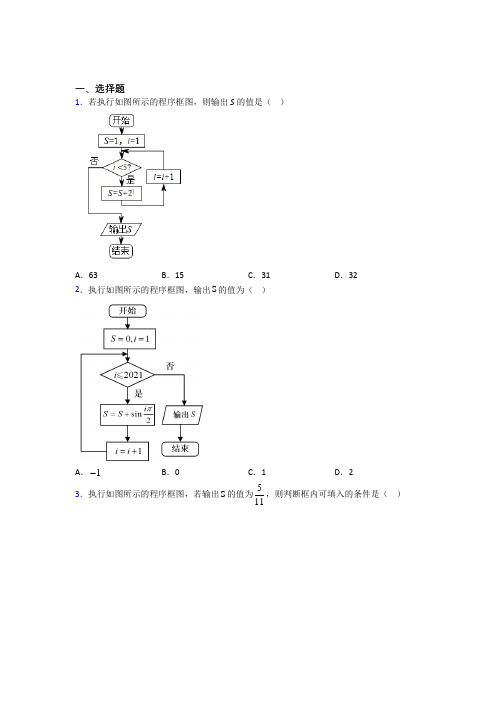
一、选择题1．若执行如图所示的程序框图，则输出S的值是（）A．63 B．15 C．31 D．32 2．执行如图所示的程序框图，输出S的值为（）A．1 B．0 C．1 D．23．执行如图所示的程序框图，若输出S的值为511，则判断框内可填入的条件是（）A ．4i ≤B ．5i ≤C ．5i <D ．6i ≤ 4．如图给出的是计算1232018⨯⨯⨯⨯的值的一个程序框图，则其中判断框内应填入的是（ ）A ．2018i <B ．2018i =C ．2018i ≤D ．2018i >5．已知函数1()(1)g x x x =+，程序框图如图所示，若输出的结果1011S =，则判断框中可以填入的关于n 的判断条件是（ ）A ． 10?n ≤B ．10?n >C ． 11?n ≤D ． 11?n > 6．明代数学家程大位（1533~1606年），有感于当时筹算方法的不便，用其毕生心血写出《算法统宗》，可谓集成计算的鼻祖．如图所示的程序框图的算法思路源于其著作中的“李白沽酒”问题．执行该程序框图，若输出的y 的值为2，则输入的x 的值为（ ）A ．74B ．5627C ．2D ．164817．某程序框图如图所示，其中21()g n n n =+，若输出的20192020S =，则判断框内可以填入的条件为（ ）A ．2020?n <B ．2020?nC ．2020?n >D ．2020?n 8．程大位是明代著名数学家，他的《新编直指算法统宗》是中国历史上一部影响巨大的著作．卷八中第33问：“今有三角果一垛，底阔每面七个．问该若干？”如图是解决该问题的程序框图．执行该程序框图，求得该垛果子的总数S 为（ ）A ．28B ．56C ．84D ．120 9．若执行如图所示的程序框图，则输出S 的值为（ ）A ．9-B ．16-C ．25-D ．36- 10．执行如图所示的程序框图，输出的结果为( )A ．201921-B ．201922-C ．202022-D ．202021- 11．执行如图所示的程序框图，若输出的结果为5，则输入的实数a 的范围是( )A ．[)6,24B ．[)24,120C ．(),6-∞D ．()5,24 12．执行如图所示程序框图，当输入的x 为2019时，输出的y (= )A．28B．10C．4D．2二、填空题13．执行如图所示的伪代码,则输出的S的值是_______.14．执行如图所示的程序框图若输人x的值为3，则输出y的值为______．15．如图，程序框图中，语句1被执行的次数为__________．16．执行如图所示的算法框图，若输入的x的值为2，则输出的n的值为__________．17．阅读如图所示的流程图，运行相应的程序，则输出n的值为______．18．将二进制数110 101（2）转为七进制数，结果为________．19．一个算法的程序框图如下图所示，若该程序输出的结果为，则判断框中应填入的条件是____．20．程序如下：以上程序输出的结果是_________________三、解答题21．现有一个算法框图如图所示。
(典型题)高中数学必修三第二章《算法初步》测试题(包含答案解析)
一、选择题1．该程序中k的值是（）A．9 B．10 C．11 D．12 2．执行如图所示的程序框图，则输出的S=（）A．1-B．2-C．2D．1 23．执行如图所示的程序框图，输出S的值为（）A ．1-B ．0C ．1D ．24．执行如图所示的程序框图，若输出的结果为126，则判断框内的条件可以为（ ）A ．5n ≤B ．6n ≤C ．7n ≤D ．8n ≤ 5．鸡兔同笼，是中国古代著名的趣味题之一.《孙子算经》中就有这样的记载：今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各有几何？设计如右图的算法来解决这个问题，则判断框中应填入的是（ ）A ．94m >B ．94m =C ．35m =D ．35m ≤6．读下面的程序：上面的程序在执行时如果输入6，那么输出的结果为()A ．6B ．720C ．120D ．50407．执行如图的程序框图，若输出的4n =，则输入的整数p 的最小值是（ ）A．4B．5C．6D．15 8．执行如图所示的程序框图，若输人的n值为2019，则S＝A．B．C．D．9．下列赋值语句正确的是 ()A．S＝S＋i2B．A＝－AC．x＝2x＋1 D．P＝10．执行如图的程序框图，则输出x的值是 ()A ．2018B ．2019C ．12 D ．211．执行如图所示的程序框图，若输出的结果为5，则输入的实数a 的范围是( )A ．[)6,24B ．[)24,120C ．(),6-∞D ．()5,24 12．执行如图的程序框图，如果输出a 的值大于100，那么判断框内的条件为()A ．5k <？B ．5k ≥？C ．6k <？D ．6k ≥？二、填空题13．根据下列算法语句，当输入x 为60时，输出y 的值为_______.14．如图所示的程序框图，输出的S的值为()A．12B．2 C．1-D．12-15．根据如图所示的伪代码可知,输出的结果为______.16．执行如下图所示的程序框图，则输出的结果n=__________．17．执行如图所示的程序框图，输出S的值为___________.18．执行下图所示的程序框图，若输入，则输出的值为_____________.19．如图所示的程序框图，输出的结果是_________.20．一个算法的程序框图如图所示，则该算法运行后输出的结果为________.三、解答题21．（1）作任意五个数12345,,,,x x x x x 中最大数及其序号的算法的流程图框图；（2）初始状态为35，24，23，47，43的五个数，当计算过程第1次，第3次，第5次到达判断框时，M ，k 的值分别为多少？22．用二分法求方程5310x x -+=在(0,1)上的近似解，精确到0.001，写出算法，并画出流程图.23．某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算：()()()0.5350=500.53+-500.8550f ωωωω⎧≤⎪⎨⨯⨯>⎪⎩.其中f (单位：元)为托运费，ω为托运物品的重量(单位：千克)，试写出一个计算费用f 的算法，并画出相应的程序框图．24．编写一个程序，要求输入两个正数a 和b 的值，输出a b 和b a 的值，并画出程序框图. 25．求两底面半径分别为2和4，高为5的圆台的表面积及体积．写出解决该问题的一个算法，并画出程序框图．26．设计算法输出1 000以内既能被3整除又能被5整除的所有正整数,画出程序框图.【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【分析】本题只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可（注意避免计算错误）．【详解】3,2,8,814x k y ===<，第一次循环，4,10,1014k y ==<；第二次循环，6,12,1214k y ==<；第三次循环，8,14,1414k y ===；第四次循环，10,16,1614k y ==>，退出循环，输出10k =，故选：B.【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.2．D解析：D【分析】列举出前四次循环，可知，该算法循环是以3为周期的周期循环，利用周期性可得出输出的S 的值.【详解】第一次循环，02020k =≤成立，1112S ==--，011k =+=； 第二次循环，12020k =≤成立，()11112S ==--，112k =+=； 第三次循环，22020k =≤成立，12112S ==-，213k =+=；第四次循环，32020k =≤成立，1112S ==--，314k =+=； 由上可知，该算法循环是周期循环，且周期为3，依次类推，执行最后一次循环，20202020k =≤成立，且202036731=⨯+，此时12S =， 202012021k =+=，20212020k =≤不成立，跳出循环体，输出S 的值为12. 故选：D.【点睛】本题考查利用程序框图计算输出结果，推导出循环的周期性是解题的关键，考查计算能力，属于中等题.3．C解析：C【分析】由函数()πsin 2x f x =，可求周期为4，()(1)(2)(3)40+++=f f f f ，由题意可知()(1)(2)(2021)=2021(1)1=+++==S f f f f f【详解】 由函数()πsin 2x f x =的周期为2π4π2T ==， ()π1sin 12f ==，()2π2sin 02f ==， ()3π3sin 12f ==-，()4π4sin 02f ==，()(1)(2)(3)40+++=f f f f ()(1)(2)(2021)=2021(1)1∴=+++==S f f f f f .故选：C【点睛】本题考查了程序框图求和，正弦型三角函数的周期等基本知识，考查了运算求解能力和逻辑推理能力，属于一般题目.4．B解析：B【分析】根据框图，模拟程序运行即可求解.【详解】根据框图，执行程序，12,2S n ==；1222,3S n =+=；⋯12222,1i S n i =++⋯+=+，令12222126i S =++⋯+=，解得6i =，即7n =时结束程序，所以6n ≤，故选 ：B【点睛】本题主要考查了程序框图，循环结构，条件分支结构，等比数列求和，属于中档题.genju 5．B解析：B【分析】由题意知i 为鸡的数量，j 为兔的数量，m 为足的数量，根据题意可得出判断条件.【详解】由题意可知i 为鸡的数量，j 为兔的数量，m 为足的数量，根据题意知，在程序框图中，当计算足的数量为94时，算法结束，因此，判断条件应填入“94m =”.故选B.【点睛】本题考查算法程序框图中判断条件的填写，考查分析问题和解决问题的能力，属于中等题. 6．B解析：B【解析】【分析】执行程序，逐次计算，根据判断条件终止循环，即可求解输出的结果，得到答案.【详解】由题意，执行程序，可得：第1次循环：满足判断条件，1,2S i ==；第2次循环：满足判断条件，2,3S i ==；第3次循环：满足判断条件，6,4S i ==；第4次循环：满足判断条件，24,5S i ==；第5次循环：满足判断条件，120,6S i ==；第6次循环：满足判断条件，720,7S i ==；不满足判断条件，终止循环，输出720S =，故选B.【点睛】本题主要考查了循环结构的程序框图的计算输出，其中解答中正确理解循环结构的程序框图的计算功能，逐次计算是解答的关键，着重考查了推理与运算能力，属于基础题. 7．A解析：A【分析】列举出算法的每一步循环，根据算法输出结果计算出实数p 的取值范围，于此可得出整数p 的最小值.【详解】0S p =<满足条件，执行第一次循环，0021S =+=，112n =+=；1S p =<满足条件，执行第二次循环，1123S =+=，213n =+=；3S p =<满足条件，执行第二次循环，2327S =+=，314n =+=.7S p =<满足条件，调出循环体，输出n 的值为4.由上可知，37p <≤，因此，输入的整数p 的最小值是4，故选A.【点睛】本题考查算法框图的应用，解这类问题，通常列出每一次循环，找出其规律，进而对问题进行解答，考查分析问题和解决问题的能力，属于中等题.8．B解析：B【分析】 根据程序框图可知，当时结束计算，此时 . 【详解】 计算过程如下表所示：周期为6 n2019 k1 2 … 2018 2019 S… k<n 是 是 是 是 否故选B.【点睛】本题考查程序框图，选用表格计算更加直观，此题关键在于判断何时循环结束. 9．B解析：B【解析】在程序语句中乘方要用“^”表示，所以A 项不正确；乘号“*”不能省略，所以C 项不正确；DSQR(x)表示，所以D 项不正确；B 选项是将变量A 的相反数赋给变量A ，则B 项正确．选B.10．D解析：D【分析】模拟执行程序框图，依次写出每次循环得到的x ，y 的值，当2019y = 时，不满足条件退出循环，输出x 的值即可得解．【详解】解：模拟执行程序框图，可得2,0x y ==.满足条件2019y <，执行循环体，1,1x y =-=；满足条件2019y <，执行循环体，1,22x y == ； 满足条件2019y <，执行循环体，2,3x y ==； 满足条件2019y <，执行循环体，1,4x y =-= ；…观察规律可知，x 的取值周期为3，由于20196733⨯＝，可得：满足条件2019y <，执行循环体，当2,2019x y == ,不满足条件2019y <，退出循环，输出x 的值为2．故选D ．【点睛】本题主要考查了循环结构的程序框图，依次写出每次循环得到的x ，y 的值，根据循环的周期，得到跳出循环时x 的值是解题的关键．11．A解析：A【解析】【分析】模拟程序的运行，依次写出每次循环得到的x ，n 的值，由题意判断退出循环的条件即可得解．【详解】模拟程序的运行，可得n ＝1，x ＝1不满足条件x ＞a ，执行循环体，x ＝1，n ＝2不满足条件x ＞a ，执行循环体，x ＝2，n ＝3不满足条件x ＞a ，执行循环体，x ＝6，n ＝4不满足条件x ＞a ，执行循环体，x ＝24，n ＝5此时，由题意应该满足条件x ＞a ，退出循环，输出n 的值为5．可得：6≤a ＜24．故选：A ．【点睛】本题考查的知识点是循环结构的程序框图的应用，当循环的次数不多，或有规律时，常采用模拟循环的方法解答，属于基础题．12．C解析：C【解析】【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算并输出变量a 的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【详解】由题意，模拟程序的运算，可得k 1=，a 1=满足判断框内的条件，执行循环体，a 6=，k 3=满足判断框内的条件，执行循环体，a 33=，k 5=满足判断框内的条件，执行循环体，a 170=，k 7=此时，不满足判断框内的条件，退出循环，输出a 的值为170．则分析各个选项可得程序中判断框内的“条件”应为k 6<？故选：C ．【点睛】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．二、填空题13．31【解析】分析程序中各变量各语句的作用再根据流程图所示的顺序可知：该程序的作用是计算并输出分段函数的函数值当时则故答案为31点睛：算法是新课程中的新增加的内容也必然是新高考中的一个热点应高度重视程 解析：31【解析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是计算并输出分段函数()0.550{250.65050x x y x x ≤=+-，，＞ 的函数值，当60x =时，则y 250.6605031=+-=（），故答案为31.点睛：算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．程序填空也是重要的考试题型，这种题考试的重点有：①分支的条件②循环的条件③变量的赋值④变量的输出．其中前两点考试的概率更大．此种题型的易忽略点是：不能准确理解流程图的含义而导致错误.14．A 【解析】【分析】模拟执行程序框图依次写出每次循环得到的k 的值当k=2012时不满足条件退出循环输出的值为【详解】模拟执行程序框图可得满足条件满足条件满足条件满足条件由此可见S 的周期为3故当k=20解析：A【解析】【分析】模拟执行程序框图，依次写出每次循环得到的k ，S 的值，当k=2012时不满足条件2011k ≤ ，退出循环，输出S 的值为12. 【详解】模拟执行程序框图，可得2,1S k ==满足条件2011k ≤，1,22S k ==， 满足条件2011k ≤，1,3S k =-=， 满足条件2011k ≤，2,4S k ==，满足条件2011k ≤，1,52S k ，== 由此可见S 的周期为3，20113670...1,÷= 故当k=2012时不满足条件2011k ≤ ，退出循环，输出S 的值为12. 故选A.【点睛】本题主要考查了循环结构的程序框图，属于基础题． 15．72【分析】模拟程序的运行依次写出每次循环得到的的值可得当时不满足条件退出循环输出的值为72【详解】模拟程序的运行可得满足条件执行循环体满足条件执行循环体；满足条件执行循环体;满足条件执行循环体；不 解析：72【分析】模拟程序的运行，依次写出每次循环得到的S i ，的值，可得当9i = 时不满足条件8i ＜，退出循环，输出S 的值为72.【详解】模拟程序的运行，可得10,i S ==， 满足条件8i ＜，执行循环体，39;i S ==，满足条件8i ＜，执行循环体，524i S ==， ；满足条件8i ＜，执行循环体，745i S ==， ;满足条件8i ＜，执行循环体，9i =，72S =；不满足条件8i ＜，退出循环，输出S 的值为72,故答案为72【点睛】本题考查循环结构的程序框图的应用，当循环的次数不多或有规律时，常采用模拟执行程序的方法解决，属于基础题．16．9【解析】模拟程序的运行可得第一次执行循环不满足则返回继续循环；不满足则返回继续循环；不满足则返回继续循环；当时则最小值为此时故答案为点睛：识别运行程序框图和完善程序框图的思路：(1)要明确程序框图 解析：9【解析】模拟程序的运行，可得0S =，1n =，第一次执行循环，20log 21S =+=，12n n =+=，不满足3S >，则返回继续循环；231log 2S =+，13n n =+=，不满足3S >，则返回继续循环；22341log log 11223S =++=+=，14n n =+=，不满足3S >，则返回继续循环；⋅⋅⋅当n k =时，222234111log log log 1log 232k k S k ++=+++⋅⋅⋅+=+，1n k =+则211log 32k S +=+>，8k ≥，k 最小值为8，此时19n k =+=. 故答案为9.点睛：识别、运行程序框图和完善程序框图的思路：(1)要明确程序框图的顺序结构、条件结构和循环结构；(2)要识别、运行程序框图，理解框图所解决的实际问题；(3)按照题目的要求完成解答并验证．17．48【解析】第1次运行成立第2次运行成立第3次运行成立第3次运行不成立故输出的值为48解析：48【解析】第1次运行，1,2,122,4i S S i ===⨯=<成立第2次运行，2,2,224,4i S S i ===⨯=<成立第3次运行，3,4,3412,4i S S i ===⨯=<成立第3次运行，4,12,41248,4i S S i ===⨯=<不成立，故输出S 的值为4818．【解析】试题分析：当时；当时；当时此时故答案为考点：程序框图的应用解析：2【解析】试题分析：当16x =时，2log 1641y ==>；当4x =时，2log 421y ==>；当2x =时，2log 21y ==，此时2x =.故答案为2.考点：程序框图的应用.19．1【解析】试题分析：根据程序框图可知该程序执行的是所以输出的的值为1考点：本小题主要考查程序框图的执行和对数的运算点评：高考中程序框图的题目一般离不开循环结构要分清是当型循环还是直到型循环要搞清楚退 解析：1【解析】 试题分析：根据程序框图可知，该程序执行的是34103410lg 2lg lg lg lg(2)lg101239239b =++++=⋅⋅⋅⋅==，所以输出的的值为1. 考点：本小题主要考查程序框图的执行和对数的运算. 点评：高考中程序框图的题目一般离不开循环结构，要分清是当型循环还是直到型循环，要搞清楚退出循环的条件，避免多执行或少执行一步. 20．1320【分析】由题意结合所给的流程图执行程序确定其输出值即可【详解】程序运行如下：首先初始化数据：第一次循环满足执行；第二次循环满足执行；第三次循环不满足跳出循环输出故答案为【点睛】识别运行程序框 解析：1320【分析】由题意结合所给的流程图执行程序，确定其输出值即可.【详解】程序运行如下：首先初始化数据：12,1i S ==，第一次循环，满足10i ≥，执行12,111S S i i i =⨯==-=；第二次循环，满足10i ≥，执行132,110S S i i i =⨯==-=；第三次循环，不满足10i ≥，跳出循环，输出1320S =.故答案为1320．【点睛】识别、运行程序框图和完善程序框图的思路：(1)要明确程序框图的顺序结构、条件结构和循环结构．(2)要识别、运行程序框图，理解框图所解决的实际问题．(3)按照题目的要求完成解答并验证．三、解答题21．（1）见解析；（2）第1次：35,1M k ==；第3次：35,1M k ==；第5次：47,4M k ==【分析】（1）直接画出流程框图得到答案.（2）直接根据流程框图计算得到答案.【详解】（1）（2）根据程序框图：35,1M k ==，24M <不成立，23M <不成立，47M <成立， 故47,4M k ==，43M <不成立，输出结果，故第1次：35,1M k ==；第3次：35,1M k ==；第5次：47,4M k ==.【点睛】本题考查了程序框图，意在考查学生的理解能力和应用能力.22．见解析【分析】利用二分法得到算法：取[,]a b 中点01()2b x a =+，判断()0()f a f x 符号，依次进行直到满足精度，再画出流程图得到答案.【详解】算法：第一步：取[,]a b 中点01()2b x a =+，将区间一分为二； 第二步：若()00f x =，则0x 就是方程的根；否则所求根*x 在0x 左侧或右侧； 若()0()0f a f x >，则()*0,x x b ∈，以0x 代替a ； 若()0()0f a f x <，则()*0,x a x ∈，以0x 代替b ；第三步：若||a b c -<，计算终止，此时*0x x ≈，否则转到第一步.【点睛】本题考查了利用二分法解方程的算法和程序框图，意在考查学生的理解能力和应用能力. 23．见解析【解析】【分析】根据分段函数的解析式，设置判断框并设置出判断条件，确定好判断框的“是”与“否”，由此可得出程序框图，即可求解．【详解】解算法如下：第一步：输入物品重量ω；第二步：如果50ω≤，那么0.53f ω＝，否则，(500.535)500.8f ω⨯⨯＝＋－；第三步：输出物品重量ω和托运费f .程序框图如下：【点睛】本题主要考查了算法与程序框图的实际应用，解答中根据分段函数的解析式，设置出判断框，并设置出判断条件是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题．24．见解析；【解析】试题分析: 先利用INPUT 语句输入两个正数a 和b 的值，再分别赋值a b 和b a 的值，最后输出a b 和b a 的值试题程序和程序框图分别如下：25．见试题解析．【解析】【分析】根据圆台的体积和表面积公式依次按顺序输入公式，写成顺序结构即可.【详解】算法步骤如下：第一步：12r =，24r =，5h =．第二步：计算()2221l r r h =-+．第三步：计算211S r π=，222S r π=，()312S r r l π=+．第四步：计算123S S S S =++，()112213V S S S S h =++． 第五步：输出S 和V ．程序框图如下图所示．【点睛】（1）程序框图是流程图的一种，程序框图有一定的规范和标准，而日常生活中的流程图则相对自由一些，可以使用不同的色彩，也可以添加一些生动的图形元素．（2）画算法的程序框图，一般需要将自然语言描述的算法的每一个步骤分解为若干输入、输出、条件结构、循环结构等基本算法单元，然后根据各单元的逻辑关系，用流程线将这些基本单元连接起来．即基本单元是构成程序框图的基本要素，基本要素之间的关系由流程线建立． 26．见解析【解析】试题分析：分析程序中各变量、各语句的作用，再根据循环语句找到能被15整除的正整数，在1000n ＞ 时结束循环体，由此设计算法及画出框图．试题算法如下:S1 n=1;S2 若n ≤66,则执行S3,否则执行S6;S3 a=15n ;S4 输出a ;S5n=n+1,重复执行S2; S6结束.程序框图如图所示.。
人教版数学高一 第一章《算法初步》单元测试题三(新人教A版必修3)
第一章算法单元测试题3（人教A 版必修3）一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代号填在题后的括号内（本大题共12个小题，每小题5分，共60分）。
1．下列语句中是算法的个数为 （ ） ①从济南到巴黎：先从济南坐火车到北京，再坐飞机到巴黎； ②统筹法中“烧水泡茶”的故事； ③测量某棵树的高度，判断其是否是大树； ④已知三角形的一部分边长和角，借助正余弦定理求得剩余的边角，再利用三角形的面积公式求出该三角形的面积。
A ．1 B ．2 C ．3 D ．4 2．（文）下图为某三岔路口交通环岛的简化模型， 在某 高峰时段，单位时间进出路口 A 、B 、 C 的机动车辆数 如图所示，图中 123,,x x x 分别表示该时段单位时间通过 路段 AB ⋂,BC ⋂CA ⋂的机动车辆数（假设：单位时间内，在 上述路段中，同一路段上驶入与驶出的车辆数相等），则（ ）A ．123x x x >>B ．132x x x >>C ．231x x x >>D ．321x x x >>（理）下列说法正确的是（ ）A ．算法就是某个问题的解题过程；B ．算法执行后可以产生不同的结果；C ．解决某一个具体问题算法不同结果不同；D ．算法执行步骤的次数不可以为很大，否则无法实施。
3．284和1024的最小公倍数是 （ ） A ．1024 B ．142 C ．72704 D ．568 4．用冒泡法对数据{7，6，3，9，2}，从小到大排序，第3趟结果是 （ ） A ．2,3,6,7,9 B ．3,6,2,7,9 C ．3,2,6,7,9 D ．2,3,7,6,9 5．给出以下四个问题, （ ）①输入一个数x ,输出它的相反数. ②求面积为6的正方形的周长. ③求三个数a,b,c 中的最大数. ④求二进数111111的值.其中不需要用条件语句来描述其算法的有 （ ）A ．1个B ．2个C ．3个D ．4个6．用秦九韶算法计算多项式654235683512)(x x x x x x f +++-+=在4-=x 时的值 时,3V 的值为（ ） A ．－144 B ．－136 C ．－57 D ．34 7．下列各数中最小的一个是 （ ） A ．111111（2） B ．210（6） C ．1000（4） D ．81（8） 8．读程序甲： i=1 乙：i=1000 S=0 S=0 WHILE i≤1000 DOS=S+i S=S+ii=i+l i=i－1WEND LOOP UNTIL i<1PRINT S PRINT SEND END对甲、乙两程序和输出结果判断正确的是（）A．程序不同结果不同B．程序不同，结果相同C．程序相同结果不同D．程序相同，结果相同9．（文）为解决四个村庄用电问题，政府投资在已建电厂与这四个村庄之间架设输电线路，现已知这四个村庄及电厂之间的距离如图所示（距离单位：公里）则能把电力输送到这四个村庄的输电线路的最短总长度应该是（）A．19.5 B．20.5 C．21.5 D．25.5（理）任何一个算法都必须有的基本结构是（）A．顺序结构B．条件结构C．循环结构D．三个都有10．有一堆形状、大小相同的珠子,其中只有一粒重量比其它的轻,某同学经过思考,他说根据科学的算法，利用天平，三次肯定能找到这粒最轻的珠子,则这堆珠子最多有几粒（）A．21 B．24 C．27 D．3011．为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密),已知加密规则为:明文a,b,c,d对应密文a+2b,2b+c,2c+3d,4d,例如,明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为（）A．4,6,1,7 B．7,6,1,4 C．6,4,1,7 D．1,6,4,712．程序：x=1y=1WHILE x<=4Z=0WHILE y<=x+2Z=Z+1y=y+1WENDPRINT Zx=x+1y=1WENDEND运行后输出的结果为（）A．3 4 5 6 B．4 5 6 7 C．5 6 7 8 D．6 7 8 9（第14题）第Ⅱ卷二、填空题：请把答案填在题中横线上（本大题共4个小题，每小题4分，共16分）。
高一数学必修三章算法初步单元测试题(含答案)
三一文库（）/高一〔高一数学必修三章算法初步单元测试题(含答案)[1]〕(时间：120分钟满分：150分)一、选择题(本大题共12小题，每小题5分，满分60分．在每小题给出的四个选项中，有且只有一项是符合题目要求的) 1．算法共有三种逻辑结构，即顺序结构、条件结构、循环结构，下列说法正确的是( )A．一个算法只能含有一种逻辑结构B．一个算法最多可以包含两种逻辑结构C．一个算法必须含有上述三种逻辑结构D．一个算法可能含有上述三种逻辑结构解析通读四个选项知，答案D最为合理，应选D.答案 D2．下列赋值语句正确的是( )A．M＝a＋1 B．a＋1＝MC．M－1＝a D．M－a＝1解析根据赋值语句的功能知，A正确．答案 A3．学了算法你的收获有两点，一方面了解我国古代数学家的杰出成就，另一方面，数学的机械化，能做许多我们用笔和纸不敢做的有很大计算量的问题，这主要归功于算法语句的( )A．输出语句 B．赋值语句C．条件语句 D．循环语句解析由题意知，应选D.答案 D4．读程序其中输入甲中i＝1，乙中i＝1000，输出结果判断正确的是( )A．程序不同，结果不同B．程序不同，结果相同C．程序相同，结果不同D．程序相同，结果相同解析图甲中用的是当型循环结构，输出结果是S＝1＋2＋3＋ (1000)而图乙中用的是直到型循环结构，输出结果是S＝1000＋999＋…＋3＋2＋1.可见这两图的程序不同，但输出结果相同，故选B.答案 B5．程序框图(如图所示)能判断任意输入的数x的奇偶性，其中判断框内的条件是( )A．m＝0? B．x＝0?C．x＝1? D．m＝1?解析阅读程序易知，判断框内应填m＝1？，应选D.答案 D6．840和1764的公约数是( )A．84 B．12C．168 D．252解析∵1764＝840×2＋84,840＝84×10，∴1764与840的公约数是84.答案 A7．用秦九韶算法求多项式：f(x)＝12＋35x－8x2＋79x3＋6x4＋5x5＋3x6在x＝－4的值时，v4的值为( )A．－57 B．220C．－845 D．3392解析f(x)＝(((((3x＋5)x＋6)x＋79)x－8)x＋35)x＋12 当x＝－4时，v0＝3；∴v1＝3×(－4)＋5＝－7；v2＝－7×(－4)＋6＝34，v3＝34×(－4)＋79＝－57；v4＝－57×(－4)－8＝220. 答案 B8．1001101(2)与下列哪个值相等( )A．115(8) B．113(8)C．114(8) D．116(8)解析先化为十进制：1001101(2)＝1×26＋23＋22＋20＝77，再化为八进制，∴77＝115(8)，∴100110(2)＝115(8)．答案 A9．下面程序输出的结果为( )A．17 B．19C．21 D．23解析当i＝9时，S＝2×9＋3＝21，判断条件9>＝8成立，跳出循环，输出S.答案 C10．已知程序：上述程序的含义是( )A．求方程x3＋3x2－24x＋3＝0的零点。
高中数学必修三第一、二章《算法初步》单元测试题
高中数学必修三第一、二章《算法初步》单元测试题(120分钟150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列推理错误的是( )A.A∈l,A∈α,B∈l,B∈α⇒l⊂αB.A∈α,A∈β,B∈α,B∈β⇒α∩β=ABC.l⊄α,A∈l⇒A∉αD.A∈l,l⊂α⇒A∈α2.一个等腰三角形绕它的底边所在直线旋转360°形成的曲面所围成的几何体是( )A.球体B.圆柱C.圆台D.两个共底面的圆锥组成的组合体3.如图所示为某一平面图形的直观图,则此平面图形可能是下图中的( )4.下列命题正确的是( )A.一直线与一个平面内的无数条直线垂直,则此直线与平面垂直B.两条异面直线不能同时垂直于一个平面C.直线与平面所成的角的取值范围是:0°<θ≤180°D.两异面直线所成的角的取值范围是:0°<θ<90°.5.用一个平行于水平面的平面去截球,得到如图所示的几何体,则它的俯视图是( )【补偿训练】某几何体的三视图如图所示,则这个几何体是( )A.三棱锥B.三棱柱C.四棱锥D.四棱柱6.已知m,n是两条不同直线,α,β是两个不同平面,则下列命题正确的是( )A.若α,β垂直于同一平面,则α与β平行B.若m,n平行于同一平面,则m与n平行C.若α,β不平行,则在α内不存在与β平行的直线D.若m,n不平行,则m与n不可能垂直于同一平面7.已知一平面平行于两条异面直线,一直线与两异面直线都垂直,那么这个平面与这条直线的位置关系是( )A.平行B.垂直C.斜交D.不能确定8.如图,将一个正方体沿相邻三个面的对角线截出一个棱锥,则棱锥的体积与原正方体的体积之比为( )A.1∶3B.1∶4C.1∶5D.1∶69.某几何体的三视图如图所示,则该几何体的表面积等于( )A.8+2B.11+2C.14+2D.15【补偿训练】已知圆台上、下底面面积分别是π,4π,侧面积是6π,则这个圆台的体积是( )A. B.2π C. D.10.在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成的角的正弦值为( )A. B. C. D.【拓展延伸】探究空间角问题(1)求空间角的基本原则求空间角时,无论哪种情况最终都归结到两条相交直线所成的角的问题上.(2)解题步骤:①找(或作)出所求角;②证明该角符合题意;③构造出含这个角的三角形,解这个三角形,求出角.(3)空间角包括以下三类:①求异面直线所成的角,关键是选取合适的点引两条异面直线的平行线,这两条相交直线所成的锐角或直角即为两条异面直线所成的角.②求直线与平面所成的角,关键是在斜线上选取恰当的点向平面引垂线,在此基础上进一步确定垂足的位置.③求二面角,关键是作出二面角的平面角,而作二面角的平面角时,首先要确定二面角的棱,然后结合题设构造二面角的平面角.一般常用两种方法:定义法,垂面法.11.矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为( )A.πB.πC.πD.π12.已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是( )A.2πR2B.πR2C.πR2D.πR2二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.设平面α∥平面β,A,C∈α,B,D∈β,直线AB与CD交于点S,且点S位于平面α,β之间,AS=8,BS=6,CS=12,则SD= .14.一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.【补偿训练】若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是.15.如图,圆锥SO中,AB,CD为底面圆的两条直径,AB∩CD=O,且AB⊥CD,SO=OB=2,P为SB的中点,则异面直线SA与PD所成角的正切值为.16.如图,AB是☉O的直径,C是圆周上不同于A,B的点,PA垂直于☉O所在的平面,AE⊥PB于E,AF⊥PC于F,因此, ⊥平面PBC.(填图中的一条直线)【补偿训练】如图,已知ABCD是矩形,且PA⊥平面ABCD,则下列结论中不正确的是( )A.平面PAB⊥平面PADB.平面PCD⊥平面PADC.平面PAB⊥平面PBCD.平面PCD⊥平面PBC三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)(2015·全国卷Ⅱ)如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A 1B1,D1C1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法与理由).(2)求平面α把该长方体分成的两部分体积的比值.【补偿训练】圆柱有一个内接长方体AC 1,长方体的体对角线长是10cm,圆柱的侧面展开图为矩形,此矩形的面积是100πcm 2,求圆柱的体积.18.(12分)(2015·常德高一检测)如图,在正三棱柱ABC-A 1B 1C 1中,F,F 1分别是AC,A 1C 1的中点.求证:(1)平面AB 1F 1∥平面C 1BF. (2)平面AB 1F 1⊥平面ACC 1A 1.【补偿训练】如图已知在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC=BC,M,N,P,Q分别是AA1,BB1,AB,B1C1的中点.(1)求证:面PCC1⊥面MNQ.(2)求证:PC1∥面MNQ.19.(12分)如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC.(2)求证:平面MOC⊥平面VAB.(3)求三棱锥V-ABC的体积.20.(12分)如图是一个几何体的三视图,(1)画出这个几何体的直观图.(2)求这个几何体的侧面积.(3)求这个几何体的体积.21.(12分)直三棱柱的高为6 cm,底面三角形的边长分别为3 cm,4 cm,5 cm,将棱柱削成圆柱,求削去部分体积的最小值.22.(12分)(2015·淄博高一检测)已知一四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点.(1)求四棱锥P-ABCD的体积.(2)若点E为PC的中点,AC∩BD=O,求证EO∥平面PAD.(3)是否不论点E在何位置,都有BD⊥AE?证明你的结论.【补偿训练】如图所示,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.求证:(1)直线EF∥平面PCD.(2)平面BEF⊥平面PAD.高中数学必修三第一、二章《算法初步》单元测试题参考答案(120分钟150分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列推理错误的是( )A.A∈l,A∈α,B∈l,B∈α⇒l⊂αB.A∈α,A∈β,B∈α,B∈β⇒α∩β=ABC.l⊄α,A∈l⇒A∉αD.A∈l,l⊂α⇒A∈α【解析】选C.若直线l∩α=A,显然有l⊄α,A∈l,但A∈α.2.一个等腰三角形绕它的底边所在直线旋转360°形成的曲面所围成的几何体是( )A.球体B.圆柱C.圆台D.两个共底面的圆锥组成的组合体【解析】选D.等腰三角形的底边所在直线为旋转轴,所得几何体是两个共底面的圆锥组成的组合体.3.如图所示为某一平面图形的直观图,则此平面图形可能是下图中的( )【解析】选A.由直观图知,原四边形一组对边平行且不相等为梯形,且梯形两腰不能与底垂直.4.下列命题正确的是( )A.一直线与一个平面内的无数条直线垂直,则此直线与平面垂直B.两条异面直线不能同时垂直于一个平面C.直线与平面所成的角的取值范围是:0°<θ≤180°D.两异面直线所成的角的取值范围是:0°<θ<90°.【解析】选B. A错误,一直线与一个平面内的无数条直线垂直,并不意味着和平面内的任意直线垂直,所以此直线与平面不一定垂直;B正确,由线面垂直的性质定理可知,两条异面直线不能同时垂直于一个平面;C错误,直线与平面所成的角的取值范围是:0°≤θ≤90°;D错误,两异面直线所成的角的取值范围是:0°<θ≤90°.5.(2015·深圳高二检测)用一个平行于水平面的平面去截球,得到如图所示的几何体,则它的俯视图是( )【解析】选B. D选项为正视图或侧视图,俯视图中显然应有一个被遮挡的圆,所以内圆是虚线. 【补偿训练】某几何体的三视图如图所示,则这个几何体是( )A.三棱锥B.三棱柱C.四棱锥D.四棱柱【解题指南】本题考查的是几何体的三视图,在判断时要结合三种视图进行判断.【解析】选B.由题知,该几何体的三视图为一个三角形,两个四边形,经分析可知该几何体为三棱柱.6.(2015·安徽高考)已知m,n是两条不同直线,α,β是两个不同平面,则下列命题正确的是( )A.若α,β垂直于同一平面,则α与β平行B.若m,n平行于同一平面,则m与n平行C.若α,β不平行,则在α内不存在与β平行的直线D.若m,n不平行,则m与n不可能垂直于同一平面【解析】选D.7.(2015·长白山高一检测)已知一平面平行于两条异面直线,一直线与两异面直线都垂直,那么这个平面与这条直线的位置关系是( )A.平行B.垂直C.斜交D.不能确定【解析】选B.根据线面平行的性质,在已知平面内可以作出两条相交直线与已知两条异面直线分别平行.因此,一直线与两异面直线都垂直,一定与这个平面垂直.8.如图,将一个正方体沿相邻三个面的对角线截出一个棱锥,则棱锥的体积与原正方体的体积之比为( )A.1∶3B.1∶4C.1∶5D.1∶6【解析】选D.设正方体的棱长为a,则棱锥的体积V1=××a×a×a=,又正方体的体积V2=a3,所以=.9.(2015·福建高考)某几何体的三视图如图所示,则该几何体的表面积等于( )A.8+2B.11+2C.14+2D.15【解析】选B.由三视图可知,该几何体为底面是直角梯形的直四棱柱,所以S=2×(1+2)×1×+2×2+1×2+1×2+×2=11+2.【补偿训练】已知圆台上、下底面面积分别是π,4π,侧面积是6π,则这个圆台的体积是( )A. B.2π C. D.【解析】选D.上底半径r=1,下底半径R=2.因为S侧=6π,设母线长为l,则π(1+2)·l=6π.所以l=2.所以高h==.所以V=π·(12+1×2+22)=π.10.在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成的角的正弦值为( )A. B. C. D.【解析】选D.在平面A1B1C1D1内过点C1作B1D1的垂线,垂足为E,连接BE.⇒C1E⊥平面BDD1B1,所以∠C1BE的正弦值就是所求角的正弦值.因为BC1==,C1E==,所以sin∠C1BE===.【拓展延伸】探究空间角问题(1)求空间角的基本原则求空间角时,无论哪种情况最终都归结到两条相交直线所成的角的问题上.(2)解题步骤:①找(或作)出所求角;②证明该角符合题意;③构造出含这个角的三角形,解这个三角形,求出角.(3)空间角包括以下三类:①求异面直线所成的角,关键是选取合适的点引两条异面直线的平行线,这两条相交直线所成的锐角或直角即为两条异面直线所成的角.②求直线与平面所成的角,关键是在斜线上选取恰当的点向平面引垂线,在此基础上进一步确定垂足的位置.③求二面角,关键是作出二面角的平面角,而作二面角的平面角时,首先要确定二面角的棱,然后结合题设构造二面角的平面角.一般常用两种方法:定义法,垂面法.11.矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为( )A.πB.πC.πD.π【解析】选C.球心O为AC中点,半径为R=AC=,V=πR3=π.12.(2015·滁州高二检测)已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是( )A.2πR2B.πR2C.πR2D.πR2【解析】选B.设圆柱底面半径为r,则其高为3R-3r,全面积S=2πr2+2πr(3R-3r)=6πRr-4πr2=-4π+πR2,故当r=R时全面积有最大值πR2.二、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)13.设平面α∥平面β,A,C∈α,B,D∈β,直线AB与CD交于点S,且点S位于平面α,β之间,AS=8,BS=6,CS=12,则SD= .【解析】由面面平行的性质得AC∥BD,=,解得SD=9.答案:914.(2015·天津高考)一个几何体的三视图如图所示(单位:m),则该几何体的体积为m3.【解析】由三视图可知,该几何体是中间为一个底面半径为1,高为2的圆柱,两端是底面半径为1,高为1的圆锥,所以该几何体的体积V=12×π×2+2××12×π×1=π(m3).答案:π【补偿训练】若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是.【解析】由三视图可知此几何体是由一个底面为正方形的四棱柱和一个底面是梯形的四棱柱拼接而成的,所以此几何体的体积是V=2×2×4+×(2+6)×2×4=48(cm3).答案:48cm315.如图,圆锥SO中,AB,CD为底面圆的两条直径,AB∩CD=O,且AB⊥CD,SO=OB=2,P为SB的中点,则异面直线SA与PD所成角的正切值为.【解析】连接PO,则PO∥SA,所以∠OPD即为异面直线SA与PD所成的角,且△OPD为直角三角形,∠POD为直角,所以tan∠OPD===.答案:16.(2015·福州高一检测)如图,AB是☉O的直径,C是圆周上不同于A,B的点,PA垂直于☉O 所在的平面,AE⊥PB于E,AF⊥PC于F,因此, ⊥平面PBC.(填图中的一条直线)【解题指南】将问题转化为证明AF⊥BC,AF⊥PC,从而证明AF⊥平面PBC.【解析】因为AB是☉O的直径,C是圆周上不同于A,B的点,所以BC⊥AC,因为PA垂直于☉O所在的平面,所以BC⊥PA,又PA∩AC=A,所以BC⊥平面PAC,AF⊂平面PAC,所以AF⊥BC,又AF⊥PC,BC∩PC=C,所以AF⊥平面PBC.答案:AF【补偿训练】如图,已知ABCD是矩形,且PA⊥平面ABCD,则下列结论中不正确的是( )A.平面PAB⊥平面PADB.平面PCD⊥平面PADC.平面PAB⊥平面PBCD.平面PCD⊥平面PBC【解析】选D.由题意知,直线AB⊥平面PAD,直线CD⊥平面PAD,故选项A,B均正确;直线BC ⊥平面PAB,BC⊂平面PBC,故选项C正确,选项D错误.三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)(2015·全国卷Ⅱ)如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A 1B1,D1C1上,A1E=D1F=4,过点E,F的平面α与此长方体的面相交,交线围成一个正方形.(1)在图中画出这个正方形(不必说明画法与理由).(2)求平面α把该长方体分成的两部分体积的比值.【解析】(1)交线围成的正方形EHGF如图.(2)作EM⊥AB,垂足为M,则AM=A1E=4,EB1=12,EM=AA1=8,因为四边形EHGF为正方形,所以EH=EF=BC=10.于是MH==6,AH=10,HB=6.因为长方体被平面α分成两个高为10的直棱柱,所以其体积的比值为.【补偿训练】圆柱有一个内接长方体AC 1,长方体的体对角线长是10cm,圆柱的侧面展开图为矩形,此矩形的面积是100πcm 2,求圆柱的体积.【解析】设圆柱底面半径为rcm,高为hcm.如图所示,则圆柱轴截面长方形的对角线长等于它的内接长方体的体对角线长,则所以所以V 圆柱=Sh=πr 2h=π×52×10=250π(cm 3).18.(12分)(2015·常德高一检测)如图,在正三棱柱ABC-A 1B 1C 1中,F,F 1分别是AC,A 1C 1的中点.求证:(1)平面AB 1F 1∥平面C 1BF. (2)平面AB 1F 1⊥平面ACC 1A 1.【证明】(1)在正三棱柱ABC-A 1B 1C 1中, 因为F,F 1分别是AC,A 1C 1的中点, 所以B 1F 1∥BF,AF 1∥C 1F.又因为B 1F 1∩AF 1=F 1,C 1F ∩BF=F, 所以平面AB 1F 1∥平面C 1BF. (2)在正三棱柱ABC-A 1B 1C 1中, AA 1⊥平面A 1B 1C 1,所以B 1F 1⊥AA 1. 又B 1F 1⊥A 1C 1,A 1C 1∩AA 1=A 1,所以B 1F 1⊥平面ACC 1A 1,而B 1F 1⊂平面AB 1F 1, 所以平面AB 1F 1⊥平面ACC 1A 1.【补偿训练】如图已知在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC=BC,M,N,P,Q分别是AA1,BB1,AB,B1C1的中点.(1)求证:面PCC1⊥面MNQ.(2)求证:PC1∥面MNQ.【证明】(1)因为AC=BC,P是AB的中点,所以AB⊥PC,因为AA1⊥面ABC,CC1∥AA1,所以CC1⊥面ABC,而AB在平面ABC内,所以CC1⊥AB,因为CC1∩PC=C,所以AB⊥面PCC1,又因为M,N分别是AA1,BB1的中点,四边形AA1B1B是平行四边形,所以MN∥AB,所以MN⊥面PCC1,MN在平面MNQ内,所以面PCC1⊥面MNQ.(2)连PB1与MN相交于K,连KQ,因为MN∥PB,N为BB1的中点,所以K为PB1的中点,又因为Q是C1B1的中点,所以PC1∥KQ,而KQ⊂平面MNQ,PC1⊄平面MNQ,所以PC1∥面MNQ19.(12分)(2015·北京高考)如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=,O,M分别为AB,VA的中点.(1)求证:VB∥平面MOC.(2)求证:平面MOC⊥平面VAB.(3)求三棱锥V-ABC的体积.【解析】(1)因为O,M分别为AB,VA的中点,所以OM∥VB.又因为OM⊂平面MOC,VB⊄平面MOC,所以VB∥平面MOC.(2)因为AC=BC,O为AB中点,所以OC⊥AB.因为平面VAB⊥平面ABC,交线AB,OC⊂平面ABC,所以OC⊥平面VAB. 因为OC⊂平面MOC,所以平面MOC⊥平面VAB.(3)由(2)知OC为三棱锥C-VAB的高,因为AC⊥BC且AC=BC=,所以OC=1,AB=2.因为△VAB为等边三角形,所以S△VAB=×2×=.V V-ABC=V C-VAB=××1=.20.(12分)如图是一个几何体的三视图,(1)画出这个几何体的直观图.(2)求这个几何体的侧面积.(3)求这个几何体的体积.【解析】(1)此几何体是上底边长为3,下底边长为5,高为3的正四棱台.(2)棱台侧面梯形的高为=,所以棱台的侧面积S侧=(3+5)××4=16.(3)棱台的体积V=(S++S')·h=×(52++32)×3=49.21.(12分)直三棱柱的高为6 cm,底面三角形的边长分别为3 cm,4 cm,5 cm,将棱柱削成圆柱,求削去部分体积的最小值.【解析】如图所示,只有当圆柱的底面圆为直三棱柱的底面三角形的内切圆时,圆柱的体积最大,削去部分体积才能最小,设此时圆柱的底面半径为R,圆柱的高即为直三棱柱的高6cm.因为在△ABC中,AB=3cm,BC=4cm,AC=5cm,所以△ABC为直角三角形.根据直角三角形内切圆的性质可得7-2R=5,所以R=1cm,所以V圆柱=πR2·h=6πcm3.而三棱柱的体积为V三棱柱=×3×4×6=36(cm3),所以削去部分的体积为36-6π=6(6-π)(cm3).22.(12分)(2015·淄博高一检测)已知一四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点.(1)求四棱锥P-ABCD的体积.(2)若点E为PC的中点,AC∩BD=O,求证EO∥平面PAD.(3)是否不论点E在何位置,都有BD⊥AE?证明你的结论.【解析】(1)由该四棱锥的三视图可知,该四棱锥P-ABCD的底面是边长为1的正方形,侧棱PC ⊥底面ABCD,且PC=2.所以V P-ABCD=S▱ABCD·PC=.(2)因为EO∥PA,EO⊄平面PAD,PA⊂平面PAD.所以EO∥平面PAD.(3)不论点E在何位置,都有BD⊥AE,证明如下:因为ABCD是正方形,所以BD⊥AC,因为PC⊥底面ABCD且BD⊂平面ABCD,所以BD⊥PC,又因为AC∩PC=C,所以BD⊥平面PAC,因为不论点E在何位置,都有AE⊂平面PAC,所以不论点E在何位置,都有BD⊥AE.【补偿训练】(2015·金华高二检测)如图所示,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.求证:(1)直线EF∥平面PCD.(2)平面BEF⊥平面PAD.【证明】(1)因为E,F分别为AP,AD的中点,所以EF∥PD.又因为EF⊄平面PCD,PD⊂平面PCD,所以直线EF∥平面PCD.(2)连接DB,如图,因为AB=AD,∠BAD=60°,所以△ABD为正三角形.因为点F是AD的中点,所以BF⊥AD.因为平面PAD⊥平面ABCD,BF⊂平面ABCD,平面PAD∩平面ABCD=AD,所以BF⊥平面PAD . 又因为BF⊂平面BEF,所以平面BEF⊥平面PAD.。
(典型题)高中数学必修三第二章《算法初步》测试卷(有答案解析)
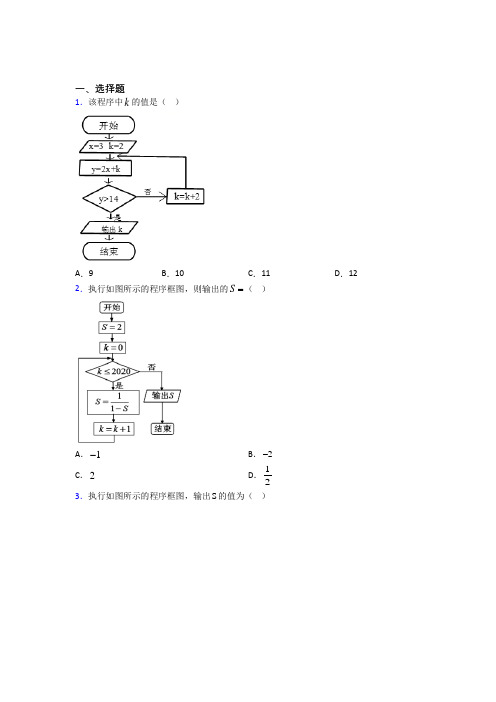
一、选择题1．该程序中k的值是（）A．9 B．10 C．11 D．12 2．执行右面的程序框图，若输入的,,a b k分别为1,2,3，则输出的M ( )A．203B．72C．165D．1583．执行如图所示的程序框图，若输入的a，b的值分别为1，1，则输出的S是（）A ．25B ．18C ．11D ．34．二分法是求方程近似解的一种方法，其原理是“一分为二，无限逼近”．执行如图所示的程序框图，若输入11x =，22x =，0.1d =，则输出n 的值为（ ）A ．2B ．3C ．4D ．55．执行如图所示的程序框图，如果输入x ＝5，y ＝1，则输出的结果是（ ）A．261 B．425 C．179 D．5446．元朝著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒，携着游春走，遇店添一倍，逢友饮一斗，店友经三处，没了壶中酒，借问此壶中，当原多少酒?”用程序框图表达如图所示，即最终输出的0x=，则一开始输入的x的值为( )A．34B．78C．1516D．31327．如图，“大衍数列”：0，2，4，8，12….来源于《乾坤谱》中对《易传》“大衍之数五十”的推论，主要用于解释中国传统文化中的太极衍生过程中曾经经历过的两仪数量总和.下图是求大衍数列前n项和的程序框图.执行该程序框图，输入10m=，则输出的S=（）A．100 B．140 C．190 D．250 8．执行如图所示的程序框图，则输出的k的值为（）A．3 B．4 C．5 D．6 9．读下面的程序：上面的程序在执行时如果输入6，那么输出的结果为()A．6 B．720 C．120 D．5040 10．执行如图所示的程序框图，若输出的值为7，则框图中①处可以填入（）A ．7SB ．21SC ．28SD ．36S 11．执行如下图的程序框图，那么输出S 的值是( )A ．2B ．1C ．12D ．-112．执行如图所示程序框图，当输入的x 为2019时，输出的y ( )A ．28B ．10C ．4D ．2二、填空题13．执行如图所示的伪代码,则输出的S 的值是_______.14．阅读如图所示的程序框图，若121log 3a =，2logb e =，ln 2c =，则输出的结果是________.15．执行如图所示的程序框图，若输入n的值为8，则输出的s的值为_____．16．执行如下图所示的程序框图，则输出的结果n __________．17．执行如图所示的程序框图，输出S 的值为___________.18．用秦九韶算法求多项式()5432357911f x x x x x x =+-+-+当4x =时的值为____________.19．将二进制数110 101（2）转为七进制数，结果为________．20．执行如图所示的程序框图，若输入，则输出的值为__________________.三、解答题21．已知数列{}n a 的递推公式111n n n a a a --=+，且11a =，请画出求其前10项的流程图. 22．已知底面半径为r ，高为h 的圆柱和一正方体的体积相等，试设计一个程序分别求圆柱的表面积和正方体的表面积，并画出程序框图(π＝3. 14).23．读下列程序，写出此程序表示的函数，并求当输出的6y =时，输入的x 的值.24．程序框图如图,运行此程序,试求输出的b 的值.25．设计程序求π的近似值可以用公式:2222π1116123=+++…+21n ,用此公式求2π6,即逐项进行累加,直到21n <0.000 01为止(该项不累加),然后求出π的近似值. 26．任意输入三个赋值变量a ，b ，c ，编写计算2235a b c -+的值的程序．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【分析】本题只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可（注意避免计算错误）．【详解】3,2,8,814x k y ===<，第一次循环，4,10,1014k y ==<；第二次循环，6,12,1214k y ==<；第三次循环，8,14,1414k y ===；第四次循环，10,16,1614k y ==>，退出循环，输出10k =，故选：B.【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.2．D解析：D【详解】试题分析：根据题意由13≤成立，则循环，即1331,2,,2222M a b n =+====;又由23≤成立，则循环，即28382,,,33323M a b n =+====;又由33≤成立，则循环，即3315815,,,428838M a b n =+====;又由43≤不成立，则出循环，输出158M =． 考点：算法的循环结构3．C【分析】该程序的功能是利用循环结构计算并输出变量S 的值，模拟程序的运行过程，分析循环中各变量的变化情况，即可得到答案. 【详解】模拟执行程序框图，可得：1,1,1a b n ===， 第1次循环，可得3,1,3,2S a b n ====； 第2次循环，可得5,3,5,3S a b n ====； 第3次循环，可得11,5,11,4S a b n ====， 满足判断条件，输出11S =. 故选：C. 【点睛】本题主要考查了循环结构的程序框图的计算与输出，其中解答中模拟程序框图的运行过程，逐次计算，结合判断条件求解是解答的关键，意在考查运算与求解能力，属于基础题.4．C解析：C 【分析】按照用二分法求函数零点近似值的步骤求解即可，注意验证精确度的要求． 【详解】解：模拟程序的运行，可得121,1,2,0.1n x x d ====，令22f xx ，则()()110,220f f =-<=>，()1.5, 1.50.250m f ==>，满足条件()()120, 1.5f m f x x <=，此时1.510.50.1-=>，不符合精确度要求；()2, 1.25, 1.250.43750n m f ===-<，不满足条件()()110, 1.25f m f x x <=，此时1.5 1.250.250.1-=>，不符合精确度要求；()3, 1.375, 1.3750.1090n m f ===-<，不满足条件()()110, 1.375f m f x x <=，此时1.5 1.3750.1250.1-=>，不符合精确度要求；()4, 1.4375, 1.43750.0660n m f ===>，满足条件()()120, 1.4375f m f x x <=，此时1.4375 1.3750.06250.1-=<，符合精确度要求． 退出循环，输出n 的值为4． 故选：C. 【点睛】本题主要考查循环结构程序框图以及用二分法求区间根的问题，属于基础题型，二分法是把函数的零点所在区间一分为二，使区间的两个端点逐步逼近零点，进而求零点近似值的5．B解析：B 【分析】根据循环结构的条件，依次运算求解，即得解. 【详解】起始值：5,1,0x y n ===，满足1105<⨯，故：5,0,2x y n ===； 满足0105<⨯，故：7,4,4x y n ===； 满足4107<⨯，故：11,36,6x y n ===； 满足361011<⨯，故：17,144,8x y n ===； 满足1441017<⨯，故：25,400,10x y n ===； 此时：4001025>⨯，满足输出条件：输出425x y += 故选：B 【点睛】本题考查了程序框图的循环结构，考查了学生逻辑推理，数学运算的能力，属于中档题.6．B解析：B 【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算输入时变量x 的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得到答案. 【详解】本题由于已知输出时x 的值，因此可以逆向求解： 输出0x =,此时4i =； 上一步：1210,2x x -==,此时3i =； 上一步：1321,24x x -==,此时2i =； 上一步：3721,48x x -==,此时1i =； 故选：B . 【点睛】本题考查了程序框图的循环结构，考查了学生逻辑推理和数学运算的能力，属于基础题.7．C解析：C 【分析】根据程序框图进行运算,直到满足判断框中的条件,就停止运行,输出结果. 【详解】第一次运行,211,0,0002n n a S -====+=,不符合n m ≥,继续运行;第二次运行,22,22n n a ===,022S =+=,不符合n m ≥,继续运行,第三次运行,213,42n n a -===,426S =+=,不符合n m ≥,继续运行,第四次运行,24,82n n a ===,8614S =+=,不符合n m ≥,继续运行,第五次运行,5n =,21122n a -==,121426S =+=, 不符合n m ≥,继续运行,第六次运行,6n =,2182n a ==,182644S =+=, 不符合n m ≥,继续运行,第七次运行,217,242n n a -===,244468S =+=, 不符合n m ≥,继续运行,第八次运行,28,322n n a ===,3268100S =+=, 不符合n m ≥,继续运行,第九次运行,219,40,401001402n n a S -====+=, 不符合n m ≥,继续运行,第十次运行,210,50,501401902n n a S ====+=,符合n m ≥,退出运行,,输出190S =.故选:C 【点睛】本题考查了程序框图中循环结构,正确理解程序框图是解题关键,属于基础题. 8．C解析：C 【分析】根据框图模拟程序运算即可. 【详解】第一次执行程序，2111S =⨯-=，25S >-，继续循环，第二次执行程序，2k =，2121S =⨯-=-，25S >-，继续循环， 第三次执行程序，3k =，2(1)35S =⨯--=-，25S >-，继续循环， 第四次执行程序，4k =，2(5)414S =⨯--=-，25S >-，继续循环，第五次执行程序，5k =，2(14)532S =⨯--=-，25S <-，跳出循环，输出5k =，结束.故选C. 【点睛】本题主要考查了程序框图，涉及循环结构，解题关键注意何时跳出循环，属于中档题.9．B【解析】 【分析】执行程序，逐次计算，根据判断条件终止循环，即可求解输出的结果，得到答案. 【详解】由题意，执行程序，可得：第1次循环：满足判断条件，1,2S i ==； 第2次循环：满足判断条件，2,3S i ==； 第3次循环：满足判断条件，6,4S i ==； 第4次循环：满足判断条件，24,5S i ==； 第5次循环：满足判断条件，120,6S i ==； 第6次循环：满足判断条件，720,7S i ==； 不满足判断条件，终止循环，输出720S =，故选B. 【点睛】本题主要考查了循环结构的程序框图的计算输出，其中解答中正确理解循环结构的程序框图的计算功能，逐次计算是解答的关键，着重考查了推理与运算能力，属于基础题.10．C解析：C 【分析】根据程序框图列出所有的循环步骤，最后一次循环中的S 满足条件，以及倒数第二次循环中S 不满足条件来选择四个选项中的判断条件． 【详解】第一次循环：1S =，不满足条件，2i =； 第二次循环：3S =，不满足条件，3i =； 第三次循环：6S =，不满足条件，4i =； 第四次循环：10S =，不满足条件，5i =； 第五次循环：15S =，不满足条件，6i =； 第六次循环：21S =，不满足条件，7i =； 第七次循环：28S =，满足条件，输出的值为7． 所以判断框中的条件可填写“28S ”． 故选C ． 【点睛】本题考查程序框图中判断条件的选择，这种类型的问题一般要列举出所有的循环步骤，利用最后一次和倒数第二次循环中变量满足与不满足来筛选判断条件，考查逻辑推理能力，属于中等题．11．A解析：A 【解析】模拟程序的运行，依次写出每次循环得到的k 和S 值，根据题意即可得到结果. 【详解】程序运行如下，k=0, S ＝112-＝﹣1， k ＝1，S ＝()111--＝12；k ＝2，S ＝12112=-；k ＝3，S ＝11-2＝-1… 变量S 的值以3为周期循环变化，当k=2018时，s=2， K=2019时，结束循环，输出s 的值为2． 故选：A ． 【点睛】本题考查程序框图，是当型结构，即先判断后执行，满足条件执行循环，不满足条件，跳出循环，算法结束，解答的关键是算准周期，是基础题．12．C解析：C 【分析】x 的变化遵循以2-为公差递减的等差数列的变化规律，到0x <时结束，得到1x =-，然后代入解析式，输出结果. 【详解】0x ≥时，每次赋值均为2x -x 可看作是以2019为首项，2-为公差的等差数列{}n x()()20191220212n x n n ⇒=+-⨯-=-当0x <时输出，所以0n x <，即202120n -< 20212n ⇒>即：10100x >，10110x < 10112021210111x ⇒=-⨯=-1314y ∴=+=本题正确选项：C 【点睛】本题结合等差数列考查程序框图问题，关键是找到程序框图所遵循的规律.二、填空题13．110【分析】分析程序中各变量各语句的作用再根据顺序可知：该程序的作用是累加并输出的值利用等差数列的求和公式计算即可得解【详解】分析程序中各变量各语句的作用根据顺序可知：该程序的作用是累加并输出满足解析：110 【分析】分析程序中各变量、各语句的作用，再根据顺序，可知：该程序的作用是累加并输出24620S =++++的值，利用等差数列的求和公式计算即可得解.【详解】分析程序中各变量、各语句的作用，根据顺序，可知： 该程序的作用是累加并输出满足条件24620S =++++的值，由于10(220)246201102S +=++++==， 故输出的S 的值为：110， 故答案是：110. 【点睛】该题考查的用伪代码表示的循环结构的程序的相关计算，考查学生的运算求解能力，属于简单题目.14．【分析】首先分析程序框图的作用是输出三个数中的最大值从而比较三个数的大小求得结果【详解】根据题中所给的程序框图可以判断出其作用是输出三者中的最大出那个数因为而所以其最大值是故答案是：【点睛】该题考查 解析：a【分析】首先分析程序框图的作用是输出三个数中的最大值，从而比较三个数的大小，求得结果. 【详解】根据题中所给的程序框图，可以判断出其作用是输出三者中的最大出那个数， 因为12221log log 3log 13a eb ==>=>，而ln 21c =<， 所以其最大值是a ， 故答案是：a . 【点睛】该题考查的是有关程序框图的输出结果的求解问题，属于简单题目.15．8【分析】根据程序框图知该程序的功能是计算并输出变量的值模拟程序的运行过程即可求解【详解】当时满足循环条件当时满足循环条件当时满足循环条件；当时不满足循环条件跳出循环输出故填【点睛】本题主要考查了程解析：8 【分析】根据程序框图知，该程序的功能是计算并输出变量s 的值，模拟程序的运行过程即可求解. 【详解】当2i =时，满足循环条件，2,4,2s i k ===，当4i =时，满足循环条件，4,6,3s i k === ， 当6i =时，满足循环条件，8,8,4s i k ===； 当8i =时，不满足循环条件，跳出循环，输出8s =. 故填8. 【点睛】本题主要考查了程序框图，循环结构，属于中档题.16．9【解析】模拟程序的运行可得第一次执行循环不满足则返回继续循环；不满足则返回继续循环；不满足则返回继续循环；当时则最小值为此时故答案为点睛：识别运行程序框图和完善程序框图的思路：(1)要明确程序框图解析：9 【解析】模拟程序的运行，可得0S =，1n =，第一次执行循环，20log 21S =+=，12n n =+=，不满足3S >，则返回继续循环；231log 2S =+，13n n =+=，不满足3S >，则返回继续循环；22341log log 11223S =++=+=，14n n =+=，不满足3S >，则返回继续循环；⋅⋅⋅当n k =时，222234111log log log 1log 232k k S k ++=+++⋅⋅⋅+=+，1n k =+则211log 32k S +=+>，8k ≥，k 最小值为8，此时19n k =+=.故答案为9.点睛：识别、运行程序框图和完善程序框图的思路： (1)要明确程序框图的顺序结构、条件结构和循环结构； (2)要识别、运行程序框图，理解框图所解决的实际问题； (3)按照题目的要求完成解答并验证．17．48【解析】第1次运行成立第2次运行成立第3次运行成立第3次运行不成立故输出的值为48解析：48 【解析】第1次运行，1,2,122,4i S S i ===⨯=<成立 第2次运行，2,2,224,4i S S i ===⨯=<成立 第3次运行，3,4,3412,4i S S i ===⨯=<成立 第3次运行，4,12,41248,4i S S i ===⨯=<不成立， 故输出S 的值为4818．【解析】依据用秦九韶算法的算理可得：将代入可得其函数值为故应填答案点睛：解答本题的关键是准确理解秦九韶算法的算法原理和算法步骤先算出再算然后算出进而后算出最后算出 解析：1559【解析】依据用秦九韶算法的算理可得：()()()()()f x x 357911x x x x =+-+-+,将x 4=代入可得其函数值为1559，故应填答案1559。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一、单项选择题（共12小题，每小题5分，共60分）1. 算法的有穷性是指（）A. 算法必须包含输出B. 算法中每个操作步骤都是可执行的C. 算法的步骤必须有限D. 以上说法均不正确【答案】C【解析】试题分析：所谓算法有穷性是指一个算法应包含有限的操作步骤，即在执行有限操作后算法结束，从而可得结论．解：一个算法必须在有限步内结束，简单的说就是没有死循环即算法的步骤必须有限故选C．点评：本题主要考查了算法的特点，属于基本概念的考查，是容易题．2.2.算法共有三种逻辑结构，即顺序结构、条件结构、循环结构，下列说法正确的是( )A. 一个算法只能含有一种逻辑结构B. 一个算法最多可以包含两种逻辑结构C. 一个算法必须含有上述三种逻辑结构D. 一个算法可以含有上述三种逻辑结构的任意组合【答案】D【解析】分析：根据算法中三种逻辑结构的定义，顺序结构是最基本的结构，每个算法一定包含顺序结构，选择结构是算法中出现分类讨论时使用的逻辑结构，循环结构一定包含一个选择结构，从而即可得出答案.详解：算法有三种逻辑结构，最基本的是顺序结构，一个算法一定包含有顺序结构，但是可以含有三种逻辑结构的任意组合.故选：D.点睛：本题考查的知识点是算法的概念及算法的特点，是对概念的直接考查，属基础题，熟练掌握相关概念是解答本题的关键.3.3.下列给出的赋值语句中正确的是（）A. B. C. D.【答案】B【解析】【分析】根据赋值语句定义判断选择.【详解】赋值语句一般格式是:变量=表达式(或变量)，所以选B.【点睛】赋值语句用符号“=”表示，其一般格式是变量=表达式(或变量)，其作用是对程序中的变量赋值；4.4.程序执行后输出的结果是（）A. －1B. 0C. 1D. 2【答案】B【解析】试题分析：开始满足，第一次循环：；满足，第二次循环：；满足，第三次循环：；满足，第四次循环：；满足，第五次循环：；此时不满足，结束循环，所以输出n的值为0。
考点：while语句。
点评：当型循环结构是最基本的循环结构之一。
当型循环结构用在先判断某些条件是否为真，然后重复执行某一段代码的情况下。
当型循环的条件是在循环体执行前进行判断的,当条件满足时进入循环，否则结束循环。
5.5.以下给出的各数中不可能是八进制数的是（）A. 312B. 10 110C. 82D. 7 457【答案】C【解析】【分析】根据八进制数不可能出现8或9，即可作出判断选择.【详解】因为八进制数不可能出现8或9，所以82不可能是八进制数，选C.【点睛】本题考查进制有关概念，考查基本判别能力.6. 如果右边程序执行后输出的结果是132，那么在程序until后面的“条件”应为( )A. i > 11B. i >=11C. i <=11D. i<11【答案】D【解析】试题分析：第一次循环：，此时应满足条件，再次循环；第二次循环：，应为输出的s的值为132，所以此时应结束循环，所until后面的“条件”应为i<11，因此选D。
考点：until语句。
点评：我们要注意“until语句”和“while语句”的区别。
while语句是先判断，再执行循环体，当条件满足时执行循环体；而until语句是先循环再判断，当条件不满足时执行循环体。
7.7.如图给出的是计算的值的一个程序框图，其中判断框内应填入的条件是（）A. B. C. D.【答案】A【解析】根据框图，i-1表示加的项数当加到时，总共经过了10次运算，则不能超过10次， i-1=10执行“是”所以判断框中的条件是“i>10”故选A8.8.用秦九韶算法在计算时，要用到的乘法和加法的次数分别为（）A. 4，3B. 6，4C. 4，4D. 3，4【答案】C【解析】【分析】先整理成秦九韶算法，再确定用到的乘法和加法的次数.【详解】因为，所以用到的乘法和加法的次数4，4，选C.【点睛】本题考查秦九韶算法，考查基本求解能力.9.9.下面的程序框图能判断任意输入的数的奇偶性,其中判断框内的条件是( )A. B. C. D.【答案】A【解析】试题分析：本题考查了选择结构，由程序框图所体现的算法可知判断一个数是奇数还是偶数，看这个数除以2的余数是1还是0，从而得到判断框条件．解：由程序框图所体现的算法可知判断一个数是奇数还是偶数，看这个数除以2的余数是1还是0．由图可知应该填m=1．故选B点评：选择结构是考试中常考的知识点，根据流程图计算运行结果是算法这一模块的重要题型，处理的步骤一般为：分析流程图，从流程图中即要分析出计算的类型，又要分析出参与计算的数据建立数学模型，根据第一步分析的结果，选择恰当的数学模型解模．10.10.二进制数10111转化为五进制数是（）A. 41B. 25C. 21D. 43【答案】D【解析】【分析】根据进制先换成十进制，再换成五进制.【详解】因为，所以，选D.【点睛】本题考查不同进制之间转换,考查基本求解能力.11.11.假设，那么在执行后的值为（）A. 0.5B. 11.5C. 10.5D. –0.5【答案】B【解析】【分析】将，代入计算得结果.【详解】因为，所以，即的值为，选B. 【点睛】本题考查除法与取整概念,考查基本求解能力.12.12.若n=1,则如图所示程序框图输出的是（）A. 2005B. 65C. 64D. 63【答案】D【解析】【分析】执行程序，计算，若不大于2004，则加1，继续计算，直到大于2004，输出值. 【详解】执行程序，结束循环，输出选D.【点睛】算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.二、填空题（共6小题，每小题5分，共30分）13.13.三个数72,120,168的最大公约数是;【答案】24【解析】试题分析：利用辗转相除法，先求出其中二个数72，120，；120，168的最大公约数，之后我们易求出三个数72，120，168的最大公约数．解：120=72×1+4872=48×1+2448=24×2∴72，120的最大公约数是24168=120×1+48120=48×2+2448=24×2故120，168的最大公约数为24三个数72，120，168的最大公约数24．故答案为：24．点评：本题考查的知识点是最大公因数，在求两个正整数的最大公因数时，辗转相除法和更相减损术是常用的方法，要熟练掌握．14.14.若输入8时，则下列程序执行后输出的结果是______.【答案】0.7【解析】试题分析：该题为条件语句，条件为t≤4，现输入8，不符合条件，故.故答案为0.7.考点：条件语句、循环语句.15.15.将二进制数化为十进制结果为______ ，再将该数化为八进制数，结果为_____ .【答案】 (1). 45 (2).【解析】试题分析：：考点：十进制与二进制的互化16.16.若，则以下程序运行后的结果是_____.【答案】4.5【解析】【分析】根据条件就是求a除以10 的整数减去a除以10 的商加上a除以10 的余数.【详解】【点睛】本题考查除法与取整、同余等概念,考查基本求解能力.17.17.以下程序运行后输出的结果为_______.【答案】22,-22【解析】【分析】先根据条件语句确定x,y，再分别计算x-y, y-x.【详解】由题意得【点睛】本题考查条件语句,考查基本求解能力.18.18.以下程序的功能是__________，如果输入的值为54，则输出结果是_____；如果输入的值为102，则输出结果是_______.【答案】 (1). 输入一个两位数，交换它的十位和个位数字 (2). 45 (3). 102 【解析】【分析】(1)由题意得，即输入一个两位数，交换它的十位和个位数字，(2)根据（1）得结果，（3）由于102>100,所以直接跳出循环得结果.【详解】（1）由题意得当且为整数时，,输出，即输入一个两位数，交换它的十位和个位数字，否则直接输出（2）输入的值为54，则输出结果是45，（3）由于102>100,所以输出结果是102.【点睛】本题考查取整、同余等概念以及条件语句,考查基本分析与求解能力.三、解答题（共6小题，每小题10分，共60分）19.19.（1）用辗转相除法求840与1 764的最大公约数；（2）用更相减损术求440 与556的最大公约数.【答案】（1）8；（2）4.【解析】【分析】（1）根据辗转相除法，求余数，直至余数为零，（2）根据更相减损术，求减数，直至减数为零.【详解】（1）用辗转相除法求840与1 764 的最大公约数.1 764 = 840×2 + 84 840 = 84×10 +0所以840与1 764 的最大公约数是84.(2)用更相减损术求440 与556的最大公约数.556－440 = 116 440－116 = 324324－116 = 208 208－116 = 92116－92 = 24 92－24 = 6868－24 = 44 44－24 = 2024－20 = 4 20－4 = 1616－4 = 12 12－4 = 88－4 = 4所以440 与556的最大公约数4.【点睛】本题考查辗转相除法与更相减损术,考查基本求解能力.20.20.编写一个程序，求的值，并画出程序框图，要求用两种循环结构编写.【答案】程序图见解析.【解析】【分析】求和程序设置一个计数变量，一个累加变量，根据结束条件设置成直到型或当型.【详解】【点睛】本题考查循环结构,考查基本分析能力.21.21.设计算法求的值.要求画出程序框图，写出用基本语句编写的程序.【答案】程序图见解析.【解析】【分析】这是一个累加求和问题，设计一个计数变量，一个累加变量，根据结束条件设置成直到型或当型. 最后对应改成基本语句.【详解】这是一个累加求和问题，共99项相加，可设计一个计数变量，一个累加变量，用循环结构实现这一算法.程序框图如下图所示【点睛】本题考查循环结构,考查基本分析能力.22.22.某电信部门规定：拨打市内电话时，如果通话时间不超过3分钟，则收取通话费0.2元，如果通话时间超过3分钟，则超过部分以每分钟0.1元收取通话费，试设计一个计算通话费用的算法.要求写出算法，画出程序框图，编写程序.【答案】程序图见解析.【解析】试题分析：我们用（单位：元）表示通话费用，（单位：分钟）表示通话时间，则依题意必有算法步骤如下：第一步：输入通话时间；第二步：如果，那么；否则令；第三步：输出通话费用。