Dimensional reduction and BRST approach to the description of a Regge trajectory
不同建筑固废再生骨料取代率下粗粒土填料永久变形特性及安定行为研究

第 55 卷第 3 期2024 年 3 月中南大学学报(自然科学版)Journal of Central South University (Science and Technology)V ol.55 No.3Mar. 2024不同建筑固废再生骨料取代率下粗粒土填料永久变形特性及安定行为研究肖源杰1, 2,王政1,AMINU Umar Faruk 1,王萌1,李昀博1,孔坤锋3,陈宇亮4,周震5,李志勇4(1. 中南大学 土木工程学院,湖南 长沙,410075;2. 重载铁路工程结构教育部重点实验室 (中南大学),湖南 长沙,410075;3. 中国铁道科学研究院集团有限公司 铁道建筑研究所,北京,100081;4. 湖南省交通科学研究院有限公司,湖南 长沙,410015;5. 广东省交通规划设计研究院集团股份有限公司,广东 广州,510440)摘要:为探究城市建筑拆除固废再生骨料部分或全部取代天然骨料用于粗粒土路基填料的可行性,开展不同再生骨料取代率、含水率、围压和剪应力比等组合下的室内大型静动三轴试验,定量研究土性参数和应力状态对试样抗剪强度和累积塑性应变特性的影响规律。
基于半对数坐标下累积塑性应变发展的多阶段特征,分别考虑不同阶段塑性变形累积速率以及相邻两阶段的塑性变形累积速率的差异,提出适用于建筑固废再生骨料路基填料的新型安定行为判定准则。
研究结果表明:再生骨料路基填料试样的累积塑性应变随含水率和剪应力比的增大而增大,当再生骨料路基填料试样在剪应力比为0.3和0.5时,抗累积变形性能与天然骨料路基填料试验所得的抗累积变形性能接近,综合考虑抗剪强度和累积塑性变形特性的再生骨料路基填料最优取代率为85%;新安定行为判定准则具有较高的准确性,可为相似路基填料的长期路用性能评定提供理论依据。
关键词:道路工程;建筑固废;再生骨料;永久变形;安定行为中图分类号:TU43 文献标志码:A 文章编号:1672-7207(2024)03-1008-15Permanent deformation characteristics and shakedown behavior of coarse-grained fill materials incorporating different proportions ofaggregates recycled from building demolition wastes收稿日期: 2023 −06 −20; 修回日期: 2023 −08 −20基金项目(Foundation item):国家自然科学基金资助项目(52178443);国家重点研发计划项目(2019YFC1904704);交通运输部重点科技项目(2022-MS5-122);中南大学研究生自主探索创新项目(2023ZZTS0019) (Project(52178443) supported by the National Natural Science Foundation of China; Project(2019YFC1904704) supported by the National Key Research & Development Program of China; Project(2022-MS5-122) supported by the Ministry of Transport Key Science & Technology Program of China; Project(2023ZZTS0019) supported by the Graduate Student Free Exploration Innovation Program of Central South University)通信作者:王萌,博士研究生,从事路基工程研究;E-mail :**************.cnDOI: 10.11817/j.issn.1672-7207.2024.03.015引用格式: 肖源杰, 王政, AMINU Umar Faruk, 等. 不同建筑固废再生骨料取代率下粗粒土填料永久变形特性及安定行为研究[J]. 中南大学学报(自然科学版), 2024, 55(3): 1008−1022.Citation: XIAO Yuanjie, WANG Zheng, AMINU Umar Faruk, et al. Permanent deformation characteristics and shakedown behavior of coarse-grained fill materials incorporating different proportions of aggregates recycled from building demolition wastes[J]. Journal of Central South University(Science and Technology), 2024, 55(3): 1008−1022.第 3 期肖源杰,等:不同建筑固废再生骨料取代率下粗粒土填料永久变形特性及安定行为研究XIAO Yuanjie1, 2, WANG Zheng1, AMINU Umar Faruk1, WANG Meng1, LI Yunbo1, KONG Kunfeng3,CHEN Yuliang4, ZHOU Zhen5, LI Zhiyong4(1. School of Civil Engineering, Central South University, Changsha 410075, China;2. MOE Key Laboratory of Engineering Structure of Heavy Haul Railway(Central South University),Changsha 410075, China;3. Railway Engineering Research Institute, China Academy of Railway Sciences Corporation Limited,Beijing 100081, China;4. Hunan Communications Research Institute Co. Ltd., Changsha 410015, China;5. Guangdong Communication Planning & Design Institute Group Co. Ltd., Guangzhou 510440, China)Abstract:In order to address the feasibility of the mixed subgrade filling of natural aggregate and recycled aggregates from construction and demolition waste(RAW), laboratory static/dynamic triaxial tests under different conditions of recycled aggregate replacement rate, moisture content, confining pressure and shear stress ratio were carried out, and the effect of index properties and stress states on the shear strength and accumulative plastic strain characteristics of the specimen were explored. Based on the multi-stage characteristics of plastic strain development under semi-logarithmic coordinates, and considering the plastic deformation accumulation rate at different stages and the difference in plastic deformation accumulation rate in adjacent two stages, a new shakedown behavior determination criterion suitable for subgrade filling mixed with RAW was proposed. The results show that the accumulative plastic strain of the specimen increases with the increase of moisture content and shear stress ratio, and the specimens mixed with RAW show similar plastic deformation resistance ability compared to natural aggregate when the shear stress ratio is 0.3 and 0.5. After comprehensive comparative analysis of strength and deformation characteristics, it is recommended to use recycled aggregate subgrade filled with 85% replacement rate. The new shakedown behavior determination criterion has high accuracy and can provide a theoretical basis for the long-term pavement performance evaluation of similar subgrade fillings.Key words: road engineering; construction and demolition waste; recycled aggregates; permanent deformation;shakedown behavior随着中国城市化进程迅速发展,新建基础设施和老旧城区改造产生的建筑垃圾量急剧攀升[1],但综合循环再生利用率距《“十四五”循环经济发展规划》提出的“到2025年,建筑垃圾综合利用率达到60%”这一目标仍存在差距。
二维过渡金属硫族化合物的制备及其在柔性传感器中的应用研究

二维过渡金属硫族化合物的制备及其在柔性传感器中的应用研究摘要:本文通过溶剂热法和电化学沉积法制备了一系列二维过渡金属硫族化合物。
研究发现这些化合物具有优良的柔性和导电性能,可作为柔性传感器中的电极材料。
在气体传感器中,这些材料对于CO、NH3和NO2等气体具有较高的响应度和选择性。
在应变传感器中,这些材料也表现出较好的敏感性和稳定性。
因此,这些二维材料可以作为柔性传感器中的重要组成部分,具有广阔的应用前景。
关键词:二维过渡金属硫族化合物;制备;柔性传感器;应用研究。
一、引言随着社会的不断发展和科学技术的不断进步,越来越多的人们开始关注人类和环境的健康问题。
传感器技术作为一种重要的检测手段,得到了广泛的应用。
其中,柔性传感器作为一种新型的传感器,具有很好的柔韧性、高灵敏度和高选择性等特点。
因此,其应用前景非常广泛。
二维过渡金属硫族化合物作为一种新型的材料,具有很好的电学特性和机械性能,因此成为了柔性传感器材料的研究重点。
二、实验方法硫族化合物。
制备方法如下:1. 溶剂热法将过渡金属盐和硫族元素按一定的比例混合,并加入适量的有机溶剂。
在加热条件下,化合物会溶解在溶剂中,并逐渐形成深色的溶液。
当溶液温度达到一定的程度时,化合物会在溶液中析出。
2. 电化学沉积法将过渡金属板作为阳极,在硫族元素的电化学反应中沉积过渡金属硫族化合物。
反应条件如下:电流密度为10mA/cm2,沉积时间为10min,溶液温度为25℃。
三、结果与讨论通过SEM、TEM、XRD等测试手段,我们发现所制备的二维过渡金属硫族化合物具有较高的结晶度和纯度。
同时,它们具有良好的柔性和导电性能。
在CO、NH3和NO2等气体传感器中,这些材料对于目标气体具有较高的响应度和选择性。
在应变传感器中,这些材料表现出较好的敏感性和稳定性。
因此,这些二维材料可以作为柔性传感器中的重要组成部分。
四、结论硫族化合物,并研究了它们在柔性传感器中的应用。
研究发现,这些化合物具有优良的柔性和导电性能,可作为柔性传感器中的电极材料,具有很好的应变传感和气体传感性能。
武汉科技大学文法学院-公共管理系

公共管理系•【公共管理系】【行管教研室】【教授】顾杰.2013-12-05•【公共管理系】【行管教研室】【教授】邓泽宏2013-12-05•【公共管理系】【行管教研室】【教授】丁宇2013-12-05•【公共管理系】【行管教研室】【教授】周均旭2013-12-05•【公共管理系】【行管教研室】【教授】何应龙2013-12-05•【公共管理系】【行管教研室】【副教授】魏敏2013-12-05•【公共管理系】【行管教研室】【副教授】雷德明2013-12-05•【公共管理系】【行管教研室】【副教授】李秋容2013-12-05•【公共管理系】【行管教研室】【副教授】吴汉军2013-12-05•【公共管理系】【行管教研室】【副教授】石秀华2013-12-05•【公共管理系】【行管教研室】【副教授】卢珂.2013-12-05•【公共管理系】【行管教研室】【副教授】程红丹2013-12-05•【公共管理系】【行管教研室】【副教授】刘文波2013-12-05•【公共管理系】【行管教研室】【副教授】张彦英2013-12-05•【公共管理系】【行管教研室】【副教授】王哲2013-07-08•【公共管理系】【行管教研室】【讲师】张雅勤2013-07-08•【公共管理系】【行管教研室】【讲师】唐青2013-07-08•【公共管理系】【社保教研室】【教授】董登新2013-07-08•【公共管理系】【社保教研室】【教授】张智勇2013-07-08•【公共管理系】【社保教研室】【教授】熊吉峰2013-07-08•【公共管理系】【社保教研室】【副教授】周云2013-07-08•【公共管理系】【社保教研室】【副教授】王伟2013-07-08•【公共管理系】【社保教研室】【副教授】罗莉2013-07-08•【公共管理系】【社保教研室】【副教授】胡荣芳2013-07-08•【公共管理系】【社保教研室】【副教授】刘珺2013-07-08•【公共管理系】【社保教研室】【讲师】卢敏2013-07-08•【公共管理系】【社保教研室】【讲师】邱莉丽2013-07-08•【公共管理系】【社保教研室】【讲师】程妍2013-07-08•【公共管理系】【社工教研室】【教授】陈秀峰.2013-07-08•【公共管理系】【社工教研室】【教授】彭惠青2013-07-08•【公共管理系】【社工教研室】【教授】张英2013-07-08•【公共管理系】【社工教研室】【副教授】李莉2013-07-08•【公共管理系】【社工教研室】【副教授】柯燕.2013-07-08•【公共管理系】【社工教研室】【讲师】冯晓平2013-07-08教师系统分析与集成社教社社数社社常社。
信号自适应衰减的多壳扩散磁共振成像方法

2021年2月第2期Vol. 42 No. 2 2021小型微 型计算 机系统Journal of Chinese Computer Systems信号自适应衰减的多壳扩散磁共振成像方法罗伶俐,王远军(上海理工大学医学影像工程研究所,上海200093)E-mail :yjusst@ 126. com摘 要:提升总体平均扩散传播算子(Ensemble Average diffusion Propagator ,EAP )的重建精度一直以来都是扩散磁共振成像领域中扩散光谱成像(Diffusion Spectrum Imaging ,DSI )的核心问题.在诸多成像算法中,用径向基函数(Radial Basis Function ,RBF)作为扩散MR 信号插值基函数的方法在纤维方向分布重建及成像统计标量重建方面均获得了理想的EAP 重建效果,为进一步提升重建效率及精度,本文基于RBF 方法提出了对信号进行自适应衰减建模的方法,并结合确保扩散张量正定性的张量求解算法,分别基于系数人仏正则化方法求解最优化参数以作对比.针对体模数据的实验结果显示,该算法在提升各项指标 重建精度及计算效率方面均取得了理想效果.关键词:扩散MRI ;扩散光谱成像;多壳扩散MR 成像中图分类号:TP391 文献标识码:A 文章编号:1000-1220(2021 )02-0374-07Multi-shell Diffusion Magnetic Resonance Imaging Method with Adaptive Signal AttenuationLUO Ling-li,WANG Yuan-jun(Institute of Medical Imaging Engineering ,University of Shanghai for Science and Technology ,Shanghai 200093 .China)Abstract : Improving the estimation accuracy of the Ensemble Average diffusion Propagator) EAP) has always been a core issue of dif fusion spectrum imaging in the field of diffusion magnetic resonance imaging. Among many methods , the radial basis function ( RBF) is used as the interpolation basis function for diffusion MR signal to obtain the ideal EAP reconstruction effect both in reconstruction offiber orientation estimation and scalar statistics. In order to further improve the calculation efficiency and reconstruction accuracy , a method modeling the signal adaptive attenuation based on the RBF is proposed in this paper. The tensor estimating method ensuring the positive definiteness of the diffusion tensor is combined , and the optimization is performed by method based on l x and l 2 regularizationrespectively for comparison. Experimental results about phantom data show that the algorithm has achieved ideal results in terms of im proving the reconstruction accuracy of various indicators and calculation efficiency.Key words : diffusion MRI ; diffusion spectrum imaging ; multi-shell diffusion MR imaging1引言扩散磁共振成像(Diffusion Magnetic Resonance Imaging ,dMRI)技术被广泛应用于诸如阿尔茨海默症、精神分裂症、脑损伤等诸多大脑疾病的研究中.dMRI 的基础原理是由于扩散加权MR 信号对器官组织中的内生水分子的随机运动十分敏感,这其中应用最为广泛的扩散加权磁共振成像(Diffu sion-weighted MRI,DW-MRI)是使用了两种在180。
弦论揭秘:自学向导 网上预览

作者简介
戴维德 • 麦克马洪是当代著名的美国物理学家。作为物理研究人员,他曾在圣迪亚 (SaБайду номын сангаасdia) 国家实验室工作过七年。 他是 《线性代数揭秘》 、 《量子力学揭秘》 、 《相对论揭秘》 、 《MATLAB®揭秘》和《复变函数揭秘》等自学导读书籍的作者。
译者简介
郑中,生于 1979 年,四川隆昌人,理学硕士、工程师。本科就读于成都理工大学资源 经济系,后考入中国科学院地球化学研究所,毕业后在矿业公司和资源规划院工作过,现仍 主要从事地质矿产工作。 译者博客:/u/warlong /cqzg
II
目 录
译者序言 作者前言 第一章 导 论(Introduction) 广义相对论快览(A Quick Overview of General Relativity) 量子论快速入门(A Quick Primer on Quantum Theory) 标准模型(The Standard Model) 量子引力场(Quantizing the Gravitational Field) 弦论中一些基本分析(Some Basic Analysis in String Theory) 统一与基本常数(Unification and Fundamental Constants) 弦论概览(String Theory Overview) 弦论类型(Types of String Theories) M论 D膜 高维 小 结 小测验 第二章 经典弦I:运动方程(The Classical String I: Equations of Motion) 相对论性点粒子(The Relativistic Point Particle) 时空中的弦(Strings in Space-Time) 弦的运动方程(Equations of Motion for the String) 波里雅科夫作用量(The Polyakov Action) 数学旁白:欧拉示性数(Mathematical Aside: The Euler Characteristic) 光锥坐标(Light-Cone Coordinates) 波动方程解(Solutions of the Wave Equation) 具有自由端点的开弦(Open Strings with Free Endpoints) 闭弦(Closed String) 具有固定端点的开弦(Open Strings with Fixed Endpoints) 泊松括号公式(Poisson Brackets) 小测验 第三章 经典弦II:对称性与世界面流(The Classical String II: Symmetries and Worldsheet Currents) 能动张量(The Energy-Momentum Tensor) 波里雅科夫作用量的对称性(Symmetries of the Polyakov Action) 庞加莱变换(Poincaré transformations) 再参数化(reparameterization) 外尔变换(Weyl transformation) 转换为平直世界面度规(Transforming to a Flat Worldsheet Metric) 源于庞加莱不变性的守恒流(Conserved Currents from Poincaré Invariance) 哈密顿公式(The Hamiltonian) 小 结 小测验
运用近红外光谱法建立盐酸二甲双胍肠溶片一致性检验模型

t e r i c . Co a t e d Ta b l e t s b y n e a r i n f r a r e d s p e c t r u m. M ETH 0 DS Me t or f mi n h y d r o c hl o r i d e e n t e ic r c o a t e d t a b l e t s we r e s c a n n e d i n t h e r a n g e o f l 2 o 00 c m t o 4 0 0 0c m一 . t h e s e c o n d d e r i v a t i v e f o l l o we d b y v e c t o r n o r ma l i z a t i o n me t h o d wa s
中 图 分 类号 : R 9 2 7 . 2 文 献 标 识码 : A 文章编号 : 1 0 0 6 - 3 7 6 5 ( 2 0 1 4 ) - 0 9 - 0 6 7 1 - 0 0 6 8 03 -
Es t a b l i s h men t o f t h e Ne a r I n f r ar e d Con f o r mi t y Te s t Mo d el o f Me t f or mi n Hy dr o c h l o r i d e En t er i c - Co a t e d Ta b l e t s
溶藻弧菌的依赖于核酸序列恒温扩增检测方法的建立

M e h d f r De e tn b o AZ D c t o o t c i g Vi i gf Z
QI h n —i N S e gl .W ANG ing a g’ J a —u n
( . le e ia 1 ColgeofCh m clEngn e ig,Qig a ie st fS in ea dTe h oo y,Qig a 6 0 2, ia ie rn n d o Unv riyo ce c n c n lg n d o 2 6 4 Chn 2 S a d n tyExtI s e to n a a i ra . h n o g En r i n p cin a d Qu rnt Bu e u,Qig a 6 0 2,Ch n ) ne n do2 6 0 i a
mmo ・L 。 C 2 5 mmo ・L 二 硫 苏 糖 醇 ] l _ Mg 1, l
2 0 L, 甲基亚 砜 2 5 L, 板 R L 弓 . 二 . 模 NA 5 , I
物 F、 1 to R( 0 o l・L 各 1 L, NTP . 一) d s 25
[
。
溶藻 弧菌 过 去一 直 被 认 为 不 致 病 或 仅 能
引起 部分创 伤性 感染 而未 受重视 , 到 1 8 直 9 0年 才
收稿 E期 :2 1 一 5 1 t 0 1O — O 基 金 项 目 :国家 质 检 总 局科 研 项 目(0 8K1 0 ; 东 出 入境 检 验检 疫 局 科 研 项 目( K2 0 2 ) 20I 4)山 S 0 8 1 作 者 简 介 : 胜 利 ( 9 9 ) 男 , 士研 究 生 . 秦 1 7 , 硕
l h Nu li i e u n e b s d Amp i c to t o .S e i ct n e stvt r i c ec Acd S q e c — a e s l ia i n me h d f p c f i a d s n ii i we e i y y t s e . e r s lss o d t a h e stv t fNAS e t d Th e u t h we h tt e s n i iy o i BA s6 9 1 f ・m L wh c wa . × 0 c u 一 ih wa i h r t a h e u to sh g e h n t e r s l f PCR me h d t o .De e tn b o a g n l t c s wi t c i g Vi i l i o y i u t NAS A h B
(武汉大学)细胞生物学研究方法
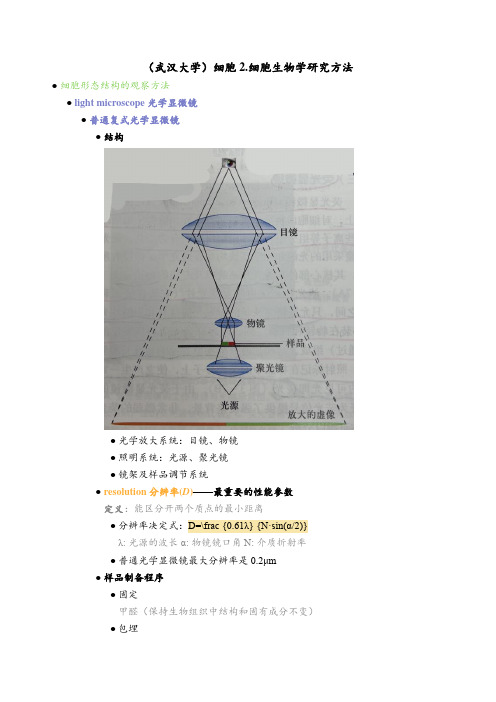
(武汉大学)细胞2.细胞生物学研究方法●细胞形态结构的观察方法●light microscope 光学显微镜●普通复式光学显微镜●结构●光学放大系统:目镜、物镜●照明系统:光源、聚光镜●镜架及样品调节系统●resolution 分辨率(D)——最重要的性能参数定义:能区分开两个质点的最小距离●分辨率决定式:D=\frac {0.61λ} {N·sin(α/2)}λ: 光源的波长α: 物镜镜口角 N: 介质折射率●普通光学显微镜最大分辨率是0.2μm●样品制备程序●固定甲醛(保持生物组织中结构和固有成分不变)●包埋石蜡(支撑生物组织的机械硬度)●切片:厚度约5μm●染色:苏木精和伊红(H-E染色)●观察●phase-contrast microscope 相差显微镜、differential-interference microscope微分干涉显微镜——观察活细胞●原理:光线穿过细胞的不同部位时,其密度不同导致光线的相位发生不同程度的改变。
通过环状光阑和相差板,将光的相位差转变为振幅差●微分干涉显微镜:以偏振光为光源●fluorescence microscope 荧光显微镜——定性定位研究组分●特殊构造●激发光滤片:只允许特定波长的光通过,让标本受激发产生荧光●双分镜:反射激发光(短波长)、透过荧光(长波长)●绿色荧光蛋白(green fluorescent protein, GFP)●将编码绿色荧光蛋白的基因与编码某种蛋白质的基因相融合,利用荧光显微镜,就可以在表达这种融合蛋白基因的活细胞中观察到该蛋白的动态变化●laser scanning confocal microscope, LSCM 激光扫描共焦显微镜●利用共焦的特点,提高图像的成像分辨率●可以通过“光学切片”改变焦点,获得一系列不同切面上的细胞图像,经叠加后重构出样品的三维结构●electron microscope, EM 电子显微镜●原理:根据物质密度的不同,利用电子穿透样品打在荧光屏上成像,观察细胞内部超微结构分辨率达到0.2nm●特点●电子束作为光源●电磁透镜聚焦●图像通过荧光屏或感光胶片记录●主要电镜制样技术●ultrathin section 超薄切片技术——解决电子束穿透能力弱的问题将细胞切成薄片,有利于电子的穿透●取材●固定:戊二醛和锇酸或低温冷冻法(保持细胞固有结构)●包埋:环氧树脂(增强细胞的机械承受力)●切片:玻璃刀40~50nm●染色:重金属盐锇酸——脂质柠檬酸铅——蛋白质乙酸双氧铀——核酸●观察●nagetive staining 负染色技术——观察细胞精细结构重金属沉积在样品周围的环境●用重金属盐对铺展在载网上的样品进行染色。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a rXiv:h ep-th/9731v128Fe b1997Preprint JINR E2-97-63Dimensional reduction and BRST approach to the description of a Regge trajectory A.Pashnev ∗and M.Tsulaia †JINR–Bogoliubov Laboratory of Theoretical Physics,141980Dubna,Moscow Region,Russia Abstract The local free field theory for Regge trajectory is described in the framework of the BRST -quantization method.The corresponding BRST -charge is constructed with the help of the method of dimensional reduction.Submitted to Modern Physics Letters A1IntroductionThe main problem in the description of the higher spin particles is removing of un-physical degrees of freedom from the theory.As was shown in[1],the corresponding lagrangian must have some invariance,which generalizes the gauge invariance of the electromagneticfield not only in the free case,but for interactingfields,as well.On the free level such lagrangians was constructed both for massive and for massless particles of any spin as well as for massless supermultiplets[2]-[10].In some sense the massless case is simpler and,hence,more investigated than the massive one.The hope is,that with the help of some Higgs-type effect some of the interacting particles acquire nonzero values of the mass.In general the lagrangians for higher spins include additionalfields.Some of them are auxiliary,others can be gauged away.The main role of thesefields is to ensure,that only physical degrees of freedom are propagating ones.It means, that the basicfield describes irreducible representation of the Poincare group-it is traceless,transverse and satisfies mass shell equation.Naturally higher spin particles arise after quantization of classical extended ob-jects such as string,relativistic oscillator[11]-[12],discrete string[13]etc.Physically they correspond to exited levels of the system and belong to Regge trajectories,each including infinite sequence of states with a spin linearly depending on the square of the mass.There are infinite number of Regge trajectories in the string and relativis-tic oscillator models and only one such trajectory in the discrete string model due to existing of additional second-class constraints.Such subdivision of all higher spin particles on Regge trajectories leads to the consideration of these Regge trajectories as independent objects for which it would be interesting to construct the lagrangian description.One of the most economic and straightforward method of construction of la-grangians for systems with constraints is the method using BRST-charge of the cor-respondingfirstly quantized theory.With the help of BRST-charge the lagrangians for the freefield theory for particular values of spins[16]and for infinite tower of massless higher spin particles were constructed[15].The analogous consideration for the massivefields is hampered by the presence of the second class constraints.The methods of converting them into thefirst class constraints with the help of additional variables were discussed in[17]-[18].Nevertheless,the strightforward application of this approach to the massive higher spins leads to the non-local lagrangian[19].In the second part of the paper we describe the auxiliary Fock space and system of constraints in it which follow from the consideration of some classical models of extended objects.In the third part of the paper we describe the massless case of[15]in D+1 dimensions which is the starting point for the consequent consideration.After that we fulfil the dimensional reduction from D+1dimensional to D dimensional space time.Formally it looks like some unitary transformation.As a result,the correct local freefield lagrangian for Regge trajectory together with its daughter trajectoriesis constructed.In the fourth part of the paper we write out as examples the lagrangians for lower spins S =0,1,2.2Constraints in auxiliary spaceTo describe all higher spins simultaneously it is convenient to introduce auxiliary Fock space generated by creation and annihilation operators a +µ,a µwith vector Lor entz index µ=0,1,2,...D −1,satisfying the following commutation relations[a µ,a +ν]=−g µν,g µν=diag (1,−1,−1,...,−1).(2.1)In addition the operators a +µ,a µcan have some internal indices leading to more complicated spectrum of physical states.For simplicity we consider in this paper a +µ,a µwithout additional indices.The general state of the Fock space|Φ = Φ(n )µ1µ2···µn (x )a +µ1a +µ2···a +µn |0 (2.2)depends on space-time coordinates x µand its components Φ(n )µ1µ2···µn (x )are tensorfields of rank n in the space-time of arbitrary dimension D .The norm of states in this Fock space is not positively definite due to the minus sign in the commutation relation (2.1)for time components of creation and annihilation operators.It means that physical states must satisfy some constraints to have positive norm.These constraints arise naturally in the considerations of classical composite systems [12]-[13].The corresponding quantum operatorsL 0=−p µ2−α′a +µa µ,L 1=p µa µ,L −1=p µa +µ=L +1,(2.3)L 2=12a +µa +µ=L +2(2.4)form the algebra[L 0,L ±1]=∓α′L ±1[L 0,L ±2]=∓2α′L ±2(2.5)(2.6)[L 1,L −2]=−L −1[L −1,L 2]=L 1(2.7)(2.8)[L 1,L −1]=−p µ2[L 2.L −2]=−a +µa µ+Dsecond class and in general this system of constraints describes single Regge trajec-tory[12]-[14].There exist some different possibilities in consideration of general system of con-straints(2.3)-(2.4).The truncated system L0,L±1describes Regge trajectory to-gether with its daughter trajectories.The operators L±1in this system are of second class as before.We describe the BRST-quantization of this system in the third part of the article.The limitα′=0of the system(2.3)corresponds to the massless infinite tower of spins with a single state at each value of the spin.In this case only the operators L±2are of second class.The BRST-quantization of this system as well as general system(2.3)-(2.4)will be given elsewhere.The simplest system offirst-class constraints˜L=−pµ2,L±1(2.10)corresponds to the massless tower of spins infinitely degenerated at each value of spin. The BRST-construction for this system of constraints was described in[15]-[16].3Massless case and dimensional reductionIn this section we consider the system with constraintsL0=−pµ2−α′a+µaµ+α0,L1=pµaµ,L−1=pµa+µ,(3.1) where parameterα0plays the role of intercept for Regge trajectory.In some sense this system is intermediate between the systems in[15]and[14]because it describes the Regge trajectory together with all daughter trajectories(due to the absence of the constraints L±2).The commutation relation[L1,L−1]=−pµ2means that L±1 are the second class constraints.To construct the BRST-charge we can try to convert them into thefirst class constraints following the prescription of[17]-[18]. We introduce new operators b and b+with the commutation relations[b,b+]=1and modify the constraints to the following expressions:˜L=−pµ2−α′a+µaµ+α0+α′b+b,(3.2)˜L=L−1+−1pµ2b,(3.4) [˜L1,˜L−1]=0,[˜L0,˜L1]=−α′˜L1,[˜L0,˜L−1]=α′˜L−1.(3.5)All of the modified constraints are offirst class and BRST-charge construc-tion is straightforward[19].Nevertheless,the corrresponding lagrangian is not sat-isfactory one.Indeed,it is non-local due to presence ofof constraints˜L±1.The natural way out of this difficulty is to replace−α′a+µaµ+α0+α′b+b,having new system of constraints with rather nontrivial commutation relations due to such complicated dependence from creation and anni-hilation operators.The simplest way to construct BRST-charge with corresponding constraints is as follows.Firstly we consider massless case in D+1dimensions with constraintsL0=−p2µ+p2D,µ=0,1,...,D−1,(3.6)L1=pµaµ−p D a D,(3.7)L−1=pµa+µ−p D a+D.(3.8) Following to the standard procedure we introduce additional set of anticommuting variablesη0,η1,η+1having ghost number one and corresponding momenta P0,P+1,P1 with commutation relations:{η0,P0}={η1,P+1}={η+1,P1}=1.(3.9) The nilpotent BRST-charge has the following form:Q=η0L0+η+1L1+η1L+1+η1η+1P0(3.10) Consider the total Fock space generated by creation operators a+µ,a+D,η+1,P+1.In addition each vector of the Fock space depends linearly on the real grassmann variable η0(P0considered as corresponding derivative P0=∂/∂η0)|χ =|χ1 +η0|χ2 .(3.11) Ghost numbers of|χ1 and|χ2 are different if the state|χ has some definite one.The BRST-invariant lagrangian in such Fock space can be written asL=− dη0 χ|Q|χ .(3.12)To be physical,lagrangian L must have zero ghost number.It means that vectors |χ and|χ1 have zero ghost numbers as well.In this case the ghost number of|χ2 is minus one.The most general expressions for such vectors are|χ1 =|S1 +η+1P+1|S2 ,(3.13)|χ2 =P+1|S3 ,(3.14) with vectors|S i having ghost number zero and depending only on bosonic creation operators a+µ,a+D|S i = φnµ1,µ2,...µn(x)a+µ1a+µ2...a+µn(a+D)n|0 .(3.15)Integration over theη0gives the following expression for the lagrangian in terms of|S iL= S1|pµ2|S1 − S2|pµ2|S2 − S3||S3 +(3.16) S1|L+1|S3 + S3|L1|S1 − S2|L1|S3 − S3|L+1|S2 .The nilpotency of the BRST-charge leads to the invariance of the lagrangian (3.12)under the following transformationsδ|χ =Q|Λ .(3.17) The parameter of transformation must have ghost number−1and can be written as |Λ =P+1|λ ,where|λ belong to the Fock space generated by a+µ,a+D and depends from the space-time coordinates.Using together this invariance and equations of motion for thefields|S i one can show,that the lagrangian(3.27)describes the infinite number of higher spin massless particles with infinite multiplicity at each value of spin[15].To obtain the description of the Regge trajectory in D dimensions one can make use of the dimensional reduction procedure to the D+1dimensional massless la-grangian.The masslessness condition in D+1dimensions isp2µ−p2D=0.(3.18) After thefixing p D=m with some arbitrary parameter m this equation describes massive particle.In principle m can depend from the spin of particle,leading to the Regge trajectory.To describe the linear Regge trajectory wefix the following x D dependence of the Fock space vector|χ in(3.12):|χ =exp(ix Dα′(−a+µaµ+a+D a D)+α′+α0a D(3.23)˜L+=pµa+µ−a+D1α′ α′+2− α′+1 (3.25) The commutator of constraints(3.23)and(3.24)has rather complicated form:[˜L1,˜L+1]=˜L0+α′+a+D X˜L1+˜L+1Xa D+a+D X2a D.(3.26)The new BRST-charge˜Q(3.21)is nilpotent due to unitarity of the transformation ˜Q=U−1QU.Our choice of square root dependence in the exponent in(3.19)leads, as we will see later,to the linear Regge trajectory.Replacement of this square root by any other function consistently gives Regge trajectory with more complicated dependence between spin and mass.The nilpotency of the BRST-charge evidently does not depend from the choice of this function.In terms of|S i the lagrangian(3.20)has the folloqing form:L=− S1|˜L0|S1 + S2|(˜L0+2α′)|S2 + S1|˜L+1|S3 + S3|˜L1|S1 −S2|(˜L1+Xa D)|S3 − S3|(˜L+1+a+D X)|S2 − S3||S3 .(3.27) The correswponding equations of motion are:˜L0|S1 −˜L+1|S3 =0,(3.28)(˜L0+2α′)|S2 −(˜L1+Xa D)|S3 =0,(3.29)|S3 −˜L1|S1 +(˜L+1+a+D X)|S2 =0.(3.30) The transformation lawδ|χ′ =˜Q|Λ has the following component form:δ|S1 =˜L+1|λ ,(3.31)δ|S2 =(˜L1+Xa D)|λ ,(3.32)δ|S3 =(˜L0+α′)|λ .(3.33) One can show that using together(3.31)and equations of motion for thefields |S i one can eliminate thefields|S2 and|S3 .Firstly we solve the equation|S3 +(˜L0+α′)|λ =0(3.34) using decompositions|S i = (a+D)n|S in ,|λ = (a+D)n|λn .(3.35) The equation(3.34)does notfix parameter|λ completely.There will be residual invariance with parameter|λ′ under the condition(˜L0+α′)|λ′ =0.(3.36)After the elimination of thefield|S2 with the help of the equation|S2 +(˜L1+ Xa D)|λ′ =0,which is consistent with the equations(3.29)and(3.36),the new parameter|λ′′ will satisfy two conditions(˜L0+α′)|λ′′ =(˜L1+Xa D)|λ′′ =0.With the help of this parameter allfields|S1n ,except|S10 can be eliminated as well.It means that only|S10 under conditionsL0|S1 =0,L1|S1 =0(3.37) is a physicalfield.The second condition kills negative norm states of the Fock space. Thefirst one-the mass shell condition-fixes the linear dependence between masses and spins of physical states.In general the Fock space vectors|χ and|χ′ have complex vawefunctions.In the massless case one can impose the following reality conditions consistent with the equations of motion and transformation law(3.17):the coefficients in|S1 and|S2 are real as opposite to the coefficients in|S3 and|λ ,which are purely imaginary. The transformation(3.19),due to its complexity destroys such reality conditions for the massive case.4ExamplesThe total lagrangian(3.27)describes all spins from zero to infinity.The maximal spin at the level m2=α0+nα′is n.Due to luck of the tracelessness constraint,there are also spins n−2,n−4...on this level.The part of the lagrangian describing this level containsfields in|S1 ,|S2 and|S3 with n,n−2and n−1total numbers of creation operators a+µand a+D.In this chapter we describe three simplest cases n=0,1,2.For n=0the onlyfield|S1 0=A|0 (4.1) gives contribution to the lagrangian:L=−A∂µ2A−α0A2(4.2) Obviously it describes spinless particle with m2=α0.For n=1correspondingfields are:|S1 1=(Aµa+µ+iAa+D)|0 and|S3 0=iC|0 (4.3) The lagrangianL=Aν∂µ2Aν−A∂µ2A+(α′+α0)Aα2−(α′+α0)A2−C2−2is invariant under the following gauge transformationsδA µ=∂µλ(4.5)δA =−√2α′+α0CA +4√2α′+α0BC (4.12)The gauge transformations with the parameter |λ =(iλµa +µ+λa +D )|0 give:for |S 1 2:δA µν=12α′+α0λµ,(4.14)δA =−√2α′+α0λ,(4.16)and for |S 3 1:δC µ=(∂ν2+2α′+α0)λµ,(4.17)δC =(∂ν2+2α′+α0)λ.(4.18)After the gauge fixing the only nonvanishing field is A µνunder conditions(∂2ρ+2α′+α0)A µν=0,∂νA µν=0.(4.19)Such equations describe simultaneously spin 2and spin 0particles.5ConclusionsIn this paper we have applied the BRST approach to the description of the free Regge trajectory.The corresponding BRST-charge was constructed with the help of dimensional reduction method.The resulting spectrum contains reducible rep-resentations of the Poincare group at each mass level due to luck of tracelessness constraint.It means that daughter trajectories also belong to the spectrum.The modification of the BRST approach to the single Regge trajectory will be given elsewhere.Acknowledgments.One of us(A.P.)would like to thank M.Vasiliev andC.Preitschopf for useful discussions.This investigation has been supported in part by the Russian Foundation of Fundamental Research,grants96-02-17634and96-02-18126,grant MXL200,joint grant RFFR-DFG96-02-00186G,and INTAS,grant 94-2317and grant of the Dutch NWO organization.References[1]M.Fierz,W.Pauli.Proc.Roy.Soc.,A173(1939)211[2]E.S.Fradkin.JETP,20(1950)27[3]L.P.H.Singh,C.R.Hagen.Phys.Rev.,D9(1974)898;Ibid D9(1974)910[4]S.J.Chang.Phys.Rev.,161(1967)1308[5]C.Fronsdal.Phys.Rev.,D18(1978)3624[6]J.Fang,C.Fronsdal.Phys.Rev.,D18(1978)3630[7]B.de Wit,D.Z.Freedman.Phys.Rev.,D21(1980)358[8]T.Curtright.Phys.Lett.,B85(1979)219[9]M.A.Vasiliev.Sov.J.Nucl.Phys.,32(1980)855(439in english translation)[10]C.Aragone,S.Deser.Nucl.Phys.,B170(1980)329[11]Y.S.Kim,Marilyn E.Noz.Phys.Rev.,D12(1975)129;ibid D15(1977)335[12]A.Barducci,D.Dominici.Nuovo Cim.,A37(1977)385[13]V.D.Gershun,A.I.Pashnev.Theor.Math.Phys.,73(1987)294[14]A.I.Pashnev.Theor.Math.Phys.,78(1989)424[15]S.Ouvry,J.Stern.,Phys.Lett.,B177(1986)335[16]Y.Meurice,Phys.Lett.,B186(1987)189[17]L.D.Faddeev,S.L.Shatashvili.Phys.Lett.,B167(1986)225[18]E.T.Egoryan,R.P.Manvelyan.Theor.Math.Phys.,94(1993)241[19]A.Pashnev,M.Tsulaia.,Preprint JINR E2-96-408,Dubna1996;hep-th/961102210。
