浙教版七年级上册第二章有理数和运算 有理数的加减专项练习(无答案)
新浙教版七年级上册数学第二章有理数的运算知识点典型例题练习(无答案)
积为
5、将一张纸按同一方向连续对折 3 次,可得到 条折痕。折 n 次,可得到
条折痕,此时若按折痕将
纸撕开,可以得到
张纸。
6、你喜欢吃拉面吗?拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合、拉伸,
反复多次,就能拉成许多细面条.如图所示:
(1)经过第 3 次捏合后,可以拉出
根细面条;
(2)到第
A. 29 B. 30 C. 59 D. 60 3、1 根 1m 长的绳子,第一次剪去一半,第二次剪去剩下的一半,如此剪下去,第 6 次剩下的绳子长度为( )
A. ( 1 )6m 2
B. ( 1 )5m 2
C. ( 1 )3m 2
D. ( 1 )12m 2
4、将一个边长为 1m 的正方形,第一次剪去一半,第二次剪去剩下的一半,如此剪下去,第六次后剩下的纸板面
By wiviee
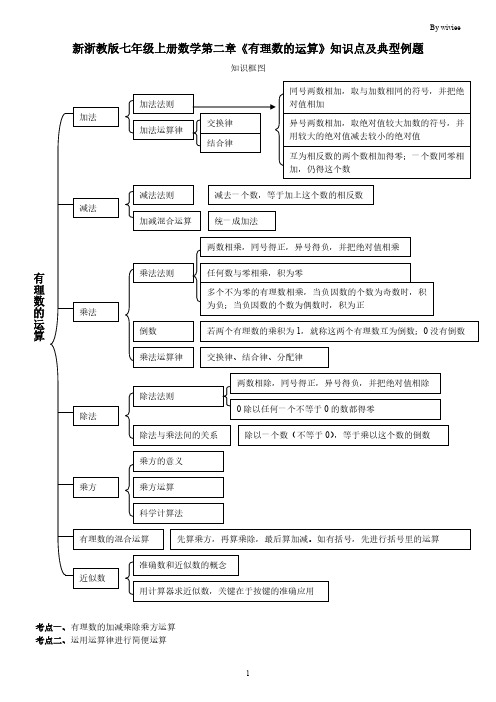
新浙教版七年级上册数学第二章《有理数的运算》知识点及典型例题
知识框图
加法
加法法则 加法运算律
交换律 结合律
同号两数相加,取与加数相同的符号,并把绝 对值相加
异号两数相加,取绝对值较大加数的符号,并 用较大的绝对值减去较小的绝对值
互为相反数的两个数相加得零;一个数同零相 加,仍得这个数
交换律、结合律、分配律
除法
除法法则
两数相除,同号得正,异号得负,并把绝对值相除 0 除以任何一个不等于 0 的数都得零
除法与乘法间的关系
除以一个数(不等于 0),等于乘以这个数的倒数
乘方的意义
乘方
乘方运算
科学计算法
有理数的混合运算
先算乘方,再算乘除,最后算加减。如有括号,先进行括号里的运算
近似数
新浙教版七年级上册数学第二章《有理数的运算》知识点及典型例题

新浙教版七年级上册数学第二章《有理数的运算》知识点及典型例题将考点与相应习题联系起来考点一、有理数的加减乘除乘方运算1、 (-3)3÷214×(-23)2 – 4-23×(- 232) 2、 -32+(-2)3 –(0.1)2×(-10)33、 -0.5-(-314)+2.75+(-712) 4、(-23)-(-5)+(-64)-(-12)5、如果()()0132122=-+-++c b a ,求333c a abc -+的值.考点二、运用运算律进行简便运算1、-(-5.6)+10.2-8.6+(-4.2)2、(-12+16-34+512)×(-12) 3、(117512918--)×36-6×1.43+3.93×6 4、492425×(-5)考点三、与数轴相关的计算或判断1、已知有理数a,b,c 在数轴上的位置如图所示,下列错误的是( ) A 、b+c<0B 、-a+b+c<0C 、|a+b|<|a+c|D 、|a+b|>|a+c|2、a ,b 在数轴上的位置如图所示,则a ,b ,a +b ,a -b 中,负数的个数是( ) A .1个 B .2个 C .3个 D .4个3、若a .b .c 在数轴上位置如图所示,则必有( )a -2-1A .abc >0B .ab -ac >0C .(a +b )c >0D .(a -c )b >04、有理数a ,b 在数轴上的位置如图所示,则在a +b ,a -b ,ab ,3a ,23a b s 这五个数中,正数的个数是( ) A .2 B .3 C .4 D .55、有理数a 、b 在数轴上的对应的位置如图所示,则( ) A .a + b <0 B .a + b >0 C .a -b = 0 D .a -b >06、a 、b 在数轴上的位置如图,化简a = ,b a += ,1+a = 。
浙教版七上第二章有理数的运算习题精选.doc

第二章 有理数的运算2.1 有理数的加法 基础训练一、填空: 1、(+ 3.5)+(– 8.5 )= ( – 0.7 )+( – 0.3 )= 2、三个不同的有理数(不全同号)和为1,请你写出一个算式 3、用“>”,“<”或“=”连接下列各式:│(– 4)+(– 5)│ │– 4│+│– 5│ │(– 4)+(+ 5)│ | – 4| + |+ 5| 二、选择题:4、若 a 比10大–3,则a=( )A 、 13B 、7C 、8D 、125、在数轴原点的左边3个单位处有一点A ,向数轴正方向移动了4.5个单位.则点A 最后停在( )处A 、–1.5B 、– 7.5C 、 1.5D 、 7.5 6、下列计算正确的是 ( )A 、(– 4 )+( – 5 )= – 9B 、 5 +( –6 )=11C 、( – 7 )+10= –3D 、( – 2 )+ 2 = 4 7、下列说法正确的是 ( )A 、两个数的和一定大于每一个加数B 、互为相反数的两个数的和等于零C 、若两数和为正,则这两个数都是正数D 、若│a │=│b │、则a=b 8、一小商店,一周盈亏情况如下:(亏为负,单位:元):128.3 、– 25.6 、–15 、27、– 7、36.5、98,则小商店该周的盈亏情况是 ( )A 、 盈240元B 、亏240元C 、盈242.2元D 、亏 242.2元 三、解答题:9、在数轴上表示下列有理数的运算,并求出计算结果 1)、( – 2.5 )+( – 3. 5 ) 2)、7 + ( – 9 )10、用简便方法计算,并说明理由: 1)、(– 243)+ 143 + 131 + (– 531)2)、(– 1.8)+ 0.2 + ( – 1.5 ) + ( – 0.3 ) + 1.5 + 0.1综合提高一、填空1、算式( –10 )+ 7和的符号为 ,和的绝对值是 ,计算结果是2、小丽沿着东西方向的道路行走,她先向正东方向走77米,再向正西方向走108 米,最后小丽停在出发点 方向 米处。
浙教版七年级数学上 第2章:有理数的运算培优练习题 有理数的加法和减法(无答案)

有理数培优练习一、有理数的加法和减法1、若一个数的相反数的倒数是自然数,则这个数是( )A. 51B.31- C.3 D.--5 2、不能使等式()()+-=+-3.113.11成立的数是( )A. 任意一个数B.任意一个正数C.任一个负数D.任一个非负数3、不能使等式()()+-=--19.09.0成立的数是( )A. 任一个负数B.任一个非负数C.任一个正数D.任一个非正数4、使等式()()+-=+-817817成立的数是( ) A. 任一个正数 B.任一个非正数 C.小于1的数 D.任意一个数5. ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+---3.05.261315.0等于( ) A.2.2 B.--3.2 C.--2.2 D.3.26. ⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛------32143421313等于( ) A. 12117- B.12116- C.1218- D.12118- 7. 欲使两数和的绝对值等于这两个数差的绝对值,这两个数必须是怎样的数?8. 欲使两数和的绝对值不大于这两数的差的绝对值,这两个数必须是怎样的数?9. 欲使两数和的绝对值不小于这两数的绝对值的和,这两个数必须是怎样的数?二、有理数的乘法、除法和乘方10. ()22225.03.0-÷⨯÷-的值是() A. 1009-B.1009C.4009D.4009- 11. ()()()()4223301.01.03.0-÷-⨯-÷-的值是( ) A. 400003- B.3000001- C.3000001 D.30001- 12. 若b a b a ⋅<⋅,则下列正确的结论是( )A. 0,0<<b aB.0,0<>b aC.0,0><b aD.0<⋅b a13. 下列数中与()527--相等的数是( ) A. ()()5527-+- B.514- C.103 D.103- 14. 如果()0125>-ab ,则下列结论正确的是( )A. 0<a bB.0>ba C.0,0<>b a D.0.0><b a15. 如果等式2a a =成立,则a 的可能的取值是( )A.1个B.2个C.3个D.不确定16.a 为任意整数,则下列四组数中的数字都不可能是2a 的末尾数字的应是( ) A.3,4,9,0 B.2,3,7,8 C.4,5,6,7 D.1,5,6,916. 四个各不相等的整数a,b,c,d,它们的积9=⋅⋅⋅d c b a ,那么a+b+c+d 的值是() A.0 B.4 C.8 D.不确定17. 如果有理数c cb ba ac b a c b a ++≠⋅⋅求满足,0,,的所有可能值得立方和。
浙教版数学七年级上册第二章 有理数的运算单元测试卷(含答案)

浙教版数学七年级上册第二章有理数的运算一、选择题1.下列各对数中,互为相反数的是( )A.+(﹣2)与﹣(+2)B.﹣(﹣3)与|﹣3|C.﹣32与(﹣3)2D.﹣23与(﹣2)32.已知数549039用四舍五入法后得到的是5.490×105,则所得近似数精确到( ).A.十位B.百位C.千分位D.万位3.两数相加,如果和小于任何一个加数,那么这两个数( )A.同为正数B.同为负数C.一正数一负数D.一个为0,一个为负数4.下列说法正确的是( )A.1是最小的自然数B.平方等于它本身的数只有1C.任何有理数都有倒数D.绝对值最小的数是05.用“▲”定义一种新运算:对于任何有理数a和b,规定a▲b=ab+b2,如2▲3=2×3+32=15,则(−4)▲2的值为( )A.−4B.4C.−8D.86.有理数a,b在数轴上的对应点如图所示,则下列式子中错误的是( )A.ab>0B.a+b<0C.a﹣b<0D.b﹣a<07.一件衣服的进价为100元,商家提高80%进行标价,为了吸引顾客,商店进行打7折促销活动,商家出售这件衣服时,获得的利润是( )A.26元B.44元C.56元D.80元8.若x、y二者满足等式x2−3y=3x+y2,且x、y互为倒数,则代数式x2−3(x+y)+5−y2−4xy的值为( )A.1B.4C.5D.99.如图是节选课本110页上的阅读材料,请根据材料提供的方法求和:11×2+12×3+13×4+⋅⋅⋅+12020×2021,它的值是( )上题是利用一系列等式相加消去项达到求和,这种方法不仅限于整数求和,如1−12=11×2①12−13=12×3②13−14=13×4③14−15=14×5④……继续写出上述第n 个算式,并把这些算式两边分别相加,会得到:11×2+12×3+13×4+⋅⋅⋅+1n ×(n +1).A .1B .20202021C .20192020D .1202110.计算机利用的是二进制数,它共有两个数码0,1,将一个十进制数转化为二进制,只需将该数写为若干个2n 的数字之和,依次写出1或0的系数即可,如十进制数字19可以写为二进制数字10011,因为19=16+2+1=1×24+0×23+0×22+1×21+1×20,32可以写为二进制数字100000,因为32=32=1×25+0×24+0×23+0×22+0×21+0×20,则十进制数字70是二进制下的( )A .4位数B .5位数C .6位数D .7位数二、填空题11.2022年11月20日晚,卡塔尔世界杯正式开幕,仅两天时间,抖音世界杯总话题播放量高达21480000000次,其中数21480000000用科学记数法表示为 .12.计算(−1)2023÷(−1)2004= .13.一个数的立方等于它本身,这个数是 14.如图所示的程序图,当输入﹣1时,输出的结果是 .15.若a ,b ,c 都不为0,则 a |a|+b |b|+c |c|+abc|abc|的值可能是 .16.如图,商品条形码是商品的“身份证”,共有13位数字.它是由前12位数字和校验码构成,其结构分别代表“国家代码、厂商代码、产品代码、校验码”.其中,校验码是用来校验商品条形码中前12位数字代码的正确性.它的编制是按照特定的算法得来的.其算法为:步骤1:计算前12位数字中偶数位数字的和a ,即a =9+1+3+5+7+9=34;步骤2:计算前12位数字中奇数位数字的和b ,即b =6+0+2+4+6+8=26;步骤3:计算3a 与b 的和c ,即c =3×34+26=128;步骤4:取大于或等于c 且为10的整数倍的最小数d ,即d =130;步骤5:计算d 与c 的差就是校验码X ,即X =130−128=2.如图,若条形码中被污染的两个数字的和是5,则被污染的两个数字中右边的数字是 .三、解答题17.小明有5张写着不同数字的卡片,完成下列各问题:(1)把卡片上的5个数在数轴上表示出来;(2)从中取出3张卡片,将这3张卡片上的数字相乘,乘积的最大值为 ;(3)从中取出2张卡片,将这2张卡片上的数字相除,商的最小值为 18.一名足球守门员练习折返跑,从球门线出发,向前记作正数,返回记作负数,他的记录如下(单位:米):+5,−3,+10,−8,−6,+12,−10.(1)守门员最后是否回到了球门线的位置?(2)在练习过程中,守门员离开球门线的最远距离是多少米?(3)守门员全部练习结束后,他共跑了多少米?19.已知a、b互为倒数,c、d互为相反数,|m|=3,n是最大的负整数,求代数式(−ab)2024−3(c+d)−n+m2的值.20.在一条不完整的数轴上从左到右有A,B,C三点,其中AB=2,BC=1,如图所示,设点A,B,C所对应数的和是p.(1)若以C为原点,写出点A,B所对应的数,计算p的值;(2)若p的值是﹣1,求出点A,B,C所对应的数;(3)在(2)的条件下,在数轴上表示|﹣0.5|、(﹣1)3和A,B,C所对应的数,并把这5个数进行大小比较,用“<”连接.21.现定义一种新运算“*”,对任意有理数a、b,规定a*b=ab+a﹣b,例如:1*2=1×2+1﹣2.(1)求2*(﹣3)的值;(2)求(﹣3)*[(﹣2)*5]的值.22.目前,某城市“一户一表”居民用电实行阶梯电价,具体收费标准如下.一户居民一个月用电量(单位:度)电价(单位:元/度)第1档不超过180度的部分0.5第2档超过180度的部分0.7(1)若该市某户12月用电量为200度,该户应交电费 元;(2)若该市某户12月用电量为x度,请用含x的代数式分别表示0≤x≤180和x>180时该户12月应交电费多少元;(3)若该市某户12月应交电费125元,则该户12月用电量为多少度?23.如图,已知数轴上有A,B两点,分别代表−40,20,两只电子蚂蚁甲,乙分别从A,B两点同时出发,甲沿线段AB以1个单位长度秒的速度向右运动,到达点B处时运动停止;乙沿BA方向以4个单位长度秒的速度向左运动.(1)A,B两点间的距离为 个单位长度;乙到达A点时共运动了 秒.(2)甲,乙在数轴上的哪个点相遇?(3)多少秒时,甲、乙相距10个单位长度?(4)若乙到达A点后立刻掉头并保持速度不变,则甲到达B点前,甲,乙还能在数轴上相遇吗?若能,求出相遇点所对应的数;若不能,请说明理由.答案解析部分1.【答案】C2.【答案】B3.【答案】B4.【答案】D5.【答案】A6.【答案】D7.【答案】A8.【答案】A9.【答案】B10.【答案】D11.【答案】2.148×101012.【答案】−113.【答案】0或±114.【答案】715.【答案】0或4或﹣416.【答案】417.【答案】(1)解:如图所示(2)50(3)-818.【答案】(1)守门员最后回到了球门线的位置(2)12米(3)54米19.【答案】解:∵a、b互为倒数,c、d互为相反数,|m|=3,n是最大的负整数,∴ab=1,c+d=0,m2=9,n=−1,∴(−ab)2024−3(c+d)−n+m2=(−1)2024−3×0−(−1)+9=1−0+1+9=11.20.【答案】(1)解:若以C为原点,∵AB=2,BC=1,∴B表示﹣1,A表示﹣3,此时,p=(﹣3)+(﹣1)+0=﹣4;(2)解:设B对应的数为x,∵AB=2,BC=1,则A点表示的数为x﹣2,C表示的数为x+1,p=x+x+1+x﹣2=﹣1;x=0,则B点为原点,∴A表示﹣2,C表示1;(3)解:如图所示:故﹣2<(﹣1)3<0<|﹣0.5|<1.21.【答案】(1)解:2*(﹣3)=2×(﹣3)+2﹣(﹣3)=﹣6+2+3=﹣1;(2)解:(﹣3)*[(﹣2)*5]=(﹣3)*[(﹣2)×5+(﹣2)﹣5]=(﹣3)*(﹣17)=(﹣3)×(﹣17)+(﹣3)﹣(﹣17)=51﹣3+17=65.22.【答案】(1)104(2)解:当0≤x≤180时,该户12月应交电费为0.5x元;当x>180时,该户12月应交电费为0.5×180+0.7(x−180),=90+0.7x−126,=(0.7x−36)(元).(3)解:∵104<125,∴x>180,∴0.7x−36=125,∴x=230.答:该户12月用电量为230度.23.【答案】(1)60;15(2)解:60÷(4+1)=12,−40+12=−28.答:甲,乙在数轴上的−28点相遇(3)解:两种情况:相遇前,(60−10)÷(4+1)=10;相遇后,(60+10)÷(4+1)=14,答:10秒或14秒时,甲、乙相距10个单位长度;(4)解:乙到达A点需要15秒,甲位于−40+15=−25,乙追上甲需要25÷(1+4)=5(秒)此时相遇点的数是−25+5=−20,故甲,乙能在数轴上相遇,相遇点表示的数是−20.。
初中数学浙教版七年级上册第2章 有理数的运算2.2 有理数的减法-章节测试习题(24)

章节测试题1.【答题】某天的最高气温是7℃,最低气温是-5℃,则这一天的最高气温与最低气温的差是()A. 2℃B. -2℃C. 12℃D. -12℃【答案】C【分析】本题考查了有理数的减法法则:减去一个数等于加上这个数的相反数.这是需要熟记的内容.这天的温差就是最高气温与最低气温的差,列式计算.【解答】这天的温差就是最高气温与最低气温的差,即7-(-5)=7+5=12℃.选C.2.【答题】某市2009年元旦的最高气温为2℃,最低气温为-8℃,那么这天的最高气温比最低气温高()A. -10℃B. -6℃C. 6℃D. 10℃【答案】D【分析】本题考查了有理数的意义和实际应用,运算过程中应注意有理数的减法法则.这天的最高气温比最低气温高多少,即是求最高气温与最低气温的差.【解答】∵2-(-8)=10,∴这天的最高气温比最低气温高10℃.选D.3.【答题】比1小2的数是()A. -3B. -1C. 1D. 3【答案】B【分析】本题考查了有理数的减法法则:减去一个数等于加上这个数的相反数.这是需要熟记的内容.比1小2的数是多少,即求1与2的差是多少.【解答】1-2=-1.选B.4.【答题】我市某天的最高气温是6℃,最低气温是﹣2℃,那么当天的日温差是______℃.【答案】8【分析】本题考查了有理数的减法,熟记减去一个数等于加上这个数的相反数是解题的关键.用最高温度减去最低温度,然后根据减去一个数等于加上这个数的相反数进行计算即可得解.【解答】6﹣(﹣2)=6+2=8℃.故答案为8.5.【答题】气象部门测定,高度每增加1千米,气温大约下降5℃,现在地面气温是15℃,那么4千米高空的气温是______℃.【答案】-5【分析】本题考查有理数的减法运算.根据题意列出算式,计算即可得到结果.【解答】根据题意得:15﹣4×5=15﹣20=﹣5,则4千米高空的气温是﹣5℃.故答案为﹣5.6.【答题】存折中有2676元,取出1082元,又存入600元,在不考虑利息的情况下,你能算出存折中还有______元.【答案】2194【分析】本题考查有理数的加减混合运算.根据题意列出算式2676﹣1082+600,然后计算即可.【解答】根据题意得:2676﹣1082+600=2194,∴存折中还有2194元.7.【答题】“早穿皮袄午穿纱”这句民谣形象地描绘了新疆奇妙的气温变化现象.乌鲁木齐五月的某天,最高气温17℃,最低气温-2℃,则当天的最大温差是______℃.【答案】19【分析】本题考查有理数的减法运算.【解答】17-(-2)=19(℃).8.【答题】-21-11=______.【答案】-32【分析】本题考查有理数的减法运算.【解答】-21-11=-(21+11)=-32.9.【答题】-22-12=______.【答案】-34【分析】本题考查有理数的减法运算.【解答】-22-12=-(22+12)=-34.10.【答题】-24-14=______.【答案】-38【分析】本题考查有理数的减法运算.【解答】-24-14=-(24+14)=-38.11.【答题】某地某天早上气温为22℃,中午上升了4℃,夜间又下降了10℃,那么这天夜间的气温是______℃.【答案】16【分析】气温上升用加下降用减,列出算式后运用有理数的加减混合运算法则计算.【解答】根据题意列算式得22+4-10=26-10=16(℃).∴这天夜间的气温是16℃.故应填16.12.【答题】一天早晨的气温是-5℃,中午又上升了10℃,半夜又下降了8℃,则半夜的气温是______℃.【答案】-3【分析】本题考查用正负来表示具有相反意义的量,做题时一定要注意单位.气温上升为正,下降为负,列出算式求解即可.【解答】根据题意列式为-5+10-8=-13+10=-3(℃).故应填-3.13.【答题】我市某天上午的温度是15℃,中午又上升了3℃,夜间又下降了8℃,则这天夜间的温度是______℃.【答案】10【分析】把温度上升计为正,下降计为负,列出算式后进行有理数的加减混合运算.【解答】根据题意,可列式15+3+(-8)=18-8=10(℃).故应填10.14.【答题】某地上午气温为10℃,下午上升2℃,到半夜又下降15℃,那么半夜的气温为______℃.【答案】-3【分析】本题考查了有理数的加减混合运算,熟练掌握运算法则是解本题的关键.根据题意列出算式,计算即可得到结果.【解答】根据题意得10+2-15=12-15=-3(℃),则半夜的气温为-3℃.故答案为-3.15.【答题】如果崇左市市区某中午的气温是36℃,到下午下降了4℃,那么下午的气温是______℃.【答案】32【分析】本题考查了有理数的减法,是基础题,熟记运算法则是解题的关键.用中午的温度减去下降的温度,然后根据有理数的减法运算法则进行计算即可得解.【解答】36℃-4℃=32℃.16.【答题】如果崇左市市区某中午的气温是35℃,到下午下降了5℃,那么下午的气温是______℃.【答案】30【分析】本题考查了有理数的减法,熟记运算法则是解题的关键.用中午的温度减去下降的温度,然后根据有理数的减法运算法则进行计算即可得解.【解答】35℃-5℃=30℃.17.【答题】计算:3-(-1)=______.【答案】4【分析】本题考查了有理数加减法则,能理解熟记法则是解题的关键.先根据有理数减法法则,把减法变成加法,再根据加法法则求出结果.【解答】3-(-1)=3+1=4,故答案为4.18.【答题】计算:2000-2015=______.【答案】-15【分析】本题考查了有理数的减法,熟记运算法则是解题的关键.根据有理数的减法运算进行计算即可得解.【解答】2000-2015=-15.故答案为-15.19.【答题】计算:0-7=______.【答案】-7【分析】本题考查了有理数的减法运算,熟练掌握减法法则是本题的关键.根据有理数的减法法则进行计算即可,减去一个数等于加上这个数的相反数.【解答】0-7=-7;故答案为-7.20.【答题】比-1℃低2℃的温度是______℃.(用数字填写)【答案】-3【分析】本题考查了有理数的减法运算,熟记减去一个数等于加上这个数的相反数是解题的关键.用-1减去2,然后根据减去一个数等于加上这个数的相反数进行计算即可得解.【解答】-1-2=-1+(-2)=-3.故答案为-3.。
浙教版七上第二章有理数的运算习题精选

第二章 有理数的运算2.1 有理数的加法 基础训练一、填空: 1、(+ 3.5)+(– 8.5 )= ( – 0.7 )+( – 0.3 )= 2、三个不同的有理数(不全同号)和为1,请你写出一个算式 3、用“>”,“<”或“=”连接下列各式:│(– 4)+(– 5)│ │– 4│+│– 5│ │(– 4)+(+ 5)│ | – 4| + |+ 5| 二、选择题:4、若 a 比10大–3,则a=( )A 、 13B 、7C 、8D 、125、在数轴原点的左边3个单位处有一点A ,向数轴正方向移动了4.5个单位.则点A 最后停在( )处A 、–1.5B 、– 7.5C 、 1.5D 、 7.5 6、下列计算正确的是 ( )A 、(– 4 )+( – 5 )= – 9B 、 5 +( –6 )=11C 、( – 7 )+10= –3D 、( – 2 )+ 2 = 4 7、下列说法正确的是 ( )A 、两个数的和一定大于每一个加数B 、互为相反数的两个数的和等于零C 、若两数和为正,则这两个数都是正数D 、若│a │=│b │、则a=b 8、一小商店,一周盈亏情况如下:(亏为负,单位:元):128.3 、– 25.6 、–15 、27、– 7、36.5、98,则小商店该周的盈亏情况是 ( )A 、 盈240元B 、亏240元C 、盈242.2元D 、亏 242.2元 三、解答题:9、在数轴上表示下列有理数的运算,并求出计算结果 1)、( – 2.5 )+( – 3. 5 ) 2)、7 + ( – 9 )10、用简便方法计算,并说明理由: 1)、(– 243)+ 143 + 131 + (– 531)2)、(– 1.8)+ 0.2 + ( – 1.5 ) + ( – 0.3 ) + 1.5 + 0.1综合提高一、填空1、算式( –10 )+ 7和的符号为 ,和的绝对值是 ,计算结果是2、小丽沿着东西方向的道路行走,她先向正东方向走77米,再向正西方向走108 米,最后小丽停在出发点 方向 米处。
浙教版七年级数学上册第二章:有理数的运算(练习1,无答案)

有理数的运算2015.9班级 ___________ 姓名 ___________ 学号_______一、选择题1、计算: (-4)+(+7)= ( )A 、-3B 、3C 、-11D 、112、(-5)3的底数是__________ ( )A 、-5B 、5C 、3D 、-33、光年是天文学中的距离单位,1光年大约是9500 000 000 000 km ,用科学记数法可表示为( )A 、9.5×1013 kmB 、9.5×1012 kmC 、9.5×1011 kmD 、9.5×1010 km4、下列计算中,正确的是 ( )A、(-2)-(-5)=-7 B、(-2)+(-3)=-1C、(-2)×(-3)=-6 D、(-12)÷(-2)=65、“5的二次幂与(-3)的商”可以写做 ( )A、2)3(5-÷ B、)3(52-÷ C 、)3(25-÷÷ D、2)]3(5[-÷6、某种红茶菌的繁殖速度是每天增加一倍,若经过18天红茶菌能长满整个缸面,那么长满半个缸面需要 ( )A 、7天B 、9天C 、16天D 、17天二、填空题1、0乘以任何数都得__________2、)2()2()2(-⨯-⨯-用乘方表示,可记做__________。
3、72-的倒数是__________。
4、对985000取近似值(要求保留三个有效数字)为 。
5、比较大小:(1)25______52; (2)21-______3)21(- (3)(-2)4______0。
三、解答题1、计算:(1))4()8(+÷- (2)(+18)-(-12)(3)(4132-)×48 (4)2、计算:(1))5()4131(12-÷-⨯ (2)4)21(21)1(22⨯-+÷-3、如图,一块长方形草地中央有一个圆形花坛。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有理数加法和减法专项
① 同号两数相加法则
② 异号两数相加的法则
重点分析: 1.有理数加法法则:
(1)同号相加取相同符号,并把绝对值相加
(2)绝对值不等的异号加减,取绝对值较大的加数符号,并用较大的绝对值减去较小的绝对值,互为相反教的两个数相加得0. (3)一个数同0相加,仍得这个数.
同号两数相加,取与加数相同的符号,并把绝对值相加
同为负数:如(-2)+(-3)=-(2+3)=-5
同为正数:如(+3)+(+9)=+(3+9)=12
两加数同号
异号两数相加,取绝对值较大的数的符号,并用较大绝对值减去较小的绝对值
绝对值相等:如(-2)+(+2)=0
绝对值不相等:如(+3)+(-9)=-(9-3)=-6
两加数异号
2.加法交换律:a+b=b+a,两个数相加,交换加数的位置,和不变.
加法结合律:a+b+c=(a+b) +c=a+(b+c),三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
3.有理数减法法则:减去一个非零的数,等于加上这个数的相反数. 两变:减法运算变加法运算,减数变成它的相反数;
一不变:被减数不变,可以表示成:a- b=a+(-b).
难点分析:
1.在进行有理数加法运算时,首先判断两个加数的符号:是同号还是异号,是否有0,从而确定用哪一条法则,在应用过程中,一定要牢记“先符号,后绝对值”,熟练以后就不会出错了:
2.在进行有理数加法运算时,一般采取:
(1) 互为相反数的先加(抵消)(2)同号的先加。
(3)同分母的先加(4)能凑整数的先加,(5)异分母分数相加,先通分,再计算。
例题:
1.有理数加减法的计算:
(1)( +7.6)+ (-18)+ ( +3.4)+ (-12) (2)(-83)+ ( +26)+ (-17)+ (-26)+ ( +15)
(3)(+14)+(+18)+(−38)+6+(−5
8)+(−6)
以下题目用拆项法
(4)10−(+55
6)−(+23
7)+(−21
6)−(+44
7) (5) (-2.5)+(+21
4)+(+1.75)+(−31
2
)
(6)(−72
3)−(+1
4)+(−1
3)+(+5)−(−31
4) (7) 22
13+8−(+92
13)+(−12
5)+(−23
5)
(8) (−32
3)−(−21
4)−(−12
3)−(+1.75) (9) (−47
8)−(−51
2)+(−41
2)−(+31
8)
2. 若|x-3|与|y+2|互为相反数,求x+y+3的值。
3. 设a 是最小的正整数,b是最大的负整数,c是绝对值最小的数,则a-b-c等于( )
A.1
B.0
C.2
D.2或0
4. 振子从一点A开始左右来回振动,振动七次后停止振动,如果规定向右为正,向左为负,则这七次振动记录为(单位:cm):
+ 10,-9,+8, -6,+7, -5, +3.
(1)求振子停止振动时位于A点什么方向,距离A点多远;
(2)如果振子每移动1cm需0.2s,则这七次振动共用多少秒?
5. 某次数学单元检测,七年级(8)班A1小组六位同学计划平均成绩达到80分,组长在登记成绩时,以80分为基准,超过80分的分数记为正,不足80分的分数记为负,成绩记录如下(单位:分):+ 10,-2,+15,+8,-13,- 7.
(1)本次检测成绩最好的为多少分?
(2)该小组实际总成绩与计划相比是超过还是不足,超过或不足多少分?
(3)本次检测AI小组六位同学中得分最高与最低相差多少分?
6. 已知a,b,c,d为有理数,其中a,b,c,d在数轴上对应的点的位置如图所示,试求|a-b|-|b-c|+|c|-|b+d|的值
7. 已知有理数a,b,c在数轴上对应的点的位置如图所示
(1)判断下列各式的符号:a-b, b-c, c-a
(2)若|a|=2,|b|=1
2,|c|=1,试比较c-b与b-a之间的大小关系
0 0。
