求抛物线表达式
抛物线解析式的求法

4.当x=1时,y=0; x=0时,
y=-2,x=2时,y=3;
5. 顶点坐标为(-1,-2),且通 过点(1,10);
6. 对称轴为x=2,函数的最小值为 3,且图象经过点(-1,5).
7.已知抛物线 y ax2 bx c 经过三点
A(2,6),B(-1,2),C(0,1)
,那么它的解析式是
x轴的两个交点间的距离为4,此抛物线
的解析式是
.
11.如图,有一个二次函数的图象,三位学生分 别说出了它的一些特点:
甲:对称轴是直线x=4。
y
C
乙:与x轴两个交点A、B点的横坐标
都是整数。
OA
x B
丙:与y轴的交点C点的纵坐标也是整数, x=4
且S⊿ABC= 3。 请你写出满足上述条件的全部特点的所有的
二次函数解析式的几种表达式
• 一般式:y=ax2+bx+c • 顶点式:y=a(x+h)2+k
• 两根式:y=a(x-x1)(x-x2)
根据下列条件求关于x 的二次函数的解析式
1.当x=3时,y最小值=-1,且图象 过(0,7);
2.图象过点(0,-2)(1,2)且 对称轴为直线 x=1.5;
3.图象经过点(0,1)(1,0) (3,0);
,
变:
(1)已知二次函数图象经过(-1,10),
(2,7)和(轴交于点(-1,0)和
(3,0),且过点(0, 3 ),那么抛物
线的解析式是
2
;淘宝账号购买 淘宝账号出售 / 淘宝账号购买 淘宝账号出售 ;
灵魂会随着老黄牛的-头撞死而颤栗,更会因主人庆幸少花钱的高兴嘴脸而悲哀。 2.文中画线处的景物描写分别有怎样的作用?请简要分析。 3.小说结尾处主人对
高考数学抛物线复习
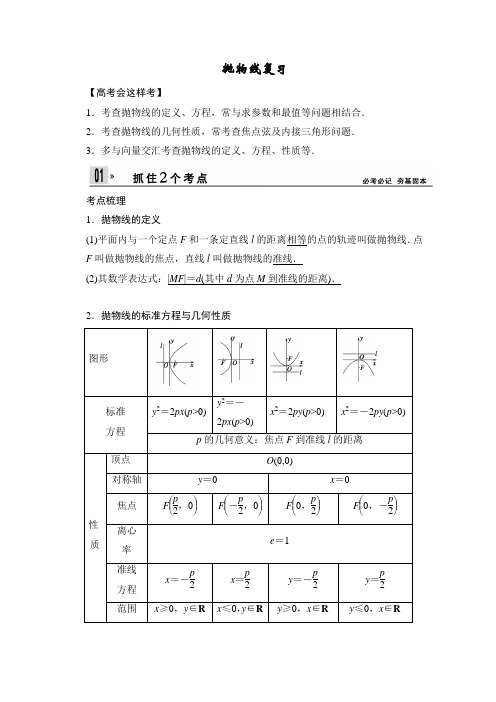
抛物线复习【高考会这样考】1.考查抛物线的定义、方程,常与求参数和最值等问题相结合.2.考查抛物线的几何性质,常考查焦点弦及内接三角形问题.3.多与向量交汇考查抛物线的定义、方程、性质等.考点梳理1.抛物线的定义(1)平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.(2)其数学表达式:|MF|=d(其中d为点M到准线的距离).2.抛物线的标准方程与几何性质图形标准方程y2=2px(p>0)y2=-2px(p>0)x2=2py(p>0) x2=-2py(p>0) p的几何意义:焦点F到准线l的距离性质顶点O(0,0)对称轴y=0 x=0焦点F⎝⎛⎭⎪⎫p2,0F⎝⎛⎭⎪⎫-p2,0F⎝⎛⎭⎪⎫0,p2F⎝⎛⎭⎪⎫0,-p2离心率e=1准线方程x=-p2x=p2y=-p2y=p2范围x≥0,y∈R x≤0,y∈R y≥0,x∈R y≤0,x∈R开口 方向向右 向左 向上 向下【助学·微博】一个重要转化 一次项的变量与焦点所在的坐标轴的名称相同,一次项系数的符号决定抛物线的开口方向,即“对称轴看一次项,符号决定开口方向”. 六个常见结论直线AB 过抛物线y 2=2px (p >0)的焦点,交抛物线于A (x 1,y 1),B (x 2,y 2)两点,如图. ①y 1y 2=-p 2,x 1x 2=p 24.②|AB |=x 1+x 2+p ,x 1+x 2≥2x 1x 2=p ,即当x 1=x 2时,弦长最短为2p . ③1|AF |+1|BF |为定值2p .④弦长AB =2psin 2α(α为AB 的倾斜角). ⑤以AB 为直径的圆与准线相切.⑥焦点F 对A ,B 在准线上射影的张角为90°. 考点自测1.(陕西)设抛物线的顶点在原点,准线方程x =-2,则抛物线的方程是( ). A .y 2=-8x B .y 2=-4x C .y 2=8x D .y 2=4x2.(辽宁)已知F 是抛物线y 2=x 的焦点,A ,B 是该抛物线上的两点,|AF |+|BF |=3,则线段AB 的中点到y 轴的距离为( ). A.34 B .1 C.54 D.743.(四川)已知抛物线关于x 轴对称,它的顶点在坐标原点O ,并且经过点M (2,y 0).若点M 到该抛物线焦点的距离为3,则|OM |=( ).A.2 2 B.2 3 C.4 D.2 54.已知动圆过点(1,0),且与直线x=-1相切,则动圆的圆心的轨迹方程为________.5.(新乡模拟)若抛物线y2=2px的焦点与双曲线x26-y23=1的右焦点重合,则p的值为________.考向一抛物线的定义及其应用【例1】►已知抛物线y2=2x的焦点是F,点P是抛物线上的动点,又有点A(3,2),求|P A|+|PF|的最小值,并求出取最小值时P点的坐标.【训练1】设P是曲线y2=4x上的一个动点,则点P到点B(-1,1)的距离与点P到直线x=-1的距离之和的最小值为________.考向二抛物线的标准方程及几何性质【例2】►(1)以原点为顶点,坐标轴为对称轴,并且经过P(-2,-4)的抛物线方程为________.(2)设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是().A.(0,2) B.[0,2] C.(2,+∞) D.[2,+∞)【训练2】(郑州一模)如图,过抛物线y2=2px(p>0)的焦点F的直线交抛物线于点A,B,交其准线l于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线的方程为().A.y2=9x B.y2=6x C.y2=3x D.y2=3x考向三抛物线的焦点弦问题【例3】►已知过抛物线y2=2px(p>0)的焦点,斜率为22的直线交抛物线于A (x 1,y 1),B (x 2,y 2)(x 1<x 2)两点,且|AB |=9. (1)求该抛物线的方程;(2)O 为坐标原点,C 为抛物线上一点,若OC →=OA →+λOB →,求λ的值.【训练3】 若抛物线y 2=4x 的焦点为F ,过F 且斜率为1的直线交抛物线于A ,B 两点,动点P 在曲线y 2=-4x (y ≥0)上,则△P AB 的面积的最小值为________.方法优化——有关抛物线焦点弦的解题技巧【真题探究】► (安徽)过抛物线y 2=4x 的焦点F 的直线交该抛物线于A ,B 两点,O 为坐标原点.若|AF |=3,则△AOB 的面积为( ).A.22B. 2C.322 D .2 2【试一试】 已知抛物线y 2=4x 的焦点为F ,过F 的直线与该抛物线相交于A (x 1,y1),B(x2,y2)两点,则y21+y22的最小值是().A.4 B.8 C.12 D.16A级基础演练(时间:30分钟满分:55分)一、选择题(每小题5分,共20分)1.(辽宁)已知F 是抛物线y 2=x 的焦点,A ,B 是该抛物线上的两点,|AF |+|BF |=3,则线段AB 的中点到y 轴的距离为 ( ). A.34 B .1C.54D.742.(东北三校联考)若抛物线y 2=2px (p >0)上一点P 到焦点和抛物线的对称轴的距离分别为10和6,则p 的值为 ( ).A .2B .18C .2或18D .4或163.(全国)已知抛物线C :y 2=4x 的焦点为F ,直线y =2x -4与C 交于A ,B 两点,则cos ∠AFB = ( ).A.45B.35C .-35D .-454.(山东)已知双曲线C 1:x 2a 2-y 2b 2=1(a >0,b >0)的离心率为2.若抛物线C 2:x 2=2py (p >0)的焦点到双曲线C 1的渐近线的距离为2,则抛物线C 2的方程为( ). A .x 2=833yB .x 2=1633yC .x 2=8yD .x 2=16y二、填空题(每小题5分,共10分)5.(郑州模拟)设斜率为1的直线l过抛物线y2=ax(a>0)的焦点F,且和y轴交于点A,若△OAF(O为坐标原点)的面积为8,则a的值为________.6.(陕西)如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米.水位下降1米后,水面宽________米.三、解答题(共25分)7.(12分)已知抛物线C:y2=2px(p>0)过点A(1,-2).(1)求抛物线C的方程,并求其准线方程;(2)是否存在平行于OA(O为坐标原点)的直线l,使得直线l与抛物线C有公共点,且直线OA与l的距离等于55?若存在,求出直线l的方程;若不存在,说明理由.8.(13分)(温州十校联考)已知椭圆x 2a 2+y 2b 2=1(a >b >0)的离心率为33,以原点为圆心、椭圆短半轴长为半径的圆与直线y =x +2相切. (1)求a 与b ;(2)设该椭圆的左、右焦点分别为F 1,F 2,直线l 1过F 2且与x 轴垂直,动直线l 2与y 轴垂直,l 2交l 1于点P .求线段PF 1的垂直平分线与l 2的交点M 的轨迹方程,并指明曲线类型.B 级 能力突破(时间:30分钟 满分:45分)一、选择题(每小题5分,共10分)1.设F 为抛物线y 2=4x 的焦点,A ,B ,C 为该抛物线上三点,若F A →+FB →+FC →=0,则|F A →|+|FB→|+|FC →|=( ).A .9B .6C .4D .32.(洛阳统考)已知P 是抛物线y 2=4x 上一动点,则点P 到直线l :2x -y +3=0和y 轴的距离之和的最小值是( ).A. 3B. 5 C .2 D.5-1二、填空题(每小题5分,共10分)3.(北京)在直角坐标系xOy 中,直线l 过抛物线y 2=4x 的焦点F ,且与该抛物线相交于A ,B 两点,其中点A 在x 轴上方.若直线l 的倾斜角为60°,则△OAF 的面积为________.4.(重庆)过抛物线y 2=2x 的焦点F 作直线交抛物线于A ,B 两点,若|AB |=2512,|AF |<|BF |,则|AF |=________.三、解答题(共25分)5.(12分)已知抛物线C :y 2=4x ,过点A (-1,0)的直线交抛物线C 于P 、Q 两点,设AP→=λAQ →. (1)若点P 关于x 轴的对称点为M ,求证:直线MQ 经过抛物线C 的焦点F ; (2)若λ∈⎣⎢⎡⎦⎥⎤13,12,求|PQ |的最大值.6.(13分)(新课标全国)设抛物线C:x2=2py(p>0)的焦点为F,准线为l,A为C 上一点,已知以F为圆心,F A为半径的圆F交l于B,D两点.(1)若∠BFD=90°,△ABD的面积为4 2,求p的值及圆F的方程;(2)若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值.。
抛物线解析式的求法

初三某班的学生在问题中出现争论:
求方程x2
1 2
x
3的解时,几乎所有学生都将方程化为
x2
1 2
x
3
0,画出函数图象,观察它与x轴的交点得, 出
方程的解,唯独小刘没有将方程移项,而是分别画出函数
变:抛物线与x轴的两个交点的横坐标是 -3和1,且过点(0, 3 ),此抛物线
2
的解析式是
9. 已知二次函数的图象顶点坐标(2,1)
,且与x 轴相交两点的距离为2,则其
表达式为
.
10.抛物线的顶点为(-1,-8),它与
x轴的两个交点间的距离为4,此抛物线
的解析式是
.
11.如图,有一个二次函数的图象,三位学生分 别说出了它的一些特点:
甲:对称轴是直线x=4。
y
C
乙:与x轴两个交点A、B点的横坐标
都是整数。
OA
x B
丙:与y轴的交点C点的纵坐标也是整数, x=4
且S⊿ABC= 3。 请你写出满足上述条件的全部特点的所有的
二次函数的解析式为- 2,0),在y轴上的截距 为- 3,对称轴 x=2,求它的 解析式.
y
x2和y
1 2
x
3的图象,他认为它们的交点AB,的横坐
标
3 2
和
2就是原
方程的解.
17.你能否画出适当的函数图象,求方程
x2 1 x 3 2
的解?
图 26.3.3
18.已知:二次函数y=x2+2ax-2b+1和 y=-x2+(a-3)x+b2-1的图象都经过 x轴上两个不同的点M、N,求 a, b的值.
抛物线求最大值和最小值的公式

抛物线求最大值和最小值的公式
抛物线是一种常见的二次函数,其一般表达式为f(x)=ax2+bx+c,其中a、b、c为常数且a eq0。
抛物线在数学和物理等各个领域都有着重要的应用,求解其最大值和最小值是常见的问题之一。
求最大值和最小值的方法
要求抛物线的最大值和最小值,可以通过求导数的方法实现。
抛物线的导数是
一条切线的斜率,当切线水平时,抛物线取得最大值或最小值。
首先考虑抛物线f(x)=ax2+bx+c,计算其导数f′(x),再令f′(x)=0求得
切线水平的点,即为抛物线的最值点。
求解最值的公式
假设抛物线为f(x)=ax2+bx+c,其导数为:
f′(x)=2ax+b
当f′(x)=0时,有:
$$ 2ax + b = 0 \\Rightarrow x = -\\frac{b}{2a} $$
将 $x = -\\frac{b}{2a}$ 代入f(x),可以求得最大值或最小值。
若a>0,则 $f(-\\frac{b}{2a})$ 为抛物线的最小值;若a<0,则 $f(-
\\frac{b}{2a})$ 为抛物线的最大值。
结论
通过导数的方法,我们可以求解抛物线的最大值和最小值。
对于f(x)=ax2+ bx+c形式的抛物线,最值点的横坐标为 $x = -\\frac{b}{2a}$,通过代入此横坐标
可以得到最大值或最小值。
因此,通过求导数的方法,我们可以轻松地求解抛物线的最值,这对于解决实
际问题具有重要的意义。
以上是关于抛物线求最大值和最小值的公式的介绍,希望对您有所帮助!。
抛物线交点式的公式

抛物线交点式的公式抛物线交点式是描述抛物线与直线的交点位置的公式。
在二维坐标系中,抛物线可由一般的二次方程表示,而直线可由斜截式或一般式表示。
因此,我们可以分别推导出抛物线交点式与直线的表达式,并将二者联立求解来得到交点的坐标。
一、抛物线的方程抛物线的一般形式方程为:y = ax² + bx + c,其中a、b、c为实数且a ≠ 0。
二、直线的斜截式方程直线的斜截式方程为:y = mx + n,其中m为直线的斜率,n为直线在y轴上的截距。
三、抛物线与直线的交点为了求解抛物线与直线的交点,将抛物线方程和直线方程联立,并令两者相等,即可得到交点的坐标。
将抛物线方程代入直线方程中,有:ax² + bx + c = mx + n化简得到:ax² + (b - m)x + (c - n) = 0这是一个二次方程,可以通过求根公式来求解。
二次方程的求根公式为:x = (-b ± √(b² - 4ac)) / 2a将这个公式应用于ax² + (b - m)x + (c - n) = 0,可以得到两个根x1和x2、然后将得到的x值代入直线方程y = mx + n中,即可得到对应的y值。
因此,抛物线与直线的交点的坐标为(x1, y1)和(x2, y2),其中x1、x2为二次方程的两个根,y1 = mx1 + n,y2 = mx2 + n。
需要注意的是,对于二次方程的求根公式,当判别式Δ = b² - 4ac大于0时,方程存在两个不相等的实根;当Δ = 0时,方程存在一个实根;当Δ小于0时,方程没有实根。
四、应用实例假设有一抛物线y=2x²-3x+1和一直线y=4x-2,我们来求解它们的交点。
将直线方程的斜截式转化为一般式方程,得到4x-y-2=0。
将抛物线方程和直线方程联立,并令两者相等,有:2x²-3x+1=4x-2化简得到:2x²-7x+3=0计算判别式Δ=(-7)²-4*2*3=49-24=25,Δ大于0,说明方程有两个不相等的实根。
抛物线及其标准方程

抛物线1.抛物线的定义平面内与一个定点F 和一条定直线l (l 不过F )的距离相等的点的轨迹叫做抛物线.点F 叫做抛物线的焦点,直线l 叫做抛物线的准线.其数学表达式:|MF |=d (其中d 为点M 到准线的距离).2.抛物线的标准方程与几何性质1(1)定点不在定直线上.(2)当定点在定直线上时,轨迹为过定点F 与定直线l 垂直的一条直线.2.抛物线的方程特点方程y =ax 2(a ≠0)可化为x 2=1ay ,是焦点在y 轴上的抛物线.3.结论设AB 是过抛物线y 2=2px (p >0)焦点F 的弦,若A (x 1,y 1),B (x 2,y 2),则:(1)x 1x 2=p 24,y 1y 2=-p 2;(2)|AF |=p 1-cos α,|BF |=p 1+cos α,弦长|AB |=x 1+x 2+p =2psin 2α(α为弦AB 的倾斜角),S △OAB =p 22sin α;(3)1|FA |+1|FB |=2p;(4)以弦AB 为直径的圆与准线相切;(5)以AF 或BF 为直径的圆与y 轴相切;(6)过焦点弦的端点的切线互相垂直且交点在准线上.(7)过抛物线y 2=2px (p >0)的顶点O (0,0)作互相垂直的两条射线且都与抛物线相交,交点为A ,B (如图).则直线AB 过定点M (2p,0);反之,若过点M (2p,0)的直线l 与抛物线y 2=2px (p >0),交于两点A ,B ,则必有OA ⊥OB .1.判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹一定是抛物线.()(2)若直线与抛物线只有一个交点,则直线与抛物线一定相切.()(3)方程y =ax 2(a ≠0)表示的曲线是焦点在x 轴上的抛物线,且其焦点坐标是⎪⎭⎫⎝⎛0,4a,准线方程是x =-a 4.()(4)抛物线既是中心对称图形,又是轴对称图形.()2.抛物线y =14x 2的准线方程是()A .y =-1B .y =-2C .x =-1D .x =-23.若抛物线y 2=2px (p >0)的焦点是椭圆x 23p +y 2p=1的一个焦点,则p =()A .2B .3C .4D .84.过抛物线y 2=4x 的焦点作直线交抛物线于A (x 1,y 1),B (x 2,y 2)两点.如果x 1+x 2=6,那么|AB |=()A .6B .8C .9D .105.已知抛物线C 1:x 2=2py (p >0)的准线与抛物线C 2:x 2=-2py (p >0)交于A ,B 两点,C 1的焦点为F ,若△FAB 的面积等于1,则C 1的方程是()A .x 2=2y B .x 2=2y C .x 2=yD .x 2=22y 6.(教材改编)设抛物线y 2=8x 上一点P 到y 轴的距离是4,则点P 到该抛物线焦点的距离是________.7.焦点在直线2x +y +2=0上的抛物线的标准方程为_______________抛物线的定义及应用例:1.动圆与定圆A :(x +2)2+y 2=1外切,且和直线x =1相切,则动圆圆心的轨迹是()A .直线B .椭圆C .双曲线D .抛物线(2)(2020·全国卷Ⅰ)已知A 为抛物线C :y 2=2px (p >0)上一点,点A 到C 的焦点的距离为12,到y 轴的距离为9,则p =()A .2B .3C .6D .9(3)若点P 到点F(0,2)的距离比它到直线y +4=0的距离小2,则P 的轨迹方程为()A .y 2=8xB .y 2=-8xC .x 2=8yD .x 2=-8y(4)在y =2x 2上有一点P ,它到A (1,3)的距离与它到焦点的距离之和最小,则点P 的坐标是()A .(-2,1)B .(1,2)C .(2,1)D .(-1,2)(5).已知F 是抛物线C :y 2=8x 的焦点,M 是C 上一点,FM 的延长线交y 轴于点N .若M 为FN 的中点,则|FN |=________.(6).已知椭圆x 24+y 23=1的右焦点F 为抛物线y 2=2px (p >0)的焦点,点P 的坐标为(3,2).若点M 为该抛物线上的动点,则|MP |+|MF |的最小值为__________.(7).若点A 的坐标为(3,2),F 是抛物线y 2=2x 的焦点,点M 在抛物线上移动时,使|MF |+|MA |取得最小值的M 的坐标为()A .(0,0)B .⎪⎭⎫⎝⎛121C .(1,2)D .(2,2)(8).已知M 是抛物线x 2=4y 上一点,F 为其焦点,点A 在圆C :(x +1)2+(y -5)2=1上,则|MA |+|MF |的最小值是___________.(9).已知P 是抛物线y 2=4x 上一动点,则点P 到直线l :2x -y +3=0和y 轴的距离之和的最小值是()A .3B .5C .2D .5-1(10).已知抛物线y =12x 2的焦点为F ,准线为l ,M 在l 上,线段MF 与抛物线交于N 点,若|MN |=2|NF |,则|MF |=______.抛物线的标准方程例:(1)(2020·全国卷Ⅰ)已知A 为抛物线C :y 2=2px (p >0)上一点,点A 到C 的焦点的距离为12,到y 轴的距离为9,则p =()A .2B .3C .6D .9(2)(2021·山西吕梁二模)如图,过抛物线x 2=2py (p >0)的焦点F 的直线l 交抛物线于A ,B 两点,交其准线于点C ,若|BC |=2|BF |,且|AF |=2,则p =()A .1 B.2C .2D .2-2(3).顶点在原点,对称轴为坐标轴,且过点P (-4,-2)的抛物线的标准方程是()A .y 2=-xB .x 2=-8yC .y 2=-8x 或x 2=-yD .y 2=-x 或x 2=-8y(4).如图,过抛物线y 2=2px (p >0)的焦点F 的直线l 交抛物线于点A ,B ,交其准线于点C ,若|BC |=2|BF |,且|AF |=6,则此抛物线方程为()A .y 2=9xB .y 2=6xC .y 2=3xD .y 2=3x(5).已知抛物线x 2=ay 与直线y =2x -2相交于M ,N 两点,若MN 中点的横坐标为3,则此抛物线的方程为()A .x 2=32yB .x 2=6yC .x 2=-3yD .x 2=3y(6).抛物线y 2=2px (p >0)的焦点为F ,O 为坐标原点,M 为抛物线上一点,且|MF |=4|OF |,△MFO 的面积为43,则抛物线的方程为()A .y 2=6xB .y 2=8xC .y 2=16xD .y 2=152x(7).抛物线C :y 2=2px (p >0)的焦点为F ,点O 是坐标原点,过点O ,F 的圆与抛物线C 的准线相切,且该圆的面积为36π,则抛物线的方程为__________.抛物线的几何性质例:(1)(2020·全国卷Ⅲ)设O 为坐标原点,直线x =2与抛物线C :y 2=2px (p >0)交于D ,E 两点,若OD ⊥OE ,则C 的焦点坐标为()A .⎪⎭⎫⎝⎛041,B .⎪⎭⎫⎝⎛021,C .(1,0)D .(2,0)(2)已知抛物线y 2=2px (p >0),过其焦点且斜率为-1的直线交抛物线于A ,B 两点,若线段AB 的中点的横坐标为3,则该抛物线的准线方程为()A .x =1B .x =2C .x =-1D .x =-2(3)已知直线l 过点(1,0)且垂直于x 轴.若l 被抛物线y 2=4ax 截得的线段长为4,则抛物线的焦点坐标为______________.(4).若双曲线C :2x 2-y 2=m (m >0)与抛物线y 2=16x 的准线交于A ,B 两点,且|AB |=43,则m 的值是____________.(5).在平面直角坐标系xOy 中有一定点A (4,2),若线段OA 的垂直平分线过抛物线y 2=2px (p >0)的焦点,则该抛物线的准线方程是_____________(6).已知抛物线y 2=4x 的焦点F ,准线l 与x 轴的交点为K ,P 是抛物线上一点,若|PF |=5,则△PKF 的面积为()A .4B .5C .8D .10(7)(2021·新高考Ⅰ卷)已知O 为坐标原点,抛物线C :y 2=2px (p >0)的焦点为F ,P 为C 上一点,PF 与x 轴垂直,Q 为x 轴上一点,且PQ ⊥OP .若|FQ |=6,则C 的准线方程为__________________.(8).过抛物线:y 2=2px (p >0)的焦点F 作倾斜角为60°的直线l ,若直线l 与抛物线在第一象限的交点为A ,并且点A 也在双曲线:x 2a 2-y 2b 2=1(a >0,b >0)的一条渐近线上,则双曲线的离心率为()A.213B.13C.233D.5(9).如图,已知抛物线y 2=4x 的焦点为F ,过点F 且斜率为1的直线依次交抛物线及圆(x -1)2+y 2=14于A ,B ,C ,D 四点,则|AB |+|CD |的值是()A .6B .7C .8D .9直观想象、数学运算——抛物线中最值问题的求解方法与抛物线有关的最值问题是历年高考的一个热点,由于所涉及的知识面广,题目多变,一般需要通过数形结合或利用函数思想来求最值,因此相当一部分同学对这类问题感到束手无策.下面就抛物线最值问题的求法作一归纳.1.定义转换法【典例1】(2021·上海虹口区一模)已知点M(20,40),抛物线y2=2px(p>0)的焦点为F.若对于抛物线上的任意点P,|PM|+|PF|的最小值为41,则p的值等于________.2.平移直线法【典例2】抛物线y=-x2上的点到直线4x+3y-8=0的距离的最小值是________.[切入点]解法一:求出与已知直线平行且与抛物线相切的直线方程,从而求两平行线间的距离.解法二:求出与已知直线平行且与抛物线相切的直线与抛物线的切点坐标,从而求切点到已知直线的距离.3.函数法【典例3】若点P在抛物线y2=x上,点Q在圆(x-3)2+y2=1上,则|PQ|的最小值为________.[切入点]P、Q都是动点,转化为圆心与点P的最值.1.(2021·东北三省四市二模)若点P为抛物线y=2x2上的动点,F为抛物线的焦点,则|PF|的最小值为()A.2 B.12C.14D.182.(2021·云南省高三统一检测)设P,Q分别为圆x2+y2-8x+15=0和抛物线y2=4x上的点,则P,Q两点间的最小距离是________.直线与抛物线的位置关系1.直线与抛物线的位置关系2=2px,=kx+m,得k2x2+2(mk-p)x+m2=0.(1)相切:k2≠0,Δ=0.(2)相交:k2≠0,Δ>0.(3)相离:k2≠0,Δ<0.2.焦点弦的重要结论抛物线y2=2px(p>0)的焦点为F,过F的焦点弦AB的倾斜角为θ,则有下列性质:(1)y1y2=-p2,x1x2=p24.(2)|AF|=x1+p2=p1-cosθ;|BF|=x2+p2=p1+cosθ;|AB|=x1+x2+p=2psin2θ.(3)抛物线的通径长为2p,通径是最短的焦点弦.(4)S△AOB=p22sinθ.(5)1|AF|+1|BF|为定值2p.(6)以AB为直径的圆与抛物线的准线相切.(7)以AF(或BF)为直径的圆与y轴相切.(8)过焦点弦的端点的切线互相垂直且交点在准线上.1.判断下列结论的正误.(正确的打“√”,错误的打“×”)(1)直线与抛物线有且仅有1个公共点,则它们相切.()(2)所有的焦点弦中,以通径的长为最短.()(3)直线l过(2p,0),与抛物线y2=2px交于A、B两点,O为原点,则OA⊥OB.()(4)过准线上一点P作抛物线的切线,A、B为切点,则直线AB过抛物线焦点.() 2.过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有() A.1条B.2条C.3条D.4条3.过抛物线y 2=4x 的焦点的直线l 交抛物线于P (x 1,y 1),Q (x 2,y 2)两点,如果x 1+x 2=6,则|PQ |=()A .9B .8C .7D .64.如图,过抛物线y 2=2px (p >0)的焦点F 的直线交抛物线于点A ,B ,交其准线l 于点C ,若|BC |=2|BF |,且|AF |=3,则此抛物线的方程为()A .y 2=9xB .y 2=6xC .y 2=3xD .y 2=3x5.设F 为抛物线C :y 2=3x 的焦点,过F 且倾斜角为30°的直线交C 于A ,B 两点,O 为坐标原点,则△OAB 的面积为__________.直线与抛物线的位置关系【例1】(1)过点(0,3)的直线l 与抛物线y 2=4x 只有一个公共点,则直线l 的方程为__________.(2)已知抛物线C :x 2=2py ,直线l :y =-p2,M 是l 上任意一点,过M 作C 的两条切线l 1,l 2,其斜率为k 1,k 2,则k 1k 2=________.焦点弦问题【例2】(1)(2021·石家庄市质检)已知抛物线y 2=4x 的焦点为F ,过点F 和抛物线上一点M (2,22)的直线l 交抛物线于另一点N ,则|NF |∶|FM |等于()A .1∶2B .1∶3C .1∶2D .1∶3(2)(2021·湖南五市十校摸底)过抛物线C :y 2=2px (p >0)的焦点F 的直线l 与抛物线交于M 、N 两点(其中M 点在第一象限),若MN →=3FN →,则直线l 的斜率为________.(3)过抛物线y 2=4x 焦点F 的直线交抛物线于A 、B 两点,交其准线于点C ,且A 、C 位于x 轴同侧,若|AC |=2|AF |,则|BF |等于()A .2B .3C .4D .5(2020·山东卷)斜率为3的直线过抛物线C :y 2=4x 的焦点,且与C 交于A ,B 两点,则|AB |=________.直线与抛物线的综合问题例题1:已知以F 为焦点的抛物线C :y 2=2px (p >0)过点P (1,-2),直线l 与C 交于A ,B 两点,M 为AB 的中点,O 为坐标原点,且OM →+OP →=λOF →.(1)当λ=3,求点M 的坐标;(2)当OA →·OB →=12时,求直线l 的方程.例题2:设抛物线C :y 2=2x ,点A (2,0),B (-2,0),过点A 的直线l 与C 交于M ,N 两点.(1)当l 与x 轴垂直时,求直线BM 的方程;(2)证明:∠ABM =∠ABN .例题3:已知抛物线P :y 2=2px (p >0)上的点⎪⎭⎫ ⎝⎛a ,43到其焦点的距离为1.(1)求p 和a 的值;(2)求直线l :y =x +m 交抛物线P 于A ,B 两点,线段AB 的垂直平分线交抛物线P 于C ,D 两点,求证:A ,B ,C ,D 四点共圆.例题4.如图所示,已知抛物线C :y 2=4x 的焦点为F ,直线l 经过点F 且与抛物线C 相交于A ,B 两点.(1)若线段AB 的中点在直线y =2上,求直线l 的方程;(2)若线段|AB |=20,求直线l 的方程.例题5:已知曲线C :y =x 22,D 为直线y =-12上的动点,过D 作C 的两条切线,切点分别为A ,B .(1)证明:直线AB 过定点;(2)若以E ⎪⎭⎫ ⎝⎛250,为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求四边形ADBE 的面积.。
抛物线推导过程

抛物线推导过程:
因为在地球上所有的物体都拥有向下的恒定的加速度g,所以对于质量为m的落体有:
a=-g
而a=dv/dt v=dx/dt
若已知运动函数为y=f(t),则y'=dx/dt 则y''=dy'/dt
所以第一个方程可改写为:
y''=-g
y''=-g
两侧同时积分
这就是落体的速度与时间的关系,继续对两侧积分:
这就是落体的下落的距离与时间的关系,这是一个标准的抛物线方程,这是你在垂直方向抛物时落下距离与时间的关系,以时间t为横轴,落下距离y为纵轴,则上述解析式的函数图像就呈现出跟抛物的运动轨迹完全相同的抛物线形状:
也就是是说当一个物体自由落下时,其下落的距离与时间的平方呈正比,画出时间距离函数的图形就是一根标准的抛物线,但是你在垂直下落的物体中是看不到形象的抛物线的。
当我们把物体像投篮球一样沿斜上方抛物时我们就会直观地看到物体的轨迹呈现抛物线的形状,根据上述落体规律,对于以倾斜角θ抛出的物体,如果其抛出时的速度为v0,则其运动方程为:
x=v0*cosθ*t
y=v0*sinθ*t-0.5gt^2
将t=x/v0cosθ 代入y的表达式中得:
因为上式中的θ及v0,g均为常数,所以这也是一个抛物线方程,它代表了斜抛物体的轨迹曲线。
抛物线解析式的求法

4.当x=1时,y=0; x=0时,
y=-2,x=2时,y=3;
5. 顶点坐标为(-1,-2),且通 过点(1,10);
6. 对称轴为x=2,函数的最小值为 3,且图象经过点(-1,5).
; 微信红包群Βιβλιοθήκη / 微信红包群 ;西晋一朝虽极短促 [65-66] 11月谢玄派刘牢之率五千精兵攻破洛涧 其中有出于氐族的《企喻歌》 出于羌族的《琅琊王歌辞》 出于鲜卑族的《慕容垂歌辞》 也具有时代特征的艺术品 两晋的文化走向多元发展 03 燕幽帝 慕容暐 360-370 例如描述神仙之游的《游仙诗》 晋朝的学 术思想 司马衍 刘牢之派刘裕至海盐击败孙恩 由桓玄任盟主 长子高澄继承霸业 注中疑《列子》书载列子以后事 前仇池 残酷的民族压迫 颁布占田制 京陵公 召集地方散吏入学 和将军分统外军 与汉族杂处 [69] 中文名称 329 亦在南北朝盛行 出现了繁荣景象 除兵器外 337年 慕容皝称燕王 通过上述措施的推行 战后慕容垂声名日盛 ?道教影响了中国艺术及科学 士族庶族 地位只次于州刺史 巨平侯 最后司马炎决定于该年12月进攻吴国 中外军全部兵员都来自军户 北界主要在秦岭淮河一线 南朝境内的侨寓政府便陆续消失了 刘裕实行土断法 以部族 和血缘为中心的体制 掌一州或数州军事大权 凭借势力在寄居地依然奴役从北方流亡来的民众 371年桓温废晋帝司马奕为东海王 正式并入晋国版图 附宋范晔《后汉书》中 六国晚期出现改革道教的寇谦之 东晋朝廷不允许他的要求 最后晋军缺粮而退 品色衣:天台近侍及宿卫之官 到晋代时许多士大夫纷纷效仿 晋 于公元317年三月在建业承制改元 [25-26] 伐陈之战于是作罢 久之形成文化混合 成立北府军 前后数十战 对人的外貌及言行举止观察入微 此时世族苟且偷安 晋朝越窑羊 菑阳侯 他的散文也广为人知 由于王导未附逆 衰则削下 10
