重庆市合川太和中学2013-2014学年高二下期期中考试数学(理)试题 Word版含答案
重庆市合川太和中学2013-高二下期期中考试数学(理)试题

太和中学2013—2014学年度下期期中考试高二数学试题(理科)(总分:150分 考试时间:120分钟)一、选择题(本大题共10个小题,每个小题5分,共50分,每个小题只有一个正确答案,将正确答案填涂在答题卡的相应位置) 1.设复数21z i=+(其中i 为虚数单位),则z 的虚部为( ) A.iB.1C.1-D.i -2.函数x y sin =在点)23,3(π处的切线的斜率为( )A.1B.21 C.22 D.23 3. 设x x x f ln )(=,若2)(0='x f ,则=0x ( )A . eB .2eC .ln 22D .ln 24. 若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合,则p 的值为( )A .2-B .2C .4-D .45. “a=1”是“函数f (x )=|x ﹣a|在区间1,+∞)上为增函数”的( ) A . 充分不必要条件 B . 必要不充分条件 C . 充要条件D . 既不充分也不必要条件6. 如图:在平行六面体1111D C B A ABCD -中,M 为11C A 与11D B 的交点。
若=,=,c AA =1则下列向量中与相等的向量是( )A.1122a b c -++B.1122a b c ++C.1122a b c --+D.1122a b c -+7.下列说法中正确的是( ).A 命题“若x y >,则22x y >”的否命题为假命题.B 命题“,R x ∈∃使得21x x ++0<”的否定为“x R ∀∈,满足210x x ++>” .C 设,x y 为实数,则“1x >”是“lg 0x >”的充要条件 .D 若“p q ∧”为假命题,则p 和q 都是假命题 8.方程x 3﹣6x 2+9x ﹣4=0的实根的个数为( ) A .0 B . 1 C . 2 D . 39.定义域为R 的函数f (x )满足f (1)=1,且f (x )的导函数1()2f x '>,则满足2()1f x x <+的x 的集合为( )A . {x |x <1}B .{x |-1<x <1}C .{x |x <-1或x >1}D .{x |x >1}10. 设双曲线22221x y a b -=的两条渐近线与直线2a x c=分别交于A,B 两点,F 为该双曲线的右焦点.若6090AFB ︒<∠<︒, 则该双曲线的离心率的取值范围是( )A . (1,2)B .(2,2)C . (1,2)D .(2,)+∞ 二、填空题(本大题共5个小题,每个小题5分,共25分,将正确答案填写在答题卡上的相应位置)11. 211(2)x dx x-=⎰ .12.用火柴棒按图的方法搭三角形:按图示的规律搭下去,则所用火柴棒数a n 与所搭三角形的个数n 之间的关系式可以是 .13.抛物线y =x 2到直线 2x -y =4距离最近的点的坐标是 . 14. 已知直线1y kx =+与曲线ln y x =有公共点,则实数k 的取值范围是 .15.函数()ln f x a x x =+,对任意的1[]x e e∈,时,()0f x ≥恒成立,则a 的范围为 .三、解答题(本大题共6个小题,前三个解答题每个13分,后三个解答题每个12分,共75分,将解答过程填写在答题卡上的相应位置) 16.(本小题满分13分)已知322()(23)()f x x ax a x a a =+-++∈R .(1)若曲线()y f x =在1x =-处的切线与直线210x y --=平行,求a 的值; (2)当2a =-时,求()f x 的单调区间.17.(本小题满分13分)在数列{n a }中,61=a ,且111++=---n na a a n n n )2,(*≥∈n N n , (1)求432,,a a a 的值;(2)猜测数列{n a }的通项公式,并用数学归纳法证明。
重庆市重庆一中2013-2014学年高二下学期期中考试理科数学试卷(解析版)

重庆市重庆一中2013-2014学年高二下学期期中考试理科数学试卷(解析版)一、选择题1.设i 为虚数单位,则2(1)i -=( )A.2B.1i +C.2i -D.22i - 【答案】C 【解析】试题分析:利用复数的运算法则,2(1)i -=1-2i-1=-2i . 考点:复数的基本运算2.设0,0a b <<.则下列不等式一定成立的是( ) A.0a b -<B.2|11|(1)(1)204b a a b π+≥--≤--≤> C.||a b ab +≤D.2a b+≤【答案】D 【解析】试题分析:由0,0a b <<得不到0a b -<,故A 错误.利用基本不等式得2b aa b+≥,故B错误;令a=-1,b=-1得|11|(1)(1)--≤--,即21≤,故C 错误;02a b+<0>,故选D.考点:不等式的基本性质;基本不等式。
3.某人将英语单词“apple ”记错字母顺序,他可能犯的错误次数最多是(假定错误不重犯)( )A.60B.59C.58D.57 【答案】B 【解析】试题分析:任意5个不相同的字母可排列成A 55个不同顺序的词,由于本题中出现两个p ,所以总个数应除以2,∴错误个数是12(5×4×3×2×1)-1=59个.故选B . 考点:排列组合及简单的计数问题4.若一几何体的正视图与侧视图均为边长为1的正方形,且其体积为12.则该几何体的俯视图可以是( )ABCD【答案】C 【解析】试题分析:若俯视图为A ,则V=1;若俯视图为B ,则V=π;若俯视图为C ,则V=12; 若俯视图为D ,则V=4π,根据几何体的体积为12,∴C 正确.故选C . 考点:简单空间图形的三视图 5.设1212min{,,...,},max{||,||,...,||}(3)n n m x x x M x x x n ==≥,其中(1,2i x R i n ∈=.那么“12...n x x x ===”是“m M =”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.非充分非必要条件【答案】B 【解析】试题分析:令12...n x x x ====-1,则m=-1,M=1,所以12...nx x x ===¿m M =,而m M =,则12...n x x x ===.故选B.考点:充要条件的判断方法.6.已知双曲线22221(0,0)x y a b a b-=>>的一条渐近线方程为340x y +=,则双曲线离心率e =( )A.54 B.53 C.43 D.45【答案】A 【解析】试题分析::∵双曲线22221(0,0)x y a b a b-=>>的焦点在x 轴上,∴渐近线方程为y=±b x a ,又∵渐近线方程为y=34x -,∴34b a =∴22916b a = ∵222b c a =-,联立得:222916a c a =-,化简得e=54.故选A考点:双曲线的性质及其方程;渐近线方程;离心率 7.若曲线12y x-=在点12(,)a a -处的切线与两坐标轴围成的三角形面积为18.则a =( )A.64B.32C.16D.8 【答案】A 【解析】试题分析:求导数可得3'212y x -=-,所以在点12,a a -⎛⎫ ⎪⎝⎭处的切线方程为:31221322y a x a --=-+,令x=0,得y =1232a -;令y=0,得x=3a .所以切线与两坐标轴围成的三角形的面积 S =1122139318224a a a -⨯⨯==,解得a=64故选A .考点:导数的几何意义,利用导数研究曲线上某点切线方程.8.设点,A P 为椭圆2212x y +=上两点.点A 关于x 轴对称点为B (异于点P ).若直线,AP BP 分别与x 轴交于点,M N , 则OM ON ⋅=( )【答案】D 【解析】试题分析:如图,取特殊值,令椭圆的上顶点为A ,下顶点为B ,左端点为P ,则A (0,1),B (0,-1),P),M),N),∴()2,0OM ON ==,2OM ON ⋅=,故选:D .考点:椭圆中向量的数量积的求法,椭圆的简单性质.9.若27270127(1)(2)(2)...(2)x x a a x a x a x ++=+++++++.则2a =( ) A.20 B.19 C.20- D.19- 【答案】C 【解析】试题分析:设t=x+2,则x=t-2,则多项式等价为2723 70123721t t a a t a t a t a t -+-=++++⋯+()(),则2a 为左边展开式中2t 的系数.由r 1=r n r r n T C a b -+,左边展开式中2t 的系数为1+()5571C -=1-21=20-.故选:C .考点:二项式定理的应用.二项式定理系数的性质; 利用换元法将多项式转化思想的应用.10.有六种不同颜色,给如图的六个区域涂色,要求相邻区域不同色,不同的涂色方法共有( )625321A.4320B.2880C.1440D.720 【答案】A【解析】试题分析:第一个区域有6种不同的涂色方法,第二个区域有5区域有4种不同的涂色方法,第四个区域有3种不同的涂色方法,第六个区域有4种不同的涂色方法,第五个区域有3种不同的涂色方法,根据乘法原理6543344320⨯⨯⨯⨯⨯=,故选:A .考点:乘法原理.二、填空题11.设随机变量2~(10,)5B ξ,则D ξ= . 【答案】125【解析】试题分析::∵随机变量ξ服从二项分布,且2~(10,)5B ξ,∴D ξ=10×25×(1-25)=125,故答案为:125考点:二项分布的方差,二项分布与n 次独立重复试验的模型. 12.已知正态分布密度曲线22()2()x p x μσ--=,且max ()(20)p x p ==,则方差为 . 【答案】2 【解析】试题分析:正态分布密度曲线22()2()x p x μσ--=可知对称轴为μ=20,所以函数的最大值是(20)p =所以=,即σ2. 考点:正态分布曲线的特点; 正态分布曲线所表示的意义.13.在61(2)x x-展开式中,常数项等于 .【答案】160-【解析】试题分析:由通项公式r 1=r n r rn T C a b -+:设第r+1项为常数,则()6r 161=2rrr T C x x -+⎛⎫- ⎪⎝⎭=()()()66612rr r rrC x x ---,所以6-r=r,即r=3;那么常数项为()()333621160C -=-,故答案为160-.考点:二项式定理系数的性质;二项式定理的应用.14.一大学生毕业找工作,在面试考核中,他共有三次答题机会(每次问题不同).假设他能正确回答每题的概率均为23,规定有两次回答正确即通过面试,那么该生“通过面试”的概率为 . 【答案】2027【解析】试题分析:有已知条件可知分为三类情况:第一次第一次答对的概率为224339⨯=; 第一次答对第二次答错第三次答对的概率为212433327⨯⨯=; 第一次答错第二次答对第三次答对的概率为122433327⨯⨯=;那么该生“通过面试”的概率为444202727927++=,故答案为2027. 考点:相互独立事件的概率. 15.若,(0,1)m n ∈.则(1)()(1)(1)mn m n m n m n --+--的最大值是 .【答案】18【解析】试题分析:只要考虑0<m ,n <1,m+n <1的情形即可. 令x=m ,y=n ,z=1-m-n ,则x+y+z=1.(1)()(1)(1)mn m n m n m n --+--=()()()222xyz xyz xy yz xz x y y z x z ≤⋅⋅++⋅=+18 考点:基本不等式;换元法.三、解答题16.已知()|||1|f x x x =-+. (1)求不等式()0f x ≤的解集A;(2)若不等式10mx m +->对任何x A ∈恒成立,求m 的取值范围. 【答案】(1)1[,)2A =-+∞ (2)(2,)+∞ 【解析】试题分析:(1)把不等式()0f x ≤转化为22(1)x x ≤+即可. (2)1,102x mx m ∀≥-+->恒成立转化为11m x >+,即max 1()21m x >=+. (1)22|||1|(1)x x x x ≤+⇔≤+12x ⇔≥-∴1[,)2A =-+∞ (2)1,102x mx m ∀≥-+->恒成立11m x ⇔>+对12x ≥-恒成立.max 1()21m x ⇔>=+∴m 取值范围是(2,)+∞考点:绝对值不等式的解法;简单的不等式恒成立的问题.17.(13分)已知函数2()()4ln(1)f x x t x =+++的图象在点(1,(1))f 处的切线垂直于y 轴. (1)求实数t 的值; (2)求()f x 的极值.【答案】(1)t=-2 (2)极大值为4极小值14ln 2+ 【解析】试题分析:(1)先求'()f x ,然后利用'(1)0f =即可; (2)由(1)知2(1)()(1)1x x f x x x -'=>-+,然后找出极值点,判断出单调区间,进而求出极值.(1)4()2(),1f x x t x '=+++ 由(1)02f t '=⇒=-. (2)∵2(1)()(1)1x x f x x x -'=>-+ 显见10x -<<时, ()0f x '>, 01x <<时, ()0f x '<. 1x >时,()0f x '> ∴()(0)4f x f ==极大值. ()(1)14ln 2f x f ==+极小值.考点:导数的几何意义;函数的单调性与极值. 18.某电视台“挑战60秒”活动规定上台演唱(I)连续达到60秒可转动转盘(转盘为八等分圆盘)一次进行抽奖,达到90秒可转两次,达到120秒可转三次(奖金累加).(2)转盘指针落在I 、II 、III 区依次为一等奖(500元)、二等奖(200元)、三等奖(100元),落在其它区域不奖励.(3)演唱时间从开始到三位评委中至少1人呜啰为止,现有一演唱者演唱时间为100秒. ①求此人中一等奖的概率;②设此人所得奖金为ξ,求ξ的分布列及数学期望E ξ.【答案】(1) 1564(2)200 【解析】试题分析:(1)由题意可知转一次奖获得一等奖的概率是18,分成三类情况:①两次都中中一等奖②第一次中一等奖,第二次未中;③第一次未中一等奖,第二次中; (2)分别计算出奖金为ξ每一种情况的概率,然后列出分布列,再计算出期望值即可.解 ①1117711588888864P =⨯+⨯+⨯= ②故12810020064E p ξξ=⋅=⨯=∑ 考点:相互独立事件的概率;离散型随机变量的分布列和数学期望19.如图,四棱柱1111ABCD A BC D -中,1DD ABCD ⊥底面.ABCD 为平行四边形,60DAB ∠=︒, 12 2.3AB AD DD ===, ,EF 分别是AB 与1D E 的中点.C 1CA 1(1)求证CE DF ⊥;(2)求二面角A EF C --的平面角的余弦值. 【答案】(1)见解析(2) 【解析】试题分析:(1) 先证明△ADE 为正△,再利用余弦定理可求CE ,然后证明出CE ⊥DE ,CE ⊥DD 1 ,最后得到CE ⊥平面DD 1E, 即可证明出CE ⊥DF. (2)先建立以直线AB, AA 1分别为x 轴,z 轴建立空间直角坐标系,然后根据点坐标求出法向量(0,m =-,(3,n =-,再利用夹角公式求出二面角A EF C --的平面角的余弦值cos θ=. (1)AD=AE, ∠DAB=60° ∴△ADE 为正△ 在△CDE 中,由余弦定理可求又22212+=.由勾股定理逆定理知CE ⊥DE又DD 1⊥平面ABCD, CE ⊂平面ABCD. ∴CE ⊥DD 1 ∴CE ⊥平面DD 1E, 又DF ⊂平面DD 1E. ∴CE ⊥DF.(2)以直线AB, AA 1分别为x 轴,z 轴建立空间直角坐标系,由题设A(0,0,0), E(1,0,0),D 1(1,22), C 5(,,0)22可求平面AEF 的一个法向量为(0,m =-平面CEF 的一个法向量为(3,n =- ∴平面角θ满足||130|cos |13||||m n m n θ⋅==又θ为纯角 ∴cos 13θ=-注本题(1)也可建坐标直接证明.(2)的坐标系建法不唯一.考点:余弦定理;勾股定理逆定理;线面垂直的性质与判定定理;法向量;夹角公式. 20.已知抛物线2:2(0)C y px p =>的焦点F 到准线的距离为12.过点0(,0)A x 01()8x ≥ 作直线l 交抛物线C 与,P Q 两点(P 在第一象限内). (1)若A 与焦点F 重合,且||2PQ =.求直线l 的方程;(2)设Q 关于x 轴的对称点为M .直线PM 交x 轴于B . 且BP BQ ⊥.求点B 到直线l 的距离的取值范围.【答案】(1) 4410x y --=或4410x y +-= ;(2) 1)2d ∈ 【解析】试题分析:(1) 首先求出抛物线2:C y x = 再与1:()4l y k x =- 联立得到关于x 的一元二次方程,最后利用焦半径公式求出斜率即可.(2)先求出1PB k =,进而转换为21212()41y y y y +-=,再由l 与C 联立得200y my x --=,借助于根与系数的关系求出m 的取值范围,然后由点到直线的距离公式得到d 的表达式,最后根据基本不等式求出范围. 由题2:C y x =(1)A 与下重合,则1(,0)4A 设222221:()(1)04216l y k x k k k x x y x ⎫=-⎪⇒-++=⎬⎪=⎭又由焦半径公式有12121||22PQ x x p x x =++=++= 可求21k = ∴1k =±.所求直线l 为4410x y --=或4410x y +-=(2)可求0(,0)B x -.故△BQM 为等腰直角三角形,设1122(,),(,)P x y Q x y1PB k =. 即2121212121211()41y y y y y y y y x x +=⇒-=⇒+-=-.设0202:0l x x my y my x y x -=⎫⇒--=⎬=⎭ ∴201212040m x y y m y y x⎧=+>⎪+=⎨⎪⋅=-⎩ 从而2041m x +=, 即20140m x =->, 又018x ≥. ∴2102m <≤. 点0(,0)B x -到直线0:0l x my x --=的距离为2d ====∴1[)122d ∈ 考点:抛物线的性质;焦半径公式;根与系数的关系;点到直线的距离公式;基本不等式. 21.给定数列{n a (1)判断2a 是否为有理数,证明你的结论;(2)是否存在常数0M >.使n a M <对*n N ∈都成立? 若存在,找出M 的一个值, 并加以证明; 若不存在,说明理由.【答案】(1) 2a 是无理数 (2) 3M =(或4M =等).则对*n N ∀∈,均有3n a <成立.证明略.【解析】试题分析:(1) 设2a 是无理数, 利用反证法推出矛盾即可;(2)先设(1,2,...,)k b n k ==然后得到2n b n =,用放缩法证出1b 12341 (24822)n n n n -+≤+++++,再借助错位相减法得1b <3,即对*n N ∀∈,均有3n a <成立.解(1)2a 是无理数, 若不然,r Q =∈.则21r =21r =-必为有理数,.(2)设1,2,...,)k b k ==则2211, (1,2,...,1),n k k n b a b k b k n b n +==+=-=. 于是21221111222222b b b b ++≤=+=+ 23212123222244b b +≤+⋅=++ 234123123424422488b b +≤++⋅=+++ 523452481616b ≤++++ ...≤11234 (24822)n n n b n --≤+++++ 21112341 (248222)n n n b n --+≤+++++⋅ 12341 (24822)n n n n -+=+++++ 令12341 (24822)n n n n n S -+=+++++. 则3332n n n S +=-<. 从而可取3M =(或4M =等).则对*n N ∀∈,均有3n a <成立.考点:反证法;错位相减法;放缩法.。
太和中学高二理科复习(1)答案

ʹ辻
ʹ4 ʹ
.
‶分
ʹ ‶
14 1
1辻 ʹ
1
‶
ʹ㲀 ʹ4
‶
;
1辻 1ʹ辻 1辻
所以的分布列为
15
20
p
1
1
‶
ʹ
辻
1.
辻
25 1辻
30
1 辻
数学期望
辻辻 1ʹ辻辻 辻辻 1ʹ辻 ʹ1. 1ʹ 分
1ʹ辻
18. 求满足下列条件的方程.
1 求焦点为 辻㭀 4 ,且渐近线为
的双曲线的标准方程;
ʹ 求过点 㭀‶ 的抛物线的标准方程.
太和中学高二理科数学复习(一)
一、选择题
1. 复数
4 的共轭复数
㲀1
z
等于
A. 㲀 ʹ ʹ
【答案】A
B. 㲀 ʹ 㲀 ʹ
C. ʹ ʹ
D. ʹ 㲀 ʹ
【解析】解:
4 㲀1
4 㲀1㲀 㲀1 㲀1㲀
㲀 ʹ 㲀 ʹ , 复数
4 的共轭复数
㲀1
z
等于㲀
ʹ
ʹ.
ʹ. 1 㲀 ‶ 开式的二项式系数和为 512,则开式的常数项为
݂ ,得
݂ 㲀 ʹ 辻,
令
㲀 ʹ ,可得 ݂
݂ 㲀 ʹ 辻,
则
㲀 ʹ 在 辻㭀 上为减函数,
由
ʹ 1 ,得
㲀ʹ 辻 辻 ,
是定义在 R 上的偶数,即
㲀 ʹ 辻,
又 㲀 ʹ 辻,
㲀 ʹ 辻 ʹ ,即
ʹ,
由
㲀 ʹ 在 辻㭀 上为减函数,
得 ʹ 且 辻,得㲀 ʹ
ʹ.
不等式
ʹ 1 的解集为 㲀 ʹ㭀辻 辻㭀ʹ .
重庆市合川太和中学2013-2014学年高二下期期中考试数学(文)试题 Word版含答案

太和中学2013—2014学年度下期期中考试高二数学试题(文科)(总分:150分 考试时间:120分钟)一、选择题(本大题共10个小题,每个小题5分,共50分,每个小题只有一个正确答案,将正确答案填涂在答题卡的相应位置)1. “21sin =A ”是“︒=30A ”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件2.函数x y sin =在点)23,3(π处的切线的斜率为( )A.1B.21 C.22 D.23 3. 设x x x f ln )(=,若2)(0='x f ,则=0x ( )A . eB .2eC . ln 22 D .ln 24. 若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合,则p 的值为( ) A .2- B .2 C .4- D .45.有下列关系:①人的年龄与他(她)拥有的财富之间的关系;②曲线上的点与该点的坐标之间的关系;③苹果的产量与气候之间的关系;④森林中的同一种树木,其横断面直径与高度之间的关系,其中有相关关系的是 ( )A .①②③B .①②C .②③D .①③④6.在独立性检验中,统计量2K 有两个临界值:3.841和6.635;当2K >3.841时,有95%的把握说明两个事件有关,当2K >6.635时,有99%的把握说明两个事件有关,当2K ≤3.841时,认为两个事件无关.在一项打鼾与患心脏病的调查中,共调查了2000人,经计算的2K =20.87,根据这一数据分析,认为打鼾与患心脏病之间 ( )A .有95%的把握认为两者有关B .约有95%的打鼾者患心脏病C .有99%的把握认为两者有关D .约有99%的打鼾者患心脏病 7.下列说法中正确的是( ).A 命题“若x y >,则22x y >”的否命题为假命题.B 命题“,R x ∈∃使得21x x ++0<”的否定为“x R ∀∈,满足210x x ++>”.C 设,x y 为实数,则“1x >”是“lg 0x >”的充要条件 .D 若“p q ∧”为假命题,则p 和q 都是假命题8.右面的程序框图,如果输入三个实数a ,b ,c ,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入下面四个选项中的( )A .c x >B .x c >C .c b >D .b c >9.定义域为R 的函数f (x )满足f (1)=1,且f (x )的导函数1()2f x '>,则满足2()1f x x <+的x 的集合为( )A . {x |x <1}B .{x |-1<x <1}C .{x |x <-1或x >1}D .{x |x >1}10. 设双曲线22221x y a b -=的两条渐近线与直线2a x c=分别交于A,B 两点,F 为该双曲线的右焦点.若6090AFB ︒<∠<︒, 则该双曲线的离心率的取值范围是( )A .B .C . (1,2)D .)+∞二、填空题(本大题共5个小题,每个小题5分,共25分,将正确答案填写在答题卡上的相应位置)11. 已知F 1、F 2为椭圆192522=+y x 的两个焦点,过F 1的直线交椭圆于A 、B 两点,若1222=+B F A F ,则AB = _____________ . 12必过点 . 13.用火柴棒按图的方法搭三角形:按图示的规律搭下去,则所用火柴棒数a n 与所搭三角形的个数n 之间的关系式可以是 .14.已知函数y=f (x )的图象在M (1,f (1))处的切线方程是+2,则f (1)+f′(1)= .15. 已知直线1y kx =+与曲线ln y x =有公共点,则实数k 的取值范围是 .三、解答题(本大题共6个小题,前三个解答题每个13分,后三个解答题每个12分,共75分,将解答过程填写在答题卡上的相应位置) 16.(本小题满分13分)已知322()(23)()f x x ax a x a a =+-++∈R .(1)若曲线()y f x =在1x =-处的切线与直线210x y --=平行,求a 的值; (2)当2a =-时,求()f x 的单调区间.17.(本小题满分13分)设数列{}n a 的前n 项和为n S ,且满足2n n a S =-()n *∈N .(1)求1a ,2a ,3a ,4a 的值并写出其通项公式;(2)证明数列{}n a 是等比数列.18.(本小题满分13分)以下是某地搜集到的新房屋的销售价格y (万元)和房屋的面积x (2m )的数据 ,若由资料可知y 对x 呈线性相关关系。
重庆市重庆八中2013-2014学年高二下学期期中考试 数学理试题
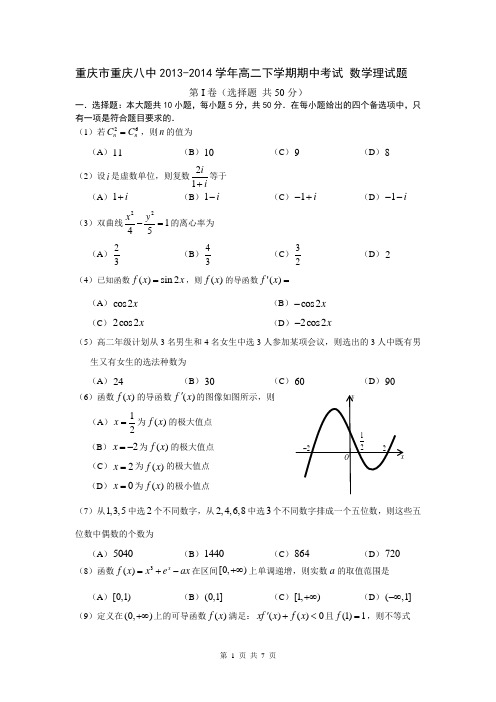
重庆市重庆八中2013-2014学年高二下学期期中考试 数学理试题第I 卷(选择题 共50分)一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个备选项中,只有一项是符合题目要求的.(1)若26n nC C =,则n 的值为 (A )11 (B )10 (C )9 (D )8(2)设i 是虚数单位,则复数21ii +等于 (A )1i +(B )1i -(C )1i -+ (D )1i --(3)双曲线22145x y -=的离心率为 (A )23(B )43(C )32(D )2(4)已知函数()sin 2f x x =,则)(x f 的导函数=)('x f(A )cos 2x (B )cos 2x -(C )2cos 2x(D )2cos 2x -(5)高二年级计划从3名男生和4名女生中选3人参加某项会议,则选出的3人中既有男生又有女生的选法种数为 (A )24(B )30(C )60(D )90(6)函数()f x 的导函数()f x '的图像如图所示,则(A )12x =为()f x 的极大值点 (B )2x =-为()f x 的极大值点 (C )2x =为()f x 的极大值点 (D )0x =为()f x 的极小值点(7)从1,3,5中选2个不同数字,从2,4,6,8中选3个不同数字排成一个五位数,则这些五位数中偶数的个数为 (A )5040(B )1440(C )864(D )720(8)函数3()x f x x e ax =+-在区间[0,)+∞上单调递增,则实数a 的取值范围是 (A )[0,1)(B )(0,1](C )[1,)+∞(D )(,1]-∞(9)定义在(0,)+∞上的可导函数()f x 满足:()()0xf x f x '+<且(1)1f =,则不等式()1xf x >的解集为(A )(,1)-∞(B )(0,1)(C )(1,)+∞(D )(0,1](10)如果小明在某一周的第一天和第七天分别吃了3个水果,且从这周的第二天开始,每天所吃水果的个数与前一天相比,仅存在三种可能:或“多一个”或“持平”或“少一个”,那么,小明在这一周中每天所吃水果个数的不同选择方案共有 (A )50种(B )51种(C )140种(D )141种第Ⅱ卷(非选择题 共100分)二.填空题:本大题共5小题,每小题5分,共25分.请把答案填在答题卡上.(11)2213x dx ⎰= (用数字作答). (12)若6名学生排成一列,则学生甲、乙、丙三人互不相邻的排位方法种数为 . (13)曲线()321f x x x =++在点()()1,1f 处的切线方程为 .(14)将5名大学生分配到3个乡镇去当村官,每个乡镇至少一名,则不同的分配方案有种.(15)把正整数按一定的规则排成了如图所示的三角形数表. 设(),ij a i j N +∈是位于这个三角形数表中从上往下数第i 行、从左往右数第j 个数,如428a =.若2014ij a =, 则i j += .三.解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. (16)(本题共13分,第(Ⅰ)问6分,第(Ⅱ)问7分)某研究性学习小组有6名同学.(Ⅰ)这6名同学排成一排照相,则同学甲与同学乙相邻的排法有多少种?(Ⅱ)从6名同学中选4人参加班级4100⨯接力比赛,则同学丙不跑第一棒.....的安排方法有多少种?(17)(本题共13分,第(Ⅰ)问6分,第(Ⅱ)问7分)124357681012911131517141618202224已知函数1()ln 1f x a x x=+-在1x =处取极值. (Ⅰ)求a 的值;(Ⅱ)求()f x 在21[,]e e上的最大值和最小值.(18)(本题共13分,第(Ⅰ)问4分,第(Ⅱ)问9分)已知椭圆2222:1(0)x y C a b a b +=>>过点(0,1)(Ⅰ)求椭圆C 的方程;(Ⅱ)若斜率为1的直线l 交C 于,A B 两点,且85AB =,求直线l 的方程.(19)(本题共12分,第(Ⅰ)问4分,第(Ⅱ)问8分)如图,四棱锥S ABCD -中,AD AB ⊥,CD AB //,33CD AB ==,平面SAD ⊥平面ABCD ,E 是线段AD 上一点,AE ED ==AD SE ⊥.(Ⅰ)证明:BE ⊥平面SEC ;(Ⅱ)若1SE =,求直线CE 与平面SBC 所成角的正弦值.(20)(本题共12分,第(Ⅰ)问5分,第(Ⅱ)问7分) 已知函数()2axf x x e =⋅(a 为小于0的常数).(Ⅰ)当1a =-时,求函数()x f 的单调区间; (Ⅱ)存在[1,2]x ∈使不等式44()f x e≥成立,求实数a 的取值范围.(21)(本题共12分,第(Ⅰ)问4分,第(Ⅱ)问8分)已知数列{}n a 满足112a =,1121n n n a a a ++=⋅+. (Ⅰ)求234,,a a a 的值,由此猜测{}n a 的通项公式,并证明你的结论;(Ⅱ)证明:13521n a a a a -⋅⋅⋅⋅<<.重庆八中2013---2014学年度(下)半期考试高二年级数学试题(理科)答案一、选择题:DACCB 、ACDBD10.解:设*(1n 7,)n a n N ≤≤∈,则776655443a (a-a )+(a-=⇒0766554433221(a -a )+(a -a )+(a -a )+(a -a )+(a -a )+(a -a )=令*1(11,N )n n n n n a a x x x +-=-≤≤∈∴1234560x x x x x x +++++=所以共有的方法数为32211664651141C C C C C +++=(按0个0,2个0,4个0,6个0分类的)二、填空题11.7 12. 144 13. 52y x =- 14. 150 15. 79 三、解答题:16.解:(Ⅰ)5252240A A ⋅=; (Ⅱ)1355300C A =.17.解:(Ⅰ)()21ax f x x -'=,由题(1)0f '=,则1a =; (Ⅱ)由(Ⅰ)知()21x f x x-'=,则()f x 在21,e ⎡⎤⎣⎦上单调递增,在1,1e ⎡⎤⎢⎥⎣⎦上单调递减⇒()()()min10f x f ==;又12f e e ⎛⎫=- ⎪⎝⎭,()2211f ee =+⇒()()22max 1()1f x f e e==+. 18.解 (Ⅰ)由题知1b =,c a =,解得24a = 则椭圆C 的方程为2214x y +=. (Ⅱ)设1122(,),(,)A x y B x y ,直线:l y x m =+ 由2244y x m x y =+⎧⎨+=⎩可得:2258440x mx m ++-= 则1285m x x +=-,212445m x x -=则85AB ===,解得m =y x =C 有两个交点. 故直线l的方程为y x =±19. (Ⅰ)证明:由已知条件可得:30,60AEB DEC ∠=︒∠=︒,90BEC BE EC ⇒∠=︒⇒⊥又因平面S A D ⊥平面A B C D ,AD SE ⊥⇒SE ⊥面BEC BE SE ⇒⊥ 所以BE ⊥平面SEC ;(Ⅱ)如图分别以EB 、EC 、ES 所在的直线为x 、y 、z 轴建立空间直角坐标系,则C ,(0,0,1)S ,(2,0,0)B ,设平面SBC 的法向量(,,)n x y z =,则有:(3,1,20n SB n n SC ⎧⋅=⎪⇒=⎨⋅=⎪⎩,设直线直线CE 与平面SBC 所成角为θ,有 1sin 4CE nCE n θ⋅==⋅20. 解:2()(2)axf x e ax x '=+(Ⅰ) 当1a =-时,2()(2)(2)x xf x e x x e x x --'=-+=-⋅-,令()0f x '=,得0x =或2x =所以()f x 的单调递增区间为(0,2),递减区间为(,0)-∞和(2,)+∞. (Ⅱ) 2()(2)ax f x e ax x '=+,令()0f x '=,得0x =或2x a=- (1)当22a-≥时,即10a -≤<时,()f x 在[1,2]上单调递增, 则2max 44()(2)4af x f e e==≥,解得2a ≥-,所以10a -≤<满足题意.(2)当212a <-<时,即21a -<<-时,()f x 在2[1,]a -上单调递增,2[,2]a-上单调递减,故2max 24244()()f x f e a a e -=-=⋅≥,解得e a e -≤≤,所以当21a -<<-时满足题意.(3)当21a-≤时,即2a ≤-时,()f x 在[1,2]上单调递减,故max 44()(1)af x f e e==≥,解得ln 44a ≥-,所以ln 442a -≤≤-时满足题意综上所述,[ln 44,)a ∈-+∞.21. 解:(Ⅰ)令1,2,3n =可知223a =,334a =,445a =猜想1n na n =+,下用数学归纳法证明.(1)1n =时,显然成立;(2)假设n k =时,命题成立.即1k ka k =+.当1n k =+时,由题可知11112221k k k a k a k k ++===-+-+. 故1n k =+时,命题也成立.由(1)(2)可知,1n na n =+.(Ⅱ)证明:∵=方法一:放缩法:212nn -<==135211321242n n a a a a n --⋅⋅⋅⋅⋅⋅⋅=⨯⨯⋅⋅⋅⨯<=∴13521n a a a a -⋅⋅⋅⋅⋅⋅⋅<方法二:数学归纳法(略) 由于=,可令函数x x x f sin 2)(-=,则()1cos f x x '=,令()0f x '=,得22cos =x ,给定区间)4,0(π,则有()0f x '<,则函数)(x f 在)4,0(π上单调递减,∴0)0()(=<f x f ,即x x s i n 2<在)4,0(π恒成立,又4311210π<≤+<n ,则有121sin2121+<+n n<.。
2013届太和中学高三月考数学试卷

2013届太和中学高三数学试卷赵玉苗 整理 2013-05-13一、选择题(每小题5分,共60分)1.已知数列{a n }的首项a 1=1,a n +1=3S n (n ≥1),则下列结论正确的是( )A 数列a 2,a 3,…,a n ,…是等比数列B 数列{a n }是等比数列C 数列a 2,a 3,…,a n ,…是等差数列D 数列{a n }是等差数列2 等差数列{a n }中,27,39963741=++=++a a a a a a ,则数列{a n }的前9项的和n S 是( )A 99B 66C 297D 1443.已知等差数列}{n a ,n S 表示前n 项的和,,0,0993<>+S a a 则n S S S ,,21中最小的是( )A 4SB 5SC 6SD 9S4 若四个正数a ,b ,c ,d 成等差数列,x 是a 和d 的等差中项,y 是b 和c 的等比中项,则x 和y 的大小关系是 ( ) A x <y B x >y C x =y D x ≥y5(理)设等比数列{}n a 中, 前n 项和为S n ,若n n S a a a a 212531)(3=++++- ,8321=a a a ,则nn n a S ∞→lim = A 0 B21C 2D 86. 2003年3月.全世界爆发“非典” 科学家经过深入的研究,终于发现了一种细菌M 在杀死“非典”病毒N 的同时能够自身复制,已知1个细菌M 可以杀死1个病毒N ,并且生成2个细菌M ,那么1个细菌M 和2048个“非典”病毒N 最多可生成M 的数值是( ) A 1024 B 2048 C 2049 D 无法确定7 数列{}n a 中,{}1,0+>n n n a a a 且是公比为)0(>q q 的等比数列,满足211++++n n n n a a a a )(32N n a a n n ∈>++,则公比q 的取值范围是 ( )A 2210+<<q B 2510+<<qC 2210+-<<q D 2510+-<<q8 (理)数列{}=+++∈=+=→++)(lim *,,56,51,21111n n x n n n n a a a N n a a a a 则中 ( )A52 B 72 C 41 D 2549 等差数列{a n }的前n 项和为S n ,若 1062a a a ++是一个定值,则下各数中也为定值( )A 6SB 11SC 12SD 13S10 (理)将1,2,…,9这9个数平均分成三组,则每组的三个数都成等差数列的概率为( )A561 B 701 C 3361D420111. 把正整数按下图所示的规律排序,则从2003到2005的箭头方向依次为12 在数列{}n a 中,如果存在非零常数T ,使得m T m a a +=对于任意的非零自然数m 均成立,那么就称数列{}n a 为周期数列,其中T 叫数列{}n a 的周 已知数列{}n x 满足()112,n n n x x x n n N +-=-≥∈,如果()121,,0x x a a R a ==∈≠ ,当数列{}n x 的周期最小时,该数列前2005项的和是A 668B 669C 1336D 1337200届高三数列数学试卷(一) 班级_________,姓名________ 选择题(每小题5分,共60分)二、填空题:本大题共5小题;每小题4分,共20分 13 等差数列{}n a 中,公差d ≠0,a 1,a 3 ,a 9 成等比数列,则1042931a a a a a a ++++= ____ .14.在数列{a n }中,a 1=1,a 2=2,且)( )1(12*+∈-+=-N n a a n n n 则100S =_____15一个项数为偶数的等比数列,它的偶数项和是奇数项和的2倍,又它的首项为1,且中间两项的和为24,此等比数列的项数为____________________.16 已知等差数列{}n a 的前n 项和为n S ,若1,m m N >∈,且211210,38m m m m a a a S -+-+-==,则m 等于_____________. 17 已知8079--=n n a n (n ∈N +),则在数列{a n }的前50项中最大项的项数是三、解答题(本大题共6小题,共70分,解答题应写出文字说明,证明过程或演算步骤) 18 (12分)(理)已知:g(x )= 214x+-(x >0),点A n (a n ,11+-n a )在曲线y =g (x )上(n ∈*N ),且a 1=1. (I)证明数列{21na }为等差数列;(II) 求数列{a n }的通项公式;(Ⅲ) 设b n =1111++n n a a ,记S n =b 1+b 2+……+b n ,求S n .19 (12分)(理)已知等差数列}{n a 的首项为a ,公差为b ;等比数列}{n b 的首项为b ,公比为a ,其中a ,+∈N b ,且2211a b a b a <<<<(1)求a 的值;(2)若对于任意+∈N n ,总存在+∈N m ,使n m b a =+3,求b 的值;(3)在(2)中,记}{n c 是所有}{n a 中满足n m b a =+3, +∈N m 的项从小到大依次组成的数列,又记n S 为}{n c 的前n 项和,n T 是}{n a 的前n 项和,求证:n S ≥n T (+∈N n20. (理)(10分) 已知函数223)(x ax x f -=的最大值不大于61,又当.81)(,]21,41[≥∈x f x 时(1)求a 的值;(2)设.11.),(,21011+<∈=<<++n a N n a f a a n n n 证明21`. (本题满分12分)有人玩掷骰子移动棋子的游戏,棋盘分为A B 两方,开始时棋子放在A 方,根据下列① ② ③的规定移动棋子:①骰子出现1点时,不能移动棋子;②出现2 3 4 5点时,把棋子移向对方;③出现6点时,如果棋子在A 方就不动,如果棋子在B 方就移至A 方(1)求将骰子连掷2次,棋子掷第一次后仍在A 方而掷第二次后在B 方的概率 (2)将骰子掷了n 次后,棋子仍在A 方的概率记为P n , 求P n22 (理)(12分)设点n A (n x ,0),1(,2)n n n P x -和抛物线n C :y =x 2+a n x +b n (n ∈N*),其中a n =-2-4n -112n -,n x 由以下方法得到:x 1=1,点P 2(x 2,2)在抛物线C 1:y =x 2+a 1x +b 1上,点A 1(x 1,0)到P 2的距离是A 1到C 1上点的最短距离,…,点11(,2)n n n P x ++在抛物线n C :y =x 2+a n x +b n 上,点n A (n x ,0)到1n P +的距离是n A 到n C 上点的最短距离(Ⅰ)求x 2及C 1的方程(Ⅱ)证明{n x }是等差数列2013届太和中学高三数学试卷答卷13 等差数列{}n a 中,公差d ≠0,a 1,a 3 ,a 9 成等比数列,则1042931a a a a a a ++++= _1613___ . 14.在数列{a n }中,a 1=1,a 2=2,且)( )1(12*+∈-+=-N n a a n n n 则100S =_2600____15一个项数为偶数的等比数列,它的偶数项和是奇数项和的2倍,又它的首项为1,且中间两项的和为24,此等比数列的项数为________8____________.16 已知等差数列{}n a 的前n 项和为n S ,若1,m m N >∈,且211210,38m m m m a a a S -+-+-==,则m 等于_______10______. 17 918 (Ⅰ)∵点A n (a n ,11+-n a )在曲线y =g (x )上(n ∈N +),∴11+-n a =g (a n )=214na +-,并且a n >021141nn a a +=∴+,),1(411221N n n a a nn ∈≥=-∴+,∴数列{21na }为等差数列(II)∵数列{21na }为等差数列,并且首项为211a =1,公差为4,∴21na =1+4(n —1),∴3412-=n a n ,∵a n >0,∴341-=n a n ,(III)b n =1111++n n a a =4341414341--+=++-n n n n ,∴S n =b 1+b 2+…+b n =43414 (45)9415--+++-+-n n =4114-+n19 解:(1)∵ b a ab b a a 2+<<+<,a ,+∈N b ,∴ ⎩⎨⎧+<<+.2,b a ab ab b a ∴ ⎪⎪⎩⎪⎪⎨⎧-<->.121b b a b b a , ∴⎪⎪⎩⎪⎪⎨⎧-+<-+>.122111b a b a , ∴ ⎩⎨⎧<>41a a ,…………4分 ∴ a =2或a =3(a =3时不合题意,舍去) ∴a =2 …………5分(2)b m a m )1(2-+=,12-⋅=n n b b ,由n m b a =+3可得 2)1(5-⋅=-+n b b m ∴ )12(1=+--m b n∴ b =5 …………8分 (3)由(2)知35-=n a n ,125-⋅=n n b , ∴ 2531-=-=-⋅n n m b a∴ 251-=-⋅n n C ∴ n S n n 3)12(5--=,15(21-=n n T n ……10分 ∵ 211==T S ,22==T S …………11分当n ≥3时,]121212[52---=-n n T S nn n ]12121)11[(52---+=n n n]12121)1[52321---++++=n n C C C n n n0]121212)1(1[52=----++>n n n n n ∴ n T S > 综上得 n n T S ≥)(+∈N n …………14分20 (1)解:由于223)(x ax x f -=的最大值不大于,61所以 .1,616)3(22≤≤=a a a f 即 ① ………………3分 又,81)(]21,41[≥∈x f x 时所以1.813234,81832,81)41(,81)21(≥⎪⎪⎩⎪⎪⎨⎧≥-≥-⎪⎪⎩⎪⎪⎨⎧≥≥a a a f f 解得即. ② 由①②得.1=a ………………6分(2)证法一:(i )当n=1时,2101<<a ,不等式110+<<n a n 成立; 因2,3161)(0),32,0(,0)(12=<≤=<∈>n a f a x x f 故所以时不等式也成立.(ii )假设)2(≥=k k n 时,不等式110+<<k a k 成立,因为223)(x x x f -=的对称轴为,31=x 知]31,0[)(在x f 为增函数,所以由311101≤+<<k a 得 )11()(0+<<k f a f k ………………8分于是有,21)2()1(24212121)1(123110221+<+++-+=+-+++⋅-+<<+k k k k k k k k k a k …………12分所以当n=k+1时,不等式也成立.根据(i )(ii )可知,对任何*∈N n ,不等式11+<n a n 成立.…………14分21 解:(1)将骰子连掷2次,棋子掷第一次后仍在A 方而掷第二次后在B 方的概率P=⨯6264=92(2)设把骰子掷了n +1次后,棋子仍在A 方的概率为P n +1,有两种情况:①第n 次棋子在A 方,其概率为P n ,且第n +1次骰子出现1点或6点,棋子不动,其概率为3162= ②第n 次棋子在B 方,且第n +1次骰子出现2,3,4,5或6点,其概率为65 ∴)1(65311n n n P P P -+=+,即)95(21951--=-+n n P P ,P 0=1,31)1(6531001=-+=P P P , 215951-=--+n n P P , ∴{95-n P }是首项为92951-=-P ,公比为21-的等比数列∴1)21(9295---=-n n P ⇒ 229)1(95-⋅-+=n n n P 22 解:(Ⅰ)由题意得()21111,0,:7A C y x x b =-+, 设点(),P x y 是1C 上任意一点, 则1||A P ==令()()()222117f x x x x b =-+-+则()()()()21212727f x x x x b x '=-+-+-由题意得()20f x '=,即()()()222122127270x x x b x-+-+-=又()22,2P x 在1C 上,222127x x b∴=-+ 解得213,14x b ==故1C 的方程为2714y x x =-+(Ⅱ)设点(),P x y 是n C 上任意一点,则||n A P ==令()()()222n n ng x x x x a x b =-+++则()()()()2222n n nng x x x x a x b x a '=-++++由题意得()10n g x +'=即()()()21112220n n n n nn n x x x a x b xa +++-++++=又1212n n n n n x a x b ++=++ ,()()()112201n n n n n x x x a n ++∴-++=≥,即()()111220*n n n n n x x a +++-+=下面用数学归纳法证明21n x n =-, ①当1n =时,11x =,等式成立;②假设当n k =时,等式成立,即21k x k =-,则当1n k =+时,由()*知()111220k k k k k x x a +++-+=, 又11242k k a k -=---,1122112k k k k k x a x k ++-∴==++, 即1n k =+时,等式成立由①②知,等式对*n N ∈成立, 故{}n x 是等差数列。
重庆市合川太和中学2013-2014学年高二下期期中考试理科数学试卷(带解析)

重庆市合川太和中学2013-2014学年高二下期期中考试理科数学试卷(带解析)1.设复数21z i=+(其中i 为虚数单位),则z 的虚部为( ) A.i B.1 C.1- D.i -【答案】C 【解析】试题分析:因为()()()()22121211111i i z i i i i i--====-++--,所以z 的虚部为1-。
故C 正确。
考点:复数的运算。
2.函数sin y x =在点(,)32π处的切线的斜率为( )A.1B.12C.2 【答案】B 【解析】试题分析:令()sin y f x x ==,则()'cos f x x =,所以1'cos 332f ππ⎛⎫==⎪⎝⎭。
由导数的几何意义可知在点(,32π处的切线的斜率1'32k f π⎛⎫== ⎪⎝⎭。
故B 正确。
考点:导数的几何意义。
3.设2k ,若2k ,则135101S =++++( )A .101?A ≥B .101?A =C .101?A ≤D .101?A >【答案】A 【解析】试题分析:因为()()1''ln ln 'ln ln 1f x x x x x x x x x=+=+⋅=+,所以当()00'ln 12f x x =+=时,解得0ln 1x =,所以0x e =。
故A 正确。
考点:导数的计算。
4.若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合,则p 的值为( )A .321(3)10x k dx +=⎰B .2C .4-D .4【答案】D 【解析】试题分析:由椭圆方程可知226,2a b ==,所以222624c a b =-=-=,即2c =。
所以椭圆右焦点为()2,0。
即抛物线的焦点为()2,0,可知22p=,解得4p =。
故D 正确。
考点:椭圆及抛物线的方程和简单几何性质。
5.“a=1”是“函数f (x )=|x ﹣a|在区间[1,+∞)上为增函数”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 【答案】A 【解析】试题分析:当1a =时,()()()1,111,1x x f x x x x -≥⎧⎪=-=⎨-<⎪⎩,此时函数()f x 在[)1,+∞上单调递增;当函数()f x x a =-在[)1,+∞上单调递增时,则在[)1,+∞上0x a -≥即a x ≤恒成立,所以1a ≤。
2024届重庆市合川区太和中学中考三模数学试题含解析

2024届重庆市合川区太和中学中考三模数学试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上。
将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.下列计算正确的是( ) A .B .C .D .2.在平面直角坐标系中,二次函数y =a (x –h )2+k (a <0)的图象可能是A .B .C .D .3.如图,将矩形沿对角线折叠,使落在处,交于,则下列结论不一定成立的是( )A .B .C .D .4.已知点()P m,n ,为是反比例函数3y=-x上一点,当-3n<-1≤时,m 的取值范围是( ) A .1m<3≤B .-3m<-1≤C .1<m 3≤D .-3<m -1≤5.tan45º的值为( ) A .12B .1C .22D 26.图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A,B在围成的正方体中的距离是()A.0 B.1 C.2D.37.方程23x1x=-的解是A.3 B.2 C.1 D.08.小明调查了班级里20位同学本学期购买课外书的花费情况,并将结果绘制成了如图的统计图.在这20位同学中,本学期购买课外书的花费的众数和中位数分别是()A.50,50 B.50,30 C.80,50 D.30,509.已知a35a等于()A.1 B.2 C.3 D.410.如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是A.B.C.D.11.如图,⊙O 是等边△ABC 的外接圆,其半径为3,图中阴影部分的面积是()A.πB.32πC.2πD.3π12.如图,在▱ABCD中,AB=2,BC=1.以点C为圆心,适当长为半径画弧,交BC于点P,交CD于点Q,再分别以点P,Q为圆心,大于12PQ的长为半径画弧,两弧相交于点N,射线CN交BA的延长线于点E,则AE的长是()A.12B.1 C.65D.32二、填空题:(本大题共6个小题,每小题4分,共24分.)13.如图,在△ABC中,AB=AC=15,点D是BC边上的一动点(不与B,C重合),∠ADE=∠B=∠α,DE交AB 于点E,且tan∠α=,有以下的结论:①△ADE∽△ACD;②当CD=9时,△ACD与△DBE全等;③△BDE为直角三角形时,BD为12或;④0<BE≤,其中正确的结论是 ________(填入正确结论的序号).14.如图,在△ABC中,AB=2,BC=3.5,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为_____.15.不等式1253x->的解集是________________16.因式分解:a2﹣a=_____.17.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是_____.18.在直角坐标平面内有一点A(3,4),点A与原点O的连线与x轴的正半轴夹角为α,那么角α的余弦值是_____.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)中央电视台的“朗读者”节目激发了同学们的读书热情,为了引导学生“多读书,读好书“,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本书最少的有5本,最多的有8本,并根据调查结果绘制了不完整的图表,如图所示:本数(本)频数(人数)频率5 a 0.26 18 0.17 14 b8 8 0.16合计50 c我们定义频率=频数抽样人数,比如由表中我们可以知道在这次随机调查中抽样人数为50人课外阅读量为6本的同学为18人,因此这个人数对应的频率就是1850=0.1.(1)统计表中的a、b、c的值;(2)请将频数分布表直方图补充完整;(3)求所有被调查学生课外阅读的平均本数;(4)若该校八年级共有600名学生,你认为根据以上调查结果可以估算分析该校八年级学生课外阅读量为7本和8本的总人数为多少吗?请写出你的计算过程.20.(6分)先化简,再求值:(m+2﹣52m-)•243mm--,其中m=﹣12.21.(6分)某超市在春节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣和优惠,在每个转盘中指针指向每个区域的可能性均相同,若指针指向分界线,则重新转动转盘,区域对应的优惠方式如下,A1,A2,A3区域分别对应9折8折和7折优惠,B1,B2,B3,B4区域对应不优惠?本次活动共有两种方式.方式一:转动转盘甲,指针指向折扣区域时,所购物品享受对应的折扣优惠,指针指向其他区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针均指向折扣区域时,所购物品享受折上折的优惠,其他情况无优惠.(1)若顾客选择方式一,则享受优惠的概率为;(2)若顾客选择方式二,请用树状图或列表法列出所有可能顾客享受折上折优惠的概率.22.(8分)我们已经知道一些特殊的勾股数,如三连续正整数中的勾股数:3、4、5;三个连续的偶数中的勾股数6、8、10;事实上,勾股数的正整数倍仍然是勾股数.另外利用一些构成勾股数的公式也可以写出许多勾股数,毕达哥拉斯学派提出的公式:a=2n+1,b=2n2+2n,c=2n2+2n+1(n为正整数)是一组勾股数,请证明满足以上公式的a、b、c 的数是一组勾股数.然而,世界上第一次给出的勾股数公式,收集在我国古代的着名数学着作《九章算术》中,书中提到:当a=12(m2﹣n2),b=mn,c=12(m2+n2)(m、n为正整数,m>n时,a、b、c构成一组勾股数;利用上述结论,解决如下问题:已知某直角三角形的边长满足上述勾股数,其中一边长为37,且n=5,求该直角三角形另两边的长.23.(8分)如图,已知点A(﹣2,0),B(4,0),C(0,3),以D为顶点的抛物线y=ax2+bx+c过A,B,C三点.(1)求抛物线的解析式及顶点D的坐标;(2)设抛物线的对称轴DE交线段BC于点E,P为第一象限内抛物线上一点,过点P作x轴的垂线,交线段BC于点F,若四边形DEFP为平行四边形,求点P的坐标.24.(10分)某通讯公司推出了A,B两种上宽带网的收费方式(详情见下表)设月上网时间为x h(x为非负整数),请根据表中提供的信息回答下列问题(1)设方案A的收费金额为y1元,方案B的收费金额为y2元,分别写出y1,y2关于x的函数关系式;(2)当35<x<50时,选取哪种方式能节省上网费,请说明理由25.(10分)如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.(1)求抛物线的解析式;(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.26.(12分)某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.若苗圃园的面积为72平方米,求x;若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由;27.(12分)雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.(1)如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、D【解题分析】分析:根据合并同类项、同底数幂的乘法、幂的乘方、同底数幂的除法的运算法则计算即可.解答:解:A、x+x=2x,选项错误;B、x?x=x2,选项错误;C、(x2)3=x6,选项错误;D、正确.故选D.2、B【解题分析】根据题目给出的二次函数的表达式,可知二次函数的开口向下,即可得出答案.【题目详解】二次函数y=a(x﹣h)2+k(a<0)二次函数开口向下.即B成立.故答案选:B.【题目点拨】本题考查的是简单运用二次函数性质,解题的关键是熟练掌握二次函数性质.3、C【解题分析】分析:主要根据折叠前后角和边相等对各选项进行判断,即可选出正确答案.详解:A、BC=BC′,AD=BC,∴AD=BC′,所以A正确.B、∠CBD=∠EDB,∠CBD=∠EBD,∴∠EBD=∠EDB,所以B正确.D、∵sin∠ABE=,∵∠EBD=∠EDB∴BE=DE∴sin∠ABE=.由已知不能得到△ABE∽△CBD.故选C.点睛:本题可以采用排除法,证明A,B,D都正确,所以不正确的就是C,排除法也是数学中一种常用的解题方法.4、A【解题分析】直接把n的值代入求出m的取值范围.【题目详解】解:∵点P(m,n),为是反比例函数y=-3x图象上一点,∴当-1≤n<-1时,∴n=-1时,m=1,n=-1时,m=1,则m的取值范围是:1≤m<1.故选A.【题目点拨】此题主要考查了反比例函数图象上点的坐标性质,正确把n的值代入是解题关键.5、B【解题分析】解:根据特殊角的三角函数值可得tan45º=1,故选B.【题目点拨】本题考查特殊角的三角函数值.6、C【解题分析】试题分析:本题考查了勾股定理、展开图折叠成几何体、正方形的性质;熟练掌握正方形的性质和勾股定理,并能进行推理计算是解决问题的关键.由正方形的性质和勾股定理求出AB的长,即可得出结果.解:连接AB,如图所示:根据题意得:∠ACB=90°,由勾股定理得:AB==;故选C.考点:1.勾股定理;2.展开图折叠成几何体.7、A【解题分析】试题分析:分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解:去分母得:2x=3x﹣3,解得:x=3,经检验x=3是分式方程的解.故选A.8、A【解题分析】分析:根据扇形统计图分别求出购买课外书花费分别为100、80、50、30、20元的同学人数,再根据众数、中位数的定义即可求解.详解:由扇形统计图可知,购买课外书花费为100元的同学有:20×10%=2(人),购买课外书花费为80元的同学有:20×25%=5(人),购买课外书花费为50元的同学有:20×40%=8(人),购买课外书花费为30元的同学有:20×20%=4(人),购买课外书花费为20元的同学有:20×5%=1(人),20个数据为100,100,80,80,80,80,80,50,50,50,50,50,50,50,50,30,30,30,30,20,在这20位同学中,本学期计划购买课外书的花费的众数为50元,中位数为(50+50)÷2=50(元).故选A.点睛:本题考查了扇形统计图,平均数,中位数与众数,注意掌握通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.9、B【解题分析】1,进而得出答案.【题目详解】∵a∴a=1.故选:B.【题目点拨】考查了估算无理数大小,正确得出无理数接近的有理数是解题关键.10、A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
太和中学2013—2014学年度下期期中考试高二数学试题(理科)(总分:150分 考试时间:120分钟)一、选择题(本大题共10个小题,每个小题5分,共50分,每个小题只有一个正确答案,将正确答案填涂在答题卡的相应位置)1.设复数21z i =+(其中i 为虚数单位),则z 的虚部为( )A.iB.1C.1-D.i -2.函数x y sin =在点)23,3(π处的切线的斜率为( )A.1B.21 C.22 D.23 3. 设x x x f ln )(=,若2)(0='x f ,则=0x ( )A . eB .2eC .ln 22D .ln 24. 若抛物线22y px =的焦点与椭圆22162x y +=的右焦点重合,则p 的值为( ) A .2- B .2 C .4- D .456. 如图:在平行六面体1111D C B A ABCD -中,M 为11C A 与11D B 的交点。
若=,=,=1则下列向量中与相等的向量是( )A.1122a b c -++B.1122a b c ++C.1122a b c --+D.1122a b c -+7.下列说法中正确的是( ).A 命题“若x y >,则22x y >”的否命题为假命题.B 命题“,R x ∈∃使得21x x ++0<”的否定为“x R ∀∈,满足210x x ++>” .C 设,x y 为实数,则“1x >”是“lg 0x >”的充要条件 .D 若“p q ∧”为假命题,则p 和q 都是假命题 8.方程x 3﹣6x 2+9x ﹣4=0的实根的个数为( )9.定义域为R 的函数f (x )满足f (1)=1,且f (x )的导函数()2f x '>,则满足2()1f x x <+的x 的集合为( )A . {x |x <1}B .{x |-1<x <1}C .{x |x <-1或x >1}D .{x |x >1}10. 设双曲线22221x y a b -=的两条渐近线与直线2a x c =分别交于A,B 两点,F 为该双曲线的右焦点.若6090AFB ︒<∠<︒, 则该双曲线的离心率的取值范围是( )A .B .C . (1,2)D .)+∞二、填空题(本大题共5个小题,每个小题5分,共25分,将正确答案填写在答题卡上的相应位置)11. 211(2)x dx x -=⎰ .12.用火柴棒按图的方法搭三角形:按图示的规律搭下去,则所用火柴棒数a n 与所搭三角形的个数n 之间的关系式可以是 .13.抛物线y =x 2到直线 2x -y =4距离最近的点的坐标是 .14. 已知直线1y kx =+与曲线ln y x =有公共点,则实数k 的取值范围是 . 15.函数()ln f x a x x =+,对任意的1[]x e e∈,时,()0f x ≥恒成立,则a 的范围为 . 三、解答题(本大题共6个小题,前三个解答题每个13分,后三个解答题每个12分,共75分,将解答过程填写在答题卡上的相应位置) 16.(本小题满分13分)已知322()(23)()f x x ax a x a a =+-++∈R .(1)若曲线()y f x =在1x =-处的切线与直线210x y --=平行,求a 的值; (2)当2a =-时,求()f x 的单调区间.17.(本小题满分13分)在数列{n a }中,61=a ,且111++=---n na a a n n n )2,(*≥∈n N n , (1)求432,,a a a 的值;(2)猜测数列{n a }的通项公式,并用数学归纳法证明。
18.(本小题满分13分)在如图所示的多面体ABCDE 中,AB ⊥平面ACD,DE ⊥平面ACD ,AC=AD=CD=DE=2,AB=1。
(1)请在线段CE 上找到一点F ,使得直线BF ∥平面ACD ,并证明; (2)求平面BCE 与平面ACD 所成锐二面角的大小;19.(本题满分12分)已知椭圆C的两焦点分别为()()12F F 、,长轴长为6,⑴求椭圆C 的标准方程;⑵已知过点(0,2)且斜率为1的直线交椭圆C 于A 、B 两点,求线段AB 的长度。
.BADCE18题图20. (本题满分12分)设函数()2ln af x ax x x=--. (1)若()f x 在2x =时有极值,求实数a 的值和()f x 的极大值; (2)若()f x 在定义域上是增函数,求实数a 的取值范围.21.如图,椭圆12222=+by a x 上的点M 与椭圆右焦点2F 的连线2MF 与x 轴垂直,且OM (O是坐标原点)与椭圆长轴和短轴端点的连线AB 平行. (1)求椭圆的离心率;(2)F 1是椭圆的左焦点,C 是椭圆上的任一点,证明:122F CF π∠≤;(3)过F 1且与AB 垂直的直线交椭圆于P 、Q ,若1PFQ ∆的面积是20 3 ,求此时椭圆的方程.太和中学2013—2014学年度下期期中考试高二数学试题(理科)参考答案一. 1-5 CBADA 6-10 ACCAB二.11. 3-ln2 12. a n =2n+1 13. (1,1) 14.21(,]e-∞ 15. 1[]e e-,三.16.解:(1) 由题意得2()32(23)f x x ax a '=+-+时∴(1)32(23)2f a a '-=--+=∴12a =- ……………………………6分(2) ∵ 2a =-,∴32()24f x x x x =-++∴ 2()341f x x x '=-+,令()0f x '>,得113x x ><或令()0f x '<,得113x <<∴()f x 单调递增区间为1()3-∞,,(1)+∞, ()f x 单调递减区间为1(1)3, ……………………………13分17、(13分)解:(1)30,20,12432===a a a ……………………………6分(2)猜测)2)(1(++=n n a n 。
下用数学归纳法证明:①当4,3,2,1=n 时,显然成立;②假设当k n =),4(N k k ∈≥时成立,即有)2)(1(++=k k a k ,则当1+=k n 时,由111++=---n na a a n n n 得111+++=-n a n n a n n ,故2)2)(1(12111111++++++=++++++=+k k k k k k a k k a k k )3)(2()2()2(2++=+++=k k k k ,故1+=k n 时等式成立;③由①②可知,)2)(1(++=n n a n 对一切*N n ∈均成立。
……………………………13分 18(13分)解法一:以D 点为原点建立如图所示的空间直角坐标系,使得x 轴和z 轴的正半轴分别经过点A 和点E ,则各点的坐标为(0,0,0)D ,(2,0,0)A ,(0,0,2)E ,(2,0,1)B,(1,0)C , (1)点F 应是线段CE 的中点,下面证明: 设F 是线段CE 的中点,则点F 的坐标为1(,2F,∴3(,0)2BF =- DE BF DE BF DE ⊥∴=⋅∴=,0),2,0,0(,而是平面ACD 的一个法向量,此即证得BF ∥平面ACD ; ……………………………6分 (2)设平面BCE 的法向量为(,,)n x y z =,则n CB ⊥,且n CE ⊥,由(1,CB =,(1,CE =-,∴020x z x z ⎧-+=⎪⎨-+=⎪⎩,不妨设y =12x z =⎧⎨=⎩,即(1,3,2)n =,∴所求角θ满足(0,0,2)cos ||2n n θ⋅==⨯4πθ=; ……………………………13分解法二:(1)由已知AB ⊥平面ACD ,DE ⊥平面ACD ,∴AB//ED ,设F 为线段CE 的中点,H 是线段CD 的中点,连接FH ,则//FH =12ED ,∴//FH =AB ,∴四边形ABFH 是平行四边形,∴//BF AH ,由BF ⊄平面ACD 内,AH ⊂平面ACD ,//BF ∴平面ACD (2)由已知条件可知ACD ∆即为BCE ∆在平面ACD 上的射影,设所求的二面角的大小为θ,则cos ACDBCES S θ∆∆=, 易求得BC=BE =CE =1||2BCE S CE ∆== 而2||ACDS AC ∆==,∴cos ACD BCE S S θ∆∆==02πθ<<, ∴4πθ= 19.解:⑴由()()12F F 、,长轴长为6 得:3c a ==所以1b =∴椭圆方程为22191x y += …………………………………………………5分⑵设1122(,),(,)A x y B x y ,由⑴可知椭圆方程为22191x y +=①,∵直线AB 的方程为2y x =+②……………………………7分把②代入①得化简并整理得21036270x x ++=∴12121827,x x x x +=-= ……………………………10分又AB ……………………………12分 20.(1)∵()f x 在2x =时有极值,∴有(2)0f '=又22()a f x a x x '=+- ∴410a a +-=, ∴45a =……………………2分 ∴有2224422()(252)555f x x x x x x'=+-=-+由()0f x '=得112x =,22x =又0x >∴由()0f x '>得102x <<或2x >由()0f x '<得122x <<∴()f x 在区间1(0,)2和(2,)+∞上递增,在区间1(,2)2上递减……………5分BA DCE19题图∴()f x 的极大值为16()2ln 225f =-……………6分 (2)若()f x 在定义域上是增函数,则()0f x '≥在0x >时恒成立()22222'a ax x af x a x x x-+=+-=, ∴需0x >时220ax x a -+≥恒成立,……………………………9分化220ax x a -+≥为221xa x ≥+恒成立,222111x x x x =≤++, ∴1a ≥为所求。
………………………12分 21.(1)易得222(,),,,,OM AB b b b b b c M c k k b c a e a ac a ac a a ==∴=⇒=⇒=∴==……………………………4分(2)证:由椭圆定义得:2221212121212||||||||||2,cos 2||||FC F C F F FC F C a FCF FC F C +-+=∠=222121212442||||2 1.2||||||||a c FC F C b FC F C FC F C --==-22221212121222||||22||||(),cos 110,.222FC F C b c FC F C a FCF FCF a c π+≤=∴∠≥-=-=∴∠≤ ……………………………8分 (3)解:设直线PQ的方程为(),)ay x c y x c b=--=-即 .代入椭圆方程消去x 得:221y b +=,整理得:22212122520,,.55c y c y y y y --=∴+=⋅=-∴22222212128481().2||25,5252PF Q c c y y S c y y c ∆-=+==⋅⋅-===因此a 2=50,b 2=25,所以椭圆方程为22 1.5025x y += ……………………………12分。
