product_binary
C语言实现读写二进制文件

.LIBPATTERNS: lib%.so lib%.a
vpath % .
vpath %.c src
vpath %.h include
OBJS = mysql_binary.o
$(PRODUCT): $(OBJS)
$(CXX) $(OBJS) -o $@ $(LIBS)
读:
FILE *fp = fopen("file.dat","r");
fread(plist,sizeof(Point),100,fp);
fread的返回值为实际读入的结构体Point的元素个数。
写:
FILE *fp = fopen("file.dat","w");
fwrite(plist,sizeof(Point),100,fp);
length = mysql_fetch_lengths(res_set);
for (i=0; i<mysql_num_fields(res_set); i++) {
fwrite(row[0], 1, length[0], fp);
}
}
fclose(fp);
mysql_close(conn);
free(sql);
exit(1);
}
if ((n = fread(buf, 1, *size, fp)) < 0) { //n=*size
perror("fread file" );
exit(1);
}
sql = (char *)malloc(sizeof(char)*n*2+256); //2n+1+strlen(other sql)
Binary relation - Wikipedia, the free encyclopedia

Binary relationFrom Wikipedia, the free encyclopediaIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = A×A. More generally, a binary relation between two sets A and B is a subset of A×B. The terms dyadic relation and 2-place relation are synonyms for binary relations.An example is the "divides" relation between the set of prime numbers P and the set of integers Z, in which every prime p is associated with every integer z that is a multiple of p (and not with any integer that is not a multiple of p). In this relation, for instance, the prime 2 is associated with numbers that include −4, 0, 6, 10, but not 1 or 9; and the prime 3 is associated with numbers that include 0, 6, and 9, but not 4 or 13.Binary relations are used in many branches of mathematics to model concepts like "is greater than", "is equal to", and "divides" in arithmetic, "is congruent to" in geometry, "is adjacent to" in graph theory, "is orthogonal to" in linear algebra and many more. The concept of function is defined as a special kind of binary relation. Binary relations are also heavily used in computer science.A binary relation is the special case n = 2 of an n-ary relation R⊆A1× … ×A n, that is, a set of n-tuples where the j th component of each n-tuple is taken from the j th domain A j of the relation.In some systems of axiomatic set theory, relations are extended to classes, which are generalizations of sets. This extension is needed for, among other things, modeling the concepts of "is an element of" or "is a subset of" in set theory, without running into logical inconsistencies such as Russell's paradox.Contents1 Formal definition1.1 Is a relation more than its graph?1.2 Example2 Special types of binary relations3 Relations over a set4 Operations on binary relations4.1 Complement4.2 Restriction5 Sets versus classes6 The number of binary relations7 Examples of common binary relations8 See also9 Notes10 References11 External linksFormal definitionA binary relation R is usually[citation needed] defined as an ordered triple[citation needed] (X, Y, G) where X and Y are arbitrary sets (or classes), and G is a subset of the Cartesian product X×Y. The sets X and Y are called the domain (or the set of departure) and codomain (or the set of destination), respectively, of the relation, and G is called its graph.The statement (x,y) ∈R is read "x is R-related to y", and is denoted by xRy or R(x,y). The latter notation corresponds to viewing R as the characteristic function on "X" x "Y" for the set of pairs of G.The order of the elements in each pair of G is important: if a≠b, then aRb and bRa can be true or false, independently of each other.A relation as defined by the triple (X, Y, G) is sometimes referred to as a correspondence instead.[1] In this case the relation from X to Y is the subset G of X×Y, and "from X to Y" must always be either specified or implied by the context when referring to the relation. In practice correspondence and relation tend to be used interchangeably.Is a relation more than its graph?According to the definition above, two relations with the same graph may be different, if they differ in the sets and . For example, if , then , , and arethree distinct relations.Some mathematicians, especially in set theory, do not consider the sets and to be part of the relation, and define a binary relation as a set of ordered pairs, identifying binary relations with their graphs. The domain of a binary relation is then defined as the set of all such that there exists at least one such that , the range of is defined as the set of all such that there exists at least one such that , and the field of is the union of its domain and its range.[2][3][4]A special case of this difference in points of view applies to the notion of function. Many authors insist on distinguishing between a function's codomain and its range. Thus, a single "rule," like mapping every real number x to x2, can lead to distinct functions and , depending on whether the images under that rule are understood to be reals or, more restrictively, non-negative reals. But others view functions as simply sets of ordered pairs with unique first components. This difference in perspectives does raise some nontrivial issues. As an example, the former camp considers surjectivity—or being onto—as a property of functions, while the latter sees it as a relationship that functions may bear to sets.Either approach is adequate for most uses, provided that one attends to the necessary changes in language, notation, and the definitions of concepts like restrictions, composition, inverse relation, and so on. The choice between the two definitions usually matters only in very formal contexts, like category theory.ExampleExample: Suppose there are four objects {ball, car, doll, gun} and four persons {John, Mary, Ian, Venus}. Suppose that John owns the ball, Mary owns the doll, and Venus owns the car. Nobody owns the gun and Ian owns nothing. Then the binary relation "is owned by" is given asR=({ball, car, doll, gun}, {John, Mary, Ian, Venus}, {(ball, John), (doll, Mary), (car, Venus)}).Thus the first element of R is the set of objects, the second is the set of people, and the last element is a set of ordered pairs of the form (object, owner).The pair (ball, John), denoted by ball R John means that the ball is owned by John.Two different relations could have the same graph. For example: the relation({ball, car, doll, gun}, {John, Mary, Venus}, {(ball,John), (doll, Mary), (car, Venus)})is different from the previous one as everyone is an owner. But the graphs of the two relations are the same. Nevertheless, R is usually identified or even defined as G(R) and "an ordered pair (x, y) ∈ G(R)" is usually denoted as "(x, y) ∈R".Special types of binary relationsSome important types of binary relations R between X and Y are listed below.Uniqueness properties:injective (also called left-unique[5]): for all x and z in X and y in Y it holds that if xRy and zRy then x = z.functional (also called right-unique[5] or right-definite[citation needed]): for all x in X, and y and z in Y it holds that if xRy and xRz then y = z; such a binary relation is called a partial function.one-to-one (also written 1-to-1): injective and functional.Totality properties:left-total:[5] for all x in X there exists a y in Y such that xRy, i.e., R is a multivalued function (thisproperty, although sometimes also referred to as total, is different from the definition of total in the next section).surjective (also called right-total[5]): for all y in Y there exists an x in X such that xRy.Uniqueness and totality properties:A function: a relation that is functional and left-total.A bijection: a one-to-one correspondence; such a relation is a function and is said to be bijective.Relations over a setIf X = Y then we simply say that the binary relation is over X, or that it is an endorelation over X. Some types ofendorelations are widely studied in graph theory, where they're known as directed graphs.The set of all binary relations Rel(X) on a set X is the set 2X×X which is a Boolean algebra augmented with the involution of mapping of a relation to its inverse relation. For the theoretical explanation see Relation algebra. Some important types of binary relations over a set X are:reflexive: for all x in X it holds that xRx. For example, "greater than or equal to" is a reflexive relation but "greater than" is not.irreflexive (or strict): for all x in X it holds that not xRx. "Greater than" is an example of an irreflexive relation.coreflexive: for all x and y in X it holds that if xRy then x = y. "Equal to and odd" is an example of acoreflexive relation.symmetric: for all x and y in X it holds that if xRy then yRx. "Is a blood relative of" is a symmetricrelation, because x is a blood relative of y if and only if y is a blood relative of x.antisymmetric: for all distinct x and y in X, if xRy then not yRx.asymmetric: for all x and y in X, if xRy then not yRx. (So asymmetry is stronger than anti-symmetry. In fact, asymmetry is equivalent to anti-symmetry plus irreflexivity.)transitive: for all x, y and z in X it holds that if xRy and yRz then xRz. (Note that, under the assumption of transitivity, irreflexivity and asymmetry are equivalent.)total: for all x and y in X it holds that xRy or yRx (or both). "Is greater than or equal to" is an example of a total relation (this definition for total is different from left total in the previous section).trichotomous: for all x and y in X exactly one of xRy, yRx or x = y holds. "Is greater than" is an example of a trichotomous relation.Euclidean: for all x, y and z in X it holds that if xRy and xRz, then yRz (and zRy). Equality is a Euclidean relation because if x=y and x=z, then y=z.serial: for all x in X, there exists y in X such that xRy. "Is greater than" is a serial relation on the integers.But it is not a serial relation on the positive integers, because there is no y in the positive integers such that 1>y.[6] However, the "Is less than" is a serial relation on the positive integers (the natural numbers), the rational numbers and the real numbers. Every reflexive relation is serial.set-like: for every x in X, the class of all y such that yRx is a set. (This makes sense only if we allowrelations on proper classes.) The usual ordering < on the class of ordinal numbers is set-like, while its inverse > is not.A relation that is reflexive, symmetric, and transitive is called an equivalence relation. A relation that is reflexive, antisymmetric, and transitive is called a partial order. A partial order that is total is called a total order, simple order, linear order, or a chain.[7] A linear order where every nonempty set has a least element is called a well-order. A relation that is symmetric, transitive, and serial is also reflexive.Operations on binary relationsIf R is a binary relation over X and Y, then the following is a binary relation over Y and X:Inverse or converse: R−1, defined as R−1 = { (y, x) | (x, y) ∈R }. A binary relation over a set is equal to its inverse if and only if it is symmetric. See also duality (order theory).If R is a binary relation over X, then each of the following is a binary relation over X:Reflexive closure: R =, defined as R = = { (x, x) | x∈X } ∪R or the smallest reflexive relation over X containing R. This can be seen to be equal to the intersection of all reflexive relations containing R.Reflexive reduction: R ≠, defined as R ≠ = R \ { (x, x) | x∈X } or the largest irreflexive relation over X contained in R.Transitive closure: R +, defined as the smallest transitive relation over X containing R. This can be seen to be equal to the intersection of all transitive relations containing R.Transitive reduction: R −, defined as a minimal relation having the same transitive closure as R.Reflexive transitive closure: R *, defined as R * = (R +) =, the smallest preorder containing R.Reflexive transitive symmetric closure: R ≡, defined as the smallest equivalence relation over Xcontaining R.If R, S are binary relations over X and Y, then each of the following is a binary relation:Union: R∪S⊆X×Y, defined as R∪S = { (x, y) | (x, y) ∈R or (x, y) ∈S }.Intersection: R∩S⊆X×Y, defined as R∩S = { (x, y) | (x, y) ∈R and (x, y) ∈S }.If R is a binary relation over X and Y, and S is a binary relation over Y and Z, then the following is a binary relation over X and Z: (see main article composition of relations)Composition: S ∘ R, also denoted R ; S (or more ambiguously R ∘ S), defined as S ∘ R = { (x, z) | there exists y∈Y, such that (x, y) ∈R and (y, z) ∈S }. The order of R and S in the notation S ∘ R, used here agrees with the standard notational order for composition of functions.ComplementIf R is a binary relation over X and Y, then the following too:The complement S is defined as x S y if not x R y.The complement of the inverse is the inverse of the complement.If X = Y the complement has the following properties:If a relation is symmetric, the complement is too.The complement of a reflexive relation is irreflexive and vice versa.The complement of a strict weak order is a total preorder and vice versa.The complement of the inverse has these same properties.RestrictionThe restriction of a binary relation on a set X to a subset S is the set of all pairs (x, y) in the relation for which x and y are in S.If a relation is reflexive, irreflexive, symmetric, antisymmetric, asymmetric, transitive, total, trichotomous, a partial order, total order, strict weak order, total preorder (weak order), or an equivalence relation, its restrictions are too.However, the transitive closure of a restriction is a subset of the restriction of the transitive closure, i.e., in general not equal.Also, the various concepts of completeness (not to be confused with being "total") do not carry over to restrictions. For example, on the set of real numbers a property of the relation "≤" is that every non-empty subset S of R with an upper bound in R has a least upper bound (also called supremum) in R. However, for a set of rational numbers this supremum is not necessarily rational, so the same property does not hold on the restriction of the relation "≤" to the set of rational numbers.The left-restriction (right-restriction, respectively) of a binary relation between X and Y to a subset S of its domain (codomain) is the set of all pairs (x, y) in the relation for which x (y) is an element of S.Sets versus classesCertain mathematical "relations", such as "equal to", "member of", and "subset of", cannot be understood to be binary relations as defined above, because their domains and codomains cannot be taken to be sets in the usual systems of axiomatic set theory. For example, if we try to model the general concept of "equality" as a binary relation =, we must take the domain and codomain to be the "class of all sets", which is not a set in the usual set theory.In most mathematical contexts, references to the relations of equality, membership and subset are harmless because they can be understood implicitly to be restricted to some set in the context. The usual work-around to this problem is to select a "large enough" set A, that contains all the objects of interest, and work with the restriction =A instead of =. Similarly, the "subset of" relation ⊆ needs to be restricted to have domain and codomain P(A) (the power set of a specific set A): the resulting set relation can be denoted ⊆A. Also, the "member of" relation needs to be restricted to have domain A and codomain P(A) to obtain a binary relation ∈A that is a set.Another solution to this problem is to use a set theory with proper classes, such as NBG or Morse–Kelley set theory, and allow the domain and codomain (and so the graph) to be proper classes: in such a theory, equality, membership, and subset are binary relations without special comment. (A minor modification needs to be made to the concept of the ordered triple (X, Y, G), as normally a proper class cannot be a member of an ordered tuple; or of course one can identify the function with its graph in this context.) [8] With this definition one can for instance define a function relation between every set and its power set.The number of binary relationsThe number of distinct binary relations on an n-element set is 2n2 (sequence A002416 in OEIS):Number of n-element binary relations of different typesn all transitive reflexive preorder partialordertotalpreordertotalorderequivalencerelation011111111122111111 21613443322 35121716429191365 46553639944096355219752415OEIS A002416A006905A053763A000798A001035A000670A000142A000110 Notes:The number of irreflexive relations is the same as that of reflexive relations.The number of strict partial orders (irreflexive transitive relations) is the same as that of partial orders.The number of strict weak orders is the same as that of total preorders.The total orders are the partial orders that are also total preorders. The number of preorders that are neither a partial order nor a total preorder is, therefore, the number of preorders, minus the number of partial orders, minus the number of total preorders, plus the number of total orders: 0, 0, 0, 3, and 85, respectively.the number of equivalence relations is the number of partitions, which is the Bell number.The binary relations can be grouped into pairs (relation, complement), except that for n = 0 the relation is its own complement. The non-symmetric ones can be grouped into quadruples (relation, complement, inverse, inverse complement).Examples of common binary relationsorder relations, including strict orders:greater thangreater than or equal toless thanless than or equal todivides (evenly)is a subset ofequivalence relations:equalityis parallel to (for affine spaces)is in bijection withisomorphydependency relation, a finite, symmetric, reflexive relation.independency relation, a symmetric, irreflexive relation which is the complement of some dependency relation.Binary relations by propertyreflexive symmetric transitive symbol exampledirected graph→undirected graph No Yestournament No No pecking orderdependency Yes Yesweak order Yes≤preorder Yes Yes≤preferencepartial order Yes No Yes≤subsetpartial equivalence Yes Yesequivalence relation Yes Yes Yes∼, ≅, ≈, ≡equalitystrict partial order No No Yes<proper subsetSee alsoConfluence (term rewriting)Hasse diagramIncidence structureLogic of relativesOrder theoryRelation algebraTriadic relationNotes1. ^Encyclopedic dictionary of Mathematics (/books?id=azS2ktxrz3EC&pg=PA1331&hl=en&sa=X&ei=glo6T_PmC9Ow8QPvwYmFCw&ved=0CGIQ6AEwBg#v=onepage &f=false). MIT. 2000. pp. 1330–1331. ISBN 0-262-59020-4.2. ^ Suppes, Patrick (1972) [originally published by D. van Nostrand Company in 1960]. Axiomatic Set Theory. Dover.ISBN 0486616304.3. ^ Smullyan, Raymond M.; Fitting, Melvin (2010) [revised and corrected republication of the work originally publishedin 1996 by Oxford University Press, New York]. Set Theory and the Continuum Problem. Dover. ISBN 9780486474847.4. ^ Levy, Azriel (2002) [republication of the work published by Springer-Verlag, Berlin, Heidelberg and New York in1979]. Basic Set Theory. Dover. ISBN 0486420795.5. ^ a b c d Kilp, Knauer and Mikhalev: p. 36. ^ Yao, Y.Y.; Wong, S.K.M. (1995). "Generalization of rough sets using relationships between attribute values"(http://www2.cs.uregina.ca/~yyao/PAPERS/relation.pdf). Proceedings of the 2nd Annual Joint Conference onInformation Sciences: 30–33..7. ^ Joseph G. Rosenstein, Linear orderings, Academic Press, 1982, ISBN 012597680, p. 48. ^ Tarski, Alfred; Givant, Steven (1987). A formalization of set theory without variables. American MathematicalSociety. p. 3. ISBN 0-8218-1041-3.ReferencesM. Kilp, U. Knauer, A.V. Mikhalev, Monoids, Acts and Categories: with Applications to WreathProducts and Graphs, De Gruyter Expositions in Mathematics vol. 29, Walter de Gruyter, 2000, ISBN 3-11-015248-7.Gunther Schmidt, 2010. Relational Mathematics. Cambridge University Press, ISBN 978-0-521-76268-7. External linksHazewinkel, Michiel, ed. (2001), "Binary relation" (/index.php?title=p/b016380), Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4Retrieved from "/w/index.php?title=Binary_relation&oldid=554422047" Categories: Mathematical relationsThis page was last modified on 10 May 2013 at 09:48.Text is available under the Creative Commons Attribution-ShareAlike License; additional terms may apply. By using this site, you agree to the Terms of Use and Privacy Policy.Wikipedia® is a registered trademark of the Wikimedia Foundation, Inc., a non-profit organization.。
MULTIPLY

32-bit Multiplicand reg, 32 -bit ALU,
64-bit Product reg, (0-bit Multiplier reg)
Multiplicand
32 bits
32-bit ALU Shift Right Product (Multiplier) Write Control 64 bits
Op
0001111000 sub
Middle of run of 1s 0001111000 none
0
0
1
0
End of run of 1s
0001111000 add
Middle of run of 0s 0001111000 none
Originally for Speed (when shift was faster than add)
Product Multiplier Multiplicand
Add
SRL
SLL
0000 0000 0011
Add
0000 0010
2. Shift the Multiplicand register left 1 bit. 3. Shift the Multiplier register right 1 bit. 32nd repetition? No: < 32 repetitions
11 -> nop, shiftR
01 -> add shift done
(= 14)
13
Booths Example (2 x -3 = 0010 x 1101)
Operation Multiplicand Product next?
10 -> sub shiftR P (sign ext) 01 -> add shift P 10 -> sub shiftR P (sign ext) 11 -> nop shiftR P (sign ext) done 0. Initial value m = 0010 0000 1101 0 1a. P = P - m - 0010 = + 1110 1110 1101 0 1b. 2a. 2b. 3a. 3b. 4a 4b. 0010 1111 0110 1 + 0010 0001 0110 1 0010 0000 1011 0 - 0010 = + 1110 0010 0010 0010 1110 1011 0 1111 0101 1 1111 0101 1 1111 1010 1
二进制数据镜像函数

二进制数据镜像函数英文回答:Binary data mirroring is a function that involves reversing the order of the bits in a binary data stream. This means that the least significant bit becomes the most significant bit, and vice versa. This function is commonly used in various applications, such as data encryption, image processing, and network protocols.One way to implement the binary data mirroring function is by using bitwise operations in programming languages. For example, in C++, you can use the bitwise shift operators to reverse the order of the bits. Here is a simple code snippet that demonstrates this:cpp.unsigned int mirrorBits(unsigned int num) {。
unsigned int mirroredNum = 0;int numBits = sizeof(num) 8; // Assuming 32-bit integer.for (int i = 0; i < numBits; i++) {。
mirroredNum <<= 1; // Left shift by 1 bit.mirroredNum |= (num & 1); // Set the least significant bit.num >>= 1; // Right shift by 1 bit.}。
stm32编译的二进制程序的格式

stm32编译的二进制程序的格式在STM32编译的二进制程序格式方面,主要参考内容如下:1. ELF(Executable and Linkable Format)格式:ELF是一种可执行文件格式,用于将编译后的程序转换为二进制文件。
它定义了如何组织和加载可执行文件的各个部分,包括代码段、数据段、符号表等。
ELF格式具有良好的可扩展性和灵活性,可以适应不同的硬件和目标平台。
2. HEX(Intel Hex)格式:HEX格式是一种常用的非执行文件格式,用于表示二进制数据。
它将数据以十六进制的形式表示,并在文件中以行为单位进行存储。
每行包含数据的起始地址、数据长度、数据本身和校验和等信息。
HEX格式通常用于将二进制程序下载到STM32芯片中。
3. BIN(Binary)格式:BIN格式是一种简单的二进制文件格式,直接将二进制数据以字节序列的形式存储在文件中。
它没有头部信息,也没有指示地址和长度的字段,只包含纯粹的二进制数据。
BIN格式适用于将程序直接烧录到STM32芯片的存储器中。
4. SREC(Motorola S-record)格式:SREC格式是一种用于表示二进制数据的文件格式,广泛应用于早期的Motorola微处理器和微控制器。
它将数据以ASCII字符的形式表示,并在文件中以行为单位进行存储。
每行包含数据的类型、起始地址、长度、数据本身和校验和等信息。
SREC格式通常用于将二进制程序下载到STM32芯片中。
除了这些常见的二进制程序格式,STM32编译还可以生成其他格式的输出文件,例如:5. IHEX(Intel Hex Extended)格式:IHEX格式是对HEX格式的扩展,增加了附加数据和可执行代码等内容。
它可以更好地支持STM32芯片的特殊功能,如EEPROM和Flash的编程。
6. AOut(Assembler Output)格式:AOut格式是汇编器的输出格式,包含有关汇编指令和数据的详细信息。
建表常用字段

建表常用字段摘要:一、引言二、数据库表的设计原则三、建表时需要考虑的关键字段四、实例分析五、总结正文:一、引言在我国,数据库技术被广泛应用于各个领域,为了有效地管理和存储数据,设计合理的数据库表结构至关重要。
数据库表的设计涉及到多个方面,其中选择合适的字段是关键。
本文将介绍在建立数据库表时常用的一些字段类型。
二、数据库表的设计原则1.合理的数据类型选择2.遵循规范命名规范3.保持数据表的整洁性4.考虑数据表之间的关系三、建表时需要考虑的关键字段1.主键(Primary Key)2.外键(Foreign Key)3.唯一约束(Unique Constraint)4.非空约束(Not Null Constraint)5.自动递增(Auto Increment)6.日期和时间字段(Date and Time Fields)7.字符串字段(String Fields)8.数字字段(Number Fields)9.布尔字段(Boolean Fields)10.二进制数据字段(Binary Data Fields)四、实例分析以一个简单的电商数据库为例,包括以下表:1.商品表(Product Table)- 商品ID(Product ID,主键)- 商品名称(Product Name,字符串)- 商品类别(Product Category,字符串)- 商品价格(Product Price,数字)- 商品库存(Product Stock,数字)- 创建时间(Create Time,日期和时间)- 更新时间(Update Time,日期和时间)2.用户表(User Table)- 用户ID(User ID,主键)- 用户名(User Name,字符串)- 用户密码(User Password,字符串)- 用户邮箱(User Email,字符串)- 创建时间(Create Time,日期和时间)- 更新时间(Update Time,日期和时间)3.订单表(Order Table)- 订单ID(Order ID,主键)- 用户ID(User ID,外键)- 商品ID(Product ID,外键)- 订单状态(Order Status,字符串)- 订单金额(Order Amount,数字)- 创建时间(Create Time,日期和时间)- 更新时间(Update Time,日期和时间)五、总结在建立数据库表时,选择合适的字段类型对于数据的存储和管理至关重要。
物联网中英文词汇对照表
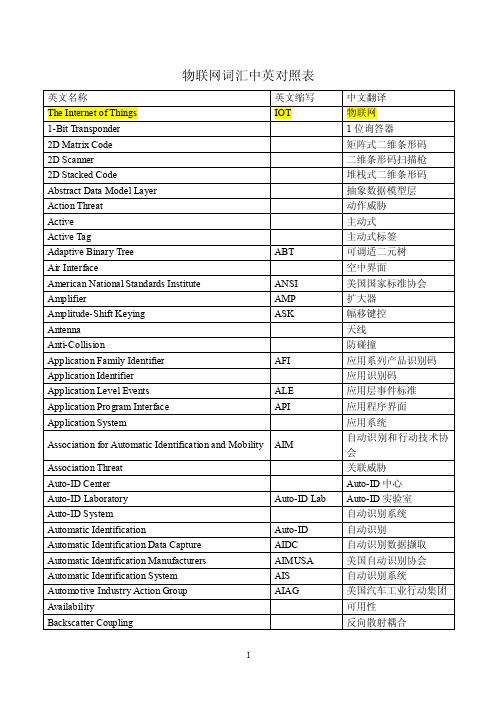
英文缩写 XML FMCG FSK GID GCI GDD GDSN GLN GPC GR GSMP GTAG GTIN
HLS HIBCC HF
ID Code
ISO ISBN ISSN
4
中文翻译 可延伸式标记语言 法拉第笼 快速移转消费产品 定位图形 频移键控 GDSN 服务 基础编码方式 一般管理者代码 全球商务创建会 全球化数据字典 全球数据同步网络 全球位置码 全球产品分类系统 GS1 全球注册中心 全球标准管理程序 全球标准标签 全球交易品项识别代码 手持式读取器 杂凑锁 杂凑链 标头 健康医疗产业 美国制药团体事务管理 协会 高频 本地数据库 恶意编码传播 识别码 照相扫描枪 感应耦合 基础建设威胁 店内条形码 真确性 标准化国际组织 国际标准书号 国际标准期刊号
Auto-ID Lab
Auto-ID AIDC AIMUSA AIS AIAG
中文翻译 物联网 1 位询答器 矩阵式二维条形码 二维条形码扫描枪 堆栈式二维条形码 抽象数据模型层 动作威胁 主动式 主动式标签 可调适二元树 空中界面 美国国家标准协会 扩大器 幅移键控 天线 防碰撞 应用系列产品识别码 应用识别码 应用层事件标准 应用程序界面 应用系统 自动识别和行动技术协 会 关联威胁 Auto-ID 中心 Auto-ID 实验室 自动识别系统 自动识别 自动识别数据撷取 美国自动识别协会 自动识别系统 美国汽车工业行动集团 可用性 反向散射耦合
英文名称 Data Character Data Definition Layer Data Field Data Transfer Rate Decoder Defense Logistics Agency Denial of Service Domain Name Service Dot Double-Sideband Amplitude Shift Keying EAN International EAN.UCC EAN.UCC System EANCOM Eavesdropping Electromagnetic Backscatter Coupling Electronic Article Surveillance Electronic Bill of Rights Electronic Data Interchange Electronic Privacy Information Center Electronic Product Code Enterprise Resource Planning Entity and Economy TRON EPC Information Services EPCglobal EPCglobal C hina EPCglobal Network Erasure Correction Error Correction Error Correction Character Error Detection European Article Number
Metasys

Network Control Engine Catalog PageLIT-19004552018-12-17 Release 9.0.7MS-NCE25xx-xJohnson ControlsIntroductionThe Metasys® Network Control Engine (NCE) Series controllers provide a cost-effective solution designed for integrating central plants and large built-up air handlers into your existing Metasys networks.These network control engines combine the network supervisor capabilities and IP network connectivity of a Network Automation Engine (NAE) with the I/O point connectivity and direct digital control capabilities of a Field Equipment Controller (FEC), making them the ideal choice for expanding and improving your Metasys installation for greater data visibility and control over your energy usage.NCEs provide supervisory control of a specified field bus trunk with up to 32 field controllers. NCE25 Series controllers provide integration to many network protocols, including BACnet®/IP, BACnet MS/TP, N2 Bus, Modbus® RTU, Modbus TCP, M-Bus (EN 13757-3), KNX IP, and other third-party protocols. The MS-NCE2500-0 and MS-NCE2506-0 models, which are available in Europe only, do not provide a physical field controller trunk connection.All NCE models feature 33 integral I/O points and a Sensor/Actuator (SA) Bus, which allow you to increase the NCE's I/O field point capacity and integrate NS Series Network Sensors, and VFDs into your NCE application.Some NCE models feature an integral field controller display screen with a navigation keypad, allowing for easy modifications in the field.Application documentationRefer to the Network Engines Product Bulletin (LIT-12012138) for important product application information.Repair informationIf the network engine fails to operate within its specifications, replace the unit. For a replacement network engine, contact the nearest Johnson Controls® representative.Features and benefitsUse of commonly accepted IT standards at the automation and enterprise level Allows you to install the network engine on the existing IT infrastructure within a buildingor enterprise and use standard IT communication services over the company intranet, WAN, or public Internet with firewall protection. Communication between the network engine and clients is encrypted with Hypertext Transfer Protocol Secure (https).Web-based user interfaceAllows you to access, monitor, and control the network engine from a supported webbrowser connected to the network.Secure Linux® operating systemProvides a high level of protection from threats with the adoption of the Linux operatingsystem, a full replacement of the recently expired Windows® CE operating system. Supervision of controller networks including Johnson Controls and third-party protocol devicesSupports connectivity to open network standards for complete flexibility in the selection of field devices. Supported protocols are model and software release dependent. They include BACnet MS/TP, BACnet/IP, N2 Bus, Modbus RTU, Modbus TCP, M-Bus (EN 13757-3), KNX IP,and other third-party protocols. Prior to Metasys system Release 9.0.7, only the NetworkIntegration Engines (NIE29s) provided the Modbus, M-Bus, and KNX integrations. At Release9.0.7, these third-party integrations are included with all NCEs.Multiple connection options for data accessAllow connection of a web browser through the IP network using the Ethernet port. AtRelease 9.0 or earlier, you can use the optional internal or external modem for a dial-upconnection. Modem functions are not available for an NCE25 at Release 9.0.7.Integral field controller with 33 I/O pointsProvides field-level control of central plant and large air-handler applications combined with enterprise level IP network connectivity.Expandable I/O point capacity, NS sensor connectivity, and VFD control on field controller SA BusAllow you to connect multiple IOMs, NS Series Network Sensors, and VFDs to the fieldcontroller SA Bus, which greatly expands the network engine's field level control capabilities. No hardware to replaceUpgrade from Windows CE to Linux OS using a simple network download.Point type countsTable 1: Point type countsOrdering informationContact the nearest Johnson Controls representative to order an NCE25 or accessories. Specify the desired product code number using the following NCE ordering information tables.Table 3: NCE25 accessories ordering informationTechnical specifications Table 4: NCE25Network and Serial Interfaces (Depending on the NCE model.)•One Ethernet port; 10/100 Mbps; 8-pin RJ-45 connector•One optically isolated RS-485 SA Bus port; with a pluggable and keyed 4-position terminal block (on all NCE25 models)•One optically isolated RS-485 port; with a pluggable and keyed 4-position terminal block (only on NCE25 models that support an N2 Bus or MS/TP bus trunk)•One LonWorks port; FTT10 78 Kbps; pluggable, keyed 3-position terminal block (only on NCE25 models that support a LonWorks Network trunk). The LonWorks models are supported to run the Metasys Release 9.0 software, but not the Release 9.0.7 update.•One RS-232-C serial port with a standard 9-pin sub-D connector that supports standard baud rates•One USB serial port with a standard USB connector that supports an optional, user-supplied external modem. Modem functions are available with Metasys Release 9.0, but are not available after the NCE is updated with Release 9.0.7.•Option: One telephone port for the internal modem; up to 56 Kbps; 6-pin modular connector (NCE models with an optional internal modem have one RS-232-C serial port only; not supported for an engine with Release 9.0.7).Analog Input/Analog Output Point Resolution •Analog Input Points: 16-bit resolution•Analog Output Points: 16-bit resolution and ±200 mV accuracy on 0-10 VDC applicationsInput/Output Capabilities •10-Universal Inputs: Defined as 0–10 VDC, 4–20 mA, 0–600k ohm, or Binary Dry Contact•8-Binary Inputs: Defined as Dry Contact Maintained or Pulse/ Accumulator Mode•4-Analog Outputs: Defined as 0–10 VDC or 4–20 mA•7-Binary Outputs: Defined as 24 VAC Triac (selectable internal or external source power)•4-Configurable Outputs: Defined as 0–10 VDC or 24 VAC Triac BODimensions (Height x Width x Depth)155 mm x 270 mm x 64 mm (6.1 in. x 10.6 in. x 2.5 in.), minimum mounting space required: 250 mm x 370 mm x 110 mm (9.8 in. x 14.6 in. x 4.3 in.)Housing Plastic housingPlastic material: ABS and polycarbonateProtection: IP20 (IEC60529)Mounting On a flat surface with screws, on three mounting clips, or a single 35mm DIN railShipping Weight 1.2 kg (2.7 lb)United States: UL Listed, File E107041, CCN PAZX, UL 916, EnergyManagement Equipment; FCC Compliant to CFR47, Part 15, Subpart B,Class AComplianceCanada: UL Listed, File E107041, CCN PAZX7, CAN/CSA C22.2 No. 205,Signal Equipment Industry Canada Compliant, ICES-003Europe: CE Mark - Johnson Controls declares that this product isin compliance with the essential requirements and other relevantprovisions of the EMC Directive.Australia and New Zealand: RCM Mark, Australia/NZ EmissionsCompliantBACnet International: BTL 135-2010 Listed B-BC at Metasys systemRelease 8.1The performance specifications are nominal and conform to acceptable industry standard. For application at conditions beyond these specifications, consult the local Johnson Controls office. Johnson Controls shall not be liable for damages resulting from misapplication or misuse of its products. North American emissions complianceCanadaThis Class (A) digital apparatus meets all the requirements of the Canadian Interference-Causing Equipment Regulations.Cet appareil numérique de la Classe (A) respecte toutes les exigences du Règlement sur lematériel brouilleur du Canada.United StatesThis equipment has been tested and found to comply with the limits for a Class A digital device pursuant to Part 15 of the FCC Rules. These limits are designed to provide reasonable protection against harmful interference when this equipment is operated in a commercial environment. This equipment generates, uses, and can radiate radio frequency energy and, if not installed and used in accordance with the instruction manual, may cause harmful interference toradio communications. Operation of this equipment in a residential area may cause harmful interference, in which case the users will be required to correct the interference at their own expense.Points of single contactAPAC Europe NA/SAJOHNSON CONTROLSC/O CONTROLS PRODUCT MANAGEMENTNO. 32 CHANGJIJANG RD NEW DISTRICTWUXI JIANGSU PROVINCE 214028CHINAJOHNSON CONTROLSWESTENDHOF 345143 ESSENGERMANYJOHNSON CONTROLS507 E MICHIGAN STMILWAUKEE WI 53202USA© 2018 Johnson Controls. All rights reserved. All specifications and other information shown were current as of document。
