华师大版九年级数学下册课后练习相似三角形的应用课后练习二及详解
2014-2015学年华师大版九年级数学下册课后练习:相似三角形有关的综合问题1+课后练习一及详解

学科:数学专题:相似三角形有关的综合问题 1重难点易错点解析题面:如图,四边形ABCD是菱形,∠A=60°,直线EF经过点C,分别交AB、AD的延长线于E、F两点,连接ED、FB相交于点H.(1)找出图中与△BEC相似的三角形,并选一对给予证明;(2)如果菱形的边长是3,DF=2,求BE的长.金题精讲题面:如图,点D在△ABC的边BC上,DC=AC=BD,∠ACB的平分线CF交AD于F,点E是AB 的中点,连接EF.(1)求证:△AEF∽△ABD.(2)若△AEF的面积为1,求△ABC的面积.满分冲刺题面:如图,Rt△ABC中,∠BCA=90°,AC=BC,点D是BC的中点,点F在线段AD上,DF=CD,BF交CA于E点,过点A作DA的垂线交CF的延长线于点G,下列结论:①CF2=EF?BF;②AG=2DC;③AE=EF;④AF?EC=EF?EB.其中正确的结论有.课后练习详解重难点易错点解析答案:(1)△BEC ∽△AEF ;(2)BE =4.5.详解:(1)△BEC ∽△DCF ;△BEC ∽△AEF ,∵四边形ABCD 是菱形,∴BC ∥AF ,∴△BEC ∽△AEF ;(2)∵四边形ABCD 是菱形,∴BC ∥AD ,∴△BCE ∽△AFE ,∴=BEBC AE AF,即3=35BE BE ,即BE =4.5.金题精讲答案:(1)△AEF ∽△ABD ;(2)8.详解:(1)证明:∵DC =AC ,CF 是∠ACB 的平分线,∴AF =DF ,∵点E 是AB 的中点,即AE =BE ,∴EF 是△ABD 的中位线,∴EF ∥BD ,∴△AEF ∽△ABD ;(2)∵△AEF ∽△ABD ,∴2=AEF ABD S AE S AB,∵AE =12AB ,S △AEF =1,∴S △ABD =4,∵BD =CD ,∴S △ABC =2S △ABD =8.满分冲刺答案:①②④.。
2020—2021年最新华东师大版九年级数学下册《圆周角与相似三角形》专题练习及答案.docx

(新课标)华东师大版九年级下册第27章圆圆周角与相似三角形专题练习题1. 如图,在⊙A中,点B是弦DC,EF延长线的交点.求证:BC·BD=BF·BE.2.如图,BC是⊙A的直径,△DBE的各个顶点在⊙A上,BF⊥DE于点F.求证:BD·BE=BC·BF3.如图,在⊙A中,BC是⊙A的直径,点D在⊙A上,DE⊥BC于点E.求证:DE2=CE·BE.4.如图,△BCD的各个顶点都在⊙A上,BC=BD,弦BE交CD于点F.求证:BD2=BE·BF.5.如图,△BCD的各个顶点都在⊙A上,△BCD的角平分线BF交CD于点E,交⊙A于点F,连接CF.求证:BE2=BC·BD-EC·ED.答案:1.解:连结CE ,DF ,则∠E =∠D , 又∵∠B =∠B ,∴△CBE ∽△FBD , ∴CB BE =FB BD ,∴BC ·BD =BF·BE 2.解:连结CD ,则∠BDC =∠BFE =90°, ∠C =∠E ,∴△BDC ∽△BFE , ∴BD BF =BC BE ,∴BD ·BE =BC·BF 3.解:如图,连结BD ,CD ,则∠BDC =90° ∴∠C +∠B =90°,∵∠BED =∠DEC =90° ∴∠C +∠CDE =90°,∴∠B =∠CDE∴△BED ∽△DEC ,∴DE BE =CE DE ,∴DE 2=CE·BE4.解:连结ED ,则∠C =∠E ,∵BC =BD ,∴∠BCD =∠BDC , ∴∠E =∠BDC ,又∵∠EBD =∠DBF ,∴△BED ∽△BDF ,∴BD BF =BE BD ,∴BD 2=BE·BF5.解:∵∠F =∠D ,∠FBC =∠DBE ,∴△BCF ∽△BED ,∴BF BD =BC BE, ∴BC ·BD =BE·BF =BE·(BE +EF ) =BE 2+BE·EF ,∵∠F =∠D , ∠FCE =∠DBE ,∴△CFE ∽△BDE ∴EC EB =EF ED,∴BE ·EF =EC·ED , ∴BC ·BD =BE 2+BE·EF =BE 2+EC·ED ∴BE 2=BC·BD -EC·ED。
华师大版九年级数学下册课后练习:解直角三角形 课后练习二及详解(1)
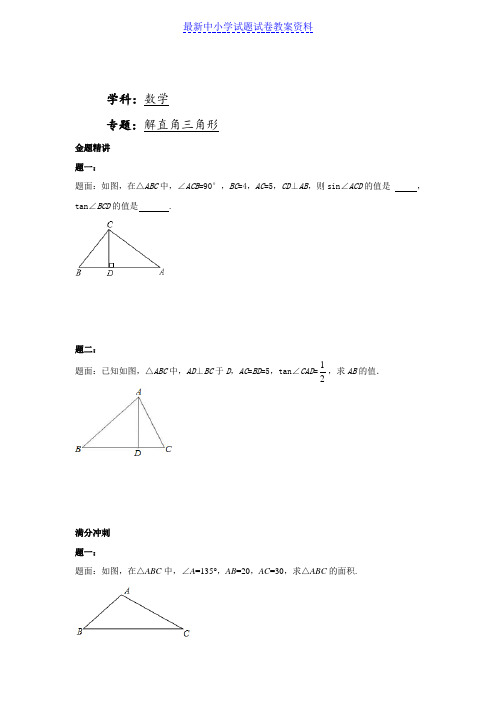
学科:数学专题:解直角三角形金题精讲题一:题面:如图,在△ABC中,∠ACB=90°,BC=4,AC=5,CD⊥AB,则sin∠ACD的值是,tan∠BCD的值是 .题二:题面:已知如图,△ABC中,AD⊥BC于D,AC=BD=5,tan∠CAD=12,求AB的值.满分冲刺题一:题面:如图,在△ABC中,∠A=135°,AB=20,AC=30,求△ABC的面积.题二:题面:如图,已知AD是Rt△ABC斜边BC上的高,且AB=6,BC=10.则AC= ,sin a= .题三:2,求AB的长.题面:如图,在△ABC中,∠A=30°,∠B=45°,AC=3课后练习详解金题精讲题一:答案:41;45详解:∵△ABC 中,∠ACB =90°,BC =4,AC =5,CD ⊥AB ,∴AB在Rt△ABC 与Rt△ACD 中,∠A +∠B =90°,∠A +∠ACD =90°,∠ADC =∠ACB =90°. ∴∠B =∠ACD .Rt△ABC ∽Rt△ACD ,∠BCD =∠A .故sin∠ACD =sin∠B =AC AB , tan∠BCD =tan∠A =BC AC =45. 题二:答案: 详解:∵AD ⊥BC ,△ADC 为Rt△,又在Rt△ADC 中tan ∠CAD =1=2CD AD , ∴设CD =x ,AD =2x , 由:CD 2+AD 2=AC 2得 x 2+4x 2=25,∵x >0∴x ∴在Rt△ADB 中AB =,即AB 长为满分冲刺题一:答案:详解:过点B 作BE ⊥AC ,∵∠A =135°,∴∠BAE =180°-∠A =180°-135°=45°,∴∠ABE =90°-∠BAE =90°-45°=45°,在Rt △BAE 中,∵AB =20,∴BE =,∵AC =30,∴S △ABC =12AC •BE =12×30×=题二:答案:8;45.详解:在Rt△ABC 中,AC =8;AB 2=BD •BC ,∴BD =3.6,CD =6.4,在Rt△ACD 中,sin a =CD AC =45. 题三:答案:详解:过点C 作CD ⊥AB 于D ,在Rt △ACD 中,∠A =30°,AC ==. ∴CD=AC×sin A=0.5,AD=AC×cos A=32在Rt△BCD中,∠B=45°,则BD=CD AB=AD+BD。
九年级下数学相似三角形经典习题(含答案)

九年级下数学相似三角形经典习题例1 从下面这些三角形中,选出相似的三角形.例2 已知:如图,ABCD 中,2:1:=EB AE ,求A E F ∆与CDF ∆的周长的比,如果2cm 6=∆AEF S ,求C D F S ∆. 例3 如图,已知ABD ∆∽ACE ∆,求证:ABC ∆∽ADE ∆.例4 下列命题中哪些是正确的,哪些是错误的?(1)所有的直角三角形都相似. (2)所有的等腰三角形都相似.(3)所有的等腰直角三角形都相似. (4)所有的等边三角形都相似.例5 如图,D 点是ABC ∆的边AC 上的一点,过D 点画线段DE ,使点E 在ABC ∆的边上,并且点D 、点E 和ABC ∆的一个顶点组成的小三角形与ABC ∆相似.尽可能多地画出满足条件的图形,并说明线段DE 的画法. 例6 如图,一人拿着一支刻有厘米分画的小尺,站在距电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上约12个分画恰好遮住电线杆,已知手臂长约60厘米,求电线杆的高.例7 如图,小明为了测量一高楼MN 的高,在离N 点20m 的A 处放了一个平面镜,小明沿NA 后退到C 点,正好从镜中看到楼顶M 点,若5.1=AC m ,小明的眼睛离地面的高度为1.6m ,请你帮助小明计算一下楼房的高度(精确到0.1m ).例8 格点图中的两个三角形是否是相似三角形,说明理由.例9 根据下列各组条件,判定ABC ∆和C B A '''∆是否相似,并说明理由:(1),cm 4,cm 5.2,cm 5.3===CA BC AB cm 28,cm 5.17,cm 5.24=''=''=''A C C B B A .(2)︒='∠︒='∠︒=∠︒=∠35,44,104,35A C B A .(3)︒='∠=''=''︒=∠==48,3.1,5.1,48,6.2,3B C B B A B BC AB .例10 如图,下列每个图形中,存不存在相似的三角形,如果存在,把它们用字母表示出来,并简要说明识别的根据.例11 已知:如图,在ABC ∆中,BD A AC AB ,36,︒=∠=是角平分线,试利用三角形相似的关系说明AC DC AD ⋅=2.例12 已知ABC ∆的三边长分别为5、12、13,与其相似的C B A '''∆的最大边长为26,求C B A '''∆的面积S . 例13 在一次数学活动课上,老师让同学们到操场上测量旗杆的高度,然后回来交流各自的测量方法.小芳的测量方法是:拿一根高3.5米的竹竿直立在离旗杆27米的C 处(如图),然后沿BC 方向走到D 处,这时目测旗杆顶部A 与竹竿顶部E 恰好在同一直线上,又测得C 、D 两点的距离为3米,小芳的目高为1.5米,这样便可知道旗杆的高.你认为这种测量方法是否可行?请说明理由.例14.如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点A ,再在河的这一边选点B 和C ,使BC AB ⊥,然后再选点E ,使BC EC ⊥,确定BC 与AE 的交点为D ,测得120=BD 米,60=DC 米,50=EC 米,你能求出两岸之间AB 的大致距离吗?例15.如图,为了求出海岛上的山峰AB 的高度,在D 和F 处树立标杆DC 和FE ,标杆的高都是3丈,相隔1000步(1步等于5尺),并且AB 、CD 和EF 在同一平面内,从标杆DC 退后123步的G 处,可看到山峰A 和标杆顶端C 在一直线上,从标杆FE 退后127步的H 处,可看到山峰A 和标杆顶端E 在一直线上.求山峰的高度AB 及它和标杆CD 的水平距离BD 各是多少?(古代问题)例16 如图,已知△ABC 的边AB =32,AC =2,BC 边上的高AD =3.(1)求BC 的长;(2)如果有一个正方形的边在AB 上,另外两个顶点分别在AC ,BC 上,求这个正方形的面积.相似三角形经典习题答案例1. 解 ①、⑤、⑥相似,②、⑦相似,③、④、⑧相似例2. 解 ABCD 是平行四边形,∴CD AB CD AB =,//,∴AEF ∆∽CDF ∆, 又2:1:=EB AE ,∴3:1:=CD AE ,∴AEF ∆与CDF ∆的周长的比是1:3. 又)cm (6,)31(22==∆∆∆AEF CDF AEF S S S ,∴)cm (542=∆CDF S . 例3 分析 由于ABD ∆∽ACE ∆,则C A E B A D ∠=∠,因此DAE BAC ∠=∠,如果再进一步证明AE CA AD BA =,则问题得证.证明 ∵ABD ∆∽ACE ∆,∴CAE BAD ∠=∠.又DAC BAD BAC ∠+∠=∠ ,∴CAE DAC DAE ∠+∠=∠,∴DAE BAC ∠=∠.∵ABD ∆∽ACE ∆,∴AEAC AD AB =. 在ABC ∆和ADE ∆中,∵AE AC AD AB ADE BAC =∠=∠,,∴ABC ∆∽ADE ∆ 例4.分析 (1)不正确,因为在直角三角形中,两个锐角的大小不确定,因此直角三角形的形状不同.(2)也不正确,等腰三角形的顶角大小不确定,因此等腰三角形的形状也不同.(3)正确.设有等腰直角三角形ABC 和C B A ''',其中︒='∠=∠90C C ,则︒='∠=∠︒='∠=∠45,45B B A A ,设ABC ∆的三边为a 、b 、c ,C B A '''∆的边为c b a '''、、, 则a c b a a c b a '=''='==2,,2,, ∴a a c c b b a a '=''=',,∴ABC ∆∽C B A '''∆. (4)也正确,如ABC ∆与C B A '''∆都是等边三角形,对应角相等,对应边都成比例,因此ABC ∆∽C B A '''∆. 答:(1)、(2)不正确.(3)、(4)正确.例5.解:画法略.例6.分析 本题所叙述的内容可以画出如下图那样的几何图形,即60=DF 厘米6.0=米,12=GF 厘米12.0=米,30=CE 米,求BC .由于ADF ∆∽ACAF EC DF AEC =∆,,又ACF ∆∽ABC ∆,∴BC GF EC DF =,从而可以求出BC 的长.解 EC DF EC AE //,⊥ ,∴EAC DAF AEC ADF ∠=∠∠=∠,,∴ADF ∆∽AEC ∆.∴ACAF EC DF =. 又EC BC EC GF ⊥⊥,,∴ABC AGF ACB AFG BC GF ∠=∠∠=∠,,//, ∴AGF ∆∽ABC ∆,∴BC GF AC AF =,∴BCGF EC DF =. 又60=DF 厘米6.0=米,12=GF 厘米12.0=米,30=EC 米,∴6=BC 米.即电线杆的高为6米.例7.分析 根据物理学定律:光线的入射角等于反射角,这样,BCA ∆与MNA ∆的相似关系就明确了. 解 因为MAN BAC AN MN CA BC ∠=∠⊥⊥,,,所以BCA ∆∽MNA ∆.所以AC AN BC MN ::=,即5.1:206.1:=MN .所以3.215.1206.1≈÷⨯=MN (m ). 说明 这是一个实际应用问题,方法看似简单,其实很巧妙,省却了使用仪器测量的麻烦. 例8.分析 这两个图如果不是画在格点中,那是无法判断的.实际上格点无形中给图形增添了条件——长度和角度.解 在格点中BC AB EF DE ⊥⊥,,所以︒=∠=∠90B E ,又4,2,2,1====AB BC DE EF .所以21==BC EF AB DE .所以DEF ∆∽ABC ∆. 说明 遇到格点的题目一定要充分发现其中的各种条件,勿使遗漏.例9.解 (1)因为7128cm 4cm ,7117.5cm 2.5cm ,7124.5cm 3.5cm ==''==''==''A C CA C B BC B A AB ,所以ABC ∆∽C B A '''∆; (2)因为︒=∠-∠-︒=∠41180B A C ,两个三角形中只有A A '∠=∠,另外两个角都不相等,所以ABC ∆与C B A '''∆不相似;(3)因为12,=''='''∠=∠C B BC B A AB B B ,所以ABC ∆相似于C B A '''∆. 例10.解 (1)ADE ∆∽ABC ∆ 两角相等; (2)ADE ∆∽ACB ∆ 两角相等;(3)CDE ∆∽CAB ∆ 两角相等; (4)EAB ∆∽ECD ∆ 两边成比例夹角相等;(5)ABD ∆∽ACB ∆两边成比例夹角相等; (6)ABD ∆∽ACB ∆ 两边成比例夹角相等. 例11.分析 有一个角是65°的等腰三角形,它的底角是72°,而BD 是底角的平分线,∴︒=∠36CBD ,则可推出ABC ∆∽BCD ∆,进而由相似三角形对应边成比例推出线段之间的比例关系. 证明 AC AB A =︒=∠,36 ,∴︒=∠=∠72C ABC .又BD 平分ABC ∠,∴︒=∠=∠36CBD ABD .∴BC BD AD ==,且A B C ∆∽BCD ∆,∴BC CD AB BC ::=,∴CD AB BC ⋅=2,∴CD AC AD ⋅=2. 说明 (1)有两个角对应相等,那么这两个三角形相似,这是判断两个三角形相似最常用的方法,并且根据相等的角的位置,可以确定哪些边是对应边.(2)要说明线段的乘积式cd ab =,或平方式bc a =2,一般都是证明比例式,b d c a =,或c a a b =,再根据比例的基本性质推出乘积式或平方式.例12分析 由ABC ∆的三边长可以判断出ABC ∆为直角三角形,又因为ABC ∆∽C B A '''∆,所以C B A '''∆也是直角三角形,那么由C B A '''∆的最大边长为26,可以求出相似比,从而求出C B A '''∆的两条直角边长,再求得C B A '''∆的面积.解 设ABC ∆的三边依次为,13,12,5===AB AC BC ,则222AC BC AB += ,∴︒=∠90C . 又∵ABC ∆∽C B A '''∆,∴︒=∠='∠90C C .212613==''=''=''B A AB C A AC C B BC , 又12,5==AC BC ,∴24,10=''=''C A C B . ∴12010242121=⨯⨯=''⨯''=C B C A S . 例13.分析 判断方法是否可行,应考虑利用这种方法加之我们现有的知识能否求出旗杆的高.按这种测量方法,过F 作AB FG ⊥于G ,交CE 于H ,可知AGF ∆∽EHF ∆,且GF 、HF 、EH 可求,这样可求得AG ,故旗杆AB 可求.解 这种测量方法可行.理由如下:设旗杆高x AB =.过F 作AB FG ⊥于G ,交CE 于H (如图).所以AGF ∆∽EHF ∆. 因为3,30327,5.1==+==HF GF FD ,所以5.1,25.15.3-==-=x AG EH . 由AGF ∆∽EHF ∆,得HF GF EH AG =,即33025.1=-x ,所以205.1=-x ,解得5.21=x (米) 所以旗杆的高为21.5米.说明 在具体测量时,方法要现实、切实可行.例14. 解:︒=∠=∠∠=∠90,ECD ABC EDC ADB ,∴ABD ∆∽ECD ∆,1006050120,=⨯=⨯==CD EC BD AB CD BD EC AB (米),答:两岸间AB 大致相距100米. 例15. 答案:1506=AB 米,30750=BD 步,(注意:AK FE FH KE AK CD DG KC ⋅=⋅=,.) 例16. 分析:要求BC 的长,需画图来解,因AB 、AC 都大于高AD ,那么有两种情况存在,即点D 在BC 上或点D 在BC 的延长线上,所以求BC 的长时要分两种情况讨论.求正方形的面积,关键是求正方形的边长. 解:(1)如上图,由AD ⊥BC ,由勾股定理得BD =3,DC =1,所以BC =BD +DC =3+1=4. 如下图,同理可求BD =3,DC =1,所以BC =BD -CD =3-1=2.(2)如下图,由题目中的图知BC =4,且162)32(2222=+=+AC AB ,162=BC ,∴222BC AC AB =+.所以△ABC 是直角三角形.由AE G F 是正方形,设G F =x ,则FC =2-x ,∵G F ∥AB ,∴AC FC AB GF =,即2232x x -=. ∴33-=x ,∴3612)33(2-=-=AEGF S 正方形. 如下图,当BC =2,AC =2,△ABC 是等腰三角形,作CP ⊥AB 于P ,∴AP =321=AB , 在Rt △APC 中,由勾股定理得CP =1,∵GH ∥AB ,∴△C GH ∽△CBA ,∵x x x-=132,32132+=x ∴121348156)32132(2-=+=GFEH S 正方形 因此,正方形的面积为3612-或121348156-.。
华师大版九年级数学下册课后练习:相似三角形有关的综合问题1 课后练习二及详解

学科:数学专题:相似三角形有关的综合问题1重难点易错点解析题面:己知在平行四边形ABCD 中,AD =6,点E 在直线AD 上,且DE =3,连接BE 与对角线AC 相交于点M ,则AM MC = .金题精讲题面:如图,△ABC 中,∠ACB =90°,CD 是AB 边上的高,∠CAB 的角平分线分别交BC 、CD 于点E 、F ;过点E 作EG ⊥AB ,垂足为G .(1)求证:CF =CE ;(2)求证:CE :BE =AC :AB ;(3)若AB =10,AC =6,求CF 的长.满分冲刺题面:如图,在△ABC 中,∠ACB =90°,CD 是斜边AB 上的高,ED ⊥DF ,且DE 、DF 分别交AC 、BC 于E 、F .求证:=CF CD AE AD.课后练习详解重难点易错点解析答案:12或32.详解:分两种情况:(1)点E在线段AD上时,△AEM∽△CBM,则1==2 AM AEMC BC;(2)点E在线段AD的延长线上时,△AME∽△CMB,则3==2 AM AEMC BC.金题精讲答案:(1)CF=CE;(2)CE:BE=AC:AB;(3)3.详解:(1)∵AE平分∠CAB,∠ ACB=90°,EG⊥AB∴EG=CE∴△ACE≌△AGE∴∠AEC=∠AEG∵CD⊥AB,EG⊥AB∴CD∥EG∴∠GEF=∠CFE∴∠CEF=∠CFE∴CF=CE(2)证明:∵∠ACB=90°,EG⊥AB,∠B=∠B。
【最新】2019-2020精选华师大版九年级数学下册课后练习:相似三角形的应用 课后练习二及详解

题三:
题面:如图,在Rt△ABC中,∠C=90°,正方形DEFC内接于三角形, AC=1,BC=2,则AF:FC等于 .
课后练习详解
重难点易错点解析
题一:
答案:A.
详解:∵,∴.
又∵EF∥BC,∴△AEF∽△ABC.∴.∴9S△AEF=S△ABC.
又∵S四边形BCFE=8,∴9(S△ABC﹣8)=S△ABC,解得S△ABC=9.故选A.
则CD=DE=EF=CF=x,AF=1x,BD=2x,
∵四边形DEFC是正方形,
∴∠AFE=∠AFE=∠CDE=∠EDB=90°,EF∥BC,
∴∠AEF=∠B,∠AFE=∠EDB,
∴△AFE∽△EDB,
∴,
∴,
解得:x=,
∴CF=,AF=1=,
∴.
【最新】2019-2020精选华师大版九年级数学下册课后练习:相似三角形的应用+课后练习二及详解
专题:相似三角形的应用
重难点易错点解析
题一:
题面:如图,在△ABC中,EF∥BC,,S四边形BCFE=8,则S△ABC=( )
A.9 B.10 C.12 D.13
金题精讲
题面:如图所示,以正方形ABCD的边AB为直径,在正方形内部作半圆,圆心为O,DF切半圆于E,交AB的延长线于点F,BF=4.求证:△EFO∽△AFD,并求的值.
金题精讲
答案:.
详解:易知∠OEF=∠FAD=90°,而∠OFE=∠DFA,
故△EFO∽△AFD,
所以,
而EO=AO=AB=AD,
即.
满分冲刺
题一:
答案:4.2米.
详解:过点D作DE⊥AB于点E,则BE=CD=1.2米,
【解析版】华师大版九年级数学下册课后练习:相似三角形有关的综合问题1+课后练习一及详解

学科:数学专题:相似三角形有关的综合问题1重难点易错点解析题面:如图,四边形ABCD是菱形,∠A=60°,直线EF经过点C,分别交AB、AD的延长线于E、F两点,连接ED、FB相交于点H.(1)找出图中与△BEC相似的三角形,并选一对给予证明;(2)如果菱形的边长是3,DF=2,求BE的长.金题精讲题面:如图,点D在△ABC的边BC上,DC=AC=BD,∠ACB的平分线CF交AD于F,点E是AB 的中点,连接EF.(1)求证:△AEF∽△ABD.(2)若△AEF的面积为1,求△ABC的面积.满分冲刺题面:如图,Rt△ABC中,∠BCA=90°,AC=BC,点D是BC的中点,点F在线段AD上,DF=CD,BF交CA于E点,过点A作DA的垂线交CF的延长线于点G,下列结论:①CF2=EF•BF;②AG=2DC;③AE=EF;④AF•EC=EF•EB.其中正确的结论有.课后练习详解重难点易错点解析答案:(1)△BEC ∽△AEF ;(2)BE =4.5.详解:(1)△BEC ∽△DCF ;△BEC ∽△AEF ,∵四边形ABCD 是菱形,∴BC ∥AF ,∴△BEC ∽△AEF ;(2)∵四边形ABCD 是菱形,∴BC ∥AD ,∴△BCE ∽△AFE , ∴=BE BC AE AF, 即 3=35BE BE +, 即BE =4.5.金题精讲答案:(1)△AEF ∽△ABD ;(2)8.详解:(1)证明:∵DC =AC ,CF 是∠ACB 的平分线,∴AF =DF ,∵点E 是AB 的中点,即AE =BE ,∴EF 是△ABD 的中位线,∴EF ∥BD ,∴△AEF ∽△ABD ;(2)∵△AEF ∽△ABD , ∴2=AEF ABD S AE S AB ⎛⎫ ⎪⎝⎭, ∵AE =12AB ,S △AEF =1, ∴S △ABD =4,∵BD =CD ,∴S △ABC =2S △ABD =8.满分冲刺答案:①②④.详解:∵DF =CD ,∴∠DCF =∠DFC ,∵AC =BC ,点D 是BC 的中点,∴DF =DB =DC ,∴∠DBF =∠DFB ,又∵∠DBF +∠DFB +∠DFC +∠DCF =180°,∴∠BFC =12×180°=90°, ∴CF ⊥BE ,∴Rt △BCF ∽Rt △CEF , ∴=BF CF CF EF, ∴CF 2=EF •BF ,故①正确;∵AG ⊥AD ,∴∠G +∠AFG =90°,又∵∠ACG +∠DCF =90°,∠DCF =∠DFC =∠AFG , ∴∠G =∠ACG ,∴AG =AC ,∵AC =BC ,∴AG =BC ,又∵∠CBE =∠ACG ,∴∠CBE =∠G ,在△BCE 和△AGF 中,∵∠GAF =∠BCE =90°,∠CBE =∠G , AG =BC ,∴△BCE ≌△AGF (AAS ),∴AG =BC ,∵点D 是BC 的中点,∴BC =2DC ,∴AG =2DC ,故②正确;根据角的互余关系,∠EAF +∠ADC =90°,∠AFE +∠DFC =90°, ∵tan ∠ADC =2,∴∠ADC ≠60°,∵∠DCF =∠DFC ,∴∠FDC ≠∠DFC ,∴∠EAF ≠∠EFA ,∴AE ≠EF ,故③错误;∵∠ACB =90°,CF ⊥BE ,∴△CEF ∽△BCE , ∴=EF EC EC EB, ∴EC 2=EF •EB ,∵△BCE ≌△AGF (已证),∴AF =EC ,∴AF •EC =EF •EB ,故④正确;所以,正确的结论有①②④.。
【解析版】华师大版九年级数学下册课后练习:相似三角形的性质+课后练习一及详解

学科:数学专题:相似三角形的性质重难点易错点解析题一:题面:两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF 的位置,AB=12,DH=3,平移距离为4,求阴影部分的面积.金题精讲题面:如图△ABC中,AD为△ABC的角平分线,求证:AB•DC=AC•BD.满分冲刺题一:题面:如图,Rt△ABC中,有三个正方形,DF=9cm,GK=6cm,则第三个正方形的边长PQ= .题二:题面:已知AB⊥BC于B,CD⊥BC于C,AB=4,CD=6,BC=14,P为BC上一点,试问BP= _________时,△ABP与△PCD相似.题三:题面:如图1,在△ABC中,D、E、F分别为三边的中点,G点在边AB上,△BDG与四边形ACDG的周长相等,设BC=a,AC=b,AB=c.(1)求线段BG的长;(2)求证:DG平分∠EDF;(3)连接CG,如图2,若△BDG与△DFG相似,求证:BG⊥CG.课后练习详解重难点易错点解析题一:答案:42.详解:∵AB=12,∴DE=12,又∵DH=3,∴HE=12-3=9,∵HE∥AB,∴HE EC AB BC=,即9124ECEC=+,故EC=12,∴S△DEF=12DE•EF=12×12×(4+12)=96;S△HEC=12HE•EC=12×9×12=54;∴S阴影部分DHCF=96-54=42.金题精讲答案:AB•DC=AC•BD.详解:过C作CE∥AB交AD延长线于E,∴△ABD∽△ECD,∴AB BD CE DC=,∵AD是△ABC的角平分线,∴∠1=∠2,∵CE∥AB,∴∠1=∠E,∴∠2=∠E,∴AC=CE,∴AB BD AC DC=,∴AB•DC=AC•BD.满分冲刺题一:答案:4cm.详解:由已知可得PK∥EF∥AC,∴△QPK∽△KGF∽△FDA,∴由相似三角形的性质和正方形的性质可得:QP KGPK GF=,又∵PK=KG-QP,GF=DF-GK,DF=9cm,GK=6cm,∴QP KG PK GF=即6696QPQP=--,解得QP=4cm.题二:答案:2或12或5.6.详解:∵AB⊥DB,CD⊥DB,∴∠C=∠B=90°,设BP=x,当PB:DC=AB:PC时,△PAB∽△DPC,∴4614xx=-,解得BP=2或12;当PB:PC=AB:DC时,△PAB∽△PDC,∴4 146xx=-,解得x=5.6;解得BP=2或12或5.6.题三:答案:22BG AB ACb c=++=;DG 平分∠EDF ;BG ⊥CG .详解:(1)∵D 、E 、F 分别是△ABC 三边中点,∴DE =12AB ,DF =12AC . 又∵△BDG 与四边形ACDG 周长相等,即BD +DG +BG =AC +CD +DG +AG , ∴BG =AC +AG . ∵BG =AB -AG ,∴22AB AC b c BG ++==. (2)证明:2b cBG +=,222b c cbFG BG BF +=-=-=,∴FG =DF .∴∠FDG =∠FGD .又∵DE ∥AB ,∴∠EDG =∠FGD .∴∠FDG =∠EDG .∴DG 平分∠EDF .(3)在△DFG 中,∠FDG =∠FGD ,∴△DFG 是等腰三角形. ∵△BDG 与△DFG 相似,∴△BDG 是等腰三角形.∴∠B =∠BGD .∴BD =DG .∴CD = BD =DG .∴B 、G 、C 三点共圆.∴∠BGC =90°.∴BG ⊥CG .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学科:数学
专题:相似三角形的应用
重难点易错点解析
题一:
题面:如图,在△ABC中,EF∥BC,
1
2
AE
EB
,S四边形BCFE=8,则S△ABC=()
A.9 B.10 C.12 D.13
金题精讲
题面:如图所示,以正方形ABCD的边AB为直径,在正方形内部作半圆,圆心为O,DF切半
圆于E,交AB的延长线于点F,BF=4.求证:△EFO∽△AFD,并求FE
FA
的值.
满分冲刺
题一:
题面:小明想知道学校旗杆的高,他在某一时刻测得直立的标杆高1米时影长0.9米,此时他测旗杆影长时,因为旗杆靠近建筑物,影子不全落在地面上,有一部分影子在墙上,他测得落在地面上的影长BC为2.7米,又测得墙上影高CD为1.2米,请你求旗杆AB的高度.
题二:
题面:如图,在平面直角坐标系中,以原点为中心,将△ABO 扩大到原来的2倍,得到△A ′B ′O .若点A 的坐标是(1,2),则点A ′的坐标是( )
A.(2,4)
B.(1-,2-)
C.(2-,4-)
D.(2-,1-)
题三:
题面:如图,在Rt △ABC 中,∠C =90°,正方形DEFC 内接于三角形, AC =1,BC =2,则AF :FC 等于 .
课后练习详解
重难点易错点解析
题一:
答案:A . 详解:∵
12AE EB =,∴11123
AE AE AB AE EB ===++. 又∵EF ∥BC ,∴△AEF ∽△ABC .∴2S 11()S 39AEF ABC ∆∆==.∴9S △AEF =S △ABC . 又∵S 四边形BCFE =8,∴9(S △ABC ﹣8)=S △ABC ,解得S △ABC =9.故选A .
金题精讲 答案:12
FE FA =. 详解:易知∠OEF =∠FAD =90°,而∠OFE =∠DFA ,
故△EFO ∽△AFD , 所以
EF EO AF AD
=, 而EO =AO =12AB =12
AD , 即12FE FA =.
满分冲刺
题一:
答案:4.2米.
详解:过点D 作DE ⊥AB 于点E ,则BE =CD =1.2米,
∵他在某一时刻测得直立的标杆高1米时影长0.9米, ∴
10.9
AE ED =, 即12.70.9AE =,解得AE =3米, ∴AB =AE +BE =3+1.2=4.2米.
答:旗杆的高度是4.2米.
题二:
答案:C.
详解:根据以原点O为中心,将△ABO扩大到原来的2倍,即可得出对应点的坐标应乘以-2,即可得出点A′的坐标:
∵点A的坐标是(1,2),∴点A′的坐标是(-2,-4),故选C.
题三:
答案:
1
2 AF
FC
=.
详解:在Rt△ACB中,AC=1,BC=2,由勾股定理得:AB5
设正方形CFED的边长是x,
则CD=DE=EF=CF=x,AF=1-x,BD=2-x,
∵四边形DEFC是正方形,
∴∠AFE=∠AFE=∠CDE=∠EDB=90°,EF∥BC,
∴∠AEF=∠B,∠AFE=∠EDB,
∴△AFE∽△EDB,
∴AF EF DE BD
=,
∴1
2
x x
x x -
=
-
,
解得:x=2
3
,
∴CF=2
3
,AF=1-
2
3
=
1
3
,
∴
1
2 AF
FC
=.。
