2019-2020年高考数学一轮复习解三角形教案理
2019版高考数学一轮复习第3章三角函数解三角形3.5两角和与差的正弦余弦与正切公式课件理

动态演示
结合动画演示,直观地呈现三角函数的计算过 程。
总结
1 重点内容概括
回顾本章重点内容,检 查概念与公式的掌握程 度。
2 解题方法总结
总结解题技巧和常用公 式,为下一步的练习做 好准备。
3 知识点巩固提示
练习做题、做笔记,多 次温习概念与公式,通 过追溯源头的方式加深 理解。
正弦、余弦、正切公式
正弦公式
三角形任意两边的比值相等,即a/sinA=b/sinB=c/sinC。
余弦公式
根据勾股定理和余弦函数,得到c²=a²+b²-2ab*cosC。
正切公式
将正弦公式与余弦公式相除得到tanA=a/b*tanC-b/a。
解题技巧
1
使用两角和/差公式
判断题中是否存在三角形两个角之和/
合理运用公式
2
差,使用对应的公式。
根据题目中所给的信息,选择合适的
公式,并化简,变形运用。
3注意化简Fra bibliotek将多个三角函数合并为一个统一的三 角函数,然后进行化简,避免表达式 过于复杂。
练习题
求第三个角度
已知三角形内两角的度数,求第三个角的度数。
求解三角形的边长
已知部分边长与角度,求解三角形剩余边长度。
复杂问题
数学一轮复习:三角函数 解三角形
本课件旨在帮助你理解三角形的两角和与差,掌握正弦、余弦、正切公式, 并运用解题技巧快速解决问题。
三角形的两角和与差
两角和公式
两个角的和为第三个角的补角,即A+B=180°-C, 其中C为第三个角的度数。
两角差公式
两个角的差的余角等于这两个角的余角之积,即 A-B=C-》sinA*sinB=sinC*sin(A+B)。
高考数学一轮复习 第三章 三角函数、解三角形 第一节 任意角、弧度制及任意角的三角函数学案 文(含解

第一节 任意角、弧度制及任意角的三角函数2019考纲考题考情1.角的有关概念(1)从运动的角度看,角可分为正角、负角和零角。
(2)从终边位置来看,角可分为象限角与轴线角。
(3)若β与α是终边相同的角,则β用α表示为β=2k π+α,k ∈Z 。
2.弧度与角度的互化 (1)1弧度的角长度等于半径长的弧所对的圆心角叫做1弧度的角。
(2)角α的弧度数如果半径为r 的圆的圆心角α所对弧的长为l ,那么角α的弧度数的绝对值是|α|=l r。
(3)角度与弧度的换算①1°=π180rad ;②1 rad = ⎛⎪⎫180π°。
(4)弧长、扇形面积的公式设扇形的弧长为l ,圆心角大小为α(rad),半径为r ,则l =|α|r ,扇形的面积为S =12lr =12|α|·r 2。
3.任意角的三角函数(1)定义:设α是一个任意角,它的终边与单位圆交于点P (x ,y ),那么sin α=y ,cos α=x ,tan α=yx(x ≠0)。
(2)几何表示:三角函数线可以看作是三角函数的几何表示。
正弦线的起点都在x 轴上,余弦线的起点都是原点,正切线的起点都是点(1,0)。
如图中有向线段MP ,OM ,AT 分别叫做角α的正弦线,余弦线和正切线。
1.区分两个概念(1)第一象限角未必是锐角,但锐角一定是第一象限角。
(2)不相等的角未必终边不相同,终边相同的角也未必相等。
2.一个口诀三角函数值在各象限的符号:一全正、二正弦、三正切、四余弦。
3.三角函数定义的推广设点P (x ,y )是角α终边上任意一点且不与原点重合,r =|OP |,则sin α=y r,cos α=x r ,tan α=y x。
一、走进教材1.(必修4P 10A 组T 7改编)角-225°=________弧度,这个角在第________象限。
答案 -5π4二2.(必修4P 15练习T 2改编)设角θ的终边经过点P (4,-3),那么2cos θ-sin θ=________。
高考数学:解三角形(复习学案)
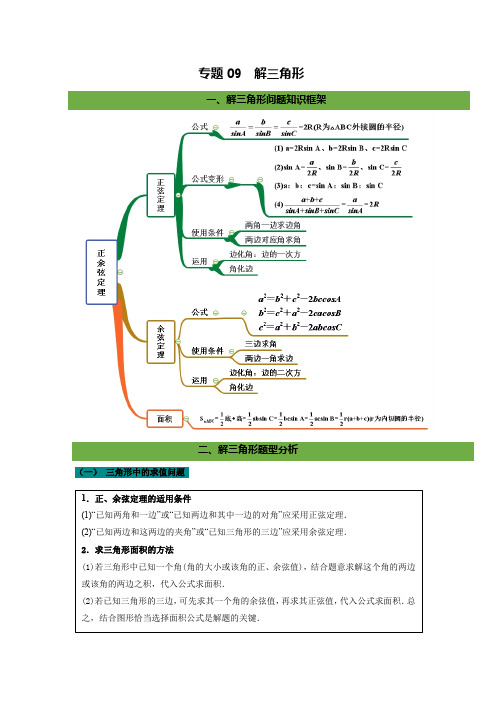
专题09 解三角形(一) 三角形中的求值问题1.例题【例1】设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若a =2,c =23,cos A =32,且b <c ,则b =( )A . 3B .2C .2 2D .3【例2】在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,若1a =,cos )cos 0A C C b A ++=,则角A =( )A .23π B .3π C .6π D .56π 【例3】在ABC ∆中,角A ,B ,C 的对边分别是a ,b ,c ,4a =,b =cos (2)cos c B a b C =-,则ABC ∆的面积为______.【例4】(2017·全国高考真题(理))△ABC 的内角、、A B C 的对边分别为a b c 、、, 已知△ABC 的面积为23sin a A.(1)求sin sin B C ;(2)若6cos cos 1,3,B C a ==求△ABC 的周长.【例5】如图,在△ABC 中,∠B =π3,AB =8,点D 在BC 边上,且CD =2,cos ∠ADC =17.(1)求sin ∠BAD ; (2)求BD ,AC 的长.2.巩固提升综合练习【练习1】(2019·全国高考真题)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知a sin A -b sin B =4c sin C ,cos A =-14,则bc =( )A .6B .5C .4D .3【练习2】(2018·全国高考真题)△ABC 的内角A , B , C 的对边分别为a , b , c ,已知bsinC +csinB =4asinBsinC ,b 2+c 2−a 2=8,则△ABC 的面积为________. 【练习3】 在ABC ∆中,已知AB 边上的中线1CM =,且1tan A ,1tan C ,1tan B成等差数列,则AB 的长为________.【练习4】在△ABC 中,已知AB =2,AC =5,tan ∠BAC =-3,则BC 边上的高等于( ) A .1 B .2 C . 3 D .2【练习5】已知圆内接四边形ABCD 的边长AB =2,BC =6,CD =DA =4,求四边形ABCD 的面积S .【练习6】 △ABC 的内角A ,B ,C 的对边分别为a ,b ,c 已知c cos B =(3a -b )cos C . (1)求sin C 的值;(2)若c =26,b -a =2,求△ABC 的面积.(二)三角形中的最值或范围问题1.例题【例1】在△ABC中,已知c=2,若sin2A+sin2B-sin A sin B=sin2C,则a+b的取值范围为________.【例2】已知在锐角ABC∆中,角A,B,C的对边分别为a,b,c,若2cos cosb Cc B=,则111tan tan tanA B C++的最小值为()A B C D.【例3】已知△ABC的外接圆半径为R,角A,B,C所对的边分别为a,b,c,若a sin B cos C +32c sin C=2R,则△ABC面积的最大值为( )A.25B.45C.255D.125【例4】在ABC∆中,角A,B,C的对边分别为a,b,c,且cos Ccos cos cos2ab Ac A B+=,ABC∆,则ABC∆周长的最小值为______.2.巩固提升综合练习【练习1】 设锐角三角形ABC 的内角,,A B C 所对的边分别为,,a b c ,若2,2a B A ==,则b 的取值范围为( )A .(0,4)B .(2,C .D .4)【练习2】 在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若bc =1,b +2c cos A =0,则当角B 取得最大值时,△ABC 的周长为( ) A .2+3 B .2+2 C .3D .3+2【练习3】已知ABC ∆1,且满足431tan tan A B+=,则边AC 的最小值为_______.【练习4】在ABC ∆中,23BAC π∠=,已知BC 边上的中线3AD =,则ABC ∆面积的最大值为__________.(三)解三角形的实际应用必备知识:实际测量中的有关名称、术语南偏西60°指以正南方向为始边,转向目标方向线形成的角1.例题【例1】在海岸A处,发现北偏东45°方向,距离A处(3-1)n mile的B处有一艘走私船,在A处北偏西75°的方向,距离A 2 n mile的C处的缉私船奉命以10 3 n mile的速度追截走私船.此时,走私船正以10 n mile/h的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?【例2】如图,A,B两点在河的同侧,且A,B两点均不可到达,测出A,B的距离,测量者可以在河岸边选定两点C,D,测得CD=a,同时在C,D两点分别测得∠BCA=α,∠ACD=β,∠CDB=γ,∠BDA=δ.在△ADC和△BDC中,由正弦定理分别计算出AC和BC,再在△ABC中,应用余弦定理计算出AB.若测得CD=32km,∠ADB=∠CDB=30°,∠ACD=60°,∠ACB=45°,求A,B两点间的距离.【例3】某人在点C测得塔顶A在南偏西80°,仰角为45°,此人沿南偏东40°方向前进100米到D,测得塔顶A的仰角为30°,则塔高为____________米.2.巩固提升综合练习【练习1】甲船在A处,乙船在甲船正南方向距甲船20海里的B处,乙船以每小时10海里的速度向正北方向行驶,而甲船同时以每小时8海里的速度由A处向北偏西60°方向行驶,问经过多少小时后,甲、乙两船相距最近?【练习2】如图,一艘船自西向东匀速航行,上午10时到达一座灯塔P 的南偏西75°距塔68海里的M 处,下午2时到达这座灯塔的东南方向的N 处,则这艘船航行的速度为( )A.1762海里/时B .346海里/时 C.1722海里/时D .342海里/时【练习3】某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:A 、B 、C 三地位于同一水平面上,在C 处进行该仪器的垂直弹射,观测点A 、B 两地相距100米,∠BAC =60°,在A 地听到弹射声音的时间比在B 地晚217秒.在A 地测得该仪器弹至最高点H 时的仰角为30°,求该仪器的垂直弹射高度CH .(声音的传播速度为340米/秒)1.在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若a ,b ,c 成等比数列,且a 2=c 2+ac -bc ,则cb sin B =( )A .32B .233C .33D .32.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,a =3,c =23,b sin A =a cos ⎪⎭⎫⎝⎛+6πB 则b =( ) A .1 B.2 C.3D.53.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若a =2,c =32,tan B =2tan A ,则△ABC 的面积为( ) A .2 B .3 C .32D .423.如图,在△ABC 中,∠C =π3,BC =4,点D 在边AC 上,AD =DB ,DE ⊥AB ,E 为垂足.若DE =22,则cos A 等于( ) A .223B .24C .64D .634.在锐角三角形ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若B =2A ,则2ba的取值范围是( ) A .(2,2) B .(2,6) C .(2,3)D .(6,4)5.在ΔABC 中,角A 、B 、C 所对的边分别为a ,b ,c ,a =2,B =45°,若三角形有两解,则b 的取值范围是_______.6.已知a ,b ,c 是△ABC 中角A ,B ,C 的对边,a =4,b ∈(4,6),sin 2A =sin C ,则c 的取值范围为________.7.设△ABC 的内角A ,B ,C 的对边a ,b ,c 成等比数列,cos(A -C )-cos B =12,延长BC至点D ,若BD =2,则△ACD 面积的最大值为________.8.(2019·高考全国卷Ⅱ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若b =6,a =2c ,B =π3,则△ABC 的面积为________. 9.若满足3ABC π∠=, AC =3, ,BC m ABC =恰有一解,则实数m 的取值范围是______.10.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,外接圆的半径为1,且tan A tan B =2c -bb ,则△ABC 面积的最大值为________.11.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且a 2+c 2-b 2=ab cos A +a 2cos B . (1)求角B ;(2)若b =27,tan C =32,求△ABC 的面积.12.已知ABC ∆中,角A B C 、、的对边分别为a b c ,,,若cos sin a b C c B =+(Ⅰ)求B ;(Ⅰ)若2b = ,求ABC ∆面积的最大值。
2020版高考数学一轮总复习课件5.3 正弦、余弦定理及解三角形

2
;sin
A
2
B
=cos
C 2
;cos
A
2
B
=sin
C 2
.
2.三角形形状的判断方法
要判断三角形的形状,应围绕三角形的边角关系进行思考,依据已知条
件中的边角关系判断时,主要有以下两种途径:
(1)化角为边:利用正弦、余弦定理把已知条件转化为只含边的关系,通
过因式分解、配方等得出边的相应关系,从而判断三角形的形状.
ABC的外接圆半径为R.
(1)S= 1 ah(h为BC边上的高);
2
(2)S= 1 absin C= 1 acsin B= 1 bcsin A;
2
2
2
(3)S=2R2sin Asin Bsin C;
(4)S= abc ;
4R
(5)S=
p(
p
a)(
p
b)(
p
c)
p
1 2
(a
b
c)
.
考向基础 1.距离的测量
数学(浙江专用)
5.3 正弦、余弦定理及解三角形
考向基础 1.正、余弦定理
考点清单
考点一 正弦、余弦定理
2.解斜三角形的类型 (1)已知两角及一边,用正弦定理,有解时,只有一解. (2)已知两边及其中一边的对角,用正弦定理,有解时可分为几种情况.在 △ABC中,已知a、b和角A,解的情况如下:
55
∵B=2C,∴cos B=cos 2C=2cos2C-1=2× 4 -1= 3 ,
55
∴sin B= 4 .
5
∵A+B+C=π,∴sin A=sin(B+C)=sin Bcos C+cos Bsin C= 4 × 2 5 + 3× 5 =
高考数学一轮复习第三章三角函数解三角形考前增分微课2解三角形的综合应用课件理新人教A版 (2)

第六节 解三角形2019考纲考题考情1.正弦定理asin A=b sin B =csin C=2R 其中2R 为△ABC 外接圆直径。
变式:a =2R sin A ,b =2R sin B ,c =2R sin C 。
a ∶b ∶c =sin A ∶sin B ∶sin C 。
2.余弦定理a 2=b 2+c 2-2bc cos A ;b 2=a 2+c 2-2ac cos B ; c 2=a 2+b 2-2ab cos C 。
变式:cos A =b 2+c 2-a 22bc ;cos B =a 2+c 2-b 22ac ;cos C =a 2+b 2-c 22ab。
sin 2A =sin 2B +sin 2C -2sin B sin C cos A 。
3.解三角形(1)已知三边a,b ,c 。
运用余弦定理可求三角A ,B ,C 。
(2)已知两边a ,b 及夹角C 。
运用余弦定理可求第三边c 。
(3)已知两边a ,b 及一边对角A 。
先用正弦定理,求sin B ,sin B =b sin Aa。
①A 为锐角时,若a <b sin A ,无解;若a =b sin A ,一解;若b sin A <a <b ,两解;若a ≥b ,一解。
②A 为直角或钝角时,若a ≤b ,无解;若a >b ,一解。
(4)已知一边a 及两角A ,B (或B ,C )用正弦定理,先求出一边,后求另一边。
4.三角形常用面积公式(1)S =12a ·h a (h a 表示a 边上的高)。
(2)S =12ab sin C =12ac sin B =12bc sin A =abc 4R 。
(3)S =12r (a +b +c )(r 为内切圆半径)。
在△ABC 中,常有以下结论: 1.∠A +∠B +∠C =π。
2.任意两边之和大于第三边,任意两边之差小于第三边。
3.sin(A +B )=sin C ;cos(A +B )=-cos C ;tan(A +B )=-tan C ;sin A +B2=cos C 2;cos A +B 2=sin C2。
高考数学一轮复习 第3章 三角函数、解三角形 第2讲 同角三角函数的基本关系及诱导公式创新教学案(含

第2讲 同角三角函数的基本关系及诱导公式[考纲解读] 1.理解同角三角函数的基本关系式:sin 2α+cos 2α=1,sin αcos α=tan α,并能熟练应用同角三角函数关系进行化简求值.(重点)2.能利用单位圆中的三角函数线推导出π2±α,π±α的正弦、余弦、正切的诱导公式,理解“奇变偶不变,符号看象限〞的含义,并能利用诱导公式进行化简.(重点、难点) [考向预测] 从近三年高考情况来看,本讲内容在高考中一般不单独命题,但它是三角函数的基础.预测2021年高考将以诱导公式为基础内容,结合同角三角函数关系式及三角恒等变换进行考查,试题以客观题为主,难度小,具有一定的技巧性.对应学生用书P0631.同角三角函数的基本关系(1)平方关系:01 sin 2α+cos 2α=1.(2)商数关系:02 sin αcos α=tan α⎝ ⎛⎭⎪⎫α≠π2+k π,k ∈Z .2.三角函数的诱导公式一 二三四五 六 角2k π+α(k ∈Z )π+α-απ-απ2-α π2+α 正弦sin α01 -sin α 02 -sin α 03sin α 04cos α 05 cos α 余弦cos α06 -cos α07cos α 08 -cos α 09sin α10 -sin α正切tan α11 tan α12 -tan α13 -tan α ——口诀 函数名不变,符号看象限函数名改变,符号看象限1.概念辨析(1)对任意α,β∈R ,有sin 2α+cos 2β=1.( ) (2)假设α∈R ,那么tan α=sin αcos α恒成立.( )(3)(sin α±cos α)2=1±2sin αcos α.( )(4)sin(π+α)=-sin α成立的条件是α为锐角.( ) 答案 (1)× (2)× (3)√ (4)× 2.小题热身 (1)假设sin α=55,π2<α<π,那么tan α=________. 答案 -12解析 因为sin α=55,π2<α<π, 所以cos α=-1-sin 2α=-1-⎝⎛⎭⎪⎫552=-255, 所以tan α=sin αcos α=-12.(2)化简:cos 2α-1sin αtan α=________.答案 -cos α解析 原式=-sin 2αsin α·sin αcos α=-cos α.(3)sin 2490°=________;cos ⎝ ⎛⎭⎪⎫-52π3=________.答案 -12-12解析 sin2490°=sin(7×360°-30°)=-sin30°=-12.cos ⎝ ⎛⎭⎪⎫-52π3=cos ⎝ ⎛⎭⎪⎫16π+π+π3=cos ⎝⎛⎭⎪⎫π+π3 =-cos π3=-12.(4)sin ⎝⎛⎭⎪⎫π2+α=35,α∈⎝ ⎛⎭⎪⎫0,π2,那么sin(π+α)=________.答案 -45解析 因为sin ⎝⎛⎭⎪⎫π2+α=cos α=35,α∈⎝⎛⎭⎪⎫0,π2,所以sin α=1-cos 2α=45,所以sin(π+α)=-sin α=-45.对应学生用书P063题型 一 同角三角函数关系式的应用角度1 化简与求值1.(2019·某某模拟)角α的顶点为坐标原点,始边与x 轴的非负半轴重合,终边上一点A (2sin α,3),那么cos α=( )A.12 B .-12C.32D .-32答案 A解析 由任意角三角函数的定义得tan α=32sin α,即sin αcos α=32sin α,所以3cos α=2sin 2α=2(1-cos 2α).整理得2cos 2α+3cos α-2=0,解得cos α=12或cos α=-2(舍去).角度2 sin α+cos α、sin αcos α、sin α-cos α三者之间的关系2.(2019·某某石室中学模拟)α为第二象限角,且sin α+cos α=15,那么cos α-sin α=( )A.75 B .-75C .±75D.2425答案 B解析 因为sin α+cos α=15,所以(sin α+cos α)2=125,即1+2sin αcos α=125,所以2sin αcos α=-2425.所以(cos α-sin α)2=1-2sin αcos α=1+2425=4925.又因为α为第二象限角.所以cos α<0,sin α>0.所以cos α-sin α<0.所以cos α-sin α=-75.角度3“齐次式〞问题3.sin α+3cos α3cos α-sin α=5,那么cos 2α+sin αcos α的值是() A.35 B .-35C .-3D .3 答案 A 解析 因为sin α+3cos α3cos α-sin α=5,所以tan α+33-tan α=5,解得tan α=2,所以cos 2α+sin αcos α=cos 2α+sin αcos αsin 2α+cos 2α=1+tan αtan 2α+1=1+222+1=35.1.应用同角三角函数关系式化简、求值的方法(1)利用sin 2α+cos 2α=1可实现α的正弦、余弦的互化,利用sin αcos α=tan α可以实现角α的弦切互化.如举例说明1.(2)由一个角的任一三角函数值可求出这个角的另外两个三角函数值,因为利用“平方关系〞公式,需求平方根,会出现两解,需根据角所在的象限判断符号,当角所在的象限不明确时,要进行分类讨论.2.sin α+cos α,sin αcos α,sin α-cos α之间的关系问题(1)方法:利用(sin α±cos α)2=1±2sin αcos α可以知一求二.(2)关注点:根据角α终边的位置确定sin α+cos α,sin α-cos α的符号.如举例说明2.3.sin α,cos α的齐次式的解法 (1)常见的结构①sin α,cos α的二次齐次式(如a sin 2α+b sin αcos α+c cos 2α)的问题常采用“切〞代换法求解;②sin α,cos α的齐次分式⎝ ⎛⎭⎪⎫如a sin α+b cos αc sin α+d cos α的问题常采用分式的基本性质进行变形.(2)巧用“1〞的变换:1=sin 2α+cos 2α.如举例说明3.1.假设α是第二象限角,那么tan α1sin 2α-1化简的结果是( ) A .-1 B .1 C .-tan 2α D .tan 2α答案 A解析 因为α是第二象限角,所以sin α>0,cos α<0,所以tan α1sin 2α-1=sin αcos α·⎪⎪⎪⎪⎪⎪cos αsin α=-sin αcos α·cos αsin α=-1. 2.假设sin(π-α)=-2sin ⎝ ⎛⎭⎪⎫π2+α,那么sin αcos α的值等于( ) A .-25B .-15C.25或-25D.25答案 A解析 由sin(π-α)=-2sin ⎝ ⎛⎭⎪⎫π2+α,可得sin α=-2cos α,那么tan α=-2,所以sin αcos α=sin αcos αsin 2α+cos 2α=tan α1+tan 2α=-25. 3.α∈⎝⎛⎭⎪⎫0,π4,sin αcos α=229,那么sin α-cos α=________.(提示(22-1)2=9-42)答案1-223解析 因为sin αcos α=229,所以(sin α-cos α)2=1-2sin αcos α =1-429=9-429=⎝ ⎛⎭⎪⎫22-132.又因为α∈⎝⎛⎭⎪⎫0,π4,所以sin α-cos α<0,所以sin α-cos α=1-223.题型 二 诱导公式的应用1.化简sin(-1071°)sin99°+sin(-171°)sin(-261°)的结果为( ) A .1 B .-1 C .0 D .2答案 C解析 原式=(-sin1071°)sin99°+sin171°sin261°=-sin(3×360°-9°)sin(90°+9°)+sin(180°-9°)·sin(270°-9°)=sin9°cos9°-sin9°cos9°=0.2.(2019·某某六校教育研究会联考)假设sin ⎝ ⎛⎭⎪⎫α-π4=55,那么cos ⎝ ⎛⎭⎪⎫α+π4的值为( )A.255 B .-255C.55D .-55 答案 D解析 cos ⎝ ⎛⎭⎪⎫α+π4=cos ⎣⎢⎡⎦⎥⎤π2+⎝⎛⎭⎪⎫α-π4=-sin ⎝ ⎛⎭⎪⎫α-π4=-55. 3.假设cos ⎝ ⎛⎭⎪⎫π6-θ=a ,那么cos ⎝ ⎛⎭⎪⎫5π6+θ+sin ⎝ ⎛⎭⎪⎫2π3-θ的值为________.答案 0 解析 因为cos ⎝⎛⎭⎪⎫5π6+θ=cos ⎣⎢⎡⎦⎥⎤π-⎝ ⎛⎭⎪⎫π6-θ=-cos ⎝ ⎛⎭⎪⎫π6-θ=-a .sin ⎝⎛⎭⎪⎫2π3-θ=sin ⎣⎢⎡⎦⎥⎤π2+⎝ ⎛⎭⎪⎫π6-θ=cos ⎝ ⎛⎭⎪⎫π6-θ=a , 所以cos ⎝⎛⎭⎪⎫5π6+θ+sin ⎝ ⎛⎭⎪⎫2π3-θ=0.(1)诱导公式的两个应用方向与原那么①求值,化角的原那么与方向:负化正,大化小,化到锐角为终了. ②化简,化简的原那么与方向:统一角,统一名,同角名少为终了. (2)应用诱导公式的基本流程(3)巧用口诀:奇变偶不变,符号看象限.(4)注意观察角与所求角的关系,如果两者之差或和为π2的整数倍,可考虑诱导公式,如举例说明2中⎝⎛⎭⎪⎫α+π4-⎝ ⎛⎭⎪⎫α-π4=π2.1.(2020·某某高三摸底)在平面直角坐标系xOy 中,角α的终边经过点P (3,4),那么sin ⎝ ⎛⎭⎪⎫α-2021π2=( )A .-45B .-35C.35D.45答案 B解析 因为角α的终边经过点P (3,4). 所以cos α=332+42=35. 所以sin ⎝ ⎛⎭⎪⎫α-2021π2=sin ⎝ ⎛⎭⎪⎫α-π2-1010π =sin ⎝ ⎛⎭⎪⎫α-π2=-sin ⎝ ⎛⎭⎪⎫π2-α=-cos α=-35. 2.k ∈Z ,化简:sin k π-αcos[k -1π-α]sin[k +1π+α]cos k π+α=________.答案 -1解析 当k 为偶数时,原式=sin -αcos -π-αsin π+αcos α=-sin α-cos α-sin αcos α=-1.当k 为奇数时,原式=sin π-αcos -αsin αcos π+α=sin αcos αsin α-cos α=-1.综上知,原式=-1.题型 三 同角三角函数基本关系式和诱导公式的综合应用1.(2019·某某模拟)cos ⎝ ⎛⎭⎪⎫2019π2+α=12,α∈⎝ ⎛⎭⎪⎫π2,π,那么cos α=( )A.12 B .-12C .-32D.32答案 C 解析 因为cos ⎝⎛⎭⎪⎫2019π2+α=cos ⎝ ⎛⎭⎪⎫1008π+3π2+α=cos ⎝ ⎛⎭⎪⎫3π2+α=sin α=12,又α∈⎝⎛⎭⎪⎫π2,π,所以cos α=-1-sin 2α=-32.2.在△ABC 中,3sin ⎝ ⎛⎭⎪⎫π2-A =3sin(π-A ),且cos A =-3cos(π-B ),那么C 等于( )A.π3 B.π4 C.π2D.2π3答案 C解析 因为3sin ⎝⎛⎭⎪⎫π2-A =3sin(π-A ),所以3cos A =3sin A ,所以tan A =33,又0<A <π,所以A =π6.因为cos A =-3cos(π-B ),即cos A =3cos B ,所以cos B =13cos π6=12,又0<B <π,所以B =π3,所以C =π-(A +B )=π2.应选C. 3.(2019·某某六中第一次阶段性检测)f (α)=⎣⎢⎡⎦⎥⎤sin ⎝ ⎛⎭⎪⎫π2-αtan π+α-cos π-α2-14sin ⎝ ⎛⎭⎪⎫3π2+α+cos π-α+cos 2π-α.(1)化简f (α);(2)假设-π3<α<π3,且f (α)<14,求α的取值X 围.解 (1)f (α)=cos αtan α+cos α2-1-4cos α-cos α+cos α=sin α+cos α2-1-4cos α=2sin αcos α-4cos α=-12sin α.(2)由得-12sin α<14,∴sin α>-12,∴2k π-π6<α<2k π+7π6,k ∈Z .∵-π3<α<π3,∴-π6<α<π3.故α的取值X 围为⎝⎛⎭⎪⎫-π6,π3.同角三角函数关系式和诱导公式综合应用题的解法(1)使用诱导公式把求解的三角函数式化为只含一个角的三角函数式.如举例说明3.(2)使用同角三角函数的基本关系式求解该三角函数式的值,求解中注意公式的准确性.1.(2019·某某八校联考)sin(π+α)=-13,那么tan ⎝ ⎛⎭⎪⎫π2-α=() A .2 2 B .-2 2 C.24D .±2 2答案 D解析 因为sin(π+α)=-sin α=-13,所以sin α=13,所以cos α=±1-sin 2α=±223, 所以tan ⎝ ⎛⎭⎪⎫π2-α=sin ⎝ ⎛⎭⎪⎫π2-αcos ⎝ ⎛⎭⎪⎫π2-α=cos αsin α=±2 2. 2.1+2sin π-3cos π+3化简的结果是( ) A .sin3-cos3 B .cos3-sin3 C .±(sin3-cos3) D .以上都不对答案 A解析 因为sin(π-3)=sin3,cos(π+3)=-cos3,所以原式=1-2sin3·cos3=sin3-cos32=|sin3-cos3|.因为π2<3<π,所以sin3>0,cos3<0,即sin3-cos3>0,所以原式=sin3-cos3.3.tan100°=k ,那么sin80°的值等于( ) A.k1+k2B .-k1+k2kk答案 B解析 由得tan100°=k =tan(180°-80°)=-tan80°,所以tan80°=-k ,又因为tan80°=sin80°cos80°=sin80°1-sin 280°,所以sin 280°1-sin 280°=k 2,注意到k <0,可解得sin80°=-k1+k2.对应学生用书P277组 基础关1.计算:sin 11π6+cos 10π3=( )A .-1B .1C .0 D.12-32答案 A 解析 sin 11π6+cos 10π3=sin ⎝ ⎛⎭⎪⎫2π-π6+cos ⎝⎛⎭⎪⎫3π+π3=-sin π6-cos π3=-12-12=-1.2.sin(π+θ)=-3cos(2π-θ),|θ|<π2,那么θ等于( )A .-π6B .-π3C.π6D.π3答案 D解析 因为sin(π+θ)=-3cos(2π-θ),所以-sin θ=-3cos θ,所以tan θ=sin θcos θ= 3.又因为|θ|<π2,所以θ=π3. 3.cos31°=a ,那么sin239°·tan149°的值是( ) A.1-a2aB.1-a 2a答案 B解析 sin239°·tan149°=sin(270°-31°)·tan(180°-31°)=(-cos31°)·(-tan31°)=sin31°=1-a 2.4.假设0≤2x ≤2π,那么使1-sin 22x =cos2x 成立的x 的取值X 围是( )A.⎝⎛⎭⎪⎫0,π4B.⎝⎛⎭⎪⎫3π4,πC.⎝⎛⎭⎪⎫π4,5π4D.⎣⎢⎡⎦⎥⎤0,π4∪⎣⎢⎡⎦⎥⎤3π4,π答案 D解析 显然cos2x ≥0,因为0≤2x ≤2π,所以0≤2x ≤π2或3π2≤2x ≤2π,所以x ∈⎣⎢⎡⎦⎥⎤0,π4∪⎣⎢⎡⎦⎥⎤3π4,π.5.(2019·某某二中模拟)角α终边上一点P 的坐标是(2sin2,-2cos2),那么sin α等于( )A .sin2B .-sin2C .cos2D .-cos2答案 D 解析 因为r =2sin22+-2cos22=2,由任意角的三角函数的定义,得sin α=y r=-cos2.6.假设sin θ,cos θ是方程4x 2+2mx +m =0的两根,那么m 的值为( ) A .1+ 5 B .1- 5 C .1± 5 D .-1- 5答案 B解析 由得Δ=(2m )2-4×4×m =4m (m -4)≥0,所以m ≤0或m ≥4,排除A ,C.又因为sin θ+cos θ=-m 2,sin θcos θ=m4,(sin θ+cos θ)2=1+2sin θcos θ,所以m 24=1+m2,解得m =1-5或m =1+5(舍去).7.tan α=3,那么1+2sin αcos αsin 2α-cos 2α的值是( )A.12 B .2C .-12D .-2答案 B解析 因为tan α=3,所以1+2sin αcos αsin 2α-cos 2α=sin 2α+cos 2α+2sin αcos αsin 2α-cos 2α=tan 2α+1+2tan αtan 2α-1 =32+1+2×332-1=2. 8.化简:(1+tan 2α)(1-sin 2α)=________. 答案 1解析 (1+tan 2α)(1-sin 2α)=⎝ ⎛⎭⎪⎫1+sin 2αcos 2α·cos 2α=cos 2α+sin 2α=1.9.化简:sin α+πcos π-αsin ⎝ ⎛⎭⎪⎫5π2-αtan -αcos 3-α-2π=________. 答案 -1解析 原式=-sin α-cos αsin ⎝ ⎛⎭⎪⎫π2-α-tan αcos 3α=sin αcos αcos α-sin αcos αcos 3α=sin αcos 2α-sin αcos 2α=-1. 10.cos(75°+α)=13,那么sin(α-15°)+cos(105°-α)的值是________.答案 -23解析 因为cos(75°+α)=13,所以sin(α-15°)=sin[(75°+α)-90°]=-cos(75°+α)=-13.cos(105°-α)=cos[180°-(75°+α)]=-cos(75°+α)=-13.所以sin(α-15°)+cos(105°-α)=-23.组 能力关1.2θ是第一象限的角,且sin 4θ+cos 4θ=59,那么tan θ=( )A.22B .-22C. 2 D .- 2答案 A解析 因为sin 4θ+cos 4θ=59,所以(sin 2θ+cos 2θ)2-2sin 2θcos 2θ=59,所以sin θcos θ=23,所以sin θcos θsin 2θ+cos 2θ=23,所以tan θtan 2θ+1=23,解得tan θ=22(tan θ=2,舍去,这是因为2θ是第一象限的角,所以tan θ为小于1的正数).2.(2019·某某模拟)当θ为第二象限角,且sin ⎝ ⎛⎭⎪⎫θ2+π2=13时,1-sin θcos θ2-sinθ2的值是( )A .1B .-1C .±1D .0答案 B解析 ∵sin ⎝ ⎛⎭⎪⎫θ2+π2=13,∴cos θ2=13,∴θ2在第一象限,且cos θ2<sin θ2,∴1-sin θcos θ2-sin θ2=-⎝⎛⎭⎪⎫cos θ2-sin θ2cos θ2-sinθ2=-1.3.-π2<α<0,sin α+cos α=15,那么1cos 2α-sin 2α的值为() A.75 B.257 C.725D.2425答案 B解析 因为-π2<α<0,所以cos α>0,sin α<0,可得cos α-sin α>0,因为(sin α+cos α)2+(cos α-sin α)2=2,所以(cos α-sin α)2=2-(sin α+cos α)2=2-125=4925,cos α-sin α=75,cos 2α-sin 2α=15×75=725,所以1cos 2α-sin 2α的值为257. 4.(2020·某某摸底)假设1+cos αsin α=2,那么cos α-3sin α=( )A .-3B .3C .-95D.95答案 C解析 因为1+cos αsin α=2,所以cos α=2sin α-1.又因为sin 2α+cos 2α=1,所以sin 2α+(2sin α-1)2=1.整理得5sin 2α-4sin α=0,因为sin α≠0,所以sin α=45.所以cos α=2sin α-1=35.所以cos α-3sin α=35-125=-95.5.cos ⎝⎛⎭⎪⎫5π12+α=13,且-π<α<-π2,那么cos ⎝ ⎛⎭⎪⎫π12-α等于( )A.223B.13 C .-13D .-223答案 D 解析 因为⎝ ⎛⎭⎪⎫5π12+α+⎝ ⎛⎭⎪⎫π12-α=π2,所以cos ⎝ ⎛⎭⎪⎫π12-α=sin ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫π12-α=sin ⎝⎛⎭⎪⎫5π12+α.因为-π<α<-π2,所以-7π12<α+5π12<-π12.又cos ⎝ ⎛⎭⎪⎫5π12+α=13>0,所以-π2<α+5π12<-π12,所以sin ⎝ ⎛⎭⎪⎫5π12+α=-1-cos 2⎝⎛⎭⎪⎫5π12+α=-1-⎝ ⎛⎭⎪⎫132=-223.6.sin 21°+sin 22°+sin 23°+…+sin 289°=________. 答案 44.5解析 因为sin(90°-α)=cos α,所以当α+β=90°时,sin 2α+sin 2β=sin 2α+cos 2α=1, 设S =sin 21°+sin 22°+sin 23°+…+sin 289°, 那么S =sin 289°+sin 288°+sin 287°+…+sin 21°,两个式子相加得2S =1+1+1+…+1=89,S =44.5. 7.α∈⎝ ⎛⎭⎪⎫π,3π2,且满足 1-sin α1+sin α+1cos α=2,那么cos 2α+2sin2α=________.答案 95解析 因为α∈⎝⎛⎭⎪⎫π,3π2,所以 1-sin α1+sin α+1cos α=1-sin α1-sin α1+sin α1-sin α+1cos α=1-sin α-cos α+1cos α=sin αcos α,那么sin αcos α=2,tan α=2,而cos 2α+2sin2α=cos 2α+4sin αcos αsin 2α+cos 2α=1+4tan αtan 2α+1=95. 8.sin α=255,求tan(α+π)+sin ⎝ ⎛⎭⎪⎫5π2+αcos ⎝ ⎛⎭⎪⎫5π2-α的值.解 tan(α+π)+sin ⎝ ⎛⎭⎪⎫5π2+αcos ⎝ ⎛⎭⎪⎫5π2-α=tan α+cos αsin α=sin αcos α+cos αsin α=1sin αcos α. ∵sin α=255>0,∴α为第一或第二象限角.当α为第一象限角时,cos α=1-sin 2α=55, 那么原式=1sin αcos α=52;当α为第二象限角时,cos α=-1-sin 2α=-55, 那么原式=1sin αcos α=-52.。
2019-2020学年高考数学一轮复习-第2讲-平面向量、解三角形教学案

2019-2020学年高考数学一轮复习 第2讲 平面向量、解三角形教学案【学习目标】(1)正弦定理、余弦定理及其应用(B 级)(2)处理与三角形有关的三角综合问题,除正确运用好正弦定理、余弦定理、面积公式及己知的三角函数关系式外,对隐含的很多条件,如三角函数的定义、三角形的内角和、诱导公式、勾股定理,向量有关知识等等,都要综合考虑,这样才能有效的解决问题【知识要点】1.已知两个非零向量a 与b ,它们的夹角是θ,则有a =⋅b __________,其中夹角θ的取值范围是________,规定=⋅a 0___ _;向量的数量积的结果是一个_____ _ 2.平面向量数量积的坐标表示: 已知),,(),,(2211y x b y x a ==则=⋅b a _____ ________;记a 与b 的夹角为θ,则=θcos _____________ __=||a ___ __ ____3.向量的平行的充要条件:设),(11y x a =,),(22y x b =,且0≠a ,则⇔b a // ⇔4.两非零向量垂直的充要条件:设),,(),,(2211y x b y x a ==则⇔⊥b a _____ __5.正弦定理: .6.余弦定理:第一形式:=2a ,第二形式: =A cos7.三角形的面积公式【自主学习】1. (必修4 P90习题19改编)已知向量a =(6,-3),b =(2,x +1),若a ⊥b ,则实数x = .2. (必修4 P80例5改编)已知向量a =(1,0),b =(2,1),则当k = 时,向量k a -b 与a +3b 平行.3. (必修5 P10习题4改编)在△ABC 中,已知b a a +=sin sin -sin B B A , 且2sin Asin B=2sin 2C ,则△ABC 的形状为4. (必修5 P16习题1(3)改编)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知a =7,b =43,c =13,则△ABC 最小的内角为 .【课堂探究】例1 (2015·江苏卷)在△ABC 中,已知AB=2,AC=3,角A=60°.(1) 求BC 的长;(2) 求sin 2C 的值.例2 在△ABC中,角A,B,C所对的边分别为a,b,c.已知sin2sin-sinCA C=222222----b a cc a b.(1) 求角B的大小;(2) 设T=sin2A+sin2B+sin2C,求T的取值范围.例3 (2015·陕西卷)在△ABC中,已知角A,B,C所对的边分别为a,b,c,向量m=(a,3b)与n=(cos A,sin B)平行.(1) 求角A的大小;(2) 若a7b=2,求△ABC的面积.【针对训练】1. (2015·安徽卷)在△ABC中,已知6A=75°,B=45°,则AC= .2. (2015·南京调研)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a+2c=2b,sin B=2sin C,则cos A= .3. (2014·常州期末)在△ABC中,角A,B,C的对边分别为a,b,c,若tanA=7tanB,22 -a bc=3,则c= . 【巩固提升】1. 已知向量a,b满足|a|=1,|b|=2,|a-b|=2,则|a+b|=2. (2015·苏锡常镇宿一调)如图,在平行四边形ABCD中,E为DC的中点,AE与BD交于点M,AB=2,AD=1,且MA·MB=-16,则AB·AD= .3. (2015·福建卷)在△ABC中,若AC=3,A=45°,C=75°,则BC= .4.(2015·镇江期末)已知△ABC的面积为S,且AB·AC=2S.(1) 求sin A的值;(2) 若|AB|=3,|AB-AC|=23,求sin B的值.5. (2015·苏北四市)已知向量a=(1,2sin θ),b=πsin13θ⎛⎫⎛⎫+⎪⎪⎝⎭⎝⎭,,θ∈R.(1) 若a⊥b,求tan θ的值;(2) 若a∥b,且θ∈π2⎛⎫⎪⎝⎭,,求θ的值.。
高考数学第一轮复习教案 专题6三角函数、三角恒等变换与解三角形

专题六 三角函数、三角恒等变换与解三角形一、考试内容:角的概念的推广.弧度制.任意角的三角函数.单位圆中的三角函数线.同角三角函数的基本关系式.正弦、余弦的诱导公式.两角和与差的正弦、余弦、正切.二倍角的正弦、余弦、正切.正弦函数、余弦函数的图像和性质.周期函数.函数y=Asin(ωx+φ)的图像.正切函数的图像和性质.已知三角函数值求角. 正弦定理.余弦定理.斜三角形解法. 二、考试要求:(1)理解任意角的概念、弧度的意义能正确地进行弧度与角度的换算.(2)掌握任意角的正弦、余弦、正切的定义;了解余切、正割、余割的定义;掌握同角三角函数的基本关系式;掌握正弦、余弦的诱导公式;了解周期函数与最小正周期的意义. (3)掌握两角和与两角差的正弦、余弦、正切公式;掌握二倍角的正弦、余弦、正切公式. (4)能正确运用三角公式,进行简单三角函数式的化简、求值和恒等式证明.(5)理解正弦函数、余弦函数、正切函数的图像和性质,会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+φ)的简图,理解A.ω、φ的物理意义.(6)会由已知三角函数值求角,并会用符号arcsinx\arc-cosx\arctanx 表示. (7)掌握正弦定理、余弦定理,并能初步运用它们解斜三角形. (8)“同角三角函数基本关系式:sin2α+cos2α=1,sin α/cos α=tan α,tan α•cos α=1”. 三、命题热点高考对给部分考查的主要内容为:任意角的概念和弧度制、任意角的三角函数的概念、诱导公式、同角三角函数关系、三角函数的图像和性质、两角和与差的三角函数公式、二倍角公式、正弦定理、余弦定理,并能步运用它们解斜三角形,并结合平面向量的概念和线性运算、平面向量的数量积、平面向量的应用。
高考对该部分的考查重基础,虽然该部分内容在试卷中试题数量多、占有的分值较多,但是试题以考查基础为主,试题的难度一般是中等偏下。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图二abc CBA图一cabA BC2019-2020年高考数学一轮复习解三角形教案理知识梳理:1、直角三角形各元素之间的关系:如图1,在Rt ABC中,C=,BC=a,AC=b,Ab=c。
(1)、三边之间的关系:+=;(勾股定理)(2)、锐角之间的关系:A+B=(3)、边角之间的关系:(锐角三角函数的定义):sinA=cosB= sinB=cosA= ,tanA2、斜三角形各元素之间的关系:如图2,ABC中,A、B、C为其内角,a、b、c分别表示A、B、C的对边。
(1)、三角形内角之间的关系:A+B+C=;sin(A+B)=sinC,cos(A+B)=-cosC;tan(A+B)=-tanCsin; cos;(2)、三边之间的关系:两边之和大于第三边,两边之差小于第三边;(3)、正弦定理:在一个三角形中,各边和它所对角的正弦值的比相等;即=2R (2R为外接圆的直径)正弦定理变形:a=2R ;;;;;a:b:c=(4)、余弦定理:=-2bccosA; =-2accosB;-2abcosC;余弦定理变形:cosA= ; cosB=; cosC=3、三角形的面积公式:(1)、=a=b=c(,,分别表示a,b,c三边上的高)(2)、=absinC=bcsinA=casinB(3)、=2=(4)、=;(5)、=rs(r为内切圆半径,)4、解三角形:由三角形的六个元素(即三个内角和三条边)中的三个元素(其中至少有一个是边)求其它未知元素的问题叫做解三角形,这里所说的元素还可以包括三角形的高、中线、角平分线、内切圆半径、外接圆半径、面积等等,解三角形问题一般可以分为下面两个情形:若给出是直角三角形,则称为解直角三角形;若给出的三角形为斜三角形,则称为解斜三角形。
5、实际问题中的应用。
(1)、仰角和俯角:(2)、方位角:指从正北方向顺时针转到目标方向线的角。
(3)、坡度角:坡面与水平面所成的二面角的度数。
(4)、距离、角度的测量测量距离问题;测量高度问题;测量角度问题。
βαDCBAβαHGE D EBA二、题型探究探究一:利用正余弦定理解三角形 例1: (2014安徽)(本小题满分12分)设△ABC 的内角A,B,C 所对边的长分别是a,b,c,且b=3,c=1,A=2B.(Ⅰ)求a 的值;(Ⅱ)求⎪⎭⎫⎝⎛+4sin πA 的值. (Ⅰ)因为B A 2=,所以B B B A cos sin 22sin sin ==.由正、余弦定理得 acb c a b a 22222-+⋅=.因为3=b ,1=c ,所以122=a ,32=a .(Ⅱ)由余弦定理得31612192cos 222-=-+=-+=bc a c b A . 由于π<<A 0,所以322911cos 1sin 2=-=-=A A . 故62422)31(223224sincos 4cossin )4sin(-=⨯-+⨯=+=+πππA A A 例2: 在中,已知a 、b 、c 分别表示A 、B 、C 的对边,已知a ,b ,c 成等比数列,且-=ac-bc ,求A 及 (,)探究二:求三角形的面积例3:已知a 、b 、c 分别表示A 、B 、C 的对边,A ,B ,C 成等差数列,cosA= ,b=(1)、求sinC 的值 (2)、求的面积。
例4:已知三个内角A、B、C成等差数列,其外接圆的半径为1,且有sinA-sinC+ cos(A-C)=(1)、求A,B,C大小;因为三个内角A、B、C成等差数列,所以B=sinA-sinC=2cos,所以= ,所以A-C=又A+C=12,所以A=,B=C=,(2)、求的面积。
=2=例5:已知三个内角A,B,C成等差数列,三边a、b、c成等比数列,证明为正三角形。
探究三:判断三角形的形状例5:在中,已知asinA=bsinB,试判断三角形的形状;例6:在中,已知acosA=bcosB,试判断三角形的形状;例7:在中,已知acosB=bcosA,试判断三角形的形状;探究四:正余定理的实际应用(2014上海)(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.如图,某公司要在A B 、两地连线上的定点C 处建造广告牌CD ,其中D 为顶端,AC 长35米,CB 长80米,设A B 、在同一水平面上,从A 和B 看D 的仰角分别为βα和.(1)设计中CD 是铅垂方向,若要求βα2≥,问CD 的长至多为多少(结果精确到0.01米)?(2)施工完成后.CD与铅垂方向有偏差,现在实测得,, 45.1812.38==βα求CD 的长(结果精确到0.01米)?【解析】(1).米的最大长度是所以,解得)(即则令28.2828.2822000,h -8080h 280h -180h2≥35h 0βtan -12tan ββ2tan ≥αtan ∴0β2≥α2π80hCB h βtan ,35h DC h αtan ,2222AC h h DC ≈≤<>•=•>=>>=====三、方法提升: (1)、解斜三角形的常规思维方法: 已知两角和一边,可先用正弦定理解;已知两边和夹角,先用余弦定理,之后再用正弦定理;已知两边及一边所对的角,应用正弦定理,再由正弦定理或余弦定理求解,这种情况要结合图形讨论解的情况; 已知三边,用余弦定理。
(2)、三角形的内切圆半径R= ,特别地,=(3)、三角形中中射影定理 (4)、两内角与正弦关系:在中,A<B,……(5)、三角形中的重要结论:tanAtanBtanC=tanA+tanB+tanC(斜三角形) (6)、锐角三角形中,sinA+sinB+sinC>cosA+cosB+cosC; tanAtanBtanC>1四、反思感悟五、课时作业正弦、余弦定理的应用一、选择题(每小题6分,共60分) 1在△ABC 中,“︒>30A ”是“21sin >A ”的 ( ) A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2△ABC 中,∠A ,∠B 的对边分别为a ,b ,且∠A=60°,4,6==b a ,那么满足条件的△ABC ( )A .有一个解B .有两个解C .无解D .不能确定3在三角形ABC 中, 如果B A cos sin =, 那么这个三角形是 ( ) A .直角三角形 B . 锐角三角形C .钝角三角形D . 直角三角形或钝角三角形4已知ABC △中,a =b =60B =,那么角A 等于 ( )A .135B .90C .45D .305ABC ∆的内角A 、B 、C 的对边分别为a 、b 、c ,若a 、b 、c 成等比数列,且2c a =,则cos B =A .14 B .34C .4D .36在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,A =3π,a =3,b =1,则c = ( ) A 1 B 2 C 3—1 D 3 7在ABC ∆中,AB=3,AC=2,BC=10,则AB AC ⋅= ( ) A .23-B .32-C .32D .238在△ABC 中,角A 、B 、C 的对边分别为a 、b 、c ,若a 2+c 2-b 2=,则角B 的值为 ( ) A.6π B.3π C.6π或56π D.3π或23π 9设A 是△ABC 中的最小角,且11cos +-=a a A ,则实数a 的取值范围是( ) A .a ≥3 B .a >-1 C .-1<a ≤3 D .a >010在△ABC 中,若三个内角A ,B ,C 成等差数列且A <B <C ,则cos cos A C 的取值范围是( )A .11(,]24-B .31[,]44-C .11(,)24-D .31(,)44-11在△ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,已知3,30,a b C ===︒ 则A =12在△ABC 中,若B=300,AB=23,AC=2,则△ABC 的面积S 是13△ABC 的内角A B C ,,的对边分别为a b c ,,,若()C a A c b cos cos 3=-,则=A cos14在△ABC 中,已知AB=l ,∠C=50°,当∠B= 时,BC 的长取得最大值.三、解答题(15、16、17题每题16分,18题18分,共66分)15已知ABC △1,且sin sin A B C +=.(I )求边AB 的长;(II )若ABC △的面积为1sin 6C ,求角C 的度数.16在ABC △中,角A B C ,,的对边分别为tan a b c C =,,,(1)求cos C ;(2)若52CB CA =,且9a b +=,求c .17在ABC △中,内角A B C ,,对边的边长分别是a b c ,,,已知2c =,3C π=.(Ⅰ)若ABC △,求a b ,; (Ⅱ)若sin 2sin B A =,求ABC △的面积正余弦定理的应用参考答案15解:(I )由题意得1AB BC AC ++=,BC AC +=,两式相减,得1AB =.(II )由ABC △的面积11sin sin 26BC AC C C =,得13BC AC =,222cos 2AC BC AB C AC BC +-=22()2122AC BC AC BC AB AC BC +--==,60C =.16解:(1)sin tan cos C C C =∴=22sin cos 1C C += 解得1c o s 8C =±. tan 0C >,C ∴是锐角. 1cos 8C ∴=.17解:(Ⅰ)由余弦定理得,224a b ab +-=,又1sin 2ab C =4ab =.(Ⅱ)已知条件化为2b a =,联立方程组2242a b ab b a ⎧+-=⎨=⎩,,解得3a =,b =.所以ABC △的面积1sin 2S ab C ==。
