2017版高中人教A版数学必修1课时作业13 Word版含解析
高中人教A版数学必修1课时作业3Word版含解析

那么 ( )
ห้องสมุดไป่ตู้
A.P M C. M= P 答案: C 二、填空题
B.M P D.M P
x+y=1, 6.若 A= x, y
x-y-3= 0
,B={( x,y)|y=ax2+1} ,且
A? B,则 a=________.
1
x+ y=1,
答案: -2 解析: A= x,y x- y-3=0
={(2 ,- 1)} ,
∵ A?
B,∴-
1=
a×
22+
1,∴
a=-
1 2.
7.已知 ? { x|x2-x+ a=0} ,则实数 a 的取值范围是 ________.
答案: a a≤14
解析: ∵? { x|x2- x+a=0} ,
∴
Δ=
(
-
1)2-
4a≥
0,∴
a≤
1 4.
8.设 A={ x|x2-8x+15=0} ,B={ x|x-a=0} ,若 B? A,则实
1a≥- 1, ∴
2 a≤ 1,
∴a≥ 2.
(3)当 a<0 时, A= x 2a<x<1a ,
2a≥- 1, ∵ A? B,∴
1a≤ 1,
∴a≤- 2.
综上所述, a 的取值范围是 { a|a=0 或 a≥2 或 a≤- 2} . 13.设集合 A={ x|a-2<x<a+2} ,B={ x|x<1} ,若 A? B,求 实数 a 的取值范围. 解: 如图所示,
1 = x x=6 6a+1 ,a∈ Z ,
B= x x=b2-13,b∈Z
1 = x x=6 3b-2 ,b∈ Z
1 = x x=6[3 b+1 -2],b∈Z
2017-2018学年人教A版高中数学必修1课时作业:作业12 1.2习题课 Word版含解析
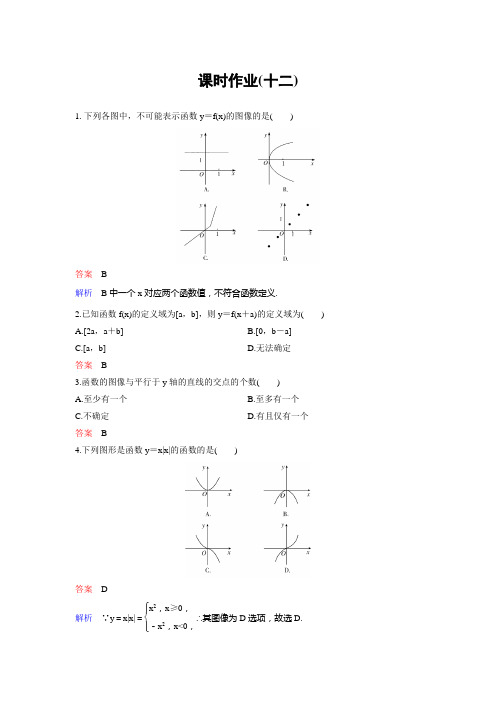
课时作业(十二)1.下列各图中,不可能表示函数y =f(x)的图像的是( )答案 B解析 B 中一个x 对应两个函数值,不符合函数定义.2.已知函数f(x)的定义域为[a ,b],则y =f(x +a)的定义域为( ) A.[2a ,a +b] B.[0,b -a] C.[a ,b] D.无法确定答案 B3.函数的图像与平行于y 轴的直线的交点的个数( ) A.至少有一个 B.至多有一个 C.不确定 D.有且仅有一个 答案 B4.下列图形是函数y =x|x|的函数的是( )答案 D解析 ∵y =x|x|=⎩⎪⎨⎪⎧x 2,x ≥0,-x 2,x<0,∴其图像为D 选项,故选D.5.某农贸市场出售西红柿,当价格上涨时,供给量相应增加,而需求量相应减少,具体调查结果如下表: 表1 市场供给表表2( ) A.(2.3,2.6)内 B.(2.4,2.6)内 C.(2.6,2.8)内 D.(2.8,2.9)内答案 C6.如图所示,函数f(x)的图像是曲线OAB ,其中点O ,A ,B 的坐标分别为(0,0),(1,2),(3,1),则f(1f (3))的值等于________.答案 2解析 ∵f(3)=1,1f (3)=1,∴f(1f (3))=f(1)=2.7.若函数f(x)的定义域为[-1,2],则y =f(x)+f(-x)的定义域为________. 答案 [-1,1]8.设函数y =f(x)的定义域为R +,且f(xy)=f(x)+f(y),f(8)=3,则f(2)等于__________. 答案 12解析 ∵f(8)=f[(2)6]=6f(2)=3,∴f(2)=12.9.设f(x)=2x -3,g(x -2)=f(x),则g(x)=________. 答案 2x +110.已知函数f(x)满足f(x +4)=x 3+2,当f(x)=1时,x 的值为________. 答案 311.已知函数f(1-x1+x)=x ,求f(2)的值.解析 由1-x 1+x=2,解得x =-13.所以f(2)=-13.12.(1)已知函数f(x)的定义域是[1,5],求函数f(x 2+1)的定义域. (2)已知函数f(2x 2-1)的定义域是[1,5],求f(x)的定义域.解析 (1)由f(x)定义域为[1,5],知f(x 2+1)中需1≤x 2+1≤5,解得-2≤x ≤2. ∴f(x 2+1)的定义域为[-2,2].(2)由f(2x 2-1)定义域为[1,5],得1≤x 2≤25,1≤2x 2-1≤49,故f(x)定义域为[1,49]. 13.如图,该曲线表示一人骑自行车离家的距离与时间的关系.骑车者9时离开家,15时回家.根据这个曲线图,请你回答下列问题:(1)最初到达离家最远的地方是什么时间?离家多远? (2)何时开始第一次休息?休息多长时间? (3)第一次休息时,离家多远? (4)11:00到12:00他骑了多少千米?(5)他在9:00~10:00和10:00~10:30的平均速度分别是多少? (6)他在哪段时间里停止前进并休息用午餐?解析 (1)最初到达离家最远的地方的时间是12时,离家30千米. (2)10:30开始第一次休息,休息了半小时. (3)第一次休息时,离家17千米. (4)11:00至12:00他骑了13千米.(5)9:00~10:00的平均速度是10千米/时;10:00~10:30的平均速度是14千米/时. (6)从12时到13时停止前进,并休息用午餐较为符合实际情形. ►重点班·选做题14.设函数f(x)=[x],[x]表示不超过x 的最大整数,x ∈(-2.5,2]时,写出函数f(x)的解析式.答案 f(x)=⎩⎪⎨⎪⎧-3, x ∈(-2.5,-2),-2, x ∈[-2,-1),-1, x ∈[-1,0),0, x ∈[0,1),1, x ∈[1,2),2, x =21.客车从甲地以60 km/h 的速度匀速行驶1小时到达乙地,在乙地停留了半小时,然后以80 km/h 的速度匀速行驶1小时到达丙地.下列描述客车从甲地出发,经过乙地,最后到达丙地所经过的路程s 与时间t 之间关系的图像中,正确的是()答案 C解析 图像经过(0,0),(1,60),(1.5,60),(2.5,140)的三段折线,故选C.2.如图所示的四个容器高度都相同.将水从容器顶部一个孔中以相同的速度注入其中,注满为止.用下面对应的图像显示该容器中水面的高度h 和时间t 之间的关系,其中不正确的个数为()A.1B.2C.3D.4答案 A解析 对于第一图,水面的高度h 的增加应是均匀的,因此不正确,其他均正确,选A. 3.某商场经营一批进价为30元/件的商品,在市场试销中发现,此商品的销售单价x 元与日销售量y 件之间有如下所表示的关系.(1)y 与x 的一个函数关系式y =f(x);(2)设经营此商品的日销售利润为P 元,根据上述关系,写出P 关于x 的函数关系式,并指出销售单价x 为多少时,才能获得最大日销售利润?解析 (1)由表作出点(30,60),(40,30),(45,15),(50,0).如图,它们近似地在一条直线上,设它们共线于直线y =kx +b ,∴⎩⎪⎨⎪⎧50k +b =0,45k +b =15,解得⎩⎪⎨⎪⎧k =-3,b =150.∴y =-3x +150,(x ∈N ).经检验(30,60),(40,30)也在此直线上. ∴所求函数解析式为y =-3x +150,(x ∈N ).(2)依题意P =y(x -30)=(-3x +150)(x -30)=-3(x -40)2+300, 当x =40时,P 有最大值300,故销售价为40元时,才能获得最大利润.4.《国务院关于修改〈中华人民共和国个人所得税法实施条例〉的决定》已于2008年3月1日起施行,个人所得税税率表如下:(1)若某人2008年4月份的收入额为4 200元,求该人本月应纳税所得额和应纳的税费; (2)设个人的月收入额为x 元,应纳的税费为y 元.当0<x ≤3 600时,试写出y 关于x 的函数关系式.解析 (1)本月应纳税所得额为4 200-2 000=2 200元; 应纳税费由表格,得500×5%+1 500×10%+200×15%=205元. (2)y =⎩⎪⎨⎪⎧0,0<x ≤2 000,(x -2 000)·5%,2 000<x ≤2 500,25+(x -2 500)·10%,2 500<x ≤3 600.。
高中数学(人教版A版必修一)配套课时作业:第一章 集合与函数的概念 1.3习题课 Word版含解析

§1.3 习题课课时目标 1.加深对函数的基本性质的理解.2.培养综合运用函数的基本性质解题的能力.1.若函数y =(2k +1)x +b 在R 上是减函数,则( ) A .k >12B .k <12C .k >-12D .k <-122.定义在R 上的函数f (x )对任意两个不相等的实数a ,b ,总有f (a )-f (b )a -b >0成立,则必有( ) A .函数f (x )先增后减 B .函数f (x )先减后增 C .f (x )在R 上是增函数 D .f (x )在R 上是减函数3.已知函数f (x )在(-∞,+∞)上是增函数,a ,b ∈R ,且a +b >0,则有( ) A .f (a )+f (b )>-f (a )-f (b ) B .f (a )+f (b )<-f (a )-f (b ) C .f (a )+f (b )>f (-a )+f (-b ) D .f (a )+f (b )<f (-a )+f (-b )4.函数f (x )的图象如图所示,则最大、最小值分别为( )A .f (32),f (-32)B .f (0),f (32)C .f (0),f (-32) D .f (0),f (3)5.已知f (x )=ax 2+bx +3a +b 是偶函数,定义域为[a -1,2a ],则a =________,b =________.6.已知f (x )=⎩⎪⎨⎪⎧12x -1, x ≥0,1x ,x <0,若f (a )>a ,则实数a 的取值范围是______________.一、选择题1.设f (x )是定义在R 上的偶函数,且在(-∞,0)上是增函数,已知x 1>0,x 2<0,且f (x 1)<f (x 2),那么一定有( ) A .x 1+x 2<0B .x 1+x 2>0C .f (-x 1)>f (-x 2)D .f (-x 1)·f (-x 2)<0 2.下列判断:①如果一个函数的定义域关于坐标原点对称,那么这个函数为偶函数; ②对于定义域为实数集R 的任何奇函数f (x )都有f (x )·f (-x )≤0; ③解析式中含自变量的偶次幂而不含常数项的函数必是偶函数; ④既是奇函数又是偶函数的函数存在且唯一. 其中正确的序号为( ) A .②③④B .①③C .②D .④3.定义两种运算:a ⊕b =ab ,a ⊗b =a 2+b 2,则函数f (x )=2⊕x(x ⊗2)-2为( )A .奇函数B .偶函数C .既不是奇函数也不是偶函数D .既是奇函数也是偶函数4.用min{a,b}表示a,b两数中的最小值,若函数f(x)=min{|x|,|x+t|}的图象关于直线x=-12对称,则t的值为()A.-2B.2C.-1D.15.如果奇函数f(x)在区间[1,5]上是减函数,且最小值为3,那么f(x)在区间[-5,-1]上是()A.增函数且最小值为3B.增函数且最大值为3C.减函数且最小值为-3D.减函数且最大值为-36.若f(x)是偶函数,且当x∈[0,+∞)时,f(x)=x-1,则f(x-1)<0的解集是()A.(-1,0) B.(-∞,0)∪(1,2)C.(1,2) D.(0,2)二、填空题7.若函数f(x)=-x+abx+1为区间[-1,1]上的奇函数,则它在这一区间上的最大值为____.8.已知函数f(x)是定义域为R的奇函数,且当x>0时,f(x)=2x-3,则f(-2)+f(0)=________.9.函数f(x)=x2+2x+a,若对任意x∈[1,+∞),f(x)>0恒成立,则实数a的取值范围是________.三、解答题10.已知奇函数f(x)的定义域为(-∞,0)∪(0,+∞),且f(x)在(0,+∞)上是增函数,f(1)=0.(1)求证:函数f(x)在(-∞,0)上是增函数;(2)解关于x的不等式f(x)<0.11.已知f(x)=x2+ax+bx,x∈(0,+∞).(1)若b≥1,求证:函数f(x)在(0,1)上是减函数;(2)是否存在实数a,b,使f(x)同时满足下列两个条件:①在(0,1)上是减函数,(1,+∞)上是增函数;②f(x)的最小值是3.若存在,求出a,b的值;若不存在,请说明理由.能力提升12.设函数f(x)=1-1x+1,x∈[0,+∞)(1)用单调性的定义证明f(x)在定义域上是增函数;(2)设g(x)=f(1+x)-f(x),判断g(x)在[0,+∞)上的单调性(不用证明),并由此说明f(x)的增长是越来越快还是越来越慢?13.如图,有一块半径为2的半圆形纸片,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,设CD=2x,梯形ABCD 的周长为y.(1)求出y关于x的函数f(x)的解析式;(2)求y的最大值,并指出相应的x值.1.函数单调性的判定方法 (1)定义法.(2)直接法:运用已知的结论,直接判断函数的单调性,如一次函数,二次函数,反比例函数;还可以根据f (x ),g (x )的单调性判断-f (x ),1f (x ),f (x )+g (x )的单调性等.(3)图象法:根据函数的图象判断函数的单调性. 2.二次函数在闭区间上的最值对于二次函数f (x )=a (x -h )2+k (a >0)在区间[m ,n ]上最值问题,有以下结论: (1)若h ∈[m ,n ],则y min =f (h )=k ,y max =max{f (m ),f (n )}; (2)若h ∉[m ,n ],则y min =min{f (m ),f (n )}, y max =max{f (m ),f (n )}(a <0时可仿此讨论). 3.函数奇偶性与单调性的差异.函数的奇偶性是相对于函数的定义域来说的,这一点与研究函数的单调性不同,从这个意义上说,函数的单调性是函数的“局部”性质,而奇偶性是函数的“整体”性质,只是对函数定义域内的每一个值x ,都有f (-x )=-f (x )[或f (-x )=f (x )],才能说f (x )是奇函数(或偶函数).§1.3 习题课双基演练1.D [由已知,令2k +1<0,解得k <-12.] 2.C [由f (a )-f (b )a -b >0,知f (a )-f (b )与a -b 同号,由增函数的定义知选C.]3.C [∵a +b >0,∴a >-b ,b >-a .由函数的单调性可知,f (a )>f (-b ),f (b )>f (-a ). 两式相加得C 正确.]4.C[由图象可知,当x=0时,f(x)取得最大值;当x=-32时,f(x)取得最小值.故选C.]5.130解析偶函数定义域关于原点对称,∴a-1+2a=0.∴a=1 3.∴f(x)=13x2+bx+1+b.又∵f(x)是偶函数,∴b=0. 6.(-∞,-1)解析若a≥0,则12a-1>a,解得a<-2,∴a∈∅;若a<0,则1a>a,解得a<-1或a>1,∴a<-1.综上,a∈(-∞,-1).作业设计1.B[由已知得f(x1)=f(-x1),且-x1<0,x2<0,而函数f(x)在(-∞,0)上是增函数,因此由f(x1)<f(x2),则f(-x1)<f(x2)得-x1<x2,x1+x2>0.故选B.]2.C[判断①,一个函数的定义域关于坐标原点对称,是这个函数具有奇偶性的前提条件,但并非充分条件,故①错误.判断②正确,由函数是奇函数,知f(-x)=-f(x),特别地当x=0时,f(0)=0,所以f(x)·f(-x)=-[f(x)]2≤0.判断③,如f(x)=x2,x∈[0,1],定义域不关于坐标原点对称,即存在1∈[0,1],而-1 [0,1];又如f(x)=x2+x,x∈[-1,1],有f(x)≠f(-x).故③错误.判断④,由于f(x)=0,x∈[-a,a],根据确定一个函数的两要素知,a取不同的实数时,得到不同的函数.故④错误.综上可知,选C.]3.A[f(x)=2xx2+2,f(-x)=-f(x),选A.] 4.D[当t>0时f(x)的图象如图所示(实线)对称轴为x=-t2,则t2=12,∴t=1.]5.D[当-5≤x≤-1时1≤-x≤5,∴f(-x)≥3,即-f(x)≥3.从而f(x)≤-3,又奇函数在原点两侧的对称区间上单调性相同,故f(x)在[-5,-1]上是减函数.故选D.]6.D[依题意,因为f(x)是偶函数,所以f(x-1)<0化为f(|x-1|)<0,又x∈[0,+∞)时,f(x)=x-1,所以|x-1|-1<0,即|x-1|<1,解得0<x<2,故选D.]7.1解析f(x)为[-1,1]上的奇函数,且在x=0处有定义,所以f(0)=0,故a=0.又f(-1)=-f(1),所以--1-b+1=1b+1,故b=0,于是f(x)=-x.函数f(x)=-x在区间[-1,1]上为减函数,当x取区间左端点的值时,函数取得最大值1. 8.-1解析∵f(-0)=-f(0),∴f(0)=0,且f(2)=22-3=1.∴f(-2)=-f(2)=-1,∴f(-2)+f(0)=-1.9.a>-3解析∵f(x)=x2+2x+a=(x+1)2+a-1,∴[1,+∞)为f(x)的增区间,要使f(x)在[1,+∞)上恒有f(x)>0,则f(1)>0,即3+a>0,∴a>-3.10.(1)证明设x1<x2<0,则-x1>-x2>0.∵f(x)在(0,+∞)上是增函数,∴f(-x1)>f(-x2).∵f(x)是奇函数,∴f(-x1)=-f(x1),f(-x2)=-f(x2),∴-f(x1)>-f(x2),即f(x1)<f(x2).∴函数f(x)在(-∞,0)上是增函数.(2)解若x>0,则f(x)<f(1),∴x<1,∴0<x<1;若x<0,则f(x)<f(-1),∴x<-1.∴关于x的不等式f(x)<0的解集为(-∞,-1)∪(0,1).11.(1)证明设0<x1<x2<1,则x1x2>0,x1-x2<0.又b>1,且0<x1<x2<1,∴x1x2-b<0.∵f(x1)-f(x2)=(x1-x2)(x1x2-b)x1x2>0,∴f(x1)>f(x2),所以函数f(x)在(0,1)上是减函数.(2)解设0<x1<x2<1,则f(x1)-f(x2)=(x1-x2)(x1x2-b)x1x2由函数f(x)在(0,1)上是减函数,知x1x2-b<0恒成立,则b≥1. 设1<x1<x2,同理可得b≤1,故b=1.x∈(0,+∞)时,通过图象可知f(x)min=f(1)=a+2=3.故a=1.12.(1)证明设x1>x2≥0,f(x1)-f(x2)=(1-1x1+1)-(1-1x2+1)=x1-x2(x1+1)(x2+1).由x1>x2≥0⇒x1-x2>0,(x1+1)(x2+1)>0,得f(x1)-f(x2)>0,即f(x1)>f(x2).所以f(x)在定义域上是增函数.(2)解g(x)=f(x+1)-f(x)=1(x+1)(x+2),g(x)在[0,+∞)上是减函数,自变量每增加1,f(x)的增加值越来越小,所以f(x)的增长是越来越慢.13.解(1)作OH,DN分别垂直DC,AB交于H,N,连结OD.由圆的性质,H是中点,设OH=h,h=OD2-DH2=4-x2.又在直角△AND中,AD=AN2+DN2=(2-x)2+(4-x2)=8-4x=22-x,所以y=f(x)=AB+2AD+DC=4+2x+42-x,其定义域是(0,2).(2)令t=2-x,则t∈(0,2),且x=2-t2,所以y=4+2·(2-t2)+4t=-2(t-1)2+10,当t=1,即x=1时,y的最大值是10.。
高中人教A版数学必修1课时作业18 Word版含解析

=×+=+=.
.已知=,求的值.
解:由=,得=-=,
∴==.
.设={},={,-},是否存在的值,使∩={}?
解:不存在的值,使∩={}成立.
若=,则=,此时-=,从而-==,与集合元素的互异性矛盾;
若=,则=,此时无意义;
若=,此时=,从而∩={},与条件不符;
若-=,则=,从而=,与集合元素的互异性矛盾.
.若=,则()
.=.=
.=.=
答案:解析:由=,得=,
∴()=(),则=.
-+的值为()Biblioteka ..答案:解析:-+=-·
=×=.
二、填空题
.[()]=.
答案:解析:原式=[()]=()==.
.已知=,=,则=.
答案:解析:由题意得,=,=,
∴==-=-=.
.设=,=,则+=.
答案:解析:∵=,=,∴=,=,
课时作业(十八)对 数
一、选择题
.已知=,则=()
.±.
..
答案:解析:由=,可知=,∴=±,
又>且≠,∴=.
.方程=的解是()
.
答案:解析:原方程即为=-,
∴=-,∴=-=.
.有以下四个结论:
①( )=;
②( )=;
③若=,则=;
④若=,则=.
其中正确的是()
.①③.②④.①②.③④
答案:解析:( )= =,( )= =,故①②正确;若= ,则=,故③错误;若= ,则=,故④错误.
∴+=()·=×=.
三、解答题
.已知=,=(>,且≠),求=的值.
解:由=,得=,
由=,得=,
所以==·[(·-)]
=·(·-)=·=()·()
高中数学必修一 人教A版·数学·必修1课时作业13指数函数及其性质 Word版含解析

所以x<0,
所以0<2x<1.
所以0<a-1<1.
所以1<a<2.
【答案】(1,2)
8.函数y= 的值域是________.
【解析】令t=x2-x- = 2- .
则t∈ ,
因此y= t∈ =(0, ].
【答案】(0, ]
三、解答题(每小题10分,共20分)
9.设f(x)=3x,g(x)= x.
(1)求函数f(x)的解析式;
(2)若函数g(x)= ,试判断函数g(x)的奇偶性并给出证明.
【解析】(1)由已知得
解得k=1,a= .
故f(x)= -x=2x.
(2)由(1)知g(x)= ,函数g(x)为奇函数.
证明:函数g(x)的定义域为R,
又g(-x)= = =-
故函数g(x)是奇函数.
【答案】B
5.函数y=ax在区间[0,1]上的最大值和最小值的和为3,则函数y=3ax-1在区间[0,1]上的最大值是()
A.6 B.1
C.5 D.
【解析】由于函数y=ax在[0,1]上为单调函数,
所以有a0+a1=3,即a=2.
所以函数y=3ax-1,即y=6x-1在[0,1]上单调递增,其最大值为y=6×1-1=5.故选C.
(1)在同一坐标系中作出f(x),g(x)的图象;
(2)计算f(1)与g(-1),f(π)与1)函数f(x)与g(x)的图象如图所示:
(2)f(1)=31=3,g(-1)= -1=3;
f(π)=3π,g(-π)= -π=3π;
f(m)=3m,g(-m)= -m=3m.
课时作业
|
一、选择题(每小题5分,共25分)
2017-2018学年人教A版高中数学必修1课时作业:作业3 1.1.1-3集合的含义与表示 Word版含解析

课时作业(三)1.设x ∈N ,且1x ∈N ,则x 的值可能是( )A.0B.1C.-1D.0或1答案 B解析 首先x ≠0,排除A ,D ;又x ∈N ,排除C ,故选B.2.下面四个关系式:π∈{x|x 是正实数},0.3∈Q ,0∈{0},0∈N ,其中正确的个数是( ) A.4 B.3 C.2 D.1 答案 A解析 本题考查元素与集合之间的关系,由数集的分类可知四个关系式均正确. 3.集合{x ∈N |-1<x<112}的另一种表示方法是( )A.{0,1,2,3,4}B.{1,2,3,4}C.{0,1,2,3,4,5}D.{1,2,3,4,5} 答案 C解析 ∵x ∈N ,且-1<x<112,∴集合中含有元素0,1,2,3,4,5,故选C.4.已知集合A ={x ∈N *|-5≤x ≤5},则必有( ) A.-1∈A B.0∈A C.3∈A D.1∈A 答案 D解析 ∵x ∈N *,-5≤x ≤5,∴x =1,2,即A ={1,2},∴1∈A. 5.集合M ={(x ,y)|xy<0,x ∈R ,y ∈R }是( ) A.第一象限内的点集 B.第三象限内的点集 C.第四象限内的点集 D.第二、四象限内的点集 答案 D解析 根据描述法表示集合的特点,可知集合表示的是横、纵坐标异号的点的集合,这些点在第二、四象限内.6.若a ,b ,c ,d 为集合A 的四个元素,则以a ,b ,c ,d 为边长构成的四边形可能是( ) A.矩形B.平行四边形C.菱形D.梯形答案 D解析 由于集合中的元素具有“互异性”,故a ,b ,c ,d 四个元素互不相同,即组成四边形的四条边互不相等.7.集合A ={x|x ∈N ,且42-x ∈Z },用列举法可表示为A =________.答案 {0,1,3,4,6}解析 注意到42-x ∈Z ,因此,2-x =±2,±4,±1,解得x =-2,0,1,3,4,6,又∵x ∈N ,∴x =0,1,3,4,6.8.一边长为6,一边长为3的等腰三角形所组成的集合中有________个元素. 答案 1解析 这样的三角形只有1个,是两腰长为6,底边长为3的等腰三角形. 9.点P(1,3)和集合A ={(x ,y)|y =x +2}之间的关系是________. 答案 P ∈A解析 在y =x +2中,当x =1时,y =3,因此点P 是集合A 的元素,故P ∈A. 10.用列举法表示集合A ={(x ,y)|x +y =3,x ∈N ,y ∈N *}为________. 答案 {(0,3),(1,2),(2,1)}解析 集合A 是由方程x +y =3的部分整数解组成的集合,由条件可知,当x =0时,y =3;当x =1时,y =2;当x =2时,y =1.故A ={(0,3),(1,2),(2,1)}.11.若A ={-2,2,3,4},B ={x|x =t 2,t ∈A},用列举法表示集合B =________. 答案 {4,9,16}解析 由题意可知集合B 是由集合A 中元素的平方构成,故B ={4,9,16}.12.下列集合中:A ={x =2,y =1},B ={2,1},C ={(x ,y)|⎩⎪⎨⎪⎧x +y =3,x -y =1},D ={(x ,y)|x =2且y =1},与集合{(2,1)}相等的共有________个. 答案 2解析 因为集合{(2,1)}的元素表示的是有序实数对,由已知集合的代表元素知,元素为有序实数对的是C ,D ,而A 表示含有两个元素x =2,y =1的集合,B 表示含有2个元素的集合.13.设A 是满足x<6的所有自然数组成的集合,若a ∈A ,且3a ∈A ,求a 的值.解析 ∵a ∈A 且3a ∈A ,∴a<6且3a<6,∴a<2. 又∵a 是自然数,∴a =0或1.14.已知集合A 含有两个元素a 和a 2,若1∈A ,求实数a 的值.解析 本题中已知集合A 中有两个元素且1∈A ,据集合中元素的特点需分a =1和a 2=1两种情况,另外还要注意集合中元素的互异性. 若1∈A ,则a =1或a 2=1,即a =±1. 当a =1时,集合A 有重复元素,∴a ≠1;当a =-1时,集合A 含有两个元素1,-1,符合互异性. ∴a =-1. ►重点班·选做题15.已知集合A ={0,2,5,10},集合B 中的元素x 满足x =ab ,a ∈A ,b ∈A 且a ≠b ,写出集合B.解析 当⎩⎪⎨⎪⎧a =0,b ≠0或⎩⎪⎨⎪⎧a ≠0,b =0时,x =0;当⎩⎪⎨⎪⎧a =2,b =5或⎩⎪⎨⎪⎧a =5,b =2时,x =10; 当⎩⎪⎨⎪⎧a =2,b =10或⎩⎪⎨⎪⎧a =10,b =2时,x =20; 当⎩⎪⎨⎪⎧a =5,b =10或⎩⎪⎨⎪⎧a =10,b =5时,x =50.所以B ={0,10,20,50}.1.已知A ={x|3-3x>0},则有( ) A.3∈A B.1∈A C.0∈A D.-1∉A答案 C解析 因为A ={x|3-3x>0}={x|x<1},所以0∈A.2.“今有三女,长女五日一归,中女四日一归,小女三日一归,问三女何时相会”.(选自《孙子算经》),请将三女前三次相会的天数用集合表示出来.解析 三女相会的日数,即为5,4,3的公倍数,它们的最小公倍数为60,因此三女前三次相会的天数用集合表示为{60,120,180}.3.数集M 满足条件:若a ∈M ,则1+a1-a ∈M(a ≠±1且a ≠0),已知3∈M ,试把由此确定的集合M 的元素全部求出来.解析 ∵a =3∈M ,∴1+a 1-a =1+31-3=-2∈M ,∴1-21+2=-13∈M.∴1-131+13=12∈M ,∴1+121-12=3∈M.即M =⎩⎨⎧⎭⎬⎫3,-2,-13,12.4.设集合A ={x ,y},B ={0,x 2},若集合A ,B 相等,求实数x ,y 的值. 解析 因为A ,B 相等,则x =0或y =0.(1)当x =0时,x 2=0,则B ={0,0},不满足集合中元素的互异性,故舍去. (2)当y =0时,x =x 2,解得x =0或x =1.由(1)知x =0应舍去. 综上知:x =1,y =0.5.集合A ={x|⎩⎪⎨⎪⎧y =x ,y =x 2}可化简为________. 以下是两位同学的答案,你认为哪一个正确?试说明理由.学生甲:由⎩⎪⎨⎪⎧y =x ,y =x 2,得x =0或x =1,故A ={0,1}; 学生乙:问题转化为求直线y =x 与抛物线y =x 2的交点,得到A ={(0,0),(1,1)}. 解析 同学甲正确,同学乙错误.由于集合A 的代表元素为x ,因此满足条件的元素只能为x=0,1;而不是实数对⎩⎪⎨⎪⎧x =0,y =0,⎩⎪⎨⎪⎧x =1,y =1.故同学甲正确.。
高中人教A版数学必修1课时作业3 Word版含解析

课时作业(三)集合间的基本关系一、选择题.适合条件{}⊆{}的集合的个数是( )....答案:解析:因为集合中必须包含元素,但从元素中至多选取个,于是集合的个数是-=(个),故选..已知集合=,=∈,则( )... 与关系不确定. =答案:解析:在集合中,=,∈,当=时,=,∈;当=-时,=-,∈,故按子集的定义,必有..已知集合={-<<,∈},则下列集合是集合的子集的为( ).={-}.={-}.={-π<<-,∈}.={≤,∈}答案:.已知集合={++≤},={-≤},若⊆,则实数的取值范围是( ). [,+∞). [-].. (-∞,-]答案:解析:由题意知={-≤≤-},所以要使⊆,显然有<,所以={≤≤},根据集合的关系可知≤-..已知集合={(,)+<,>}和={(,)<,<},那么( )....=答案:二、填空题.若=错误!,={(,)=+},且⊆,则=.答案:-解析:=错误!={(,-)},∵⊆,∴-=×+,∴=-..已知∅{-+=},则实数的取值范围是.答案:解析:∵∅{-+=},∴Δ=(-)-≥,∴≤..设={-+=},={-=},若⊆,则实数=.答案:或解析:={-+=}={},={=},若⊆,则=或=..已知集合{},且中至多有个奇数,则这样的集合共有个.答案:解析:若中有且只有个奇数,则={}或{}或{}或{};若中没有奇数,则={}或∅..已知集合=,=错误!错误!,=错误!,则,,之间的关系是.答案:=解析:==,====.。
高中人教A版数学必修1课时作业5 Word版含解析

课时作业(五)补集及综合应用一、选择题.已知全集=,集合={≤或≥},集合={<<+,∈},且(∁)∩≠∅,则实数的取值范围为( ). {<或>}. {<<}. {<<}. {-<<}答案:解析:∁={<<},(∁)∩≠∅,∴<<或<+<.解得<<..设全集是实数集,={>或<-},={≥或<}都是的子集,则图中阴影部分所表示的集合是( ).{-≤<}.{-≤≤}.{<}.{<≤}答案:解析:∵图中阴影部分表示:∈且∉,∴∈(∩∁).又∁={-≤≤},∴∩∁={-≤<}.故选..已知为全集,,,都是的子集,且⊆,⊆,则∁(∩)=( ). {∈∉,且∉}. {∈∉,或∉}. {∈∉,且∉}. {∈∉,或∉}答案:解析:由题意知,∩={∈,且∈},所以∁(∩)={∈∉,或∉}..设全集={},集合={,-},∁={},则的值是( )...或.-或答案:解析:∵∪∁=,∴-=,∴=或..已知全集={},集合={-+=},={=,∈},则集合∁(∪)中元素的个数为( )....答案:解析:={},={=,∈}={},∴∪={},∴∁(∪)={},故选.二、填空题.有人进入家电超市,其中买电视机的有人,买电脑的有人,两种均买的有人,则两种均没买的有人.答案:解析:如图,两种均没买的人数为-(++)=..设集合={+≥},={-<<},全集=,且(∁)∩=∅,则实数的取值范围为.答案:{≥} 解析:∁={<-},。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课时作业(十三) 单调性与奇偶性的综合应用一、选择题1.设f (x )是定义在[-6,6]上的偶函数,且f (4)>f (1),则下列各式一定成立的是( )A .f (0)<f (6)B .f (4)>f (3)C .f (2)>f (0)D .f (-1)<f (4)答案:D 解析:∵f (x )是定义在[-6,6]上的偶函数,∴f (-1)=f (1).又f (4)>f (1),∴ f (4)>f (-1).2.已知定义在R 上的奇函数f (x ),当x >0时,f (x )=x 2+|x |-1,那么x <0时,f (x )的解析式为f (x )=( )A .x 2-|x |+1B .-x 2+|x |+1C .-x 2-|x |-1D .-x 2-|x |+1答案:D 解析:设x <0,则-x >0,f (-x )=x 2+|x |-1,∵f (-x )=-f (x ),∴-f (x )=x 2+|x |-1,∴f (x )=-x 2-|x |+1.3.若f (x )是偶函数,其定义域为(-∞,+∞),且在[0,+∞)上是减函数,则f ⎝ ⎛⎭⎪⎫-32与fa 2+2a +52的大小关系是( ) A .f ⎝ ⎛⎭⎪⎫-32>f ⎝ ⎛⎭⎪⎫a 2+2a +52 B .f ⎝ ⎛⎭⎪⎫-32<f ⎝⎛⎭⎪⎫a 2+2a +52 C .f ⎝ ⎛⎭⎪⎫-32≥f ⎝ ⎛⎭⎪⎫a 2+2a +52 D .f ⎝ ⎛⎭⎪⎫-32≤f ⎝ ⎛⎭⎪⎫a 2+2a +52答案:C 解析:a 2+2a +52=(a +1)2+32≥32,f (x )为偶函数,且在[0,+∞)上是减函数,所以f ⎝ ⎛⎭⎪⎫-32=f ⎝ ⎛⎭⎪⎫32≥f ⎝ ⎛⎭⎪⎫a 2+2a +52. 4.若p (x ),g (x )都是R 上的奇函数,f (x )=ap (x )+bg (x )+2在(0,+∞)上有最大值5,则f (x )在(-∞,0)上有( )A .最小值-5B .最大值-5C .最小值-1D .最大值-3答案:C 解析:∵p (x ),g (x )都是R 上的奇函数,∴f (x )-2=ap (x )+bg (x )为奇函数.又f (x )在(0,+∞)上有最大值5,∴f (x )-2在(0,+∞)上有最大值3,∴f (x )-2在(-∞,0)上有最小值-3,∴f (x )在(-∞,0)上有最小值-1.5.偶函数的定义域为R ,当x ∈[0,+∞)时,f (x )是增函数,则不等式f (x )>f (1)的解集是( )A .(1,+∞)B .(-∞,-1)C .(-1,1)D .(-∞,-1)∪(1,+∞)答案:D 解析:f (x )是偶函数有f (|x |)=f (x ),所以f (x )>f (1)可转化为f (|x |)>f (1),又x ∈[0,+∞)时,f (x )是增函数,所以|x |>1,即x ∈(-∞,-1)∪(1,+∞).6.偶函数y =f (x )在区间[0,4]上单调递减,则有( )A .f (-1)>f ⎝ ⎛⎭⎪⎫π3>f (-π) B .f ⎝ ⎛⎭⎪⎫π3>f (-1)>f (-π) C .f (-π)>f (-1)>f ⎝ ⎛⎭⎪⎫π3 D .f (-1)>f (π)>f ⎝ ⎛⎭⎪⎫π3 答案:A 解析:∵y =f (x )为偶函数,∴f (-1)=f (1),f (-π)=f (π).∵0<1<π3<π<4,y =f (x )在[0,4]上单调递减,∴f (1)>f ⎝ ⎛⎭⎪⎫π3>f (π),∴f (-1)>f ⎝ ⎛⎭⎪⎫π3>f (-π). 7.定义在R 上的偶函数f (x )满足:对任意的x 1,x 2∈(-∞,0](x 1≠x 2),有(x 2-x 1)·[f (x 2)-f (x 1)]>0,则当n ∈N *时,有( )A .f (-n )<f (n -1)<f (n +1)B .f (n -1)<f (-n )<f (n +1)C .f (n +1)<f (-n )<f (n -1)D .f (n +1)<f (n -1)<f (-n )答案:C 解析:由(x 2-x 1)[f (x 2)-f (x 1)]>0,得f (x )在x ∈(-∞,0]为增函数.又f (x )为偶函数,所以f (x )在x ∈[0,+∞)为减函数.又f (-n )=f (n )且0≤n -1<n <n +1,∴f (n +1)<f (n )<f (n -1),即f (n +1)<f (-n )<f (n -1).二、填空题8.若f (x )为奇函数,g (x )为偶函数,且f (x )-g (x )=x 2+3x +2,则f (x )+g (x )=________.答案:-x 2+3x -2解析:∵f (x )-g (x )=x 2+3x +2,∴f (-x )-g (-x )=x 2-3x +2,又f (x )为奇函数,g (x )为偶函数,∴-f (x )-g (x )=x 2-3x +2,∴f (x )+g (x )=-x 2+3x -2.9.若函数f (x )=⎩⎪⎨⎪⎧x 2+2x ,x ≥0,g (x ),x <0为奇函数,则f (g (-1))=________.答案:-15 解析:当x <0时,则-x >0,因为f (x )是奇函数, 所以f (-x )=-f (x )=(-x )2-2x =x 2-2x ,所以f (x )=-x 2+2x ,即g (x )=-x 2+2x ,因此,f (g (-1))=f (-3)=-9-6=-15.10.若函数f (x )=(x +a )(bx +2a )(常数a ,b )是偶函数,值域为(-∞,4],则该函数的解析式f (x )=________.答案:-2x 2+4 解析:由于f (x )=(x +a )(bx +2a )=bx 2+(ab +2a )x +2a 2,所以f (-x )=bx 2-(ab +2a )x +2a 2,∴ab +2a =0,∴a =0或b =-2.又f (x )最大值4,所以b =-2,且f (0)=2a 2=4,∴a =±2,∴f (x )=-2x 2+4.11.老师给出一个函数,请三位同学各说出了这个函数的一条性质:①此函数为偶函数;②定义域为{x ∈R |x ≠0};③在(0,+∞)上为增函数.老师评价说其中有一个同学的结论错误,另两位同学的结论正确.请你写出一个(或几个)这样的函数______________________.答案:y =x 2或y =⎩⎪⎨⎪⎧1-x ,x >0,1+x ,x <0或y =-2x (答案不唯一) 解析:本题为开放型题目,答案不唯一,可结合条件来找.如:y =x 2或y =⎩⎨⎧ 1-x ,x >0,1+x ,x <0或y =-2x .三、解答题12.已知函数y =f (x )在(0,+∞)上为增函数,且f (x )<0(x >0),试判断F (x )=1f (x )在(0,+∞)上的单调性并给出证明过程. 解:F (x )在(0,+∞)上为减函数.证明如下:任取x 1,x 2∈(0,+∞),且x 1< x 2,∴F (x 2)-F (x 1)=1f (x 2)-1f (x 1)=f (x 1)-f (x 2)f (x 2)f (x 1). ∵y =f (x )在(0,+∞)上为增函数,且x 1< x 2,∴f (x 1)<f (x 2),∴f (x 1)-f (x 2)<0.而f (x 1)<0,f (x 2)<0,∴f (x 1)f (x 2)>0.∴F (x 2)-F (x 1)<0,即F (x 1)>F (x 2),∴F (x )在(0,+∞)上为减函数.13.若偶函数f (x )在(-∞,0]上是增函数,且f (a +1)>f (3-a ),求a 的取值范围.解:∵f (x )是偶函数,且在(-∞,0]上是增函数,∴f (x )在[0,+∞)上是减函数.∵f (a +1)>f (3-a ),∴f (|a +1|)>f (|3-a |),∴|a +1|<|3-a |,∴a 2+2a +1<9-6a +a 2,∴a <1,∴a 的取值范围为(-∞,1).14.设f (x )为定义在R 上的偶函数,当x ≤-1时,f (x )=x +b ,且f (x )的图象经过点(-2,0).又在y =f (x )的图象中,有一部分是顶点为(0,2),且过(-1,1)的一段抛物线.(1)试求出f (x )的表达式;(2)求出f (x )的值域.解:(1)∵f (x )的图象经过点(-2,0),∴0=-2+b ,即b =2.∴当x ≤-1时,f (x )=x +2.又∵f (x )为偶函数,∴当x ≥1时,f (x )=f (-x )=-x +2.当-1<x <1时,依题意设f (x )=ax 2+2,则1=a (-1)2+2,∴a =-1,∴当-1<x <1时,f (x )=-x 2+2.综上,f (x )=⎩⎪⎨⎪⎧ x +2,x ≤-1,-x 2+2,-1<x <1,-x +2,x ≥1.(2)当x ≤-1时,f (x )=x +2∈(-∞,1];当-1<x <1时,f (x )=-x 2+2∈(1,2];当x ≥1时,f (x )=-x +2∈(-∞,1].综上所述,f (x )的值域为(-∞,2].尖子生题库15.已知奇函数f (x )=⎩⎪⎨⎪⎧ -x 2+2x ,x >0,0,x =0,x 2+mx ,x <0.(1)求实数m 的值,并在给出的直角坐标系中画出y =f (x )的图象;(2)若函数f (x )在区间[-1,a -2]上单调递增,试确定a 的取值范围.解:(1)当x <0时,-x >0,f (-x )=-(-x )2+2(-x )=-x 2-2x .又f (x )为奇函数,∴f (-x )=-f (x )=-x 2-2x ,∴f (x )=x 2+2x ,∴m =2.y =f (x )的图象如图所示.(2)由(1)知,f (x )=⎩⎪⎨⎪⎧ -x 2+2x ,x >0,0,x =0,x 2+2x ,x <0,由图象可知,f (x )在[-1,1]上单调递增, 要使f (x )在[-1,a -2]上单调递增,只需⎩⎪⎨⎪⎧a -2>-1,a -2≤1,解得1<a ≤3. 故a 的取值范围是(1,3].。
