光纤光栅的特性
光纤光栅光学特性的测量

光纤光栅光学特性的测量一、实验目的和内容1. 了解光纤Bragg 光栅的原理及其主要光学特性。
2. 掌握Digtal lock-in Amplifier 工作原理和使用要领。
3. 掌握测量光纤Bragg 光纤反射光谱及其它光学特性的方法二、实验基本原理1. 光纤布拉格光栅的理论模型光敏光纤布拉格光栅(FBG,fiber Bragg grating )的原理是由于光纤芯折射率周期变化造成光纤波导条件的改变,导致一定波长的光波发生相应的模式耦合,使的其透射光谱和反射光谱对该波长出现奇异性,图1表示了其折射率分布模型。
这只是一个简化图形,实际上光敏折射率改变的分布将由照射光的光强分布所决定。
对于整个光纤曝光区域,可以由下列表达式给出折射率分布较一般的描述:⎪⎩⎪⎨⎧≥≤≤≤+=2321211)],,(1[),,(a r n a r a n a r z r F n z r n ϕϕ 式中),,(z r F ϕ为光致折射率变化函数。
具有如下特性: 1),,(),,(n z r n z r F ϕϕ∆=)(0),,()0(),(1maxmax L z z r F L z n n z r F >=<<∆=ϕϕ式中1a 为光纤纤芯半径;2a 为光纤包层半径;相应的1n 为纤芯初始折射率;2n 为包层折射率;),,(z r n ϕ∆为折射率最大变化量。
因为制作光纤光栅是需要去掉包层,所以这里的3n 一般指空气折射率。
之所以式中出现ϕ和r 坐标项,是为了描述折射率分布在横截面上的精细结构。
在式(1)中隐藏了如下两点假设:第一,光纤为理想的阶跃型光纤,并且折射率沿轴向均匀分布;第二,光纤包层为纯石英,由紫外光引起的折射率变化极其微弱,可以忽略不计。
这两点假设有实际意义,因为目前实际由于制作光纤光栅的光栅,多数是采用改进化学汽相沉积法(MCVD )制成,且使纤芯重掺锗以提高光纤的紫外光敏性,这就使得实际的折射率分布很接近于理想阶跃型,因此采用理想阶跃型光纤模型不会引入于实际情况相差很大的误差。
光纤光栅

天津爱天光电子科技有限公司是美国 AT.photonics公司在天津的独资分公司, 简称天津爱天公司。公司按国际规范进行 产品质量管理。 主要运营方向是开发、生产和销售不 同用途的各种光学器件以及用于光传感和 光通信领域的光源、光纤光栅传感器、光 纤光栅传感实验仪以及各类光纤光栅传感 监测及测量仪器。
5、 石油化学工业:光纤光栅本质安全, 特别适合于石化厂、油田中的温度、液位 等的监控 6、 医学:如可遥测核磁共振机中实地 温度,可进行心脏有效率的测量等 7、 核工业中的应用:监视废料站的情 况,监测反应堆建筑的情况等 8、 光纤光栅还可以应用于水听器、机 器人手臂传感、识别安全系统等
谢 谢
光纤光栅的中心波长即随温 度的变化而变化,也随应变的变化 而变化,在光通信领域中,这成为 光纤光栅应用的难题之一,而在传 感领域,它又成为必要的技术基础。
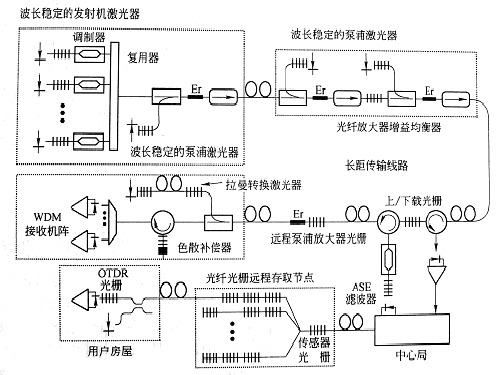
4.光纤光栅传感系统
三、光纤光栅传感系统
光纤光栅传感器是用光纤光栅制成的 一种新型光纤传感器。光纤光栅是20世纪 90年代发展起来的一种新型全光纤无源器 件,它具有体积小、重量轻、与光纤兼容、 插入损耗低、性能长期稳定性好等特点。 利用光纤光栅制成多种传感器如温度、应 变、应力、加速度、压强等传感器。不同 的光纤光栅传感器可具有不同的工作波长, 因此可以利用波分复用技术,在一根光纤 级联多个光纤光栅传感器作分布式测量。
光纤光栅传感器主要特点: A. 全光纤无源器件,抗电磁干扰,可 用于一些恶劣环境的测量; B. 与光纤兼容,传输损耗低,容易实 现对被测信号的远距离检测; C. 为波长检测器件,感应光信号与传 输线路损耗无关; D. 灵敏度高,长期稳定性好; E. 耐腐蚀,可靠性高; F. 反应灵敏,可实时测量; G. 可级联使用,作分布测量。
光栅布拉格光栅及其传感特性研究

光栅布拉格光栅及其传感特性研究2一光纤光栅概述21.1 光纤光栅的耦合模理论21.2 光纤光栅的类型31.2.1 均匀周期光纤布拉格光栅31.2.2 线性啁啾光纤光栅31.2.3 切趾光纤光栅31.2.4 闪耀光纤光栅41.2.5 相移光纤光栅41.2.6 超结构光纤光栅41.2.7 长周期光纤光栅4二光纤布拉格光栅传感器52.1 光纤布拉格光栅应力传感器52.2 光纤布拉格光栅温度传感器62.3 光纤布拉格光栅压力传感器62.4 基于双折射效应的光纤布拉格光栅传感器7三光纤光栅传感器的敏化与封装103.1 光纤光栅传感器的温度敏化103.2 光纤光栅传感器的应力敏化103.2 光纤光栅传感器的交叉敏感及其解决方法10四光纤光栅传感网络与复用技术104.1 光纤光栅传感网络常用的波分复用技术114.1.1 基于波长扫描法的波分复用技术124.1.2 基于波长分离法的波分复用技术134.1.3 基于衍射光栅和CCD阵列的复用技术134.1.4 基于码分多址(CDMA)和密集波分复用(DWDM)技术144.2光纤光栅传感网络常用的空分复用技术144.3光纤光栅传感网络常用的时分复用技术164.4 光纤光栅传感网络的副载波频分复用技术184.4.1 光纤光栅传感副载波频分复用技术184.4.2 FBG传感网络的光频域反射复用技术184.5 光纤光栅传感网络的相干复用技术184.6 混合复用FBG传感网络184.6.1 WDM/TDM混合FBG网络184.6.2 SDM/WDM混合FBG网络184.6.3 SDM/TDM混合FBG网络184.6.4 SDM/WDM/TDM混和FBG网络184.6.5 光频域反射复用/波分复用混合FBG传感网络18五光栅光栅传感信号的解调方法18六激光传感器18光栅布拉格光栅及其传感特性研究一 光纤光栅概述1.1 光纤光栅的耦合模理论光纤光栅的形成基于光纤的光敏性,不同的曝光条件下、不同类型的光纤可产生多种不同的折射率分布的光纤光栅。
光纤光栅

(k = 0,1,2,3…)
N=2 d=3a N=3 d=3a N=4 d=3a N=5 d=3a
-2 -1 0 1 2
衍射图样
归一化强度分布(N为狭缝数目)
光栅衍射图样及强度分布
1.光纤光栅的定义
光纤光栅:在一定长度的光纤上,在光纤的纤芯或者
包层中,周期性的改变折射率。
边界条件
dR ( z ) ˆ i R ( z ) i S ( z ) dz dS ( z ) ˆS ( z ) i R ( z ) i dz
d 令D dz
ˆ R ikS D i ˆ S ikR D i
光栅衍射
平行光垂直照到光栅平面时, 光波将在每个狭缝处发生衍射, a b 衍射光干涉后再经透镜会聚到 屏幕上,使屏幕上出现细亮的 等间距条纹。 是单缝衍射与各个缝之间干 涉的综合效果
d
θ
f
o
P
θ
o
f
光栅衍射
光栅方程(亮纹条件) :
(a b) sin k
N=1
d=a+b 为光栅常量 亮纹到中心的距离:
*
ˆ
2
neff
1 d 是光纤光栅的直流自耦合系数 2 dz
neff 表示光纤光栅的交流耦合系数
布拉格波长 2neff
均匀光纤光栅耦合模方程组的解析解
R L / 2 1
L z , S ( L / 2) 0 光栅长度外无反向传输光存在 2
光栅的相位变化即chirp
2 neff ( z) neff ( z)1 v cos z ( z) * f ( z)
光纤光学8-光纤光栅
Ⅱ类光栅:温度稳定性好(800℃)、脉冲激光
极高UV曝光量,瞬间局部温度达上千度、物理破坏引 起折射率变化(融化石英基质,物理性损伤)、折射 率变化⊿n可达10-2
三、光纤光栅的制作技术
内部写入法
干涉写入法
逐点写入法
1、内部写入法
光纤中沿相反方向传播的两列相干光波可表示为
E f A sin(kz wt ) Eb A sin(kz wt )
B 布拉格波数; B 2 B B 布拉格波长;
与布拉格光栅周期关系 B 2n0
n
NL
小,我们暂不考虑。
1 n2 E 2
2
表征非线性折射率变化,由于其值很
根据耦合模理论,应包括向前和向后传播的光, 因而光纤中的光场是正向传播的模式和反向传播的模 式的线性叠加,各个模式的系数是随着传输距离的变 换发生变化的。
4、 相位掩膜技术
相位掩模是采用电子束平板印刷术或全息曝光 蚀刻于硅基片表面的一维周期性透射相位光栅,其 实质是一种特殊设计的光学衍射元件。
相位掩模的高级衍射波强度较弱,通常只考虑0 级和±1级衍射波,在正入射情况下±1衍射波的强度 相等。衍射角满足光栅 sin m sin i m (n )
光纤光栅的分类:I型、IIA型和II型
Ⅰ类光栅:温度稳定性较差(300℃)、脉冲或连续 较低掺杂浓度、较低UV曝光量、局部缺陷引起折射 率变化、折射率变化⊿n~ 10-5—10-3 ⅡA类光栅:温度稳定性较好(500℃)、脉冲或连续 掺杂浓度较高(eg >25mol% GeO2)、 较高UV曝光 量( > 500J/cm2),、结构重构引起折射率变化、 折射率变化⊿n<0
提出了多种模型,没有一种可以解释所 有的实验结果。
啁啾光纤光栅特性及应用

啁啾光纤光栅特性及应用光纤光栅是一种利用光纤中的周期性折射率变化来实现光的分布式反射和耦合的光学器件。
它可以通过改变光纤中的折射率分布来实现光的选择性反射和耦合,从而实现光的分布式传输和处理。
光纤光栅具有许多优良特性和广泛的应用领域。
1. 特性:光纤光栅具有很多特殊的特性,使其在光学器件中得到广泛应用。
(1)完全内反射:光纤光栅可以实现光的完全内反射,使光在光纤中分布非常均匀,降低光线的损耗和失真。
(2)波长选择性耦合:利用光纤光栅的周期性折射率变化,可以实现对特定波长的光线的选择性耦合,使光纤光栅成为波分复用和光通信中的重要组件。
(3)光纤传感:光纤光栅可以通过改变光纤中的折射率分布来实现对光线的敏感性,可以用于测量温度、压力、形变等物理量的传感器。
(4)光谱分析:光纤光栅可以通过对光在光纤中的反射和耦合的特性进行分析,实现光谱分析和光谱测量。
2. 应用:光纤光栅具有广泛的应用领域,以下是其中一些典型的应用。
(1)光通信:光纤光栅在光通信中有广泛的应用,可以用于实现波分复用、光纤传感、光纤光栅滤波器等。
比如,光纤光栅滤波器可以实现波分复用中的光信号的分离和提取,提高光通信系统的传输性能。
(2)光纤传感:利用光纤光栅的敏感性,可以实现对温度、压力、形变等物理量的测量。
光纤光栅传感器具有实时、分布式和高精度等特点,被广泛应用于工业、环境监测、化学生物等领域。
(3)光谱分析:光纤光栅可以通过对光谱的分析,实现对光信号的光谱分析和光谱测量。
光纤光栅光谱仪可以用于光谱分析、化学测量、生物医学等领域。
(4)激光调制:光纤光栅可以用作光调制器,在激光通信和激光传感中发挥重要作用。
通过改变光纤光栅的折射率分布,可以实现对激光光束的控制和调制。
总之,光纤光栅具有许多独特的特性和广泛的应用领域。
它在光通信、光传感、光谱分析和激光调制等领域起到重要作用,对光学器件的发展和光学通信的进步起到了重要推动作用。
随着技术的不断发展,相信光纤光栅在未来会有更加广泛的应用和更高的性能。
光纤布拉格光栅基本参数

光纤布拉格光栅基本参数光纤光栅的形成方式主要是使用各类激光使光纤产生轴向的折射率周期性变化,从而形成永久性空间的相位光栅,其作用实质上是在纤芯内形成一个(透射或反射)滤波器或反射镜,将确定频率/波长的导模反射,原理类似多层增反膜,其滤波波长称为布拉格波长,在确定条件下布拉格波长=光栅所在位置的有效折射率*2光栅周期(在相位掩膜版法刻写时,此数值为相位掩膜版的周期,即相位掩膜版的周期=2*光栅周期)即λ(波长)=2*neff(折射率)*Λ(光栅周期),而有效折射率和光栅周期会随温度和应力状态改变,这也是光纤光栅应用于应力及温度传感的基础。
注:本段依据Dream的提问内容于2022年4月19日作出修改,去掉了不正规的表述内容。
光纤光栅的基础特征参数包括:光纤类型、光栅类型、中心波长,峰宽/带宽/3dB带宽/FWHM,反射率,边模/旁瓣抑制比,光栅长度。
高端特征参数包括:刻写环境温度、测试模式、反射峰的线型(近高斯,近洛伦兹型,卷积型等),色散值,啁啾率,光栅阶数等光纤类型:由于不同光纤的折射率及内部结构均有所差别,所以光纤类型是光纤光栅的重要特征参数。
光栅类型:光纤光栅有多种不同类型,例如均匀、啁啾、长周期、相移、取样、倾斜等,不同类型的光纤光栅用于不同的用途,也是光纤光栅的重要特征参数。
中心波长:中心波长一般可用光纤光谱仪测得,由于光纤光对温度及应力均比较敏感,所以一般需在悬空不受力且温度恒定的位置测量比较标准(精度要求特别高的,还需要标定测试模式),按照光纤类型的不同,其温度变化系数大约为10-20Pm/℃(升温红移,降温蓝移),所以制造时的环境温度也是光纤光栅的一个重要参数。
峰宽/带宽/3dB带宽/FWHM:一般商用光纤光栅均使用3dB带宽来进行表征,在激光用途,光纤激光器腔镜一般为低功率高反2nm低反1nm,高功率则选择高反3-4nm低反1nm的配置,而用于外腔半导体腔外稳频用途的光纤光栅,一般带宽都在0.1nm左右,而用于光纤DFB激光器中产生单频激光用途的光纤光栅,则一般选用相移光纤光栅,其相移峰带宽一般小于100MHz,而用于DBR激光器的光栅对,其低反一般需要到0.05nm以下。
光纤布拉格光栅(FBG)介绍

光纤布拉格光栅(FBG)介绍1 介绍FBG是Fiber Bragg Grating的缩写,即光纤布拉格光栅。
在纤芯内形成的空间相位周期性分布的光栅,其作用的实质就是在纤芯内形成一个窄带的(透射或反射)滤波器或反射镜。
利用这一特性可制造出许多性能独特的光纤器件。
这些器件具有反射带宽范围大、附加损耗小、体积小,易与光纤耦合,可与其它光器件兼容成一体,不受环境尘埃影响等一系列优异性能。
目前应用主要集中在光纤通信领域(光纤激光器、光纤滤波器)和光纤传感器领域(位移、速度、加速度、温度的测量)。
近年来,随光纤光栅的重要性被人们所认识,各种光纤光栅的制作方法层出不穷,这些方法各有其优缺点,下面分别进行评述。
2光纤光栅制作方法2.1光敏光纤的制备采用适当的光源和光纤增敏技术,可以在几乎所有种类的光纤上不同程度的写人光栅。
所谓光纤中的光折变是指激光通过光敏光纤时,光纤的折射率将随光强的空间分布发生相应的变化,如这种折射率变化呈现周期性分布,并被保存下来,就成为光纤光栅。
光纤中的折射率改变量与许多参数有关,如照射波长、光纤类型、掺杂水平等。
如果不进行其它处理,直接用紫外光照射光纤,折射率增加仅为(10的负4次方)数量级便已经饱和,为了满足高速通信的需要,提高光纤光敏性日益重要,目前光纤增敏方法主要有以下几种:1)掺入光敏性杂质,如:锗、锡、棚等。
2)多种掺杂(主要是B/Ge 共接)。
3)高压低温氢气扩散处理。
4)剧火。
2.2成栅的紫外光源光纤的光致折射率变化的光敏性主要表现在244nm紫外光的错吸收峰附近,因此除驻波法用488nm可见光外,成栅光源都是紫外光。
大部分成栅方法是利用激光束的空间干涉条纹,所以成栅光源的空间相干性特别重要。
目前,主要的成栅光源有准分子激光器、窄线宽准分子激光器、倍频Ar离子激光器、倍频染料激光器、倍频OPO激光器等,根据实验结果,窄线宽准分子激光器是目前用来制作光纤光栅最为适宜的光源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
光纤光栅的特性1.光纤布喇格光栅的理论模型:假设光纤为理想的纤芯掺锗阶跃型光纤,并且折射率沿轴向均匀分布,包层为纯石英,此种光纤在紫外光的照射下,纤芯的折射率会发生永久性变化,对包层的折射率没有影响。
利用目前的光纤光栅制作技术:如全息相干法,分波面相干法及相位模板复制法等。
生产的光纤光栅大多数为均匀周期正弦型光栅。
纤芯中的折射率分布(如图1)所示。
)(1Z n 为纤芯的折射率,m ax n ∆为光致折射率微扰的最大值,)0(1n 为纤芯原折射率,Λ为折射率变化的周期(即栅距),L 为光栅的区长度。
若忽略光栅横截面上折射率分布的不均匀性,光栅区的折射率分布可表示为:)2cos()0()(max 11Z n n z n Λ∆+=π…………………………………………………(1.1)显而易见,其折射率沿纵向分布,属于非正规光波导中的迅变光波导,在考虑模式耦合的时候,只能使用矢量模耦合方程,其耦合主要发生在基模的正向传输导模与反向传输导模之间。
2.单模光纤的耦合方程由于纤芯折射率非均匀分布,引起了纤芯中传输的本征模式间发生耦合。
在弱导时, 忽 略偏振效应,吸收损耗和折射率非均匀分布引起了模式泄漏,则非均匀波导中的场Φ( x , y ,z ) 满足标量波动方程:0),,(}),,({222202=Φ∂∂++∇z y x zz y x n sk t…………………(2.1)其中:λπ/20=k ,λ是自由空间的光波长。
22221}{1ϕ∂∂+∂Φ∂∂∂=Φ∇Φr r r r r t…………………………………………………(2.2) 由于折射率非均匀分布引起波导中模式耦合只发生在纤芯中,因此非均匀波导中的场 可以表示为均匀波导束缚模式),(y x φ之和:),()}exp()exp()({),()(),,(y x z i a z i z a y x z A z y x l l l l l ll l lφββφ-+-∑=∑=Φ………(2.3))(1z A 则表示与),(1y x φ相联系的全部随z 变化的关系。
本节讨论省去了所有对结论无影响的)exp(t j ω的因子。
其中),(1y x φ满足方程:0}),({22202=-+∇l t aver t y x n k φβ…………………………(2.4)将∑⋅=Φll lAφ代入2.1中,并利用2.4消去含有l t φ2∇的项,并按模式耦合理论的一般方法进行处理,化简时略去高次项,则可以得到一个正向传输模与同一反向传输模间的模式耦合方程:)2exp(2)2exp(21111z i a Ddz da z i a Ddz da ββββ--=-=--……………………………………………(2.5)ηφφββaver aver A A aver n n n ik dA dAn n ik D co2)()(22220222220-=-=⎰⎰∞…………………………(2.6) 其中dAdAA A co⎰⎰∞=22φφη…………………………………………………………(2 .7)是芯层中的功率百分比。
在阶跃折射率剖面光纤中,基模可以用高斯函数近似代替,代入2.7式中得:211V-=η,其中V 为光栅的结构常数。
其中βββ=-=-11 为传播常数。
根据射线理论,光纤中模场的传播常数λπβ/2n =。
在单模光纤中n 近似等于原纤芯折射率)0(1n 。
由于)cos(2222222z n n n n n n n n n n n n n n aver aver averaver averaver aver aver aver θ∆=-=-≈-=-……(2.8) 其中:Λ=πθ2 所以)cos(2)cos(20z n i z n ik D θηλπθηβ∆=∆=……………………………………(2.9) 令耦合系数ηλπn C ∆=………………………………………………………………(2.10) 将2.8,2.9代入2.5和2.6得:)2exp()cos(2)2exp()cos(21111z i z a C i dzda z i z a C i dz da βθβθ⋅-=⋅-=--………………………………………………(2.11)又)(21)2cos()cos(22Λ-Λ+=Λ=πππθi i e e z z 代入2.6,并省略高次项])(2exp[z i βπ+Λ则 ]2exp[]2exp[1111z i a iC dzda z i a iC dzda ββ∆-⋅-=∆⋅-=--………………………………………………………(2.12)其中Λ-=∆πββ设折射率扰动区间)(2,1Z Z ,长度为L ,不难得到边界条件:在1Z 处L =0,1)0(1=a ,在2Z 处,0)(1=-L a 。
利用此边界条件,可解出方程2.7)](sinh[)]cosh()[sinh()exp()()]}(cosh[)](sinh[{)]cosh()sinh([)exp()(11L z S SL iS SL z i C Z a L z S iS L z S SL iS SL z i Z a --∆-⋅=-+-∆-∆∆-=-ββββ(2.13)其中:222β∆-=C S因此得到端口处( z = 0) 当22β∆≥C 时入射光的反射率为:)(cosh )(sinh )(sinh )0()0(),(222222211SL S SL SL C a a L R +∆==-βλ…………………………… (2.14)当0=∆β,即Λ=n 2λ时,满足相位匹配条件,2.9可以化为:)(tanh 2max CL R =当22β∆<C 时,入射光的反射率QLk QL C a a L R 22222211cos )(sin )0()0(),(-∆==-βλ…………………………………………(2.15) 其中222C Q -∆=β由R 的表达式可以求得反射谱的半高全宽度(FWHM) 为:2122])()2[(Ln n B FWHMΛ+∆≈∆λλ……………………………………………………(2.16)对弱反射(峰值反射率较低) 光栅一般还须在上式右端乘以系数0. 5 加以修正。
3光线光栅的特性分析a ):反射率与光栅长度的关系反射率是光纤光栅的一个重要参数2.14和2.15直接描述了反射率R 和光栅长度L 的关系。
下面图3.1,3.2,.3.3分别描述了不同耦合系数(即不同n ∆)时候,R 和L 的关系。
光栅中心波长nm 5.827=λ,V =2.405,)11(*2Vn n C -∆=∆=λπηλπ折射率扰动n ∆分别为444410*4,10*3,10*2,10*1----。
图3.1 反射率与光栅长度的关系可见对折射率扰动大的光栅,长度较短也可以达到高的反射率。
图3.2描述n ∆分别为334410*2,10*1,10*8,10*6----时,反射率与光栅长度的关系。
图3.2反射率与光栅长度的关系图3.3描述n ∆分别为555510*4,10*3,10*2,10*1----时,反射率与光栅长度的关系。
图3.3反射率与光栅长度的关系b ):有效长度c L 与折射率扰动的关系取反射率R =0.9时,光栅长度为有效长度c L ,可得有效长度c L 与n ∆的关系。
n ∆从0变化到410*5-,其他参数仍照上面选取,可以得到如下曲线:图 3.4 光栅有效长度和折射率扰动的关系可见在反射率一定的情况下,折射率扰动越大,光栅的长度可以做的越短。
图3.5,3.6描述了n ∆从0变化到310*5-,0变化到510*5- 时候c L 与n ∆的关系。
图 3.5 光栅有效长度和折射率扰动的关系图 3.6 光栅有效长度和折射率扰动的关系c ):谱线宽度光栅的另一个重要特性是谱线宽度,我们取半峰谱线宽度为光栅线宽λ∆。
图.3.7描述了n ∆变化对λ∆的影响。
折射率扰动大会加宽谱线带宽,光栅的谱线宽度λ∆还与光栅长度L 有关。
图3.8描述了410*1-=∆n 时,线宽λ∆和光栅长度L 的关系。
根据公式2122])()2[(Ln n B FWHMΛ+∆≈∆λλ,我们取中心波长m b 610*5497.1-=λ,n =1.462,710*3.5-=Λ,m L 410*6-=,510*5~0-=∆n图3.7 线宽与折射率的关系3.8 线宽与光栅长度的关系d :)光纤光栅反射光谱特性 根据公式:)(cosh )(sinh )(sinh )0()0(),(222222211SL S SL SL C a a L R +∆==-βλ…………………………… (2.14)当0=∆β,即Λ=n 2λ时,满足相位匹配条件,2.9可以化为:)(tanh 2max CL R =当22β∆<C 时,入射光的反射率QLk QL C a a L R 22222211cos )(sin )0()0(),(-∆==-βλ…………………………………………(2.15) 其中222C Q -∆=β我们假设光纤各项参数为:m b 610*5497.1-=λ,n =1.462,710*3.5-=Λ,m L 410*6-=,310*4-=∆n ,V =2.405得到3.9光栅反射光谱特性曲线3.9光栅反射光谱特性曲线从上图我门可以得出2个结论: (1):存在峰值反射率。
当δβ=0 时,有峰值反射率;当δβ≠0 时,反射谱有边带存在,边带的反射率大大降低。
δβ= 0 时有λ= 2n Λ= B λ,这称为光纤光栅的Bragg 条件,其中B λ为Bragg 波长。
即在一阶Bragg 波长2 n Λ=B λ 处,有最大反射率)(tanh 2max CL R =。
(2): λ=B λ 时,由上式可以看出:耦合系数愈高,峰值反射率愈高,愈接近于1 ,反射谱边带的峰值反射率也相应增大。
