指数函数图象的平移
指数函数图象的翻折平移.ppt

1 : y 3x
2 : y (1)x 3
思考:y ax与y ax的图象有什么关系?
函数图象的变换
思考:y ax与y ax的图象有什么关系?
观察它们的图象
令f (x) ax ,则ax f (x) f (x) 图象关于y轴对称 f (x)
思考:y ax与y ax的图象有什么关系?
观察它们的图象
小结:
小结:
练习1:已知f (x) 2x , 作出| f (x) 1| 和f (| x 1|)的图象
练习2:方程2|x| x 2的实根的个数
2、图象的平移变换
(1)
f (x) 沿x轴正方向平 移a个单位 f (x a), (a 0)
(2)
f (x) 沿x轴负方向平移a个单位 f (x a), (a 0)
(3)
f (x) 沿y轴正方向平移b个单位 f (x) b, (b 0)
(4)
f (x) 沿y轴负方向平移b个单位 f (x) b, (b 0)
观察它们的图象
令f (x) ax ,则 ax f (x) f (x) 图象关于x轴对称 f (x)
思考:y ax与y ax的图象有什么关系?
观察它们的图象
令f (x) ax ,则 ax f (x)
f (x) 图象关于原点对称 f (x)
1、图象的对称变换
(1)
f (x) 图象关于y轴对称 f x 1的图象
x
x 1
y x 1 1 2 x 1 x 1
y 2 向左 平移1 y 2
y
x
x 1
y 1 2 向上平移1 x 1
1
2 1 0 1 2
x
3、图象的翻折变换
指数函数的图像和性质教案设计

指数函数的图像和性质教案设计第一章:指数函数的引入1.1 生活中的实例引入通过生活中的实例,如细胞分裂、放射性衰变等,引入指数函数的概念。
引导学生观察实例中的规律,引发对指数函数的好奇心。
1.2 指数函数的定义给出指数函数的数学定义:形如f(x) = a^x 的函数,其中a 是正常数。
解释指数函数与幂函数的关系。
1.3 指数函数的图像利用数学软件或图形计算器,绘制几个简单的指数函数图像。
引导学生观察图像的形状和特点,如随着x 的增大,函数值增大或减小等。
第二章:指数函数的性质2.1 指数函数的单调性探讨指数函数的单调性,即随着x 的增大,函数值是增大还是减小。
引导学生通过观察图像或数学推理来得出结论。
2.2 指数函数的渐近行为分析指数函数在x 趋向于正无穷和负无穷时的渐近行为。
引导学生理解指数函数的快速增长和减趋行为。
2.3 指数函数的零点和极限探讨指数函数的零点,即函数值为零的x 值。
引导学生理解指数函数的极限概念,如x 趋向于某个值时函数的极限。
第三章:指数函数的应用3.1 人口增长模型利用指数函数模型描述人口增长,介绍人口增长的基本规律。
引导学生通过指数函数来分析和预测人口变化。
3.2 放射性衰变模型利用指数函数模型描述放射性物质的衰变过程,介绍放射性衰变的基本规律。
引导学生通过指数函数来分析和预测放射性物质的变化。
3.3 投资增长模型利用指数函数模型描述投资的复利增长,介绍投资增长的基本规律。
引导学生通过指数函数来分析和预测投资的变化。
第四章:指数函数的图像和性质的综合应用4.1 指数函数图像的变换探讨指数函数图像的平移、缩放等变换规律。
引导学生通过变换规律来理解和绘制更复杂的指数函数图像。
4.2 指数函数性质的综合应用结合前面的学习,解决一些综合性的问题,如求指数函数的零点、极值等。
引导学生运用指数函数的性质来解决实际问题。
第五章:复习和拓展5.1 复习指数函数的图像和性质通过复习题和小测验,巩固学生对指数函数图像和性质的理解。
指数函数定义域,值域,复合函数单调性,平移,轴对称

指数函数定义域,值域,复合函数单调性,平移,轴对称对你有一定的帮助!1.若函数1.若函数f ( x) = 2 x 3 + 3 的图像恒过定试求P的坐标。
点P,试求P的坐标。
2. 函数y=a x-1+4 恒过定点_____. 恒过定点_____ _____. = -3.方程2 3(2 ) 4 = 0的解为:____2x x对你有一定的帮助!一.求指数型复合函数的定义域、值域:求指数型复合函数的定义域、值域:(1) y = 0.4x1 x 1(2) y = 35 x 1(3) y = 2 + 1(4) y = 4 + 2xx+1+1对你有一定的帮助!二.求下列函数的定义域、值域:求下列函数的定义域、值域:(1) y = 31 2 x1 (2) y = ( ) 2x 11 x2 4x x (3) y = ( ) (4) y =3 + 1 4对你有一定的帮助!复合函数单调性复合函数的单调性,同增异减” 复合函数的单调性,根据“同增异减”的原则处理.u = g (x)增减增减f ( x) = a增减减增uf ( x) = a增增减减g ( x)对你有一定的帮助!练习讨论下列函数的定义域、值域、1、讨论下列函数的定义域、值域、单调区间(1) y = 2x 1(2) y = 3x2 2 x( 3) y = 3x1 ( 4) y = 3x2 2 x对你有一定的帮助!作业1、求函数的定义域、值域和单调区间. 求函数的定义域、值域和单调区间.(1) y = 0.5 (2) y = 21 2 x + x22x + 2 x +1对你有一定的帮助!求下列函数的的定义域、值域、求下列函数的的定义域、值域、单调区间(1) y = log2 ( x + 2x + 5)2(2) y = log 1 ( x + 4x + 5)2 3对你有一定的帮助!2 1 例已知函数f (x) = x 2 +1x(1)确定f(x)的奇偶性;(1)确定f(x)的奇偶性;奇函数确定f(x)的奇偶性(2)判断f(x)的单调性;(2)判断f(x)的单调性;R上是单调递增判断f(x)的单调性在(3)求f(x)的值域. (3)求f(x)的值域. 的值域值域( 值域(-1,1)对你有一定的帮助!练习: 练习:解下列不等式(1) 6x2 + x 211 x2 8 2x (2) ( )3 3 1 x2 x2 2 x (3) a ( ) ( a 0且a ≠ 1) a对你有一定的帮助!一、指数函数图象的变换1.说明下列函数图象与指数函数=2x的说明下列函数图象与指数函数y= 说明下列函数图象与指数函数图象关系,并画出它们的图象: 图象关系,并画出它们的图象(1) y = 2xx+1, y=2x+2;(2) y = 2x 1, y=2x 2;(3) y = 2 + 1, y = 2 1.x对你有一定的帮助!(1) y = 2xx+1, y=2-2x+2作出图象,显示出函数数据表作出图象,-3x -11 2 42 43 8y=20.125 0.25 0.5 1 0.25 0.5 0.5 1 1 2 2 4y=2y=2x+18 16x+28 16 32对你有一定的帮助!比较函数y=2xy9 8 7 6 5 4 3 2 1 -4 -2 O 2 4y=2x+1x+2y=2. 的图象关系x对你有一定的帮助!比较函数y=2xy9 8 7 6 5 4 3 2 1 -4 -2 O 2 4 y=2x+1x+2y=2. 的图象关系x对你有一定的帮助!比较函数y=2xy9 8 7 6 5 4 3 2 1 -4 -2 O 2 4 y=2x+1x+2y=2. 的图象关系x对你有一定的帮助!(2) y = 2xx 1, y=2x 2作出图象,显示出函数数据表作出图象,-3x -2 0.25 0.125-1 0.5 0.250 1 0.51 2 12 3 4 8 2 4y=2y=20.125 0.0625x 1y=2x 20.03125 0.0625 0.125 0.25 0.5 1 2对你有一定的帮助!比较函数y=2y=2__ 1y9 8 7 6 5 4 3 2 1 -4 -2 O 2 4y=2x 2. 的图象关系x对你有一定的帮助!比较函数y=2y=2__ 1y9 8 7 6 5 4 3 2 1 -4 -2 O 2 4 y=2x 2. 的图象关系x对你有一定的帮助!比较函数y=2y=2__ 1y9 8 7 6 5 4 3 2 1 -4 -2 O 2 4 y=2x 2. 的图象关系x对你有一定的帮助!。
高中新教材数学必修件时指数函数的图象与性质

对称变换规律
01
指数函数$y=a^x$($a>0$,$aneq 1$)的图像关于 原点对称。即当$x$取相反数时,$y$也取相反数。
02
指数函数图像也关于直线$y=x$对称。即当函数形式为 $y=a^x$和$x=a^y$时,两个函数的图像关于直线 $y=x$对称。
03
对称变换不改变图像的形状和开口方向,只改变图像的 位置和对称轴。
当$0 < a < 1$时,指数函数的 图像在$x$轴上方,但随着$x$ 的增大,函数值逐渐减小,图像
向右下方延伸。
指数函数的图像都经过点$(0, 1)$。
指数函数性质总结
01
指数函数的值域为$(0, +infty)$。
02
指数函数在其定义域内是连续的。
03
指数函数在其定义域内是可导的,且导数等 于其自身乘以一个常数。
03
电磁辐射衰减
在通信和电磁学领域,指数函数可用于描述电磁辐射在传播过程中的衰
减。根据衰减常数和传播距离,可以计算信号强度的变化。
复合增长问题中指数函数应用
复利计算
在金融领域,指数函数用于计算 复利问题。通过给定本金、年利 率和存款期限,可以计算存款到
期时的本息总额。
连续增长模型
在经济学和生物学等领域,指数 函数可用于描述连续增长的模型 。通过分析历史数据,可以估算 出连续增长率,并预测未来某一
时刻的数量或规模。
化学反应动力学
在化学领域,指数函数用于描述 化学反应的动力学过程。通过分 析反应速率与反应物浓度的关系 ,可以了解反应的动力学特性和
反应机理。
05 典型例题解析与课堂互动环节
典型例题解析过程展示
01
指数、对数、幂函数对比
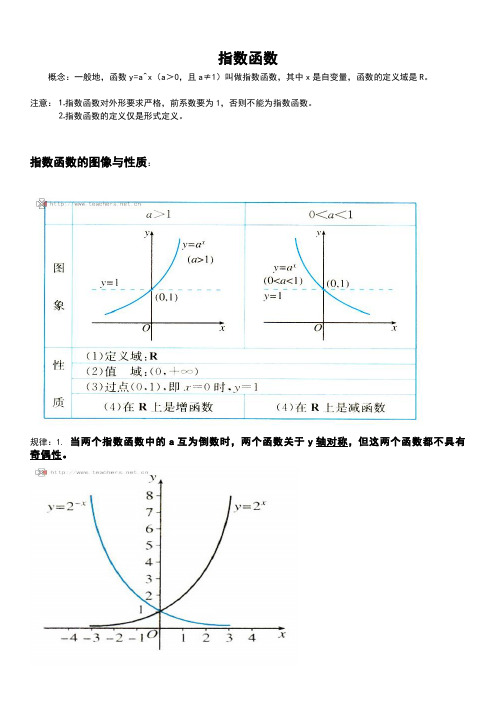
指数函数概念:一般地,函数y=a^x(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R。
注意:⒈指数函数对外形要求严格,前系数要为1,否则不能为指数函数。
⒉指数函数的定义仅是形式定义。
指数函数的图像与性质:规律:1. 当两个指数函数中的a互为倒数时,两个函数关于y轴对称,但这两个函数都不具有奇偶性。
2.当a>1时,底数越大,图像上升的越快,在y轴的右侧,图像越靠近y轴;当0<a<1时,底数越小,图像下降的越快,在y轴的左侧,图像越靠近y轴。
在y轴右边“底大图高”;在y轴左边“底大图低”。
3.四字口诀:“大增小减”。
即:当a>1时,图像在R上是增函数;当0<a<1时,图像在R上是减函数。
4. 指数函数既不是奇函数也不是偶函数。
比较幂式大小的方法:1.当底数相同时,则利用指数函数的单调性进行比较;2.当底数中含有字母时要注意分类讨论;3.当底数不同,指数也不同时,则需要引入中间量进行比较;4.对多个数进行比较,可用0或1作为中间量进行比较底数的平移:在指数上加上一个数,图像会向左平移;减去一个数,图像会向右平移。
在f(X)后加上一个数,图像会向上平移;减去一个数,图像会向下平移。
对数函数1.对数函数的概念由于指数函数y=a x在定义域(-∞,+∞)上是单调函数,所以它存在反函数,我们把指数函数y=a x(a >0,a ≠1)的反函数称为对数函数,并记为y=log a x(a >0,a ≠1).因为指数函数y=a x的定义域为(-∞,+∞),值域为(0,+∞),所以对数函数y=log a x 的定义域为(0,+∞),值域为(-∞,+∞).2.对数函数的图像与性质对数函数与指数函数互为反函数,因此它们的图像对称于直线y=x . 据此即可以画出对数函数的图像,并推知它的性质.为了研究对数函数y=log a x(a >0,a ≠1)的性质,我们在同一直角坐标系中作出函数y=log 2x ,y=log 10x ,y=log 10x,y=log 21x,y=log101x 的草图由草图,再结合指数函数的图像和性质,可以归纳、分析出对数函数y=log a x(a >0,a ≠1)的图像的特征和性质.见下表.]图象a>1 a<1性质(1)x>0(2)当x=1时,y=0(3)当x>1时,y>00<x<1时,y<0(3)当x>1时,y<00<x<1时,y>0 (4)在(0,+∞)上是增函数(4)在(0,+∞)上是减函数补充性质设y1=log a x y2=log b x其中a>1,b>1(或0<a<1 0<b<1) 当x>1时“底大图低”即若a>b则y1>y2当0<x<1时“底大图高”即若a>b,则y1>y2比较对数大小的常用方法有:(1)若底数为同一常数,则可由对数函数的单调性直接进行判断.(2)若底数为同一字母,则按对数函数的单调性对底数进行分类讨论.(3)若底数不同、真数相同,则可用换底公式化为同底再进行比较.(4)若底数、真数都不相同,则常借助1、0、-1等中间量进行比较.3.指数函数与对数函数对比名称指数函数对数函数一般形式y=a x(a>0,a≠1) y=log a x(a>0,a≠1) 定义域(-∞,+∞) (0,+∞)值域(0,+∞) (-∞,+∞)函数值变化情况当a>1时,⎪⎩⎪⎨⎧<<==>>)0(1)0(1)0(1xxxa x当0<a<1时,⎪⎩⎪⎨⎧<>==><)0(1)0(1)0(1xxxa x当a>1时⎪⎩⎪⎨⎧<<==>>)1(0)1(0)1(0logxxxxa当0<a<1时,⎪⎩⎪⎨⎧<>==><)1(0)1(0)1(0logxxxxa单调性当a>1时,a x是增函数;当0<a<1时,a x是减函数.当a>1时,log a x是增函数;当0<a<1时,log a x是减函数.图像y=a x的图像与y=log a x的图像关于直线y=x对称.幂函数幂函数的图像与性质幂函数n y x =随着n 的不同,定义域、值域都会发生变化,可以采取按性质和图像分类记忆的方法.熟练掌握n y x =,当112,1,,,323n =±±±的图像和性质,列表如下. 从中可以归纳出以下结论:① 它们都过点()1,1,除原点外,任何幂函数图像与坐标轴都不相交,任何幂函数图像都不过第四象限.② 11,,1,2,332a =时,幂函数图像过原点且在[)0,+∞上是增函数. ③ 1,1,22a =---时,幂函数图像不过原点且在()0,+∞上是减函数.④ 任何两个幂函数最多有三个公共点.n y x =奇函数 偶函数 非奇非偶函数 1n >01n <<0n <OxyOxyOxyOxyOxyOxyOxyOxyOxy定义域 R R R奇偶性奇奇奇非奇非偶 奇在第Ⅰ象限的增减性 在第Ⅰ象限单调递增 在第Ⅰ象限单调递增 在第Ⅰ象限单调递增在第Ⅰ象限单调递增在第Ⅰ象限单调递减幂函数y x α=(x ∈R ,α是常数)的图像在第一象限的分布规律是:①所有幂函数y x α=(x ∈R ,α是常数)的图像都过点)1,1(;②当21,3,2,1=α时函数y x α=的图像都过原点)0,0(;③当1=α时,y x α=的的图像在第一象限是第一象限的平分线(如2c );④当3,2=α时,y x α=的的图像在第一象限是“凹型”曲线(如1c )⑤当21=α时,y x α=的的图像在第一象限是“凸型”曲线(如3c )⑥当1-=α时,y x α=的的图像不过原点)0,0(,且在第一象限是“下滑”曲线(如4c )当0>α时,幂函数y x α=有下列性质:(1)图象都通过点)1,1(),0,0(;(2)在第一象限内都是增函数;(3)在第一象限内,1>α时,图象是向下凸的;10<<α时,图象是向上凸的; (4)在第一象限内,过点)1,1(后,图象向右上方无限伸展。
指数函数平移

指数函数平移指数函数的平移是数学中的一个重要概念,它是指把指数函数的原点做出一定的变化,让指数函数的图像在坐标系中左右、上下移动。
平移是指数函数参数调整过程中的一种操作,它可以帮助我们更改指数函数的图形,以便更好地理解指数函数的特性和表达式。
指数函数的平移也称之为参数调整,它可以帮助我们更好地理解和表达指数函数的特性。
通常情况下,可以通过平移来增大或减小指数函数的值,并改变指数函数的曲线。
指数函数的平移可以分为三种,即水平平移,上下平移,和参数调整。
水平平移是指沿着x轴将指数函数进行左右移动,移动的方向与移动量有关。
上下平移是指沿着y轴将指数函数进行上下移动,移动的方向与移动量有关。
最后,参数调整是指修改指数函数的参数,使指数函数的函数图发生变化。
在指数函数的平移中,水平平移是最重要的一种操作,它可以将一个指数函数的中心点转向另一个位置,从而使指数函数的函数图发生变化。
举个例子,如果我们想要将y=2^x函数的中心点向右平移3个单位,则可以将其写成y=2^(x-3)的形式。
这里的-3表示的是右平移的量,而+3表示的是左平移的量。
而上下平移则涉及到指数函数的另一个参数,也就是“指数自变量”。
像y=2^x一样,“2”这个数字就是指数函数的一个参数,也就是“指数自变量”。
这个参数使指数函数得以变化,也就是说可以通过改变这个参数来使指数函数本身进行上下平移。
最后,改变指数函数参数也是一个有效的指数函数平移方法,但其处理方式与水平平移和上下平移有些不同。
如果想要改变指数函数的函数图,首先要找出函数中的(?x),其中的参量x表示的是指数函数的参数。
我们可以将这个参量乘以一个系数来改变函数的大小,也可以对函数进行 x加减操作来改变函数的形状。
指数函数的平移能够让我们更好地理解指数函数的特性和表达式,从而帮助我们更好地应用指数函数。
它分为三个方面:水平平移、上下平移和参数调整。
水平平移是指沿着x轴将指数函数进行左右移动;上下平移是指沿着 y将指数函数进行上下移动;参数调整是指修改指数函数的参数,使指数函数的函数图发生变化。
计算指数函数的平移和缩放
计算指数函数的平移和缩放指数函数是数学中的重要函数之一,它具有形如f(x) = a⋅bˣ的表达式,其中a和b都是常数,b被称为底数。
在研究指数函数时,我们常常需要考虑平移和缩放对其图像的影响。
一、指数函数的平移平移是指将函数图像上下或左右移动的操作,它可以通过改变指数函数中的常数项来实现。
设原始的指数函数为f(x) = a⋅bˣ,若我们将其上下平移h个单位,则得到新的指数函数f(x) = a⋅bˣ + h。
当h为正值时,函数图像将向上平移,而当h为负值时,函数图像将向下平移。
平移的距离是|h|,也就是h的绝对值。
举例来说,考虑指数函数f(x) = 2ˣ。
如果我们将其上移2个单位,则得到新的指数函数f(x) = 2ˣ + 2。
相比于原来的函数,新函数的图像将整体上移2个单位。
二、指数函数的缩放缩放是指将函数图像进行拉伸或压缩的操作,它可以通过改变指数函数中的底数来实现。
设原始的指数函数为f(x) = a⋅bˣ,若我们将其按横轴方向缩放k倍(k>0),则得到新的指数函数f(x) = a⋅(b/k)ˣ。
当k大于1时,函数图像将被水平拉伸,而当0<k<1时,函数图像将被水平压缩。
缩放倍数是k的倒数,也就是1/k。
举例来说,考虑指数函数f(x) = 2ˣ。
如果我们将其在横轴方向压缩为原来的一半,则得到新的指数函数f(x) = 2ˣ/2 = 2ˣ/4。
相比于原来的函数,新函数的图像将在横轴方向缩短一半。
三、平移和缩放的综合应用在实际问题中,我们常常需要同时考虑指数函数的平移和缩放。
此时,我们可以先进行缩放操作,再进行平移操作。
设原始的指数函数为f(x) = a⋅bˣ,若我们将其按横轴方向缩放k倍,并将结果向左平移h个单位,则得到新的指数函数f(x) = a⋅(b/k)ˣ + h。
这里的缩放倍数是k,平移距离是|h|,分别决定了函数图像的水平压缩程度和水平平移距离。
举例来说,考虑指数函数f(x) = 2ˣ。
3. 指数函数图像
当0 x 1 时,y 0 ;当x 1 时,y 0 , 故选B
4.翻折变化:
1 y f x 去掉y 轴左边图,保 留y 轴右 边图 y f x 将y 轴右边的图像翻折到左边去
① f x ex f x = e x
② f x = e x f x 2 = e x-2
指数函数的图象
知识点
1.当 当0a
1 a
时, 底数a 越大,图象在x 1 时,底数a 越小,图象在x
0
时越接近y 轴,在x 0 0 时越接近x 轴,在x
时越接近x 轴 0 时越接近y 轴
2.平移变换:左加右减
1 f x 向左平移a 个单位 f x a 2 f x 向上平移 a个单位 f x a 3 f x 向右平 移 a个单位 f x a 4 f x 向下平移a个单位 f x a
解析:① 有界性:由函数的定义域得x 0 , A错; 当x 0 时,y 0 ,B错;
② 指数爆炸,当x , y 0 ,D错
例7 函数y x3 x 2 x 的图象大致是
解析:① 奇偶性:f x x3 x 2 x f x ,故函数为奇函数,C错; ② 有界性:令y 0 ,则 x3 x 2 x 0
D. a b 1 d c
例2 已知1 n m 0 ,则指数函数① y mx ,
② y nx 的图象为
例3 已知函数y ax b a 0且 a 1 的图象经过
第二、三、四象限,则有
A. 0 a 1 ,b 1
知识讲解_指数函数及其性质_基础
指数函数及其性质要点一、指数函数的概念:函数y=a x (a>0且a ≠1)叫做指数函数,其中x 是自变量,a 为常数,函数定义域为R. 要点诠释:(1)形式上的严格性:只有形如y=a x (a>0且a ≠1)的函数才是指数函数.像23xy =⋅,12xy =,31xy =+等函数都不是指数函数.(2)为什么规定底数a 大于零且不等于1:①如果0a =,则000x x ⎧>⎪⎨≤⎪⎩xx时,a 恒等于,时,a 无意义.②如果0a <,则对于一些函数,比如(4)xy =-,当11,,24x x ==⋅⋅⋅时,在实数范围内函数值不存在.③如果1a =,则11xy ==是个常量,就没研究的必要了. 要点二、指数函数的图象及性质:y=a x0<a<1时图象a>1时图象图象性质 ①定义域R ,值域 (0,+∞)②a 0=1, 即x=0时,y=1,图象都经过(0,1)点 ③a x =a ,即x=1时,y 等于底数a④在定义域上是单调减函数 ④在定义域上是单调增函数 ⑤x<0时,a x >1 x>0时,0<a x <1⑤x<0时,0<a x <1 x>0时,a x >1⑥ 既不是奇函数,也不是偶函数(1)当底数大小不定时,必须分“1a >”和“01a <<”两种情形讨论。
(2)当01a <<时,,0x y →+∞→;当1a >时,0x y →-∞→。
当1a >时,a 的值越大,图象越靠近y 轴,递增速度越快。
当01a <<时,a 的值越小,图象越靠近y 轴,递减的速度越快。
(3)指数函数xy a =与1xy a ⎛⎫= ⎪⎝⎭的图象关于y 轴对称。
要点三、指数函数底数变化与图像分布规律 (1)① xy a = ②xy b = ③x y c = ④x y d =则:0<b <a <1<d <c又即:x ∈(0,+∞)时,x x x x b a d c <<< (底大幂大) x ∈(-∞,0)时,x x x x b a d c >>> (2)特殊函数112,3,(),()23x x x x y y y y ====的图像:要点四、指数式大小比较方法(1)单调性法:化为同底数指数式,利用指数函数的单调性进行比较. (2)中间量法 (3)分类讨论法 (4)比较法比较法有作差比较与作商比较两种,其原理分别为:①若0A B A B ->⇔>;0A B A B -<⇔<;0A B A B -=⇔=; ②当两个式子均为正值的情况下,可用作商法,判断1A B >,或1AB<即可. 【典型例题】类型一、指数函数的概念例1.函数2(33)xy a a a =-+是指数函数,求a 的值. 【答案】2【解析】由2(33)xy a a a =-+是指数函数,可得2331,0,1,a a a a ⎧-+=⎨>≠⎩且解得12,01,a a a a ==⎧⎨>≠⎩或且,所以2a =.【总结升华】判断一个函数是否为指数函数:(1)切入点:利用指数函数的定义来判断;(2)关键点:一个函数是指数函数要求系数为1,底数是大于0且不等于1的常数,指数必须是自变量x .举一反三:【变式1】指出下列函数哪些是指数函数(1)4xy =;(2)4y x =;(3)4xy =-;(4)(4)xy =-;(5)1(21)(1)2xy a a a =->≠且;(6)4x y -=.【答案】(1)(5)(6)【解析】(1)(5)(6)为指数函数.其中(6)4x y -==14x⎛⎫ ⎪⎝⎭,符合指数函数的定义,而(2)中底数x 不是常数,而4不是变数;(3)是-1与指数函数4x 的乘积;(4)中底数40-<,所以不是指数函数.类型二、函数的定义域、值域 例2.求下列函数的定义域、值域.(1)313xxy =+;(2)y=4x -2x +1;(4)y =为大于1的常数)【答案】(1)R ,(0,1);(2)R [+∞,43);(3)1,2⎡⎫-+∞⎪⎢⎣⎭[)0,+∞;(4)(-∞,-1)∪[1,+∞) [1,a)∪(a ,+∞)【解析】(1)函数的定义域为R (∵对一切x ∈R ,3x ≠-1).∵ (13)1111313x x xy +-==-++,又∵ 3x >0, 1+3x >1, ∴ 10113x <<+, ∴ 11013x-<-<+,∴ 101113x<-<+, ∴值域为(0,1). (2)定义域为R ,43)212(12)2(22+-=+-=x x x y ,∵ 2x >0, ∴ 212=x即 x=-1时,y 取最小值43,同时y 可以取一切大于43的实数,∴ 值域为[+∞,43). (3)要使函数有意义可得到不等式211309x --≥,即21233x --≥,又函数3x y =是增函数,所以212x -≥-,即12x ≥-,即1,2⎡⎫-+∞⎪⎢⎣⎭,值域是[)0,+∞.(4)∵011112≥+-=-+x x x x ∴ 定义域为(-∞,-1)∪[1,+∞), 又∵111011≠+-≥+-x x x x 且,∴ a ay a y x x x x≠=≥=-+-+1121121且, ∴值域为[1,a)∪(a ,+∞).【总结升华】求值域时有时要用到函数单调性;第(3)小题中值域切记不要漏掉y>0的条件,第(4)小题中112111≠+-=+-x x x 不能遗漏. 举一反三:【变式1】求下列函数的定义域: (1)2-12x y =(2)y =(3)y =(4)0,1)y a a =>≠【答案】(1)R ;(2)(]-3∞,;(3)[)0,+∞;(4)a>1时,(]-0∞,;0<a<1时,[)0+∞,【解析】(1)R(2)要使原式有意义,需满足3-x ≥0,即3x ≤,即(]-3∞,.(3) 为使得原函数有意义,需满足2x -1≥0,即2x ≥1,故x ≥0,即[)0,+∞(4) 为使得原函数有意义,需满足10xa -≥,即1xa ≤,所以a>1时,(]-0∞,;0<a<1时,[)0+∞,.【总结升华】本题中解不等式的依据主要是指数函数的单调性,根据所给的同底指数幂的大小关系,结合单调性来判断指数的大小关系.类型三、指数函数的单调性及其应用例3.讨论函数221()3x xf x -⎛⎫= ⎪⎝⎭的单调性,并求其值域.【思路点拨】对于x ∈R ,22103x x-⎛⎫> ⎪⎝⎭恒成立,因此可以通过作商讨论函数()f x 的单调区间.此函数是由指数函数及二次函数复合而成的函数,因此可以逐层讨论它的单调性,综合得到结果.【答案】函数()f x 在区间(-∞,1)上是增函数,在区间[1,+∞)上是减函数 (0,3] 【解析】解法一:∵函数()f x 的定义域为(-∞,+∞),设x 1、x 2∈(-∞,+∞)且有x 1<x 2,∴222221()3x x f x -⎛⎫= ⎪⎝⎭,211211()3x x f x -⎛⎫= ⎪⎝⎭,222222121212121122()()(2)2211()113()3313x x x x x x x x x x x x f x f x -----+--⎛⎫ ⎪⎛⎫⎛⎫⎝⎭=== ⎪ ⎪⎝⎭⎝⎭⎛⎫ ⎪⎝⎭. (1)当x 1<x 2<1时,x 1+x 2<2,即有x 1+x 2-2<0.又∵x 2-x 1>0,∴(x 2―x 1)(x 2+x 1―2)<0,则知2121()(2)113x x x x -+-⎛⎫> ⎪⎝⎭.又对于x ∈R ,()0f x >恒成立,∴21()()f x f x >. ∴函数()f x 在(-∞,1)上单调递增.(2)当1≤x 1<x 2时,x 1+x 2>2,即有x 1+x 2-2>0. 又∵x 2-x 1>0,∴(x 2―x 1)(x 2+x 1―2)>0,则知2121()(2)1013x x x x -+-⎛⎫<< ⎪⎝⎭.∴21()()f x f x <.∴函数()f x 在[1,+∞)上单调递减.综上,函数()f x 在区间(-∞,1)上是增函数,在区间[1,+∞)上是减函数.∵x 2―2x=(x ―1)2―1≥-1,1013<<,221110333x x--⎛⎫⎛⎫<≤= ⎪⎪⎝⎭⎝⎭. ∴函数()f x 的值域为(0,3].解法二:∵函数()f x 的下义域为R ,令u=x 2-2x ,则1()3uf u ⎛⎫= ⎪⎝⎭.∵u=x 2―2x=(x ―1)2―1,在(―∞,1]上是减函数,1()3uf u ⎛⎫= ⎪⎝⎭在其定义域内是减函数,∴函数()f x 在(-∞,1]内为增函数.又1()3uf u ⎛⎫= ⎪⎝⎭在其定义域内为减函数,而u=x 2―2x=(x ―1)2―1在[1,+∞)上是增函数,∴函数()f x 在[1,+∞)上是减函数.值域的求法同解法一.【总结升华】由本例可知,研究()f x y a =型的复合函数的单调性用复合法,比用定义法要简便些,一般地有:即当a >1时,()f x y a=的单调性与()y f x =的单调性相同;当0<a <1时,()f x y a=的单调与()y f x =的单调性相反.举一反三:【变式1】求函数2323xx y -+-=的单调区间及值域.【答案】3(,]2x ∈-∞上单增,在3[,)2x ∈+∞上单减. 14(0,3]【解析】[1]复合函数——分解为:u=-x 2+3x-2, y=3u ;[2]利用复合函数单调性判断方法求单调区间; [3]求值域. 设u=-x 2+3x-2, y=3u ,其中y=3u 为R 上的单调增函数,u=-x 2+3x-2在3(,]2x ∈-∞上单增, u=-x 2+3x-2在3[,)2x ∈+∞上单减, 则2323xx y -+-=在3(,]2x ∈-∞上单增,在3[,)2x ∈+∞上单减.又u=-x 2+3x-22311()244x =--+≤, 2323x x y -+-=的值域为14(0,3].【变式2】求函数2-2()(01)xxf x a a a =>≠其中,且的单调区间.【解析】当a>1时,外层函数y=a u 在()-∞+∞,上为增函数,内函数u=x 2-2x 在区间(1)-∞,上为减函数,在区间[)1+∞,上为增函数,故函数2-2()(-1)x xf x a =∞在区间,上为减函数,在区间[)1+∞,上为增函数; 当0<a<1时,外层函数y=a u 在()-∞+∞,上为减函数,内函数u=x 2-2x 在区间(1)-∞,上为减函数,在区间[)1+∞,上为增函数,故函数2-2()xxf x a =在区间(1)-∞,上为增函数,在区间[)1,+∞上为减函数.例4.证明函数1()(1)1x xa f x a a -=>+在定义域上为增函数. 【思路点拨】利用函数的单调性定义去证明。
指数函数图象的特点
y
7 6
5
y 2x1 4
3
2
y 2x y 2x1
1 4 3 2 1 O
1 2 3 4x
要掌握指数函数的图象及性质 在比较几个指数的大小时要先看底数
是大于1还是小于1
(2)的底数小于1,再由(3),(4)
中比较c,d的大小,由(1),(2)
中比较a,b的大小
例3 说明 y 2x1的图象与 y 2x的图象的关系,
并画出它们的示意图
y 2x1与y 2x的图象的关系呢?
解:比较函数 y 2x1与 y 2x的关系
y 231与y x2相等
我们来研究下面的问 题。
某种细胞分裂时,由1个分裂成2个, 2个分裂成4个……
1个这样的细胞分裂x次后,得 的细胞个数y与x的函数关系是
分裂x次后呢?
这个函数里,自变量x作为指数,而 底数2是一个大于0且不等于1的的常 量。
指数函数的定义
一般地,我们把行如
的
函数叫做指数函数。
? 其中x是自变量,函数的定义域是R
在R上是增函数(如图)
Y
y 1.7x
2.5 3
1.72.5 1.73
(2).分析 考察指数函数 y 0.8x。由于
底数 0.8 < 1,所以指数函数 y 0.8x
在R上是减函数(如图)
0.1 0.2
o
X
Y
y 0.8x
0.80.1 0.80.2
o
X
例2 如图指数函数,1.y ax 2,.y bx 3,.y cx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y= f(x- m)
y=f(x)
上下移
y = f(x)+n
规律小结:左加右减,上加下减
练:函数y=2-x-1+1的图象可由函数y=2-x的图象 (B) A.向右平移一个单位,再向上平移一个单位得到 B.向左平移一个单位,再向上平移一个单位得到 C.向右平移一个单位,再向下平移一个单位得到 D.向左平移一个单位,再向下平移一个单位得到
比较函数 y 2 、y 2
x
x 1与y2x2的关系y2 y2
x x
向左平行移动1个单位长度 向左平行移动2个单位长度
y2
x 1 x2
y2
y
8 7 6 5 4 3 2 1
● ●
y=2x
y=2x+1
● ●
y= 2x +2
●
● ●
●
● ●
-5 -4 -3 -2-1 O 1 2 3 4 5
2.
y x的图象怎样平移得到y x 3
y 2x的图象怎样平移得到y 2x 3
练习
• 由y=2x 的图像怎样得到y=2x+2 , y=2x+3, y=2x-4, y=2x-5的图像?
思考:为了得到y=2x-3-1的图像,只需把 y=2x的图像 向右平移3个单位,再向下平移1个单位
3. 指数函数的性质
(1) 定义域: R
性 (2) 值域:(0,+ ∞) 质 (3) 过点(0, 1),即x = 0 时,y=1
(4)在R上是增函数 (4)在R上是减函数
二.指数函数图像的平移
1. 实例 说明下列函数图像与指数函数y=2x
图像的关系, 并画出它们的示意图:
(1) y 2
x 1
(2) y 2
x2
思路:通过分析函数解析式的数量关系,分 析出该函数图像与指数函数图像上的点的 坐标关系,再归纳出函数图像间的关系.
分析:(1)比较函数 y=2x+1与y=2x数量关系:
y=2-2+1与y=2-1的值相等, y=2-1+1与 y=20的值相等, y=22+1与 y=23的值相等, … … y=2(t-1)+1与y=2t 的值相等.
x
练习
x 1 y 5 1. 的图象向右平移2个单位得到的 x 图象的解析式为 y 2 .
课堂小结
(1) 本节学习了指数函数图像的平移,并拓展到 一般函数图像平移的情形;
(2) 掌握平移方法,利用平移画出相关函数图像,
理解平移方向与正负号的关系.
y
y=2x+1 y 2 x
(t, 2t)
1
(t-1, 2t)
-1
2 1 O
所以,两函数图像上点的坐标存在关系: 点(t-1, 2t)
左移1
x
点(t, 2t)
结论: 指数函数y=2x的图像向左平移1个
2
2 1
单位,可得到函数y=2x+1的图像.
(2)类似可比较函数y=2x-2与y=2x的关系:
就得到函数y=2x-2的图像 (如图)
2. 方法小结:
(1) 函数y=ax的图像左移m (m>0) 个单位,得y=a x + m的图像. (2)函数y=ax图像右移m 个单位,得y=a
x - m的图像.
y
y=a x
y=ax+m
1
O
y=ax-m x
(3)平移后产生新函数——复合函数,它已 不再是指数函数了.
∵y=2-1-2与y=2-3 相等
y=20-2与y=2-2 相等
y=23-2 与y=21 相等 ∴y=2(t+2)-2与y=2t 相等
两个函数图像上纵坐标相等 的点的横坐标恰好相差 2
y
y2
x
y=2x-2
… …
1
O
x
点(t,
2t)
右移2
点(t+2, 2t)
结论:将指数函数y=2x的图像向右平移2个单位
指数函数及其性质3
一. 指数函数的定义、图像与性质
1. 指数函数定义
一般地,函数
y= a x ( a > 0, a 1) 叫做
指数函数,其中x是自变量,函数定义域是R
2. 叙述指数函数y= a x ( a > 0, a 1)图像特征
y=ax
(a>1) 1
y
y
y=ax
(0<a<1)
1
O
x
O
x
三.函数图像一般平移规律
(1)沿x 轴左右平移(m>0) y y=f(x)
右移m
y=f(x+m)
左移m
y=f(x-m) x
O
注意: 数与形变化的变化规律
(2) 沿y 轴上下平移 (n>0)
y y=f(x)+n y=f(x)
上移n
y=f(x)-n
O 下移n
x
(3)函数f (x) 平移的一般规律
左右移
x
图像平移练习 1. 说明下列函数的图像与指数函数.
y( )
(1) y
1 x的图像的关系,并画出示意图 3
1
3
x2
1 (2) y x 1 3
2. 说明函数 y=4x-3的图像与函数 y=4x
的关系,并画出示意图.
练习
1. f (x) 图像向右平移2个单位后为 x 则 f (x ) = . y2
比较函数 y 2 、y 2
x
x 1
与
y2
x2
的关系
y2 y2
x x
向左平行移动1个单位长度 向左平行移动2个单位长度
y2
x 1 x2
y2
y
8 7 6 5 4 3 2 1
● ●
y=2x
y=2x+1
● ●
y= 2x +2
●
● ●
●
● ●
-5 -4 -3 -2-1 O 1 2 3 4 5
