平行线分线段成比例定理基础练11习
平行线分线段成比例经典例题与变式练习

平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=.2. 平行线分线段成比例定理的推论:如图,在三角形中, 如果DE BC ∥,则AD AE DEAB AC BC==3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
1、如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
2、 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.3、如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=.4、如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.l 3l 2l 1FE D CB A ABCDEE DC B AEDCBAFE DCBAFEDCBAECA5、如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作 EF CD ∥交AD BC ,于E F ,,求EF 的长。
6、(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
7、(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =,连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AFFC FD+ 的值为( ) A.52 B.1 C.32D.28、如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD于点O . (1)当1A 2AE C =时,求AOAD 的值; (2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想.9、如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.10、如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
平行线分线段成比例经典例题与变式练习

平行线分线段成比例平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=.2. 平行线分线段成比例定理的推论:如图,在三角形中, 如果DE BC ∥,则AD AE DEAB AC BC==3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
1、如图,DE BC ∥,且DB AE =,若510AB AC ==,,求AE 的长。
2、 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.3、如图,AB BD ⊥,CD BD ⊥,垂足分别为B 、D ,AC 和BD 相交于点E ,EF BD ⊥,垂足为F .证明:111AB CD EF+=.4、如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.l 3l 2l 1FE D CB A ABCDEE DC B AEDCBAFE DCBAFEDCBAFE DCBA5、如图,在梯形ABCD 中,AB CD ∥, 129AB CD ==,,过对角线交点O 作 EF CD ∥交AD BC ,于E F ,,求EF 的长。
6、(上海市数学竞赛题)如图,在梯形ABCD 中,AD BC ∥,AD a BC b E F ==,,,分别是AD BC ,的中点,AF 交BE 于P ,CE 交DF 于Q ,求PQ 的长。
7、(1)如图(1),在ABC ∆中,M 是AC 的中点,E 是AB 上一点,且14AE AB =,连接EM 并延长,交BC 的延长线于D ,则BCCD=_______. (2)如图(2),已知ABC ∆中,:1:3AE EB =,:2:1BD DC =,AD 与CE 相交于F ,则EF AFFC FD+ 的值为( ) A.52 B.1 C.32D.28、如图,在ABC ∆中,D 为BC 边的中点,E 为 AC 边上的任意一点,BE 交AD 于点O .(1)当1A 2AE C =时,求AOAD的值;(2)当11A 34AE C =、时,求AOAD的值; (3)试猜想1A 1AE C n =+时AOAD的值,并证明你的猜想.9、如图,AD 是ABC ∆的中线,点E 在AD 上,F 是BE 延长线与AC 的交点.(1)如果E 是AD 的中点,求证:12AF FC =; (2)由(1)知,当E 是AD 中点时,12AF AEFC ED=⋅成立,若E 是AD 上任意一点(E 与A 、D 不重合),上述结论是否仍然成立,若成立请写出证明,若不成立,请说明理由.10、如图,已知ABC ∆中,AD 是BC 边上的中线,E 是AD 上的一点,且BE AC =,延长BE 交AC 于F 。
平行线分线段成比例专题培优提高训练

平行线分线段成比率专题训练知识梳理平行线分线段成比率定理及其推论1. 平行线分线段成比率定理以下列图,假如 l 1 ∥ l 2 ∥ l 3 ,则BCEF,ABDE, AB AC .AC DFACDFDEDFADl 1BEl 2CFl 32. 平行线分线段成比率定理的推论:如图,在三角形中,假如 DE ∥ BC ,则AD AE DE ABACBCAEDDEA3. 平行的判断定理:如上图,假如有AD AE DE,那么 DE ∥ BC 。
AB ACBCBC BC专题解说专题一、平行线分线段成比率定理及其推论基本应用【例 1】如图, DE ∥ BC ,且 DB AE ,若 AB 5 ,AC 10 ,求 AE 的A长。
DEBC【例 2】如图,已知 AB / /EF / /CD ,若 ABa , CDb , EFc ,求证:1 1 1 .CcabAEBFD【稳固】如图, ABBD ,CD BD ,垂足分别为 B 、D , AC 和BD 订交于点 E , EFBD ,垂足为 F .证明:11 1 . CABCDEFAEBFD【例 3】如图,在梯形ABCD中,AB∥CD,AB12 ,CD 9,过对角线交点 O 作EF∥CD 交 AD,BC于 E,F ,求EF的长。
D CE FOA B【稳固】(上海市数学比赛题)如图,在梯形 ABCD 中, AD∥BC ,AD a ,BC b ,E ,F 分别是 AD ,BC 的中点,AF交BE于P, CE 交DF于 Q ,求PQ 的长。
AED P QBFC专题二、定理及推论与中点相关的问题【例 4】(2007 年北师大附中期末试题)(1)如图( 1),在ABC中,M是AC的中点,E是AB上一点,且AE 1AB ,4连结 EM 并延伸,交BC的延伸线于 D ,则BC_______.2)如图(2),已知ABC中,AE : EB CD2:1 ,AD与CE 订交于F,(1:3 ,BD : DC则 EF AF的值为()FC FDA 5A.32AEC.2E MFB DB CD C(1)(2)( 2001 年河北省中考试题)如图,在 ABC 中, D 为 BC 边的中点, E 为 AC 边上的随意一点, BE 交 AD 于点 O .(1)当AE1时,求AO的值;AC 2 AD( 2)当AE 1 1 时,求AO的值;AA C3 、 AD4(3)试猜想AE1 时AO的值,并证明你的猜想 .EA C n1ADOB D C【例 5】(2010 年湖北恩施中考题) 如图, AD 是 ABC 的中线,点 E 在 AD 上, F是 BE 延伸线与 AC 的交点 .(1)假如 E 是 AD 的中点,求证:AF1 ;FC2(2)由(1)知,当 E 是 AD 中点时,AF1AE建立,若 E 是 AD 上随意一点FC2 ED( E 与 A 、 D 不重合),上述结论能否仍旧建立, 若建立请写出证明, 若不建立,请说明原因 .AFEBDC【稳固】 如图,已知 ABC 中, AD 是 BC 边上的中线, E 是 AD上的一点,且 BEAC ,延伸 BE 交 AC 于 F 。
平行线分线段成比例定理的_典型例题

平行线分线段成比例的一些学习技巧平行线分线段成比例是相似三角形学习的基础,但学习的策略是相同的,我认为需要掌握一定数量的基本图形,需要有学习者个单独的独特的解答策略。
而很多同学往往都只是用原有的方法解决后来学习的内容,这对几何学习,尤其是相似三角形的学习是相当不利的。
下面介绍一些平行线分线段成比例的基本习题。
例1(1)已知,则=(2)如果,那么的值是()A.7 B.8 C.9 D.10分析本考题主要考查比与代数式比的互换.第(1)小题可将代数式比的形式转化成积的形式:,整理后再转化成比的形式,便有对于第(2)小题,可连续运用两次等比定理,得出,即,其比的比值为9,故选C,但这里需要注意的是:第一,等比定理本身隐含着一个约束条件——分母为零;第二,“比”与“比值”是两个不同的概念,比是一种运算,而比的比值是运算的结果.例2、已知:1、、2三个数,请你再添上个数,写出一个比例式 .分析这是一道开放型试题,旨在考查学生的发散思维能力,由于题中没有明确告知求1、、2的第四比例项,因此,所添的数可能是前三数的第四比例项,也可能不是前三数的第四比例项,这样本考题便有多种确定方法,如从可求出,便有比例式或,从,又能求出,也得到比例式等等.例3如下图,BD=5:3,E为AD的中点,求BE:EF的值.分析应设法在已知比例式BD:DC与未知比例式BE:EF之间架设桥梁,即添平行线辅助线.解过D作DG∥CA交BF于G,则中点,DG∥AF,例 4如下图,AC∥BD,AD、BC相交于E,EF∥BD,求证:分析待证式可变形为.依AC∥EF∥BD,可将线段的比例式与化归为同一直线AB上的线段比而证得.证明AC∥EF∥BD,.说明证明线段倒数和的关系的常见方法是先变形为证线段比的和为一定值,然后化归为同一直线上的线段比.例5、已知a、b、c均为非零的实数,且满足求的值.解设则三式相加,得当时,有时,则,这时原式=例6如下图,中,D是AB上一点,E是内一点,DE∥BC,过D作AC的平行线交CE的处长线于F,CF与AB交于P,求证BF∥AE.证明DE∥AC,∥,..BF∥AE.。
九年级数学上册第23章图形的相似23.1成比例线段23.1.2平行线分线段成比例同步练习华东师大版

23.1.2 平行线分线段成比例知识点 1 平行线分线段成比例1.如图23-1-3,AD ∥BE ∥CF ,直线m ,n 与这三条平行线分别交于点A ,B ,C 和点D ,E ,F ,根据平行线分线段成比例,可得AB BC =()() ,若AB =5,BC =10,DE =4,可得()()=()(),解得EF =________.图23-1-32.如图23-1-4,在四边形ABCD 中,点E ,F 分别在AD 和BC 上,AB ∥EF ∥DC ,且DE =3,DA =5,CF =4,则FB 的长为( )A.32B.83C .5D .6图23-1-43.如图23-1-5,若AD ∥BE ∥CF ,直线l 1,l 2与平行线分别交于点A ,B ,C 和点D ,E ,F .若AB =BC ,则DE 与EF ________(填“相等”或“不相等”).图23-1-54.如图23-1-6,在四边形ABCD 中,AD ∥BC ,E 是AB 上一点,EF ∥BC 交CD 于点F .若AE =2,BE =6,CD =7,则FC =________.图23-1-65.如图23-1-7,已知AD ∥BE ∥CF ,它们依次交直线l 1,l 2于点A ,B ,C 和点D ,E ,F .如果AB =6,BC =10,那么DEDF的值是________.图23-1-76.[教材练习第1题变式]如图23-1-8,直线a ∥b ∥c .(1)若AC =6 cm ,EC =4 cm ,BD =8 cm ,则线段DF 的长度是多少厘米? (2)若AE ∶EC =5∶2,DB =5 cm ,则线段DF 的长度是多少厘米?图23-1-8知识点 2 平行线分线段成比例的推论7.[2016·兰州改编]如图23-1-9,在△ABC 中,因为DE ∥BC ,所以AD BD =( )( ).若AD BD =23,则AD BD =( )( )=________.图23-1-98.如图23-1-10,直线l 1∥l 2∥l 3,直线AC 与l 1,l 2,l 3分别交于点A ,B ,C ,直线DF 与l 1,l 2,l 3分别交于点D ,E ,F ,AC 与DF 相交于点G ,且AG =2,GB =1,BC =5,则DEEF的值为( )A. 12 B .2 C. 25 D. 35图23-1-109.如图23-1-11,在△ABC中,DE∥BC,且分别交AB,AC于点D,E,则下列比例式不正确的是( )A.ABAD=ACAEB.ABAC=ADAEC.ADBD=AEECD.ABDE=ACEC图23-1-1110.如图23-1-12,若AB∥DC,AC,BD相交于点E,且AE=2,EC=3,BD=10,则ED =________.图23-1-1211.如图23-1-13,在△ABC中,DE∥BC,且DB=AE.若AB=5,AC=10,求AE的长.图23-1-1312.如图23-1-14,已知AB∥CD∥EF,AD∶AF=3∶5,BE=10,那么BC的长为________.图23-1-1413.如图23-1-15,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C都在横格线上.若线段AB=4 cm,则线段BC=________cm.图23-1-1514. 如图23-1-16,AD为△ABC的中线,E为AD的中点,连结BE并延长交AC于点F,则CFAF=__________.15.如图23-1-17,在△ABC中,DF∥AC,DE∥BC,AE=4,EC=2,BC=8,求CF的长.图23-1-1716.如图23-1-18,BE平分∠ABC,DE∥BC交AB于点D,AC=8,AB=9,CE=4,求DE的长.图23-1-1817.对于平行线,我们有这样的结论:如图23-1-19①,AB∥CD,AD,BC交于点O,则AODO=BOCO.请你利用该结论解答下列问题:如图②,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.图23-1-19教师详答1.DE EF 5 10 4 EF 8 2.B [解析] ∵AB ∥EF ∥DC ,∴DE DA =CF CB .∵DE =3,DA =5,CF =4,∴35=4CB ,∴CB =203,∴FB =CB -CF =203-4=83.故选B.3.相等 [解析] 因为AD ∥BE ∥CF ,所以AB BC =DEEF.因为AB =BC ,所以DE =EF . 4. 214 [解析] 因为AD ∥EF ∥BC ,所以AE EB =DF FC .因为AE =2,BE =6,CD =7,所以26=7-FC FC ,所以FC =214. 5 . 38 [解析] ∵AD ∥BE ∥FC ,∴AB BC =DE EF.又∵AB =6,BC =10,∴DE EF =35,∴DE DF =38.6.解:(1)∵a ∥b ∥c ,∴BD DF =ACEC,即8DF =64,解得DF =163(cm). 故线段DF 的长度是163 cm.(2)∵a ∥b ∥c ,∴BF DF =AE EC =52,即5+DF DF =52,解得DF =103(cm). 故线段DF 的长度是103 cm.7.AE EC AE EC 238.D [解析] ∵AG =2,GB =1,∴AB =AG +GB =3.∵直线l 1∥l 2∥l 3,∴DE EF =AB BC =35.故选D.9.D 10.611.解:∵DE ∥BC ,∴AB DB =ACEC,∴5AE =1010-AE ,∴AE =103. 12. [解析] ∵AB ∥CD ∥EF ,∴BC BE =AD AF ,即BC 10=35,解得BC =6.13. 12 [解析] 如图,过点A 作AE BD 于点D .∵练习本中的横格线都平行,且相邻两条横格线间的距离都相等,∴AB BC =AD DE ,即4BC =26,∴BC =12(cm).14. 2 [解析] 如图,过点D 作∥,交于点G , 则AF FG =AE ED ,FG GC =BDDC.又∵E 为AD 的中点,AD 为△ABC 的中线, ∴AE =ED ,BD =DC , ∴AF FG =AE ED =1,FG GC =BD DC=1, ∴AF =FG ,FG =GC , ∴CF =2AF ,∴CF AF=2. 15.解:∵DE ∥BC ,∴AD AB =AE AC =46=23. ∵DF ∥AC ,∴AD AB =CF BC =23,∴CF 8=23,∴CF =163. 16.解:∵DE ∥BC , ∴AB DB =AC CE, ∴9DB =84,∴DB =92. ∵BE 平分∠ABC ,∴∠ABE =∠CBE . ∵DE ∥BC ,∴∠CBE =∠DEB , ∴∠ABE =∠DEB ,∴DE =DB =92.17.解:过点C 作CE ∥AB 交AD 的延长线于点E, 则 BD DC =ADDE.又∵BD =2DC ,AD =2, ∴DE =1. ∵CE ∥AB ,∴∠AEC =∠BAD =75°.又∵∠CAD=30°,∴∠ACE=75°,∴AC=AE=AD+DE=3.。
初三数学平行线分线段成比例专题习题
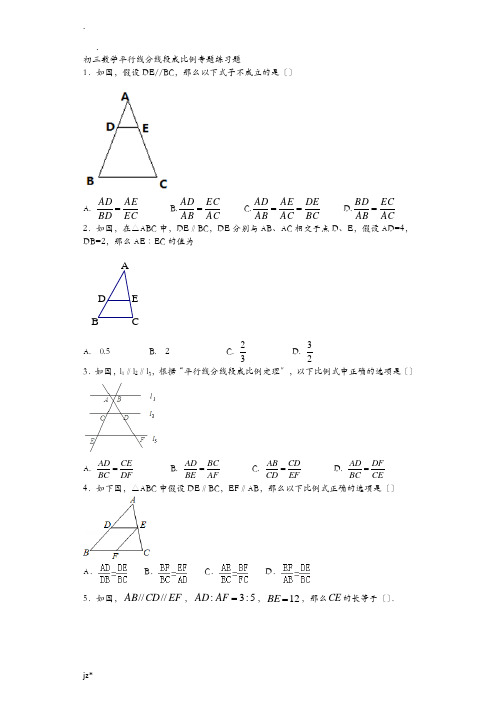
7.如图,AD∥BE∥CF,直线l1、l2这与三条平行线分别交于点A、B、C和点D、E、F.AB=l,BC=3,DE =2,那么EF'的长为〔〕
A.4 B.5 C.6 D.8
8.如图, ∥ ∥ ,两条直线与这三条平行线分别交于点A、B、C和D、E、F. ,那么 的值为〔〕
考点:平行线分线段成比例.
20.8.
【解析】
试题分析:由DE∥BC,AD:DB=3:2,得到 ,再由EF∥AB, ,可设BF=3k,FC=2k,得到BC=BF+FC=5k=20cm,解出k的值即可得到FC的长.
试题解析:∵DE∥BC,AD:DB=3:2,∴ ,∵EF∥AB, ,设BF=3k,FC=2k,∴BC=BF+FC=3k+2k=5k,又BC=20cm,∴5k=20,k=4,∴FC=2k=8.
求证:〔1〕△ACE≌△BCD;
〔2〕 .
16.如图,在△ABC中,DE∥BC,AD=4,DB=8,DE=3.
〔1〕求 的值;
〔2〕求BC的长.
17.如图,a∥b∥c,
〔1〕假设AC=6cm,EC=4cm,BD=8cm,那么线段DF的长度是多少厘米?
〔2〕假设AE:EC=5:2,DB=5cm,那么线段DF的长度是多少厘米?
〔3〕∵△ABD和△ACD的高相等,
可得:△ABD和△ACD面积的比= ,
可得: .
考点:相似形综合题.
19.6cm.
【解析】
试题分析:由平行线的性质可得 , ,进而再由题中条件即可求解BC与GC的长.
试题解析:∵DC∥EF∥AB,∴ =2,又AG=5cm,∴GC=2.5cm. ,CF=2cm,
∴BC=6cm.CB的长是6cm.
初中数学《平行线与比例线段》讲义及练习

板块考试要求A 级要求B 级要求C 级要求相似三角形 会识别相似三角形掌握相似三角形的概念、判定和性质,会用相似三角形的性质和判定解决简单问题会运用相似三角形的性质和判定解决有关问题一、比例1、比例的基本性质:1),a c ad bc b d =⇔=这一性质称为比例的基本性质,由它可推出许多比例形式; 2)a c b db d ac =⇔=(反比定理); 3)a c a b b d c d =⇔=(或d cb a =)(更比定理);4)a c a b c db d b d ++=⇔=(合比定理); 5)a c a b c db d b d --=⇔=(分比定理); 6)a c a b c db d a bcd ++=⇔=--(合分比定理); 7)(0)a c m a c m a b d n bd n b d n b ++⋅⋅⋅+==⋅⋅⋅=++⋅⋅⋅+≠⇔=++⋅⋅⋅+(等比定理).2、比例中项:若::a b b c =,则b 叫做,a c 的比例中项. 3、如图,设三条平行线123l l l ∥∥,则AB DEBC EF=.此定理 称为平行线分线段成比例定理,它的逆定理仍然成立.知识点睛中考要求第一讲相似三角形l 3l 2l 1FE D CB A二、平行线分线段成比例定理及其推论1. 平行线分线段成比例定理如下图,如果1l ∥2l ∥3l ,则BC EF AC DF =,AB DE AC DF =,AB ACDE DF=. l 3l 2l 1FE D CB A2. 平行线分线段成比例定理的推论:如图,在三角形中,如果DE BC ∥,则AD AE DEAB AC BC==ABCDEEDC B A3. 平行的判定定理:如上图,如果有BCDEAC AE AB AD ==,那么DE ∥ BC 。
重点:掌握比例的基本性质,同时掌握比例的几种变形;掌握平行线分线段成比例定理的内容,能够利用平行线分线段成比例定理解决相应的题目难点:掌握定理的内容和推论及其初步运用 关键:掌握好与相似的过渡重、难点板块一、比例的基本性质【例1】 已知:a cb d=,求证:ab cd +是2222a c b d ++和的比例中项。
中考数学每日一练:平行线分线段成比例练习题及答案_2020年综合题版

中考数学每日一练:平行线分线段成比例练习题及答案_2020年综合题版答案答案答案2020年中考数学:图形的变换_图形的相似_平行线分线段成比例练习题~~第1题~~(2020宁波.中考模拟) 已知,在平面直角坐标系xoy 中,点A 的坐标为(0,2),点P (m ,n)是抛物线上的一个动点.(1)如图1,过动点P 作PB ⊥x 轴,垂足为B ,连接PA ,请通过测量或计算,比较PA 与PB 的大小关系:PAPB (直接填写“>”“<”或“=”,不需解题过程);(2) 请利用(1)的结论解决下列问题:①如图2,设C 的坐标为(2,5),连接PC ,AP+PC 是否存在最小值?如果存在,求点P 的坐标;如果不存在,简单说明理由;②如图3,过动点P 和原点O 作直线交抛物线于另一点D ,若AP=2AD ,求直线OP 的解析式.考点: 两点间的距离;垂线段最短;平行线分线段成比例;~~第2题~~(2020青浦.中考模拟) 如图,在平行四边形ABCD 中,E 为DC 上一点,AE 与BD 交于点F, DE ∶EC=2∶3.(1)求BF ∶DF 的值;(2) 如果 , ,试用 、 表示向量 .考点: 平面向量;平行线分线段成比例;~~第3题~~(2020青浦.中考模拟) 已知:如图,在△ABC中,点D 在边BC 上,AE ∥BC , BE 与AD 、AC 分别相交于点F、G ,.(1) 求证:△CAD ∽△CBG ;(2) 联结DG ,求证: .考点: 平行线分线段成比例;相似三角形的判定与性质;~~第4题~~(2020松江.中考模拟) 已知:如图,点D 、F 在△ABC 边AC 上,点E 在边BC 上,且DE ∥AB , .答案答案(1) 求证:EF ∥BD ;(2) 如果,求证:.考点: 平行线的性质;平行线分线段成比例;相似三角形的判定与性质;~~第5题~~(2020长宁.中考模拟)如图,在梯形ABCD 中,点E, F 分别在边AB , CD 上,AD ∥EF ∥BC , EF与BD 交于点G ,AD =5,BC =10,=.(1)求EF 的长;(2) 设 = , =,那么 =, =.(用向量 、 表示)考点: 平面向量;平行线分线段成比例;相似三角形的判定与性质;2020年中考数学:图形的变换_图形的相似_平行线分线段成比例练习题答案1.答案:2.答案:3.答案:4.答案:5.答案:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二课时:《平行线分线段成比例》练习
1.判断题
(1)三条平行线截两条直线,所得的线段成比例( )
(2)一条直线交△ABC 的边AB 于点D ,交AC 边于点E ,如果 AB =9,BD =5,AC =3.5,AE =2,那么DE ∥BC .( )
(3)如图1,321////l l l ,则BF
AE
DF CE BD AC ==( ) (4)如图2,在△ABC 中,DE ∥BC ,则BC DE
EC AE DB AD ==( ) 2.选择题
(1)如图3,在△ABC 中,DE ∥BC 交AB 于D ,交AC 于E ,下列 不能成立的比例式一定是( ) A .
EC AE DB AD = B .AE AC AD AB = C .DB EC AB AC = D .BC
DE
DB AD = (2)如图4,E 是□ABCD 的边CD 上一点,CD CE 3
1
=,AD =12,那么CF 的长为( )
A .4
B .6
C .3
D .12
(3)如图5,□ABCD ,E 在CD 延长线上,AB =10,DE =5,EF =6,则BF 的长为( )
A .3
B .6
C .12
D .16
(4)如图6,在ABC 中,AB=3AD, DE//BC, EF//AB, 若AB=9, DE=2, 则线段FC 的长度是( ) A. 6 B. 5 C. 4 D. 3
(5)如图3,在△ABC 中,DE ∥BC ,DE 分别与AB 、AC 相交于点D 、E ,
若AD=4,DB=2,则AE ︰EC 的值为( )
(A )0.5 (B )2 (C )32 (D )2
3
3.填空题
(1)如图8,则=________,=
________; (2)如图9,321////l l l ,AM =2,MB =3,CD =4.5,则ND =________,CN =________; (3)如图10,D 、E 分别为AB 的三等分点,DF ∥EG ∥BC ,若BC =12,则DF =___ ___,
EG =________;
(4)如图11,△ABC 中,DE ∥BC ,若AE ∶EC =2∶3,DB -AD =3,则AD =________,
DB =________;
4.如图, 已知△ABC 中AB=AC ,AD ⊥BC ,M 是AD 的中点,CM 交AB 于P , DN ∥CP 交AB 于N ,若AB=6cm ,求AP 的值.
5、如图:P 是四边形OACB 对角线的任意一点,且PM ∥CB ,PN ∥CA , 求证:OA :AN=OB :MB
6、如图,△ABC 中,AF ∶FD =1∶5,BD =DC ,求:AE ∶EC .
6、如图,在△ABC 中,EF ∥CD ,DE ∥BC ,求证:A F ·BD = AD ·F D
2
1//l l DE
AD AC AB 图6 B A C F D E 图7
E D C
B
A 图1 图2
图3 图4 图5 图11 图10 图9 图8
(如图2-2)已知直线截△ABC三边所在的直线分别于E、F、D三点且AD=BE. 求证:EF:FD=CA:CB.。
