江苏省南京外国语学校仙林分校中学部2017-2018学年高二下学期期末考试数学理试题 Word版含答案
江苏省南京市金陵中学2017-2018学年高二下学期期末考试数学试题含答案

金陵中学2017-2018学年度第二学期期末考试高二数学试卷数学I一、填空题:本大题共14小题,每小题5分,共70分.请把答案填在答题卡相应位置上. 1.设集合{2,4}A =,{2,6,8}B =,则AB = .2.已知复数2(12i)z =-,其中i 是虚数单位,则||z 的值是 .3.某校共有教师200人,男学生1200人,女学生1000人.现用分层抽样的方法从所有师生中抽取一个容量为n 的样本,已知从女学生中抽取的人数为50人,那么n 的值为 .4.如图是一算法的伪代码,则输出值为 .5.如图,在长方体1111ABCD A B C D -中, 3cm AB AD ==,12cm AA =,则三棱锥111A AB D -的体积为 .6.在平面直角坐标系xOy 中,若双曲线2221(0)x y m m-=>的一条渐近线方程为0x +=,则实数m 的值为 .7.设各项均为正数的等比数列{}n a 的前n 项和为n S ,若52378,13a a S -==,则数列{}n a 的通项公式为n a = .8.将一颗均匀的骰子连续抛掷2次,向上的点数依次记为,m n ,则“2m n >”的概率是 .9.若实数,x y 满足条件14,23,x y x y -≤+≤⎧⎨≤-≤⎩则42z x y =-的取值范围为 .10.在平面直角坐标系xOy 中,已知()cos f x x =,()g x x =,两曲线()y f x =与()y g x =在区间(0,)2π上交点为A .若两曲线在点A 处的切线与x 轴分别相交于,B C 两点,则线段BC 的为 .11.如图,在平面四边形ABCD 中, O 是对角线AC 的中点,且10OB =,6OD =. 若28DA DC ⋅=-,则BA BC ⋅的值为 .12.若对满足64x y xy ++=的任意正实数,x y ,都有22210x xy y ax ay ++--+≥,则实数a 的取值范围为 .13.在平面直角坐标系xOy 中,记椭圆22221(0)x y a b a b+=>>的左右焦点分别为12,F F ,若该椭圆上恰好有6个不同的点P ,使得12F F P ∆为等腰三角形,则该椭圆的离心率的取值范围是 .14.对于任意的实数,m n ,记min{,}m n 为,m n 中的最小值.设函数21()4f x x a x=++,()ln g x x =-,函数()min{(),()}h x f x g x =,若()h x 在(0,)+∞恰有一个零点,则实数a 的取值范围是 .二、解答题:本大题共6小题,共计90分.解答时应写出文字说明、证明过程.15.在平面直角坐标系xOy 中,设向量(sin ,1)m x =-,2(3cos ,cos )n x x =.(1)当3x π=时,求m n ⋅的值;(2)若[0,]4x π∈,且132m n ⋅=-.求cos2x 的值. 16.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,平面PAD ⊥平面ABCD ,AP AD =,点M 在棱PD 上, AM PD ⊥,点N 是棱PC 的中点,求证:(1) MN ∥平面PAB ; (2) AM ⊥平面PCD .17.如图,在一个水平面内,河流的两岸平行,河宽1(单位:千米)村庄,A B 和供电站C 恰位于一个边长为2(单位:千米)的等边三角形的三个顶点处,且,A C 位于河流的两岸,村庄A 侧的河岸所在直线恰经过BC 的中点D .现欲在河岸上,A D 之间取一点E ,分别修建电缆CE 和EA ,EB .设DCE θ∠=,记电缆总长度为()f θ (单位:千米).(1)求()f θ的解析式;(2)当DCE ∠为多大时,电缆的总长度()f θ最小,并求出最小值.18.如图,在平面直角坐标系xOy 中,已知椭圆22221(0)x y a b a b+=>>的离心率为2,且过点1)2.设F 为椭圆的右焦点, ,A B 为椭圆上关于原点对称的两点,连结,AF BF 并延长,分别交椭圆于,C D 两点.(1)求椭圆的标准方程;(2)设直线,AB CD 的斜率分别为12,k k ,是否存在实数m ,使得21k mk =?若存在,求出实数m 的值;若不存在,请说明理由.19.设数列{}n a 的前n 项的和为n S ,且满足12a =,对*n N ∀∈,都有1(1)2n n a p S +=-+ (其中常数1p >),数列{}n b 满足2121log ()n n b a a a n=.(1)求证:数列{}n a 是等比数列; (2)若220172p =,求2018b 的值;(3)若*k N ∃∈,使得2212k p +=,记3||2n n c b =-,求数列{}n c 的前2(1)k +项的和. 20.在平面直角坐标系xOy 中,已知函数()1n (R)f x c x c =∈的图像与直线2y x e=相切,其中e 是自然对数的底数.(1)求实数c 的值; (2)设函数()()a h x ax g x x =--在区间1(,e)e内有两个极值点. ①求实数a 的取值范围;②设函数()h x 的极大值和极小值的差为M ,求实数M 的取值范围 .高二数学Ⅱ(附加题)21.已知矩阵 2 11 3M -⎡⎤=⎢⎥⎣⎦, 1 12 1N ⎡⎤=⎢⎥-⎣⎦. (1)求1()MN -;(2)在平面直角坐标系xOy 中,求直线:210L x y +-=在M 对应的变换T 作用下所得直线L '的方程.22.在直角坐标系xOy 中,以原点O 为极点,以x 轴的非负半轴为极轴,取与直角坐标系xOy相同的长度单位,建立极坐标系.设曲线C 的参数方程为sin x y θθ⎧=⎪⎨=⎪⎩,(θ为参数,[0,2]θπ∈),直线l 的极坐标方程为cos()4p πθ-=(1)写出曲线C 的普通方程和直线l 的直角坐标方程;(2)求曲线C 上的点到直线l 的最大距离.23.假定某篮球运动员每次投篮命中率均为(01)p p <<.现有3次投篮机会,并规定连续两次投篮均不中即终止投篮,已知该运动员不放弃任何一次投篮机会,且恰好用完3次投篮机会的概率是2125. (1)求p 的值;(2)设该运动员投篮命中次数为X ,求X 的概率分布及数学期望()E X .24.如图,已知正四棱柱1111ABCD A B C D -的底面边长为2,侧棱长为3, 1AE A B ⊥,垂足为F ,AE 交1B B 于点E .(1)求证: 1D B ⊥平面AEC ;(2)记直线AE 与平面1ACD 所成的角θ,求sin θ的值.试卷答案一、填空题. 1. {2,4,6,8} 2. 5 3. 120 4. 45. 37. 31n-8.169. [5,13] 10.311. 36 12. 10(,]3-∞ 13. 111(,)(,1)32214. 5{|4a a <-或3}4a >- 二、解答题.15. 解(1)当3x π=时,1]m =-,1]4n =, 所以311442m n ⋅=-=.(2) 2cos cos m n x x x ⋅=-112cos2222x x =-- 1sin[2]62x π=--,若122m n ⋅=-.则11sin[2]6222x π--=-,即sin[2]6x π-=. 因为[0,]4x π∈,所以2663x πππ-≤-≤,所以cos[2]6x π-= 所以cos2cos[[2]]66x x ππ=-+cos[2]6x π=--1sin[2]62x π-⨯12=-=16.证明(1)因为在PAD ∆中, ,AP AD AM PD =⊥, 所以点M 是棱PD 的中点. 又点N 是棱PC 的中点, 所以MN 是PDC ∆的中位线, 所以MN DC ∥. 因为底面ABCD 是矩形, 以AB DC ∥, 所以MN AB ∥.又AB ⊂平面PAB , MN ⊄平面PAB ,所以MN ∥平面PAB . (2)因为平面PAD ⊥平面ABCD , CD ⊂平面ABCD , 平面PAD平面,ABCD AD CD AD =⊥,所以CD ⊥平面PAD .又AM ⊂平面PAD ,所以CD AM ⊥. 因为CD AD ⊥,CD AM ⊥, CD PD D =,CD ⊂平面PCD ,PD ⊂平面PCD ,所以AM ⊥平面PCD .17.解(1)易得AD 垂直平分BC ,1CD BD ==则1cos CE EB θ==,tan ED θ=,tan AE θ=,于是11()cos cos f θθθ=++2sin tan cos θθθ-=+因为E 在CD 之间,所以03πθ<<,故2sin ()cos f θθθ-=+,03πθ<<.(2) 22cos (2sin )(sin )()cos f θθθθθ----=,03πθ<<, 令()0f θ=,得1sin ,26πθθ==, 故当06πθ<<,()0f θ<,()f θ递减,当sin 62ππθ<<,()0f θ>,()f θ递增,所以,当6πθ=时, min ()()6f f πθ==12-+=答:当6DCE π∠=时, ()f θ最小值为18.解(1)设椭圆的方程为22221(0)x y a b a b+=>>,c =,由题意知22311,4c a a b ⎧=⎪⎪⎨⎪+=⎪⎩ 解得2,1,a b =⎧⎨=⎩所以椭圆的方程为2214x y +=. (2)设00(,)A x y ,则00(,)B x y --,010y k x =,又F , 所以直线AF的方程为y x =-.由221,4y x x y ⎧=-⎪⎪⎨⎪+=⎪⎩消去y ,得2200(7)x x --20070x -+=.因为0x x =是该方程的一个解,所以点C的横坐标C x =又点(,)C C C x y在直线y x =-上,所以C C y x =-=C的坐标为 同理,点D的坐标为,所以2k =101472y k x ==, 即存在7m =,使得217k k =.19.(1)证明:因为*n N ∀∈,都有1(1)2n n a p S +=-+,21(1)2n n a p S ++=-+所以两式相减得211(1)n n n a a p a +++-=-, 即21n n a pa ++=,当1n =时211(1)2a p a pa =-+=,所以*1,()n n a pa n N +=∈,又因为1p >,所以11n nn n a a p p++=, 所以数列{}n na p是常数列, 112,2n n n n a a a p p p p -===, 所以{}n a 是以2为首项, p 为公比的等比数列.(2)由(1)得12n n a p -=.2121log ()n n b a a a n==(1)221log (2)n n np n -=1(1)()2017n n n n -+所以20182b =.(3)由(1)得12n n a p -=.2121log ()n n b a a a n==(1)221log (2)n n n p n -=(1)2121log (22)n n n k n -+1121n k -=++. 因为322322(21)n n k b k ---=+, 所以当11n k ≤≤+时, 32n n c b =-,当2n k ≥+时,32n n c b =-. 因此数列{}n c 的前2(21)k +项的和22k T +121()k b b b +=-++++2222()k k k b b b ++++++0121k k +++=-++(1)(2)2+121k k k k ++++++ (1)221k k k +=-++2(1)(22)(1)22121k k k k k k ++++=++. 20. (1)设直线2y x e =与函数()1n f x c x =相切于点00(,1n )P x c x ,函数()1n f x c x =在点00(,1n )P x c x 处的切线方程为: 0001()c y c nx x x x -=-,02c x e=, 把0,0x y ==代入上式得0,2x e c ==. 所以,实数c 的值为2. (2)①由(1)知()21n ah x ax x x=--, 设函数()h x 在区间1(,e)e内有两个极值点1212,()x x x x <,令22()a a h x a x x x'=+--2220ax x ax -+==, 则220ax x a -+=,设2()2m x ax x a =-+,因为121x x =,故只需0,20,()0,am e ∆>⎧⎪⎪>⎨⎪>⎪⎩,所以, 2211e a e <<+.②因为121x x =,所以,121()()M f x f x ax =-=1221221n (21n )a ax ax x x x ----- 11121n a ax x x =---1111(21n )a ax x x -- 21112221n aax x x =--由21120ax x a -+=,得12121x a x =+,且111x e<<. 12111211222121x x x M x x x +=-+222111211121n 4(1n )12x x x x --=-+. 设21x t =,211t e <<,令11()4(1n )+12t t t t ϕ-=-, 221()4()(+1)2t t t ϕ'=-222(1)0(1)t t t --=<+, ()t ϕ(在21(,1)e 上单调递减,从而21(1)()()t e ϕϕϕ<<, 所以,实数M 的取值范围是28(0,)1e +. 高二数学Ⅱ(附加题)21. 解(1)由题知 2 11 3MN -⎡⎤=⎢⎥⎣⎦ 1 10 32 17 2⎡⎤⎡⎤=⎢⎥⎢⎥--⎣⎦⎣⎦,所以0 3)2l 7 det(2MN ⎡⎤==-⎢⎥-⎣⎦, 根据逆矩阵公式,得121 217)1 03(MN -⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦.(2)设由L 上的任意一点(,)P x y '''在T 作用下得到L '上对应点(,)p x y .由 2 11 3x x y y '-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦,即2,3'x y x x y y ''-=⎧⎨''+=⎩解得3+72'7x y x y x y ⎧'=⎪⎪⎨-⎪=⎪⎩,因为210x y ''+-=,所以3221077x y y x +-⨯+-=,即5470x y +-=.即直线L 的方程为5470x y +-=. 22.解(1)由,sin ,x y θθ⎧=⎪⎨=⎪⎩得22:13x C y +=,由cos ()4p πθθ-=cos sin 4p p θθ+=,即:40l x y +-=.(2)在22:13x C y +=上任取一点,sin )P θθ(02)θπ≤≤,则点P 到直线l的距离为d=|2sin()4|πθ+-=,02θπ≤≤, 当sin()13πθ+=-,即76πθ=时,max d =23. 解(1)设事件A :“恰用完3次投篮机会”,则其对立事件A :“前两次投篮均不中”, 依题意, ()1()P A P A =-2211(1)25p =--=, 解得35p =.(2)依题意, X 的所有可能值为0,1,2,3, 且24(0)(1)25P X p ==-=, 2(1)(1)P X p p ==-24(1)(1)125p p p +--=, 327(3)125P X p ===, 故(2)1(0)P X P X ==-=54(1)(3)125P X P X -=-==. X 的概率分布列为:数学期望24()2125E X =+⨯54272133125125125+⨯=.24.解(1)如图,以D 为坐标原点,分别以直线1,,DA DC DD 所在直线为x 轴, y 轴, z 轴,建立空间直角坐标系D xyz -,易得1(0,2,3)A B =-,设BE a =,则(0,2,)AE a =,因为1A B AE ⊥,所以1(0,2,3)AB AE ⋅=- (0,2,)430a a ⋅=-=, 解得43a =,即4(0,2,)3AE =, 又1(2,2,3)D B =-,(2,2,0)AC =-, 所以1(2,23)D B AE ⋅=-4 (0,2,)03⋅=,所以1D B AE ⊥, 且1(2,2,3)(2,2,0)0D B AC ⋅=-⋅-=,所以1D B AC ⊥,又AE AC A =,所以1D B ⊥平面AEC . (2) 4(0,2,)3AE =,1(2,0,3)D A =-,1(0,2,3)DC =-, 设平面1ACD 的一个法向量(,,)n x y z =, 则110,0,D A n D C n ⎧⋅=⎪⎨⋅=⎪⎩即230,230,x z y z -=⎧⎨-=⎩令0z =,则3x y ==,即(3,3,2)n =,sin |cos ,AE θ=<|||||AE n n AE n ⋅>=⋅423=2⨯⨯==22.。
2017-2018学年江苏省南京市金陵中学高二第二学期期末考试数学试题-解析版
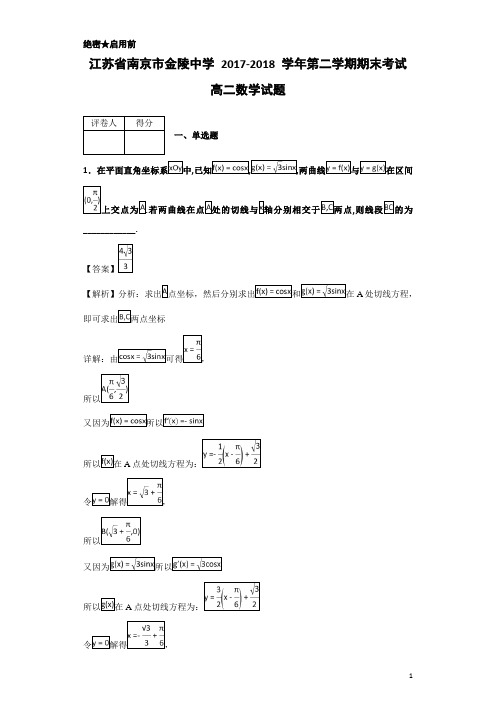
绝密★启用前江苏省南京市金陵中学2017-2018 学年第二学期期末考试高二数学试题一、单选题1,,____________.【解析】分析:求出A处切线方程,又因为A又因为A所以线段BC的长度为点睛:熟练记忆导函数公式是解导数题的前提条件,导数的几何意义是在曲线上某一点处的导数就等于该点处切线斜率,是解决曲线切线的关键,要灵活掌握.第II卷(非选择题)请点击修改第II卷的文字说明二、填空题2,【答案】{2,4,6,8}详解:A集合和B集合“加”起来的元素,重复的元点睛:在求集合并集时要注意集合的互异性.3,____________.【答案】5【解析】分析:先将复数z右边化为.4.某校共有教师200人,男学生1200人,女学生1000人.现用分层抽样的方法从所有师,已知从女学生中抽取的人数为50人,____________.【答案】120【解析】分析:根据分层抽样的原则先算出总体中女学生的比例,再根据抽取到女学生的人数计算样本容量n详解:因为共有教师200人,男学生1200人,女学生1000人女学生中抽取的人数为50人所以n=120点睛:分层抽样的实质为按比例抽,所以在计算时要算出各层所占比例再乘以样本容量即为该层所抽取的个数.5.如图是一算法的伪代码,则输出值为____________.【答案】4【解析】分析:按照循环体执行,直到跳出循环详解:第一次循环后:S=7,n=6;第二次循环后:S=13,n=5;第三次循环后:S=18,n=4;所以输出值为4点睛:程序题目在分析的时候一定要注意结束条件,逐次执行程序即可.6.如图,,为____________.【答案】3,=33点睛:在求解三棱锥体积问题时,如果所求椎体高不好确定时,往往要通过等体积转化,找到合适的高所对应的椎体进行计算,体现了数学中的转化与化归思想,要深刻体会.7,____________.x的值为x轴上,又因为该双曲线一条渐近线方程为所以的值为点睛:双曲线渐近线方程:当焦点在x y轴上时为8.,若则数列的通【解析】分析:根据基本量直接计算点睛:在等比数列问题中的未知量为首项和公比,求解这两个未知量需要两个方程,所以如果已知条件可以构造出来两个方程,则一定可以解出首项和公比,进而可以解决其他问题,因此基本量求解是这类问题的基本解法.9.将一颗均匀的骰子连续抛掷2次,则的概率是____________.【解析】分析:骰子连续抛掷2次共有366种详解:一颗均匀的骰子连续抛掷2次,(3,1),(4,1),(5,1),(6,1),(5,2),(6,2)6种点睛:古典概型概率要准确求出总的事件个数和基本事件个数,然后根据概率公式.10____________.A点处取得最小值,在C点处取得最大值所以的取值范围为点睛:点睛:线性规划要能够准确画出可行域,尤其是判断每一个不等式代表的是直线的左侧还是右侧时不能出错,常用带点方法判断比较准确。
2017-2018学年江苏省南京市外国语学校仙林分校中学部高二(上)数学期中试卷带解析答案

2017-2018学年江苏省南京市外国语学校仙林分校中学部高二(上)期中数学试卷一、填空题1.(4分)抛物线y2=x的准线方程为.2.(4分)函数y=x4﹣4x+3在区间[﹣2,3]上的最小值为.3.(4分)已知A(1,0),B(3,0),则以AB为直径的圆的方程为.4.(4分)函数f(x)=x﹣lnx的单调减区间为.5.(4分)若双曲线C的渐近线方程为y=±2x,且经过点(2,2),则C的标准方程为.6.(4分)若椭圆短轴一端点到椭圆一焦点的距离是该焦点到同侧长轴一端点距离的3倍,则椭圆的离心率e=.7.(4分)函数y=sinx的图象在点(π,0)处的切线方程为.8.(4分)圆心在x轴上且与直线l:y=2x+1切于点P(0,1)的圆C的标准方程为.9.(4分)在平面直角坐标系xOy中,已知抛物线y2=4x上一点P到焦点的距离为3,则点P的横坐标是.10.(4分)已知函数f(x)=2f′(1)lnx﹣x,则f(x)的极大值为.11.(4分)已知双曲线y2﹣4x2=16上一点M到一个焦点的距离等于2,则点M 到另一个焦点的距离为.12.(4分)设f(x)=,其中a为正实数,若f(x)为R上的单调递增函数,则a的取值范围是.13.(4分)已知椭圆的左、右焦点分别为F1,F2,P是以椭圆短轴为直径的圆上任意一点,则=.14.(4分)已知半径为2的动圆C2经过圆C1:(x﹣1)2+(y﹣1)2=8的圆心,且与直线l:x+y﹣8=0相交,则直线l被圆C2截得的弦长最大值是.二、解答题15.(11分)(1)已知双曲线C1:的离心率e∈(1,2),求实数k的取值范围.(2)过抛物线y2=2px(p>0)的焦点F作倾斜角为45°的直线交抛物线于A,B 两点,若线段AB的长为8,求p的值.16.(11分)已知椭圆(a>b>0)的右顶点A(2,0),A到右焦点的距离与其到右准线的距离之比为,(1)求椭圆的方程;(2)直线y=x+m与椭圆交于P,Q两点,问P,Q两点横坐标的平方和是否为定值?17.(11分)在边长为48cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?18.(11分)已知圆M:x2+y2﹣4x﹣8y+m=0与x轴相切.(1)求m的值;(2)求圆M在y轴上截得的弦长;(3)若点p是直线3x+4y+=0上的动点,过点p作直线PA,PB与圆M相切,A,B为切点,求四边形PAMB面积的最小值.19.(10分)已知函数f(x)=alnx+x2(a为实常数).(1)若a=﹣2,求证:函数f(x)在(1,+∞)上是增函数;(2)求函数f(x)在[1,e]上的最小值及相应的x值.20.(10分)已知椭圆(a>b>0)上的一动点P到右焦点的最短距离为,且右焦点到右准线的距离等于短半轴的长.(1)求椭圆C的方程;(2)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连接PB交椭圆C于另一点E,证明直线AE与x轴相交于定点Q;(3)在(2)的条件下,过点Q的直线与椭圆C交于M,N两点,求的取值范围.2017-2018学年江苏省南京市外国语学校仙林分校中学部高二(上)期中数学试卷参考答案与试题解析一、填空题1.(4分)抛物线y2=x的准线方程为x=﹣.【解答】解:抛物线y2=x的焦点在x轴上,且开口向右,2p=1∴∴抛物线y2=x的准线方程为x=﹣故答案为:x=﹣2.(4分)函数y=x4﹣4x+3在区间[﹣2,3]上的最小值为0.【解答】解:y′=4x3﹣4=4(x3﹣1);∴x∈[﹣2,1)时,y′<0,x∈(1,3]时,y′>0;∴x=1时,该函数取最小值0.故答案为:0.3.(4分)已知A(1,0),B(3,0),则以AB为直径的圆的方程为(x﹣2)2+y2=1.【解答】解:∵A(1,0),B(3,0),∴AB中点为(2,0),|AB|=.因此,以AB为直径的圆的圆心为(2,0),半径r=1.∴圆的方程为(x﹣2)2+y2=1.故答案为:(x﹣2)2+y2=1.4.(4分)函数f(x)=x﹣lnx的单调减区间为{x|0<x<1} .【解答】解:∵f(x)=x﹣lnx∴f'(x)=1﹣=令<0,则0<x<1故答案为:{x|0<x<1}5.(4分)若双曲线C的渐近线方程为y=±2x,且经过点(2,2),则C的标准方程为.【解答】解:由题意,∵双曲线C的渐近线方程为y=±2x,∴设双曲线C的方程为y2﹣4x2=λ∵双曲线C经过点(2,2),∴8﹣16=λ∴λ=﹣8∴双曲线C的方程为y2﹣4x2=﹣8,即故答案为:6.(4分)若椭圆短轴一端点到椭圆一焦点的距离是该焦点到同侧长轴一端点距离的3倍,则椭圆的离心率e=.【解答】解:由题意可得,即a=3a﹣3c∴2a=3c∴故答案为:7.(4分)函数y=sinx的图象在点(π,0)处的切线方程为x+y﹣π=0.【解答】解:函数y=sinx的导数为y′=cosx,在点(π,0)处的切线斜率为k=cosπ=﹣1,即有在点(π,0)处的切线方程上午y﹣0=﹣(x﹣π),即为x+y﹣π=0.故答案为:x+y﹣π=0.8.(4分)圆心在x轴上且与直线l:y=2x+1切于点P(0,1)的圆C的标准方程为(x﹣2)2+y2=5.【解答】解:设圆的标准方程为(x﹣a)2+(y﹣b)2=r2,∵圆心在x轴上,∴b=0,(1)∵与直线l:y=2x+1切于点P(0,1),∴=﹣,(2),由(1)、(2),得a=2,b=0,又∵P点在圆上,代入圆的方程得r2=5,∴所求圆的标准方程为(x﹣2)2+y2=5.故答案为(x﹣2)2+y2=5.9.(4分)在平面直角坐标系xOy中,已知抛物线y2=4x上一点P到焦点的距离为3,则点P的横坐标是2.【解答】解:∵抛物线y2=4x=2px,∴p=2,由抛物线定义可知,抛物线上任一点到焦点的距离与到准线的距离是相等的,∴|PF|=x+1=3,∴x=2,故答案为:2.10.(4分)已知函数f(x)=2f′(1)lnx﹣x,则f(x)的极大值为2ln2﹣2.【解答】解:由于函数f(x)=2f′(1)lnx﹣x,则f′(x)=2f′(1)×﹣1(x>0),f′(1)=2f′(1)﹣1,故f′(1)=1,得到f′(x)=2×﹣1=,令f′(x)>0,解得:x<2,令f′(x)<0,解得:x>2,则函数在(0,2)上为增函数,在(2,+∞)上为减函数,故f(x)的极大值为f(2)=2ln2﹣2故答案为:2ln2﹣211.(4分)已知双曲线y2﹣4x2=16上一点M到一个焦点的距离等于2,则点M 到另一个焦点的距离为10.【解答】解:双曲线y2﹣4x2=16即为﹣=1,可得a=4,设双曲线的两焦点为F1,F2,由题意可设|MF1|=2,由双曲线的定义可得||MF1|﹣|MF2||=2a=8,即有|2﹣|MF2||=8,解得|MF2|=10或﹣6(舍去).故答案为:10.12.(4分)设f(x)=,其中a为正实数,若f(x)为R上的单调递增函数,则a的取值范围是(0,1] .【解答】解:∵f(x)=,∴f'(x)=,∵f(x)为R上的单调增函数,∴f'(x)≥0在R上恒成立,又∵a为正实数,∴f'(x)≥0在R上恒成立,∴ax2﹣2ax+1≥0在R上恒成立,∴△=4a2﹣4a=4a(a﹣1)≤0,解得0≤a≤1,∵a>0,∴0<a≤1,∴a的取值范围为0<a≤1,故答案为:(0,1].13.(4分)已知椭圆的左、右焦点分别为F1,F2,P是以椭圆短轴为直径的圆上任意一点,则=2.【解答】解:椭圆如图,F1(﹣1,0),F2(1,0),设P(x0,y0),则x02+y02=3,∴=(x0+1,y0)•(x0﹣1,y0)=x02+y02﹣1=3﹣1=2.故答案为:2.14.(4分)已知半径为2的动圆C2经过圆C1:(x﹣1)2+(y﹣1)2=8的圆心,且与直线l:x+y﹣8=0相交,则直线l被圆C2截得的弦长最大值是2.【解答】解:设动圆C2的圆心为(a,b)∵半径为2的动圆C2经过圆C1:(x﹣1)2+(y﹣1)2=8的圆心,∴圆心的轨迹方程为:(a﹣1)2+(b﹣1)2=8又直线l被圆C2截得的弦长L=2,(d为圆C2的圆心(a,b)到直线l:x+y ﹣8=0的距离).∵点(a,b)的轨迹是以(1,1)为圆心,半径为2的圆.∴d的最小值为圆心(1,1)到直线l:x+y﹣8=0的距离减去半径2,即d min==则直线l被圆C2截得的弦长最大值为2=2故答案为:2二、解答题15.(11分)(1)已知双曲线C1:的离心率e∈(1,2),求实数k的取值范围.(2)过抛物线y2=2px(p>0)的焦点F作倾斜角为45°的直线交抛物线于A,B 两点,若线段AB的长为8,求p的值.【解答】解:(1)双曲线C1:(k>0)的离心率e∈(1,2),可得e==∈(1,2),解得0<k<12,即k的取值范围是(0,12);(2)过抛物线y2=2px(p>0)的焦点F(,0)作倾斜角为45°的直线交抛物线于A,B两点,可得直线y=x﹣,代入抛物线的方程可得:x2﹣3px+=1,可得x1+x2=3p,由弦长公式可得|AB|=x1+x2+p=4p=8,解得p=2.16.(11分)已知椭圆(a>b>0)的右顶点A(2,0),A到右焦点的距离与其到右准线的距离之比为,(1)求椭圆的方程;(2)直线y=x+m与椭圆交于P,Q两点,问P,Q两点横坐标的平方和是否为定值?【解答】解:(1)椭圆(a>b>0)的右顶点A(2,0),∴a=2,∵A到右焦点的距离与其到右准线的距离之比为,∴=,解得c=,∴b2=a2﹣c2=1,∴椭圆方程为+y2=1,(2)设P(x1,y1),Q(x2,y2)将y=x+m代入椭圆方程,化简得:x2+2mx+2(m2﹣1)=0,∴x1+x2=﹣2m,x1x2=2(m2﹣1),∴x12+x22=(x1+x2)2﹣2x1x2=4m2﹣4(m2﹣1)=4,∴P,Q两点的横坐标的平方和为定值.17.(11分)在边长为48cm的正方形铁片的四角切去相等的正方形,再把它的边沿虚线折起(如图),做成一个无盖的方底箱子,箱底的边长是多少时,箱底的容积最大?最大容积是多少?【解答】解:设箱底边长为xcm,则箱高h=,∴箱子容积V(x)=x2h=(48x2﹣x3)(0<x<48).求导数,得V′(x)=48x﹣x2,令V′(x)=0,解得x=0(不合题意,舍去),x=32,∵x∈(0,32)时,V′(x)>0;x∈(32,48)时,V′(x)<0,∴V(x)在区间(0,32)上为增函数,区间(32,48)上为减函数,由此可得V(x)的最大值是V(32)=8192.故箱底的边长是32cm时,箱子的容积最大,最大容积是8192cm3.18.(11分)已知圆M:x2+y2﹣4x﹣8y+m=0与x轴相切.(1)求m的值;(2)求圆M在y轴上截得的弦长;(3)若点p是直线3x+4y+=0上的动点,过点p作直线PA,PB与圆M相切,A,B为切点,求四边形PAMB面积的最小值.【解答】解:(1)圆M:x2+y2﹣4x﹣8y+m=0化为圆M:(x﹣2)2+(y﹣4)2=20﹣m,圆的圆心坐标(2,4),半径为,∵圆M:x2+y2﹣4x﹣8y+m=0与x轴相切,∴=4,解得m=4.(2)圆M:x2+y2﹣4x﹣8y+4=0,当x=0时,可得y2﹣8y+4=0,解得y1=4+2或y2=4﹣2.圆M在y轴上截得的弦长:y1﹣y2=4+2﹣4+2=4.(3)由题意知:S PAMB=2S△PAM=2וMB•PB=4PB=4,∵PM的最小值等于点M到直线3x+4y+8=0的距离,∴PM min=.∴四边形PAMB面积的最小值为4=8.19.(10分)已知函数f(x)=alnx+x2(a为实常数).(1)若a=﹣2,求证:函数f(x)在(1,+∞)上是增函数;(2)求函数f(x)在[1,e]上的最小值及相应的x值.【解答】解:(1)证明:当a=﹣2时,f(x)=x2﹣2lnx,x∈(1,+∞),其导数.故函数f(x)在(1,+∞)上是增函数.(2)根据题意,函数f(x)=alnx+x2,其导数为.当x∈[1,e],2x2+a∈[a+2,a+2e2].若a≥﹣2,f'(x)在[1,e]上非负(仅当a=﹣2,x=1时,f'(x)=0),故函数f(x)在[1,e]上是增函数.此时,[f(x)]min=f(1)=1.若﹣2e2<a<﹣2,当时,f'(x)=0.当时,f'(x)<0,此时,f(x)是减函数.当时,f'(x)<0,此时,f(x)是增函数.故.若a≤﹣2e2,f'(x)在[1,e]上非正(仅当时a=﹣2e2,x=e时,f'(x)=0)故函数f(x)在[1,e]上是减函数,此时.综上可知,当a≥﹣2时,f(x)的最小值为1,相应的x的值为1;当﹣2e2<a<﹣2时,f(x)的最小值为.相应的x值为;当a≤﹣2e2时,f(x)的最小值为a+e2,相应的x值为e.20.(10分)已知椭圆(a>b>0)上的一动点P到右焦点的最短距离为,且右焦点到右准线的距离等于短半轴的长.(1)求椭圆C的方程;(2)设P(4,0),A,B是椭圆C上关于x轴对称的任意两个不同的点,连接PB交椭圆C于另一点E,证明直线AE与x轴相交于定点Q;(3)在(2)的条件下,过点Q的直线与椭圆C交于M,N两点,求的取值范围.【解答】解:(1)由题意可得解得,∴椭圆C的方程为;(2)如图所示:设直线PB的方程为y=k(x﹣4),B(x1,y1),E(x2,y2),则A(x1,﹣y1).联立,消去y化为方程(1+2k2)x2﹣16k2x+32k2﹣4=0,∵直线PB与椭圆有两个不同的交点,∴△=(16k2)2﹣4(1+2k2)(32k2﹣4)>0.(*)x1+x2=,.直线AE的方程为,令y=0,则====.故直线AE过定点Q(1,0).(3)①当直线MN与x轴重合时,=(2,0)•(﹣2,0)=﹣4;②当直线MN与x轴不重合时,设直线MN的方程为my=x﹣1,联立消去x化为方程(2+m2)y2+2my﹣3=0,可知△>0.可得y M+y N=,y M y N=.∴=x M x N+y M y N=(my M+1)(my N+1)+y M y N=(1+m2)y M y N+m(y M+y N)+1==﹣4+,∵m2≥0,∴,∴,∴的取值范围是.综上可知:的取值范围是.。
精品解析:江苏省南京外国语学校仙林分校中学部2017--2018第一学期高二上学期期中测试数学试卷(解析版)

,解得
,即该圆的标准方程为
2
; 故填
.
二、解答题(本大题共 4 小题,每小题 13 分,共 52 分)
9.(1) 已知双曲线 :
的离心率
,求实数 的取值范围.
(2) 过抛物线
的焦点 作倾斜角为 的直线交抛物线于 , 两点,若线段 的长为 8,求 的
值.
【答案】 (1)
(2)
【解析】
试题分析: (1)利用双曲线的几何要素间的等量关系和离心率公式进行求解;
(2) 联立直线和抛物线的标准方
程,得到关于 的一元二次方程,利用根与系数的关系和两点间的距离公式进行求解
.
试题解析: (1)
,
∴
(2) 过焦点 的直线方程为
,
∴
∴
∴ ∴ 【方法点睛】本题第二问考查过抛物线的焦点的弦问题;在求过抛物线的焦点的弦的长度或焦半径时,利 用抛物线的定义(将抛物线的点到焦点的距离转化为到准线的距离)可起到事半功倍的效果,如:过抛物
因为
,所以
,所小值为 0;故填 0.
3.已知
,
,则以 为直径的圆的方程为 ___________.
【答案】 【解析】
单调递减,在区间
因为
,
,所以以 为直径的圆的圆心为
.
,半径为
4.函数 【答案】 【解析】
的单调增区间为 ____________ .
,即该圆的方程为
南外仙林分校中学部 2017-2018 学年第一学期高二年级期中测试 数学试题
第Ⅰ卷 (100 分 ) 一、填空题(本大题共 8 小题,每小题 6 分,共 48 分)
1.抛物线
的准线方程为 ________.
2017-2018学年江苏省南京外国语学校仙林分校中学部度第二学期高一年级期中测试数学学科试题

2017-2018学年江苏省南京外国语学校仙林分校中学部度第二学期高一年级期中测试数学学科试题一、填空题 1.不等式20x x-<的解为____________. 【答案】()0,2 【解析】分析:不等式20x x-<化为()20x x -<,解一元二次不等式即可. 详解:不等式20x x -<化为()20x x -<,解得02x <<, ∴不等式20x x-<的解集为()0,2,故答案为()0,2. 点睛:本题考查了分式不等式转化为一元二次不等式的解法,属于基础题 2.数列{a n }是等比数列,若a 3=1,a 5=3,则a 7的值为__________. 【答案】9【解析】分析:根据等比数列中等比中项的性质进行求解即可.详解:在等比数列中, ()2375a a a =,即2713a ⋅=,解得79a =,故答案为9. 点睛:本题主要考查等比数列性质的应用,利用等比中项的性质是解决本题的关键,属于基础题. 3.中,,则______________【答案】 【解析】由余弦定理可得:.4.正方体1AC 中,与面ABCD 的对角线AC 异面的棱有________条. 【答案】6【解析】分析:在正方体1AC 中,根据异面直线的定义列举出与面ABCD 的对角线AC 异面的所有的棱,由此能求出结果. 详解:如图,在正方体1AC 中,与面ABCD 的对角线AC 异面的棱有: 1BB , 1DD , 11A B , 11A D ,11D C , 11B C ,共6条,故答案为6.点睛:本题考查正方体中与面对角线异面的棱的条数的判断,是基础题,解题时要认真审题,注意正方体的性质的合理运用5.在等比数列{}n a 中,公比51421156q a a a a >-=-=,,,则3=a ______. 【答案】4【解析】分析:由已知条件利用等比数列的通项公式列出关于首项和公比的方程组,求出等比数列的首项和公比,由此能求出3a .详解:由已知条件得: 41131115{ 6a q a a q a q -=-=,由1q >,解得11a =, 2q =,所以2314a a q ==,故答案为4.点睛:本题考查等比数列{}n a 的通项公式求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.6.在等差数列{}n a 中, 121a a +=, 349a a +=,则56a a +=________. 【答案】17【解析】分析:由已知的第②个等式减去第①个等式可求出等差数列的性质得到差为公差d ,将所求式子用②和公差表示,即可求出结果.详解:设等差数列的公差为d ,由121a a +=①, 349a a +=② ②-①得: ()()341248a a a a d +-+==,得2d =, 则()563449817a a a a d +=++=+=,故答案为17.点睛:本题主要考查学生掌握等差数列的性质,是一道基础题,解题的突破点是求出等差数列的公差. 7.已知正数,a b 满足141a b+=,则ab 的最小值为___________. 【答案】16【解析】分析:利用基本不等式将和为定值转化为积的最值,即可得出结果详解:∵正数,a b 满足141a b +=,∴141a b +=≥ 可化为16ab ≥,当且仅当2a =, 8b =时取等号,故ab 的最小值为16,故答案为16.点睛:本题考查了基本不等式的性质,以及运算能力,属于基础题. 8.在ABC ∆中, sin cos A Ba b=,则B ∠= ________. 【答案】4π【解析】分析:利用正弦定理,结合条件,可得sin cos B B =,结合B 的取值范围,由此可求B 的值. 详解:由正弦定理可得sin sin A B a b =,∵sin cos A Ba b=, ∴sin cos B B =, 又∵0B π<<,∴4B π=,故答案为4π点睛:本题考查正弦定理和已知三角函数只求角,考查学生的计算能力,属于基础题. 9.已知2x >,则函数162y x x =+-的最小值是_______. 【答案】10【解析】分析:先判定20x ->,再由16162222y x x x x =+=-++--根据基本不等式可求得最小值.详解:∵2x >,∴20x ->,∴16162221022y x x x x =+=-++≥=--, 当且仅当1622x x -=-,即6x =时,等号成立,即函数的最小值为10. 点睛:本题主要考查了基本不等式.基本不等式求最值应注意的问题(1)使用基本不等式求最值,其失误的真正原因是对其前提“一正、二定、三相等”的忽视.要利用基本不等式求最值,这三个条件缺一不可.(2)在运用基本不等式时,要特别注意“拆”“拼”“凑”等技巧,使其满足基本不等式中“正”“定”“等”的条件.10.在ABC ∆中,若sin A C =, 30B =︒, 2b =,则ABC ∆的面积是______.【解析】分析:由正弦定理将已知条件化为a =,由余弦定理和条件求出a 、c 的值,代入三角形的面积公式求解.详解:因为sin A C =,所以由正弦定理可得a ,由余弦定理得, 2222cos b a c ac B =+-,即222432c c =+-,化简得2c =, a =111sin 2222ABCSac B ==⨯⨯=点睛:本题考查正弦、余弦定理,以及三角形的面积公式,熟练掌握公式是解题的关键;利用正弦定理实现边角之间的互化,是解三角形中常用的技巧,而当涉及三角形三边及其中一个角时主要通过余弦定理解三角形. 11.若等差数列的前项和为,,,则使得取最大值时的正整数______________ 【答案】3【解析】由等差数列的性质可得:,数列的公差: ,据此可得,数列单调递减,且:,使得取最大值时的正整数3.12.设0,0x y >>,且()1xy x y -+=,则x y +的最小值是__________.【答案】)21【解析】分析:首先根据0,0x y >>,即可得到22x y xy +⎛⎫≤ ⎪⎝⎭,代入原不等式进而得出()()214x y x y +≤-+,解关于x y +的不等式即可得出x y +的最小值.详解:∵0,0x y >>,∴22x y xy +⎛⎫≤ ⎪⎝⎭,∴()()()214x y xy x y x y +=-+≤-+,即()()2440x y x y +-+-≥,解得2x y +≥+2x y +≤-;∴x y +的最小值为2+2+点睛:考查基本不等式: a b +≥ 0a >, 0b >,以及一元二次不等式的解法,解题的关键是构造出关于x y +的不等式.13.在△ABC 中,内角,,A B C 的对边分别为,,a b c ,已知3cos 5A =, sin 2cos C B =且4a =,则△ABC 的面积为_________. 【答案】8【解析】分析:利用两角和的正弦函数公式和sin 2cos C B =即可得出sinB , cosB ,从而得出sinC ,再利用正弦定理求出b ,代入面积公式即可得出三角形的面积. 详解:∵3cos 5A =,∴4sin 5A =,∵()sin sin 2cos C A B B =+=,∴sin cos cos sin 2cos A B A B B +=, ∴43cos sin 2cos 55B B B +=,即sin 2cos B B =,∴tan 2B =,∴sin B =,cos B =,∴sin 2cos C B ==, 由正弦定理得:sin sin a b A B=,即445=b =∴1148225ABCSabsinC ==⨯⨯=,故答案为8. 点睛:本题考查了正弦定理在解三角形中的应用,两角和差的三角函数以及三角形面积的求法,属于中档题.14.在ABC 中,角,,A B C 所对的边分别是,,a b c ,若5b =, 10a c +=, 2A C =.则a c -=_________. 【答案】2【解析】分析:对已知等式2A C =两边同时取正弦,利用二倍角正弦和正弦定理相结合可得2cos a c C =,再利用余弦定理将角化为边,最后将5b =及10a c =-代入可得关于c 的一元二次方程,解出即可.详解:∵2A C =,∴sin sin22sin cos A C C C ==,由正弦定理得: 2cos a c C =,根据余弦定理可得: 22222a b c a c ab+-=,将5b =及10a c =-代入化简得29200c c -+=,解得4{6c a ==, 5{5c a ==(根据大角对大边舍去),则2a c -=,故答案为2.点睛:本题主要考查了解三角形的问题,考查了正弦定理、余弦定理的应用和方程思想的灵活运用,属于基础题.二、解答题15.解不等式: 22530x x -+->.【答案】3{|1}2x x <<【解析】分析:在不等式两边都除以1-,不等式号方向改变,把不等式的左边分解因式后,即可得原不等式的解集.详解:由原式得22530x x -+<,即()()1230x x --<所以312x <<,因此原不等式的解集为3{|1}2x x << 点睛:本题主要考查了一元二次不等式的解法,考查了转化的思想,解题的关键是正确进行因式分解,是一道基础题.16.已知空间四边形ABCD ,E 、H 分别是AB 、AD 的中点, F 、G 分别是CB 、CD 上的点,且2CF CGFB GD==.(1)求证:四边形EFGH 是梯形;(2)若BD a =,求梯形EFGH 的中位线的长. 【答案】(1)见解析;(2)712a 【解析】分析:(1)首先根据三角的中位线定理得到//EH BD ,且12EH BD =,根据三角形相似得到//FG BD ,且23FG BD =,从而//FG BD ,且23FG BD =成立,即可得结论;(2)根据梯形中位线的长度等于上底和下底之和的一半可得结果.详解:证明:(1)在ABD 中,E 、H 分别是AB 、AD 的中点, 所以//EH BD ,且12EH BD = 在CBD 中,2CF CGFB GD==, 所以//FG BD ,且23FG BD =所以四边形EFGH 中, //EH FG ,且EH FG ≠,因此,四边形EFGH 是梯形;(2)由(1)知12EH a =, 23FG a = 从而,梯形EFGH 的中位线的长为7212EH FG a +=. 点睛:本题考查直线与直线平行的判定,梯形中位线的长度,考查学生分析解决问题的能力,属于基础题. 17.在△ABC 中,C -A =2π,sin B =13.(1)求sin A 的值;(2)设AC ABC 的面积.【答案】(1(2)【解析】分析:(1)由已知2C A π-=和三角形的内角和定理得到A 与B 的关系式22B A π=-及A 的范围,然后利用二倍角的余弦函数公式化简得到一个关于sinA 的方程,即可求得结果;(2) 先根据sin sin 2C A π⎛⎫=+ ⎪⎝⎭可求出sin C 的值,再由正弦定理求出BC ,最后根据三角形面积公式可得结果. 详解:(1)由2C A π-=和A B C ++=π,得B =2π-2A , 0<A <4π.故sin cos2B A =,即1-2 2sin A =13, sin 3A =.(2)由(1)得 sin sin cos 2C A A π⎛⎫=+=== ⎪⎝⎭.又由正弦定理sin sin BC ACA B =,得BC =所以1sin 2ABCS AC BC C ∆=⋅⋅= 点睛:本题考查了同角三角函数间的基本关系、二倍角的余弦函数公式、诱导公式及三角形的面积公式和正弦定理,是一道综合题,做题时应注意角度的变换. 18.已知正项等比数列的前项和为,且,.(1)求数列的通项公式;(2)设,求数列的前项和.【答案】(1);(2).【解析】试题分析:(1)由题意求得首项和公比,则数列的通项公式为;(2)结合(1)的结果错位相减可得.试题解析:(1)设正项等比数列的公比为,若,则,不符合题意;则∴ ,解得:∴ (2)①②①②得:∴点睛:一般地,如果数列{a n }是等差数列,{b n }是等比数列,求数列{a n ·b n }的前n 项和时,可采用错位相减法求和,一般是和式两边同乘以等比数列{b n }的公比,然后作差求解.19.为了丰富改善居民生活,市招商局引进外商到开发区一次性投资72万元建起了一座蔬菜加工厂.以后每年还需要继续投资:第一年需要要各种经费为12万元,从第二年开始每年所需经费均比上一年增加4万元,该加工厂每年销售总收入为50万元. (1)若扣除投资及各种经费,该加工厂从第几年开始纯利润为正? (2)若干年后,外商为开发新项目,对加工厂有两种处理方案: ①若年平均纯利润达到最大值时,便以48万元价格出售该厂; ②若纯利润总和达到最大值时,便以16万元的价格出售该厂. 问:哪一种方案比较合算?说明理由. 【答案】(1)从第三年开始获利;(2)见解析 【解析】分析:(1)利润总额()f n 即x 年中的收入50n 减去n 年所需各种经费, ()0f n >解出结果进行判断得出何年开始赢利;(2)利用基本不等式算出第一种方案总盈利,利用二次函数性质算出第二种方案的总盈利,得到每一种方案的总盈利,比较大小选择方案.详解:由题设知,每年的经费是以12首项,4为公差的等差数列。
江苏省南京市金陵国际语言中学2018年高二物理下学期期末试题含解析

江苏省南京市金陵国际语言中学2018年高二物理下学期期末试题含解析一、选择题:本题共5小题,每小题3分,共计15分.每小题只有一个选项符合题意1. 如图所示的速度选择器中有正交的电场和磁场,有一粒子沿垂直于电场和磁场的方向飞入其中,并沿直线运动(不考虑重力作用),则此粒子()A.一定带正电B.一定带负电C.可能带正电或负电,也可能不带电D.一定不带电参考答案:C【考点】带电粒子在混合场中的运动.【分析】在速度选择器中,存在相互正交的匀强电场、磁场,带电粒子进入其中后受到电场力和洛伦兹力,只有两力平衡,粒子才能从左孔射入,从右孔射出.由左手定则判断洛伦兹力方向,当然也可以不带电,则做匀速直线运动.【解答】解:若带电粒子带正电,受到的洛伦竖直向下,电场力竖直向上,且qv0B=qE,即速度v0=,该电荷做匀速直线运动,从左向右运动;若带电粒子带负电,受到的洛伦竖直向上,电场力竖直向下,且qv0B=qE,即速度v0=,该电荷做匀速直线运动,也从左边射入,从右边射出.若不带电,则不受到任何力,所以做匀速直线运动,故C正确,ABD错误.故选:C2. (单选)仔细观察氢原子的光谱,发现它只有几条分离的不连续的亮线,其原因是()A.观察时氢原子有时发光,有时不发光B.氢原子只能发出平行光C.氢原子辐射的光子的能量是不连续的,所以对应的光的频率也是不连续的D.氢原子发出的光互相干涉的结果参考答案:C3. (单选)一物体在水平面上由静止开始在水平恒力F作用下运动t s,t s末撤去该力,物体又经过2t s停止运动,在此过程中,物体受到的摩擦力大小为()A.F/4 B.F/3 C.F/2 D.2F/3参考答案:B4. (多选)图(a)为一列简谐横波在t=2时的波形图,图(b)为媒质中平衡位置在x=1.5m处的质点的振动图像,P是平衡位置为x=2m的质点。
下列说法正确的是。
A.波速为0.5m/sB.波的传播方向向右C.0~2s时间内,P运动的路程为8cmD.0~2s时间内,P向y轴正方向运动E.当t=7s时,P恰好回到平衡位置。
江苏省南京市金陵中学2017-2018学年高二下学期期期末考试英语试题

本试卷满分120分第I卷第一部分英语知识运用(共三节,满分50分)第一节听力理解(共20题,每小题0.5分,满分10分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. Why is Ann so upset?A. She failed one of her exams.B. She is worrying about other lesson.C. She has no time to do her math homework.2. What type of food does the woman cat?A. Junk food.B. Healthy food.C. Delivered food.3. What will the man probably do to stay warm?A. Use a blanket.B. Turn on the heater.C. Drink some hot chocolate.4. What are the speakers mainly talking about?A. The man’s career.B. The man’s travel plan.C. The man’s plan after graduating.5. What are the speakers’ opinions about the painting?A. It’s simple.B. It’s colorful.C. It’s complex.听下面5段对话。
每段对话后有几个小题,从题中所给的A、B、C、三个选项中选出最佳选项,并标在试卷的相应位置,听每段对话前,你将有时间阅读各个小题,每小题5秒钟:听完后,各小题给出5秒钟的作答时间。
江苏省南京市金陵中学2017-2018学年高二下学期期末考试数学试题含答案

金陵中学2017-2018学年度第二学期期末考试高二数学试卷数学I一、填空题:本大题共14小题,每小题5分,共70分.请把答案填在答题卡相应位置上. 1.设集合{2,4}A =,{2,6,8}B =,则AB = .2.已知复数2(12i)z =-,其中i 是虚数单位,则||z 的值是 .3.某校共有教师200人,男学生1200人,女学生1000人.现用分层抽样的方法从所有师生中抽取一个容量为n 的样本,已知从女学生中抽取的人数为50人,那么n 的值为 .4.如图是一算法的伪代码,则输出值为 .5.如图,在长方体1111ABCD A B C D -中, 3cm AB AD ==,12cm AA =,则三棱锥111A AB D -的体积为 .6.在平面直角坐标系xOy 中,若双曲线2221(0)x y m m-=>的一条渐近线方程为30x y +=,则实数m 的值为 .7.设各项均为正数的等比数列{}n a 的前n 项和为n S ,若52378,13a a S -==,则数列{}n a 的通项公式为n a = .8.将一颗均匀的骰子连续抛掷2次,向上的点数依次记为,m n ,则“2m n >”的概率是 .9.若实数,x y 满足条件14,23,x y x y -≤+≤⎧⎨≤-≤⎩则42z x y =-的取值范围为 .10.在平面直角坐标系xOy 中,已知()cos f x x =,()3sin g x x =,两曲线()y f x =与()y g x =在区间(0,)2π上交点为A .若两曲线在点A 处的切线与x 轴分别相交于,B C 两点,则线段BC 的为 .11.如图,在平面四边形ABCD 中, O 是对角线AC 的中点,且10OB =,6OD =. 若28DA DC ⋅=-,则BA BC ⋅的值为 .12.若对满足64x y xy ++=的任意正实数,x y ,都有22210x xy y ax ay ++--+≥,则实数a 的取值范围为 .13.在平面直角坐标系xOy 中,记椭圆22221(0)x y a b a b+=>>的左右焦点分别为12,F F ,若该椭圆上恰好有6个不同的点P ,使得12F F P ∆为等腰三角形,则该椭圆的离心率的取值范围是 .14.对于任意的实数,m n ,记min{,}m n 为,m n 中的最小值.设函数21()4f x x a x=++,()ln g x x =-,函数()min{(),()}h x f x g x =,若()h x 在(0,)+∞恰有一个零点,则实数a 的取值范围是 .二、解答题:本大题共6小题,共计90分.解答时应写出文字说明、证明过程.15.在平面直角坐标系xOy 中,设向量(sin ,1)m x =-,2(3cos ,cos )n x x =.(1)当3x π=时,求m n ⋅的值;(2)若[0,]4x π∈,且3132m n ⋅=-.求cos2x 的值. 16.如图,在四棱锥P ABCD -中,底面ABCD 是矩形,平面PAD ⊥平面ABCD ,AP AD =,点M 在棱PD 上, AM PD ⊥,点N 是棱PC 的中点,求证:(1) MN ∥平面PAB ; (2) AM ⊥平面PCD .17.如图,在一个水平面内,河流的两岸平行,河宽1(单位:千米)村庄,A B 和供电站C 恰位于一个边长为2(单位:千米)的等边三角形的三个顶点处,且,A C 位于河流的两岸,村庄A 侧的河岸所在直线恰经过BC 的中点D .现欲在河岸上,A D 之间取一点E ,分别修建电缆CE 和EA ,EB .设DCE θ∠=,记电缆总长度为()f θ (单位:千米).(1)求()f θ的解析式;(2)当DCE ∠为多大时,电缆的总长度()f θ最小,并求出最小值.18.如图,在平面直角坐标系xOy 中,已知椭圆22221(0)x y a b a b+=>>的离心率为3,且过点1(3,)2.设F 为椭圆的右焦点, ,A B 为椭圆上关于原点对称的两点,连结,AF BF 并延长,分别交椭圆于,C D 两点.(1)求椭圆的标准方程;(2)设直线,AB CD 的斜率分别为12,k k ,是否存在实数m ,使得21k mk =?若存在,求出实数m 的值;若不存在,请说明理由.19.设数列{}n a 的前n 项的和为n S ,且满足12a =,对*n N ∀∈,都有1(1)2n n a p S +=-+ (其中常数1p >),数列{}n b 满足2121log ()n n b a a a n=.(1)求证:数列{}n a 是等比数列; (2)若220172p =,求2018b 的值;(3)若*k N ∃∈,使得2212k p +=,记3||2n n c b =-,求数列{}n c 的前2(1)k +项的和. 20.在平面直角坐标系xOy 中,已知函数()1n (R)f x c x c =∈的图像与直线2y x e=相切,其中e 是自然对数的底数.(1)求实数c 的值; (2)设函数()()a h x ax g x x =--在区间1(,e)e内有两个极值点. ①求实数a 的取值范围;②设函数()h x 的极大值和极小值的差为M ,求实数M 的取值范围 .高二数学Ⅱ(附加题)21.已知矩阵 2 11 3M -⎡⎤=⎢⎥⎣⎦, 1 12 1N ⎡⎤=⎢⎥-⎣⎦. (1)求1()MN -;(2)在平面直角坐标系xOy 中,求直线:210L x y +-=在M 对应的变换T 作用下所得直线L '的方程.22.在直角坐标系xOy 中,以原点O 为极点,以x 轴的非负半轴为极轴,取与直角坐标系xOy相同的长度单位,建立极坐标系.设曲线C 的参数方程为sin x y θθ⎧=⎪⎨=⎪⎩,(θ为参数,[0,2]θπ∈),直线l 的极坐标方程为cos()4p πθ-=(1)写出曲线C 的普通方程和直线l 的直角坐标方程;(2)求曲线C 上的点到直线l 的最大距离.23.假定某篮球运动员每次投篮命中率均为(01)p p <<.现有3次投篮机会,并规定连续两次投篮均不中即终止投篮,已知该运动员不放弃任何一次投篮机会,且恰好用完3次投篮机会的概率是2125. (1)求p 的值;(2)设该运动员投篮命中次数为X ,求X 的概率分布及数学期望()E X .24.如图,已知正四棱柱1111ABCD A B C D -的底面边长为2,侧棱长为3, 1AE A B ⊥,垂足为F ,AE 交1B B 于点E .(1)求证: 1D B ⊥平面AEC ;(2)记直线AE 与平面1ACD 所成的角θ,求sin θ的值.试卷答案一、填空题. 1. {2,4,6,8} 2. 5 3. 120 4. 45. 37. 31n-8.169. [5,13] 11. 36 12. 10(,]3-∞ 13. 111(,)(,1)32214. 5{|4a a <-或3}4a >- 二、解答题.15. 解(1)当3x π=时,1]m =-,1]4n =, 所以311442m n ⋅=-=.(2) 2cos cos m n x x x ⋅=-112cos222x x =-- 1sin[2]62x π=--,若12m n ⋅=-.则11sin[2]622x π--=-,即sin[2]6x π-=. 因为[0,]4x π∈,所以2663x πππ-≤-≤,所以cos[2]6x π-= 所以cos2cos[[2]]66x x ππ=-+cos[2]6x π=--1sin[2]62x π-⨯132326-=⨯-⨯=.16.证明(1)因为在PAD ∆中, ,AP AD AM PD =⊥, 所以点M 是棱PD 的中点. 又点N 是棱PC 的中点, 所以MN 是PDC ∆的中位线, 所以MN DC ∥. 因为底面ABCD 是矩形, 以AB DC ∥, 所以MN AB ∥.又AB ⊂平面PAB , MN ⊄平面PAB ,所以MN ∥平面PAB . (2)因为平面PAD ⊥平面ABCD , CD ⊂平面ABCD , 平面PAD平面,ABCD AD CD AD =⊥,所以CD ⊥平面PAD .又AM ⊂平面PAD ,所以CD AM ⊥. 因为CD AD ⊥,CD AM ⊥, CD PD D =,CD ⊂平面PCD ,PD ⊂平面PCD ,所以AM ⊥平面PCD .17.解(1)易得AD 垂直平分BC ,1CD BD ==则1cos CE EB θ==,tan ED θ=,tan AE θ=,于是11()cos cos f θθθ=++2sin tan cos θθθ-=+因为E 在CD 之间,所以03πθ<<,故2sin ()cos f θθθ-=+,03πθ<<.(2) 22cos (2sin )(sin )()cos f θθθθθ----=,03πθ<<, 令()0f θ=,得1sin ,26πθθ==, 故当06πθ<<,()0f θ<,()f θ递减,当sin 62ππθ<<,()0f θ>,()f θ递增,所以,当6πθ=时, min ()()6f f πθ==122-+=答:当6DCE π∠=时, ()f θ最小值为18.解(1)设椭圆的方程为22221(0)x y a b a b+=>>,c =,由题意知22311,4c a a b ⎧=⎪⎪⎨⎪+=⎪⎩ 解得2,1,a b =⎧⎨=⎩所以椭圆的方程为2214x y +=. (2)设00(,)A x y ,则00(,)B x y --,010y k x =,又F , 所以直线AF的方程为y x =-.由221,4y x x y ⎧=-⎪⎪⎨⎪+=⎪⎩消去y ,得2200(7)x x --20070x -+=.因为0x x =是该方程的一个解,所以点C的横坐标C x =又点(,)C C C x y在直线y x =-上,所以C C y x =-=C的坐标为 同理,点D的坐标为,所以2k =101472y k x ==, 即存在7m =,使得217k k =.19.(1)证明:因为*n N ∀∈,都有1(1)2n n a p S +=-+,21(1)2n n a p S ++=-+所以两式相减得211(1)n n n a a p a +++-=-, 即21n n a pa ++=,当1n =时211(1)2a p a pa =-+=,所以*1,()n n a pa n N +=∈,又因为1p >,所以11n nn n a a p p++=, 所以数列{}n na p是常数列, 112,2n n n n a a a p p p p -===, 所以{}n a 是以2为首项, p 为公比的等比数列.(2)由(1)得12n n a p -=.2121log ()n n b a a a n==(1)221log (2)n n np n -=1(1)()2017n n n n -+所以20182b =.(3)由(1)得12n n a p -=.2121log ()n n b a a a n==(1)221log (2)n n n p n -=(1)2121log (22)n n n k n -+1121n k -=++.因为322322(21)n n k b k ---=+, 所以当11n k ≤≤+时, 32n n c b =-,当2n k ≥+时,32n n c b =-. 因此数列{}n c 的前2(21)k +项的和22k T +121()k b b b +=-++++2222()k k k b b b ++++++0121k k +++=-++(1)(2)2+121k k k k ++++++ (1)221k k k +=-++2(1)(22)(1)22121k k k k k k ++++=++. 20. (1)设直线2y x e =与函数()1n f x c x =相切于点00(,1n )P x c x ,函数()1n f x c x =在点00(,1n )P x c x 处的切线方程为: 0001()c y c nx x x x -=-,02c x e=, 把0,0x y ==代入上式得0,2x e c ==. 所以,实数c 的值为2. (2)①由(1)知()21n ah x ax x x=--, 设函数()h x 在区间1(,e)e内有两个极值点1212,()x x x x <,令22()a a h x a x x x'=+--2220ax x ax -+==, 则220ax x a -+=,设2()2m x ax x a =-+,因为121x x =,故只需0,20,()0,am e ∆>⎧⎪⎪>⎨⎪>⎪⎩,所以, 2211e a e <<+.②因为121x x =,所以,121()()M f x f x ax =-=1221221n (21n )a ax ax x x x ----- 11121n a ax x x =---1111(21n )a ax x x -- 21112221n aax x x =--由21120ax x a -+=,得12121x a x =+,且111x e<<. 12111211222121x x x M x x x +=-+222111211121n 4(1n )12x x x x --=-+. 设21x t =,211t e <<,令11()4(1n )+12t t t t ϕ-=-, 221()4()(+1)2t t t ϕ'=-222(1)0(1)t t t --=<+, ()t ϕ(在21(,1)e 上单调递减,从而21(1)()()t e ϕϕϕ<<, 所以,实数M 的取值范围是28(0,)1e +. 高二数学Ⅱ(附加题)21. 解(1)由题知 2 11 3MN -⎡⎤=⎢⎥⎣⎦ 1 10 32 17 2⎡⎤⎡⎤=⎢⎥⎢⎥--⎣⎦⎣⎦,所以0 3)2l 7 det(2MN ⎡⎤==-⎢⎥-⎣⎦, 根据逆矩阵公式,得121 217)1 03(MN -⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦.(2)设由L 上的任意一点(,)P x y '''在T 作用下得到L '上对应点(,)p x y .由 2 11 3x x y y '-⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥'⎣⎦⎣⎦⎣⎦,即2,3'x y x x y y ''-=⎧⎨''+=⎩解得3+72'7x y x y x y ⎧'=⎪⎪⎨-⎪=⎪⎩, 因为210x y ''+-=,所以3221077x y y x +-⨯+-=, 即5470x y +-=.即直线L 的方程为5470x y +-=. 22.解(1)由,sin ,x y θθ⎧=⎪⎨=⎪⎩得22:13x C y +=,由cos ()4p πθθ-=cos sin 4p p θθ+=,即:40l x y +-=.(2)在22:13xC y+=上任取一点(3cos,sin)Pθθ(02)θπ≤≤,则点P到直线l的距离为|3cos sin4|2dθθ+-=|2sin()4|32πθ+-=,02θπ≤≤,当sin()13πθ+=-,即76πθ=时,max32d=.23. 解(1)设事件A:“恰用完3次投篮机会”,则其对立事件A:“前两次投篮均不中”, 依题意, ()1()P A P A=-2211(1)25p=--=,解得35p=.(2)依题意, X的所有可能值为0,1,2,3,且24(0)(1)25P X p==-=,2(1)(1)P X p p==-24(1)(1)125p p p+--=,327(3)125P X p===,故(2)1(0)P X P X==-=54(1)(3)125P X P X-=-==.X的概率分布列为:数学期望24()2125E X=+⨯54272133125125125+⨯=.24.解(1)如图,以D为坐标原点,分别以直线1,,DA DC DD所在直线为x轴, y轴, z轴,建立空间直角坐标系D xyz-,易得1(0,2,3)A B=-,设BE a=,则(0,2,)AE a=,因为1A B AE⊥,所以1(0,2,3)AB AE⋅=- (0,2,)430a a⋅=-=,解得43a=,即4(0,2,)3AE=,又1(2,2,3)D B=-,(2,2,0)AC=-,所以1(2,23)D B AE⋅=-4(0,2,)03⋅=,所以1D B AE⊥,且1(2,2,3)(2,2,0)0D B AC⋅=-⋅-=,所以1D B AC⊥,又AE AC A=,所以1D B⊥平面AEC.(2)4(0,2,)3AE=,1(2,0,3)D A=-,1(0,2,3)DC=-,设平面1ACD的一个法向量(,,)n x y z=,则110,0,D A nD C n⎧⋅=⎪⎨⋅=⎪⎩即230,230,x zy z-=⎧⎨-=⎩令0z=,则3x y==,即(3,3,2)n=,sin|cos,AEθ=<|||||AE nnAE n⋅>=⋅22222423=2342+()3+3+23⨯⨯=⨯286=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南京外国语学校仙林分校中学部2017-2018学年度第二学期高二年级 数学理期末测试第Ⅰ卷一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答卷..纸.相应位置上.1. 设复数z 满足(34i)|43i |z -=+(i 为虚数单位),则z 的虚部是___.2. 设集合}3{},4,2{},3,1,1{2=++=-=B A a a B A ,则实数a 的值为 .3. 右图是一个算法流程图,则输出的k 的值是 .4. 函数ln(1)()1x f x x +=-的定义域为 . 5.某棉纺厂为了解一批棉花的质量,从中随机抽取了100根棉花纤 维的长度(棉花纤维的长度是棉花质量的重要指标),所得数据均 在区间]40,5[中,其频率分布直方图如图所示,则在抽测的100根 中,有_ _根棉花纤维的长度小于mm 20.6. 盒子里共有大小相同的3只白球,1只黑球,若从中随机摸出两只球,则它们颜色不同的概率是_____________. 7.已知函数cos y x =与sin(2)(0)y x ϕϕπ=+≤≤,它们的图象有一个横坐标为3π的交点,则ϕ的值是___________. 8. 双曲线()2222:10,0x y C a b a b -=>> 的左、右焦点分别是12,F F ,过1F 作倾斜角为30︒的直线, 交双曲线C 右支于点M ,若2MF 垂直于x 轴,则双曲线C 的离心率为 . 9.若sin (6π﹣θ)=,则cos (23π+2θ)的值为 .10.函数()sin (0)f x x x x π=-≤≤的单调增区间是________ 11. 设函数24 6 (0)() 6 (0)x x x f x x x ⎧-+=⎨+<⎩≥,则不等式)1()(f x f >的解集是 .12. 已知函数,1)(2-+=mx x x f 若对于任意()1,+∈m m x ,都有0)(<x f 成立,则实数m 的取值范围是__________ .13.已知()f x 是定义在R 上且周期为3的函数,当[)0,3x ∈时,21()22f x x x =-+, 若函数()y f x a =-在区间[]3,4-上有10个零点(互不相同),则实数a 的取值范围是 .14. 在钝角ABC ∆中,已知2sin 216A A +=,则sin cosBC 取得最小值时,角B 等于 .二、解答题:本大题共6小题,共计90分.解答应写出文字说明、证明过程或演算步骤.请把答案写在答卷纸...相应位置上.15. (本题满分14分)已知集合A ={x |x 2-3x +2>0},B ={x |x 2-(a +1)x +a ≤0,a >1}. (1)求集合A ,B ;(2)若(C R A )∪B =B ,求实数a 的取值范围. 16.(本题满分14分)在ABC ∆中,角A ,B ,C 的对边分别为a b c ,,,已知3a =,b =2B A =. (1)求cos A 值; (2)求c 的值.17.(本题满分14分)已知()()2,ln 23+-+==x ax x x g x x x f .(Ⅰ)如果函数()x g 的单调递减区间为错误!未找到引用源。
,求函数()x g 的解析式; (Ⅱ)在(Ⅰ)的条件下,求函数y=()x g 的图像在点错误!未找到引用源。
处的切线方程; (Ⅲ)若不等式错误!未找到引用源。
的解集为P ,且错误!未找到引用源。
,求实数a 的取值范围.18.(本题满分16分)已知美国苹果公司生产某款iPhone 手机的年固定成本为40万美元,每生产1万只还需另投入16万美元.设苹果公司一年内共生产该款iPhone 手机x 万只并全部销售完,每万只的销售收入为R(x)万美元,且R(x)=(Ⅰ)写出年利润W(万美元)关于年产量x(万只)的函数解析式;(Ⅱ)当年产量为多少万只时,苹果公司在该款iPhone 手机的生产中所获得的利润最大?并求出最大利润.19. (本题满分16分)已知椭圆C :22221x y a b+=(0a b >>)的离心率为12,1F .2F 分别为椭圆C 的左.右焦点,若椭圆C 的焦距为2. (1)求椭圆C 的方程;(2)设M 为椭圆上任意一点,以M 为圆心,1F M 为半径作圆M ,当圆M 与椭圆的右准线l 有公共点时,求12FF ∆M 面积的最大值.20. (本题满分16分)已知a 为实数,函数f (x )=a ·ln x +x 2-4x .(1)是否存在实数a ,使得f (x )在x =1处取极值?证明你的结论; (2)若函数f (x )在[]2,3上存在单调递增区间,求实数a 的取值范围; (3)设g (x )=2a ln x +x 2-5x -1a x +,若存在x 0∈1,e e ⎡⎤⎢⎥⎣⎦,使得f (x 0)<g (x 0)成立,求实数a 的取值范围.第Ⅱ卷21.B (本小题满分10分)已知直线1=+y x l :在矩阵⎥⎦⎤⎢⎣⎡=10n m A 对应的变换作用下变为直线1=-'y x l :,求矩阵A .21.C (本小题满分10分) 已知直线:l 1314x ty t=+⎧⎨=--⎩ (t 为参数),以坐标原点为极点,x 轴正半轴为极轴,曲线C 的极坐标方程为)4cos(2πθρ+=.(1)将曲线C 的方程化成直角坐标方程; (2)求直线l 被曲线C 截得的弦长. 22.(本小题满分10分)已知甲箱中装有3个红球,3个黑球,乙箱中装有2个红球,2个黑球,这些球除颜色外完全相同,某商场举行有奖促销活动,设奖规则如下:每次分别从以上两个箱子中个随机摸出2个球,共4个球,若摸出4个球都是红球,则获得一等奖,摸出的球中有3个红球,则获得二等奖;摸出的球中有2个红球,则获得三等奖;其他情况不获奖,每次模球结束后将球放回原箱中(1)求在1次摸奖中,获得二等奖的概率;(2)若连续摸奖2次,求获奖次数X 的分布列及数学期望E(X)。
23.(本小题满分10分)如图,在长方体ABCD-A 1B 1C 1D 1中,AA l =AB=2AD=2,E 为AB 的中点,F 为D 1E上的一点,D 1F=2FE.(l)证明:平面DFC ⊥平面D 1EC; (2)求二面角A-DF-C 的大小.高二年级数学期终测试第Ⅰ卷一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答卷...(1,)+∞11 ﹣(3,)+∞15. 解:(1)A =(-∞,1)∪(2,+∞)---------------------------------3分 x 2-(a +1)x +a ≤0,(x -1)(x -a )≤0 ----------------5分∵a >1∴1≤x ≤a ∴B =[1,a ] --------------------------7分 (2) C R A =[1,2] ∵(C R A )∪B =B ∴C R A ⊆B , 即[1,2]⊆[1,a ] ∴a ≥2, 即所求实数a 的取值范围为[2, +∞).16.解:(1)在ABC ∆中,因为3a =,b =,2B A =,故由正弦定理得3sin =A ,所以2sin cos sin =A A A 故cos =A (2)由(1)知cos =A ,所以sin ==A ,又因为2B A =, 所以21cos cos 22cos 13==-=B A A ,从而cos 3==B 在ABC∆中,因为π++=A B C ,所以sin sin()sin cos cos sin 9=+=+=C A B A B A B 所以由正弦定理得sin 5sin ==a Cc A17. 解:(Ⅰ)错误!未找到引用源。
……1分 由题意01232<-+ax x 的解集是⎪⎭⎫⎝⎛-1,31即01232=-+ax x 的两根分别是1,31-.将1=x 或31-代入方程01232=-+ax x 得1-=a . ()223+--=∴x x x x g . ……5分(Ⅱ)由(Ⅰ)知:错误!未找到引用源。
,错误!未找到引用源。
,错误!未找到引用源。
点错误!未找到引用源。
处的切线斜率错误!未找到引用源。
错误!未找到引用源。
, ……7分错误!未找到引用源。
函数y=()x g 的图像在点错误!未找到引用源。
处的切线方程为: 错误!未找到引用源。
,即错误!未找到引用源。
. ……9分 (Ⅲ) 错误!未找到引用源。
,错误!未找到引用源。
即:123ln 22++≤ax x x x 对()+∞∈,0x 上恒成立 ……11分可得x x x a 2123ln --≥对()+∞∈,0x 上恒成立 设()xx x x h 2123ln --=, 则()()()22'213121231x x x x x x h +--=+-=……12分 令()0'=x h ,得31,1-==x x (舍)当10<<x 时,()0'>x h ;当1>x 时, ()0'<x h ∴当1=x 时,()x h 取得最大值, ()x h max =-2 2-≥∴a .a ∴的取值范围是[)+∞-,2.18.解:(1)当0<x≤40,W =xR(x)-(16x +40)=-6x 2+384x -40;........ 2分 当x>40,W =xR(x)-(16x +40)=-40000x-16x +7360............4分 所以,W =26384400404000016736040.x x x x x x ⎧<≤⎪⎨>⎪⎩-+-,,--+,....................................6分(2)①当0<x≤40,W =-6(x -32)2+6104,所以W max =W(32)=6104;.............10分②当x>40时,W =-40000x-16x +7360,由于40000x1600, 当且仅当40000x=16x ,即x =50∈(40,+∞)时,W 取最大值为5760...........14分 综合①②知,当x =32时,W 取最大值为6104..................16分19.【答案】(1) 22143x y +=解:(1)因为22c =,且12c a =,所以1c =,2a =.…………………………2分 所以23b =.…………………………4分所以椭圆C 的方程为22143x y +=.…………………………6分 (2)设点M 的坐标为()00,x y ,则2200143x y +=. 因为()1F 1,0-,24a c=,所以直线l 的方程为4x =.…………………………8分 由于圆M 与l 有公共点,所以M 到l 的距离04x -小于或等于圆的半径R . 因为()22221R F 1x y =M=++,所以()()22200041x x y -≤++,…………………………10分即20010150y x +-≥.又因为2200314x y ⎛⎫=- ⎪⎝⎭,所以20033101504x x -+-≥.…………12分解得0423x ≤≤.…………………………14分当043x =时,0y =所以()12F F max122S ∆M =⨯=……………………16分20.【答案】(1)不存在实数a ,使得f (x )在x =1处取极值;(2)a >-6;(3)上存在单调递增区间,转化为'()0f x ≥在[2,3]上恒成立,对'()f x 表达式中的分子配方,讨论分子的正负;第三问,先构造函数()()()h x f x g x =-,将存在x 0∈,使得f (x 0)<g (x 0)成立,转化为01[,]x e e∃∈,0min ()0h x ≤,求a 的范围,对()h x 求导,利用函数()h x 的正负判断函数的单调性,求函数的最小值,从而求出参数a 的取值范围.(3)法一:记F (x )=x -ln x (x >0),∴'()F x =1x x- (x >0), ∴当0<x <1时,'()F x <0,F (x )递减;当x >1时,'()F x >0,F (x )递增. ∴F (x )≥F (1)=1>0由f (x 0)≤g (x 0) 得:(x 0-ln x 0)a ≥x 20-2x 0 ………12分∴200002ln x x a x x -≥-,记22()ln x x G x x x -=-,x ∈[1e ,e ]∴22(22)(ln )(2)(1)(1)(2ln 2)()(ln )(ln )x x x x x x x x G x x x x x -------+==-- ∵x ∈[1e,e ],∴2-2ln x =2(1-ln x )≥0,∴x -2ln x +2>0 ∴x ∈(1e,1)时,'()G x <0,G (x )递减;x ∈(1,e )时,'()G x >0,G (x )递增 ∴G (x )min =G (1)=-1 ∴a ≥G (x )min =-1.故实数a 的取值范围为[-1,+∞). ………16分第Ⅱ卷21. 解:(1)设直线:1l x y +=上任意一点(,)M x y 在矩阵A 的变换作用下,变换为点(,)M x y ''' .由''01x m n x mx ny y y y +⎡⎤⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦,得x mx ny y y'=+⎧⎨'=⎩ …………5分 又点(,)M x y '''在l '上,所以1x y ''-=,即()1mx ny y +-= 依题意111m n =⎧⎨-=⎩,解得12m n =⎧⎨=⎩,1201A ⎡⎤∴=⎢⎥⎣⎦ …………10分21.C 解:(1)把)4πρθ=+化为直角坐标系中的方程为220x y x y +-+=(2) 把1314x ty t =+⎧⎨=--⎩化为普通方程为4310x y +-=∴圆心到直线的距离为110,∴弦长为75=; 22.解:.(1)设“在1次摸奖中,获得二等奖”为事件A ,则2111123223322264C C C +C C C 7()C C 30P A ==⋅. …………………………4分(2)设“在1次摸奖中,获奖” 为事件B ,则获得一等奖的概率为223212264C C 1=C C 30P =⋅; 获得三等奖的概率为221111323322322642C C +C C C C 7=C C 15P =⋅;所以17711()30301515P B =++=.……………8分 由题意可知X 的所有可能取值为0,1,2.21116(0)(1)15225P X ==-=,12111188(1)C (1)1515225P X ==-=,211121(2)()15225P X ===. 所以X 的分布列是所以()01222522522515E X =⨯+⨯+⨯=. ……………………………10分23.解:(1)以D 为原点,分别以DA 、DC 、DD 1所在直线为x 轴、y 轴、 z 轴建立如图所示空间直角坐标系,则A (1,0,0),B (1,2,0),C (0,2,0), D1(0,0,2). ∵E 为AB 的中点,∴E 点坐标为E (1,1,0),∵D 1F =2FE , ∴1122224(1,1,2)(,,)33333D F DE ==-=-,11224222(0,0,2)(,,)(,,)333333DF DD D F =+=+-=……………2分设(,,)x y z =n 是平面DFC 的法向量,则00DF DC ⎧⋅=⎪⎨⋅=⎪⎩n n ,∴222033320x y z y ⎧++=⎪⎨⎪=⎩,,取x =1得平面FDC 的一个法向量(1,0,1)=-n , …………………………………3分设(,,)x y z =p 是平面ED 1C 的法向量,则1100D F D C ⎧⋅=⎪⎨⋅=⎪⎩,,p p ∴2240333220x y z y z ⎧+-=⎪⎨⎪-=⎩,, 取y =1得平面D 1EC 的一个法向量(1,1,1)=p , ……………4分∵(1,0,1)(1,1,1)0⋅=-⋅=n p ,∴平面DFC ⊥平面D 1EC . ……………………5分 (2)设(,,)x y z =q 是平面ADF 的法向量,则00DF DA ⋅=⋅=,,q q∴22203330x y z x ⎧++=⎪⎨⎪=⎩,,取y =1得平面ADF 的一个法向量(0,1,1)=-q , …………7分 设二面角A -DF -C 的平面角为θ,由题中条件可知π(,π)2θ∈,则cos θ=-||||||⋅⋅n q n q12=-,…………………………………………9分∴二面角A -DF -C 的大小为120°. ……………………………………10分。
