江西省九江瑞昌市高丰中学九年级数学上册 各单元(含期中期末)测试试卷(图片版) 北师大版
江西省九江市九年级上学期期中数学试卷

江西省九江市九年级上学期期中数学试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)(2020·晋中模拟) 下列图形中,既是轴对称图形,又是中心对称图形的是()A .B .C .D .2. (2分) (2020九上·宁波月考) 如图,在⊙O中,如果,那么()A . AB=ACB . AB=2ACC . AB<2ACD . AB>2AC3. (2分) (2018九上·宁江期末) 二次函数y=-2x2+1的图象如图所示,将其绕坐标原点O旋转180°,则旋转后的抛物线的解析式为()B . y=2x2+1C . y=2x2D . y=2x2-14. (2分)抛物线y=,y=﹣2018x2+2019,y=2018x2共有的性质是()A . 开口向上B . 对称轴是y轴C . 当x>0时,y随x的增大而增大D . 都有最低点5. (2分) (2019九上·德惠月考) 已知关于x的一元二次方程(x+1)2-m=0有两个实数根,则m的取值范围是()A . m≥B . m≥2C . m≥1D . m≥06. (2分)若A(﹣2,y1),B(﹣1,y2),C(﹣3,y3)为二次函数y=ax2(a<0)的图象上的三点,则y1 ,y2 , y3的大小关系是()A . y1<y2<y3B . y2<y1<y3C . y3<y1<y2D . y1<y3<y27. (2分)(2020·南充模拟) 将抛物线向左平移1个单位后的解析式为()A .B .C .D .8. (2分)已知一元二次方程x2+bx﹣3=0的一根为﹣3,在二次函数y=x2+bx﹣3的图象上有三点(-,y1)、(-,y2)、(,y3),y1、y2、y3的大小关系是()A . y1<y2<y3C . y3<y1<y2D . y1<y3<y29. (2分) (2017九上·重庆开学考) 在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2﹣m的图象可能是()A .B .C .D .10. (2分) (2020九上·萍乡期末) 如图所示,在矩形中,,点在边上,平分,,垂足为,则等于()A .B . 1C .D . 211. (2分) (2017八下·嘉兴期中) 如图,在平行四边形ABCD中,∠B=60度,AB=5cm,则下面结论正确的是()A . BC=5cm,∠D=60度B . ∠C=120度,CD=5cmC . AD=5cm,∠A=60度D . ∠A=120度,AD=5cm12. (2分)如图,已知AB=AC,AD=AE,∠BAC=∠DAE.下列结论不正确的是()A . ∠BAD=∠CAEB . △ABD≌△ACEC . AB=BCD . BD=CE二、填空题 (共8题;共9分)13. (1分) (2019九上·虹口期末) 如图,在Rt△ABC中,∠ACB=90°,CD为AB边上的中线,过点A作AE⊥CD交BC于点E ,如果AC=2,BC=4,那么cot∠CAE=________.14. (1分) (2019九上·湖里期中) 一种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是57,每个支干长出________个小分支.15. (1分) (2020九上·醴陵期末) 如图,AB//CD,,E为BC上一点,且.若,,,则DE的长为________.16. (1分)(2017·安徽模拟) 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,17. (1分)如图,正六边形ABCDEF内接于⊙O,向⊙O内任意投点,则所投的点落在正六边形ABCDEF内的概率是________ .18. (1分) (2020九上·椒江月考) 用半径为4,圆心角为90°的扇形纸片围成一个圆锥的侧面,则这个圆锥的底面圆的半径为________.19. (2分) (2019七下·景县期中) 如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到长方形OABC的边时反弹,反弹时反射角等于入射角、当小球第1次碰到矩形的边时的点为P1 ,第2次碰到长方形的边时的点为P2……第n次碰到矩形的边时的点为Pn.则点P4的坐标是________,点P2019的坐标是________.20. (1分) (2020九上·丹东月考) 甲乙两人在玩转盘游戏时,把转盘A.B分别分成4等份、3等份,并在每一份内标上数字,如图所示.游戏规定,转动两个转盘停止后,指针必须指到某一数字,否则重转.甲、乙二人分别转动A.B转盘一次,则指针所指的两个数字都是方程x2−4x+3=0的解的概率是________.三、解答题 (共6题;共56分)21. (6分) (2018九上·前郭期末) 如图,平面直角坐标系中,每个小正方形边长都是1.(1)按要求作图:①以坐标原点O为旋转中心,将△ABC逆时针旋转90°得到△A1B1C1;②作出△A1B1C1关于原点成中心对称的中心对称图形△A2B2C2 .(2)△A2B2C2中顶点B2坐标为________.22. (5分)如图,在平面直角坐标系xoy中,的外接圆与y轴交于点,,求OC的长.23. (15分) (2019九上·鄞州月考) 如图,抛物线交x轴于A、B两点,直线y=kx+b经过点A,与这条抛物线的对称轴交于点M(1,2),且点M与抛物线的顶点N关于x轴对称.(1)求抛物线的函数关系式;(2)设题中的抛物线与直线的另一交点为C,已知P(x,y)为线段AC上一点,过点P作PQ⊥x轴,交抛物线于点Q.求线段PQ的最大值及此时P坐标;24. (10分) (2019九上·枣庄月考) 如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD边的延长线上,且满足∠MAN=90°,联结MN、AC , N与边AD交于点E .(1)求证;AM=AN;(2)如果∠CAD=2∠NAD ,求证:AM2=AC•AE .25. (10分)某超市销售一种牛奶,进价为每箱24元,规定售价不低于进价.现在的售价为每箱36元,每月可销售60箱.市场调查发现:若这种牛奶的售价每降价1元,则每月的销量将增加10箱,设每箱牛奶降价x元(x为正整数),每月的销量为y箱.(1)写出y与x中间的函数关系式和自变量x的取值范围;(2)超市如何定价,才能使每月销售牛奶的利润最大?最大利润是多少元?26. (10分)(2017·平谷模拟) 如图,⊙O为等腰三角形ABC的外接圆,AB=AC.AD是⊙O的直径,切线DE 与AC的延长线相交于点E.(1)求证:DE∥BC;(2)若DF=n,∠BAC=2a,写出求CE长的思路.参考答案一、选择题 (共12题;共24分)答案:1-1、考点:解析:答案:2-1、考点:解析:答案:3-1、考点:解析:答案:4-1、考点:解析:答案:5-1、考点:解析:答案:6-1、考点:解析:答案:7-1、考点:解析:答案:8-1、考点:解析:答案:9-1、考点:解析:答案:10-1、考点:解析:答案:11-1、考点:解析:答案:12-1、考点:解析:二、填空题 (共8题;共9分)答案:13-1、考点:解析:答案:14-1、考点:解析:答案:15-1、考点:解析:答案:16-1、考点:解析:答案:17-1、考点:解析:答案:18-1、考点:解析:答案:19-1、考点:解析:答案:20-1、考点:解析:三、解答题 (共6题;共56分)答案:21-1、答案:21-2、考点:解析:答案:22-1、考点:解析:答案:23-1、答案:23-2、答案:23-3、考点:解析:答案:24-1、答案:24-2、考点:解析:答案:25-1、答案:25-2、考点:解析:答案:26-1、答案:26-2、考点:解析:。
江西省九江市第三中学2024-2025学年九年级上学期期中考试数学试卷(含答案)

江西省2025届九年级期中综合评估数学▶上册◀说明:共有六个大题,23个小题,满分120分,考试时间120分钟.一、单项选择题(本大题共6小题,每小题3分,共18分)在每小题列出的四个备选项中只有一项是最符合题目要求的,请将其代码填入题后括号内错选、多选或未选均不得分.1.若关于的函数是二次函数,则的值为( )A.1B.2C.0D.32.以下是几种化学物质的结构式,其中文字上方的结构式图案属于中心对称图形的是( )A.甲醛B.甲烷 C.水 D.乙酸3.已知关于的一元二次方程有一个根为,则另一根为( )A.7B.3C.D.4.如图,四边形是的内接四边形,连接,,若,则的度数是( )A. B. C. D.5.在平面直角坐标系中,将抛物线绕顶点旋转得到新抛物线,再将新抛物线沿轴翻折得到抛物线,则,,的值分别是( )A.2,,11B.2,,5C.,,11D.,8,56.某校计划举办劳动之星颁奖典礼,想在颁奖现场设计一个如图1所示的抛物线型拱门入口.要在拱门上顺次粘贴“劳”“动”“之”“保”(分别记作点,,,)四个大字,要求与地面平行,且,抛物线最高点的五角星(点)到的距离为,,,如图2所示,则点到的距离为( )图1 图221.124.1~x 31my x x =-+m x 2520x x m -+=2-7-3-ABCD O OA OC 86AOC ∠=︒ADC ∠94︒127︒136︒137︒285y ax x =-+P 180︒x22y x bx c =++a b c 8-8-2-8-2-A B C D BC BC AD ∥E BC 0.6m 2m BC =4m AD =C ADA. B. C. D.二、填空题(本大题共6小题,每小题3分,共18分)7.一元二次方程的解为______.8.在平面直角坐标系中,点关于原点对称的点的坐标是______.9.如图,是半圆的直径,,为的中点,连接,,则的度数为______.10.《九章算术》“勾股”章有一题:“今有二人同所立.甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会,问甲、乙行各几何.”大意是说:已知甲、乙两人同时从同一地点出发,甲每单位时间走7步,乙每单位时间走3步.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多远?设甲走了步(步为古代长度单位,类似于现在的米),根据题意可列方程:____________.(结果化为一般式)11.在平面直角坐标系中,若抛物线向左平移2个单位长度后经过点,则的最大值为______.12.如图,在矩形中,连接,,,将线段绕点顺时针旋转,得到线段,连接,,当时,的周长为______三、解答题(本大题共5小题,每小题6分,共30分)13.(1)解方程:.(2)如图,将绕点逆时针旋转得到,若,且于点,求的度数.14.某件夏天T 恤的售价为100元,因换季促销,在经过连续两次降价后,现售价为81元,求平均每次降价的百分率.15.自古以来,景德镇就是中国陶瓷文化的象征,生产的瓷器闻名四方,远销世界各地.如图,这是景德镇2m 1.8m 2.4m 1.5m290x -=()2,4-BC OAB AC =D AC OD BD BDO ∠x ()()220y a x c a =-+≠()1,6-ac ABCD AC 1AB =60BAC ∠=︒AB B ()0180a α︒<≤︒BP CP DP 12PCB BAC ∠=∠DPC △()()()2131x x x x +=++ABC △A 28︒AB C ''△40C ∠'=︒AB BC '⊥E BAC ∠生产的某种瓷碗正面的形状示意图,是的一部分,是的中点,连接,与弦交于点,连接,.已知,碗深,求的长.16.如图,是的直径,点,点在上,,,请仅用无刻度的直尺按下列要求作图(保留作图痕迹).(1)如图1,在上作一点,使得是以为底边的等腰三角形.(2)如图2,在上方作一点,使得为等边三角形.图1图217.在平面直角坐标系中,已知抛物线与轴没有交点.(1)求的取值范围.(2)请直接写出抛物线顶点所在的象限.四、解答题(本大题共3小题,每小题8分,共24分)18.如图,在平面直角坐标系中,抛物线经过点.(1)求的值,并求出此抛物线的顶点坐标.(2)当时,请利用图象,直接写出的取值范围.(3)当时,请利用图象,直接写出的取值范围.19.如图,在中,,将绕点顺时针旋转,得到,连接,.(1)求证:点,,在同一条直线上.(2)若,,求的面积.AB O D AB OD AB C OA OB 18cm AB =6cm CD =OA AB O C D O 60COA ∠=︒OD AB ⊥OD E OCE △OC AB F ABF △214y x x c =-++x c 222y x xc c c =-+-24y x mx =-++()3,4A -m 20x -≤≤y 0y ≤x ABC △135BCA ︒∠=ACB △A 90︒ADE △CD CE B C D 2BC=AC =CDE △20.某主播销售一种商品,已知这种商品的成本价为20元/个,规定销售价格不低于成本价,且不高于成本价的2倍,通过前几天的销售发现,该商品每天的销售量(单位:个)与销售价格(单位:元/个)之间满足一次函数关系,部分对应数据如下表:/(元/个) (23252811)/个…540500440…(1)求出关于的函数关系式,并直接写出的取值范围.(2)求销售该商品每天的最大利润.五、解答题(本大题共2小题,每小题9分,共18分)21.追本溯源题(1)来自课本中的习题,请你完成解答,提炼方法并解答题(2).(1)如图1,,比较与的长度,并证明你的结论.方法应用(2)如图2,,是的两条弦,点,分别在,上,连接,,且,是的中点.①求证:.②若圆心到的距离为3,的半径是6,求的长.图1 图222.如图,在平面直角坐标系中,抛物线与轴相交于点和点(点在点的左侧),与轴相交于点,点与点关于轴对称,为该抛物线上一点,连接,,,.(1)求该抛物线的解析式.(2)若的面积与的面积相等,请直接写出点的横坐标.y x x y y x x AD BC = AB CDMB MD O A C MBMD AB CD AB CD =M AC BM DM =O DM O DM 25y x bx =-++x A ()5,0B A B y C D A y E AC CD DE BE BDE △ACD △E(3)当点在第一象限时,连接,设的面积为,求的最大值.六、解答题(本大题共12分)23.综合与实践如图,是等边内一点,,连接,将线段绕点顺时针旋转得到,连接.初步感知(1)如图1,的延长线与交于点,求的度数.特例应用(2)如图2,作点关于的对称点,若点在的角平分线上.①当点与点重合时,的长为______;②当点与点不重合时,判断四边形的形状,并证明.拓展延伸(3)如图2,在(2)的条件下,取的中点,记为,当点从点运动到点时,请直接写出点运动的路径长.图1图2E CE ECD △S S P ABC △2AB =CP CP C 60︒CE AE BP AE Q AQB ∠E ACF P ABC △BD P F BP P F BPEF FPG P B D G江西省2025届九年级期中综合评估数学参考答案1.B2.C3.A4.D5.A 提示:由旋转和翻折可知,,抛物线的顶点的坐标为.点关于轴的对称点的坐标为,最后得到的抛物线的解析式为,.故选A.6.B 提示:建立如图所示的平面直角坐标系.由题意易知点的坐标为,点的坐标为,则点的坐标为,故设抛物线的解析式为,将点的坐标代入上式,得,抛物线的解析式为.点的横坐标为2,点的纵坐标为,点到的距离为.故选B.7.8.9.10.11.912.3或或 提示:,,,,,.如图1,当时,此时.易证得为等边三角形,的周长为;2a =8b =-∴2285y x x =-+P ()2,3- ()2,3P -x ()2,3∴()222232811y x x x =-+=-+11c ∴=C ()1,0B ()1,0-E ()0,0.6()()11y a x x =+-E 0.6a =-∴()()0.611y x x =-+- D ∴D ()()0.62121 1.8-⨯+⨯-=-∴C AD 1.8m 3x =±()2,4-22.5︒24020049x x -=2+3+1AB = 90ABC ∠=︒60BAC ∠=︒1CD ∴=22AC AB ==BC ∴==60α=︒1302PCB BAC ∠=︒=∠DPC △DPC ∴△33CD =如图2,当时,此时,,.易证得,,的周长为;如图3,当时,此时,,,.的周长为.综上所述,的周长为3或或.图1 图2 图313.(1)(解法不唯一)解:,,,.(2)解:将绕点逆时针旋转得到.,.又,,.14.解:设平均每次降价的百分率为.由题意得,解得,(舍去).答:平均每次降价的百分率为.15.解:是的中点,,.设,则.在中,由勾股定理得,120α=︒1302PCB BAC ∠=︒=∠30PBC PCB ∴∠=∠=︒1PC BP ∴==DCP BPC ≌△△DP BC ∴==DPC ∴△2CD PC DP ++=+180a =︒1302PCB BAC ∠=︒=∠2PC AC ∴==22AP AB ==DP ∴===DPC ∴△123CD PC DP ++=+=+DPC △2+3+()()()2131x x x x +=++ ()()1230x x x ∴+--=11x ∴=-23x = ABC △A 28︒AB C ''△28BAE ∴∠=︒40C C ∠'=∠=︒AB BC '⊥ 9050EAC C ∴∠=︒-∠=︒285078BAC BAE EAC ∴∠=∠+∠=︒+︒=︒x ()2100181x -=10.110%x ==2 1.9x =10%DAB OD AB ∴⊥19cm 2AC BC AB ∴===cm OA r =()6cm OC r =-Rt OAC △222OC AC OA +=即,解得,的长为.16.解:(1)如图1,即所求.(2)如图2,即所求.图1 图217.解:(1)抛物线与轴没有交点,,即,解得.(2)第二象限.提示:,该抛物线的顶点坐标为.,,点在第二象限.18.解:(1)把代入,得,解得.,抛物线的顶点坐标为.(2)当时,的取值范围是.(3)当时,的取值范围是或.19.解:(1)证明:是由绕点顺时针旋转得到的,,,,.()22269r r -+=394r =OA ∴39cm 4OCE △ABF △ x 240b ac ∴∆=-<10c +<1c <-()2222y x xc c c x c c =-+-=-- ∴(),c c -1c <- 1c ∴->∴(),c c -()3,4A -24y x mx =-++9344m --+=3m =-223253424y x x x ⎛⎫=--+=-++ ⎪⎝⎭∴325,24⎛⎫- ⎪⎝⎭20x -≤≤y 2544y ≤≤0y ≤x 4x ≤-1x ≥ADE△ACB △A 90︒ACB ADE ∴≌△△90CAD ∠=︒AC AD ∴=()1180452ACD ADC CAD ∴∠=∠=︒-∠=︒又,,点,,在同一条直线上.(2)由(1)可知,,.,.,.20.解:(1)设关于的函数关系式为.将,代入上式.得解得.(2)设销售该商品每天的利润为元.由题意得.,,当时,取得最大值,且最大值为4500.答:销售该商品每天的最大利润为4500元.21.解:(1).证明:,,,即.(2)①证明:是的中点,.,,,,.②如图,过点作,是垂足,连接.135BCA ∠=︒ 13545180BCA ACD ∴∠+∠=︒+︒=︒∴B C D 90CAD ∠=︒AC AD=6CD ∴===135ADE BCA ︒∠=∠= 90CDE ADE ADC ︒∴∠=∠-∠=2DE BC == 1162622CDE S CD DE ∴=⋅=⨯⨯=△y x y kx b =+()23,540()25,50023540,25500,k b k b +=⎧⎨+=⎩20,1000,k b =-⎧⎨=⎩()2010002040y x x ∴=-+≤≤W ()()()22202010002014002000020354500W x x x x x =--+=-+-=--+200-< 203540<<∴35x =W AB CD=AD BC = AD BC∴= AD AC BC AC ∴+=+ AB CD=M AC AM CM∴=AB CD = AB CD∴= AB AM CMCD ∴+=+ BMDM ∴=BM DM ∴=O ON MD ⊥N OM在中,,,22.解:(1)∵抛物线与轴相交于点和点,,解得,该抛物线的解析式为.(2.(3),令,即,解得,,点的坐标为.点与点关于轴对称,点的坐标为.设点的坐标为.设直线的解析式为.由点,的坐标可知,解得直线的解析式为.如图,过点作轴,交于点.当时,,点的坐标为,, Rt OMN △3ON =6OM =MN ∴==2DM MN ∴==25y x bx =-++x A ()5,0B 25550b ∴-++=4b =∴245y x x =-++245y x x =-++ ∴0y =2450x x -++=11x =-25x =∴A ()1,0- D A y ∴D ()1,0-E ()2,45m m m -++CE y kx t =+()0,5C ()2,45E m m m -++25,45,t mk t m m =⎧⎨+=-++⎩4,5,k m t =-+⎧⎨=⎩∴CE ()45y m x =-++D DF y ∥CE F 1x =()459y m m =-++=-+∴F ()1,9m -+9DF m ∴=-则,当时,的值最大,且最大值为,故的最大值为.23.解:(1),,即.又,,(SAS ),.,.(2②四边形为平行四边形.证明:如图1,连接.图1在等边中,平分,.又,关于对称,,,,.在等边中,,,.在等边中,,,,,,,.平分,,,,为等边三角形,()2111981922228E S DF x m m m ⎛⎫=⋅⋅=-=--+ ⎪⎝⎭∴92m =S 818S 81860ACB PCE ∠=∠=︒ ACB ACP PCE ACP ∴∠-∠=∠-∠BCP ACE ∠=∠BC AC = CP CE =BCP ACE ∴≌△△CBP CAE ∴∠=∠CBP ACB CAE AQB ∠+∠=∠+∠ 60AQB ACB ︒∴∠=∠=BPEF CF ABC △BD ABC ∠BD AC ∴⊥E F AC AF AE ∴=CF CE =AC EF ∴⊥EF BP ∴∥ PCE △60PCE ∠=︒PC CE PE ==CF PC ∴= ABC △AC BC =60ACB ∠=︒ACB PCE ∴∠=∠PCB ACE ∴∠=∠()SAS BCP ACE ∴≌△△CAE CBP ∴∠=∠BP AE =BD ABC ∠30CBP ︒∴∠=30CAE FAC CBP ∴∠=∠=∠=︒60FAE ∴∠=︒AFE ∴△,.,,四边形为平行四边形.(3.提示:将图1中与的交点记为.由(2)易知.,,,即,易求得,,.如图2,当点从点运动到点时.图2,点的运动路径为图2中的长,为的中点,连接,.,同理可得,是等边三角形.是的中点,,易求得.AE EF ∴=BP EF ∴=BP EF ∥BP EF =∴BPEF AF BP M BP AF =30FAB ABP ∠=∠=︒ AM BM∴=BP BM AF AM ∴-=-PM FM =∴30MPF ∠=︒MPF ABP ∴∠=∠PF AB ∴∥P B D PF AB ∥∴G GH H AB DH HF 112DF AB == 1DH HF ==DFH ∴△G DF 1DH DF ==∴GH =。
江西省九江市九年级数学上学期期末考试试题(含解析) 新人教版-新人教版初中九年级全册数学试题

某某省某某市2016届九年级数学上学期期末考试试题一、选择题(共6小题,每小题3分,满分18分)1.一元二次方程(x﹣1)2=0的解为( )A.x=1 B.x=0 C.x=﹣1 D.x=±12.如图所示几何体三视图的主视图是( )A.B.C.D.3.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )A.1 B.2 C.3 D.44.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形5.函数y=mx﹣m与在同一直角坐标系中的图象可能是( )A.B.C.D.6.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )A.1个B.2个C.3个D.4个二、填空题(共8小题,每小题3分,满分24分)7.一元二次方程x2=x的解为__________.8.已知反比例函数的图象在第__________象限内.9.由一些大小相同的小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体的小正方体最多是__________个.10.如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为__________cm.11.如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若CD=5,则EF的长为__________.12.从﹣2,﹣1,1,2这四个数中,任取两个不同的数作为一次函数y=kx+b的系数k,b,则一次函数y=kx+b的图象不经过第四象限的概率是__________.13.如图,E(﹣6,0),F(﹣4,﹣2),以O为位似中心按比例尺1:2把△EFO缩小到第一象限,则点F的对应点F′的坐标为__________.14.如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于__________.三、解答题(共10小题,满分78分)15.解方程:x2﹣4x+1=0.16.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,请在图(1)中画出一个格点三角形,使它与图(1)中的△ABC相似.17.如图,在平行四边形ABCD中,对角线AC、BD相交于O,过点O作直线EF⊥BD,分别交AD、BC于点E和点F,求证:四边形BEDF是菱形.18.从甲学校到乙学校有A1、A2、A3三条线路,从乙学校到丙学校有B1、B2二条线路.(1)利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果;(2)小X任意走了一条从甲学校到丙学校的线路,求小X恰好经过了B1线路的概率是多少?19.已知关于x的一元二次方程x2﹣6x+k=0.(1)当它有两个实数根时,求k的X围;(2)当k=﹣11时,假设方程两根是x1,x2,求x12+x22+8的值.20.如图,路灯(P点)距地面8米,身高1.6米的小明从距离路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点(B点在A点的左边)时,身影的长度是变长了还是变短了?变长或变短了多少米?21.如图,一次函数y=kx+b与反比例函数y=的图象交于A(2,3),B(﹣3,n)两点.(1)求一次函数与反比例函数的解析式;(2)求△ABO的面积;(3)根据所给条件,请直接写出不等式kx+b>的解集.22.某某特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:(1)每千克核桃应降价多少元?(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?23.如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE 与AB相交于点E.(1)求证:AB•CF=CB•CD;(2)已知AB=15,BC=9,P是射线DE上的动点,设DP=x(x>0),四边形BCDP的面积为y.①求y关于x的函数关系式;②当PB+PC最小时,求x,y的值.24.在四边形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.(1)求点B的坐标;(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F.求直线DE的解析式;(3)点M在(2)中直线DE上,四边形ODMN是菱形,求N的坐标.2015-2016学年某某省某某市九年级(上)期末数学试卷一、选择题(共6小题,每小题3分,满分18分)1.一元二次方程(x﹣1)2=0的解为( )A.x=1 B.x=0 C.x=﹣1 D.x=±1【考点】解一元二次方程-直接开平方法.【专题】计算题.【分析】利用直接开平方法解方程即可.【解答】解:x﹣1=0,所以x1=x2=1.故选A.【点评】本题考查了解一元二次方程﹣直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程.2.如图所示几何体三视图的主视图是( )A.B.C.D.【考点】简单几何体的三视图.【分析】根据主视图是从物体正面看所得到的图形解答即可.【解答】解:如图所示几何体从正面看所得到的图形是B中图形,故选:B.【点评】本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中.主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.3.如图,在△ABC中,DE∥BC,AD=6,DB=3,AE=4,则EC的长为( )A.1 B.2 C.3 D.4【考点】平行线分线段成比例.【分析】根据平行线分线段成比例可得,代入计算即可解答.【解答】解:∵DE∥BC,∴,即,解得:EC=2,故选:B.【点评】本题主要考查平行线分线段成比例,掌握平行线分线段所得线段对应成比例是解题的关键.4.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形【考点】正方形的判定;平行四边形的性质;菱形的判定;矩形的判定.【专题】证明题.【分析】根据邻边相等的平行四边形是菱形;根据所给条件可以证出邻边相等;根据有一个角是直角的平行四边形是矩形;根据对角线相等的平行四边形是矩形.【解答】解:A、根据邻边相等的平行四边形是菱形可知:四边形ABCD是平行四边形,当AB=BC时,它是菱形,故A选项正确;B、∵四边形ABCD是平行四边形,∴BO=OD,∵AC⊥BD,∴AB2=BO2+AO2,AD2=DO2+AO2,∴AB=AD,∴四边形ABCD是菱形,故B选项正确;C、有一个角是直角的平行四边形是矩形,故C选项正确;D、根据对角线相等的平行四边形是矩形可知当AC=BD时,它是矩形,不是正方形,故D选项错误;综上所述,符合题意是D选项;故选:D.【点评】此题主要考查学生对正方形的判定、平行四边形的性质、菱形的判定和矩形的判定的理解和掌握,此题涉及到的知识点较多,学生答题时容易出错.5.函数y=mx﹣m与在同一直角坐标系中的图象可能是( )A.B.C.D.【考点】反比例函数的图象;一次函数的图象.【分析】此题分两种情况进行讨论:m>0时,m<0时,先根据反比例函数的性质判断出双曲线所在象限,再根据一次函数的性质一次函数图象所在象限,即可选出答案.【解答】解:当m>0时,双曲线在第一、三象限,一次函数y=mx﹣m图象经过第一、三、四象限;当m<0时,双曲线在第二、四象限,一次函数y=mx﹣m图象经过第一、二、四象限故选D.【点评】本题主要考查了反比例函数的图象性质和一次函数的图象性质,重点是注意系数m 的取值.6.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P的个数是( )A.1个B.2个C.3个D.4个【考点】相似三角形的判定;直角梯形.【分析】由于∠PAD=∠PBC=90°,故要使△PAD与△PBC相似,分两种情况讨论:①△APD∽△BPC,②△APD∽△BCP,这两种情况都可以根据相似三角形对应边的比相等求出AP的长,即可得到P点的个数.【解答】解:∵AB⊥BC,∴∠B=90°.∵AD∥BC,∴∠A=180°﹣∠B=90°,∴∠PAD=∠PBC=90°.AB=8,AD=3,BC=4,设AP的长为x,则BP长为8﹣x.若AB边上存在P点,使△PAD与△PBC相似,那么分两种情况:①若△APD∽△BPC,则AP:BP=AD:BC,即x:(8﹣x)=3:4,解得x=;②若△APD∽△BCP,则AP:BC=AD:BP,即x:4=3:(8﹣x),解得x=2或x=6.∴满足条件的点P的个数是3个,故选:C.【点评】本题主要考查了相似三角形的判定及性质,难度适中,进行分类讨论是解题的关键.二、填空题(共8小题,每小题3分,满分24分)7.一元二次方程x2=x的解为x1=0,x2=1.【考点】解一元二次方程-因式分解法.【分析】首先把x移项,再把方程的左面分解因式,即可得到答案.【解答】解:x2=x,移项得:x2﹣x=0,∴x(x﹣1)=0,x=0或x﹣1=0,∴x1=0,x2=1.故答案为:x1=0,x2=1.【点评】此题主要考查了因式分解法解一元二次方程,关键是把方程的右面变为0.8.已知反比例函数的图象在第二、四象限内.【考点】反比例函数的性质.【分析】根据反比例函数的性质,利用k=﹣2<0,即可得出图象所在象限.【解答】解:∵反比例函数,∴k=﹣2<0,∴反比例函数的图象在第二、四象限.故答案为:二、四.【点评】此题主要考查了反比例函数的性质,根据已知得出k的符号,熟练应用反比例函数的性质是解决问题的关键.9.由一些大小相同的小正方体搭成的几何体的主视图和俯视图,如图所示,则搭成该几何体的小正方体最多是7个.【考点】由三视图判断几何体.【专题】计算题.【分析】根据几何体主视图,在俯视图上表上数字,即可得出搭成该几何体的小正方体最多的个数.【解答】解:根据题意得:,则搭成该几何体的小正方体最多是1+1+1+2+2=7(个).故答案为:7.【点评】此题考查了由三视图判断几何体,在俯视图上表示出正确的数字是解本题的关键.10.如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为18cm.【考点】相似三角形的应用.【分析】根据题意可画出图形,再根据相似三角形的性质对应边成比例解答.【解答】解:∵DE∥BC,∴△AED∽△ABC∴=设屏幕上的小树高是x,则=解得x=18cm.故答案为:18.【点评】本题考查相似三角形性质的应用.解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.11.如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若CD=5,则EF的长为5.【考点】三角形中位线定理;直角三角形斜边上的中线.【分析】已知CD是Rt△ABC斜边AB的中线,那么AB=2CD;EF是△ABC的中位线,则EF应等于AB的一半.【解答】解:∵△ABC是直角三角形,CD是斜边的中线,∴CD=AB,又∵EF是△ABC的中位线,∴AB=2CD=2×5=10cm,∴EF=×10=5cm.故答案为:5.【点评】此题主要考查了三角形中位线定理以及直角三角形斜边上的中线等知识,用到的知识点为:(1)直角三角形斜边的中线等于斜边的一半;(2)三角形的中位线等于对应边的一半.12.从﹣2,﹣1,1,2这四个数中,任取两个不同的数作为一次函数y=kx+b的系数k,b,则一次函数y=kx+b的图象不经过第四象限的概率是.【考点】列表法与树状图法;一次函数图象与系数的关系.【专题】数形结合.【分析】列举出所有情况,看不经过第四象限的情况数占总情况数的多少即可.【解答】解:共16种情况,不经过第四象限的一次函数图象有4种,所以概率为.故答案为:.【点评】考查概率的求法;用到的知识点为:概率=所求情况数与总情况数之比.得到不经过第四象限的一次函数图象是解决本题的难点.13.如图,E(﹣6,0),F(﹣4,﹣2),以O为位似中心按比例尺1:2把△EFO缩小到第一象限,则点F的对应点F′的坐标为(2,1).【考点】位似变换;坐标与图形性质.【分析】以O为位似中心,按比例尺1:2,把△EFO缩小,结合图形得出,则点F的对应点F′的坐标是E(﹣4,﹣2)的坐标同时乘以﹣计算即可.【解答】解:根据题意可知,点F的对应点F′的坐标是F(﹣4,﹣2)的坐标同时乘以﹣,所以点F′的坐标为(2,1),故答案为:(2,1).【点评】本题考查了位似变换及坐标与图形性质的知识,关于原点成位似的两个图形,若位似比是k,则原图形上的点(x,y),经过位似变化得到的对应点的坐标是(kx,ky)或(﹣kx,﹣ky).14.如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于4或8.【考点】平移的性质;解一元二次方程-因式分解法;平行四边形的判定与性质;正方形的性质.【专题】几何动点问题.【分析】根据平移的性质,结合阴影部分是平行四边形,△AA′H与△HCB′都是等腰直角三角形,则若设AA′=x,则阴影部分的底长为x,高A′D=12﹣x,根据平行四边形的面积公式即可列出方程求解.【解答】解:设AC交A′B′于H,∵∠A=45°,∠D=90°∴△A′HA是等腰直角三角形设AA′=x,则阴影部分的底长为x,高A′D=12﹣x∴x•(12﹣x)=32∴x=4或8,即AA′=4或8cm.故答案为:4或8.【点评】考查了平移的性质及一元二次方程的解法等知识,解决本题关键是抓住平移后图形的特点,利用方程方法解题.三、解答题(共10小题,满分78分)15.解方程:x2﹣4x+1=0.【考点】解一元二次方程-配方法.【专题】计算题;配方法.【分析】移项后配方得到x2﹣4x+4=﹣1+4,推出(x﹣2)2=3,开方得出方程x﹣2=±,求出方程的解即可.【解答】解:移项得:x2﹣4x=﹣1,配方得:x2﹣4x+4=﹣1+4,即(x﹣2)2=3,开方得:x﹣2=±,∴原方程的解是:x1=2+,x2=2﹣.【点评】本题考查了用配方法解一元二次方程、解一元一次方程的应用,关键是配方得出(x ﹣2)2=3,题目比较好,难度适中.16.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,请在图(1)中画出一个格点三角形,使它与图(1)中的△ABC相似.【考点】作图—相似变换.【专题】作图题.【分析】利用网格特点可判断△ABC为直角三角形,两直角边分别为和2,于是把△ABC 放大得到直角三角形A′B′C′.【解答】解:如图2,△A′B′C′为所作.【点评】本题考查了作图﹣相似变换:两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到.17.如图,在平行四边形ABCD中,对角线AC、BD相交于O,过点O作直线EF⊥BD,分别交AD、BC于点E和点F,求证:四边形BEDF是菱形.【考点】菱形的判定;全等三角形的判定与性质;平行四边形的性质.【专题】证明题.【分析】由四边形ABCD是平行四边形,即可得AD∥BC,OB=OD,易证得△OED≌△OFB,可得DE=BF,即可证得四边形BEDF是平行四边形,又由EF⊥BD,即可证得平行四边形BEDF 是菱形.【解答】证明:∵四边形ABCD是平行四边形,∴AD∥BC,OB=OD,∵∠EDO=∠FBO,∠OED=∠OFB,∴△OED≌△OFB(AAS),∴DE=BF,又∵ED∥BF,∴四边形BEDF是平行四边形,∵EF⊥BD,∴▱BEDF是菱形.【点评】此题考查了平行四边形的判定与性质,菱形的判定以及全等三角形的判定与性质.此题难度不大,解题的关键是注意数形结合思想的应用.18.从甲学校到乙学校有A1、A2、A3三条线路,从乙学校到丙学校有B1、B2二条线路.(1)利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果;(2)小X任意走了一条从甲学校到丙学校的线路,求小X恰好经过了B1线路的概率是多少?【考点】列表法与树状图法.【分析】(1)依据题意先用列表法或画树状图法分析所有等可能的出现结果,注意要不重不漏;(2)依据表格或树状图即可求得小X从甲学校到丙学校共有6条不同的线路,其中经过B1线路有3条,然后根据概率公式即可求出该事件的概率.【解答】解:(1)利用列表或树状图的方法表示从甲校到丙校的线路所有可能出现的结果如下:A1A2A3B1(A1、B1)(A2、B1)(A3、B1)B2(A1、B2)(A2、B2)(A3、B2)(2)∴小X从甲学校到丙学校共有6条不同的线路,其中经过B1线路有3条,∴P(小X恰好经过了B1线路)=.【点评】本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.19.已知关于x的一元二次方程x2﹣6x+k=0.(1)当它有两个实数根时,求k的X围;(2)当k=﹣11时,假设方程两根是x1,x2,求x12+x22+8的值.【考点】根的判别式;根与系数的关系.【专题】探究型.【分析】(1)根据关于x的一元二次方程x2﹣6x+k=0有两个实数根,可得△≥0,从而可以得到k的X围;(2)根据k=﹣11,方程两根是x1,x2,可以得到两根之和与两根之积,从而可以得到x12+x22+8的值.【解答】解:(1)∵关于x的一元二次方程x2﹣6x+k=0,∴当它有两个实数根时,△=(﹣6)2﹣4×1×k≥0,解得,k≤9,即k的取值X围是k≤9;(2)∵k=﹣11,∴x2﹣6x﹣11=0,∴,∴x12+x22+8==62﹣2×(﹣11)+8=66,即x12+x22+8的值是66.【点评】本题考查根的判别式和根与系数的关系,解题的关键是明确根的判别式△的取值不同,根的情况也不同和根与系数的关系,巧妙变化得到所求问题需要的条件.20.如图,路灯(P点)距地面8米,身高1.6米的小明从距离路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点(B点在A点的左边)时,身影的长度是变长了还是变短了?变长或变短了多少米?【考点】相似三角形的应用;中心投影.【分析】由题意得出△MAC∽△MOP,△NBD∽△NOP,即可由相似三角形的性质求解.【解答】解:∵∠MAC=∠MOP=90°,∠AMC=∠OMP,∴△MAC∽△MOP.∴=,即=,解得,MA=5米;同理,由△NBD∽△NOP,可求得NB=1.5米,∴小明的身影变短了,变短了5﹣1.5=3.5(米).【点评】本题考查了相似三角形的应用;解题时关键是找出相似的三角形,根据对应边成比例列出方程.21.如图,一次函数y=kx+b与反比例函数y=的图象交于A(2,3),B(﹣3,n)两点.(1)求一次函数与反比例函数的解析式;(2)求△ABO的面积;(3)根据所给条件,请直接写出不等式kx+b>的解集.【考点】反比例函数与一次函数的交点问题.【分析】(1)根据反比例函数y=的图象过点A(2,3),利用待定系数法求出m,进而得出B点坐标,然后利用待定系数法求出一次函数解析式;(2)将三角形AOB分割为S△AOB=S△BOC+S△AOC,求出即可.(3)根据A、B的横坐标结合图象即可得出答案.【解答】解:(1)∵反比例函数y=的图象交于A(2,3),B(﹣3,n)两点.∴m=2×3=﹣3n.∴m=6,n=﹣2,∴反比例函数的解析式为y=.B的坐标是(﹣3,﹣2).把A(2,3)、B(﹣3,﹣2)代入y=kx+b.得:,解得,∴一次函数为y=x+1.(2)设直线y=x+1与x轴交于C,C(﹣1,0).所以:S△AOB=S△BOC+S△AOC=×1×2+×1×3=2.5.(3)kx+b>的解集是﹣3<x<0或x>2.【点评】此题主要考查了待定系数法求出反比例函数、一次函数解析式以及求三角形面积等知识,根据已知得出B点坐标以及得出S△AOB=S△BO C+S△AOC是解题关键.22.某某特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:(1)每千克核桃应降价多少元?(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?【考点】一元二次方程的应用.【专题】增长率问题.【分析】(1)设每千克核桃降价x元,利用销售量×每件利润=2240元列出方程求解即可;(2)为了让利于顾客因此应下降6元,求出此时的销售单价即可确定几折.【解答】(1)解:设每千克核桃应降价x元.…1分根据题意,得(60﹣x﹣40)(100+×20)=2240.…4分化简,得 x2﹣10x+24=0 解得x1=4,x2=6.…6分答:每千克核桃应降价4元或6元.…7分(2)解:由(1)可知每千克核桃可降价4元或6元.因为要尽可能让利于顾客,所以每千克核桃应降价6元.此时,售价为:60﹣6=54(元),.…9分答:该店应按原售价的九折出售.…10分【点评】本题考查了一元二次方程的应用,解题的关键是根据题目中的等量关系列出方程.23.如图,四边形ABCD中,AD=CD,∠DAB=∠ACB=90°,过点D作DE⊥AC,垂足为F,DE 与AB相交于点E.(1)求证:AB•CF=CB•CD;(2)已知AB=15,BC=9,P是射线DE上的动点,设DP=x(x>0),四边形BCDP的面积为y.①求y关于x的函数关系式;②当PB+PC最小时,求x,y的值.【考点】相似形综合题.【专题】压轴题;数形结合.【分析】(1)首先证得△DCF∽△ABC,利用相似三角形的性质可得结论;(2)①由勾股定理可得BC的长,利用梯形的面积公式可得结果;②首先由垂直平分线的性质可得点C关于直线DE的对称点是点A,PB+PC=PB+PA,故只要求PB+PA最小即可,因为当P、A、B三点共线时PB+PA最小,由中位线的性质可得EF=,由(1)知CF:BC=CD:AB,可得CD,即得AD,在Rt△ADF中,由勾股定理可得DF,易得DE,即得x,代入①可得y.【解答】(1)证明:如图1,∵AD=CD,DE⊥AC,∴DE垂直平分AC,∴AF=CF,∠DFA=∠DFC=90°,∠DAF=∠DCF,∵∠DAB=∠DAF+∠CAB=90°,∠CAB+∠B=90°,∴∠DCF=∠DAF=∠B,在Rt△DCF和Rt△ABC中,∠DFC=∠ACB=90°,∠DCF=∠B,∴△DCF∽△ABC,∴,∴AB•CF=CB•CD;(2)解:①∵AB=15,BC=9,∠ACB=90°,∴AC===12,∴CF=AF=6,∴y=(x+9)×6=3x+27(x>0);②由(1)知点C关于直线DE的对称点是点A,∴PB+PC=PB+PA,故只要求PB+PA最小,显然当P、A、B三点共线时PB+PA最小,此时DP=DE,PB+PA=AB,∵EF∥BC,∴EF=,∵CF:BC=CD:AB,即6:9=CD:15,∴CD=10=AD,Rt△ADF中,AD=10,AF=6,∴DF=8,∴DE=DF+EF=8+=,∴x=,此时y=.【点评】本题主要考查了相似三角形的性质及判定,垂直平分线的性质及判定定理及最短路径问题,分析出当P、A、B三点共线时PB+PA最小是解答此题的关键.24.在四边形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3.分别以OA、OC边所在直线为x轴、y轴建立如图所示的平面直角坐标系.(1)求点B的坐标;(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F.求直线DE的解析式;(3)点M在(2)中直线DE上,四边形ODMN是菱形,求N的坐标.【考点】一次函数综合题.【分析】(1)作BH⊥OA于H,根据矩形的性质求出OH的长,根据勾股定理求出BH的长,得到点B的坐标;(2)作EG⊥OA于G,得到△OGE∽△OHB,根据题意和相似三角形的性质求出点E、D的坐标,运用待定系数法求出直线DE的解析式;(3)作MP⊥y轴于点P,得到△MPD∽△FOD,根据相似三角形的性质和勾股定理计算即可.【解答】解:如图1,作BH⊥OA于H,则四边形OHBC为矩形,∴OH=CB=3,∴AH=OA﹣OH=3,∴BH==6,∴点B的坐标为(3,6);(2)如图1,作EG⊥OA于G,则EG∥BH,∴△OGE∽△OHB,∴==,∵OE=2EB,∴=,又OH=3,BH=6,∴OG=2,EG=4,∴点E的坐标为(2,4),∵OC=BH=6,OD=5,∴点D的坐标为(0,5),设直线DE的解析式为y=kx+b,∴,解得,,∴直线DE的解析式为y=﹣x+5;(3)如图2,作MP⊥y轴于点P,∵四边形ODMN是菱形,∴DM=MN=NO=OD=5,∵MP∥OA,∴△MPD∽△FOD,∴==,当y=0,即﹣x+5=0时,x=10,∴点F的坐标为(0,10),∴DF==5,∴==,解得,MP=2,PD=,∴OP=5+,∴N的坐标为(﹣2,).【点评】本题考查的是一次函数知识的综合运用,掌握矩形的性质定理、菱形的性质定理、相似三角形的判定和性质定理以及待定系数法求函数解析式的步骤是解题的关键.。
江西省九江市2022-2023学年九年级上学期期末数学试题(含答案)
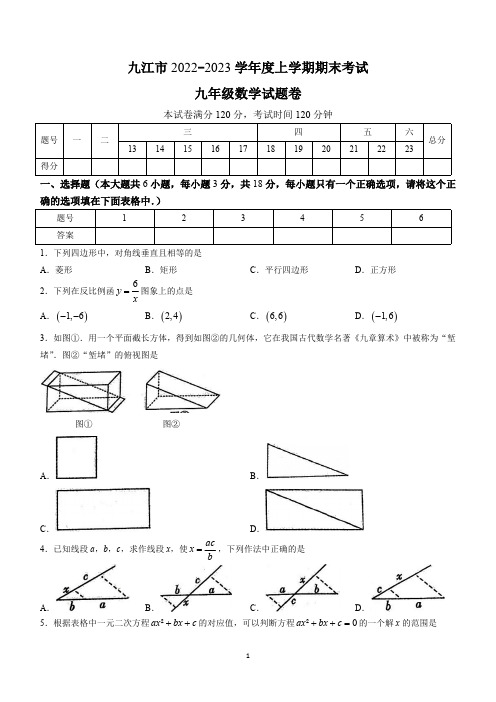
九江市2022-2023学年度上学期期末考试九年级数学试题卷本试卷满分120分,考试时间120分钟三四五六题号一二1314151617181920212223总分得分一、选择题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项,请将这个正确的选项填在下面表格中.)题号123456答案1.下列四边形中,对角线垂直且相等的是A .菱形B .矩形C .平行四边形D .正方形2.下列在反比例函图象上的点是A .B .C .D .3.如图①.用一个平面截长方体,得到如图②的几何体,它在我国古代数学名著《九章算术》中被称为“堑堵”.图②“堑堵”的俯视图是图①图②A .B .C .D .4.已知线段a ,b ,c ,求作线段x ,使,下列作法中正确的是A .B .C .D .5.根据表格中一元二次方程的对应值,可以判断方程的一个解x 的范围是6y x=()1,6--()2,4()6,6()1,6-acx b=²ax bx c ++²0ax bx c ++=x 00.51 1.52-1-0.51 3.57A .0<x <0.5B .0.5<x <1C .1<x <1.5D .1.5<x <26.已知:如图,直线与双曲线在第一象限交于点,与x 轴、y 轴分别交于A ,B 两点,则下列结论错误的是(第6小题图)A .t =2B .△AOB 等腰直角三角形C .k =1D .当x >1时,二、填空题(本题满分18分,共有6道小题,每小题3分)7.一元二次方程的解是 .8.菱形ABCD 的对角线AC 与BD 相交于点O ,若,,则BD 的长为 cm .9.如图所示的电路图,同时闭合两个开关能形成闭合电路的概率是 .(第9题)10.如图,△ABC 与△DEF 位似,点O 为位似中心,相似比为2∶3.若△ABC 的周长为4,则△DEF 的周长 .(第10题)²ax bx c++11y kx=+22y x=()1,P t 21y y >240x -=AB =4cm AC =11.如图,在矩形ABCD 中,AB =2,AD =3,E 、F 分别是边AB 、CD 的中点,点P 是AD 上一点,∠PFB =3∠FBC ,则AP 的长为 .(第11题)12.正方形ABCD 的边长为3,点P 、Q 在正方形不同的边上与点A 构成等腰三角形,若等腰△APQ 的底边长为APQ 的腰长是 .三、解答题(本大题共5小题,每小题6分,共30分)13.解方程(1)解方程:(2)如图,在平行四边形ABCD 中,AC 平分∠DAB ,求证:四边形ABCD 为菱形.14.已知关于x 的一元二次方程.(1)请说明无论m 为何实数,该方程总有两个实数根;(2)如果方程的一个实数根为1,求m 值及另一根.15.如图,在△ABC 中,点D ,E ,F 分别在边AB ,AC ,BC 上,连接DE ,EF ,已知四边形BFED 是平行四边形,.若△ADE 的面积为1,求平行四边形BFED 的面积.16.请用学过的方法研究一类新函数(k 为常数,k ≠0)的图象和性质.(1)在给出的平面直角坐标系中画出函数的图象;2230x x --=210x mx --=14DE BC =ky x=6y x=(2)对于函数,当自变量x 的值增大时,函数值y 怎样变化?17.按要求作出萎形(仅用无刻度的直尺作图,保留作图痕迹,不写作法)(1)如图1,在矩形ABCD 中,E ,F 分别是边AB ,AD 的中点,以EF 为边作出一个菱形;图1(2)如图2,在正方形ABCD 中,E 是对角线BD 上任意一点(BE >DE ),以AE 为边作出一个菱形.图2四、解答题(本大题共3小题,每小题8分,共24分)18.如图,线段DE 与AF 分别为△ABC 的中位线与中线.(1)求证:AF 与DE 互相平分(2)当线段AF 与BC 满足怎样的数量关系时,四边形ADFE 为矩形?请说明理由.ky x19.第十四届国际数学教育大会(ICME -14)会微的主题图案有着丰富的数学元素,展现了我国古代数学的文化魅力,其右下方的“卦”是用我国古代的计数符号写出的八进制数3745.八进制是以8作为进位基数的数字系统,有0~7共8个基本数字.八进制数3745换算成十进制数是,表示ICME -14的举办年份.(1)八进制数3746换算成十进制数是 ;(2)小华设计了一个n 进制数143,换算成十进制数是120,求n 的值。
九江市九年级上学期数学期中考试试卷

九江市九年级上学期数学期中考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分) (2020七上·鹿邑期末) 下列选项中,不能由已知等式a=b推出的是()A . a+3x=b+3xB . a﹣2=b﹣2C . ac=bcD .2. (2分)如图①是一个正三棱柱毛坯,将其截去一部分,得到一个工件如图②.则这个工件的俯视图、主视图依次是()A . c、aB . c、dC . b、dD . b、a3. (2分)若方程x2﹣3x+c=0无实数解,那么c的取值范围是()A . c<B . c>C . c≥D . c≤4. (2分)当棱长为20的正方体的某个面平行于投影面时,这个面的正投影的面积为()A . 20B . 300C . 400D . 6005. (2分)某花木场有一块形如等腰梯形ABCD的空地,各边的中点分别是E,F,G,H,测量得对角线AC=10米,现想用篱笆围成四边形EFGH的场地,则需篱笆总长度是()A . 40米B . 30米C . 20米D . 10米6. (2分)在△ABC中,点D,E,F分别在边AB,AC,BC上,若DE∥BC,EF∥AB,则下面所列比例式中正确的是()A .B .C .D .7. (2分) (2016八下·西城期末) 若A(1,y1),B(2,y2)两点都在反比例函数y= 的图象上,则y1与y2的大小关系是()A . y1<y2B . y1=y2C . y1>y2D . 无法确定8. (2分)在Rt△ABC中,∠C=90°,若sinA= ,AB=2,则AC长是()A .B .C .D . 29. (2分) (2016九下·澧县开学考) 若一次函数y=kx+b的图象经过第二、三、四象限,则反比例函数y=的图象在()A . 一、三象限B . 二、四象限C . 一、二象限D . 三、四象限10. (2分)一个三角形的周长是36cm,则以这个三角形各边中点为顶点的三角形的周长是()A . 6cmB . 12cmC . 18cmD . 36cm11. (2分)从长为10cm、7cm、5cm、3cm的四条线段中任选三条能够成三角形的概率是()A .B .C .D .12. (2分)(2014·湖州) 在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是()A .B .C .D .二、填空题 (共4题;共4分)13. (1分)一元二次方程x2-3x=0的根是________ .14. (1分) (2015九上·罗湖期末) 在某校组织的知识竞赛中共有三种试题,其中语文类4题,综合类8题,数学类若干题.已知从中随机抽取一题,是数学类的概率是,则数学类有________题.15. (1分)(2011·苏州) 如图,已知△ABC是面积为的等边三角形,△ABC∽△ADE,AB=2AD,∠BAD=45°,AC与DE相交于点F,则△AEF的面积等于________(结果保留根号).16. (1分)如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,若∠APD=60°,则CD 的长为________.三、解答题 (共7题;共71分)17. (10分)已知下列n(n为正整数)个关于x的一元二次方程:①x2﹣1=0,②x2+x﹣2=0,③x2+2x﹣3=0,…(n)x2+(n﹣1)x﹣n=0.(1)请解上述一元二次方程①、②、③、(n);(2)请你指出这n个方程的根具有什么共同特点,写出一条即可.18. (11分)(2018·毕节) 2017年9月,我国中小学生迎来了新版“教育部统编义务教育语文教科书”,本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读,某校对A《三国演义》、B《红楼梦》、C《西游记》、D《水浒》四大名著开展“最受欢迎的传统文化经典著作”调查,随机调查了若干名学生(每名学生必选且只能选这四大名著中的一部)并将得到的信息绘制了下面两幅不完整的统计图:(1)本次一共调查了________名学生;(2)请将条形统计图补充完整;(3)某班语文老师想从这四大名著中随机选取两部作为学生暑期必读书籍,请用树状图或列表的方法求恰好选中《三国演义》和《红楼梦》的概率.19. (5分) (2019九上·六安期末) 如图,以点O为位似中心,在网格内将△ABC放大2倍得到△A′B′C′,若A点坐标为(﹣1,1).请写出A′点的坐标.20. (10分)(2013·连云港) 小林准备进行如下操作实验;把一根长为40cm的铁丝剪成两段,并把每一段各围成一个正方形.(1)要使这两个正方形的面积之和等于58cm2,小林该怎么剪?(2)小峰对小林说:“这两个正方形的面积之和不可能等于48cm2.”他的说法对吗?请说明理由.21. (10分)(2018·阜宁模拟) 如图,△ABC中,AB=BC.(1)用直尺和圆规作△ABC的中线BD;(不要求写作法,保留作图痕迹);(2)在(1)的条件下,若BC=6,BD=4,求的值.22. (15分)如图,在平面直角坐标系中,(1)分别写出△ABC的顶点坐标;(2)设小方格的边长为1,求出△ABC的面积(3)若以点A,B,C,D四点构成行四边形,直接写出点D的坐标.23. (10分)(2011·绍兴) 抛物线y=﹣(x﹣1)2+3与y轴交于点A,顶点为B,对称轴BC与x轴交于点C.(1)如图1.求点A的坐标及线段OC的长;(2)点P在抛物线上,直线PQ∥BC交x轴于点Q,连接BQ.①若含45°角的直角三角板如图2所示放置.其中,一个顶点与点C重合,直角顶点D在BQ上,另一个顶点E在PQ上.求直线BQ的函数解析式;②若含30°角的直角三角板一个顶点与点C重合,直角顶点D在直线BQ上,另一个顶点E在PQ上,求点P 的坐标.参考答案一、选择题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共7题;共71分)17-1、17-2、18-1、18-2、18-3、19-1、20-1、20-2、21-1、21-2、22-1、22-2、22-3、23-1、。
2023-2024学年江西省九江市九年级(上)期末数学试卷+答案解析

2023-2024学年江西省九江市九年级(上)期末数学试卷一、选择题:本题共6小题,每小题3分,共18分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.方程的二次项系数、一次项系数和常数项分别是()A.0,5,2B.0,5,C.1,5,D.1,5,22.如图是一根空心方管,它的俯视图是()A.B.C.D.3.在一个不透明的盒子中装有n个除颜色外完全相同的球,其中有4个红球.若每次将球充分搅匀后,任意摸出1个球记下颜色再放回盒子,通过大量重复试验后,发现摸到红球的频率稳定在左右,则n的值大约为()A.16B.18C.20D.244.如图,已知,直线m分别交直线a、b、c于点A、B、C,直线n分别交直线a、b、c于点D、E、F,若,则的值是()A.B.C.D.15.矩形具有而菱形不具有的性质是()A.两组对边分别平行B.对角线互相垂直C.对角线相等D.两组对角分别相等6.如图,在平面直角坐标系中,的顶点A,B分别在y轴、x轴上,,斜边轴.若反比例函数的图象经过AC的中点D,则k的值为()A.4B.5C.6D.8二、填空题:本题共6小题,每小题3分,共18分。
7.关于x的一元二次方程的一个根为,则m的值为______.8.用数字0,1,2,3组成个位数字与十位数字不同的两位数,其中是偶数的概率为______.9.如图,在菱形ABCD中,,,则BD的长为______.10.如图,在矩形ABCD中,点E,F分别是AD,BC边的中点,连接EF,若矩形ABFE与矩形ABCD相似,,则矩形ABCD的面积为______.11.如图,是反比例函数和在第一象限的图象,直线轴,并分别交两条曲线于A、B两点,则______.12.如图,为边长为7cm的等边三角形,,,P为BC上动点,以的速度从B向C运动,假设P点运动时间为t秒,当______秒时,与相似.三、计算题:本大题共1小题,共6分。
13.《杨辉算法》中有这么一道题:“直田积八百六十四步,只云长阔共六十步,问长多几何?”意思是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多了多少步?四、解答题:本题共10小题,共78分。
2020-2021学年第一学期江西省九江市九年级(上)期中考试数学试卷 解析版

2020-2021学年江西省九江市九年级(上)期中数学试卷一、选择题(本大题共6小题,每小题3分,共18分。
每小题只有一个正确选项)1.一元二次方程x2﹣9=0的根是()A.x=9B.x=±9C.x=3D.x=±32.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球实验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45,则口袋中白色球的个数很可能是()个.A.12B.24C.36D.483.下列几何图形中,即是轴对称图形,又是中心对称图形的是()A.等边三角形B.平行四边形C.菱形D.对角线相等的四边形4.为了加强视力保护意识,小明要在书房里挂一张视力表.由于书房空间狭小,他想根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.如图,如果大视力表中“E”的高度是3.5cm,那么小视力表中相应“E”的高度是()A.3cm B.2.5cm C.2.3cm D.2.1cm5.生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2米,则a约为()A.1.24米B.1.38米C.1.42米D.1.62米6.如图,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为()A.B.C.D.二、填空题(本大题共6小题,每小题3分,共18分)7.顺次连接一个对角线互相垂直的四边形各边中点,所得的四边形是形.8.现有四张正面分别标有数字﹣1,1,2,3的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数字,前后两次抽取的数字分别记为m,n.则点P(m,n)在第二象限的概率为.9.已知一元二次方程x2﹣x+k=0的一根为1,则另一根为.10.在Rt△ABC中,∠C=90°,∠A=30°,点P为AC中点,经过点P的直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有条.11.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是.12.如图,在平行四边形ABCD中,AB=8,BC=12,∠B=120°,E是BC的中点,点P 在平行四边形ABCD的边上,若△PBE为等腰三角形,则EP的长为.三、(本大题共5小题,每小题6分,共30分)13.(6分)(1)用配方法解方程x2+4x﹣5=0;(2)用因式分解法解方程(x﹣3)2+4x(x﹣3)=0.14.(6分)在图1、2中,点E是矩形ABCD边AD上的中点,现要求仅用无刻度的直尺分别按下列要求画图.[保留画(作)图痕迹,不写画(作)法](1)在图1中,以BC为一边画△PBC,使△PBC面积=矩形ABCD面积;(2)在图2中,以BE、ED为邻边作▱BEDK.15.(6分)如图,点E,F分别在菱形ABCD的边BC,CD上,且BE=DF.求证:∠BAE =∠DAF.16.(6分)已知关于x的方程x2﹣(m+1)x+2(m﹣1)=0(1)求证:无论m取何值时,方程总有实数根;(2)若等腰三角形一边长为4,另两边恰好是此方程的根,求此三角形的另两边长.17.(6分)小红的爸爸积极参加社区抗疫志愿服务工作.根据社区的安排,志愿者被随机分到A组(体温检测)、B组(便民代购)、C组(环境消杀).(1)小红的爸爸被分到B组的概率是;(2)某中学王老师也参加了该社区的志愿者队伍,他和小红爸爸被分到同一组的概率是多少?(请用画树状图或列表的方法写出分析过程)四、(本大题共3小题,每小题8分,共24分)18.(8分)如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.(1)求证:△BDE∽△EFC;(2)若BC=12,=,求线段BE的长.19.(8分)某商店将进货为30元的商品按每件40元出售,每月可出售600件,现在采用提高商品售价减少销售量的办法增加利润,这种商品每件的销售价每提高1元,其销售量就减少10件,商品想在月销售成本不超过1万元的情况下,使每月总利润为10000元,那么此时每件商品售价应为多少元?20.(8分)如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.(1)求证:四边形ADEF是平行四边形;(2)求证:∠DHF=∠DEF.五、(本大题共2小题,每小题9分,共18分)21.(9分)如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG∥EF.(1)求证:四边形OEFG是矩形;(2)若AD=10,EF=4,求OE和BG的长.22.(9分)已知x1,x2是一元二次方程x2﹣2x+k+2=0的两个实数根.(1)求k的取值范围.(2)是否存在实数k,使得等式+=k﹣2成立?如果存在,请求出k的值;如果不存在,请说明理由.六、(本大题共12分)23.(12分)如图1,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD,EC与BD相交于点G,与AD相交于点F,AF=AB.(1)求证:BD⊥EC;(2)若AE=2,求AB的长;(3)如图2,连接AG,请探究线段EG、AG、DG之间的数量美系,并说明理由.2020-2021学年江西省九江市九年级(上)期中数学试卷参考答案与试题解析一、选择题(本大题共6小题,每小题3分,共18分。
2020-2021学年江西省九江市九年级(上)期中数学试卷-解析版

2020-2021学年江西省九江市九年级(上)期中数学试卷一、选择题(本大题共6小题,共18.0分)1.一元二次方程x2−9=0的根是()A. x=9B. x=±9C. x=3D. x=±32.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有60个,除颜色外,形状、大小、质地等完全相同.小刚通过多次摸球实验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45,则口袋中白色球的个数很可能是()个.A. 12B. 24C. 36D. 483.下列几何图形中,即是轴对称图形,又是中心对称图形的是()A. 等边三角形B. 平行四边形C. 菱形D. 对角线相等的四边形4.为了加强视力保护意识,小明要在书房里挂一张视力表.由于书房空间狭小,他想根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.如图,如果大视力表中“E”的高度是3.5cm,那么小视力表中相应“E”的高度是()A. 3cmB. 2.5cmC. 2.3cmD. 2.1cm5.生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2米,则a约为()A. 1.24米B. 1.38米C. 1.42米D. 1.62米6.如图,矩形ABCD的对角线AC,BD交于点O,AB=6,BC=8,过点O作OE⊥AC,交AD于点E,过点E作EF⊥BD,垂足为F,则OE+EF的值为()A. 485B. 325C. 245D. 125二、填空题(本大题共6小题,共18.0分)7.顺次连接一个对角线互相垂直的四边形各边中点,所得的四边形是______形.8.现有四张正面分别标有数字−1,1,2,3的不透明卡片,它们除数字外其余完全相同,将它们背面朝上洗均匀,随机抽取一张,记下数字后放回,背面朝上洗均匀,再随机抽取一张记下数宇,前后两次抽取的数字分别记为m,n.则点P(m,n)在第二象限的概率为______.9.已知一元二次方程x2−x+k=0的一根为1,则另一根为______.10.在Rt△ABC中,∠C=90°,∠A=30°,点P为AC中点,经过点P的直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有______条.11.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是______.12.如图,在平行四边形ABCD中,AB=8,BC=12,∠B=120°,E是BC的中点,点P在平行四边形ABCD的边上,若△PBE为等腰三角形,则EP的长为______.三、计算题(本大题共1小题,共6.0分)13.(1)用配方法解方程x2+4x−5=0;(2)用因式分解法解方程(x−3)2+4x(x−3)=0.四、解答题(本大题共10小题,共78.0分)14.在图1、2中,点E是矩形ABCD边AD上的中点,现要求仅用无刻度的直尺分别按下列要求画图.[保留画(作)图痕迹,不写画(作)法](1)在图1中,以BC为一边画△PBC,使△PBC面积=矩形ABCD面积;(2)在图2中,以BE、ED为邻边作▱BEDK.15.如图,点E,F分别在菱形ABCD的边BC,CD上,且BE=DF.求证:∠BAE=∠DAF.16.已知关于x的方程x2−(m+1)x+2(m−1)=0(1)求证:无论m取何值时,方程总有实数根;(2)若等腰三角形一边长为4,另两边恰好是此方程的根,求此三角形的另两边长.17.小红的爸爸积极参加社区抗疫志愿服务工作.根据社区的安排,志愿者被随机分到A组(体温检测)、B组(便民代购)、C组(环境消杀).(1)小红的爸爸被分到B组的概率是______;(2)某中学王老师也参加了该社区的志愿者队伍,他和小红爸爸被分到同一组的概率是多少?(请用画树状图或列表的方法写出分析过程)18.如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE//AC,EF//AB.(1)求证:△BDE∽△EFC;(2)若BC=12,AFFC =12,求线段BE的长.19.某商店将进价为30元的商品按每件40元出售,每月可出售600件,现在采用提高商品售价减少销售量的办法增加利润,这种商品每件的销售价每提高1元,其销售量就减少10件,商店想在月销售成本不超过1万元的情况下,使每月总利润为10000元,那么此时每件商品售价应为多少元?20.如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.(1)求证:四边形ADEF是平行四边形;(2)求证:∠DHF=∠DEF.21.如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上,EF⊥AB,OG//EF.(1)求证:四边形OEFG是矩形;(2)若AD=10,EF=4,求OE和BG的长.22.已知x1,x2是一元二次方程x2−2x+k+2=0的两个实数根.(1)求k的取值范围.(2)是否存在实数k,使得等式1x1+1x2=k−2成立?如果存在,请求出k的值;如果不存在,请说明理由.23.如图1,已知四边形ABCD是矩形,点E在BA的延长线上,AE=AD,EC与BD相交于点G,与AD相交于点F,AF=AB.(1)求证:BD⊥EC;(2)若AE=2,求AB的长;(3)如图2,连接AG,请探究线段EG、AG、DG之间的数量美系,并说明理由.答案和解析1.【答案】D【解析】解:x2−9=0,移项得:x2=9,两边直接开平方得:x=±3,故选:D.首先把−9移到方程的右边,然后两边直接开平方即可.此题主要考查了直接开方法解一元二次方程,解这类问题要移项,把所含未知数的项移到等号的左边,把常数项移项等号的右边,化成x2=a(a≥0)的形式,利用数的开方直接求解.2.【答案】B【解析】解:∵小刚通过多次摸球实验后发现其中摸到红色、黑色球的频率稳定在0.15和0.45,∴估计摸到红色、黑色球的概率分别为0.15和0.45,∴摸到白球的概率为1−0.15−0.45=0.4,∴口袋中白色球的个数为60×0.4=24,即口袋中白色球的个数很可能24个.故选B.根据频率估计概率得到摸到红色、黑色球的概率分别为0.15和0.45,则摸到白球的概率为0.4,然后利用概率公式计算即可.本题考查了利用频率估计概率:大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.3.【答案】C【解析】解:A、等边三角形是轴对称图形,不是中心对称图形,故此选项不合题意;B、平行四边形不是轴对称图形,是中心对称图形,故此选项不合题意;C、菱形即是轴对称图形,也是中心对称图形,故此选项符合题意;D、对角线相等的四边形不是轴对称图形,也不是中心对称图形,故此选项不合题意;故选:C.根据轴对称图形与中心对称图形的概念求解.此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.4.【答案】D【解析】解:由题意得:CD//AB,∴CDAB =DEBE,∵AB=3.5cm,BE=5m,DE=3m,∴CD3.5=35,∴CD=2.1cm,故选:D.直接利用平行线分线段成比例定理列比例式,代入可得结论.本题考查了相似三角形的应用,比较简单;根据生活常识,墙与地面垂直,则两张视力表平行,根据平行相似或平行线分线段成比例定理列比例式,可以计算出结果.5.【答案】A【解析】解:∵雕像的腰部以下a与全身b的高度比值接近0.618,∴ab=0.618,∵b为2米,∴a约为1.24米.故选:A.根据雕像的腰部以下a与全身b的高度比值接近0.618,因为图中b为2米,即可求出a 的值.本题考查了黄金分割,解决本题的关键是掌握黄金分割定义.6.【答案】C【解析】解:∵AB=6,BC=8,∴矩形ABCD的面积为48,AO=DO=12AC=5,∵对角线AC,BD交于点O,∴△AOD的面积为12,∵EO⊥AO,EF⊥DO,∴S△AOD=S△AOE+S△DOE,即12=12AO×EO+12DO×EF,∴12=12×5×EO+12×5×EF,∴5(EO+EF)=24,∴EO+EF=245,故选:C.依据矩形的性质即可得到△AOD的面积为12,再根据S△AOD=S△AOE+S△DOE,即可得到OE+EF的值.本题主要考查了矩形的性质,解题时注意:矩形的四个角都是直角;矩形的对角线相等且互相平分.7.【答案】矩【解析】解:矩形.理由如下:∵E、F、G、H分别为各边的中点,∴EF//AC,GH//AC,EH//BD,FG//BD,(三角形的中位线平行于第三边)∴四边形EFGH是平行四边形,(两组对边分别平行的四边形是平行四边形)∵AC⊥BD,EF//AC,EH//BD,∴∠EMO=∠ENO=90°,∴四边形EMON是矩形(有三个角是直角的四边形是矩形),∴∠MEN=90°,∴四边形EFGH是矩形(有一个角是直角的平行四边形是矩形).根据三角形中位线的性质,可得到这个四边形是平行四边形,再由对角线垂直,能证出有一个角等于90°,则这个四边形为矩形.本题考查的是矩形的判定方法,常用的方法有三种:①一个角是直角的平行四边形是矩形.②三个角是直角的四边形是矩形.③对角线相等的平行四边形是矩形.8.【答案】316【解析】解:画树状图为:共有16种等可能的结果数,其中点P(m,n)在第二象限的结果数为3,.所以点P(m,n)在第二象限的概率=316.故答案为316画树状图展示所有16种等可能的结果数,利用第二象限内点的坐标特征确定点P(m,n)在第二象限的结果数,然后根据概率公式求解.本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.也考查了点的坐标.9.【答案】0【解析】解:设方程的另一个根是x2,则:1+x2=1,解得x2=0.所以另一根为0,故答案为0.根据根与系数的关系由两根之和可以求出另一个根.是解题的关键.本题考查了根与系数的关系,熟练掌握两根之和等于−ba10.【答案】3【解析】解:过点P作PE//AB交AB于点E,△CPE∽△CAB.过点P作PF//BC交AB于点F,△APF∽△ACB.过点P作PG⊥AB交AB于点G,△PGA∽△BCA.故满足条件的直线有3条,故答案为:3.根据相似三角形的判定方法,画出图形判断即可.本题考查相似三角形的判定,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型.11.【答案】8√5【解析】解:如图,连接BD交AC于点O,∵四边形ABCD为正方形,∴BD⊥AC,OD=OB=OA=OC,∵AE=CF=2,∴OA−AE=OC−CF,即OE=OF,∴四边形BEDF为平行四边形,且BD⊥EF,∴四边形BEDF为菱形,∴DE=DF=BE=BF,=2,∵AC=BD=8,OE=OF=8−42由勾股定理得:DE=√OD2+OE2=√42+22=2√5,∴四边形BEDF的周长=4DE=4×2√5=8√5,故答案为:8√5.连接BD交AC于点O,则可证得OE=OF,OD=OB,可证四边形BEDF为平行四边形,且BD⊥EF,可证得四边形BEDF为菱形;根据勾股定理计算DE的长,可得结论.本题主要考查正方形的性质、菱形的判定和性质及勾股定理,掌握对角线互相垂直平分的四边形为菱形是解题的关键.12.【答案】6或6√3或√57【解析】解:当P点在BA上,BP=BE=6,作BH⊥PE于H,如图1,则PH=EH,∵∠B=120°,∴∠BPE=∠BEP=30°,在Rt△BEH中,BH=1BE=3,EH=√3BH=23√3,∴PE=2EH=6√3;当P点在AD上,BP=PE,作BG⊥AD于G,PF⊥BE于F,如图2,则BF=EF=3,∵四边形ABCD为平行四边形,∴AD//BC,∵∠ABC=120°,∴∠A=60°,AB=4,BG=√3AG=4√3,在Rt△ABG中,AG=12∴PF=4√3,在Rt△PEF中,PE=√32+(4√3)2=√57;当点P在CD上,如图3,EB=EP=6,综上所述,PE的长为6或6√3或√57.故答案为6或6√3或√57.当P点在BA上,BP=BE=6,作BH⊥PE于H,如图1,根据等腰三角形的性质得PH=EH,再计算出∠BPE=∠BEP=30°,然后利用含30度的直角三角形三边的关系计算出EH,从而得到此时的PE的长;当P点在AD上,BP=PE,作BG⊥AD于G,PF⊥BE于F,如图2,所以BF=EF=3,先求出BG=4√3,从而得到PF=4√3,然后利用勾股定理计算出此时PE的长;当点P在CD上,如图3,EB=EP=6.本题考查了平行四边形的性质:平行四边形的对边相等;平行四边形的对角相等;平行四边形的对角线互相平分.平行线间的距离处处相等.也考查了等腰三角形的性质.13.【答案】解:(1)x2+4x=5.∴x2+4x+4=9,∴(x+2)2=9,∴x+2=±3,∴x1=−5,x2=1;(2)原方程因式分解得:(x−3)(5x−3)=0,∴x−3=0或5x−3=0,∴x1=3,x2=3.5【解析】(1)利用配方法求解即可.(2)利用因式分解法求解即可.本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.14.【答案】解:(1)如图所示,△PBC即为所求;(2)如图所示,平行四边形BEDK即为所求.【解析】(1)连接CE并延长,交BA的延长线于P,根据△APE≌△DCE,可得△PBC面积=矩形ABCD面积;(2)连接矩形ABCD的对角线,交于点O,可得BO=DO,再连接EO并延长,交BC于K,根据△BOK≌△DOE,可得EO=KO,连接DK,即可得到▱BEDK.本题主要考查了复杂作图,平行四边形的判定,矩形的性质的运用,解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.解题时注意:对角线互相平分的四边形是平行四边形.15.【答案】证明:四边形ABCD是菱形,∴∠B=∠D,AB=AD,在△ABE和△ADF中,{AB=AD ∠B=∠D BE=DF,∴△ABE≌△ADF(SAS),∴∠BAE=∠DAF.【解析】根据菱形的性质可得∠B=∠D,AB=AD,再证明△ABE≌△ADF,即可得∠BAE=∠DAF.本题考查了菱形的性质、全等三角形的判定与性质,解决本题的关键是掌握菱形的性质.16.【答案】解:(1)证明:∵Δ=[−(m+1)]2−4×2(m−1)=m2−6m+9=(m−3)2≥0,∴无论m取何值,这个方程总有实数根;(2)若腰长为4,将x=4代入原方程,得:16−4(m+1)+2(m−1)=0,解得:m=5,∴原方程为x2−6x+8=0,解得:x1=2,x2=4.组成三角形的三边长度为2、4、4;若底边长为4,则此方程有两个相等实数根,∴Δ=0,即m=3,此时方程为x2−4x+4=0,解得:x1=x2=2,由于2+2=4,不能构成三角形,舍去;所以三角形另外两边长度为4和2.【解析】本题考查了根的判别式、三角形三边关系、等腰三角形的性质以及解一元二次方程,解题的关键是:(1)牢记“当Δ≥0时,方程有实数根”;(2)代入x=4求出m值.(1)根据方程的系数结合根的判别式,即可得出Δ=(m−3)2≥0,由此即可证出:无论m取何值,这个方程总有实数根;(2)分腰长为4和底边长度为4两种情况分别求解可得.17.【答案】13【解析】解:(1)共有3种可能出现的结果,被分到“B组”的有1中,因此被分到“B ;组”的概率为13(2)用列表法表示所有可能出现的结果如下:共有9种可能出现的结果,其中“他与小红的爸爸”在同一组的有3种,∴P(他与小红爸爸在同一组)=39=13.(1)共有3种可能出现的结果,被分到“B组”的有1中,可求出概率.(2)用列表法表示所有可能出现的结果,进而计算“他与小红的爸爸”分到同一组的概率.本题考查列表法或树状图法求随机事件发生的概率,列举出所有可能出现的结果情况是正确求解的前提.18.【答案】证明:(1)∵DE//AC,∴∠DEB=∠FCE,∵EF//AB,∴∠DBE=∠FEC,∴△BDE∽△EFC;(2)∵EF//AB,∴BEEC =AFFC=12,∵EC=BC−BE=12−BE,∴BE12−BE =12,解得:BE=4.【解析】(1)由平行线的性质可得∠DEB=∠FCE,∠DBE=∠FEC,可得结论;(2)由平行线分线段成比例可得BEEC =AFFC=12,即可求解.本题考查了相似三角形的判定和性质,平行线分线段成比例,掌握相似三角形的判定是本题的关键.19.【答案】解:设每件商品售价应为x元,每月的销量为[600−10(x−40)]件,由题意,得[600−10(x−40)](x−30)=10000,解得:x1=50,x2=80.当x=50时,600−10(50−40)=500件,销售成本为:500×30=15000>10000舍去,当x=80时,600−10(80−40)=200件,销售成本为:200×30=6000<10000舍去,答:此时每件商品售价应为80元.【解析】设每件商品售价应为x元,根据利润=售价−进价建立方程求出其解并检验即可.本题考查了列一元二次方程解实际问题的运用,一元二次方程的解法的运用,利润率问题的数量关系的运用,解答时根据利润=售价−进价建立方程是关键.20.【答案】证明:(1)∵点D,E,F分别是AB,BC,CA的中点,∴DE、EF都是△ABC的中位线,∴EF//AB,DE//AC,∴四边形ADEF是平行四边形;(2)∵四边形ADEF是平行四边形,∴∠DEF=∠BAC,∵D,F分别是AB,CA的中点,AH是边BC上的高,∴DH=AD,FH=AF,∴∠DAH=∠DHA,∠FAH=∠FHA,∵∠DAH+∠FAH=∠BAC,∠DHA+∠FHA=∠DHF,∴∠DHF=∠BAC,∴∠DHF=∠DEF.【解析】(1)根据三角形的中位线平行于第三边并且等于第三边的一半可得EF//AB,DE//AC,再根据平行四边形的定义证明即可;(2)根据平行四边形的对角相等可得∠DEF=∠BAC,根据直角三角形斜边上的中线等于斜边的一半可得DH=AD,FH=AF,再根据等边对等角可得∠DAH=∠DHA,∠FAH=∠FHA,然后求出∠DHF=∠BAC,等量代换即可得到∠DHF=∠DEF.本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰三角形的性质,直角三角形斜边上的中线等于斜边的一半的性质,平行四边形的判定与性质,熟记各性质并准确识图是解题的关键.21.【答案】解:(1)∵四边形ABCD是菱形,∴BD⊥AC,∠DAO=∠BAO,∵E是AD的中点,AD,∴AE=OE=12∴∠EAO=∠AOE,∴∠AOE=∠BAO,∴OE//FG,∵OG//EF,∴四边形OEFG是平行四边形,∵EF⊥AB,∴∠EFG=90°,∴四边形OEFG是矩形;(2)∵四边形ABCD是菱形,∴BD⊥AC,AB=AD=10,∴∠AOD=90°,∵E是AD的中点,AD=5;∴OE=AE=12由(1)知,四边形OEFG是矩形,∴FG=OE=5,∵AE=5,EF=4,∴AF=√AE2−EF2=3,∴BG=AB−AF−FG=10−3−5=2.AD,推【解析】(1)根据菱形的性质得到BD⊥AC,∠DAO=∠BAO,得到AE=OE=12出OE//FG,求得四边形OEFG是平行四边形,根据矩形的判定定理即可得到结论;AD=5;由(1)知,(2)根据菱形的性质得到BD⊥AC,AB=AD=10,得到OE=AE=12四边形OEFG是矩形,求得FG=OE=5,根据勾股定理得到AF=√AE2−EF2=3,于是得到结论.本题考查了矩形的判定和性质,菱形的性质,勾股定理,直角三角形的性质,正确的识别图形是解题的关键.22.【答案】解:(1)∵一元二次方程x2−2x+k+2=0有两个实数根,∴△=(−2)2−4×1×(k+2)≥0,解得:k≤−1.(2)∵x1,x2是一元二次方程x2−2x+k+2=0的两个实数根,∴x1+x2=2,x1x2=k+2.∵1x1+1x2=k−2,∴x1+x2x1x2=2k+2=k−2,∴k2−6=0,解得:k1=−√6,k2=√6.又∵k≤−1,∴k=−√6.∴存在这样的k值,使得等式1x1+1x2=k−2成立,k值为−√6.【解析】本题考查了根与系数的关系以及根的判别式,(1)根据方程的系数结合△≥0,即可得出关于k的一元一次不等式,解之即可得出k的取值范围;(2)根据根与系数的关系可得出x1+x2=2,x1x2=k+2,结合1x1+1x2=k−2,即可得出关于k的方程,解之即可得出k值,再结合(1)即可得出结论.23.【答案】解:(1)∵四边形ABCD是矩形,点E在BA的延长线上,∴∠EAF=∠DAB=90°,又∵AE=AD,AF=AB,∴△AEF≌△ADB(SAS),∴∠AEF=∠ADB,∴∠GEB+∠GBE=∠ADB+∠ABD=90°,即∠EGB=90°,故BD⊥EC;(2)∵四边形ABCD是矩形,∴AE//CD,∴∠AEF=∠DCF,∠EAF=∠CDF,∴△AEF∽△DCF,∴AECD =AFDF,即AE⋅DF=AF⋅DC,设AE=AD=a(a>0),则有a⋅(a−1)=1,化简得a2−a−1=0,解得a=√5−1或a=−√5−1(舍去),∴AB=√5−1;(3)如图,在线段EG上取点P,使得EP=DG,在△AEP与△ADG中,AE=AD,∠AEP=∠ADG,EP=DG,∴△AEP≌△ADG(SAS),∴AP=AG,∠EAP=∠DAG,∴∠PAG=∠PAD+∠DAG=∠PAD+∠EAP=∠DAE=90°,∴△PAG为等腰直角三角形,∴EG−DG=EG−EP=PG=√2AG.【解析】(1)证明△AEF≌△ADB(SAS),则∠AEF=∠ADB,∠GEB+∠GBE=∠ADB+∠ABD=90°,即可求解;(2)证明△AEF∽△DCF,则AECD =AFDF,设AB=a(a>0),则有22−2a=a2,即可求解;(3)证明△AEP≌△ADG(SAS),则△PAG为等腰直角三角形,故EG−DG=EG−EP= PG=√2AG.本题是四边形综合题,考查了矩形的性质,相似三角形的判定与性质,全等三角形的判定与性质,等腰直角三角形的判定与性质等知识,熟练掌握全等三角形的判定与性质是解题的关键.。
