任意角的概念ppt课件
合集下载
任意角完整公开课PPT课件

任意角的度量
度量单位
角度的度量单位是度(°),弧度(rad)和密位(mil)。
度量工具
量角器、圆规、直尺等。
度量方法
通过量角器或使用三角函数值进行计算。
象限角与轴线角
象限角
在平面直角坐标系中,按逆时针方向,第一象限角为0°~90° ,第二象限角为90°~180°,第三象限角为180°~270°,第四 象限角为270°~360°。
、航向和航速。
04
THANKS
感谢观看
和差公式的应用
在解决涉及两角和与差的三角函数问题时,和差公式是必不可少的工 具。
04
三角函数的图像与性质
正弦函数的图像与性质
其图像是周期函数,呈现波浪
形。
正弦函数的性质包括:在每个 周期内,函数值从0增加到最 大值,然后又减小到0,如此
往复。
正弦函数的图像在y轴两侧对 称,其周期为360度。
01 02
任意角三角函数的定义
三角函数是描述三角形边与角之间关系的数学工具。对于任意角α,其 正弦函数sinα定义为“对边长度除以斜边长度”,余弦函数cosα定义 为“邻边长度除以斜边长度”,正切函数tanα定义为“对边长度除以 邻边长度”。
单位圆定义法
通过单位圆上点的坐标来表示三角函数值,其中正弦值等于y坐标,余 弦值等于x坐标,正切值等于y坐标除以x坐标。
正弦函数在每个周期内的变化 率是不同的,变化率最大的点
是函数的极值点。
余弦函数的图像与性质
余弦函数是三角函数的另一种形式, 其图像也是周期函数,呈现波浪形。
余弦函数的图像在y轴两侧对称,其 周期也为360度。
余弦函数的性质包括:在每个周期内 ,函数值从最大值减小到0,然后再 增加到最小值,如此往复。
任意角和弧度制PPT课件

轴线角
与x轴正方向形成的角称为轴线角 ,其大小为正负90°。
Part
02
弧度制的基本概念
弧度的定义
弧度的定义
弧度是度量角的一种方式,它是以长度来度量圆弧所对应的中心角的大小。在 圆中,长度等于半径的圆弧所对应的中心角叫做1弧度的角。
弧度的符号
用rad表示弧度,例如,1弧度可以表示为1rad。
弧度与角度的换算
任意角和弧度制ppt 课件
• 任意角的概念 • 弧度制的基本概念 • 任意角的三角函数 • 弧度制下的三角函数 • 任意角和弧度制的实际应用
目录
Part
01
任意角的概念
定义与性质
定义
任意角是平面内一条射线绕着端点从 一个位置旋转到另一个位置所形成的 角。
性质
任意角具有方向性,其正方向由旋转 方向确定;旋转量大于0°小于360°的 角称为正角,旋转量大于360°的角称 为负角。
正弦函数、余弦函数、正 切函数都具有周期性,其 周期为2π弧度。
奇偶性
正弦函数和正切函数是奇 函数,余弦函数是偶函数 。
图像
正弦函数、余弦函数、正 切函数的图像分别呈正弦 波、余弦波和直线形状, 且均在单位圆上表示。
弧度制下三角函数的应用
三角恒等式
利用三角函数的性质,可以推导 出许多三角恒等式,如sin^2(x)
电磁学中的交流电
在电磁学中,交流电的相位角可以用任意角和弧度制来表示,帮助 理解交流电的特性和规律。
振动和波动
在振动和波动的研究中,任意角和弧度制可以用来描述振动相位、 波传播方向等。
在几何学中的应用
平面几何和立体几何
任意角和弧度制可以用来描述平面几何和立体几何中的角度 和旋转,例如旋转矩阵、极坐标等。
与x轴正方向形成的角称为轴线角 ,其大小为正负90°。
Part
02
弧度制的基本概念
弧度的定义
弧度的定义
弧度是度量角的一种方式,它是以长度来度量圆弧所对应的中心角的大小。在 圆中,长度等于半径的圆弧所对应的中心角叫做1弧度的角。
弧度的符号
用rad表示弧度,例如,1弧度可以表示为1rad。
弧度与角度的换算
任意角和弧度制ppt 课件
• 任意角的概念 • 弧度制的基本概念 • 任意角的三角函数 • 弧度制下的三角函数 • 任意角和弧度制的实际应用
目录
Part
01
任意角的概念
定义与性质
定义
任意角是平面内一条射线绕着端点从 一个位置旋转到另一个位置所形成的 角。
性质
任意角具有方向性,其正方向由旋转 方向确定;旋转量大于0°小于360°的 角称为正角,旋转量大于360°的角称 为负角。
正弦函数、余弦函数、正 切函数都具有周期性,其 周期为2π弧度。
奇偶性
正弦函数和正切函数是奇 函数,余弦函数是偶函数 。
图像
正弦函数、余弦函数、正 切函数的图像分别呈正弦 波、余弦波和直线形状, 且均在单位圆上表示。
弧度制下三角函数的应用
三角恒等式
利用三角函数的性质,可以推导 出许多三角恒等式,如sin^2(x)
电磁学中的交流电
在电磁学中,交流电的相位角可以用任意角和弧度制来表示,帮助 理解交流电的特性和规律。
振动和波动
在振动和波动的研究中,任意角和弧度制可以用来描述振动相位、 波传播方向等。
在几何学中的应用
平面几何和立体几何
任意角和弧度制可以用来描述平面几何和立体几何中的角度 和旋转,例如旋转矩阵、极坐标等。
任意角 -完整公开课PPT课件

n 360 240 n 360 270 ,k Z ,
故
3 是第三象限的角 .
综上3 可知: 是第一或第二或第三象限的角 .
3
0°
360° x
如图
几何法
如图
故
2
是第三象限的角 .
综上2 可知: 是第一或第三象限的角 .
例3.若角的终边与角的终边关于x轴对称,则 + =______
例3. 已知角 是第一象限的角,
试问 2 、 、 各是第几象限的角?
23
180°
y
90°
0°
O
360° x
270°
又 k 120 k 120 30 ,k Z .
225° 45°
o
x
故S中适合不等式-360°≤ <720°的元素是:
45 2180 315, 45 1180 225, 45 1180 135, 45 2180 405, 45 0180 45, 45 3180 585.
练习3:
(1)终边在x轴上的角的集合:
y
{ | n 180 ,n Z }.
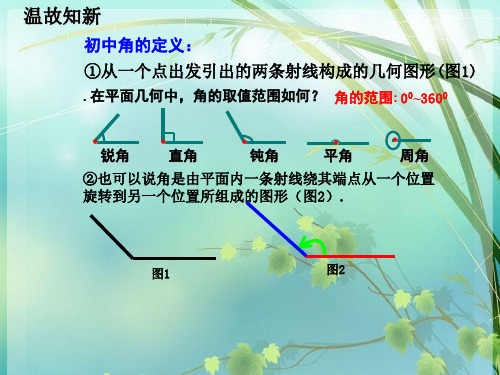
角的概念推广的必要性:
0º到360º范围内的角在生 产、生活和科学实验的实践 中已不适用。
如体操、花样滑冰、跳台跳 水中“转体三周半”,
又如车轮、钟表、罗盘的 运动规律的研究等.
1、角的概念
任意角的概念:
平面内一条射线OA绕着端点O(顶点)从一个位置
OA(始边)旋转到另一个位置OB(终边)所成的图形
3
y
90°
当 k 3n(n Z ) 时 ,
n 360 n 360 30 ,k Z , 180°
Hale Waihona Puke 故3 是第一象限的角
任意角的概念课件

02
CATALOGUE
任意角的分类
正角
定义
正角是指角度大小在$0^{circ}$和 $360^{circ}$之间的角。在平面内, 正角通常表示为逆时针旋转形成的角 。
几何表示
应用
正角在几何、三角函数等领域有广泛 应用,如时钟指针的转动、物体的旋 转等。
正角可以用实线表示,起点在坐标轴 上,逆时针旋转到终点的角度即为正 角的大小。
角的大小由其终边位置决定,与旋转 方向无关。
终边相同的角
终边相同的角表示为 $alpha = beta + 2kpi$,其中 $alpha$ 和 $beta$ 是终边相同的角, $k$ 是整数。
当 $k=0$ 时,$alpha = beta$,即两个角相等;当 $k neq 0$ 时,$alpha$ 和 $beta$ 是互补角。
象限角的集合表示为 ${alpha | npi + (-1)^n cdot frac{pi}{2} < alpha < npi + (-1)^n cdot frac{3pi}{2}, n in Z}$。
04
CATALOGU义
正弦函数是直角三角形中锐角的对边与斜边的比值,记作sin(α),其中α为锐角 。
负角
定义
负角是指角度大小在$360^{circ}$到$0^{circ}$之间的 角。在平面内,负角通常表示为
顺时针旋转形成的角。
几何表示
负角可以用虚线表示,起点在坐标 轴上,顺时针旋转到终点的角度即 为负角的大小。
应用
负角在物理学、工程学等领域有广 泛应用,如机械转动、电路分析等 。
零角
定义
零角是指角度大小为 $0^{circ}$的角。在平面 内,零角表示起点和终点 重合,没有旋转。
高中数学必修四:1.1.1《任意角》 PPT课件 图文
精讲领学
例题1 写出与下列各角终边相同的角的集合S,并把S中在 360~720范围的角写出来.
( 1 ) 6 0 ;( 2 ) 2 1 ;( 3 ) 3 6 3 1 4
解: ( 1 ) S {| k 3 6 0 6 0 , k Z }300,60,420
( 2 ) S {| k 3 6 0 2 1 , k Z }21,339,699
2、下列角中终边与330°相同的角是( ) A.30° B.-30° C.630° D.-630°
3、把-1485°转化为α+k·360° (0°≤α<360°, k∈Z)的形式是( ) A.45°-4×360° B.-45°-4×360° C.-45°-5×360° D.315°-5×360°
反馈固学
1.1.1 任意角
第一课时
(1)推广角的概念;理解并掌握正角、负角、零角的定义; (2)理解任意角以及象限角的概念; (3)掌握所有与角终边相同的角(包括角)的表示方法; (4)树立运动变化观点,深刻理解推广后的角的概念;
思考:那么工人在拧紧或拧松螺丝时,转动的角度 如何表示才比较合适?
逆时 针
4、下列结论中正确的是( ) A.小于90°的角是锐角 B.第二象限的角是钝角 C.相等的角终边一定相同 D.终边相同的角一定相等
5:任意两个角的数量大小可以相加、相减.
例如50°+80°=130°, 50°-80°=-30°, 你能解释一下这两个式子的几何意义吗?
130°是以50°角的终边为始边,逆时针旋转80°所成的角. -30°是以50°角的终边为始边,顺时针旋转80°所成的角.
注3:(1) 为任意角 (2) k Z这一条件必不可少;
(3) 终边相同的角不一定相等, 终边相等的角有无数多个,它们相差3600的整数倍.
任意角的概念说课课件ppt

角的性质
角的大小可以用度数、弧度等不同的度量单位来表示。根据 角的度数,角可分为锐角、直角、钝角等不同类型的角。此 外,还有与角相关的一系列性质,如角的平分线、角的和差 等。
为什么要引入任意角的概念
实际问题的需求
在现实生活中,很多实际问题涉及到不仅仅是0°到360°范围内的角,还可能涉 及到更大或者更小的角。因此,需要引入任意角的概念来描述这些角度。
数学理论的完善
引入任意角的概念有助于完善数学中关于角的理论体系,使其更加严密和完整 。
任意角的概念简介
01 02
任意角的定义
任意角是指大小不受限制的角,可以超过360°或小于0°。在平面直角坐 标系中,通常以x轴正方向与射线起点为参考,逆时针方向为正,顺时 针方向为负。
任意角的表示方法
任意角可以用角度、弧度两种不同的度量单位来表示。在三角函数中, 通常使用弧度作为角的度量单位。
工程技术中的任意角应用
机器人定位与导航
在机器人技术中,利用任意角可以表示机器人的朝向和位置,从 而实现精准的定位和导航。
航空航天技术
在航空航天领域,通过任意角可以描述飞行器的飞行方向和姿态, 对于飞行器的控制和导航具有重要意义。
电子工程中的相位差
在电子工程中,任意角可以用于描述信号的相位差,对于信号处理 、传输和接收等方面的研究具有重要价值。
练习1
在航海中,船只需要根据罗盘的指示来确定航向。罗盘上的度数与 任意角的概念有何关联?如何利用任意角的知识来解决航向问题?
练习2
在物理实验中,需要测量某物体做圆周运动时的角速度。如何通过 测量得到的数据,利用任意角的概念来计算物体的角速度?
练习3
在钟表中,时针、分针、秒针之间的角度关系如何运用任意角的知识 和计算来解决?
角的大小可以用度数、弧度等不同的度量单位来表示。根据 角的度数,角可分为锐角、直角、钝角等不同类型的角。此 外,还有与角相关的一系列性质,如角的平分线、角的和差 等。
为什么要引入任意角的概念
实际问题的需求
在现实生活中,很多实际问题涉及到不仅仅是0°到360°范围内的角,还可能涉 及到更大或者更小的角。因此,需要引入任意角的概念来描述这些角度。
数学理论的完善
引入任意角的概念有助于完善数学中关于角的理论体系,使其更加严密和完整 。
任意角的概念简介
01 02
任意角的定义
任意角是指大小不受限制的角,可以超过360°或小于0°。在平面直角坐 标系中,通常以x轴正方向与射线起点为参考,逆时针方向为正,顺时 针方向为负。
任意角的表示方法
任意角可以用角度、弧度两种不同的度量单位来表示。在三角函数中, 通常使用弧度作为角的度量单位。
工程技术中的任意角应用
机器人定位与导航
在机器人技术中,利用任意角可以表示机器人的朝向和位置,从 而实现精准的定位和导航。
航空航天技术
在航空航天领域,通过任意角可以描述飞行器的飞行方向和姿态, 对于飞行器的控制和导航具有重要意义。
电子工程中的相位差
在电子工程中,任意角可以用于描述信号的相位差,对于信号处理 、传输和接收等方面的研究具有重要价值。
练习1
在航海中,船只需要根据罗盘的指示来确定航向。罗盘上的度数与 任意角的概念有何关联?如何利用任意角的知识来解决航向问题?
练习2
在物理实验中,需要测量某物体做圆周运动时的角速度。如何通过 测量得到的数据,利用任意角的概念来计算物体的角速度?
练习3
在钟表中,时针、分针、秒针之间的角度关系如何运用任意角的知识 和计算来解决?
任意角的概念ppt课件

一、正角、负角、零角 〔1〕正角:按逆时针方向旋转而成的角。
〔2〕负角:按顺时针方向旋转而成的角。
〔3〕零角:射线没有旋转时,把它看成零角。 B O α
α
O
A
A B
二、象限角 角放在坐标系中, 始边OA
终边OB
Y B
顶点O
坐标原点
OX轴的正半轴
落在第几象限,就叫第几象限角。
Y B
当角的终边OB落在第一象限 时,称∠AOB是第一象限角
例1:写出与以下角终边一样的角的集合: 并指出它们是哪个象限的角:
〔1〕45º 〔3〕 240º
〔2〕 -30° 〔4〕 330º
例2:在 0º~360 º之间,找出与以下各角终边一样的角
〔1〕-120º 〔3〕 -950º
〔2〕 640º
解:(1)
∵-120º=240º-360º ∴-120º与240º角的终边一样,它是第三象限角。
所以,终边落在X轴上的角的集合为: S=S1∪S2={X|X=2K·180º, k Z}∪{X|X=〔2K+1〕·180º, k Z} ={X|X=K·180º, k Z}
小结: (1)正角、负角、零角 (2)象限角 (3)终边一样的角
作业:
谢谢观赏
终边OB对应的角是不是只有一个?
如何表示终边一样的角? Y
B
30º
A
O
X
不是:
360º+30º
OB
720º+30º
OB
-360º+30º
OB
-720º+30º
பைடு நூலகம்
OB
k·360º+30º kZ
〔四1、〕终与边3一0º样角的终角边的一集样合的角的集合: S={X|X=30º+ k·360º,kZ}
任意角的概念ppt课件

《数学》(基础版
首页
上页
五年制高职《数学》(第2册) 高等教育出版社
下页
退出
生活2 1 生3活2专5业2贴近生 活理专业4 1
论 知 识
进走 专 业
自选题 理论知识题:1号、 贴近生活题:2号、3号 走进专业题:4号、5号
归纳
1.若角 45o 则角
是第 四 象限角. 10分
返 回
2.北京时间6月4日,2010跳水世界杯在男子3米板决赛中, 中国选手何冲以546.55分夺得冠军,他也成为世界杯该 项目首位卫冕的中国人。
分类 角
锐角 直角 钝角
平角
大于平角且小于周角的角
周角
今天所学角(动态) 一条射线绕其端点 旋转而形成的图形
任意大小
正角 负角
角
零角
象限角
界限角
作业 必做: 1.导学与练习 A组 2.以小组为单位,依据本节课所 学知识编写与生活或专业相关的 问题(小组之间循环解答). 选作:
导学与练习 B组
课件部分内容来源于网络,如对 内容有异议或侵权的请及时联系 删除! 此课件可编辑版,请放心使用!
象限角
第一象限角 第二象限角 第三象限角
角
第四象限角
终边在x轴正半轴上的角
界限角
终边在x轴负半轴上的角 终边在y轴正半轴上的角
终边在y轴负半轴上的角
正男角 按角的性生别成过程 负角
零女角
角
置置于于坐社标会系中中
第教一师象限角
有象职限业角者
第医二生象限角
第三象限角
工人
第四象限角
…
终边在x轴正半轴上的角
角象限角界限角第一象限角第二象限角第三象限角第四象限角终边在xx轴正半轴上的角终边在yy轴正半轴上的角终边在xx轴负半轴上的角终边在yy轴负半轴上的角角按角的生成过程置于坐标系中正角负角零角象限角界限角第一象限角第二象限角第三象限角第四象限角性别男女置于社会中有职业者无职业者教师医生工人
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
more
(1)正角:按逆时针方向旋转而成的角。
(2)负角:按顺时针方向旋转而成的角。 (3)零角:射线没有旋转时,把它看成零角。 B O A
一、正角、负角、零角
α
O
α
A
B
二、象限角
顶点O 角放在坐标系中, 始边OA 终边OB
Y
坐标原点
OX轴的正半轴 落在第几象限,就叫第几象限角。
Y
当角的终边OB落在第一象限 时,称∠AOB是第一象限角
S={X|X=α + k· 360º,kZ}
例1:写出与下列角终边相同的角的集合: 并指出它们是哪个象限的角:
(1)45º (3) 240º (2) -30° (4) 330º
例2:在 0º ~360 º 之间,找出与下 列各角终边相同的角
(1)-120º (3) -950º (2) 640º
解:(1)
角的概念的推广
复习:
1、角的定义 射线绕着它的端点o旋转而成的图形。
B
O
O 角的项点
α
OA
A
角的始边 OB 角的终边
1、自行车轮向前行进时转动的情况
自行车车轮的转动是逆时针方向,转 动的圈数不只一圈(一圈是360度)
观察:
2、钟表指针转动的情况
钟表指针的转动是顺时针方向,转动 的圈数也不只一圈(一圈是360度)
∵-120º =240º -360º
∴-120º 与240º 角的终边相同,它是第 三象限角。 ∵640º =280º +360º ∴640º 与280º 角的终边相同,它是第 四象限角。
(2)
例3:写出终边落在X轴上的角的集合
解:终边落在X轴的正半轴上的一个角为0º ,终边落在X轴的负 半轴上的一个角为180º ,因此
Y
B
30º
O
A
X
不是:
360º +30º 720º +30º -360º +30º -720º +30º
OB OB OB OB
k· 360º +30º kZ
四、终边相同的角的集合 ( 1)与30º 角终边相同的角的集合:
S={X|X=30º+ k· 360º,kZ}
(2)与α角终边相同的角的集合:
终边落在X轴正半轴上的角的集合为:
S1={X|X=0º+ k·360º , kZ}={X|X=2K·180º, kZ}
终边落在X轴负半轴上的角的集合为:
S2={X|X=180°+k·360º , kZ}={X|X=(2K+1)·180º, kZ} 所以,终边落在X轴上的角的集合为: S=S1∪S2={X|X=2K·180º, kZ}∪{X|X=(2K+1)·180º, kZ} ={X|X=K·180º, kZ}
小结:
(1)正角、负角、零角 (2)象限角 (3)终边相同的角
作业:
B
O Y A X
B
O Y A
X 当角的终边OB落在第二象限
时,称∠AOB是第二象限角 当角的终边OB落在第三象限 时,称∠AOB是第三象限角
O
B
A X
OБайду номын сангаас
A X
B
当角的终边OB落在第四象限 时,称∠AOB是第四象限角
三、终边相同的角 设 α=30º ,在直角坐标系中做α=30º
30º 是第一象限角,终边OB。 问题:终边OB对应的角是不是只有一个? 如何表示终边相同的角?
(1)正角:按逆时针方向旋转而成的角。
(2)负角:按顺时针方向旋转而成的角。 (3)零角:射线没有旋转时,把它看成零角。 B O A
一、正角、负角、零角
α
O
α
A
B
二、象限角
顶点O 角放在坐标系中, 始边OA 终边OB
Y
坐标原点
OX轴的正半轴 落在第几象限,就叫第几象限角。
Y
当角的终边OB落在第一象限 时,称∠AOB是第一象限角
S={X|X=α + k· 360º,kZ}
例1:写出与下列角终边相同的角的集合: 并指出它们是哪个象限的角:
(1)45º (3) 240º (2) -30° (4) 330º
例2:在 0º ~360 º 之间,找出与下 列各角终边相同的角
(1)-120º (3) -950º (2) 640º
解:(1)
角的概念的推广
复习:
1、角的定义 射线绕着它的端点o旋转而成的图形。
B
O
O 角的项点
α
OA
A
角的始边 OB 角的终边
1、自行车轮向前行进时转动的情况
自行车车轮的转动是逆时针方向,转 动的圈数不只一圈(一圈是360度)
观察:
2、钟表指针转动的情况
钟表指针的转动是顺时针方向,转动 的圈数也不只一圈(一圈是360度)
∵-120º =240º -360º
∴-120º 与240º 角的终边相同,它是第 三象限角。 ∵640º =280º +360º ∴640º 与280º 角的终边相同,它是第 四象限角。
(2)
例3:写出终边落在X轴上的角的集合
解:终边落在X轴的正半轴上的一个角为0º ,终边落在X轴的负 半轴上的一个角为180º ,因此
Y
B
30º
O
A
X
不是:
360º +30º 720º +30º -360º +30º -720º +30º
OB OB OB OB
k· 360º +30º kZ
四、终边相同的角的集合 ( 1)与30º 角终边相同的角的集合:
S={X|X=30º+ k· 360º,kZ}
(2)与α角终边相同的角的集合:
终边落在X轴正半轴上的角的集合为:
S1={X|X=0º+ k·360º , kZ}={X|X=2K·180º, kZ}
终边落在X轴负半轴上的角的集合为:
S2={X|X=180°+k·360º , kZ}={X|X=(2K+1)·180º, kZ} 所以,终边落在X轴上的角的集合为: S=S1∪S2={X|X=2K·180º, kZ}∪{X|X=(2K+1)·180º, kZ} ={X|X=K·180º, kZ}
小结:
(1)正角、负角、零角 (2)象限角 (3)终边相同的角
作业:
B
O Y A X
B
O Y A
X 当角的终边OB落在第二象限
时,称∠AOB是第二象限角 当角的终边OB落在第三象限 时,称∠AOB是第三象限角
O
B
A X
OБайду номын сангаас
A X
B
当角的终边OB落在第四象限 时,称∠AOB是第四象限角
三、终边相同的角 设 α=30º ,在直角坐标系中做α=30º
30º 是第一象限角,终边OB。 问题:终边OB对应的角是不是只有一个? 如何表示终边相同的角?
