第七章 GPS卫星定位误差
GPS的误差

GPS卫星定位的误差由于微波适合作长距离传送,且具有不易受天候,水气干扰的特性,因此GPS讯号发送是采用高频,波长短的微波来对地球传送。
早期由于美俄冷战的关系,因此在民生用途的GPS讯号中都会被加入所谓的SA干扰讯号(Selective Availability)让定位精确度只能达到100~150 公尺,后来美俄冷战结束美国才终于放手让GPS系统精确度提升到目前的10~15公尺。
目前GPS发送的讯号内包含了三种讯号:SPS, PPS, Y code。
第一种讯号称为:标准定位服务(Standard Position Service),它采用C/A码来作编码。
所谓C/A码就是美国提供给全世界的讯号,也是冷战前被加入SA干扰讯号的讯号,使用的频道称为L1(Link 1,约1575.42MHz)。
第二种讯号称为:精确定位服务(Precision Position Service),又简称为P code,频道为L2(Link2,约为1227.6MHz),看到精确两字就知道比SPS来得更加精确。
此部份的定位信息曾经在波湾战争中发挥到公分级的定位水准。
最后一种讯号称为:Y code,是在战时用来防止L2频道被敌方窃取的反制码,也是美国在解除C/A 干扰讯号保留的后门,以确保只有美国人才能享受最佳的定位效果。
回到现实生活根据上面提到的原理,我们使用L2 band 应该就可以享受到公分级的定位信息才对,但事实上却不然。
由于GPS是在外层空间跟着地球旋转,因此GPS卫星讯号要进入地表,中间必定会经过大气层,而大气层中又包含了:电离层以及气流循环旺盛的对流层。
电离层内的离子浓度会影响电波传送的速度;同时对流层内的空气温度,密度以及气候因素(云层厚度,风暴发生)都会影响到GPS讯号的传送速度或传送路径。
中间对GPS讯号的影响虽然极为小,(通常不到0.01秒),但对于计算相对卫星的距离及定位精准度都会有影响。
除了这些固定的因素之外,还有一个不固定的因素就是:太阳黑子的运作周期。
GPS导航定位误差详解

GPS导航定位误差详解GPS导航定位误差详解GPS卫星导航定位,是基于被动式测距原理,亦即,GPS信号接收机被动的测量来自GPS卫星的定位信号和传播时延,而测得GPS信号接收天线相位中心和GPS卫星发射天线相位中心之间的距离(即站星距离),进而将它和GPS卫星在轨位置联合解算出用户的三维坐标。
由此可见,GPS卫星导航定位的误差主要分成下述的3大类。
(1)GPS信号的自身误差即认为得SA误差,简称卫星误差;(2)GPS信号从卫星传播到用户接收天线的船舶误差;(3)GPS信号接收机所产生的GPS信号测量误差,简称接受误差。
本节从基本概念入手,较详细地论述了GPS卫星导航定位测量的偏差和误差,以及他们的削弱方法,并论述了GPS 现代化对提高GPS 卫星导航定位精度的作用和影响。
GPS卫星导航定位的精度、误差与偏差广义而论,精度(accuracy)表示一个量的观测值与其真值接近或一致的程度,常以其相应值—误差(error)予以表述。
对GPS卫星导航而言,精度,直观地概括为同GPS信号所测定的载体在航点位与载体实际点位之差。
对于GPS卫星测地而言,精度,是用GPS信号所测定的地面点位与其实地点位之差。
现代卫星导航定位中几个常用的技术术语进行较详细地论述。
4.2.1 均方根差(RMS)均方根差,应文名为root mean square error,测绘界的中国学者将其称为“中误差”或曰“标准差”。
它的探测概率,是以置信椭圆(confidence ellipse,用于二维定位)和置信椭球(confidence ellispsoid,用于三维定位)来表述。
置信椭圆的长短半轴,分别表示二维位置坐标分量的标准差(如经度的σλ和纬度的σφ)。
一倍标准差(1σ)的概率值是68.3%,二倍标准差(2σ)的概率值为95.5%;三倍标准差(3σ)的概率值是99.7%。
许多中外文献所述的“精度”多为一倍标准差(1σ),且用“距离均方根差”(DRMS)表示二维定位精度,距离均方根差(DRMS),也称为圆径向误差(circular radial error)或曰均方位置误差,另有一些作者常采用“双倍距离均方根差”(2DRMS)。
GPS卫星定位误差来源

GPS 卫星定位的误差来源分析GPS是一个庞大的系统(由GPS卫星、用户和地面的监控站三部分组成) ,GPS 测量是通过地面接收设备接收卫星传送来的信息,计算同一时刻地面接收设备到多颗卫星之间的伪距离,采用空间距离后方交会方法,来确定地面点的三维坐标。
误差的组成也很复杂:根据不同的研究方向和研究重点, 误差的分类各有不同。
通常是按误差的性质将其分为系统误差和偶然误差两类;而从误差的来源又可以将其分为与GPS卫星有关的误差、与GPS卫星信号传播有关的误差和与GPS信号接收机有关的误差。
此篇文章主要论述除钟差、电离层、对流层、多路径效应以外的GPS卫星定位的误差来源。
在高精度的GPS测量中,还应注意到与地球整体运动有关的地球潮汐、负荷潮及相对论效应等影响。
1、与GPS卫星有关的误差(1)卫星星历误差由星历所给出的卫星在空间的位置与实际位置之差称为卫星星历误差。
卫星星历分为广播星历和精密星历。
广播星历是通过GPS卫星发送的一种预报星历。
因为我们不能充分了解卫星上存在的各种摄动因素,所以预报星历钟存在较大的误差。
精密星历是根据实测资料进行拟合处理而得出的。
它需要在一些已知精密位置的点上跟踪卫星来计算观测瞬间的卫星真是位置,从而获得准确可靠的精密星历。
(2)相对论效应相对论效应是由于卫星钟和接收机钟所处的状态(运动速度和重力位)不同而引起卫星钟和接收机钟之间产生相对钟误差的现象。
在广义和狭义相对论的综合影响下,钟安放在卫星上比安放在地面上要快,为消除这一影响,一般将卫星钟的标准频率减小4.5×10-3Hz。
(3)美国的SA 政策和AS 政策美国军方为限制非特许用户利用GPS 进行高精度定位, 采用了降低系统精度的政策: SA ( Select iv e Availability )政策和AS( Anti - Spoofing ) 政策。
SA 政策即选择可用性技术, 通过ε( dither) 和δ( epsilon) 两种技术实现。
GPS定位误差的产生原因分析与减小方法

GPS定位误差的产生原因分析与减小方法引言:在现代社会,全球定位系统(Global Positioning System,GPS)已经成为了人们生活中不可或缺的一部分。
无论是导航、交通监控还是地理信息系统等领域都离不开GPS定位技术。
然而,随着GPS定位的广泛应用,人们也逐渐发现定位误差问题的存在。
本文将从GPS定位误差产生的原因入手,探讨解决这一问题的方法。
一、GPS定位误差的原因分析:1. GPS系统误差:GPS系统本身存在着一些系统误差,例如卫星钟差、伪距观测误差、大气延迟等。
这些误差会直接影响到GPS定位的准确性。
2. 空间几何因素:GPS定位需要至少4颗卫星进行定位计算,卫星的位置和空间几何分布对定位精度有着重要影响。
当卫星分布不均匀或存在遮挡物时,会导致定位误差增大。
3. 电离层和大气影响:电离层和大气中的湿度、温度等因素都会对GPS信号产生影响,导致信号传播延迟或折射,从而引起定位误差。
4. 载波相位等伪距测量误差:GPS定位是通过测量卫星发射的信号和接收器接收的信号之间的时间差来计算位置的。
然而,由于载波相位的波长较短,测量精度更高,但受到多普勒效应的影响,会产生伪距测量误差。
二、减小GPS定位误差的方法:1. 多路径效应抑制:多路径效应是指GPS信号在传播过程中发生反射、散射等现象,致使接收器接收到多个信号,在信号合成过程中引入误差。
为了减小多路径效应,可以利用天线设计和信号处理技术,选择适合的接收天线和增加抗多路径干扰的算法。
2. 差分定位:差分定位是通过引入一个参考站与基准站的距离进行辅助定位,利用参考站的精确位置和信号传播速度信息来对GPS定位结果进行修正。
差分定位可以大幅度减小系统误差和信号传播误差的影响,提高定位精度。
3. 增加卫星数量和分布:通过增加卫星数量和改善卫星的空间分布,可以提高GPS定位的可见卫星数目和几何配置,从而减小定位误差。
可以使用卫星信噪比、可视卫星数等指标来优选卫星,并避开存在遮挡物的区域。
GPS信号的误差
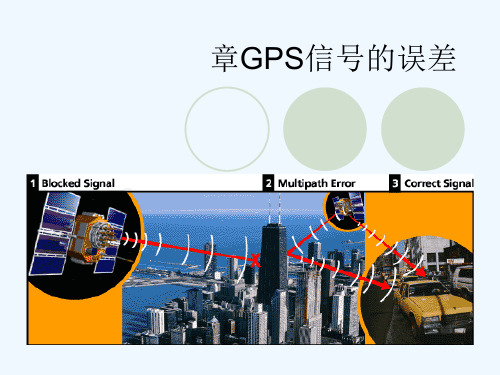
电离层和对流层的划分
电离层折射误差
1.电离层及其影响 电离层是指距地表50~1000公里之间 的大气层。按照电离层距离地面高度的不 同,将其划分为D、E、F1、F2四个电离 区。
D区:50~90km,由强烈的x射线和α辐射产生。 它不产生时延影响,夜间可忽略。 E区:90~140km,由弱x射线电离产生。有较小 的时延影响。 F1区:140~210km,与E区的共同影响占电离层 时延影响的10%。 F2区:21~1000km,由原子氧电离产生,产生最 大时延影响。 氢离子区:大于1000km,质子层,由氢原子电 离产生的H+组成。对时延的影响在白天为10%, 夜间为50%。
(2)轨道松弛法:在平差模型中将星历中给 出的卫星轨道参数作为未知数纳入平差模 型,通过平差同时求得测站位置及轨道偏 差改正数。 (3)利用同步观测值求差分 当两站距离较近时效果非常好,但基线的 相对精度随距离的增加而降低。
卫星时钟误差
物理同步误差: 一般在1ms左右; ※1ms的钟误差 300Km的距离误差! 可利用下面公式进行改正:
cm~dm --dm 1m
1m
cm~dm
10~50m
cm~dm
2~100m 2~100m dm 5m dm 5m
接收 误差
观测噪声误差
内时延误差 天线相位中心误差
0.1~1m
dm~m mm~cm
0.1~1m
dm~m mm~cm
1~10m
m
1~10m
m
mm~cm mm~cm
(一)与卫星有关的误差
星历误差(卫星轨道误差) GPS卫星星历误差是指卫星星历所提供的卫 星空间位置与实际位置的偏差。
GPS测量误差
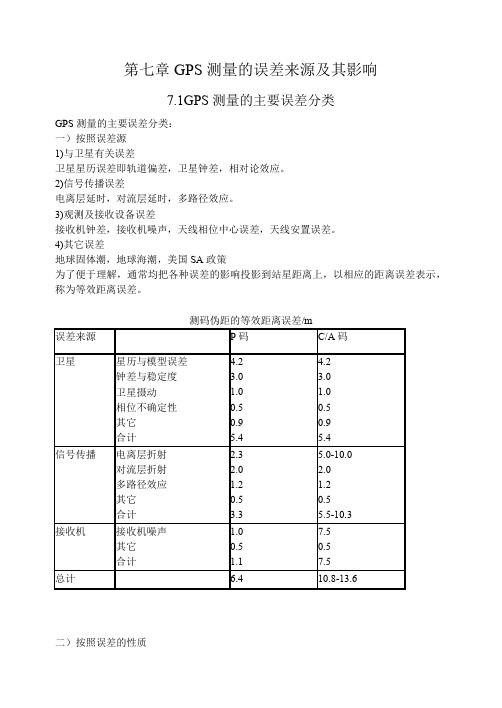
第七章GPS测量的误差来源及其影响7.1GPS测量的主要误差分类GPS测量的主要误差分类:一)按照误差源1)与卫星有关误差卫星星历误差即轨道偏差,卫星钟差,相对论效应。
2)信号传播误差电离层延时,对流层延时,多路径效应。
3)观测及接收设备误差接收机钟差,接收机噪声,天线相位中心误差,天线安置误差。
4)其它误差地球固体潮,地球海潮,美国SA政策为了便于理解,通常均把各种误差的影响投影到站星距离上,以相应的距离误差表示,称为等效距离误差。
测码伪距的等效距离误差/m二)按照误差的性质1、系统误差 包含:轨道误差、钟差、大气折射。
减弱方法:1)作为未知参数一并解算;2)建立误差模型,对观测量加于修正。
3)同步观测求差法;4)简单忽略。
2、偶然误差 包含:多路径效应、观测误差减弱方法:从观测技术、手段、方法上,严格操作。
7.2与信号传播有关的误差与卫星信号有关的误差主要包括大气折射误差和多路径效应。
7.2.1电离层折射的影响电离层属于弥散性介质,即电磁波的传播速度和频率有关。
GPS 卫星信号通过电离层时,将受到这一介质弥散特性的影响,便其信号的传播路径发生变化。
电离层会反射、折射、散射、吸收无线电信号,导致无线电信号的延迟以及相位、振幅的不规则变化等。
特征:电离层延迟与信号频率的平方成反比关系,即:2211f f t I ∝∝δδI δ为距离延迟;t δ为时间延迟 当GPS 卫星处于天顶方向时,电离层折射对信号传播路径的影响最小,而当卫星接近地平线时,则影响最大。
为了减弱电离层的影响,在GPS 定位中通常采用下面措施 (1)利用双频观测由于电离层的影响是信号频率的函数,所以利用不同频率的电磁波信号进行观测。
便能多确定其影响,而对观测量加以修正。
2211212211)(54573.2)(54573.1dion S dion S dion dion +=+=-=-=ρρρρρρ(7-1)(2)利用电离层模型加以修正对于单频GPS 接收机,为了减弱电离层的影响,一般是采用导航电文提供的电离层模型,或其它适合的电离层模型对观测量加以修正,但是这种模型至今仍在完善之中,目前模型改正的有效率约为75%。
GPS测量的误差来源及其影响

R NedR
dion
用➢
➢电离层改正的大小 主要取决于电子总量 和信号频率
dion c 40.28
f2
R N e dR
6
电离层对载波影响
G
P
S 测
•载波是正弦波 •在电离层中以相速度传播
ng 1 40.28Nf 2
量 原
dion tc 40.28
f2
R N e dR
理
及
•电离层影响与太阳黑子活动有关
理
3
及
A
n
n m
应
n0 3
用
n
n0
m 为地磁强度
模型改正的有效率约为75%
9
G P S 测 量 原 理 及 应
用
10
G P S 测 量 原 理 及 应
用
11
➢利用同步观测值求差
G
P ⑴二站同 S 步观测求
测差
量 原 理
⑵电离层 折射影响 显著减弱
及
应 相距 ≦20km
用 ⑶单频机
常采用的
应
卫星的地心距近似取26560k m,则
f2 5.2841010 f
用 – 结论:在广义相对论效应作用下,卫星上钟的频率将
变快
28
相对论效应对卫星钟的影响③
G
P • 相对论效应对卫星钟的影响
S 测
– 狭义相对论+广义相对论
量 原
令:f1 fs
理
在狭义相对论效应和广义相对论效应的共同作用下,卫星上
S
测
量
原
理
及
应
用
•差分方法也可以消除
14
关于对流层折射的影响,一般有以下几种处理方法:
第七章GPS测量误差及其影响

星历误差的大小 主要取决于卫星跟踪系统的质量(
如跟踪站的数量及空间分布;观测值的数量及精度,轨道计 算时所用的轨道模型及定轨软件的完善程度等)。此外和星 历的预报间隔(实测星历的预报间隔可视为零)也有直接关 系。由于美国政府的SA技术,星历误差中还引入了大量人为 原因而造成的误差,它们主要也呈系统误差特性。 卫星星历误差对相距不远的两个测站的定位结果产生的 影响大体相同,各个卫星的星历误差一般看成是互相独立的 。然而由于SA技术的实施,这一特性很可能破坏。
当观测量较少时,增加估计参数很容易导致方 程病态,使解算结果不准确。
回避法
原理:选择合适的观测地点,避开易产生 误差的环境;采用特殊的观测方法;采 用特殊的硬件设备,消除或减弱误差的 影响 适用情况:对误差产生的条件及原因有所 了解;具有特殊的设备。如对于电磁波 干扰、多路径效应等的应对方法等。
7.2 与卫星有关的误差
实测星历(精密星历) 实测星历(精密星历)
实测星历(精密星历)是根据实测资料进行事后处理 而直接得出的星历,精度较高。这种星历用于进行精密定 位的事后处理,对于提高精密定位精度,减少观测时间和 作业费用等具有重要作用,还可以使数据处理较为简便。 由于这种星历要在观测后一段时间(例如1~2个星期)才 能得到,所以对导航和实时定位无任何意义。 目前,许多国家和组织都在建立自己的GPS卫星跟踪网 开展独立的定轨工作。如由国际大地测量协会(IAG)第 八委员会领导的国际GPS协作网(CIGNET),Aero Service的GPS跟踪网等。
1) 忽略卫星钟的数学同步误差 导航和低精度的单点定位 2)利用测码伪距单点定位法来确定接收机的钟差 解算接收机接收瞬间的钟差 3)通过获取精确的卫星钟差值 通过IGS获得精确的卫星钟差 4)通过差分方法来消除公共的钟差项 载波相位测量
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.4
G P S 测 量 原 理 及 应 用
中 南 大 学
接收机有关误差
观测误差
约为信号波长的1% 约为信号波长的1% •天线的安置对中误差以及量取天线高的误差 天线的安置对中误差以及量取天线高的误差
•观测的分辨误差 观测的分辨误差
接收机的钟差
•作为未知数求解 作为未知数求解 •利用多项式钟差模型改正 利用多项式钟差模型改正 •星间差分可消除 星间差分可消除
中 南 大 学
•二站同步 观测求差 •电离层折 射影响显著 减弱 •相距 ≦20km •单频机常 采用的方法
G P S 测 量 原 理 及 应 用
中 南 大 学
7.2.2 对流层影响
从地面到高空40KM大气层 大气层 从地面到高空 为对流层; 为对流层; 电磁波经过对流层会产生 延 和温度、湿度、 迟,和温度、湿度、气压有 关; 天顶方向可达2.3m, , 天顶方向可达 高度角10 可达13m。 高度角 o,可达 。
电离层对C/A码影响 码影响 电离层对
G P S 测 量 原 理 及 应 用 •C/A码是方波 码是方波
ng = 1+ 40.28Nf
−2
•在电离层中以 在电离层中以 群速Vg传播 群速
c Vg = = c(1− 40.28Nf −2 ) ng
中 电离层改正的大小 南 •电离层改正的大小 大 主要取决于电子总 学 量和信号频率
G P S 测 量 原 理 及 应 用
中 南 大 学
第七章 GPS测量的误差来源及 测量的误差来源及 其影响
7.1 GPS测量主要误差分类 测量主要误差分类 测量主要
G P S 测 量 原 理 及 应 用
中 南 大 学
一、与卫星有关误差 三、观测及接收设备误差
卫星星历误差: 卫星星历误差:轨道偏差 卫星钟差 相对论效应 接收机钟差 接收机噪声 天线相位中心误差 天线安置误差
2
中 南 Ws −WT 1 1 µ f = 2 f( − ) 大 ∆f 2 = 2 R r C C 学
广义相对论
= 5.284 ×10 f
10
总的影响
∆f = ∆f1 + ∆f 2 = 4.449×10−10 f
卫星时钟频率预调为10.23MHz ×(1-4.449×10-10)=10.22 999 999 545 原 理 及 应 用
中 南 大 学
卫星轨道误差处理方法
•忽略轨道误差 忽略轨道误差 •建立自己的卫星跟踪网独立定轨 建立自己的卫星跟踪网独立定轨 •采用轨道改进法处理观测数据 采用轨道改进法处理观测数据 •同步观测值求差 同步观测值求差
7.3.2 卫星钟误差
G P S 测 量 原 理 及 应 用
减弱电离层影响方法
G P S 测 量 原 理 及 应 用
中 南 大 学
利用双频观测 令 A = −C × 40.28∫ Neds
S = ρ1 + A/ f12
s′
S = ρ2 + A/ f 22
A A A f12 − f22 ∆ρ = ρ1 − ρ2 = 2 − 2 = 2 ( ) 2 f1 f2 f1 f2 f1 2 = dion1[( ) −1] = 0.6469 dion1 f2
G P S 测 量 原 理 及 应 用
中 南 大 学
7.5.2 地球潮汐改正
主要是固体潮和海潮的影响,可使测站的位移达到80cm。 主要是固体潮和海潮的影响,可使测站的位移达到80cm。 80cm 引起的测站的位移值
n U3 hi′σ i U2 δ r = h2 g + h3 g + 4πGR ∑ ( 2i + 1) g i =1 ∂U 3 4πGR n li′ ∂σ i l2 ∂U 2 + l3 + δ ϕ = ∑ 2i + 1 ∂ϕ g ∂ϕ ∂ϕ g i =1 ∂U 3 4πGR n li′ ∂σ i l2 ∂U 2 δ = λ g ∂λ + l3 ∂λ + g ∑ 2i + 1 ∂λ i =1
中 南 大 学
7.5 其它误差
7.5.1 地球自转的影响 旋转角
∆α = ω∆τ i < 1.5′′
j
∆X 0 卫星的瞬时 坐标改正 : ∆Y = − ∆α ∆Z 0
∆α 0 0
0 X j Y j 0 Z j 0
二、信号传播误差
电离层延时 对流层延时 多路径效应
四、其它误差
地球自转的影响 地球固体潮、 地球固体潮、海潮
G P S 测 量 原 理 及 应 用
中 南 大 学
7.2 与信号传播有关误差
7.2.1 电离层 折射
由地面50由地面5050 1000km高空中由 1000km高空中由 太阳幅射造成气 体电离形成电离 层。电磁波信号 经过电离层速度 发生变化。 发生变化。
dion1 =1.54573(ρ1 − ρ2 ) dion2 = 2.54573(ρ1 − ρ2 )
S = ρ1 + dion1
利用电离层模型加以修正(Klobachar) 利用电离层模型加以修正
G P S 测 量 原 理 及 应 用
中 南 大 学
Klobachar电离层模型: 电离层模型: 电离层模型
讨论:应用非差模型进行高精度定位时,主要考虑哪些误差 的影响?
G P S 测 量 原 理 及 应 用
中 南 大 学
本章小结
GPS定位误差主要分为:与卫星有关、与传播路 径有关、与接收机有关的误差和其他影响; 其减弱与消除办法主要分为: •利用模型改正 对流层延迟、电离层延迟、卫星钟差、相对 论的影响、地球自转影响、地球潮汐的影响。 •利用观测值的线性组合 差分消除对流层、电离层误差、轨道误差影 响、卫星钟差的残差等。 •作为未知参数参与平差或其他方法 接收机钟差作为未知数,天线相位中心的改正 选择合适的观测环境和时间避开一些不利因素。
−2
•在电离层中以相速度传播 在电离层中以相速度传播
40.28 dion = tc 2 ∫ R Ne dR f
•电离层影响与太阳黑子活动有关 电离层影响与太阳黑子活动有关
•与卫星到接收机方向有关,天顶方向最大50m延迟 与卫星到接收机方向有关,天顶方向最大 与卫星到接收机方向有关 延迟 高度角20° 高度角 °时150m延迟 延迟
Tg = Dc + A cos
3
2π (t − Tp ) P DC = 5ns, TP = 14h
n A = ∑ α nϕ m n =0 3
ρ = ∑ β nϕ
n =0
ϕ m 为地磁纬度
模型改正的有效率约为75% 模型改正的有效率约为75% 75
利用同步 观测值求差
G P S 测 量 原 理 及 应 用
7.3.3 相对论效应
G P S 测 量 原 理 及 应 用
相对论效应: 相对论效应:由于卫星钟和接收机钟
所处运动状态和重力位不同引起卫星钟和 接收机钟之间产生相对钟误差的现象 。
狭义相对论
Vs 2 12 Vs f s = f [1− ( ) ] = f (1− 2 ) c 2c
2
Vs ∆f s = f s − f = − 2 2c
G P S 测 量 原 理 及 应 用
中 南 大 学
目前减弱多路径效应影响的措施
安置接收机天线的环境, 安置接收机天线的环境,应避开较强的反射面 ; 选择造型适宜且屏蔽良好的天线等 ; 适当延长观测时间, 适当延长观测时间,削弱多路径效应的周期性影响 ; 改善GPS接收机的电路设计, 改善GPS接收机的电路设计,为了减 GPS接收机的电路设计 弱多路径效应的影响 ; 建立适当的改正模型。 建立适当的改正模型
天线的相位中心位置偏差
•检测其大小并加以改正(应小于5mm) 检测其大小并加以改正(应小于5mm) 检测其大小并加以改正 5mm •按天线附有的方位标进行定向 按天线附有的方位标进行定向 •同步观测求差,以削弱相位中心偏移的 同步观测求差, 同步观测求差 影响
G P S 测 量 原 理 及 应 用
中 南 大 学
卫星钟有偏差和漂移, 1ms,相当于300km; 卫星钟有偏差和漂移,差1ms,相当于300km; 300km 导航电文中提供修正模型
∆t = a0 + a1(t − t0 ) + a2 (t − t0 )
s
2
为参考历元, t0为参考历元, 改正后可达到20ns 20ns, 6m误差 改正后可达到20ns,约6m误差 二站同步观测相对定位可消除其影响
G P S 测 量 原 理 及 应 用
中 南 大 学
7.3 与卫星有关的误差
7.3.1 卫星星历误差
广播星历: 广播星历:由地面监测站测定卫星轨道外推轨道,精度25m。 精密星历:实测后处理提供星历,精度优于5cm 精密星历: IGS站上可获取。 星历对定位影响
ds
db ds 20m = = = 1ppm b ρ 20万km
对流层改正模型
G P S 测 量 原 理 及 应 用
中 南 大 学
模型: 如Hopfield 模型: (注意各参数的单位 )
Kd KW δp = + 2 1/ 2 Sin( E + 0.25) Sin( E 2 + 2.25)1/ 2 −7 P s K d = 155.2 ×10 (hd − hs ) Ts KW = 155.2 ×10 hW = 11000m
40.28 R = ∫ ∆tVg dt = ρ − c 2 ∫ R NedR f •其速度与频率有关 其速度与频率有关 = ρ + dion
40.28 dion = −c 2 ∫ R Ne dR f
