1.2同位角、内错角、同旁内角
合集下载
1.2 同位角、内错角、同旁内角

思考 上图中有几对同位角,几对内错角,几对同旁内角?
课堂讲解 1.同位角、内错角、同旁内角的概念和识别
【典例 1】 如图 1.2-1,∠1,∠2,∠3 分别与∠A 是由 哪两条直线被第三条直线所截构成的什么角?
图 1.2-1
【点拨】 在复杂图形中确定角的位置关系及截线和被 截线时,应避开无关的线、角进行分析,分解出“三线 八角”的基本图形(如图 1.2-2),以便观察.
()
A.∠2 C.∠4
(第 2 题) B.∠3 D.∠5
【解】 ∠1 与∠2 是对顶角,∠1 与∠3 是同位角,∠1 与∠4 是内错角,∠1 与∠5 是同旁内角,故选 D.
【答案】 D
3.如图,AB,CD 相交于点 O.若∠1=∠2,则图中和
∠1 相等的角还有
,和∠1 互补的角
有
.
(第 3 题)
【解】 ∵∠1=∠2,∠2=∠BOD,∠2+∠BOC=180 °,∠2+∠AOD=180°, ∴∠1=∠BOD,∠1+∠BOC=180°,∠1+∠AOD= 180°. 【答案】 ∠BOD ∠BOC 和∠AOD
按时完成B本P2-P3课后训练
点此进入
图 1.2-3 【点拨】 若三条直线两两相交,则任何一条直线都可以 看做是截线,故有时需分类讨论. 【解析】 ∠1 的同 位角 应与∠1 有一 条公 共边 DE 或 BC.若公共边是 DE,则 DE 为截线,BA,BC 为被截线, 此时∠1 的同位角是∠5;若公共边是 BC,则 BC 为截线, DE,BA 为被截线,此时∠1 的同位角是∠B.同理, ∠B 的同旁内角也有两个,分别是∠2,∠3.
2.同位角、内错角、同旁内角的相关计算
【典例 3】 如图 1.2-4,直线 l2,l3 被直线 l1 所截.若∠1 =∠2,请你说出下列各对角的数量关系,能说明理 由的尽量说明理由.
课堂讲解 1.同位角、内错角、同旁内角的概念和识别
【典例 1】 如图 1.2-1,∠1,∠2,∠3 分别与∠A 是由 哪两条直线被第三条直线所截构成的什么角?
图 1.2-1
【点拨】 在复杂图形中确定角的位置关系及截线和被 截线时,应避开无关的线、角进行分析,分解出“三线 八角”的基本图形(如图 1.2-2),以便观察.
()
A.∠2 C.∠4
(第 2 题) B.∠3 D.∠5
【解】 ∠1 与∠2 是对顶角,∠1 与∠3 是同位角,∠1 与∠4 是内错角,∠1 与∠5 是同旁内角,故选 D.
【答案】 D
3.如图,AB,CD 相交于点 O.若∠1=∠2,则图中和
∠1 相等的角还有
,和∠1 互补的角
有
.
(第 3 题)
【解】 ∵∠1=∠2,∠2=∠BOD,∠2+∠BOC=180 °,∠2+∠AOD=180°, ∴∠1=∠BOD,∠1+∠BOC=180°,∠1+∠AOD= 180°. 【答案】 ∠BOD ∠BOC 和∠AOD
按时完成B本P2-P3课后训练
点此进入
图 1.2-3 【点拨】 若三条直线两两相交,则任何一条直线都可以 看做是截线,故有时需分类讨论. 【解析】 ∠1 的同 位角 应与∠1 有一 条公 共边 DE 或 BC.若公共边是 DE,则 DE 为截线,BA,BC 为被截线, 此时∠1 的同位角是∠5;若公共边是 BC,则 BC 为截线, DE,BA 为被截线,此时∠1 的同位角是∠B.同理, ∠B 的同旁内角也有两个,分别是∠2,∠3.
2.同位角、内错角、同旁内角的相关计算
【典例 3】 如图 1.2-4,直线 l2,l3 被直线 l1 所截.若∠1 =∠2,请你说出下列各对角的数量关系,能说明理 由的尽量说明理由.
1.2 同位角、内错角、同旁内角 课件1(浙教版七下)

F C
(2)如果把图看成是直线CD,EF被直线AB所截, 那么∠1与∠5是一对什么角? (同旁内 角) ∠4与∠5呢? (
A
E B
5
2
3
F C
(3)哪两条直线被哪一条直线所截,∠2与∠5 是同位角? (直线AB和CD被直线EF所截)
例2
如图:直线DE交∠ABC的边BA于 点 F. 如果内错角∠1与∠2相等,那么你 能找出图中其它相等的角吗?请说明理 同位角∠1与∠4相等 由。 有互补的角吗?
①在直线EF的同侧
②在直线AB、CD的内侧
1
3 4
B
4
A
6
5
7 8
5
C
D
F
∠ 3和 ∠ 6
如图:直线a、b被直线 l 截的8个角中
1
a b 5
l 2
同位角:∠1与∠5;
4
6 7
3
∠2与∠6; ∠4与∠8; ∠3与∠7.
内错角:∠3与∠5;
∠4与∠6.
8
同旁内角: ∠4与∠5; ∠3与∠6.
同位角、内错角和同旁内角的结构特征:
l3
2 1 3 4 6 5 7 8
l1
l2
如图:两只手的食子和拇 指在同一平面内,它们构 成的一对角可以看成是什 么角?类似地,你还能用 两只手的手指构成同位角 和同旁内角吗?
例1 如图,直线DE截AB,AC,构成8个角。指出
所有的同位角、内错角和同旁内角。 1.若DE,AB被AC所截呢?
2.若DE,AC被AB所截呢?
关键:要先分 清哪两条直线 被哪一条直线 所截
D
2 3 4 1
A
5 6
8 7
E C
1.2同位角 内错角 同旁内角

旁内角?
9
a
6 7 8 5 2
b
1
3
4
c
分 离 基 本 图 形 法
变式2:∠9与∠2是哪两条 线被哪一条线所截形成的一 对什么角?∠9与∠6呢?
9
a
b b
2
3
c
6
7 8
5
1
4
c
c
变式3:图中共有几对同位角? 按截线分类讨论:
a b
c
“手”可以千变万化, 能“变”出很多美妙的图形!
例2:如图,直线DE与BC被直线AB所截。 (1)1 与 2 、 1 与 3 、 1与 4 各是 一对什么角?
1
2
1
2
(1)来自( 1)2
2
(
)
(
)
让我们一起来归纳
完成学习单
两条直线被第三条直线所截
同位角
1
同旁内角
内错角
2
1
2
形状 边的 特征
F
U
Z
两个角有一条边共截线.
变式1:已知直线a,c被直线b 例1:已知直线a,b被c所 直线a,c被直线b 注意:上述三类关系角类似于 所截 所截,∠9与∠1是一对什么 截,指出所有的同位角、 对应角都是成对出现。不能说 哪个角是同位角、内错角、同 关系的角?∠9与∠3呢? 内错角、同旁内角.
1.2 同位角、内错角、同旁内角
c
2 1 4 5
已知直线a、b被c所截,观 察∠1与∠5 的位置特征? c
同位角
1
3
a b
4 5
a b 两直线a、b 的同侧
6
7
8
截线c的同旁
∠1与∠5是直线a、b被直线c所截形 你还发现哪些同位角? 成的同位角. c
9
a
6 7 8 5 2
b
1
3
4
c
分 离 基 本 图 形 法
变式2:∠9与∠2是哪两条 线被哪一条线所截形成的一 对什么角?∠9与∠6呢?
9
a
b b
2
3
c
6
7 8
5
1
4
c
c
变式3:图中共有几对同位角? 按截线分类讨论:
a b
c
“手”可以千变万化, 能“变”出很多美妙的图形!
例2:如图,直线DE与BC被直线AB所截。 (1)1 与 2 、 1 与 3 、 1与 4 各是 一对什么角?
1
2
1
2
(1)来自( 1)2
2
(
)
(
)
让我们一起来归纳
完成学习单
两条直线被第三条直线所截
同位角
1
同旁内角
内错角
2
1
2
形状 边的 特征
F
U
Z
两个角有一条边共截线.
变式1:已知直线a,c被直线b 例1:已知直线a,b被c所 直线a,c被直线b 注意:上述三类关系角类似于 所截 所截,∠9与∠1是一对什么 截,指出所有的同位角、 对应角都是成对出现。不能说 哪个角是同位角、内错角、同 关系的角?∠9与∠3呢? 内错角、同旁内角.
1.2 同位角、内错角、同旁内角
c
2 1 4 5
已知直线a、b被c所截,观 察∠1与∠5 的位置特征? c
同位角
1
3
a b
4 5
a b 两直线a、b 的同侧
6
7
8
截线c的同旁
∠1与∠5是直线a、b被直线c所截形 你还发现哪些同位角? 成的同位角. c
1.2同位角、内错角、同旁内角

A D B F
2 3 1 4
解:∵∠1=∠2 (已知)
E
∠2=∠4 (对顶角相等) ∴∠1=∠4
C ∵∠2+∠3=180° (已知)
∴∠1+∠3=180° 海亮外国语学校初中数学教研组 20
巩固提升:
E
D C
根据个人需求 添加(如:本 页所讲知识点 等)
A F
B
请找出图中所有的同位角、内错角和同旁内角。
浙教版七年级 (下册)
第一章第二节 《同位角、内错角、同旁内 角 》
1
海亮外国语学校初中数学教研组
1.平面上两条直线有哪两种位置关系?
根据个人需求 添加(如:本 页所讲知识点 等)
平行和相交 传说中的
2.两条直线相交有几个角 “ 线 ?这些角之间有哪些 角图 位置关系?
三 八
形成4个角;对顶角 3.两条直线与第三条直线相交呢?
,那么∠1与∠2是一对什么角?同位角
∠3与∠4呢? 内错角 同旁内角
13
∠2与∠4呢?
海亮外国语学校初中数学教研组
练一练
E B
5
D
1 4
A
根据个人需求 添加(如:本 页所讲知识点 等)
2
3
F C
(2)如果把图看成是直线CD,EF被直线AB所截 ,那么∠1与∠5是一对什么角? 同旁内角 ∠4与∠5呢?
海亮外国语学校初中数学教研组
21
小结
1.同位角 2.内错角
XXXXXXX
3.同旁内角
22
XXXXXXXXXXXXX XXXXXXXX
海亮外国语学校初中数学教研组
14
内错角
海亮外国语学校初中数学教研组
同位角,内错角,同旁内角的规律

同位角,内错角,同旁内角的规律
同位角、内错角、同旁内角是三角形中的特殊角度关系。
同位角(对顶角):同位角是指两条平行线被一条直线截断时,直线与平行线之间的对应角,它们的度数相等。
内错角:内错角是指两条平行线被一条直线截断时,直线与平行线之间的交叉角,它们的度数相等。
同旁内角:同旁内角是指两条平行线被一条直线截断时,直线两侧同旁相对的角,它们的度数之和为180度。
总结规律:
1. 同位角的度数相等;
2. 内错角的度数相等;
3. 同旁内角的度数之和为180度。
这些规律在解决平行线相关问题时很有用,可以通过利用这些关系来推导、求解未知的角度。
同位角内错角同旁内角

1.2 同位角,内错角,同旁内角
一、创设情景
1.1 同位角,内错角,同旁内角
平面上,两条直线有相交和平 行两种位置关系.
1.1 同位角,内错角,同旁内角
l
a
直线a、b被直线l所截.
b
1.1 同位角,内错角,同旁内角
直线a、b被直线l所截,有几对对 顶角,它们分别是哪些角?
b
α
有4对对顶角, ∠2与∠4,∠5与∠7,∠6 与∠8, ∠1和∠3分别是对顶角.
l
1
2
3 4
56 87
二、探索交流 1 观察交流
l
12
b
3 4
从直线 l 来看,∠1与∠5处于哪个位置? 5 6
∠1与∠5处于直线 l 的同一侧. α
87
对于直线a、b,∠1与∠5又处于哪个位置?
1
∠1与∠5都处于直线a、b的同一方.
这样的一对角( ∠1与∠5 )就是同位角. 5
图中的同位角还有哪些?
学校与游乐场所在的角 形成一(同位角 )角
学校与超市所在的角形 成一对( 同旁内角 )角
学校与飞机场所在的角 形成一对( 内错角 )角
游乐 场
超市 学校 学
解放路
马 人飞机场
鞍 民
池 路
路
六、例题精讲
例2 如图,直线DE交∠ABC的边BA于点 F,如果∠1=∠2,那么:
F
①同位角∠1和∠4相等,
②同旁内角∠1和∠3互补。
b
这样的一对角( ∠4与∠6 )就是内错角
l
12 3
4
56 87
图中的内错角还有哪些? 内错角还有∠3与∠5.
4
6
(Z型)
三、类比交流 变式图形:图中的∠1与∠2都是内错角.
一、创设情景
1.1 同位角,内错角,同旁内角
平面上,两条直线有相交和平 行两种位置关系.
1.1 同位角,内错角,同旁内角
l
a
直线a、b被直线l所截.
b
1.1 同位角,内错角,同旁内角
直线a、b被直线l所截,有几对对 顶角,它们分别是哪些角?
b
α
有4对对顶角, ∠2与∠4,∠5与∠7,∠6 与∠8, ∠1和∠3分别是对顶角.
l
1
2
3 4
56 87
二、探索交流 1 观察交流
l
12
b
3 4
从直线 l 来看,∠1与∠5处于哪个位置? 5 6
∠1与∠5处于直线 l 的同一侧. α
87
对于直线a、b,∠1与∠5又处于哪个位置?
1
∠1与∠5都处于直线a、b的同一方.
这样的一对角( ∠1与∠5 )就是同位角. 5
图中的同位角还有哪些?
学校与游乐场所在的角 形成一(同位角 )角
学校与超市所在的角形 成一对( 同旁内角 )角
学校与飞机场所在的角 形成一对( 内错角 )角
游乐 场
超市 学校 学
解放路
马 人飞机场
鞍 民
池 路
路
六、例题精讲
例2 如图,直线DE交∠ABC的边BA于点 F,如果∠1=∠2,那么:
F
①同位角∠1和∠4相等,
②同旁内角∠1和∠3互补。
b
这样的一对角( ∠4与∠6 )就是内错角
l
12 3
4
56 87
图中的内错角还有哪些? 内错角还有∠3与∠5.
4
6
(Z型)
三、类比交流 变式图形:图中的∠1与∠2都是内错角.
同位角、内错角、同旁内角七年级数学下册

练一练
A
1、
1 2
B
C 4
3
D
(1)∠1的内错角是 ∠3 ;同旁内角是 ∠4,∠A。
(2)∠2的内错角是 ∠4;同旁内角是 ∠3, ∠D 。
同位 内 同旁
2、(1)如果把图看成是直线AB, EF被直线CD所截,那么∠1与
∠2是一对什么角?
∠3与∠4呢?∠2与∠4呢?
∠1与∠2是一对同位角, ∠3与∠4是一对内错角, ∠2与∠4是一对同旁内角.
D
A
1
4
E5
2
3F
(2如果把图看成是直线CD,
EF被直线AB所截,
B
C
那么∠1与∠5是一对什么角(3?) 哪两条直线被哪一条直线所截,
∠4与∠5呢?
∠ 2与∠ 5是同位角
∠1与∠5是一对同旁内角, 直线AB,CD被直线EF所截 ∠4与∠5内错角.检来自:1、根据图形按要求填空:
(1)∠1与∠2是直线 A
如图,直线DE、BC被直线AB所截。 (1)∠1与∠2、∠1与∠3、∠1与∠4各是什么角?
(2)如果∠1=∠4,那么∠1和∠2相等吗? A
∠1和∠3互补吗?为什么?
D
4
E
解:⑴ ∠1与∠2是内错角、
23
∠1与∠3是同旁内角、 ∠1与∠4是同位角。 B
1
C
⑵ 如果∠1=∠4
∵∠4+∠3=180 °(邻补角互补)
AB与DE 被AC所截, 是同旁内角
∠A与∠4呢?
AC与DE 被AB所截, 是同位角
D
2 1
3
4
B
58
67 E
C
例3:∠1与∠2是不是同位角? a
1.2同位角、内错角、同旁内角
1 B A C 3 2 C D
4
A
1 B
3 4 2 C
D
B
5.看图填空: (1)若ED,BF被AB所截, 则∠ 1与 ∠2 是同位角;
B E 1 3 2
A
D 4 F C
(2)若ED,BC被AF所截, 则∠3与 ∠4 是内错角;
(3)∠1与∠3是AB和AF被 ED 所截 构成的 内错 角; (4)∠2 与∠4是 AB 和 AF BC所截构成的 同位 角。 被
3
2 1 4
5
6
8 7
E
C
注意:
B
解题关键是明确哪两条直线被哪条直线所截!
例2 如图,直线DE交∠ABC的 边BA于点 F. 如 果内错角∠1与∠2相等,求证:同位角∠1与 ∠4相等,同旁内角∠1与∠3互补。
A
D
2
F
3
4
E
1
B
C
“同位角相等、内错角相等、同旁内角互补” 这三者中若有一个成立,则另两个也成立!
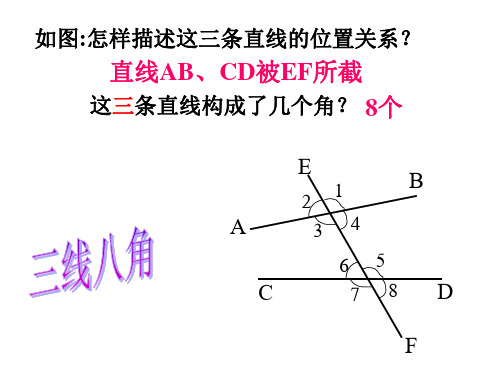
如图:怎样描述这三条直线的位置关系?
直线AB、CD被EF所截
这三条直线构成了几个角? 8个 E
2
1
3 4
B
A
6
5
7 8
C
D F
1.2同位角、内错角、同旁内角
同位角、内错角和同旁内角的结构特征:
l3
2 1 3 4 6 5 7 8
l1
l2
截线 同旁 两旁 同旁 被截线 同侧 之间 之间 结构特征
同位角 内错角 同旁内角
A C
B D
H
F
说能出你这节课的收获和体验让大家
与你分享吗?
随堂练习
AB 与直线____ CD 被直线______ BD 1、如图,(1) 和 是直线_____ 内错角 。 所截形成的__________
4
A
1 B
3 4 2 C
D
B
5.看图填空: (1)若ED,BF被AB所截, 则∠ 1与 ∠2 是同位角;
B E 1 3 2
A
D 4 F C
(2)若ED,BC被AF所截, 则∠3与 ∠4 是内错角;
(3)∠1与∠3是AB和AF被 ED 所截 构成的 内错 角; (4)∠2 与∠4是 AB 和 AF BC所截构成的 同位 角。 被
3
2 1 4
5
6
8 7
E
C
注意:
B
解题关键是明确哪两条直线被哪条直线所截!
例2 如图,直线DE交∠ABC的 边BA于点 F. 如 果内错角∠1与∠2相等,求证:同位角∠1与 ∠4相等,同旁内角∠1与∠3互补。
A
D
2
F
3
4
E
1
B
C
“同位角相等、内错角相等、同旁内角互补” 这三者中若有一个成立,则另两个也成立!
如图:怎样描述这三条直线的位置关系?
直线AB、CD被EF所截
这三条直线构成了几个角? 8个 E
2
1
3 4
B
A
6
5
7 8
C
D F
1.2同位角、内错角、同旁内角
同位角、内错角和同旁内角的结构特征:
l3
2 1 3 4 6 5 7 8
l1
l2
截线 同旁 两旁 同旁 被截线 同侧 之间 之间 结构特征
同位角 内错角 同旁内角
A C
B D
H
F
说能出你这节课的收获和体验让大家
与你分享吗?
随堂练习
AB 与直线____ CD 被直线______ BD 1、如图,(1) 和 是直线_____ 内错角 。 所截形成的__________
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)两个角有一边在同一直线上,则这条直线就是截线,其余两边所在的直线是两直线。
2、练一练、
课本第7页做一做1.课内练习1
例如图,直线DE交∠ABC的边BA于点F,如果 ∠1=∠2,那么同位角∠1和∠4相等,同旁内角∠1和∠3互补。请说明理由
分析:如果∠1=∠2,由对顶角相等,得∠2=∠4,那么∠1=∠4。因为∠2与∠3互补,即∠2+∠3=180°,又因为∠1=∠2,所以∠1+∠3=180°,即∠1和∠3互补。
应用拓展
(1)第8页课内练习2
(2)图中,∠1与∠2,∠3与∠4各是哪一条直线截哪两条直线而成的?它们各是什么角?
小结:
本讲主要讲述了同位角、内错角、同旁内角的概念以及识别它们的方法:
【活动6】作业
作业本1
对顶角指的两条直线相交成胡角
同位角,内错角,同旁内角指的是两组角之间的关系
同位角、内错角、同旁内角都是两条直线被第三条直线所截时产生的,究其实质,它们主要是反映了直线相交产生的角中,相互位置所具有的特征:(1)两个同位角就是与直线的位置关系而言具有“同上、同右”、“同上、同左”“同下、同右”或“同下、同左”的特征。(2)内错角具有“同内、异侧”的特征。(3)同旁内角具有“同内、同侧”的
1.2同位角、内错角、同旁内角
教学目标:
知识与技能目标:了解同位角、内错角、同旁内角的概念。
过程与方法目标:会识别同位角、内错角、同旁内角。
情感与态度目标:在活动中培养学生乐于探索、合作学习的习惯,培养学生“用数学”的意识和能力。
教学重点:重点:已知两直线和截线,判断同位角、内错角、同旁内角。
教学难点::已知两个角,要判别是哪两条直线被第3条直线所截而形成的什么位置关系的角
变式图形:图中的∠1与∠2都是同位角。
图形特征:在形如字母“F”的图形中有同位角。
2、再看∠3与∠5,这两个角都在直线AB、CD之间,且∠3在直线EF左侧,∠5在直线EF右侧,像这样的一对角叫做内错角。同样,∠4与∠6也具有类似位置特征,∠4与∠6也是内错角。
变式图形:图中的∠1与∠2都是有内错角。
请用三根竹条或小木棍制作一个如图的风筝骨架,观察风筝骨架中(图自己画)有几个角,请把它画成几何图形,并用符号表示这些角,然后分别指出所有的对顶角,同位角,内错角,同旁内角
归纳:(1)寻找同位角,内错角,同旁内角关键要分清两条直线和截线,然后按相互的位置特征进行判别
(2)归纳:变式是例题的逆向思维,即已知两角,如何寻找两直线和截线,引导学生得出
3、在图(1)中,∠3和∠6也在直线AB、CD之间,但它们在直线EF的同一旁像这样的一对角,我们称它为同旁内角。具有类似的位置特征的还有∠4与∠5,因此它们也是同旁内角。
变式图形:图中的∠1与∠2都是同旁内角。
图形特征:在形如“N”的图形中有同旁内角。
4、辩一辩
5,做一做(请一位学生上台展示学习成果)
掌握辩别这些角的关键是看哪两条直线被哪一条直线所截、分清哪一条直线截哪两条直线形成了哪些角,是作出正确判定的前提,在截线的同旁找同位角,同旁内角,在截线的不同旁,找内错角。特征。
板书设计:
后记:①辨别三种角抓住角的特征,分清截线被截线
②复杂图像采取分离法还是比较成功的
③給角的关系判断截线和被截线还有部分学生不会
(3)两条直线被第3条直线所截形成几个角?这8个角中有多种关系,
如∠2与∠4,∠5与∠7,∠6与∠8,∠1和∠3是对顶角,除了对顶
角,还有没有其它新的关系的角呢?这节课我们就来研究同位角,内错角,同旁内角。
合作交流,探索新知
1、先看图中∠1和∠5,这两个角分别在直线AB、CD的上方,并且都在直线EF的右侧,像这样位置相同的一对角叫做同位角。在图(1)中,像这样具有类似位置关系的角还有吗?如果你仔细观察,会发现∠2与∠6,∠3与∠7,∠4与∠8也是同位角。
关键:弄清是哪两条直线被第三条直线所截而成的同位角、内错角、同旁内角。
教学过程:
教学设计
备注
创设情景,引入新课
(1)平面上的两条直线有相交和平行两种位置关系,两直线相交形成几个角?称之谓什么角?
(2)在实际生活中,还存在着两条直线被第3条直线所截的情况,如斜拉桥的灯柱子与其横梁,脚手架的钢管,交通线路中的道路,将这些事物抽象成几何图形,就是如图所示的图形
2、练一练、
课本第7页做一做1.课内练习1
例如图,直线DE交∠ABC的边BA于点F,如果 ∠1=∠2,那么同位角∠1和∠4相等,同旁内角∠1和∠3互补。请说明理由
分析:如果∠1=∠2,由对顶角相等,得∠2=∠4,那么∠1=∠4。因为∠2与∠3互补,即∠2+∠3=180°,又因为∠1=∠2,所以∠1+∠3=180°,即∠1和∠3互补。
应用拓展
(1)第8页课内练习2
(2)图中,∠1与∠2,∠3与∠4各是哪一条直线截哪两条直线而成的?它们各是什么角?
小结:
本讲主要讲述了同位角、内错角、同旁内角的概念以及识别它们的方法:
【活动6】作业
作业本1
对顶角指的两条直线相交成胡角
同位角,内错角,同旁内角指的是两组角之间的关系
同位角、内错角、同旁内角都是两条直线被第三条直线所截时产生的,究其实质,它们主要是反映了直线相交产生的角中,相互位置所具有的特征:(1)两个同位角就是与直线的位置关系而言具有“同上、同右”、“同上、同左”“同下、同右”或“同下、同左”的特征。(2)内错角具有“同内、异侧”的特征。(3)同旁内角具有“同内、同侧”的
1.2同位角、内错角、同旁内角
教学目标:
知识与技能目标:了解同位角、内错角、同旁内角的概念。
过程与方法目标:会识别同位角、内错角、同旁内角。
情感与态度目标:在活动中培养学生乐于探索、合作学习的习惯,培养学生“用数学”的意识和能力。
教学重点:重点:已知两直线和截线,判断同位角、内错角、同旁内角。
教学难点::已知两个角,要判别是哪两条直线被第3条直线所截而形成的什么位置关系的角
变式图形:图中的∠1与∠2都是同位角。
图形特征:在形如字母“F”的图形中有同位角。
2、再看∠3与∠5,这两个角都在直线AB、CD之间,且∠3在直线EF左侧,∠5在直线EF右侧,像这样的一对角叫做内错角。同样,∠4与∠6也具有类似位置特征,∠4与∠6也是内错角。
变式图形:图中的∠1与∠2都是有内错角。
请用三根竹条或小木棍制作一个如图的风筝骨架,观察风筝骨架中(图自己画)有几个角,请把它画成几何图形,并用符号表示这些角,然后分别指出所有的对顶角,同位角,内错角,同旁内角
归纳:(1)寻找同位角,内错角,同旁内角关键要分清两条直线和截线,然后按相互的位置特征进行判别
(2)归纳:变式是例题的逆向思维,即已知两角,如何寻找两直线和截线,引导学生得出
3、在图(1)中,∠3和∠6也在直线AB、CD之间,但它们在直线EF的同一旁像这样的一对角,我们称它为同旁内角。具有类似的位置特征的还有∠4与∠5,因此它们也是同旁内角。
变式图形:图中的∠1与∠2都是同旁内角。
图形特征:在形如“N”的图形中有同旁内角。
4、辩一辩
5,做一做(请一位学生上台展示学习成果)
掌握辩别这些角的关键是看哪两条直线被哪一条直线所截、分清哪一条直线截哪两条直线形成了哪些角,是作出正确判定的前提,在截线的同旁找同位角,同旁内角,在截线的不同旁,找内错角。特征。
板书设计:
后记:①辨别三种角抓住角的特征,分清截线被截线
②复杂图像采取分离法还是比较成功的
③給角的关系判断截线和被截线还有部分学生不会
(3)两条直线被第3条直线所截形成几个角?这8个角中有多种关系,
如∠2与∠4,∠5与∠7,∠6与∠8,∠1和∠3是对顶角,除了对顶
角,还有没有其它新的关系的角呢?这节课我们就来研究同位角,内错角,同旁内角。
合作交流,探索新知
1、先看图中∠1和∠5,这两个角分别在直线AB、CD的上方,并且都在直线EF的右侧,像这样位置相同的一对角叫做同位角。在图(1)中,像这样具有类似位置关系的角还有吗?如果你仔细观察,会发现∠2与∠6,∠3与∠7,∠4与∠8也是同位角。
关键:弄清是哪两条直线被第三条直线所截而成的同位角、内错角、同旁内角。
教学过程:
教学设计
备注
创设情景,引入新课
(1)平面上的两条直线有相交和平行两种位置关系,两直线相交形成几个角?称之谓什么角?
(2)在实际生活中,还存在着两条直线被第3条直线所截的情况,如斜拉桥的灯柱子与其横梁,脚手架的钢管,交通线路中的道路,将这些事物抽象成几何图形,就是如图所示的图形
