伸展体传热特性实验报告
传热学实验报告

传热学实验报告传热学实验报告摘要:本实验通过研究传热学的基本原理和实验方法,探究了不同材料的导热性能和热传导规律。
通过实验数据的分析和处理,得出了一系列结论,对于进一步研究传热学提供了重要的参考。
引言:传热学作为热力学的一个重要分支,研究了热能在物质之间传递的规律和过程。
在工程领域中,传热学的应用非常广泛,例如热交换器、散热器等设备的设计和优化都需要依靠传热学的理论和实验研究。
本实验旨在通过实验手段,深入了解传热学的基本原理和实验方法,并通过实验数据的分析和处理,得出一些有价值的结论。
实验方法:1. 实验仪器和材料的准备本实验所需的仪器包括导热仪、温度计等,实验材料包括不同导热性能的物体,如金属、塑料等。
2. 实验步骤(1) 将不同材料的样品放置在导热仪的传热面上,并确保与传热面接触良好。
(2) 打开导热仪,记录下初始温度。
(3) 记录下不同时间间隔内的温度变化,并计算出相应的传热速率。
(4) 将实验数据整理并进行分析。
实验结果与讨论:通过实验数据的分析,我们得出了以下几个结论:1. 不同材料的导热性能存在明显差异。
在实验中,我们发现金属材料的导热性能要远远高于塑料等非金属材料。
这是因为金属材料中的自由电子能够在材料内部快速传递热能,而非金属材料中的分子结构则限制了热能的传导速度。
2. 传热速率与温度差成正比。
根据实验数据的分析,我们发现传热速率与传热面和环境之间的温度差成正比。
这是因为温度差越大,热能的传递速度越快。
3. 传热速率与传热面积成正比。
我们还观察到传热速率与传热面积成正比的规律。
这是因为传热面积越大,热能的传递面积也就越大,传热速率也就越快。
结论:通过本次实验,我们深入了解了传热学的基本原理和实验方法。
通过实验数据的分析和处理,我们得出了一系列结论,对于进一步研究传热学提供了重要的参考。
在实际应用中,我们应根据不同的工程需求,选择合适的材料和设计合理的传热面积,以提高传热效率和节约能源。
传热实验的实验报告

一、实验目的1. 理解传热的基本原理和过程;2. 掌握传热系数的测定方法;3. 分析影响传热效率的因素;4. 熟悉传热实验设备的操作和数据处理方法。
二、实验原理传热是指热量在物体内部或物体之间传递的过程。
根据热量传递的方式,传热可分为三种:导热、对流和辐射。
本实验主要研究导热和对流两种传热方式。
1. 导热:热量通过物体内部的分子或原子振动、碰撞等方式传递。
根据傅里叶定律,导热速率Q与物体面积A、温差ΔT和材料导热系数K成正比,即Q = K A ΔT。
2. 对流:热量通过流体(气体或液体)的流动传递。
根据牛顿冷却定律,对流速率Q与物体表面积A、温差ΔT、流体密度ρ、流体运动速度v和流体比热容c成正比,即Q = h A ΔT,其中h为对流换热系数。
三、实验设备与材料1. 实验设备:传热实验装置(包括套管换热器、温度计、流量计、搅拌器等);2. 实验材料:水、空气、酒精、石蜡等。
四、实验步骤1. 装置调试:将传热实验装置连接好,调试好温度计、流量计等设备,确保实验顺利进行。
2. 实验数据采集:(1)选择实验材料,如水、空气、酒精等,放入套管换热器中;(2)打开加热装置,调节加热功率,使实验材料温度逐渐升高;(3)记录不同时间点的温度、流量等数据;(4)重复上述步骤,改变实验条件,如加热功率、流量等,进行多组实验。
3. 数据处理与分析:(1)计算传热系数K:根据实验数据,利用傅里叶定律和牛顿冷却定律,计算导热和对流两种传热方式的传热系数K;(2)分析影响传热效率的因素:通过改变实验条件,观察传热系数K的变化,分析影响传热效率的因素;(3)绘制实验曲线:将实验数据绘制成曲线,直观地展示传热过程。
五、实验结果与分析1. 实验结果:(1)通过实验,得到不同条件下导热和对流两种传热方式的传热系数K;(2)分析实验数据,得出影响传热效率的因素。
2. 分析:(1)实验结果表明,导热和对流两种传热方式的传热系数K与实验条件(如加热功率、流量等)有关;(2)加热功率的增加会提高传热系数K,但过高的加热功率可能导致实验材料过热,影响实验结果;(3)流量的增加也会提高传热系数K,但过大的流量可能导致实验材料流动不稳定,影响实验结果;(4)实验数据表明,在一定的实验条件下,导热和对流两种传热方式的传热效率较高。
伸展体的稳态导热特性2

伸展体的稳态导热特性工程上常有许多沿着细长伸展体传递热量的问题,其基本特征是:温度一定的基面伸入与其温度不同的介质中,热量从其横截面沿伸展方向传递的同时,还通过其表面与液体进行对流换热,因而沿伸展体伸展方向温度也相应变化。
本实验是测量一等截面紫铜圆管在与液体进行对流换热的条件下沿管长的温度变化。
一、实验目的及要求1.通过实验,求解具有对流换热条件下伸展体导热的特性(如温度沿轴线分布规律,对流换热系数α,最小过余温度的位置及散热量Q等);2.了解热电偶测温的方法。
二、实验装置及测量系统本实验装置由风道、风机、伸展体、加热器及测温系统所组成,详见图3-1所示,伸展体是一内径为Φ1=10mm,外径为Φ2=11.5mm,长度为L=200mm,导热系数为的等截面紫铜管,水平置于有机玻璃制成的近似矩形的风道中,轴流风机固定在风道尾部上平面,由于风机的抽吸,风道中空气均匀横向掠过伸展体表面造成强迫对流换热工况,伸展体两端分别装有一组电加热器,各由一只调压器提供电源并控制其功率,以维持二端处于所要求的温度t1和t2。
为了改变空气在流过圆管表面时的速度,以达到改变换热系数的目的,风机转速可调(分为高、中、低三档),采用铜—康铜热电偶测量伸展体轴向过余温度,热端安装在一可移动的拉杆上,与伸展体内壁相接触,冷端则置于风道中,并分别用导线接到电子电位差计上,热端所处位置由拉杆及标尺确定。
三、实验原理具有对流换热条件的等截面伸展体,当长度与横截面积之比很大时,可视为一维导热,若为常物性,其导热微分方程式为:(3-1)式中m——系数,(1/米);θ——过余温度,(℃);——伸展体x截面处的温度(℃);——伸展体周围介质的温度(℃);U——伸展体横截面的周长(米);A——伸展体横截面积(米2)伸展体内的温度分布规律是由边界条件及m值来决定的,本实验装置的边界条件是:当当于是方程(3-1)的解为:(3-2)当时,伸展体过余温度分布曲线如图3-2所示。
传热实验实验报告

传热实验实验报告导言传热实验是研究物体内部热量传递过程的实验。
在实际应用中,传热实验可以帮助我们更好地理解材料和环境的热特性,并为工程领域提供依据。
在这份实验报告中,我们将介绍本次实验的目的、实验设计、实验过程以及实验结果和分析。
实验目的本次实验的目的是研究物体内部热量传递的过程,特别是对于导热系数的测量。
导热系数是描述物体传热能力的指标,它是单位时间内导热量与单位面积温度梯度的比值。
我们需要测量尽可能多的样品并记录测量结果,以便对材料和环境的热特性进行更深入的理解。
实验设计在本次实验中,我们使用的设备是传热系数测定仪,包括导热率计和实验样品。
我们将在实验样品中加热并记录样品表面和内部的温度变化,以计算出导热系数。
在实验中,我们将对不同材料和形状的样品进行测量,以确定它们的导热系数差异。
实验过程在实验前,我们需要将导热系数测定仪进行校准。
校准的结果将用于计算本次实验样品的导热系数。
接下来,选取不同材料的样品,进行实验。
实验的过程中需要加热样品,同时记录样品表面和内部的温度变化,以确定导热系数。
实验过程中需要注意材料的形状和大小,以及实验环境的温度和湿度等因素。
实验结果和分析在实验结果分析中,我们将展示各个材料的导热系数测量结果,并讨论实验中的关键发现。
实验结果表明,不同材料的导热系数差异较大,且导热系数受材料形状和温度等因素的影响较大。
此外,我们还发现在不同的环境下,导热系数也存在很大的差异。
结论本次实验通过测量不同材料和形状的样品的导热系数,深入了解了材料和环境的热特性。
各材料的导热系数主要受材料种类和形状的影响,需要在实际应用中仔细考虑。
这些结果对于实际工程和科学研究中的热传导问题具有重要的参考价值。
传热实验报告实验现象

实验时间:2021年X月X日实验地点:实验室一、实验目的1. 熟悉传热的基本原理和实验方法。
2. 了解传热过程中的实验现象,如温度变化、流量变化等。
3. 通过实验验证传热学的基本定律,如牛顿冷却定律、热传导定律等。
二、实验原理传热是指热量从高温物体传递到低温物体的过程。
传热方式主要有三种:传导、对流和辐射。
本实验主要研究传导和对流两种传热方式。
1. 传导传热:热量通过物体内部从高温部分传递到低温部分的过程。
本实验中,采用导热系数较高的金属棒进行实验。
2. 对流传热:热量通过流体(如空气、水等)的流动传递的过程。
本实验中,采用空气作为传热介质。
三、实验现象1. 传导传热现象(1)实验现象:将一端加热的金属棒置于室温环境中,观察到金属棒另一端温度逐渐升高。
(2)分析:这是由于金属棒内部热量通过传导方式传递,导致另一端温度升高。
(3)实验数据:金属棒长度L=100mm,导热系数k=45W/(m·K),加热时间t=30s,另一端温度升高ΔT=20℃。
2. 对流传热现象(1)实验现象:将加热后的金属棒放入装有空气的密闭容器中,观察到金属棒温度逐渐降低。
(2)分析:这是由于金属棒表面空气被加热,密度减小,上升;冷空气下降,形成对流,使热量传递给空气,导致金属棒温度降低。
(3)实验数据:金属棒长度L=100mm,导热系数k=45W/(m·K),加热时间t=30s,另一端温度降低ΔT=10℃。
3. 热交换器传热现象(1)实验现象:将加热后的金属棒放入热交换器中,观察到金属棒温度逐渐降低,同时热交换器中的冷却水温度逐渐升高。
(2)分析:这是由于金属棒与冷却水之间发生热交换,热量从金属棒传递给冷却水,导致金属棒温度降低,冷却水温度升高。
(3)实验数据:金属棒长度L=100mm,导热系数k=45W/(m·K),加热时间t=30s,金属棒温度降低ΔT=15℃,冷却水温度升高ΔT=5℃。
四、实验结论1. 通过实验验证了传导和对流两种传热方式的存在。
上海大有仪器 伸展体的导热特性实验台 DYR039

上海大有仪器伸展体的导热特性实验台
型号:DYR039
一.实验目的
1.通过实验,求解具有对流换热条件的伸展体导热的特性(如温度沿轴线分布规律、对流换热系数、最小过余温度的位置Xmin等);
2.了解热电偶测温的方法。
二.技术指标
1.工作电源AC220V、50Hz,单相三线制、功率1500W;安全保护:具有接地保护、漏电保护、过流保护;
2.电源线路及控制线的安装:须使用环保阻燃电气配线槽,规范整理符合国家标准,具有绝缘、防弧、阻燃自熄等特点,布线整齐,安装可靠,便于查找、维修和调换线路;
3.装置外形尺寸:1000×450×1110mm。
三.主要配置及参数
1.有机玻璃风管、加热器、高温电压表、高温调节、加热管(试件)、位移尺、引风机、热电偶;
2.电源控制系统:双面亚光密纹喷塑电控箱1只、漏电保护器(德力西)、带灯自锁按钮开关(正泰)、调节旋钮、线槽等组成,控制箱面板采用铝质凹字技术制作;
3.双面亚光密纹喷塑实验桌(配万向轮及禁锢脚、调整角可调整桌面水平及固定);
4.提供实验报告测试样本(作为调试验收标准)等。
具有对流换热条件的伸展体传热特性试验

五.具有对流换热条件的伸展体传热特性实验一、实验目的通过本实验和对实验数据的分析,加深对传热学教学内容的理解,掌握和了解伸展体传热的特性和求解具有对流换热条件的方法。
二、实验方法与设备1. 设备的组装将位于箱体风道中部的伸展体试验的封头取下,将图4所示的伸展体试件按铜管表面的刻线贴好热电偶(用单独的热电偶组)后插入风道,并使热电偶在背风处,如图16所示。
将单独一组10对的热电偶接入热电偶组(一)接口,将伸展体试件的加热导线接入位于面板最右端的接线柱。
图16 伸展体试件安装于风道内2. 实验原理本实验所用试件为一圆紫铜管,其外径0d =19mm ,内径1d =17mm ,长度L=260mm ,具有对流换热的等截面伸展体(常物性),如图17所示,取导热微分方程为:图17 等截面伸展体对流换热示意图0222=-θϑm dxd (1) 式中:m ——系数,cA hp m λ=, (m 1) θ——过余温度,f t t -=θ, (℃);t ——伸展体温度, (℃);f t ——伸展体周围介质温度, (℃);h ——空气对壁面的表面传热系数,(cm W ο⋅2); p ——横截面的周长,0d p π=,(m );λ——空气的导热系数,(m.℃)c A ——伸展体横截面面积,4)(10d d A c -=π,(2m ); 伸展体内的温度分布规律取决于边界条件和m 值得大小。
本实验采用的试件两端为第一类边界条件,即:f w fw t t L x t t x -===-===2211,,0ϑϑϑϑ ; (2)由此,试件内的温度分布规律为式(3),伸展体在壁面1和壁面2的热流量分别用式(4)和式(5)计算。
伸展体表面和流体之间的对流换热量用式(6)计算。
)()]([)(12mL sh x L m sh mx sh -+=ϑϑϑ (3))(])([)(2101mL sh mL ch m A dx d A c x c θϑλθλφ-=== (4) )()]([)(212mL sh mL ch m A dx d A c L x c θϑλθλφ-=== (5) )(]1)()[(2121mL sh mL ch mA c --=-=θϑλφφφ (6) 根据0=dxd θ,可寻求过余温度最低值处的位置m in x })(/]/)([{12min mmL sh mL ch arcth x θθ-= (7) 3. 实验过程、数据的测量和整理被测试验件被安置在风道中,当风机运行后,气流均匀地横向流过管子表面,由于被测试验件是均质的,因此,其表面传热系数基本相同。
伸展体传热特性实验报告
具有对流换热条件的伸展体传热特性试验之实验报告实验人:刘罗勤 学号:PB07013045 班级:0701301 一、实验题目:具有对流换热条件的伸展体传热特性试验 二、通过实验和对试验数据的分析,使我们更深入了解伸展体传热的特性并掌握求解具有对流换热条件的伸展体传热特性的方法。
三、基本原理 略 四、实验要求1. 解方程 2220d m dx θθ-=(1) 棒沿X 方向的过余温度ft t θ=-分布式:()x θθ=;221122*********210;,cosh()sinh()cosh(),cosh()sinh(),sinh()cosh()sinh ()sinh()cosh()sinh()sinh()sinh()d m T T T T A mx B mx dxmL A A mL B mL A B mL mL m L x mx mx mx mL mL θθθθθθθθθθθθθθθθ∞∞-==-=-⇒=+-==+⇒==--+∴=+=(2)分析沿X 方向,棒的温度分布曲线的可能形状。
分析各参数:L 、U 、f 、λ、α、1W t 、2W t 、f t 对温度分布的影响(由第2题数据得出)。
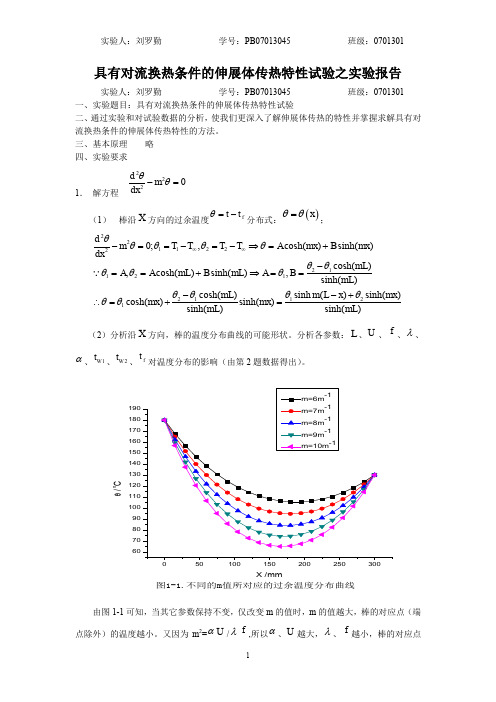
60708090100110120130140150160170180190θ / oCX /mm图1-1.不同的m值所对应的过余温度分布曲线由图1-1可知,当其它参数保持不变,仅改变m 的值时,m 的值越大,棒的对应点(端点除外)的温度越小。
又因为m 2=αU /λf ,所以α、U 越大,λ、f 越小,棒的对应点(端点除图1-1.不同的m 值所对应的过余温度分布曲线外)的温度越小。
由图1-2知,当其它参数保持不变,仅改变t f 的值时,t f 的值越大,棒的对应点(端点除外)的过余温度越小。
而由图1-3知,当仅改变t f 的值时,t f 的值越大,棒的对应点(端点除外)的温度也越大。
由图1-4知,当仅改变t w 的值时,t w 的值越大,棒的对应点的温度也越大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
具有对流换热条件的伸展体传热特性试验之实验报告
实验人:刘罗勤 学号:PB07013045 班级:0701301 一、实验题目:具有对流换热条件的伸展体传热特性试验 二、通过实验和对试验数据的分析,使我们更深入了解伸展体传热的特性并掌握求解具有对流换热条件的伸展体传热特性的方法。
三、基本原理 略 四、实验要求
1. 解方程 22
2
0d m dx θθ-=
(1) 棒沿X 方向的过余温度
f
t t θ=-分布式:
()
x θθ=;
221122*********
210;,cosh()sinh()cosh()
,cosh()sinh(),sinh()
cosh()sinh ()sinh()
cosh()sinh()sinh()sinh()
d m T T T T A mx B mx dx
mL A A mL B mL A B mL mL m L x mx mx mx mL mL θ
θθθθθθθθθθθθθθθ∞∞-==-=-⇒=+-==+⇒==--+∴=+=
(2)分析沿X 方向,棒的温度分布曲线的可能形状。
分析各参数:L 、U 、f 、λ、
α、1W t 、2W t 、f t 对温度分布的影响(由第2题数据得出)。
60
708090100110120130
140150160170180190θ / o
C
X /mm
图1-1.不同的m值所对应的过余温度分布曲线
由图1-1可知,当其它参数保持不变,仅改变m 的值时,m 的值越大,棒的对应点(端点除外)的温度越小。
又因为m 2=αU /λf ,所以α、U 越大,λ、f 越小,棒的对应点
(端点除图1-1.不同的m 值所对应的过余温度分布曲线外)的温度越小。
由图1-2知,当其它参数保持不变,仅改变t f 的值时,t f 的值越大,棒的对应点(端点除外)的过余温度越小。
而由图1-3知,当仅改变t f 的值时,t f 的值越大,棒的对应点(端点除外)的温度也越大。
由图1-4知,当仅改变t w 的值时,t w 的值越大,棒的对应点的温度也越大。
由图1-5知,
θ/ o
C
X /mm
图1-2.不同的tf值所对应的过余温度分布曲线
θ / o
C
X /mm 图1-4.不同的tw1值所对应的过余温度分布曲线 图
50
607080
90100
110120130
140
150160170180
190θ /o
C
X /mm
图1-5.不同的L值所对应的过余温度分布曲线
t / o
C
X/mm
图1-3.不同的tf值所对应的温度分布曲线
当仅改变L 的值时,L 的值越大,棒的对应点(端点除外)的温度越小。
(3)棒的最低温度截面的位置表达式(当0x L <<存在最低温度值时);
121221
cosh ()cosh 1
0ln()sin 22mL mL m m L x m mx e d L x dx hmL m e θθθθθθθ--+-==⇒=+- (4)棒两端由壁导入的热量
1
Q 及
2
Q -。
120
x x L
d d Q f
Q f
dx
dx
θθλλ===-==+=2.计算:直径为25mm ,长为300mm 的钢棒(0
50/W m C λ=)两端分别相连接。
0012200,150W W t C t C ==,
20f t C
=,
20
20/W m C α=⋅。
a. 计算温度分布;
由第1题的表达式可得 m= 8 (m -1)
012sinh ()sinh()
32.93sinh(2.48)23.78sinh8()sinh()
m L x mx x x C mL θθθ-+=
=-+
0()32.93sinh(2.48)23.78sinh820()f t x t x x C θ⇒=+=-++
b. 求棒的最低温度点的位置及其温度值,绘出该棒的温度分布曲线;
12
1
ln()0.1745()2mL mL e L x m θθ-=+= 0min (0.1745)103.99()t t C ==
80
100
120
140
160
180
θ / o
C
X/mm
图2-1.给定条件下所对应的温度分布曲线
c. 分别求出壁面1和壁面2导入棒的导热量
121299.5();809.9()Q W Q W ==
d. 求棒向空气的散热量
121299.5809.92109.4()Q Q Q W =+=+=
e. 在
2
W t 为什么值时,壁面2为绝热面?并画出温度分布曲线。
求每小时散入空气的
热量
2
W t =52.4 0C Q=5203 kJ/h
20
406080100120
140160180200
θ / o
C
X /mm
图2-2.壁面2为绝热壁时所对应的过余温度分布曲线
3.实验要求
注:由U 转化到为乘以转化因子250C/mV . 直接由上表数据编程可得m 的值:
m=11.4155 11.3350 11.3766 11.4837 11.6778 11.9073 12.4999 12.9075 15.7894(m -1)
实际上,由于第一个和最后一个数据是靠近壁面测得的,而该处的对流换热系数一般不等于中间段的,所以可以将首尾两个数据剔除。
剔除后的数据为:
于是可得m 的值(单位 m -1):
m=10.6917 10.6916 10.6994 10.7437 10.7033 10.9683 10.0459(m -1) 已知管子外径: d 0=12.5mm ,管子内径:d 1=11mm ,管子导热系数:k=398W/m o C 由m 2=au/(kf) 得a= m 2kf/u,最后可得空气对壁面的换热系数的值:
a=32.0752 32.0746 32.1209 32.3878 32.1443 33.7561 28.3170(W/m 2 o C )
25
30
35
40
45
θ / o
C
X /cm
图3-1 剔除首尾点后不同 x 位置过余温度 θ
-1
由结果可知,理论值与实测值相当符合,说明在棒的中段空气对流换热系数近似为常值 的假定是合理的。
而理论值与实测值得符合程度可从图3-2很好地看出:
25
30
35
40
45
θ / o
C
X /cm
图3-2 不同 x 位置过余温度 θ 的实测值与理论值。
