物理竞赛[热学] [2017]
2017第34届全国中学生物理竞赛决赛真题几答案解析

12π2π第34 届全国中学生物理竞赛决赛试题与参考解答一、(35 分)如图,质量分别为ma、m b 的小球a 、b 放置在光滑绝缘水平面上,两球之间用一原长为l0 、劲度系数为k的绝缘轻弹簧连接。
(1)t 时,弹簧处于原长,小球a 有一沿两球连线向右的初速度v,小球b 静止。
若运动过程中弹簧始终处于弹性形变范围内,求两球在任一时刻t(t ) 的速度。
(2)若让两小球带等量同号电荷,系统平衡时弹簧长度为L,记静电力常量为K 。
求小球所带电荷量和两球与弹簧构成的系统做微振动的频率(极化电荷的影响可忽略)。
参考解答:(1)如图,t 时刻弹簧的伸长量为ul l有d 2udt2式中ku ①mamb ②mamb为两小球的约化质量。
由①②式知,弹簧的伸长量u 服从简谐振动的动力学方程,振动频率为f2π③最后一步利用了②式。
t 时刻弹簧的伸长量u 的表达式为u A sin t B cos t ④式中A 、B 为待定常量。
t 时,弹簧处于原长,即u B将 B 代入④式得a 相对于b 的速度为u A sin t ⑤vdradrbduA cos t ⑥a dt dt dtt 时有专业知识--整理分享kL = - va (0) v 0 0 A⑦由⑥⑦式得v a v 0 cost⑧系统在运动过程中动量守恒小球 a 相对于地面的速度为m a v 0m av am b vb⑨v a v av b⑩由③⑧⑨⑩式可得, t 时刻小球a 和小球b 的速度分别为m (m m ) mvbcosa b 0t a vmm m 0 a (m m )a bmvaa⑫m 0a bab(2)若两球带等量同号电荷,电荷量为 q ,系统平衡时有q 2K 2k 0 (L 0 l 0 ) ⑬由⑬式得设t 时刻弹簧的长度为 L (见图 II ),有q L 0 ⑭d 2 L q 2dt 2k 0 (L l 0 ) K L 2⑮图 II令 xLL 0 为t 时刻弹簧相对平衡时弹簧长度 L 0的伸长量,⑮式可改写为d 2x q 2xdt 2 k 0 x k 0 (L 0 l 0 ) KL2L⑯系统做微振动时有x因而xxx 2LLOL⑰b a L 0WORD格式-可编辑专业知识--整理分享WORD格式-可编辑12π2πL3L利用上式,⑯式可写为d 2x q2q2x 2dt2k0 (L0 l0 ) K L2k2KL3x OL⑱x20 0 0略去OL,并利用⑬或⑭式,⑱式可写为d 2 x q2 3L 2lk 2K x 0 0 kx ⑲dt2 0由⑲式知,3Ll,系统的微振动服从简谐振动的动力学方程,振动频率为f ⑳最后一步利用了②式。
2017年初中物理竞赛试题参考答案和评分标准

2017年初中物理竞赛试题参考答案和评分标准一、单项选择题(每小题3分,共18分)1.B2.C3.D4.A5.A6.A二、填空题(第7-8题每题3分,第9题4分,第10题3分,共13分)7.保持F竖直向上8.6N9. 0 1010.红绿蓝白反射红光三、实验设计题(每题6分,共18分)11.器材:篮球、带阀门(夹子)的胶管、打气筒、天平、量筒、水、水槽操作步骤:(1)取一球胆(篮球)接一根带阀门(夹子)的胶管,用打气筒向球内打足气后,用天平称出其质量m1.(2)如图所示,用排水集气法在量筒中收集气体,集气完毕后,拧紧夹子,上下移动量筒,使其内外水平面一样高,以保证内外气体压强相等,然后由量筒刻度读出气体体积V.(3)再用天平称出放出气体后篮球的质量m2,篮球体积不变,避免篮球浮力对测量的影响。
则量筒内气体的质量为m1-m2.(4)空气的密度注:实验要考虑到压强和浮力对实验的影响,否则最多得3分12.如图(有错不给分) 13.如图(有错不给分)四、计算题(共27分)14.开关S 闭合,L 1和L 2并联后与L 3串联。
L 3为“6V 、 1W ”,它的电阻为:R 3=U 2/P 3=36Ω。
(1分)L 1和L 2为“6V 10W ”,电阻均为R=U 2/P=3.6Ω。
总电阻R 总=R 3+R/2=37.8Ω(1分) 通过L 3的电流I 3=U /R 总=0.16A (1分)L 3的功率P 3=I 2R=0.92W ,与L 3的额定功率(1W)相差不多,L 3能发光.(2分) L 1和L 2并联,通过每只灯泡的电流I 1=I 2=I 3/2=0.08A ,L 1的实际功率为P 1=I 2R=0.023W ,比它的额定功率10W 小得多,L 1不能发光。
同理,L 2也不能发光。
(2分)15.解:(1)F 浮=ρ水gV 排 =1×103kg/m 3×10N/kg ×4×10-2m 3=400N (2分) (2)P =Fυ P 1= F 1υ绳=2 F 1υ P 2= F 2υ绳 =2 F 2υ21F F =21P P =1516 ① (2分) (3)在匀速提升水中物体M 的过程中,以动滑轮A 和物体M 为研究对象,受力分析如图3甲所示;在匀速提升水中物体M 的过程中,以动滑轮B 和物体M 为研究对象,受力分析如图图32F 1 F 浮 G 1G 甲 2F 2F 浮G 2G 乙3乙所示。
17全国中学生物理竞赛决赛试题及答案

第27届全国中学生物理竞赛决赛试题及答案一、(25分)填空题1.一个粗细均匀的细圆环形橡皮圈,其质量为M,劲度系数为k,无形变时半径为R。
现将它用力抛向空中,忽略重力的影响,设稳定时其形状仍然保持为圆形,且在平动的同时以角速度ω绕通过圆心垂直于圆面的轴线匀速旋转,这时它的半径应为。
2.鸽哨的频率是f。
如果鸽子飞行的最大速度是u,由于多普勒效应,观察者可能观测到的频率范围是从到。
(设声速为V。
)3.如图所示,在一个质量为M、内部横截面积为A的竖直放置的绝热气缸中,用活塞封闭了一定量温度度为T的理想气体。
活塞也是绝热的,活塞质量以及活塞和气缸之间的摩擦力都可忽略不计。
已知大气压强为p,重力加速度为g,现将活塞缓慢上提,当活塞到达气缸开口处时,气缸刚好离开地面。
已知理想气体在缓慢变化的绝热过程中pVγ保持不变,其中p是气体的压强,V是气体的体积,γ是一常数。
根据以上所述,可求得活塞到达气缸开口处时气体的温度为。
4.(本题答案保留两位有效数字)在电子显微镜中,电子束取代了光束被用来“照射”被观测物。
要想分辨101.010m -⨯(即原子尺度)的结构,则电子的物质波波长不能大于此尺度。
据此推测电子的速度至少需被加速到 。
如果要想进一步分辨121.010m -⨯尺度的结构,则电子的速度至少需被加速到 ,且为使电子达到这一速度,所需的加速电压为。
已知电子的静止质量319.110kge m -=⨯,电子的电量191.610C e -=-⨯,普朗克常量346.710J s h -=⨯⋅,光速813.010m s c -=⨯⋅。
二、(20分)图示为一利用传输带输送货物的装置,物块(视为质点)自平台经斜面滑到一以恒定速度v运动的水平长传输带上,再由传输带输送到远处目的地,已知斜面高 2.0mh=,水平边长 4.0mL=,传输带宽 2.0md=,传输带的运动速度 3.0m/sv=。
物块与斜面间的摩擦系数10.30μ=。
初中物理竞赛热学训练试题

热学训练题(二)班级_______学号_________姓名__________得分____________第一部分选择题(75分)1、5℃的冷水和60℃的热水混合,得到50℃的温水。
若不计热损失,可以判断( )(A)混合前热水的热量不一定比冷水的热量多;(B)混合前热水的热量一定比冷水的热量多;(C)热水质量不一定比冷水质量大;(D)(D)热水质量一定比冷水质量小。
2、 在用混合法测定固体或液体比热的实验中,即使操作完全正确,但热损失仍然存在。
考虑到热量的损失,那么测出的比热数值大小与其真实值相比较,应当( )(E)一定大于真实值; (B)一定小于真实值;(C)只要经过多次测量取平均值,就一定完全等于真实值;(D)如果被测物质是放热物质,则测量值一定小于真实值;若是吸热物质,则测量值一定大于真实值。
3、把两只质量为m 、初温度为100℃的铜球和铁球,分别投入两杯质量也为m 、初温度为0℃的水中。
不考虑热损失,则它们分别达到热平衡后,可能出现的情况是(已知铜的比热小于铁的比热)( )(A)两杯水的混合温度可能相等; (B)放铜球的混合温度较高;(C)放铁球的混合温度较高; (D)两球放出的热量相等、温度变化相同。
4、甲乙两种液体可以相互混和,它们的密度之比为ρ甲:ρ乙=5:4;混合前的体积之比为V 甲:V 乙=2:3;比热之比为c 甲:c 乙=1:2。
假设它们的初温度不等,混和后的共同温度为t ,不计混和过程中的热损失,则它们达到热平衡后各自相对于它们原来的初温度的温度变化量之比Δt 甲:Δt 乙为( )(A)2:5; (B)5:12; (C)16:15; (D)15:165、某学生用两个相同的热源分别对质量为m 1,比热为c 1的甲物质和质量为m 2、比热为c 2的乙物质加热,并根据实验测得的数据分别画出甲、乙两物质的温度随加热时间变化的图线,如图10所示。
根据图线情况,作出如下推断,其中正确的是( )(A)若m 1=m 2,则c 1<c 2; (B)若m 1<m 2,则c 1>c 2;(C)若c 1=c 2,则m 1<m 2; (D)若c 1>c 2,则m 1<m 2。
17全国中学生物理竞赛预赛试题及答案
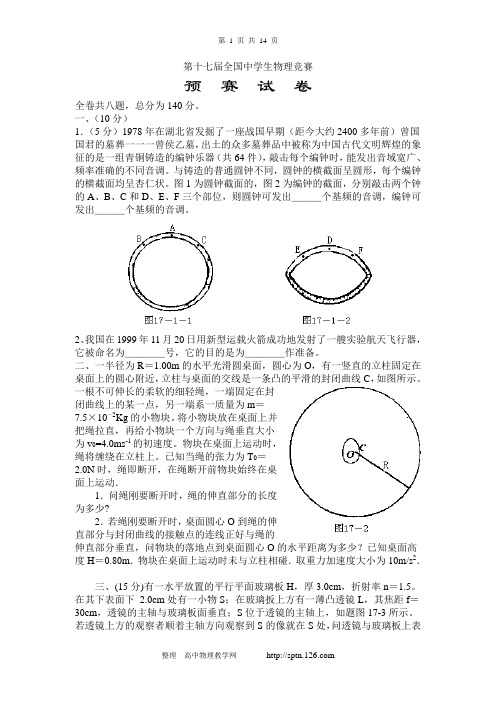
第十七届全国中学生物理竞赛预赛试卷全卷共八题,总分为140分。
一、(10分)1.(5分)1978年在湖北省发掘了一座战国早期(距今大约2400多年前)曾国国君的墓葬一一一曾侯乙墓,出土的众多墓葬品中被称为中国古代文明辉煌的象征的是一组青铜铸造的编钟乐器(共64件),敲击每个编钟时,能发出音域宽广、频率准确的不同音调。
与铸造的普通圆钟不同,圆钟的横截面呈圆形,每个编钟的横截面均呈杏仁状。
图1为圆钟截面的,图2为编钟的截面,分别敲击两个钟的A、B、C和D、E、F三个部位,则圆钟可发出___个基频的音调,编钟可发出___个基频的音调。
2、我国在1999年11月20日用新型运载火箭成功地发射了一艘实验航天飞行器,它被命名为____号,它的目的是为____作准备。
二、一半径为R=1.00m的水平光滑圆桌面,圆心为O,有一竖直的立柱固定在桌面上的圆心附近,立柱与桌面的交线是一条凸的平滑的封闭曲线C,如图所示。
一根不可伸长的柔软的细轻绳,一端固定在封闭曲线上的某一点,另一端系一质量为m=7.5×10-2Kg的小物块。
将小物块放在桌面上并把绳拉直,再给小物块一个方向与绳垂直大小为v0=4.0ms-1的初速度。
物块在桌面上运动时,绳将缠绕在立柱上。
已知当绳的张力为T0=2.0N时,绳即断开,在绳断开前物块始终在桌面上运动.1.问绳刚要断开时,绳的伸直部分的长度为多少?2.若绳刚要断开时,桌面圆心O到绳的伸直部分与封闭曲线的接触点的连线正好与绳的伸直部分垂直,问物块的落地点到桌面圆心O的水平距离为多少?已知桌面高度H=0.80m.物块在桌面上运动时未与立柱相碰.取重力加速度大小为10m/s2.三、(15分)有一水平放置的平行平面玻璃板H,厚3.0cm,折射率n=1.5。
在其下表面下 2.0cm处有一小物S;在玻璃扳上方有一薄凸透镜L,其焦距f=30cm,透镜的主轴与玻璃板面垂直;S位于透镜的主轴上,如题图17-3所示。
大学物理竞赛-热学试题

等T膨胀:
dEk=0; 内压强引起的势能变化:
dEP
PidV
a
Va2
dV
d( a V
)
dE
dEk
dEP
d ( V
)
E V2 d ( a ) a( a a )
V1
V
V1 V2
(3)
Q吸
A
E
RT
ln
V2 V1
b b
例 真实气体在气缸内以温度T1等温膨胀,推动活 塞做功,活塞移动距离为L。若仅考虑分子占有体 积去计算功,比不考虑时为——;若仅考虑分子 间存在作用力去计算功,比不考虑时——;
(a)大; (b)小; (c)都一样;
答案:(a); (b)
解:(P
a V2
)(V
b)
RT
a:反映分子间引力;b:反映气体分子本身体积;
气体对外做功:A V2 PdV
V2 ( RT1
a V1 )dV
V1 V b V 2
RT1
ln
V2 V1
b b
a( 1 V2
1) V1
(1)仅考虑分子体积: a=0, ln V2 b ln V2
V1 b
V1
, 作功增加;
(2)仅考虑分子间引力: b=0, a( 1 1 ) 0
V2 V1
,作功减小;
一、理想气体状态方程 • PV=RT • P n k T
真实气体: 范德瓦尔斯方程
(P
a V2
)(V
b)
RT
• P RT
M
*
二、气体动理论
1. 微观量与宏观量的关系
•
P
2 3
n
t
t
若把某一初态定为参考态,则:S
高中物理竞赛热学部分优题选
高中物理竞赛——热学题选1.一个老式的电保险丝,由连接在两个端纽之间的一根细而均匀的导线构成。
导线按斯特藩定律从其表面散热。
斯特藩定律指出:辐射功率P 跟辐射体表面积S 以及一个与温度有关的函数成正比,即(),44外辐T T S P -∞试说明为什么用保险丝时并不需要准确的长度。
2.有两根长度均为50cm 的金属丝A 和B 牢固地焊在一起,另两端固定在牢固的支架上(如图21-3)。
其线胀系数分别为αA =1.1×10-5/℃,αB =1.9×10-5/℃,倔强系数分别为K A =2×106N/m ,K B =1×106N/m ;金属丝A 受到450N 的拉力时就会被拉断,金属丝B 受到520N 的拉力时才断,假定支架的间距不随温度改变。
问:温度由+30°C 下降至-20°C 时,会出现什么情况?(A 、B 丝都不断呢,还是A 断或者B 断呢,还是两丝都断呢?)不计金属丝的重量,在温度为30°C 时它们被拉直但张力为零。
3.长江大桥的钢梁是一端固定,另一端自由的。
这是为什么?如果在-10℃时把两端都固定起来,当温度升高到40℃时,钢梁所承担的胁强(压强)是多少?(钢的线胀系数为12×10-6/℃,弹性模量为2.0×105N/mm 2,g=10m/s 2)4.厚度均为a=0.2毫米的钢片和青铜片,在T 1=293开时,将它们的端点焊接起来,成为等长的平面双金属片,若钢和青铜的线膨胀系数分别为10-5/度和2×10-5/度,当把它们的温度升高到T 2=293开时,它们将弯成圆弧形,试求这圆弧的半径,在加热时忽略厚度的变化。
5.在负载功率P 1=1kW ,室温t 0=20℃时,电网中保险丝的温度达到t 1=120℃,保险丝的材料的电阻温u C 图21-13度系数α=4×10-3K-1,保险丝的熔断温度t2=320℃,其所释放的热量与温度差成正比地增加,请估计电路中保险丝熔断时负载的功率。
2017年第34届全国中学生物理竞赛决赛真题及答案(高清pdf版)
f 1 2π
3L0 L0
2l0
k0
1
2π
3L0 L0
2l0
ma mb ma mb
k0
⑳
最后一步利用了②式。 评分参考:第(1)问 24 分,①②③④⑤⑥⑦⑧⑨⑩⑪⑫式各 2 分;第(2)问 11 分,⑬⑭⑮式各 2 分,⑰式 1 分,⑲⑳式各 2 分。
二、(35 分) 参考解答: (1)两体系统的相对运动相当于质量为 Mm 的质点在固定力场中的运动,其运动方程是
人在 A 处完全下蹲,在 A A 过程中系统重力势能减少,(因受到摆底板的限制)动能仍然为零。人
在 A 处时系统的机械能为 U A' K A VA 0 mg(d l)(1 cos A )
②
mg
l
l
d
(h1
d
)
人在 B 仍处位于完全下蹲状态,在 A B 过程中系统机械能守恒。人在 B 处的动能为
0 为平衡位置、圆频率
6BI 、周期 T 2π m
m 6BI
、振幅为0 的简谐运动。
(3)线框在做上述运动的过程中,当逆时针转至 ab 边与 X 轴正向重合时,
0 ,且0 0
6BI , m
⑨
此时 P 、 Q 形成断路,线框内没有了电流,不再受到安培力的力矩。由于没有阻力,线框将保持作角
三、(35 分)参考解答:
(1)假定在始终完全蹲下和始终完全站立过程中没 有机械能损失。将人和秋千作为一个系统。人在 A
处位于完全站立状态,此时系统的机械能为
U A K A VA 0 mg[l(1 cos A ) d ] mgh1 ① 式中,K A 0 和VA mgh1 分别是人在 A 处时系统的动 能和重力势能, A 是秋千与竖直方向的夹角(以 下使用类似记号)如图所示。
物理竞赛热学压轴题及答案
热学压轴题精选一、秘制气球生物在“执杖”星附近的行星上有稠密的大气,其中生活着一种气球状生物,当有人向它们询问小猪是否很会装13的时候,它们会回复BIBIBI的响声,我们暂且将这些生物命名为气球。
气球的半径和质量基本稳定,它们通过调节自身气囊内的气体温度,从而改变密度,用来调节自身的飞行高度。
这些生物白天由于日照,温度上升,飞行在空中捕食,夜晚温度下降,停落在地面上休息。
气球的质量为m0,半径为r,地面气温为T0,压强为p0,密度为ρ0。
取绝热大气模型,即大气不同地方为常数,其中γ=7/5,大气的定体摩尔热容量为C V=2.5R。
在高度h = 25m变化不大的范围内,可以认为大气的温度、密度和压强随高度线性变化。
重力加速度为g。
各参数取值如下:m0=202kg,T0=300K,ρ0=1.174kg/m3r=10m,g=10.6m/s2,p0=1.01×105Pa,κ=43.0Jm-2K-1s-1=2040Jm-2 s-1(1)气球在休息的时候,体内的气体和大气自由交换。
清晨它向外深深吐一口气,将体内压降减少到p0−Δp,于是恰好起飞,能稳定在h高度飞行。
这个过程很短,热量来不及交换。
求Δp为多少?(2)飞行了一段时间后,由于日照和气球自身的特殊生理结构能输运热量,气球的压强上升到和周围一样。
(于是它舒服的不用忍受压强差了)求此时气球内温度为多少?(3)气球皮内外温差为ΔT时,单位时间内单位面积上的的散热本领为κ=ΔQΔSΔTΔt,阳光正入射的时候,单位时间内单位面积提供的热量为λ=ΔQΔSΔt。
则气球为了舒服,单位时间需要搬运给内部气体多少热量,q=ΔQΔt?(4)考虑热力学第二定律,气球为了搬运这些热量,单位时间内至少应当做功W为多少?一、神奇的高压锅如图一个容积为V0的高压锅,初态温度为T0,内部有压强为p0的理想气体,该气体定体摩尔热容量为C V=2.5R。
气阀的面积为S,上面的重物质量为m,重力加速度为g,外面大气压强为p0.(1)至少需要升温到T1为多少才能把重物顶起?(2)如果这个过程中不考虑容器壁散热,则高压锅至少需要吸热Q1为多少才能把重物顶起?(3)如果高压锅吸热总量为Q2>Q1,则此时高压锅内的温度T2为多少?(4)之后再将温度降低到初态,但是气体不会从气阀回到高压锅内,则此时锅内压强p3为多少?二、气球猪若把猪皮看做不会收缩也不会伸长的柔软的导热性能良好的材料,给小猪肚子充气,制成的气球猪(因为小猪不服第一题的气球生物,决定挑战他们),肚皮和猪头(视为质点)质量M=12kg(由于小猪身体“被掏空”,忽略其他质量),小猪肚子的最大容积为V f=12.5m3。
热学试题(1)
大学物理竞赛训练题 热学(1)一、选择题(每题3分)1. 在标准状态下,任何理想气体在1 m 3中含有的分子数都等于 [ ](A) ×1023. (B)×1021.(C) ×1025. (D)×1023.(玻尔兹曼常量k =×1023 J ·K 1) 2. 若理想气体的体积为V ,压强为p ,温度为T ,一个分子的质量为m ,k 为玻尔兹曼常量,R 为普适气体常量,则该理想气体的分子数为: [ ](A) pV / m . (B) pV / (kT ).(C) pV / (RT ). (D) pV / (mT ).3. 若室内生起炉子后温度从15℃升高到27℃,而室内气压不变,则此时室内的分子数减少了 [ ] (A)00. (B) 400.(C) 900. (D) 2100.4. 两瓶不同种类的理想气体,它们的温度和压强都相同,但体积不同,则单位体积内的气体分子数n ,单位体积内的气体分子的总平动动能(E K /V ),单位体积内的气体质量,分别有如下关系: [ ](A) n 不同,(E K /V )不同,不同. (B) n 不同,(E K /V )不同,相同. (C) n 相同,(E K /V )相同,不同. (D) n 相同,(E K /V )相同,相同.5. 在一容积不变的封闭容器内理想气体分子的平均速率若提高为原来的2倍,则(A) 温度和压强都提高为原来的2倍. [ ](B) 温度为原来的2倍,压强为原来的4倍.(C) 温度为原来的4倍,压强为原来的2倍.(D)温度和压强都为原来的4倍.6. 关于温度的意义,有下列几种说法:(1) 气体的温度是分子平均平动动能的量度.(2) 气体的温度是大量气体分子热运动的集体表现,具有统计意义.(3) 温度的高低反映物质内部分子运动剧烈程度的不同.(4) 从微观上看,气体的温度表示每个气体分子的冷热程度.这些说法中正确的是 [ ](A) (1)、(2) 、(4). (B) (1)、(2) 、(3).(C) (2)、(3) 、(4). (D) (1)、(3) 、(4).7. 一瓶氦气和一瓶氮气密度相同,分子平均平动动能相同,而且它们都处于平衡状态,则它们 [ ](A) 温度相同、压强相同.(B) 温度、压强都不相同.(C) 温度相同,但氦气的压强大于氮气的压强.(D) 温度相同,但氦气的压强小于氮气的压强.8. 三个容器A 、B 、C 中装有同种理想气体,其分子数密度n 相同,而方均根速率之比为()()()2/122/122/12::C B A v v v =1∶2∶4,则其压强之比A p ∶B p ∶C p 为: [ ](A) 1∶2∶4. (B) 1∶4∶8.(C) 1∶4∶16. (D) 4∶2∶1.9. 水蒸气分解成同温度的氢气和氧气,内能增加了百分之几(不计振动自由度和化学能)(A) %. (B) 50%. [ ](C) 25%. (D) 0.10. 有容积不同的A 、B 两个容器,A 中装有单原子分子理想气体,B 中装有双原子分子理想气体,若两种气体的压强相同,那么,这两种气体的单位体积的内能(E / V )A 和(E / V )B的关系 [ ](A) 为(E / V )A <(E / V )B .(B) 为(E / V )A >(E / V )B .(C) 为(E / V )A =(E / V )B .(D) 不能确定.11. 有N 个分子,其速率分布如图所示,v > 5v 0时分子数为0,则: [ ] (A) a = N / (2 v 0). (B) a = N / (3 v 0). (C) a = N / (4 v 0). (D) a = N / (5 v 0). 12. 设图示的两条曲线分别表示在相同温度下氧气和氢气分子的速率分布曲线;令()2O p v 和()2H p v 分别表示氧气和氢气的最概然速率,则 [ ](A) 图中a表示氧气分子的速率分布曲线;()2O p v /()2H p v =4. (B) 图中a表示氧气分子的速率分布曲线;()2O p v /()2H p v =1/4. (C) 图中b表示氧气分子的速率分布曲线;()2O p v /()2H p v =1/4. (C) 图中b表示氧气分子的速率分布曲线;()2O p v /()2H p v = 4. 13. 下列各图所示的速率分布曲线,哪一图中的两条曲线能是同一温度下氮气和氦气的分子速率分布曲线 [ ]2a/a/ 00000f (v )14. 若氧分子[O 2]气体离解为氧原子[O]气后,其热力学温度提高一倍,则氧原子的平均速率是氧分子的平均速率的 [ ](A) 1 /2倍. (B) 2倍. (C) 2倍. (D) 4倍.15. 已知分子总数为N ,它们的速率分布函数为f (v ),则速率分布在v 1~v 2区间内的分子的平均速率为 [ ](A)⎰21d )(v v v v v f . (B) ⎰21d )(v v v v v f /⎰21d )(v v v v f . (C) ⎰21d )(v v v v v f N . (D) ⎰21d )(v v v v v f /N . 16. 气缸内盛有一定量的氢气(可视作理想气体),当温度不变而压强增大一倍时,氢气分子的平均碰撞频率Z 和平均自由程λ的变化情况是: [ ] (A) Z 和λ都增大一倍. (B) Z 和λ都减为原来的一半. (C) Z 增大一倍而λ减为原来的一半. (D) Z 减为原来的一半而λ增大一倍.17. 一固定容器内,储有一定量的理想气体,温度为T ,分子的平均碰撞次数为 1Z ,若温度升高为2T ,则分子的平均碰撞次数2Z 为 [ ] (A) 21Z . (B) 12Z . (C) 1Z . (D) 121Z .18. 在恒定不变的压强下,气体分子的平均碰撞频率Z 与气体的热力学温度T 的关系为 (A) Z 与T 无关. (B) Z 与T 成正比. [ ] (C) Z 与T 成反比. (D) Z 与T 成正比.19. 容积恒定的容器内盛有一定量某种理想气体,其分子热运动的平均自由程为0λ,平均碰撞频率为0Z ,若气体的热力学温度降低为原来的1/4倍,则此时分子平均自由程λ和平均碰撞频率Z 分别为 [ ] (A) λ=0λ,Z =0Z . (B) λ=0λ,Z =210Z .v v(C) λ=20λ,Z =20Z . (D) λ=20λ,Z =210Z . 20. 一定量的理想气体,在体积不变的条件下,当温度降低时,分子的平均碰撞频率Z 和平均自由程λ的变化情况是: [ ] (A) Z 减小,但λ不变. (B) Z 不变,但λ减小.(C) Z 和λ都减小. (D) Z 和λ都不变.21. 在一个体积不变的容器中,储有一定量的理想气体,温度为T 0时,气体分子的平均速率为0v ,分子平均碰撞次数为0Z ,平均自由程为0λ.当气体温度升高为4T 0时,气体分子的平均速率v ,平均碰撞频率Z 和平均自由程λ分别为: [ ](A) v =40v ,Z =40Z ,λ=40λ.(B) v =20v ,Z =20Z ,λ=0λ.(C) v =20v ,Z =20Z ,λ=40λ.(D) v =40v ,Z =20Z ,λ=0λ.二、填空题1. (3分) 已知某种理想气体分子的最概然速率为p v ,气体的压强为p .则此气体的密度为__________.2. (3分) 氢分子的质量为 ×1024 g ,如果每秒有1023 个氢分子沿着与容器器壁的法线成45°角的方向以105 cm / s 的速率撞击在 2.0 cm 2 面积上(碰撞是完全弹性的),则此氢气的压强为____________.3. (3分) A 、B 、C 三个容器中皆装有理想气体,它们的分子数密度之比为n A ∶n B ∶n C =4∶2∶1,而分子的平均平动动能之比为A w ∶B w ∶C w =1∶2∶4,则它们的压强之比A p ∶B p ∶C p =__________.4. (3分) 若某种理想气体分子的方均根速率()4502/12=vm/ s ,气体压强为p =7×104 Pa ,则该气体的密度为=_______________.5. (5分) 某容器内分子数密度为10 26 m -3,每个分子的质量为 3×10-27 kg ,设其中 1/6分子数以速率v = 200 m / s 垂直地向容器的一壁运动,而其余 5/6分子或者离开此壁、或者平行此壁方向运动,且分子与容器壁的碰撞为完全弹性的.则(1) 每个分子作用于器壁的冲量ΔP =_______________;(2) 每秒碰在器壁单位面积上的分子数0n =________________;(3) 作用在器壁上的压强p =___________________.6. (3分)下面给出理想气体的几种状态变化的关系,指出它们各表示什么过程.(1) p d V= (M / M mol)R d T表示____________________过程.(2) V d p= (M / M mol)R d T表示____________________过程.(3) p d V+V d p= 0 表示____________________过程.7. (3分) 某理想气体在温度为27℃和压强为×10-2 atm情况下,密度为 g/m3,则这气体的摩尔质量M mol=____________.(普适气体常量R= J·mol1·K1)8. (3分)在一个以匀速度u运动的容器中,盛有分子质量为m的某种单原子理想气体.若=________________.使容器突然停止运动,则气体状态达到平衡后,其温度的增量T9. (5分) 容器中储有1 mol 的氮气,压强为 Pa,温度为 7 ℃,则(1) 1 m3中氮气的分子数为_____________;(2) 容器中的氮气的密度为_________________;(3) 1 m3中氮分子的总平动动能为___________.(玻尔兹曼常量k=×1023 J·K1 , N2气的摩尔质量M mol=28×103 kg·mol1 , 普适气体常量R= J·mol1·K1 )10. (5分) 在相同的温度和压强下,氢气(视为刚性双原子分子气体)与氦气的单位体积内能之比为____________,氢气与氦气的单位质量内能之比为___________.11. (3分) 储有某种刚性双原子分子理想气体的容器以速度v=100 m/s运动,假设该容器突然停止,气体的全部定向运动动能都变为气体分子热运动的动能,此时容器中气体的温度上升K,由此可知容器中气体的摩尔质量M mol=_____. (普适气体常量R= J·mol1·K1) 12. (3分) 一铁球由10 m高处落到地面,回升到 m高处.假定铁球与地面碰撞时损失的宏观机械能全部转变为铁球的内能,则铁球的温度将升高______.(已知铁的比热c=J·kg1·K1)13. (3分) 一能量为1012 eV的宇宙射线粒子,射入一氖管中,氖管内充有 mol的氖气,若宇宙射线粒子的能量全部被氖气分子所吸收,则氖气温度升高了_______________K.(1 eV=×1019J,普适气体常量R= J/(mol·K))14. (3分) 1 mol的单原子分子理想气体,在1 atm的恒定压强下,从0℃加热到100℃,则气体的内能改变了_______________J.(普适气体常量R= J·mol1·K1 )15. (3分) 一氧气瓶的容积为V,充入氧气的压强为p1,用了一段时间后压强降为p2,则瓶中剩下的氧气的内能与未用前氧气的内能之比为__________.16.(3分)若某容器内温度为 300 K的二氧化碳气体(视为刚性分子理想气体)的内能为×103 J,则该容器内气体分子总数为___________________.(玻尔兹曼常量k=×10-23 J·K1,阿伏伽德罗常量N A=×1023 mol1)17. (3分)体积和压强都相同的氦气和氢气(均视为刚性分子理想气体),在某一温度T下混合,所有氢分子所具有的热运动动能在系统总热运动动能中所占的百分比为_________.18. (3分)一气体分子的质量可以根据该气体的定体比热来计算.氩气的定体比热c V = k J·kg1·K1,则氩原子的质量m=__________.(波尔兹曼常量k=×1023 J / K)19. (3分)若某容器内温度为 300 K的二氧化碳气体(视为刚性分子理想气体)的内能为×103 J,则该容器内气体分子总数为___________________.(玻尔兹曼常量k =×10-23 J ·K 1,阿伏伽德罗常量N A =×1023 mol 1)20. (3分)一定量H 2气(视为刚性分子的理想气体),若温度每升高1 K ,其内能增加 J ,则该H 2气的质量为________________.(普适气体常量R = J ·mol 1·K 1)21. (3分) 体积为103 m 3、压强为 ×105 Pa 的气体分子的平动动能的总和为 _____________J .22.(3分)某气体在温度为T = 273 K 时,压强为p =×102 atm ,密度 = ×102 kg/m 3,则该气体分子的方均根速率为___________. (1 atm = ×105 Pa)23. (4分) 图示氢气分子和氧气分子在相同温度下的麦克斯韦速率分布曲线.则氢气分子的最概然速率为______________,氧分子的最概然速率为____________.24. 当理想气体处于平衡态时,若气体分子速率分布函数为f (v ),则分子速率处于最概然速率v p 至∞范围内的概率△N / N =________________.25. (4分) 一定量的理想气体,经等压过程从体积V 0膨胀到2V 0,则描述分子运动的下列各量与原来的量值之比是(1) 平均自由程0λλ=__________. (2) 平均速率0v v =__________. (3) 平均动能0K K εε=__________. 26.(4分)氮气在标准状态下的分子平均碰撞频率为×108 s -1,分子平均自由程为 6×10-6 cm ,若温度不变,气压降为 atm ,则分子的平均碰撞频率变为_______________;平均自由程变为_______________.27.一定量的某种理想气体,先经过等体过程使其热力学温度升高为原来的2倍;再经过等压过程使其体积膨胀为原来的2倍,则分子的平均自由程变为原来的__________倍.*28. (3分) 处于重力场中的某种气体,在高度z 处单位体积内的分子数即分子数密度为n .若f (v )是分子的速率分布函数,则坐标介于x ~x +d x 、y ~y +d y 、z ~z +d z 区间内,速率介于v ~ v + d v 区间内的分子数d N =____________________.*29. (3分) 一个很长的密闭容器内盛有分子质量为m 的理想气体,该容器以匀加速度a ϖ垂直于水平面上升(如图所示).当气体状态达到稳定时温度为T ,容器底部的分子数密度为n 0,则容器内离底部高为h 处的分子数密度n =____________. *30. (3分) 已知大气压强随高度h 变化的规律为 f ()v 1000 h n n 0 a ϖ⎪⎭⎫ ⎝⎛-=RT gh M p p mol 0exp 拉萨海拔约为 3600 m ,设大气温度t =27℃,而且处处相同,则拉萨的气压p =________________. (空气的摩尔质量M mol = 29×103 kg/mol , 普适气体常量R =J ·mol 1·K 1 , 海平面处的压强p =1 atm ,符号exp(a ) ,即e a)*31. 已知大气压强随高度h 的变化规律为 ⎪⎭⎫ ⎝⎛-=RT gh M p p mol 0exp 设气温t =5 ℃,同时测得海平面的气压和山顶的气压分别为 750 mmHg 和 590 mmHg ,则山顶的海拔h =__________m. (普适气体常量R = J ·mol -1·K -1,空气的摩尔质量M mol =29×10-3kg / mol ,p 0为h =0处的压强.符号exp(a ),即e a )三、计算题1. (5分) 一氧气瓶的容积为V ,充了气未使用时压强为p 1,温度为T 1;使用后瓶内氧气的质量减少为原来的一半,其压强降为p 2,试求此时瓶内氧气的温度T 2.及使用前后分子热运动平均速率之比21/v v .2. (5分) 黄绿光的波长是5000οA (1οA =1010 m).理想气体在标准状态下,以黄绿光的波长为边长的立方体内有多少个分子(玻尔兹曼常量k =×1023J ·K 1) 3. (10分) 一密封房间的体积为 5×3×3 m 3,室温为20 ℃,室内空气分子热运动的平均平动动能的总和是多少如果气体的温度升高 K,而体积不变,则气体的内能变化多少气体分子的方均根速率增加多少已知空气的密度= kg/m 3,摩尔质量M mol =29×103 kg /mol ,且空气分子可认为是刚性双原子分子.(普适气体常量R = J ·mol 1·K 1)4. (5分) 已知某理想气体分子的方均根速率为 400 m ·s 1.当其压强为1 atm 时,求气体的密度.5. (5分) 质量m = ×1017 g 的微粒悬浮在27℃的液体中,观察到悬浮粒子的方均根速率为1.4 cm ·s 1.假设粒子速率服从麦克斯韦速率分布,求阿伏伽德罗常数.(普适气体常量R = J ·mol 1·K 1 )6. (10分) 容积为20.0 L(升)的瓶子以速率v =200 m ·s 1匀速运动,瓶子中充有质量为100g 的氦气.设瓶子突然停止,且气体的全部定向运动动能都变为气体分子热运动的动能,瓶子与外界没有热量交换,求热平衡后氦气的温度、压强、内能及氦气分子的平均动能各增加多少(摩尔气体常量R = J ·mol -1·K 1,玻尔兹曼常量k =×10-23 J ·K 1)7. (10分)有 2×103 m 3刚性双原子分子理想气体,其内能为×102 J .(1) 试求气体的压强;(2) 设分子总数为 ×1022个,求分子的平均平动动能及气体的温度.8. (5分) 一氧气瓶的容积为V ,充了气未使用时压强为p 1,温度为T 1;使用后瓶内氧气的质量减少为原来的一半,其压强降为p 2,试求此时瓶内氧气的温度T 2.及使用前后分子热运动平均速率之比21/v v .9. (10分) 当氢气和氦气的压强、体积和温度都相等时,求它们的质量比()()e H H 2M M 和内能比()()e H H 2E E .(将氢气视为刚性双原子分子气体) 10. (5分) 计算下列一组粒子的平均速率和方均根速率.粒子数N i 2 4 6 8 2速率v i (m/s) 11. (10分) 导体中自由电子的运动可看成类似于气体中分子的运动.设导体中共有N 个自由电子,其中电子的最大速率为v m ,电子速率在v ~v + d v 之间的概率为⎩⎨⎧=0d d 2v v A N N 式中A 为常数.(1) 用N ,v m 定出常数A ;(2) 试求导体中N 个自由电子的平均速率.12. (10分) 由N 个分子组成的气体,其分子速率分布如图所示. (1) 试用N 与0v 表示a 的值.(2) 试求速率在0v ~0v 之间的分子数目.(3) 试求分子的平均速率.13. (10分) N 个粒子,其速率分布如图所示(v > 50v 时粒子数为零). (1) 试用N 与0v 表示a 的值.(2) 试求速率在 20v ─ 30v 间的粒子数.(3) 试求粒子的方均根速率. 14. (5分) 某种气体由大量分子组成,试证明:分子热运动的方均根速率恒大于或等于平均速率,即()2/12v ≥ v .15. (5分) 今测得温度为t 1=15℃,压强为p 1= m 汞柱高时,氩分子和氖分子的平均自由程分别为:Ar λ= ×108 m 和Ne λ=×108 m ,求:(1) 氖分子和氩分子有效直径之比d Ne / d Ar =(2) 温度为t 2=20℃,压强为p 2= m 汞柱高时,氩分子的平均自由程/Ar λ=16. (5分) 在什么条件下,气体分子热运动的平均自由程λ与温度T 成正比在什么条件下,λ与T 无关(设气体分子的有效直径一定)aNf (v ) v v 0 0O a/3 a 2a/3Nf (v ) v v 0 2v 0 3v 0 4v 0 5v 0 O0≤v ≤v mv >v m答:从()p d kT 2π2/=λ可见,对于分子有效直径一定的气体,当压强p 恒定时,λ与T 成正比.从()n d 2π2/1=λ和n = N / V 可见,对于分子有效直径一定的气体,当分子 总数N 和气体体积V 恒定时,λ与T 无关.17. (5分) 在A 、B 、C 三个容器中,装有不同温度的同种理想气体,设其分子数密度之比n A ∶n B ∶n C =1∶2∶4,方均根速率之比()()()2/122/122/12::C B A v v v =1∶2∶4.则其算术平均速率之比为C B A v v v ::=1∶4∶16,压强之比为p A ∶p B ∶p C =1∶4∶16. 以上关于算术平均速率之比值与压强之比值是否正确如有错误请改正.18.(10分) 根据22123v m n p =和kT m 23212=v 两式,从气体分子动理论角度推导气体实验三定律:即玻意耳马略特定律、盖吕萨克定律和查理定律.19.(5分)试以分子动理论的观点解释玻意耳定律(T 不变,pV =C ).*20. (5分)试由麦克斯韦速度分布函数 )2/exp()2()(2/3kT m kTm f v v v ϖϖϖ⋅-π=导出麦克斯韦速率分布函数F (v ).*21. (10分) 假定大气层各处温度相同均为T ,空气的摩尔质量为M mol .试根据玻尔兹曼分布律 ()/kT E P n n -=e 0证明大气压强p 与高度h (从海平面算起,海平面处的大气压强为p 0)的关系是 ⎪⎪⎭⎫ ⎝⎛=p p g M RT h 0mol ln .大学物理竞赛训练题 热学(1)参考答案:一、选择题(每题3分) 1. C 2331002.6104.221⨯⨯⨯- 2. B P =nkT , nV=pV/kT 3. B P =nkT ,nkT+nk T=0 -n/n =T/T 4. C P =nkT , E K /V=n kT nw 23=,RT M M pV mol =, RT pM mol =ρ 5. D kT nw 23= 6. B7. C RT M M pV mol =, p RT M mol =ρ, kT w 23=, 8. C 231υnm p = 9. C 2H 2O. RT v E O H 26202=,RT v RT v RT v E O H 25325252000,22=+= 25.01212152222,=-=-OH OH O H E E E 2i E v RT = pV vRT = 2i E pV = 11.B N a a a a a =++++000003223υυυυυ 12. B 22p molkT RT m M υ== 14. C mol mol M RT M RT m kT 60.188≈==ππυ; 2132162222=⋅==o o o o o o T M M T υυ 15. B16. C kT p d Z υπ22=, p d kT 22πλ= 17. B n d Z υπ22=, mol M RT m kT ππυ88==18. C kTpM RT d n d Z mol ππυπ82222==19. B 20. A 21. B二、填空题 1. RTpM V M mol==ρ ,molp M RT2=υ. 22p p υρ=2. 4233274230100.210707.010103.32100.21045cos 2---⨯⨯⨯⨯⨯⨯=⨯⨯=υm p = ×10 3Pa 3. P=nkT , kT w 23=, w n w k nk p 3232==. 1∶1∶1 4. RT M M pV mol =, p RTMmol =ρ; molM RTmkT332==υ p RT M mol =ρp 22)(3υ=24)450(1073⨯⨯==1.037kg.m -3. kg ·m 35. ix ix ix m m m P υυυ2])[(=---=∆=×10-24kg m / sn 0=122826010312001061--⨯=⨯⨯==∆∆⨯⨯=s m n S S n n x x υυP n p ∆=0=4×103Pa 6. 等压; 等体; 等温. 7. g/mol 8. m u 2/ 3k9. ×1020; ×105kg/m 3; 2 J . 10. RT i v E 2=,V vRT i V E 2=, vRT pV =, p i V E 2=, 5 / 3molM RT i M E 2=, 10 / 3 11. 28×103kg / mol 12. K 13. ×10714. ×10315. p 1V =RT 1 p 2V =RT 2; E 1=21i RT 1=21i p 1V , E 2=21i RT 2=21i p 2V∴ E 2 / E 1=p 2 / p 116. kT i N E 2=, 3001038.161074.322233⨯⨯⨯⨯⨯==-ikT E N =×1023个 17. % 18. ×1026kg19. ×1023个 20. ×103kg 21. ×102 22. 495 m/s 23. mol p M RTmkT22==υ, O 2: 1000m/s , 4==molHmolOPopH M M υυ, H 2: 4000m/s,24.⎰∞pf v v v d )(25. n d 221πλ=,20==n n λλ , mol M RT πυ8=,vRT pV =,2T 0=T , 200==T T υυkT iK 2=ε 2 26. n d Z υπ22=kTpd υπ22=; pd kTn d Z 22221ππυλ=== ×107s -1; 6×10-5cm27. 2*28. dN=N f (v ) d v=n f (v )d x d y d z d v *29. kTmgh n -e0, 相对加速度g +a , kTh a g m n )(0e+-*30. 329109.836001exp 8.31300p -⎛⎫⨯⨯⨯=⨯- ⎪⨯⎝⎭=*31. 1950 三、计算题1. 解: p 1V =RT 1 p 2V =21RT 2∴ T 2=2 T 1p 2 / p 12121212P P T T ==v v2.解:理想气体在标准状态下,分子数密度为n = p / (kT )=×1025 个/ m 3以5000οA 为边长的立方体内应有分子数为N = nV =×106个.3.解:根据 kT m 23212=v , 可得 NkT m N 23212=v , 即=()RT M M mol /23=()V M RT ρmol /23=×106 . 又 ()T iR M M E ∆=∆21/mol =()T iR M V ∆21/mol ρ=×104J .及 ()()()2/1212/1222/12v v v-=∆= ()()122/1mol /3T TM R -= m/s .4.解: 223131v v ρ==nm p ∴ 90.1/32==v p ρ kg/m 35.解:据 ()m N RT M RT A /3/3mol 2/12==v,得 N A =3RT / (m 2v )=×1023mol -1.6.解:定向运动动能221v Nm ,气体内能增量T ik N ∆21,i =3 .按能量守恒应有: 221v Nm =T ik N ∆21∴ AN T iR m /2∆=v(1) ()()===∆iR M iR m N T A //2mol 2v v K(2) ()V T R M M p //mol ∆=∆=×104Pa . (3) ()T iR M M E ∆=∆21/mol =×103J .(4) T ik ∆=∆21ε=×1022 J . 7. 解:(1) 设分子数为N .据 E = N (i / 2)kT 及 p = (N / V )kT 得 p = 2E / (iV ) = ×105Pa(2) 由 kT N kT Ew2523=ϖϖ得 ()21105.75/3-⨯==N E w J又 kT NE 25= 得 T = 2 E / (5Nk )=362k 8.解: p 1V =RT 1 p 2V =21RT 2∴ T 2=2 T 1p 2 / p 12121212P P T T ==v v 9.解: 由 pV =()()mol22H H M M RT 和pV =()()mol e H e H M M RT得 ()()e H H 2M M =()()m ol m ol 2e H H M M =42=21.由 E (H 2)=()()mol 22H H M M 25RT 和RT M M E 23)He ()He ()He (mol =得 ()()e 2H E H E =()()()()molmol22e H /He 3H /H 5M M M M∵()()mol 22H M H M = ()()mole H M e H M (p 、V 、T 均相同), ∴ ()()e H E H E 2=35.10. 解:平均速率∑∑=ii i N N /v v= m/s 方均根速率 ()∑∑=iii NN 22/12v v= m/s .11. 解:(1) 根据已知条件可知电子速率分布函数为⎩⎨⎧==0d d )(2v v v A N Nf 根据速率分布函数的归一化条件1d )(0=⎰∞v v f有13d 0d 22==+⎰⎰∞m A A mmv v v v v v 0解得 33mA v =(2) 根据平均速率定义 NN ⎰=d v v可得 ⎰∞=0d )(v v v v f ⎰=mf v v v v 0d )(0≤v ≤v m v > v mm m A A mv v v v v v 4341d 402===⎰ 12. 解:(1) 由分布图可知:0→v 0: N f (v ) = ( a / v 0) v , f (v ) = av /(N v 0).v 0→2 v 0: N f (v ) = a , f (v ) = a /N .2v 0 f (v ) = 0由归一化条件1d )(0=⎰∞v v f , 有 1d /d )/(020=+⎰⎰v v v v v vv N a N a ,得: ( 3 /2 ) ( av 0 /N ) = 1 , ∴ a = ( 2 /3 ) ( N /v 0).(2) ⎰⎰==∆0000223223d d )(v v v v v v v N a NNf N 021v a =, 将a 代入得 N N N 31)3/(22100=⨯=∆v v . (3) 0→v 0: f (v ) = a v /(N v 0) = (v / N v 0)×2 N / (3 v 0) )3/(220v v =. v 0→2 v 0: f (v ) = a /N = ( 1 / N )×( 2 N / 3 v 0) = 2 / (3 v 0).⎰∞=0d )(v v v v f v vv v v v v v v v d )3/(2d )3/(20202⎰⎰⨯+⨯=0092v v +==11 v 0 /913. 解:(1) 曲线下的面积代表总分子数N ,N a a a a a =++++0000032313231v v v v v , ∴ )3(0v N a =.(2) 速率在2v 0 ─3 v 0间的粒子数3/)3/(000N N a N ===∆v v v .(3) ⎰∞=022d )(v v v v f ⎰∞=02d )()/1(v v v Nf N⎢⎢⎣⎡=⎰002d )()/1(v v v v Nf N ++⎰0022d )(v v v v v Nf⎰+00322d )(v v v v v Nf ⎰+00432d )(v v v v v Nf ⎥⎥⎦⎤+⎰00542d )(v v Nf v v v{+-+=])2[(313231311303030v v v a a N +-+-+])3()4[(3132])2()3[(3130303030v v v v a a}])4()5[(31313030v v -+a 2v 20323v =()02/1202/1277.2])3/23[(v v v ==.14.证法1:设速率分布函数为 F (v )则 1d )(0=⎰∞v v F , ⎰∞=022d )(v v v v F ,⎰∞=0d )(v v v v F由于定积分性质: 2]d )()([⎰b ax x g x f ≤⎰⋅⎰bab ax x g xx f d )]([d )]([22所以有: ()22]d )()([v v v v v ⋅⋅=⎰∞F F ≤⎰⎰∞∞⋅020d )(d )(v v v v v F F 2v =即 ()2v ≤2v 或 ()2/12v≥v证法2:因为 2)(v v -≥0而 2)(v v -22222)()(22v v v v v v v +-=+-=()22v v -= ∴ ()22v v -≥02/12)(v ≥v15. 解:(1) 据 ()p d kT 22/π=λ得 d Ne / d Ar =()2/1NeAr /λλ= .(2) /Ar λ=Ar λ(p 1 / p 2)T 2 / T 1=()()2732731221Ar ++t p t p λ=×107m .16. 答:从()p d kT 2π2/=λ可见,对于分子有效直径一定的气体,当压强p 恒定时,λ与T 成正比.从()n d 2π2/1=λ和n = N / V 可见,对于分子有效直径一定的气体,当分子总数N 和气体体积V 恒定时,λ与T 无关.17.答:以上两个比值的结果是错误的,改正如下: 对于不同温度的同种理想气体,有CB A v v v ::=()()()2/122/122/12::CB A v v v =1 : 2 : 4根据理想气体压强公式231v nm p =可得 Ap B p C p =()()()222::CC B B A A n n n v v v =1:8:6418.推导:由22123v m n p =及kT m 23212=v 得 nkT p =.即 ()kT V N nkT p /==, NkT pV =. 一定量的气体N 不变,在温度T 不变时,NkT = 恒量.故 pV = 恒量 玻意耳马略特定律 又 p = nkT , p / T = nK = (N /V )k . 一定量的气体N 不变,在体积V 不变时,(N /V )k = 恒量.故 (p / T ) = 恒量 查理定律. 再由 p = nkT = (N / V )kT 得 (V / T ) = (Nk ) / p . 一定量的气体N 不变,在压强p 不变时,Nk / p = 恒量. 故 V / T = 恒量 盖吕萨克定律19.答:当一定质量的理想气体的温度保持一定时,其压强与体积的乘积等于常量,即pV =C .也就是说:压强p 与体积V 成反比.根据分子运动论的观点,压强p 应正比于分子每次碰壁所施于器壁的平均冲量和分子在单位时间内碰撞单位面积器壁的次数这二者的乘积. 2分前者取决于分子的平均平动动能w ,也就是说取决于气体的温度T (kT w 23=),后者则正比于分子的数密度n ,而在总分子数一定时,n 又是反比于V 的.所以在T 一定的情况下,p 反比于V ,这就是玻意耳定律. 3分*20.解:设F (v )为速率分布函数,则有vv d d )(N NF =, ∴ v v d )(d NF N = ①①式的物理意义为速率分布在v ~v + d v 区间内的分子数.v ~v + d v 区间在速度空间里为一半径为v 厚度为d v 的球壳(如图所示).)(v ϖf 的物理意义为速度空间中的概率密度.在本题中)(v ϖf 为速度空间中的球对称函数.图中球壳的体积为v v d π42.速度分布在球壳中的分子数为v v v d 4)(d 2π=ϖNf N ②比较①式和②式得 24)()(v v v π=ϖf F 22v 2/32)2(4v kT m e kTm -ππ= *21.证:设空气分子的质量为m ,则在离海平面高度为h 处,空气分子的势能为E p =mgh ,于是有 h RTgM h kTN mgN h kTmg n n n n AAmol eee000---=== 2分那么,由 p = nkT =h RTgM h RTgM p kT n mol mol ee00--= 1分取对数 ln(p / p 0) =-M mol g h / RTh = RT ln (p 0/p ) / M mol g 2分。
