哈工大_计算方法实验_1拉格朗日
数值计算方法拉格朗日牛顿插值实验

实验二 插值法
实验目的
1. 掌握拉格朗日插值法、牛顿插值法、牛顿前后插值法及分段插值法的原理与算法。 2. 讨论几种方法的计算精度与误差,分析拉格朗日插值与牛顿插值法的差异。 3. 学会使用 Matlab 绘图方法,并以此方法来显示插值函数,使结果更直观更形象。
算法原理
(一)拉格朗日插值法
牛顿向前插值法 牛顿向后插值法
牛顿向前插值作业
牛顿向后插值
数据测试结果
(1)选取 n=7,拉格朗日插值结果为:
(2)选取 n=7,牛顿插值法结果为:
(3) (4)X1=1.3,x2=5.6,牛顿向前向后插值法结果为:
(一)分析讨论
1.总结 Matlab 编程的基本特点,特别是需要注意的地方。 答:能直接对矩阵进行操作,能实现简单的矩阵的乘除,方便进行数值计算。注 意的地方就是矩阵进行点乘、点除时行数列数要一样。
2.对比拉格朗日插值法和牛顿插值法的差异,特别是在计算量上的差异。 答:拉格朗日插值法与牛顿插值法都是二种常用的简便的插值法。但牛顿法
插值法则更为简便,可以节省乘、除法运算次数。拉格朗日插值法计算过程没有 继承性,每增加一个节点,整个计算过程要重新进行,牛顿插值法避免了这个问 题,减少了计算的步数。
3.对比牛顿前插和牛顿后插两种方法的差异,讨论分析同一个数值两种方法的计 算结果。
答:如果插值点 x 离 x0。比较近,则一般使用牛顿前差公式;如果插值点 x
离 x0。比较远,则一般使用牛顿后差公式。但对于同一个插值点 x 来说,不管 用牛顿前差公式还是用牛顿后差公式,得到的结果是一-样的,这两种插值公式 只是形式上的差别。 4.讨论分段插值法的意义。
答:高次插值的收敛性没有保证,实际计算稳定性也没有保证,所以当插值结 点 n 较大时,通常不采用高次多项式插值,用低次多项式插值,它能保证收敛性, 得到的结果也相对稳定。
计算方法上机实验报告——拉格朗日插值问题

计算方法上机实验报告——拉格朗日插值问题一、方法原理n次拉格朗日插值多项式为:Ln(x)=y0l0(x)+y1l1(x)+y2l2(x)+…+ynln(x) n=1时,称为线性插值,L1(x)=y0(x-x1)/(x0-x1)+y1(x-x0)/(x1-x0)=y0+(y1-x0)(x-x0)/(x1-x0) n=2时,称为二次插值或抛物线插值,精度相对高些L2(x)=y0(x-x1)(x-x2)/(x0-x1)/(x0-x2)+y1(x-x0)(x-x2)/(x1-x0)/(x1-x2)+y2(x-x0)(x-x1)/(x2-x0)/(x2-x1)二、主要思路使用线性方程组求系数构造插值公式相对复杂,可改用构造方法来插值。
对节点xi(i=0,1,…,n)中任一点xk(0<=k<=n)作一n次多项式lk(xk),使它在该点上取值为1,而在其余点xi(i=0,1,…,k-1,k+1,…,n)上为0,则插值多项式为Ln(x)=y0l0(x)+y1l1(x)+y2l2(x)+…+ynln(x)上式表明:n个点xi(i=0,1,…,k-1,k+1,…,n)都是lk(x)的零点。
可求得lk三.计算方法及过程:1.输入节点的个数n2.输入各个节点的横纵坐标3.输入插值点4.调用函数,返回z函数语句与形参说明程序源代码如下:形参与函数类型参数意义intn节点的个数doublex[n](double*x)存放n个节点的值doubley[n](double*y)存放n个节点相对应的函数值doublep指定插值点的值doublefun()函数返回一个双精度实型函数值,即插值点p处的近似函数值#include<iostream>#include<math.h>usingnamespacestd;#defineN100doublefun(double*x,double*y,intn,doublep);voidmain(){inti,n;cout<<"输入节点的个数n:";cin>>n;doublex[N],y[N],p;cout<<"pleaseinputxiangliangx="<<endl;for(i=0;i<n;i++)cin>>x[i];cout<<"pleaseinputxiangliangy="<<endl;for(i=0;i<n;i++)cin>>y[i];cout<<"pleaseinputLagelangrichazhiJieDianp="<<endl;cin>>p;cout<<"TheAnswer="<<fun(x,y,n,p)<<endl;system("pause");}doublefun(doublex[],doubley[],intn,doublep){doublez=0,s=1.0;intk=0,i=0;doubleL[N];while(k<n){if(k==0){for(i=1;i<n;i++)s=s*(p-x[i])/(x[0]-x[i]);L[0]=s*y[0];k=k+1;}else{s=1.0;for(i=0;i<=k-1;i++)s=s*((p-x[i])/(x[k]-x[i]));for(i=k+1;i<n;i++)s=s*((p-x[i])/(x[k]-x[i]));L[k]=s*y[k];k++;}}for(i=0;i<n;i++)z=z+L[i];returnz;}四.运行结果测试:五.实验分析n=2时,为一次插值,即线性插值n=3时,为二次插值,即抛物线插值n=1,此时只有一个节点,插值点的值就是该节点的函数值n<1时,结果都是返回0的;这里做了n=0和n=-7两种情况3<n<100时,也都有相应的答案常用的是线性插值和抛物线插值,显然,抛物线精度相对高些n次插值多项式Ln(x)通常是次数为n的多项式,特殊情况可能次数小于n.例如:通过三点的二次插值多项式L2(x),如果三点共线,则y=L2(x)就是一条直线,而不是抛物线,这时L2(x)是一次式。
拉格朗日插值实验报告

拉格朗日插值实验报告一、实验目的本实验旨在通过实际实验,深入理解拉格朗日插值法的原理和应用,掌握其计算过程和相关技巧。
二、实验原理Pn(x) = ∑ [yi * li(x)]其中,li(x)称为拉格朗日基函数,具体的计算公式如下:li(x) = ∏ [(x-xj)/(xi-xj)] (i≠j)利用拉格朗日插值法可以对数据进行插值计算,从而得到原函数未知的点的函数值。
三、实验步骤1.根据实验要求,选择一组离散的数据点,确保它们在横坐标轴上不共线。
2. 使用拉格朗日插值法计算插值多项式的各个基函数li(x)。
3.对插值多项式进行求和,得到最终的插值多项式Pn(x)。
4.在给定的范围内选择一些未知数据点,利用插值多项式Pn(x)计算其函数值。
5.将实际计算的函数值与原函数值进行对比,评估插值方法的准确性和精确度。
四、实验结果以实验要求给定的数据点为例,具体数据如下:x:1,2,3,4,5,6y:5,19,43,79,127,187根据拉格朗日插值法的计算公式,可以得到以下结果:l0(x)=(x-2)(x-3)(x-4)(x-5)(x-6)/(-120)l1(x)=(x-1)(x-3)(x-4)(x-5)(x-6)/120l2(x)=(x-1)(x-2)(x-4)(x-5)(x-6)/(-48)l3(x)=(x-1)(x-2)(x-3)(x-5)(x-6)/48l4(x)=(x-1)(x-2)(x-3)(x-4)(x-6)/(-20)l5(x)=(x-1)(x-2)(x-3)(x-4)(x-5)/20插值多项式Pn(x)=5*l0(x)+19*l1(x)+43*l2(x)+79*l3(x)+127*l4(x)+187*l5(x)综合以上计算结果,可以对给定范围内的未知数据点进行插值计算,从而得到相应的函数值。
五、实验分析与结论在实际实验中,我们可以利用拉格朗日插值法对任意给定的函数进行逼近计算,从而得到函数在离散数据点之间的近似值。
拉格朗日点计算公式

拉格朗日点计算公式
拉格朗日点是在两个物体之间的特定位置,使得这两个物体之间的引力与向心力平衡。
拉格朗日点是天体力学中的一个重要概念,被广泛应用于航天工程和天体物理学研究中。
计算拉格朗日点的位置需要使用拉格朗日点计算公式。
拉格朗日点有五个位置,分别命名为L1、L2、L3、L4和L5。
其中L1、L2和L3位于主天体和次天体的连线上,L4和L5则位于主天体和次天体组成的等边三角形的顶点上。
对于一个二体系统,计算L1、L2和L3点的位置可以使用以下拉格朗日点计算公式:
r1 = a * (1 - μ)^(1/3)
r2 = a * (1 + μ)^(1/3)
其中,r1和r2分别是L1和L2点到次天体的距离,a是主天体到次天体的距离,μ是主天体质量与总质量的比值。
对于一个三体系统,计算L4和L5点的位置则需要使用以下拉格朗日点计算公式:
r = ((9 * μ) / (2 * (1 - μ)))^(1/3)
其中,r是L4和L5点到主天体的距离,μ是主天体质量与次天体质量之比。
需要注意的是,这些计算公式是在假设天体为质点且忽略其他天体的干扰下得出的,因此在实际应用中可能需要考虑更多的因素,例如天体的形状、引力场的非均匀性等。
总之,拉格朗日点计算公式是计算拉格朗日点位置的重要工具,能够帮助科学家和工程师在航天和天体物理学领域进行精确的位置预测和轨道规划。
实验一 拉格朗日插值Matlab实验报告

北京理工大学珠海学院实验报告
ZHUHAI CAMPAUS OF BEIJING INSTITUTE OF TECHNOLOGY
班级2012电气2班学号xxxxxxxxx姓名陈冲指导教师张凯成绩
实验题目(实验一)拉格朗日插值实验地点及时间JD501 2013/12/26(6-7节)
一、实验目的
1.掌握用程序语言来编辑函数。
2.学会用MATLAB编写Lagrange.m函数。
二、实验环境
Matlab软件
三、实验内容
1、以书中第55页题目13为例编辑程序来实现计算结果。
2、使用MATLAB进行编写:
第一步:编写Lagrange.m函数,代码如下
第二步:利用这个函数来编辑命令:(可见实验结果中的截图)
x=[0.32,0.34,0.36];
y=[sin(0.32),sin(0.34),sin(0.36)];
x0=0.3367;
yt=Lagrange(x,y,x0)
得出抛物线插值为:0.3304
以及
x=[0.32,0.34];
y=[sin(0.32),sin(0.34)];
x0=0.3367;
yt=Lagrange(x,y,x0)
得出线性插值为:0.3304
的近似值并估计误差。
五、实验结果。
六、总结
通过这次实验我学会用MATLAB软件编辑口令进行计算,实验结果是正确的,我相信在以后的实验中,我可以做好每一步,练习好每一次的上机。
实验难度不是很大,主要要注意标点符号的正确性。
………。
长春工大计算方法实验课程指导书2016

《计算方法》实验课程指导书徐中宇2016年9月目录第一章插值法 (1)§1拉格朗日插值 (1)§2牛顿插值 (5)第二章数值积分 (8)第三章线性方程组的解法 (10)§1高斯消去法 (10)§2列主元消去法 (14)§3线性方程组的迭代解法 (18)第四章方程求根 (23)§1二分法 (23)§2牛顿迭代法 (26)§3埃特金(A ITKEN)迭代法 (28)第一章 插值法目的与要求:1. 掌握不同的输入、输出语句,注意节约内存方法。
2. 熟悉拉格朗日插值和牛顿插值公式,并体会它们不同的特点。
§1拉格朗日插值1.方法概要:拉格朗日N 次插值多项式 0()()nn i L x li x yi ==∑,其中0,()()/()ni j i j j j il x x x x x =≠=--∏可用双重循环来实现;内循环为连乘;外循环为连加。
用数组表下标变量,给出i i y x ,。
图1-1 拉格朗日插值法程序流程图3.程序及例例1.1 已知函数表:X I 0.56160 0.56280 0.56401 0.56521Y I 0.82741 0.82659 0.82577 0.82495用三次拉格朗日插值多项式求X=0.5635时的函数值。
程序为#INCLUDE "STDAFX.H"#INCLUDE <IOSTREAM.H>CONST INT N=3;CONST DOUBLE XX=0.5635;VOID MAIN(){DOUBLE X[N+1]={0.56160,0.56280,0.56401,0.56521}; DOUBLE Y[N+1]={0.82741,0.82659,0.82577,0.82495};DOUBLE L=0,LI=1;FOR (INT I=0;I<=N;I++){LI=1;FOR (INT J=0;J<=N;J++){IF (J!=I){LI=LI*(XX-X[J])/(X[I]-X[J]);}}L+=LI*Y[I];}COUT<<"THE RESULT IS:"<<L<<ENDL;}例1.2已知函数表,用拉格朗日插值多项式求0.5,0.7,0.85三点处的函数值。
哈工大计算方法上机实验指导
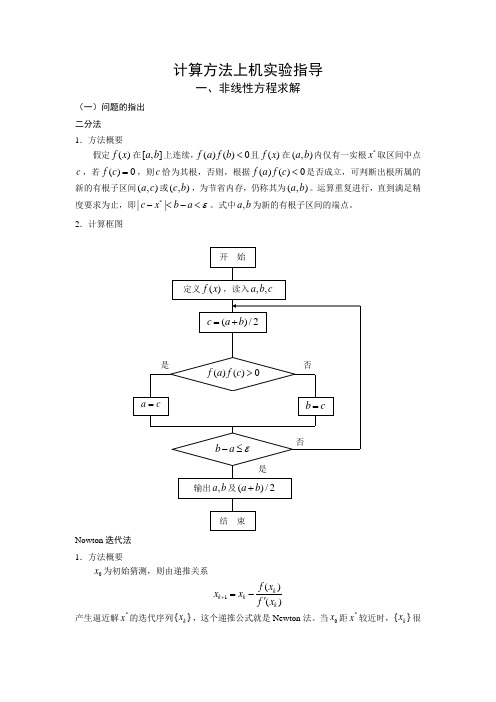
计算方法上机实验指导一、非线性方程求解(一)问题的指出 二分法 1.方法概要假定()f x 在[,]a b 上连续,()()0f a f b <且()f x 在(,)a b 内仅有一实根*x 取区间中点c ,若()0f c =,则c 恰为其根,否则,根据()()0f a f c <是否成立,可判断出根所属的新的有根子区间(,)a c 或(,)c b ,为节省内存,仍称其为(,)a b 。
运算重复进行,直到满足精度要求为止,即*||c x b a ε-<-<。
式中,a b 为新的有根子区间的端点。
2.计算框图Nowton 迭代法 1.方法概要0x 为初始猜测,则由递推关系1()()k k k k f x x x f x +=-' 产生逼近解*x 的迭代序列{}k x ,这个递推公式就是Newton 法。
当0x 距*x 较近时,{}k x 很快收敛于*x 。
但当0x 选择不当时,会导致{}k x 发散。
故我们事先规定迭代的最多次数。
若超过这个次数,还不收敛,则停止迭代另选初值。
2.计算框图(二)目的掌握二分法与牛顿法的基本原理及应用 (三)要求1.用二分法计算方程2sin 02x x -=在(1,2)内的根的近似值 2.用二分法计算方程310x x --=在(1,1.5)内的根的近似值5(0.510)ε-=⨯。
3.用牛顿法求下列非线性方程的近似根。
① 10xxe -= 00.5x = ② 310x x --= 01x =③ 2(1)(21)0x x --= 00.45x = 00.65x =4.用改进的牛顿法12()()k k k k f x x x f x +=-'计算方程20(1)(21)00.55x x x --==的近似根,并与要求3.中的③的结果进行比较。
二、Gauuss 列主元消去法(一)问题的提出由地一般线性方程组在使用Gauss 消去法求解时,从求解过程中可以清楚地看到,若(1)0k kk a -=,必须施以行交换的手续,才能使消去过程继续下去。
拉格朗日方程的三种推导方法

拉格朗日方程的三种推导方法 1 引言拉格朗日方程是分析力学中的重要方程,其地位相当于牛顿第二定律之于牛顿力学。
2 达朗贝尔原理推导达朗贝尔原理由法国物理学家与数学家让•达朗贝尔发现并以其命名。
达朗贝尔原理表明:对于任意物理系统,所有惯性力或施加的外力,经过符合约束条件的虚位移,所作的虚功的总合为零。
即:δW =∑(F i +I i )∙δr i =0i(1)其中I i 为惯性力,I i=−m i a i 。
F i 为粒子所受外力,δr i 为符合系统约束的虚位移。
设粒子 P i 的位置 r i 为广义坐标q 1,q 2,⋯,q n 与时间 t 的函数:r i =r i (q 1,q 2,⋯,q n ,t)则虚位移可以表示为:δr i =∑ðr i ðq jjδq j(2)粒子的速度v i=v i (q 1,q 2,⋯,q n ,q 1,q 2,⋯,q n ,t) 可表示为:取速度对于广义速度的偏微分:(3)首先转化方程 (1) 的加速度项。
将方程 (2) 代入:应用乘积法则:注意到的参数为,而速度的参数为,所以,。
因此,以下关系式成立:(4) 将方程(3) 与(4) 代入,加速度项成为代入动能表达式:,则加速度项与动能的关系为(5) 然后转换方程(1)的外力项。
代入方程(2) 得:(6) 其中是广义力:将方程(5) 与(6) 代入方程(1) 可得:(7) 假设所有的广义坐标都相互独立,则所有的广义坐标的虚位移也都相互独立。
由于这些虚位移都是任意设定的,只有满足下述方程,才能使方程(7) 成立:(8) 这系统的广义力与广义位势之间的关系式为代入得:定义拉格朗日量为动能与势能之差,可得拉格朗日方程:3哈密顿原理推导哈密顿原理可数学表述为:21ttLdtδ=⎰在等时变分情况下,有()dq q dt δδ•=2211()0t t t t Ldt L dt δδ==⎰⎰ (1)由拉格朗日量定义得,在等时变分情况下有L LL q q qqδδδ••∂∂=+∂∂(2)其中第一项可化为:()()()LL d d L d L q q q q dt dt dt q q q q δδδδ•••••∂∂∂∂==•-∂∂∂∂(3)将(3)代入(2)得()()d L d L LL q q qdt dt qq q δδδδ••∂∂∂=•-+∂∂∂ (4)将(4)代入(1)得2121()(())0t t t t L d L L q q q dt dt qqq δδδ••∂∂∂•+-+=∂∂∂⎰(5)在12,t t 处0q δ=,所以(5)变为21(())0t t d L Lq q dt dt qq δδ•∂∂-=∂∂⎰(6)即21[(())]0t t d L Lq dt dt qq δ•∂∂-+=∂∂⎰(7)q 是独立变量,所以拉格朗日方程:4欧拉-拉格朗日方程推导欧拉-拉格朗日方程可以表述为:设有函数和:其中是自变量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验题目1 Lagrange插值摘要给定平面上n+1个不同的数据点:则满足条件的n次拉格朗日插值多项式是存在唯一的。
若,且充分光滑,则当时,有误差估计式前言利用拉格朗日插值多项式求的近似值程序设计流程拉格朗日插值框图问题1 (1)N = 5时,程序运行如下:TestLag(inline('1./(1+x.^2)'), -5, 5, 5, :;将区间[-5,5]分为了5段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =N = 10时,程序运行如下:TestLag(inline('1./(1+x.^2)'), -5, 5, 10, :;将区间[-5,5]分为了10段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =N = 20时,程序运行如下:TestLag(inline('1./(1+x.^2)'), -5, 5, 20, :;将区间[-5,5]分为了20段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =问题1 (2)N = 5时,程序运行如下:TestLag(inline('exp(x)'), -1, 1, 5, [ ]);将区间[-1,1]分为了5段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =*N = 10时,程序运行如下:TestLag(inline('exp(x)'), -1, 1, 10, [ ]);将区间[-1,1]分为了10段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =*N = 20时,程序运行如下:TestLag(inline('exp(x)'), -1, 1, 20, [ ]);将区间[-1,1]分为了20段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =*问题2 (1)N = 5时,程序运行如下:TestLag(inline('1./(1+x.^2)'), -1, 1, 5, [ ]);将区间[-1,1]分为了5段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =N = 10时,程序运行如下:TestLag(inline('1./(1+x.^2)'), -1, 1, 10, [ ]);将区间[-1,1]分为了10段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =N = 20时,程序运行如下:TestLag(inline('1./(1+x.^2)'), -1, 1, 20, [ ]);将区间[-1,1]分为了20段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =*实验2 (2)N = 5时,程序运行如下:TestLag(inline('exp(x)'), -5, 5, 5, [ ]);将区间[-5,5]分为了5段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =N = 10时,程序运行如下:TestLag(inline('exp(x)'), -5, 5, 10, [ ]);将区间[-5,5]分为了10段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =N = 20时,程序运行如下:TestLag(inline('exp(x)'), -5, 5, 20, [ ]);将区间[-5,5]分为了20段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =*问题3 (1)N =5时,程序运行如下:TestLag2(inline('1./(1+x.^2)'), -1, 1, 5, [ ]);将区间[-1,1]分为了5段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =*N =10时,程序运行如下:TestLag2(inline('1./(1+x.^2)'), -1, 1, 10, [ ]);将区间[-1,1]分为了10段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =*N =20时,程序运行如下:TestLag2(inline('1./(1+x.^2)'), -1, 1, 20, [ ]);将区间[-1,1]分为了20段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =*问题3 (2)N =5时,程序运行如下:TestLag2(inline('exp(x)'), -1, 1, 5, [ ]);将区间[-1,1]分为了5段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =*N =10时,程序运行如下:TestLag2(inline('exp(x)'), -1, 1, 10, [ ]);将区间[-1,1]分为了10段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =*N =20时,程序运行如下:TestLag2(inline('exp(x)'), -1, 1, 20, [ ]);将区间[-1,1]分为了20段计算插值的点 xi =计算出的插值 yi =插值点处函数值 yFact =计算误差 err =*问题4(1)程序运行如下:TestLag3([1 4 9], [5 50 115 185])计算插值的点 xi =5 50 115 185计算出的插值 yi =插值点处函数值 yFact =计算误差 err =(2)程序运行如下:TestLag3([36 49 64], [5 50 115 185])计算插值的点 xi =5 50 115 185计算出的插值 yi =插值点处函数值 yFact =计算误差 err =(3)程序运行如下:TestLag3([100 121 144], [5 50 115 185])计算插值的点 xi =5 50 115 185计算出的插值 yi =插值点处函数值 yFact =计算误差 err =(4)程序运行如下:TestLag3([169 196 225], [5 50 115 185])计算插值的点 xi =5 50 115 185计算出的插值 yi =插值点处函数值 yFact =计算误差 err =实验所用函数function yh = LagInterp(x, y, xh)% LagInterp 计算拉格朗日插值%% Synopsis: yh = LagInterp(x, y, xh)%% Input: x = 一维向量,将要做插值x的值% y = 一维向量,将要做插值y的值% xh = 数值或一维向量,计算插值的位置,支持计算一列xh的值%% Output: yh = 数值或一维向量,通过计算插值的位置算出的插值if min(size(x)) > 1 | min(size(y)) > 1 %判断x,y是否为一维向量 error('x,y must be vectors!');elseif length(x) ~= length(y) %判断x,y是否有同样多的元素 error('x and y must agree!');endyh = zeros(size(xh));L = zeros(length(x) - 1);for j = 1:length(xh)for i = 1:length(x)xCal = x;xCal(i) = [];%prod(xh(j) - xCal)/prod(x(i) - xCal)为拉格朗日基函数L(i) = prod(xh(j) - xCal)/prod(x(i) - xCal);yh(j) = yh(j) + L(i) * y(i); %yh = sum(L(i) * y(i)) endendfunction TestLag(fx, a, b, n, xi)% TestLag 实验题目1 1,2%% Synopsis: TestLag(fun, a, b, n, xi)%% Input: fx = 用来验证插值计算准确率的函数% a,b = 节点选取上下限% n = 多项式次数,固定区间[-a,b]分段数% xi = 要计算插值的点x = linspace(a, b, n);y = feval(fx, x);yi = LagInterp(x, y, xi);yFact = feval(fx, xi);err = yFact - yi;fprintf('将区间[%d,%d]分为了%d段\n', a, b, n); fprintf('计算插值的点 xi =\n');disp(xi);fprintf('计算出的插值 yi =\n');disp(yi);fprintf('插值点处函数值 yFact =\n');disp(yFact);fprintf('计算误差 err =\n');disp(err);function TestLag2(fx, a, b, n, xi)% TestLag2 实验题目1 3%% Synopsis: TestLag2(fun, a, b, n, xi)%% Input: fx = 用来验证插值计算准确率的函数% a,b = 节点选取上下限% n = 多项式次数,固定区间[-a,b]分段数% xi = 要计算插值的点x = zeros(1,n);for k = 1:nx(k) = cos( (2*k-1)*pi/(2*n) ); %构造非等距节点 endy = feval(fx, x);yi = LagInterp(x, y, xi);yFact = feval(fx, xi);err = yFact - yi;fprintf('将区间[%d,%d]分为了%d段\n', a, b, n);fprintf('计算插值的点 xi =\n');disp(xi);fprintf('计算出的插值 yi =\n');disp(yi);fprintf('插值点处函数值 yFact =\n');disp(yFact);fprintf('计算误差 err =\n');disp(err);function TestLag3(x, xi)% TestLag3 实验题目1 4%% Synopsis: TestLag3(fun, a, b, n, xi)%% Input: x = 构造Lagrange插值的节点% xi = 要计算插值的点fx = inline('sqrt(x)');y = feval(fx, x);yi = LagInterp(x, y, xi);yFact = feval(fx, xi);err = yFact - yi;fprintf('计算插值的点 xi =\n'); disp(xi);fprintf('计算出的插值 yi =\n'); disp(yi);fprintf('插值点处函数值 yFact =\n'); disp(yFact);fprintf('计算误差 err =\n'); disp(err);思考题1.拉格朗日插值多项式的次数并不是越大越好,根据定义,插值式可以在节点处与实际函数匹配,但不能保证在节点之间很好的逼近实际函数。
