中考数学压轴题费马点,费马点最值问题的解法模型
【中考数学复习】2022中考数学几何模型(费马点,胡不归,阿氏圆)

12讲通关中考数学几何模型中考数学几何模型1:截长补短模型 (1)中考数学几何模型2:共顶点模型 (9)中考数学几何模型3:对角互补模型 (16)中考数学几何模型4:中点模型 (25)中考数学几何模型5:角含半角模型 (35)中考数学几何模型6:弦图模型 (44)中考数学几何模型7:轴对称最值模型 (53)中考数学几何模型8:费马点最值模型 (64)中考数学几何模型9:隐圆模型 (72)中考数学几何模型10:胡不归最值模型 (84)中考数学几何模型11:阿氏圆最值模型 (97)中考数学几何模型12:主从联动模型 (106)中考数学几何模型1:截长补短模型名师点睛拨开云雾开门见山有一类几何题其命题主要是证明三条线段长度的“和”或"差”及其比例关系.这一类题目一般可以采取“截长”或“补短”的方法来进行求解.所谓“截长”,就是将三者中最长的那条线段一分为二,使其中的一条线段与已知线段相等,然后证明其中的另一段与已知的另一段的大小关系.所谓“补短”,就是将一个已知的较短的线段延长至与另一个已知的较短的长度相等.然后求出延长后的线段与最长的已知线段的关系.有的是采取截长补短后,使之构成某种特定的三角形进行求解.典题探究启迪思维探究重点例题1.如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,若E在AD上.求证:(1)BE⊥CE;(2)BC=AB+CD.变式练习>>>1.已知△ABC的内角平分线AD交BC于D,∠B=2∠C.求证:AB+BD=AC.例题2.已知△ABC中,∠A=60°,BD,CE分别平分∠ABC和∠ACB,BD、CE交于点O,试判断BE,CD,BC的数量关系,并说明理由.2.已知:△ABC中,AB=AC,D为△ABC外一点,且∠ABD=60°,∠ADB=90°﹣∠BDC.试判断线段CD、BD与AB之间有怎样的数量关系?并证明你的结论.例题3.如图所示,在五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:DA平分∠CDE.3.如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,M是AB延长线上一点,N是CA延长线上一点,且∠MDN=60°.试探究BM、MN、CN之间的数量关系,并给出证明.例题4.在四边形ABDE中,C是BD边的中点.(1)如图(1),若AC平分∠BAE,∠ACE=90°,则线段AE、AB、DE的长度满足的数量关系为;(直接写出答案)(2)如图(2),AC平分∠BAE,EC平分∠AED,若∠ACE=120°,则线段AB、BD、DE、AE的长度满足怎样的数量关系?写出结论并证明;(3)如图(3),BD=8,AB=2,DE=8,若ACE=135°,求线段AE长度的最大值.例题5.在△ABC中,∠BAC=90°.(1)如图1,直线l是BC的垂直平分线,请在图1中画出点A关于直线l的对称点A′,连接A′C,A′B,A′C与AB交于点E;(2)将图1中的直线A′B沿着EC方向平移,与直线EC交于点D,与直线BC交于点F,过点F作直线AB的垂线,垂足为点H.①如图2,若点D在线段EC上,请猜想线段FH,DF,AC之间的数量关系,并证明;②若点D在线段EC的延长线上,直接写出线段FH,DF,AC之间的数量关系.例题6.如图1,在△ABC中,∠ACB=2∠B,∠BAC的平分线AO交BC于点D,点H为AO上一动点,过点H作直线l⊥AO于H,分别交直线AB、AC、BC、于点N、E、M.(1)当直线l经过点C时(如图2),求证:BN=CD;(2)当M是BC中点时,写出CE和CD之间的等量关系,并加以证明;(3)请直接写出BN、CE、CD之间的等量关系.达标检测领悟提升强化落实1.如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,且AC=AB+BD,求∠ABC的度数.2.如图,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F,试探究线段AB与AF,CF之间的数量关系,并证明你的结论.3.如图,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角∠NDM,角的两边分别交AB、AC边于M、N两点,连接MN.试探究BM、MN、CN之间的数量关系,并加以证明.4.如图,▱ABCD中,E是BC边的中点,连接AE,F为CD边上一点,且满足∠DFA=2∠BAE.(1)若∠D=105°,∠DAF=35°.求∠FAE的度数;(2)求证:AF=CD+CF.5.如图所示,在正方形ABCD的边CB的延长线上取点F,连结AF,在AF上取点G,使得AG=AD,连结DG,过点A作AE⊥AF,交DG于点E.(1)若正方形ABCD的边长为4,且AB=2FB,求FG的长;(2)求证:AE+BF=AF.6.如图,在四边形ABCD中,AB=AD,∠BAD=60°,∠BCD=120°,连接AC,BD交于点E.(1)若BC=CD=2,M为线段AC上一点,且AM:CM=1:2,连接BM,求点C到BM的距离.(2)证明:BC+CD=AC.7.如图,在正方形ABCD 中,点P 是AB 的中点,连接DP ,过点B 作BE ⊥DP 交DP 的延长线于点E ,连接AE ,过点A 作AF ⊥AE 交DP 于点F ,连接BF .(1)若AE =2,求EF 的长;(2)求证:PF =EP +EB .中考数学几何模型2:共顶点模型名师点睛拨开云雾开门见山共顶点模型,亦称“手拉手模型”,是指两个顶角相等的等腰或者等边三角形的顶点重合,两个三角形的两条腰分别构成的两个三角形全等或者相似。
中考数学押轴题型-费马点相关问题

费马点及其在中考中的应用一、费马点的由来费马(Pierre de Fermat ,1601 —1665) 是法国数学家、物理学家.费马一生从未受过专门的数学教育,数学研究也不过是业余爱好.然而,在17 世纪的法国还找不到哪位数学家可以与之匹敌.他是解析几何的发明者之一;概率论的主要创始人;以及独承1 7 世纪数论天地的人.一代数学大师费马堪称是17 世纪法国最伟大的数学家.尤其他提出的费马大定理更是困惑了世间智者358 年.费马曾提出关于三角形的一个有趣问题:在△ ABC 内求一点P,使PA+PB+PC 之值为最小,人们称这个点为“费马点”.二、探索费马点1 .当三角形有一个内角大于或等于120 的时候,则费马点就是这个内角的顶点.下面来验证这个结论:如图1 ,对三角形内任意一点P,延长BA 至点C′,使得AC′=AC,作∠ C′AP′=∠CAP ,并且使得AP′= AP .即把△ APC 以A 为中心做旋转变换.则△ APC ≌△ AP′C′,∵∠ BAC ≥120 °,∴∠ PAP ′≤ 6 0°.∴在等腰三角形PAP ′中,AP ≥P ∴PA+PB+PC ≥PP ′+PB+ P ′C′>BC ′= AB+AC .所以A 是费马点.2.如果三个内角都在120 °以内,那么,费马点就是三角形内与三角形三顶点的连线两两夹角为120 °的点.如图2,以 B 点为中心,将△ APB 旋转60 °到△ A′B P′.因为旋转60°,且PB=P ′ B ,所以△ P′PB 为正三角形.因此,PA+PB+PC=P ′A′+P′P+PC .由此可知当A′,P′,P,C 四点共线时,PA+PB+PC=P ′A′+P′P+PC 为最小.当A′,P′,P 共线时,∵∠ BP ′ P=60 °,∴∠ A′P B= ∠APB=120 °.同理,若P′,P,C 共线时,则∵∠ BPP ′=60°,∴∠ BPC=120 °.所以点P 为满足∠ APB= ∠BPC= ∠CPA=120 °的点.费马点相关问题等腰直角三角形 , 已知在直角平分线上的一点 P,PA+PB+PC最小值为√6+√2,求直角边的长度?解答:如图将三角形PAC 逆时针旋转60 度得三角形DEC ,则角PCD=60 度,三角形PCD 是正三角形,PC=PD 且DE=PA ,所以PA+PB+PC=DE+PD+PB ,根据两点之间线段最短,当点E、D 、P、B 在一条直线上时,DE+PD+P B 最小,这时角BPC=120 度,角APC=EDC=120 。
初三数学中考模型之费马点问题

∵ AH=BH=AB=12. ∴ ∠AGH=120°, ∠HGP=60°. ∴ A、G、P 三点一线。
再连 PD 两点。 ∵ △ABH、△GHP 和△BDH 都是等边三角形,∠GHB=30°. ∴ ∠PHD=30°,.
即 t 2 .综上, t PA PB PC 的取值范围为 3 t 2 .
“费马点”与中考试题
费尔马,法国业余数学家,拥有业余数学之王的称号,他是解析几何的发明者之一. 费马点—— 就是到三角形的三个顶点的距离之和最小的点. 费尔马的结论:对于一个各角不超过 120°的三角形,费 马点是对各边的张角都是 120°的点,对于有一个角超过 120°的三角形,费马点就是这个内角的顶点.
(2) 直线 BM 的解析式为 y 3x 6 3 (过程略).
y
E
D
C
y F
E
MD
C
A
O Bx
A
O Bx
图4
(3)如何确定点 G 的位置是本题的难点也是关健所在.设 Q 点为 y 轴上一点,P 在 y 轴上运动的速
度为 v,则 P 沿 M→Q→A 运动的时间为 MQ AQ ,使 P 点到达 A 点所用的时间最短,就是 1 MQ+AQ
(3)设 G 为 y 轴上一点,点 P 从直线 y kx b 与 y 轴的交点出发,先沿 y 轴到达 G 点,再沿 GA
到达 A 点,若 P 点在 y 轴上运动的速度是它在直线 GA 上运动速度的 2 倍,试确定 G 点的位置,使 P 点按照上述要求到达 A 点所用的时间最短.
分析和解:(1)D 点的坐标(3, 6 3 )(过程略).
第8讲费马点最值模型(解析版)
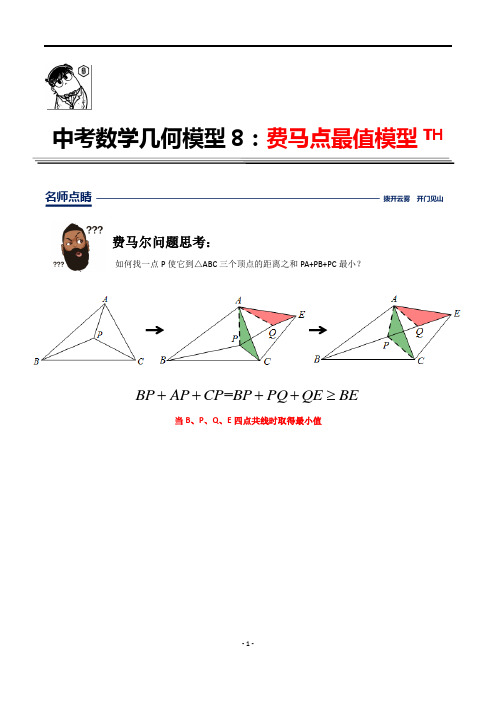
中考数学几何模型8:费马点最值模型TH名师点睛 拨开云雾 开门见山费马尔问题思考:如何找一点P 使它到△ABC 三个顶点的距离之和PA+PB+PC 最小?当B 、P 、Q 、E 四点共线时取得最小值=BP AP CP BP PQ QE BE++++≥费马点的定义:数学上称,到三角形3个顶点距离之和最小的点为费马点。
它是这样确定的:1. 如果三角形有一个内角大于或等于120°,这个内角的顶点就是费马点;2. 如果3个内角均小于120°,则在三角形内部对3边张角均为120°的点,是三角形的费马点。
费马点的性质:费马点有如下主要性质: 1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
费马点最小值快速求解:费尔马问题告诉我们,存在这么一个点到三个定点的距离的和最小,解决问题的方法是运用旋转变换.秘诀:以△ABC 任意一边为边向外作等边三角形,这条边所对两顶点的距离即为最小值典题探究 启迪思维 探究重点例题1. 已知:△ABC 是锐角三角形,G 是三角形内一点。
∠AGC=∠AGB=∠BGC=120°. 求证:GA+GB+GC 的值最小. 证明:将△BGC 逆时针旋转60°,连GP,DB.则 △CGB ≌△CPD ; ∴ ∠CPD=∠CGB=120°,CG=CP,GB=PD, BC=DC,∠GCB=∠PCD. ∵ ∠GCP=60°, ∴ ∠BCD=60°,∴ △GCP 和△BCD 都是等边三角形。
∵ ∠AGC=120°, ∠CGP=60°. ∴ A 、G 、P 三点一线。
∵ ∠CPD=120°, ∠CPG=60°. ∴ G 、P 、D 三点一线。
∴ AG 、GP 、PD 三条线段同在一条直线上。
∵ GA+GC+GB=GA+GP+PD=AD.∴ G 点是等腰三角形内到三个顶点的距离之和最小的那一点变式练习>>>1.如图,P 是边长为1的等边ABC ∆内的任意一点,求t PA PB PC =++的取值范围.解:将BPC ∆绕点B 顺时针旋转60°得到''BP C ∆, 易知'BPP ∆为等边三角形.从而''''PA PB PC PA PP P C AC ++=++≥ (两点之间线段最短),从而3t ≥.过P 作BC 的平行线分别交AB AC 、于点M N 、, 易知MN AN AM ==.因为在BMP ∆和PNC ∆中, PB MP BM <+①, PC PN NC <+②。
初中数学最值问题六种模型

初中数学最值问题有六种模型,包括将军饮马模型、一箭穿心模型、费马点模型、阿氏圆模型、胡不归模型和瓜豆原理模型。
1. 将军饮马模型:当两定点A、B在直线l同侧时,在直线上找一点P,使PA+PB最小。
可以理解为两点之间线段最短。
连接AB交直线l于点P,点P即为所求作的点。
2. 一箭穿心模型:在直线l上找M、N两点(M在左),使得AM+MN+NB最小,且MN=d。
将点A向右平移d个单位到A′,作A′关于直线l的对称点A",连接A"B交直线l 于点N,将点N向左平移d个单位到M,点M、N即为所求。
3. 费马点模型:在三角形ABC中,若D、E分别是AB、AC 上的点,则DE的延长线与BC的延长线交于费马点处,此时三角形周长最小。
4. 阿氏圆模型:以给定点A为圆心,给定距离r为半径画圆,与已知直线l相交于两点B、C,连接两点B、C并延长交于D。
则D点的轨迹是以A为圆心,r为半径的圆。
这个圆被称为阿氏圆。
5. 胡不归模型:在直角三角形ABC中,AB=c,AC=b,BC=a,AD为BC边上的高。
若点P在BC边上,问是否存在点P使得DP垂直于BC边?如果存在,求出点P的位置;
如果不存在,请说明理由。
6. 瓜豆原理模型:在一条直线上有若干个点,每个点都有一个到直线的距离,问如何选择若干个点使得这些点到直线的距离之和最小?瓜豆原理告诉我们,选择任意两个相邻的点并连接它们与直线的交点,然后选择第三个点与前两个点的距离之和最小即可。
以上是初中数学最值问题的六种模型,希望对解决这类问题有所帮助。
第8讲费马点最值模型(解析版)
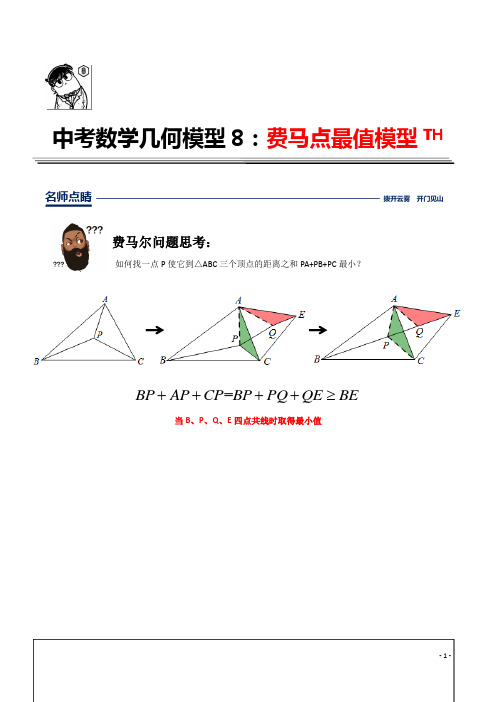
中考数学几何模型8:费马点最值模型TH名师点睛 拨开云雾 开门见山费马尔问题思考:如何找一点P 使它到△ABC 三个顶点的距离之和PA+PB+PC 最小?当B 、P 、Q 、E 四点共线时取得最小值=BP AP CP BP PQ QE BE++++≥费马点的定义:数学上称,到三角形3个顶点距离之和最小的点为费马点。
它是这样确定的:1. 如果三角形有一个内角大于或等于120°,这个内角的顶点就是费马点;2. 如果3个内角均小于120°,则在三角形内部对3边张角均为120°的点,是三角形的费马点。
费马点的性质:费马点有如下主要性质: 1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
费马点最小值快速求解:费尔马问题告诉我们,存在这么一个点到三个定点的距离的和最小,解决问题的方法是运用旋转变换.秘诀:以△ABC 任意一边为边向外作等边三角形,这条边所对两顶点的距离即为最小值典题探究 启迪思维 探究重点例题1. 已知:△ABC 是锐角三角形,G 是三角形内一点。
∠AGC=∠AGB=∠BGC=120°. 求证:GA+GB+GC 的值最小. 证明:将△BGC 逆时针旋转60°,连GP,DB.则 △CGB ≌△CPD ; ∴ ∠CPD=∠CGB=120°,CG=CP,GB=PD, BC=DC,∠GCB=∠PCD. ∵ ∠GCP=60°, ∴ ∠BCD=60°,∴ △GCP 和△BCD 都是等边三角形。
∵ ∠AGC=120°, ∠CGP=60°. ∴ A 、G 、P 三点一线。
∵ ∠CPD=120°, ∠CPG=60°. ∴ G 、P 、D 三点一线。
∴ AG 、GP 、PD 三条线段同在一条直线上。
∵ GA+GC+GB=GA+GP+PD=AD.∴ G 点是等腰三角形内到三个顶点的距离之和最小的那一点变式练习>>>1.如图,P 是边长为1的等边ABC ∆内的任意一点,求t PA PB PC =++的取值范围.解:将BPC ∆绕点B 顺时针旋转60°得到''BP C ∆, 易知'BPP ∆为等边三角形.从而''''PA PB PC PA PP P C AC ++=++≥ (两点之间线段最短),从而3t ≥.过P 作BC 的平行线分别交AB AC 、于点M N 、, 易知MN AN AM ==.因为在BMP ∆和PNC ∆中, PB MP BM <+①, PC PN NC <+②。
中考数学复习专题:几何最值模型—费马点专题
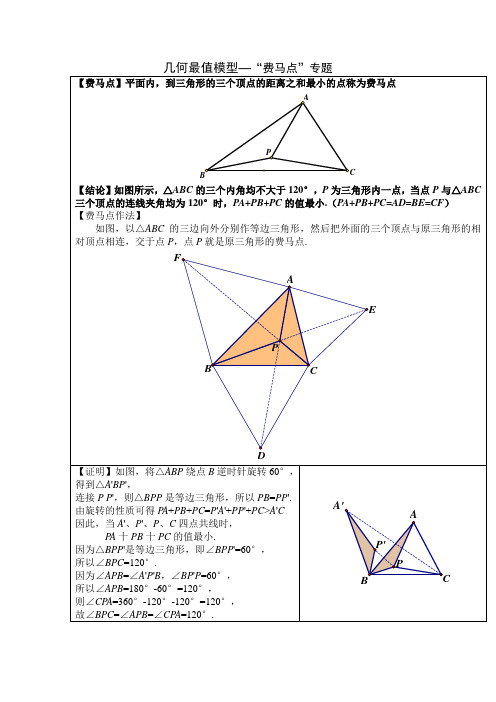
【费马点】平面内,到三角形的三个顶点的距离之和最小的点称为费马点【结论】如图所示,△ABC 的三个内角均不大于120°,P 为三角形内一点,当点P 与△ABC 三个顶点的连线夹角均为120°时,PA +PB +PC 的值最小.(PA +PB +PC=AD=BE=CF ) 【费马点作法】如图,以△ABC 的三边向外分别作等边三角形,然后把外面的三个顶点与原三角形的相对顶点相连,交于点P ,点P 就是原三角形的费马点.【证明】如图,将△ABP 绕点B 逆时针旋转60°,得到△A 'BP ',连接P P ',则△BPP 是等边三角形,所以PB =PP '. 由旋转的性质可得P A +PB +PC =P 'A '+PP '+PC >A 'C 因此,当A '、P '、P 、C 四点共线时,P A 十PB 十PC 的值最小.因为△BPP '是等边三角形,即∠BPP '=60°, 所以∠BPC =120°.因为∠APB =∠A 'P 'B ,∠BP 'P =60°, 所以∠APB =180°-60°=120°,则∠CP A =360°-120°-120°=120°, 故∠BPC =∠APB =∠CP A =120°.CBAPPDFECBAA'P'ABCP费马点结论:1) 对于一个各角不超过120°的三角形,费马点是对各边的张角都是120°的点; 2) 对于有一个角超过120°的三角形,费马点就是这个内角的顶点. 费马问题解决问题的方法是运用旋转变换.1) 利用旋转把三条共点线段转化成折线段, 2) 利用两点之间线段最短 构造直角三角形,利用勾股定理 模型巧记求到三角形三个顶点距离和的最小值,只需要以三角形的一条边为边作等边三角形,那么原三角形的第三个顶点和等边三角形的第三个顶点的距离就是最小值 例1、P 是边长是2的等边△ABC 内的一点, 求PA+PB+PC 的最小值【分析】把△APC 绕A 逆时针旋转60°,得到△AP'C',连接PP' 易知△APP'是等边三角形∴PC=P'C∴∠CAC'=60°∴P A+PB+PC=PB+PP'+PC’当且仅当BPP'C '共线时取得最小值∵AB =2;∴AD =1;BD =3∴.C'D =3∴BC =23 点评:①用旋转把三条共点线段转化成折线段 ②利用两点之间线段最短③构造直角三角形,利用勾股定理例2、P 是边长是1的正方形ABCD 内的一点, 求PA+PB+PC 的最小值【分析】把△APB 绕B 逆时针旋转,得到△BP'A',连接PP' ∴△BPP '是等边三角形 ∴BP=BP ' ∴∠PBP '=60°∴P A+PB+PC=P'A'+PP'+PC ,当且仅当CPP'A'共线时取得最小值∵AB =AB '=1;A'P'PCBA∴A'M =12;BM =32;∴CM =232;CA '=622例3、P 是△ABC 内的一点,BC=6,AC=5,∠ACB =30°, 求P A+PB+PC 的最小值 【分析】把△APC 绕C 顺时针旋转60°,得到△CP'A',连接PP' ∴△CPP '是等边三角形 ∴CP=PP'∴∠PCP '=60°∴P A+PB+PC=P 'A'+PB+PP '当且仅当BPP ’A ’共线时取得最小值 ∵CA=CA '=5;CB=6,∠ACB =30° ∴∠A 'CB =60° ∴A 'B =61什么是加权费马点问题?标准的费马点问题式中的三条线段的系数全为1。
2019年中考数学压轴题分析——最短路径问题4:费马点

2019年中考数学压轴题分析——最短路径问题4:费马点费马点问题在三角形的三边各向其外侧作等边三角形,这三个等边三角形的外接圆交于一点T,该点T即称为托里拆利点(Torricelli's point ),而三个等边三角形的外接圆称为托里拆利圆。
在一定条件下,托里拆利点和正等角中心、费尔马点等是一回事。
托里拆利点是由意大利物理学家托里拆利发现的。
该问题是费马(1601-1665)作为“求一点,使它至一三角形三顶点的距离和最小'这一著名的极值问题而向意大利物理学家托里拆利(1608-1647)提出,并为托里拆利所解决的,当三角形内角均小于120°时点K即为所求,故称K为托里拆利点,也称费马点。
以后,德国斯太纳((1796-1863)独立提出并推广了它,故又称斯太纳问题。
本篇文章中介绍的问题主要是以大家熟知的费马点为背景。
平时大家一听这名字感觉很神奇,学过之后可能感觉也就那回事。
很多数学问题、数学知识都是经历几代数学家的努力之后的成果。
除了做题,有空的时候可以多了解一些数学文化、数学史,领略数学的魅力。
话不多说,直接上题。
【题1】(2019·武汉)问题背景:如图1,将△ABC绕点A逆时针旋转60°得到△ADE,DE与BC交于点P,可推出结论:PA+PC=PE.问题解决:如图2,在△MNG中,MN=6,∠M=75°,MG=4√2.点O是△MNG内一点,则点O到△MNG三个顶点的距离和的最小值是.解答之前,大家可以先看之前的文章:旋转构造几何最值【分析】三角形内确定一点到三个顶点的距离和最小值,就是我们前面说的问题。
上辅助线先。
怎么做,圆内任取一点并连接三个顶点,再将其中一个三角形如△MOG绕点M逆时针旋转60度得△MO′G′,连接OO′。
易得四点共线时距离和最小。
点G′是定点,所以NG′的长度为定值。
∠NMG′为135°,所以容易求得NG′为2√29。
