中考数学解析版试卷分类汇编专题 动态问题
中考数学复习考点知识与题型归类解析50---动态型问题(解析版)

中考数学复习考点知识与题型归类解析50---动态型问题一、选择题9.(2020·湖北孝感)如图,在四边形ABCD 中,AD ∥BC ,∠D=90°,AB=4,BC=6,∠BAD=30°,(第9题)动点P 沿路径A →B →C →D 从点A 出发,以每秒1个单位长度的速度向点D 运动,过点P 作PH ⊥AD ,垂足为H ,设点P 运动的时间为x(单位:s),△APH 的面积为y ,则y 关于x 的函数图像大致是( ){答案}D{解析}当点P 在AB 上移动时,AP=x ,∵∠A=30°,则AH=√32x ,PH=12x ,∴y=√32x ×12x ÷2=√38x 2,y 是x 的二次函数,当x=4时,y=2√3;当点P 在BC 上移动时,即4<x ≤10时,y=x-4+2√3,y 是x 的一次函数,当x=10时,y=6+2√3; 当点P 在CD 上移动时,当10<x ≤12时,y=(6+2√3)(12-x)=-( 6+2√3)x+12×(6+2√3),y 是x 的一次函数,y 随x 的增大而减小.故选D.9.(2020·南通) 矩形ABCD 中,E 为AD 边上的一点,动点P 沿着B -E -D 运动,到D 停止,动点Q 沿着B -C 运动到C 停止,它们的速度都是1cm/s ,设它们的运动时间为x s ,△BPQ 的面积记为y cm 2,y 与x 的关系如图所示,则矩形ABCD 的面积为A .96B .84C .72D .56{答案}C{解析}由已知可得当点P 运动到与E 点重合时,x =10,过点E 作EH ⊥BC 于H ,11103022y BQ EH EH =⨯=⨯⨯=,得EH =AB =6,在Rt △ABE 中,由勾股定理求得AB =6,由右图可知当x =14时,点Q 与点C 重合,所以BC =14,所以矩形ABCD 的面积=12×6=72,故选C .(2020·本溪)10.(3分)如图,在Rt △ABC 中,∠ACB =90°,AC =BC =2√2,CD ⊥AB 于点D .点P 从点A 出发,沿A →D →C 的路径运动,运动到点C 停止,过点P 作PE ⊥AC 于点E ,作PF ⊥BC 于点F .设点P 运动的路程为x ,四边形CEPF 的面积为y ,则能反映y 与x 之间函数关系的图象是( )y/cmA.B.C.D.{答案}{解析}根据Rt△ABC中,∠ACB=90°,AC=BC=2√2,可得AB=4,根据CD⊥AB于点D.可得AD=BD=2,CD平分角ACB,点P从点A出发,沿A→D→C的路径运动,运动到点C停止,分两种情况讨论:根据PE⊥AC,PF⊥BC,可得四边形CEPF是矩形和正方形,设点P运动的路程为x,四边形CEPF的面积为y,进而可得能反映y与x之间函数关系式,从而可以得函数的图象.∵在Rt△ABC中,∠ACB=90°,AC=BC=2√2,∴AB=4,∠A=45°,∵CD⊥AB于点D,∴AD=BD=2,∵PE⊥AC,PF⊥BC,∴四边形CEPF是矩形,∴CE=PF,PE=CF,∵点P运动的路程为x,∴AP=x,x,则AE=PE=x•sin45°=√22x,∴CE=AC﹣AE=2√2−√22∵四边形CEPF 的面积为y ,∴当点P 从点A 出发,沿A →D 路径运动时, 即0<x <2时, y =PE •CE =√22x (2√2−√22x ) =−12x 2+2x=−12(x ﹣2)2+2,∴当0<x <2时,抛物线开口向下; 当点P 沿D →C 路径运动时, 即2≤x <4时,∵CD 是∠ACB 的平分线, ∴PE =PF ,∴四边形CEPF 是正方形, ∵AD =2,PD =x ﹣2, ∴CP =4﹣x ,y =12(4﹣x )2=12(x ﹣4)2. ∴当2≤x <4时,抛物线开口向上,综上所述:能反映y 与x 之间函数关系的图象是A .9.(2020·东营)如图1,点P 从△ABC 的顶点A 出发,沿A →B →C 匀速运动到点C ,图2是点P 运动时线段CP 的长度y 随时间x 变化的关系图象,其中点Q 为曲线部分的最低点,则△ABC 的边AB 的长度为( )A.12B. 8C.10D.13{答案}C{解析}本题是运动型综合题,考查了动点问题的函数图象、解直角三角形、图形面积等知识点.解题的关键是深刻理解动点的函数图象,了解图象中关键点所代表的实际意义,理解动点的完整运动过程.当P 点分别与A 、B 重合时,PC=13,由此可推出:△ABC 是等腰三角形,AC=BC=13; 当CP ⊥AB 时,PC 的值最小,即△ABC 中,AB 上的高为12,此时P 点恰好运动至AB 的中点, ∴2213125AP,∴210AB AP .9.(2020·威海)七巧板是大家熟悉的一种益智玩具.用七巧板能拼出许多有趣的图案.小李将一块等腰直角三角形硬纸板(如图①)切割七块,正好制成一副七巧板(如图②).已知AB =40cm ,则图中阴影部分的面积为( )A .25cm 2B .1003cm 2 C .50cm 2 D .75cm 2【分析】如图:设OF =EF =FG =x ,可得EH =2√2x =20,解方程即可解决问题. 【解析】:如图:设OF =EF =FG =x ,ABC∴OE=OH=2x,在Rt△EOH中,EH=2√2x,由题意EH=20cm,∴20=2√2x,∴x=5√2,∴阴影部分的面积=(5√2)2=50(cm2)故选:C.11.(2020·淄博)如图1,点P从△ABC的顶点B出发,沿B→C→A匀速运动到点A,图2是点P运动时,线段BP的长度y随时间x变化的关系图象,其中M是曲线部分的最低点,则△ABC的面积是()A.12 B.24 C.36 D.48【解析】由图2知,AB=BC=10,当BP⊥AC时,y的值最小,即△ABC中,BC边上的高为8(即此时BP=8),当y=8时,PC=2−BP2=√102−82=6,△ABC的面积=12×AC×BP=12×8×12=48,故选:D .二、填空题15.(2020·鄂州)如图,半径为2cm 的O 与边长为2cm 的正方形ABCD 的边AB 相切于E ,点F 为正方形的中心,直线OE 过F 点.当正方形ABCD 沿直线OF 以每秒(2-的速度向左运动__________秒时,O 与正方形重叠部分的面积为22cm 3π⎛- ⎝.{答案}1或1163.{解析}本题考查正方形的性质,扇形面积的计算及等边三角形的判定和性质,题目难度不大,注意分情况讨论是本题的解题关键.将正方形向左平移,使得正方形与圆的重叠部分为弓形,根据题目数据求得此时弓形面积符合题意,由此得到OF 的长度,然后结合运动速度求解即可,特别要注意的是正方形沿直线运动,所以需要分类讨论. 解:①当正方形运动到如图1位置,连接OA ,OB ,AB 交OF 于点E 此时正方形与圆的重叠部分的面积为S 扇形OAB -S △OAB 由题意可知:OA =OB =AB =2,OF ⊥AB ∴△OAB 为等边三角形 ∴∠AOB =60°,OE ⊥AB在Rt △AOE 中,∠AOE =30°,∴AE =112OA =,OE ∴S 扇形OAB -S △OAB 260π212=23π336023∴OF =1∴点F 向左运动3(31)23个单位所以此时运动时间为3=123秒②同理,当正方形运动到如图2位置,连接OC ,OD ,CD 交OF 于点E此时正方形与圆的重叠部分的面积为S 扇形OCD -S △OCD 由题意可知:OC =OD =CD =2,OF ⊥CD ∴△OCD 为等边三角形 ∴∠COD =60°,OE ⊥CD在Rt △COE 中,∠COE =30°,∴CE =1OC 12,OE ∴S 扇形OCD -S △OCD 260π212=23π336023∴OF =1∴点F 向左运动3(31)43个单位所以此时运动时间为43=116323秒 综上,当运动时间为1或1163秒时,⊙O 与正方形重叠部分的面积为22π3(cm )3故答案为:1或1163.17.(2020•湘西州)在平面直角坐标系中,O 为原点,点A (6,0),点B 在y 轴的正半轴上,∠ABO =30°,矩形CODE 的顶点D ,E ,C 分别在OA ,AB ,OB 上,OD =2.将矩形CODE 沿x 轴向右平移,当矩形CODE 与△ABO 重叠部分的面积为则矩形CODE 向右平移的距离为 .(第17题图){答案}2{解析}本题考查了矩形的性质、坐标与图形性质、勾股定理、平移的性质、直角三角形的性质、梯形面积公式等知识,熟练掌握含30°角的直角三角形的性质时是解题的关键.∵点A (6,0),∴OA =6,∵OD =2,∴AD =OA ﹣OD =6﹣2=4,∵四边形CODE 是矩形,∴DE ∥OC ,∴∠AED =∠ABO =30°,在Rt △AED 中,AE =2AD =8,ED ===,∵OD =2,∴点E 的坐标为(2,;由平移的性质得:O ′D ′=2,E ′D ′=,ME ′=OO ′=t ,D ′E ′∥O ′C ′∥OB ,∴∠E ′FM =∠ABO =30°,∴在Rt △MFE ′中,MF =2ME ′=2t ,FE ′===t ,∴S △MFE ′12=ME ′•FE ′12=⨯t22=,∵S 矩形C ′O ′D ′E ′=O ′D ′•E ′D ′=2×=S =S 矩形C ′O ′D ′E ′﹣S △MFE ′=t 1=2,t 2=-2(舍去),因此本题答案是2.17.(2020·通辽)如图①,在△ABC 中,AB =AC ,∠BAC =120°,点E 是边AB 的中点,点P 是边BC 上一动点,设PC =x ,P A +PE =y .图②是y 关于x 的函数图象,其中H 是图象上的最低点.那么a +b 的值为 .{答案}7{解析}∵点E 是边AB 的中点,∴AE =BE =12AB .从图象中可以看出,当x 的值最大时,所对应的函数值是P 恰与点B 重合.此时P A +PE =AB +12AB =32AB =AB ==AC,AE =BE E 关于BC 的对称点F ,连结AF 交BC 于点P ,此时P A +PE 有最小值,即是AF 长,连结BF .∵在△ABC 中,AB =AC ,∠BAC =120°,∴∠ABC =∠C =30°,由轴对称可得BF =BE ,∠ABC =∠FBP =30°,∴∠EBF =60°,∴△EBF 是等边三角形,∴EF =BE ,∵AE =BE ,∴AE =BE = EF ,易证△ABF 是直角三角形,∴AF =AB ·sin ∠ABF==,即a =3,在△ABF 中,∠AFB =90°,∠ABF =60°,∴∠BAF =30°,∵∠BAC =120°,∴∠P AC =∠BAC -∠BAF =90°,∴cos C =cos30°=ACPCPC223=4,即b =4,∴a +b =7.三、解答题24.(2020·温州)如图,在四边形ABCD 中,∠A =∠C =90°,DE ,BF 分别平分∠ADC ,∠ABC ,并交线段AB ,CD 于点E ,F (点E ,B 不重合).在线段BF 上取点M ,N (点M 在BN 之间),使BM =2FN .当点P 从点D 匀速运动到点E 时,点Q 恰好从点M 匀速运动到点N .记QN =x ,PD =y ,已知6125y x =-+,当Q 为BF 中点时245y =.(1)判断DE 与BF 的位置关系,并说明理由. (2)求DE ,BF 的长.E(3)若AD=6.①当DP=DF时,通过计算比较BE与BQ的大小关系.②连结PQ,当PQ所在直线经过四边形ABCD的一个顶点时,求所有满足条件的x的值.{解析}这是一道四边形动点综合题。
全国各地中考数学试卷分类汇编动态问题

动态问题一、选择题1.(2013江苏苏州,10,3分)如图,在平面直角坐标系中,Rt △OAB 的顶点A 在x 轴的正半轴上,顶点B 的坐标为(3),点C 的坐标为(12,0),点P 为斜边OB 上的一动点,则P A +PC 的最小值为( ).A B C D .【答案】B .【解析】如图,作A 关于OB 的对称点D ,连接CD 交OB 于P ,连接AP ,过D 作DN ⊥OA 于N ,则此时P A +PC 的值最小,求出AM ,求出AD ,求出DN 、CN ,根据勾股定理求出CD ,即可得出答案.解:如图,作A 关于OB 的对称点D ,连接CD 交OB 于P ,连接AP ,过D 作DN ⊥OA 于N ,则此时P A +PC 的值最小.∵DP =P A ,∴P A +PC =PD +PC =CD .∵B (3,∴AB ,OA =3,∠B =60°.由勾股定理得:OB .由三角形面积公式得:12×OA ×AB =12×OB ×AM ,即12×3=12×AM .∴AM =32.∴AD =2×32=3.∵∠AMB =90°,∠B =60°, ∴∠BAM =30°,∵∠BAO =90°,∴∠OAM =60°. ∵DN ⊥OA ,∴∠NDA =30°,∴AN =12×AD =32.由勾股定理得:DN=2. ∵C (12,0),∴CN =3-12-32=1.在Rt △DNC 中,由勾股定理得:DC 2.即P A +PC 所以应选B .【方法指导】本题考查了三角形的内角和定理,轴对称的最短路线问题,勾股定理,含30度角的直角三角形性质的应用,关键是求出P 点的位置,题目比较好,难度适中. 【易错警示】弄不清楚最小值问题,赵不到最短距离而出错.2.(2013山东临沂,14,3分)如图,正方形ABCD 中,AB =8cm ,对角线AC ,BD 相交于点O ,点E ,F 分别从B ,C 两点同时出发,以1cm/s 的速度沿BC ,CD 运动,到点C ,D 时停止运动.设运动时间为t (s ),△OEF 的面积为S (cm 2),则S (cm 2)与t (s )的函数关系可用图象表示为( )【答案】:B .3(2013四川南充,10,3分)如图1,点E 为矩形ABCD 边AD 上一点,点P ,点Q 同时从点B 出发,点P 沿BE →ED →DC 运动到点C 停止,点Q 沿BC 运动到点C 停止,它们的运动速度都是1cm/s .设P ,Q 出发秒时,△BPQ 的面积为y cm 2,已知y 与的函数关系的图象如图2(曲线OM 为抛物线的一部分).则下列结论: ①AD=BE=5cm ;②当0<≤5时,252t y =;③直线NH 的解析式为2725+-=t y ; ④若△ABE 与△QBP 相似,则429=t 秒.其中正确结论的个数为( ) A .4 B .3 C .2 D .1【答案】:B .【解析】据图(2)可以判断三角形的面积变化分为三段,可以判断出当点P 到达点E 时点Q 到达点C ,从而得到BC 、BE 的长度,再根据M 、N 是从5秒到7秒,可得ED 的长度,然后表示出AE 的长度,根据勾股定理求出AB 的长度,然后针对各小题分析解答即可. 【方法指导】本题考查了二次函数的综合应用及动点问题的函数图象,根据图(2)判断出A .D .DF点P 到达点E 时,点Q 到达点C 是解题的关键,也是本题的突破口,难度较大. 4.(2013湖北荆门,12,3分)如图所示,已知等腰梯形ABCD ,AD ∥BC ,若动直线l 垂直于BC ,且向右匀速(注:“匀速”二字为录入者所添加)平移,设扫过的阴影部分的面积为S ,BP 为x ,则S 关于x 的函数图象大致是( )【答案】A【解析】为计算的方便,不妨设AB =CD,AD =1,∠ABC =45°.分别过点A ,D 向BC 作垂线,垂足依次为E ,F ,如图3,设动直线l 移动的速度为x .①当0≤x <1时,S =12x 2,其图象是开口向上的抛物线的一部分;②当1≤x <2时,S =12+1×(x -1)=x -12,其图象是直线的一部分;③当2≤x ≤3时,S =2-12(3-x )2,其图象是开口向下的抛物线的一部分.综上所述,选A .【方法指导】判断函数大致图象的试题,一般应先确立函数关系解析式,再根据函数图象及性质做出合理的判断.解答分段函数的图象问题一般遵循以下步骤:①根据自变量的取值范围对函数进行分段;②求出每段的解析式;③由每段的解析式确定每段图象的形状. 5 (2013山东烟台,12,3分)如图1.E 为矩形ABCD 边AD 上一点,点P 从点B 沿折线BE-—ED —DC 运动到点C 时停止,点Q 从点B 沿BC 运动到点C 时停止.它们的运动速度都是1cm /s .若点P ,Q 同时开始运动,设运动时间为t (s ),⊿BPQ 的面积y (cm 2).已知y 与t 的函数关系图像如图2,则下面结论错误的是( )A . cm AE 6=B . 54sin =∠EBC C . 当100≤<t 时,252t y =D .当s t 12=时,PBQ ∆是等腰三角形A .B .C .D .(第12题)图3【答案】A【考点解剖】本题是一道典型的动点问题,主要考查了三角函数、等腰三角形的判定、二次函数的解析式、三角形的面积公式,解决本题的关键是能够根据图形中点的位置与相应线段、面积的变化来理解函数图象表达的意义,数形结合,化静为动,从而正确的解决问题. 【解析】如图:利用数形结合思想方法,结合图1、图2分别求出BE =BC =10cm ,DE =4cm ,AE =6cm ;然后利用勾股定理求出AB ,即可求出sin ∠EBC =54;当100≤<t 时,根据△BPF ∽△EBA 可求出BQ 边上的高PF t 54=,然后利用三角形面积公式即可求出y 与t 的函数关系式y =⨯t 21t 54252t =,最后利用排除法即可选D .【方法指导】点的运动问题,主要表现在运动路径与时间之间的图象关系.解决动点问题时,对题意的理解要清晰,关键是正确获取或处理题中的信息,明确哪些是变化的量,哪些是不变的量.二、填空题1.(2013杭州4分)射线QN 与等边△ABC 的两边AB ,BC 分别交于点M ,N ,且AC ∥QN ,AM =MB =2cm ,QM =4cm .动点P 从点Q 出发,沿射线QN 以每秒1cm 的速度向右移动,经过t 秒,以点P 为圆心,cm 为半径的圆与△ABC 的边相切(切点在边上),请写出t 可取的一切值(单位:秒)【思路分析】求出AB=AC=BC=4cm,MN=AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,分为三种情况:画出图形,结合图形求出即可;【解析】∵△ABC是等边三角形,∴AB=AC=BC=AM+MB=4cm,∠A=∠C=∠B=60°,∵QN∥AC,AM=BM.∴N为BC中点,∴MN=AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,分为三种情况:①如图1,当⊙P切AB于M′时,连接PM′,则PM′=cm,∠PM′M=90°,∵∠PMM′=∠BMN=60°,∴M′M=1cm,PM=2MM′=2cm,∴QP=4cm﹣2cm=2cm,即t=2;②如图2,当⊙P于AC切于A点时,连接P A,则∠CAP=∠APM=90°,∠PMA=∠BMN=60°,AP=cm,∴PM=1cm,∴QP=4cm﹣1cm=3cm,即t=3,当当⊙P于AC切于C点时,连接PC,则∠CP′N=∠ACP′=90°,∠P′NC=∠BNM=60°,CP′=cm,∴P′N=1cm,∴QP=4cm+2cm+1cm=7cm,即当3≤t≤7时,⊙P和AC边相切;③如图1,当⊙P切BC于N′时,连接PN′3则PN′=cm,∠PM\N′N=90°,∵∠PNN′=∠BNM=60°,∴N′N=1cm,PN=2NN′=2cm,∴QP=4cm+2cm+2cm=8cm,即t=8;故答案为:t=2或3≤t≤7或t=8.【方法指导】本题考查了等边三角形的性质,平行线的性质,勾股定理,含30度角的直角三角形性质,切线的性质的应用,主要考查学生综合运用定理进行计算的能力,注意要进行分类讨论啊..2(2013浙江湖州,16,4分)如图,已知点A是第一象限内横坐标为AC⊥x =-于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,轴于点M,交直线y x则点P在线段ON上运动时,A点不变,B点随之运动,求当点P从点O运动到点N时,点B运动的路径长是__▲__.【答案】【解析】(1)首先,需要证明线段B0B n就是点B运动的路径(或轨迹),如答图②所示.利用相似三角形可以证明;(2)其次,如答图①所示,利用相似三角形△AB0B n∽△AON,求出线段B0B n的长度,即点B运动的路径长.OM=N在直线y=-x上,AC⊥x轴于点M,则△OMN为等腰直角三角形,=.如答图①所示,设动点P在O点(起点)时,点B的位置为B0,动点P在N点(起点)时,点B的位置为B n,连接B0B n.∵AO⊥AB0,AN⊥AB n,∴∠OAC=∠B0AB n,又∵AB0=AO•tan30°,AB n=AN•tan30°,∴AB0:AO=AB n:AN=tan30°,∴△AB0B n∽△AON,且相似比为tan30°,∴B0B n=ON•tan30°=B0B n就是点B运动的路径(或轨迹).如答图②所示,当点P运动至ON上的任一点时,设其对应的点B为B i,连接AP,AB i,B0B i.∵AO⊥AB0,AP⊥AB i,∴∠OAP=∠B0AB i,又∵AB0=AO•tan30°,AB i=AP•tan30°,∴AB0:AO=AB i:AP,∴△AB0B i∽△AOP,∴∠AB0B i=∠AOP.又∵△AB0B n∽△AON,∴∠AB0B n=∠AOP,∴∠AB0B i=∠AB0B n,∴点B i在线段B0B n上,即线段B0B n就是点B运动的路径(或轨迹).综上所述,点B运动的路径(或轨迹)是线段B0B n,其长度为.【方法指导】本题考查坐标平面内由相似关系确定的点的运动轨迹,难度很大.本题的要点有两个:首先,确定点B 的运动路径是本题的核心,这要求考生有很好的空间想象能力和分析问题的能力;其次,由相似关系求出点B 运动路径的长度,可以大幅简化计算,避免陷入坐标关系的复杂运算之中3.(2013山东菏泽,14,3分)如图所示,在△ABC 中,BC =6,E 、F 分别是AB 、AC 的中点,动点P 在射线EF 上,BP 交CE 于点D ,∠CBP 的平分线交CE 于Q ,当CQ =13CE时, EP +BP =____________.【答案】12.【解析】延长BQ 角射线EF 于M.∵E 、F 分别是AB 、AC 的中点,∴EF//BC ,即EM//BC.∴△EQM ∽△EQB ,∴123132===CE CECQ EQ BC EM , 即26=EM ,∴EM=12.∵∠CBP 的平分线交CE 于Q ,∴∠PBM=∠CBM , ∵EM//BC ,∴∠EMB=∠CBM ,∴∠PBM=∠EMB ,∴PB=PM ,所以EP +BP =EM=12.【方法指导】本题考查三角形相似、三角形中位线性质、角平分线意义等.本题是一道动点型问题,解题时要善于从“动中求静,联想关联知识”.三、解答题1.(2013杭州4分)射线QN 与等边△ABC 的两边AB ,BC 分别交于点M ,N ,且AC ∥QN ,AM =MB =2cm ,QM =4cm .动点P 从点Q 出发,沿射线QN 以每秒1cm的速度向右移动,B(第14题)经过t秒,以点P为圆心,cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值(单位:秒)【思路分析】求出AB=AC=BC=4cm,MN=AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,分为三种情况:画出图形,结合图形求出即可;【解析】∵△ABC是等边三角形,∴AB=AC=BC=AM+MB=4cm,∠A=∠C=∠B=60°,∵QN∥AC,AM=BM.∴N为BC中点,∴MN=AC=2cm,∠BMN=∠BNM=∠C=∠A=60°,分为三种情况:①如图1,当⊙P切AB于M′时,连接PM′,则PM′=cm,∠PM′M=90°,∵∠PMM′=∠BMN=60°,∴M′M=1cm,PM=2MM′=2cm,∴QP=4cm﹣2cm=2cm,即t=2;②如图2,当⊙P于AC切于A点时,连接P A,则∠CAP=∠APM=90°,∠PMA=∠BMN=60°,AP=cm,∴PM=1cm,∴QP=4cm﹣1cm=3cm,即t=3,当当⊙P于AC切于C点时,连接PC,则∠CP′N=∠ACP′=90°,∠P′NC=∠BNM=60°,CP′=cm,∴P′N=1cm,∴QP=4cm+2cm+1cm=7cm,即当3≤t≤7时,⊙P和AC边相切;③如图1,当⊙P切BC于N′时,连接PN′3则PN′=cm,∠PM\N′N=90°,∵∠PNN′=∠BNM=60°,∴N′N=1cm,PN=2NN′=2cm,∴QP=4cm+2cm+2cm=8cm,即t=8;故答案为:t=2或3≤t≤7或t=8.【方法指导】本题考查了等边三角形的性质,平行线的性质,勾股定理,含30度角的直角三角形性质,切线的性质的应用,主要考查学生综合运用定理进行计算的能力,注意要进行分类讨论啊.2.(2013湖北孝感,25,12分)如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);(2)如图2,若点E在线段BC上滑动(不与点B,C重合).①AE=EF是否总成立?请给出证明;②在如图2的直角坐标系中,当点E滑动到某处时,点F恰好落在抛物线y=﹣x2+x+1上,求此时点F的坐标.,的坐标为3(2013·济宁,23,?分)如图,直线y=-x+4与坐标轴分别交于点A、B,与直线y=x交于点C.在线段OA上,动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,同时动点P从点A出发向点O做匀速运动,当点P、Q其中一点停止运动时,另一点也停止运动.分别过点P、Q作x轴的垂线,交直线AB、OC于点E、F,连接EF.若运动时间为t秒,在运动过程中四边形PEFQ总为矩形(点P、Q重合除外).(1)求点P运动的速度是多少?(2)当t为多少秒时,矩形PEFQ为正方形?(3)当t为多少秒时,矩形PEFQ的面积S最大?并求出最大值.考点:一次函数综合题.(1)根据直线y=-x+4与坐标轴分别交于点A、B,得出A,B点的坐标,再利用EP∥BO,分析:得出==,据此可以求得点P的运动速度;(2)当PQ=PE时,以及当PQ=PE时,矩形PEFQ为正方形,分别求出即可;(3)根据(2)中所求得出s与t的函数关系式,进而利用二次函数性质求出即可.解答:解:(1)∵直线y=-x+4与坐标轴分别交于点A、B,∴x=0时,y=4,y=0时,x=8,∴==,当t秒时,QO=FQ=t,则EP=t,∵EP∥BO,∴==,∴AP=2t,∵动点Q以每秒1个单位长度的速度从点O出发向点A做匀速运动,∴点P运动的速度是每秒2个单位长度;(2)如图1,当PQ=PE时,矩形PEFQ为正方形,则OQ=FQ=t,P A=2t,∴QP=8-t-2t=8-3t,∴8-3t=t,解得:t=2,如图2,当PQ=PE时,矩形PEFQ为正方形,∵OQ=t,P A=2t,∴OP=8-2t,∴QP=t-(8-2t)=3t-8,∴t=3t-8,解得:t=4;(3)如图1,当Q在P点的左边时,∵OQ=t,P A=2t,∴QP=8-t-2t=8-3t,当t=-=时,S矩形PEFQ的最大值为:=4,如图2,当Q在P点的右边时,∵OQ=t,P A=2t,∴QP=t-(8-2t)=3t-8,∴S矩形PEFQ=QP•QE=(3t-8)•t=3t2-8t,∵当点P、Q其中一点停止运动时,另一点也停止运动,∴0≤t≤4,当t=-=时,S矩形PEFQ的最小,∴t=4时,S矩形PEFQ的最大值为:3×42-8×4=16,综上所述,当t=4时,S矩形PEFQ的最大值为:16.点评:此题主要考查了二次函数与一次函数的综合应用,得出P ,Q 不同的位置进行分类讨论得出是解题关键.4.(2013·潍坊,24,13分)如图,抛物线c bx ax y ++=2关于直线1=x 对称,与坐标轴交于C B A 、、三点,且4=AB ,点⎪⎭⎫ ⎝⎛232,D 在抛物线上,直线是一次函数()02≠-=k kx y 的图象,点O 是坐标原点.(1)求抛物线的解析式;(2)若直线平分四边形OBDC 的面积,求k 的值.(3)把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线与直线交于N M 、两点,问在y 轴正半轴上是否存在一定点P ,使得不论k 取何值,直线PM 与PN 总是关于y 轴对称?若存在,求出P 点坐标;若不存在,请说明理由.答案:(1)因为抛物线关于直线x =1对称,AB =4,所以A(-1,0),B(3,0), 由点D(2,1.5)在抛物线上,所以⎩⎨⎧=++=+-5.1240c b a c b a ,所以3a +3b =1.5,即a +b =0.5,又12=-a b,即b =-2a ,代入上式解得a =-0.5,b =1,从而c =1.5,所以23212++-=x x y .(2)由(1)知23212++-=x x y ,令x =0,得c(0,1.5),所以CD//AB , 令kx -2=1.5,得l 与CD 的交点F(23,27k ),令kx -2=0,得l 与x 轴的交点E(0,2k),根据S 四边形OEFC =S 四边形EBDF 得:OE +CF =DF +BE ,即,511),272()23(272=-+-=+k k k k k 解得 (3)由(1)知,2)1(21232122+--=++-=x x x y所以把抛物线向左平移1个单位,再向下平移2个单位,所得抛物线的解析式为221x y -=假设在y 轴上存在一点P(0,t),t >0,使直线PM 与PN 关于y 轴对称,过点M 、N 分别向y 轴作垂线MM 1、NN 1,垂足分别为M 1、N 1,因为∠MPO =∠NPO ,所以Rt △MPM 1∽Rt △NPN 1, 所以1111PN PM NN MM =,………………(1) 不妨设M(x M ,y M )在点N(x N ,y N )的左侧,因为P 点在y 轴正半轴上, 则(1)式变为NMN M y t y t x x --=-,又y M =k x M -2, y N =k x N -2, 所以(t +2)(x M +x N )=2k x M x N ,……(2) 把y =kx -2(k ≠0)代入221x y -=中,整理得x 2+2kx -4=0, 所以x M +x N =-2k , x M x N =-4,代入(2)得t =2,符合条件, 故在y 轴上存在一点P (0,2),使直线PM 与PN 总是关于y 轴对称.考点:本题是一道与二次函数相关的压轴题,综合考查了考查了二次函数解析式的确定,函数图象交点及图形面积的求法,三角形的相似,函数图象的平移,一元二次方程的解法等知识,难度较大.点评:本题是一道集一元二次方程、二次函数解析式的求法、相似三角形的条件与性质以及质点运动问题、分类讨论思想于一体的综合题,能够较好地考查了同学们灵活应用所学知识,解决实际问题的能力。
中考数学试题汇编及解析动态几何型综合题试题

2021年中考数学试题汇编及解析动态几何型综合题纵观近5年全国各地的中考数学试卷,动态几何型综合题常常出如今一张试卷的压轴题位置,估计这一趋势在今后几年的中考中会越来越明显,这类试题往往综合性较强,往往涉及到函数、直线型、圆等初中数学的重点考察对象中的好几个,应加大训练的力度。
1、〔2021〕如图①,有两个形状完全一样的直角三角形ABC和EFG叠放在一起〔点A 与点E重合〕,AC=8cm,BC=6cm,∠C=90°,EG=4cm,∠EGF=90°,O 是△EFG斜边上的中点.如图②,假设整个△EFG从图①的位置出发,以1cm/s 的速度沿射线AB方向平移,在△EFG 平移的同时,点P从△EFG的顶点G出发,以1cm/s 的速度在直角边GF上向点F运动,当点P到达点F时,点P停顿运动,△EFG也随之停顿平移.设运动时间是为x〔s〕,FG的延长线交 AC于H,四边形OAHP的面积为y〔cm2)〔不考虑点P与G、F重合的情况〕.〔1〕当x为何值时,OP∥AC ?〔2〕求y与x 之间的函数关系式,并确定自变量x的取值范围.〔3〕是否存在某一时刻,使四边形OAHP面积与△ABC面积的比为13∶24?假设存在,求出x的值;假设不存在,说明理由.〔参考数据:1142=12996,1152=13225,1162=13456或者4.42=19.36,4.52=20.25,4.62=21.16〕[解析] 〔1〕∵Rt △EFG ∽Rt △ABC ,∴BC FG AC EG =,684FG=. ∴FG =864⨯=3cm .∵当P 为FG 的中点时,OP ∥EG ,EG ∥AC , ∴OP ∥AC .∴ x =121FG=21×3=1.5〔s 〕.∴当x 为1.5s 时,OP ∥AC .〔2〕在Rt △EFG 中,由勾股定理得:EF =5cm . ∵EG ∥AH , ∴△EFG ∽△AFH .∴FH FG AF EF AH EG ==. ∴FHx AH 3554=+=. ∴ AH =54〔 x +5〕,FH =53〔x +5〕.过点O 作OD ⊥FP ,垂足为 D . ∵点O 为EF 中点, ∴OD =21EG =2cm . ∵FP =3-x ,∴S 四边形OAHP =S △AFH -S △OFP=21·AH ·FH -21·OD ·FP =21·54〔x +5〕·53〔x +5〕-21×2×〔3-x 〕 =256x 2+517x +3〔0<x <3).〔3〕假设存在某一时刻x ,使得四边形OAHP 面积与△ABC 面积的比为13∶24.那么S 四边形OAHP =2413×S △ABC ∴256x 2+517x +3=2413×21×6×8 ∴6x 2+85x -250=0 解得 x 1=25, x 2= -350〔舍去〕. ∵0<x <3, ∴当x =25〔s 〕时,四边形OAHP 面积与△ABC 面积的比为13∶24. 2、〔2021〕如图,在Rt △ABC 中,∠C =90°,AC =12,BC =16,动点P 从点A 出发沿AC 边向点C 以每秒3个单位长的速度运动,动点Q 从点C 出发沿CB 边向点B 以每秒4个单位长的速度运动.P ,Q 分别从点A ,C 同时出发,当其中一点到达端点时,另一点也随之停顿运动.在运动过程中,△PCQ 关于直线PQ 对称的图形是△PDQ .设运动时间是为t 〔秒〕.〔1〕设四边形PCQD 的面积为y ,求y 与t 的函数关系式; 〔2〕t 为何值时,四边形PQBA 是梯形?〔3〕是否存在时刻t ,使得PD ∥AB ?假设存在,求出t 的值;假设不存在,请说明理由;〔4〕通过观察、画图或者折纸等方法,猜测是否存在时刻t ,使得PD ⊥AB ?假设存在,请估计t 的值在括号中的哪个时间是段内〔0≤t ≤1;1<t ≤2;2<t ≤3;3<t ≤4〕;假设不存在,请简要说明理由.[解析] 〔1〕由题意知 CQ =4t ,PC =12-3t ,∴S △PCQ =t t CQ PC 246212+-=⋅.PCQB∵△PCQ 与△PDQ 关于直线PQ 对称, ∴y=2S △PCQ t t 48122+-=. 〔2〕当CQCP CA CB=时,有PQ ∥AB ,而AP 与BQ 不平行,这时四边形PQBA 是梯形, ∵CA =12,CB =16,CQ =4t , CP =12-3t , ∴16412312tt =-,解得t =2. ∴当t =2秒时,四边形PQBA 是梯形.〔3〕设存在时刻t ,使得PD ∥AB ,延长PD 交BC 于点M ,如下列图,假设PD ∥AB ,那么∠QMD =∠B ,又∵∠QDM =∠C =90°,∴Rt △QMD ∽Rt △ABC , 从而ACQDAB QM =, ∵QD =CQ =4t ,AC =12,AB20,∴QM =203t . 假设PD ∥AB ,那么CP CMCA CB=,得20412331216t t t +-=, 解得t =1211. ∴当t =1211秒时,PD ∥AB . 〔4〕存在时刻t ,使得PD ⊥AB .时间是段为:2<t ≤3.3、〔2021〕如图1所示,一张三角形纸片ABC ,∠ACB=90°11AC D ∆和22BC D ∆两个三角形〔如图2所示〕.将纸片11AC D ∆沿直线2D B 〔AB 〕方向平移〔点12,,,A D D B 始终在同一直线上〕,当点1D 于点B 重合时,停顿平移.在平移过程中,11C D 与2BC 交于点E,1AC 与222C D BC 、分别交于点F 、P.CQBM(1) 当11AC D ∆平移到如图3所示的位置时,猜测图中的1D E 与2D F 的数量关系,并证明你的猜测;(2) 设平移间隔 21D D 为x ,11AC D ∆与22BC D ∆重叠局部面积为y ,请写出y 与x 的函数关系式,以及自变量的取值范围;〔3〕对于〔2〕中的结论是否存在这样的x 的值,使重叠局部的面积等于原ABC ∆面积的14. 假设存在,求x 的值;假设不存在,请说明理由.[解析] 〔1〕12D E D F =.因为1122C D C D ∥,所以12C AFD ∠=∠. 又因为90ACB ∠=︒,CD 是斜边上的中线,所以,DC DA DB ==,即112221C D C D BD AD === 所以,1C A ∠=∠,所以2AFD A ∠=∠ 所以,22AD D F =.同理:11BD D E =.又因为12AD BD =,所以21AD BD =.所以12D E D F =〔2〕因为在Rt ABC ∆中,8,6AC BC ==,所以由勾股定理,得10.AB = 即1211225AD BD C D C D ====又因为21D D x =,所以11225D E BD D F AD x ====-.所以21C F C E x == 在22BC D ∆中,2C 到2BD 的间隔 就是ABC ∆的AB 边上的高,为245. CB D A 图1PE FAD 1BC 1D 2C 2图3C 2D 2C 1BD 1A图2设1BED ∆的1BD 边上的高为h ,由探究,得221BC D BED ∆∆∽,所以52455h x-=. 所以24(5)25x h -=.121112(5)225BED S BD h x ∆=⨯⨯=- 又因为1290C C ∠+∠=︒,所以290FPC ∠=︒.又因为2C B ∠=∠,43sin ,cos 55B B ==. 所以234,55PC x PF x == ,22216225FC P S PC PF x ∆=⨯=而2212221126(5)22525BC D BED FC P ABC y S S S S x x ∆∆∆∆=--=---所以21824(05)255y x x x =-+≤≤(3) 存在. 当14ABC y S ∆=时,即218246255x x -+=整理,得2320250.x x -+=解得,125,53x x ==.即当53x =或者5x =时,重叠局部的面积等于原ABC ∆面积的14.4、〔2021〕如图1,以矩形OABC 的两边OA 和OC 所在的直线为x 轴、y 轴建立平面直角坐标系,A 点的坐标为(3)C ,0,点的坐标为(04),.将矩形OABC 绕O 点逆时针旋转,使B 点落在y 轴的正半轴上,旋转后的矩形为11111OA B C BC A B ,,相交于点M . 〔1〕求点1B 的坐标与线段1B C 的长;〔2〕将图1中的矩形111OA B C 沿y 轴向上平移,如图2,矩形222PA B C 是平移过程中的某一位置,22BC A B ,相交于点1M ,点P 运动到C 点停顿.设点P 运动的间隔 为x ,矩形222PA B C 与原矩形OABC 重叠局部的面积为y ,求y 关于x 的函数关系式,并写出x 的取值范围;〔3〕如图3,当点P 运动到点C 时,平移后的矩形为333PA B C .请你考虑如何通过图形变换使矩形333PA B C 与原矩形OABC 重合,请简述你的做法.3C[解析]〔1〕如图1,因为15OB OB ===,所以点1B 的坐标为(05),.11541B C OB OC =-=-=.〔2〕在矩形111OA B C 沿y 轴向上平移到P 点与C 点重合的过程中,点1A 运动到矩形OABC 的边BC 上时,求得P 点挪动的间隔 115x =. 当自变量x 的取值范围为1105x <≤时,如图2,由2122B CM B A P △∽△, 得1334x CM +=,此时,2221113334(1)224B A P B CM xy S S x +=-=⨯⨯-⨯+△△.即23(1)68y x =-++〔或者23345848y x x =--+〕.当自变量x 的取值范围为1145x ≤≤时,求得122(4)3PCM y S x '==-△〔或者221632333y x x =-+〕. 〔3〕局部参考答案:①把矩形333PA B C 沿3BPA ∠的角平分线所在直线对折.②把矩形333PA B C 绕C 点顺时针旋转,使点3A 与点B 重合,再沿y 轴向下平移4个单位长度.③把矩形333PA B C 绕C 点顺时针旋转,使点3A 与点B 重合,再沿BC 所在的直线对折. ④把矩形333PA B C 沿y 轴向下平移4个单位长度,再绕O 点顺时针旋转,使点3A 与点A 重合.5、〔2021〕如图1,Rt ABC △中,30CAB ∠=,5BC =.过点A 作AE AB ⊥,且15AE =,连接BE 交AC 于点P . 〔1〕求PA 的长;〔2〕以点A 为圆心,AP 为半径作⊙A ,试判断BE 与⊙A 是否相切,并说明理由; 〔3〕如图2,过点C 作CD AE ⊥,垂足为D .以点A 为圆心,r 为半径作⊙A ;以点C 为圆心,R 为半径作⊙C .假设r 和R 的大小是可变化的,并且在变化过程中保持⊙A 和⊙C 相切..,且使D 点在⊙A 的内部,B 点在⊙A 的外部,求r 和R 的变化范围. [解析] 〔1〕在Rt ABC △中,305CAB BC ∠==,,210AC BC ∴==.AE BC ∥,APE CPB ∴△∽△.::3:1PA PC AE BC ∴==. :3:4PA AC ∴=,3101542PA ⨯==. 〔2〕BE 与⊙A 相切.在Rt ABE △中,AB =,15AE =,CABCD图1图2tan 353AE ABE AB ∴∠===60ABE ∴∠=. 又30PAB ∠=,9090ABE PAB APB ∴∠+∠=∴∠=,, BE ∴与⊙A 相切.〔3〕因为553AD AB ==,,所以r 的变化范围为553r <<当⊙A 与⊙C 外切时,10R r +=,所以R 的变化范围为10535R -<<; 当⊙A 与⊙C 内切时,10R r -=,所以R 的变化范围为151053R <<+ 6、〔2021〕如图,平面直角坐标系中,直线AB 与x 轴,y 轴分别交于A (3,0),B (0,3)两点, ,点C 为线段AB 上的一动点,过点C 作CD ⊥x 轴于点D . (1)求直线AB 的解析式;(2)假设S 梯形OBCD 43,求点C 的坐标; (3)在第一象限内是否存在点P ,使得以P,O,B 为顶点的 三角形与△OBA 相似.假设存在,恳求出所有符合条件 的点P 的坐标;假设不存在,请说明理由.[解析] 〔1〕直线AB 解析式为:y=33-x+3. 〔2〕方法一:设点C坐标为〔x ,33-x+3〕,那么OD =x ,CD =33-x+3. ∴OBCD S 梯形=()2CD CD OB ⨯+=3632+-x . 由题意:3632+-x =334,解得4,221==x x 〔舍去〕 ∴ C〔2,33〕方法二:∵ 23321=⨯=∆OB OA S AOB ,OBCD S 梯形=334,∴63=∆ACD S . 由OA=3OB ,得∠BAO =30°,AD=3CD .∴ ACD S ∆=21CD ×AD =223CD =63.可得CD =33.∴ AD=1,OD =2.∴C 〔2,33〕. 〔3〕当∠OBP =Rt ∠时,如图①假设△BOP ∽△OBA ,那么∠BOP =∠BAO=30°,BP=3OB=3,∴1P 〔3,33〕. ②假设△BPO ∽△OBA ,那么∠BPO =∠BAO=30°,OP=33OB=1. ∴2P 〔1,3〕. 当∠OPB =Rt ∠时③ 过点P 作OP ⊥BC 于点P(如图),此时△PBO ∽△OBA ,∠BOP =∠BAO =30° 过点P 作PM ⊥OA 于点M .方法一: 在Rt △PBO 中,BP =21OB =23,OP =3BP =23.∵ 在Rt △P MO 中,∠OPM =30°,∴ OM =21OP =43;PM =3OM =433.∴3P 〔43,433〕.方法二:设P〔x ,33-x+3〕,得OM =x ,PM =33-x+3 由∠BOP =∠BAO,得∠POM =∠ABO .∵tan ∠POM==OMPM=x x 333+-,tan ∠ABOC=OBOA =3.∴33-x+3=3x ,解得x =43.此时,3P 〔43,433〕. ④假设△POB ∽△OBA(如图),那么∠OBP=∠BAO =30°,∠POM =30°.∴ PM =33OM =43. ∴ 4P 〔43,43〕〔由对称性也可得到点4P 的坐标〕.7、〔2021课改〕图14-1至图14-7的正方形霓虹灯广告牌ABCD 都是20×20的等距网格〔每个小方格的边长均为1个单位长〕,其对称中心为点O .如图14-1,有一个边长为6个单位长的正方形EFGH 的对称中心也是点O ,它以每秒1个单位长的速度由起始位置向外扩大〔即点O 不动,正方形EFGH 经过一秒由6×6扩大为8×8;再经过一秒,由8×8扩大为10×10;……〕,直到充满正方形ABCD ,再以同样的速度逐步缩小到起始时的大小,然后一直不断地以同样速度再扩大、再缩小.另有一个边长为6个单位长的正方形MNPQ 从如图14-1所示的位置开场,以每秒1个单位长的速度,沿正方形ABCD 的内侧边缘按A →B →C →D →A 挪动〔即正方形MNPQ 从点P 与点A 重合位置开场,先向左平移,当点Q 与点B 重合时,再向上平移,当点M 与点C 重合时,再向右平移,当点N 与点D 重合时,再向下平移,到达起始位置后仍继续按上述方式挪动〕.正方形EFGH 和正方形MNPQ 从如图14-1的位置同时开场运动,设运动时间是为x 秒,它们的重叠局部面积为y 个平方单位.〔1〕请你在图14-2和图14-3中分别画出x 为2秒、18秒时,正方形EFGH 和正方图14-7B ADQ形MNPQ 的位置及重叠局部〔重叠局部用阴影表示〕,并分别写出重叠局部的面积;〔2〕①如图14-4,当1≤x ≤3.5时,求y 与x 的函数关系式;②≤x ≤7时,求y 与x 的函数关系式;③如图14-6,当7≤x ≤10.5时,求y 与x 的函数关系式; ④≤x ≤13时,求y 与x 的函数关系式.〔3〕对于正方形MNPQ 在正方形ABCD 各边上挪动一周的过程,请你根据重叠局部面积y 的变化情况,指出y 获得最大值和最小值时,相对应的x 的取值情况,并指出最大值和最小值分别是多少.[解析] 〔1〕相应的图形如图2-1,2-2.当x =2时,y =3; 当x =18时,y =18.图14-6B A DQ图14-2图14-3B A D B AD 图14-4 BADQ图14-1 BA (P ) D Q图14-5 B A DQ〔2〕①当1≤x ≤3.5时,如图2-3,延长MN 交AD 于K ,设MN 与HG 交于S ,MQ 与FG 交于T ,那么MK =6+x ,SK =TQ =7-x ,从而MS =MK -SK =2x -1,MT =MQ -TQ =6-〔7-x 〕= x -1. ∴y=MT ·MS =〔x -1〕〔2x -1〕=2x 2-3x +1. ②≤x ≤7时,如图2-4,设FG 与MQ 交于T ,那么TQ =7-x ,∴MT =MQ -TQ =6-〔7-x 〕=x -1.∴y=MN ·MT =6〔x -1〕=6x -6.③当7≤x ≤10.5时,如图2-5,设FG 与MQ 交于T ,那么TQ=x -7,∴MT =MQ -TQ =6-〔x -7〕=13-x .∴y = MN ·MT =6〔13-x 〕=78-6x .④≤x ≤13时,如图2-6,设MN 与EF 交于S ,NP 交FG 于R ,延长NM 交BC 于K ,那么MK =14-x ,SK =RP =x -7,∴SM =SK -MK=2x -21,从而SN =MN -SM =27-2x ,NR =NP -RP =13-x .图2-4BA D图2-5BA D 图2-6BAD图2-3BADQ图2-2BA D 图2-1 BA DQ∴y=NR·SN=〔13-x〕〔27-2x〕=2x2-53x+351.〔3〕对于正方形MNPQ,①在AB边上挪动时,当0≤x≤1及13≤x≤14时,y获得最小值0;当x=7时,y获得最大值36.②在BC边上挪动时,当14≤x≤15及27≤x≤28时,y获得最小值0;当x=21时,y获得最大值36.③在CD边上挪动时,当28≤x≤29及41≤x≤42时,y获得最小值0;当x=35时,y获得最大值36.④在DA边上挪动时,当42≤x≤43及55≤x≤56时,y获得最小值0;当x=49时,y获得最大值36.励志赠言经典语录精选句;挥动**,放飞梦想。
全国各地中考数学试卷解析版分类汇编 动态问题

动态问题一、选择题1. (2014•山东潍坊,第8题3分)如图,已知矩形ABCD 的长AB 为5,宽BC 为4.E 是BC 边上的一个动点,AE ⊥上EF ,EF 交CD 于点F .设BE =x ,FC =y ,则点 E 从点B 运动到点C 时,能表示y 关于x 的函数关系的大致图象是( )考点:动点问题的函数图象.分析:易证△ABE ∽△ECF ,根据相似比得出函数表达式,在判断图像. 解答:因为△ABE ∽△ECF ,则BE :CF =AB :EC ,即x :y =5:(4-x )y , 整理,得y =-51(x -2)2+54, 很明显函数图象是开口向下、顶点坐标是(2,54)的抛物线.对应A 选项. 故选:A .点评:此题考查了动点问题的函数图象,关键列出动点的函数关系,再判断选项. 2. (2014•山东烟台,第12题3分)如图,点P 是▱ABCD 边上一动点,沿A →D →C →B 的路径移动,设P 点( )经过的路径长为x ,△BAP 的面积是y ,则下列能大致反映y 与x 的函数关系的图象是A .B .C .D .考点:平行四边形的性质,函数图象.分析:分三段来考虑点P沿A→D运动,△BAP的面积逐渐变大;点P沿D→C移动,△BAP的面积不变;点P沿C→B的路径移动,△BAP的面积逐渐减小,据此选择即可.解答:点P沿A→D运动,△BAP的面积逐渐变大;点P沿D→C移动,△BAP的面积不变;点P沿C→B的路径移动,△BAP的面积逐渐减小.故选:A.点评:本题主要考查了动点问题的函数图象.注意分段考虑.3.(2014•甘肃兰州,第15题4分)如图,在平面直角坐标系中,四边形OBCD是边长为4的正方形,平行于对角线BD的直线l从O出发,沿x轴正方向以每秒1个单位长度的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l运动的时间为t(秒),下列能反映S与t之间函数关系的图象是()B二、填空题1. (2014•江苏徐州,第18题3分)如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△P AQ的面积为ycm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为y=﹣3x+18.考点:动点问题的函数图象.12999数学网分析:根据从图②可以看出当Q点到B点时的面积为9,求出正方形的边长,再利用三角形的面积公式得出EF所在的直线对应的函数关系式.解答:解:∵点P沿边DA从点D开始向点A以1cm/s的速度移动;点Q沿边AB、BC 从点A开始向点C以2cm/s的速度移动.∴当P点到AD的中点时,Q到B点,从图②可以看出当Q点到B点时的面积为9,∴9=×(AD)•AB,∵AD=AB,∴AD=6,即正方形的边长为6,当Q点在BC上时,AP=6﹣x,△APQ的高为AB,∴y=(6﹣x)×6,即y=﹣3x+18.故答案为:y=﹣3x+18.点评:本题主要考查了动点函数的图象,解决本题的关键是求出正方形的边长.三、解答题1. (2014•四川巴中,第31题12分)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣4与x轴交于点A(﹣2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.(1)求抛物线的解析式;(2)若两动点M,H分别从点A,B以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到达原点时,点H立刻掉头并以每秒个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,经过点M的直线l⊥x轴,交AC或BC 于点P,设点M的运动时间为t秒(t>0).求点M的运动时间t与△APH的面积S的函数关系式,并求出S的最大值.考点:二次函数综合题.分析:(1)根据抛物线y=ax2+bx﹣4与x轴交于点A(﹣2,0),直线x=1是该抛物线的对称轴,得到方程组,解方程组即可求出抛物线的解析式;(2)由于点M到达抛物线的对称轴时需要3秒,所以t≤3,又当点M到达原点时需要2秒,且此时点H立刻掉头,所以可分两种情况进行讨论:①当0<t≤2时,由△AMP∽△AOC,得出比例式,求出PM,AH,根据三角形的面积公式求出即可;②当2<t≤3时,过点P作PM⊥x轴于M,PF⊥y轴于点F,表示出三角形APH的面积,利用配方法求出最值即可.解答:(1)∵抛物线y=ax2+bx﹣4与x轴交于点A(﹣2,0),直线x=1是该抛物线的对称轴,∴,解得:,∴抛物线的解析式是:y=x2﹣x﹣4,(2)分两种情况:①当0<t≤2时,∵PM∥OC,∴△AMP∽△AOC,∴=,即=,∴PM=2t.解方程x2﹣x﹣4=0,得x1=﹣2,x2=4,∵A(﹣2,0),∴B(4,0),∴AB=4﹣(﹣2)=6.∵AH=AB﹣BH=6﹣t,∴S=PM•AH=×2t(6﹣t)=﹣t2+6t=﹣(t﹣3)2+9,当t=2时S的最大值为8;②当2<t≤3时,过点P作PM⊥x轴于M,作PF⊥y轴于点F,则△COB∽△CFP,又∵CO=OB,∴FP=FC=t﹣2,PM=4﹣(t﹣2)=6﹣t,AH=4+(t﹣2)=t+1,∴S=PM•AH=(6﹣t)(t+1)=﹣t2+4t+3=﹣(t﹣)2+,当t=时,S最大值为.综上所述,点M的运动时间t与△APQ面积S的函数关系式是S=,S的最大值为.点评:本题是二次函数的综合题型,其中涉及到运用待定系数法求二次函数的解析式,三角形的面积,二次函数的最值等知识,综合性较强,难度适中.运用数形结合、分类讨论及方程思想是解题的关键.2.(2014•湖南怀化,第24题,10分)如图1,在平面直角坐标系中,AB=OB=8,∠ABO=90°,∠yOC=45°,射线OC以每秒2个单位长度的速度向右平行移动,当射线OC经过点B时停止运动,设平行移动x秒后,射线OC扫过Rt△ABO的面积为y.(1)求y与x之间的函数关系式;(2)当x=3秒时,射线OC平行移动到O′C′,与OA相交于G,如图2,求经过G,O,B 三点的抛物线的解析式;(3)现有一动点P在(2)中的抛物线上,试问点P在运动过程中,是否存在三角形POB 的面积S=8的情况?若存在,求出点P的坐标,若不存在,请说明理由.,=4+﹣4+,=4+﹣4+﹣4+3.(2014•湖南张家界,第25题,12分)如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+bx+c(a≠0)过O、B、C三点,B、C坐标分别为(10,0)和(,﹣),以OB为直径的⊙A经过C点,直线l垂直x轴于B点.(1)求直线BC的解析式;(2)求抛物线解析式及顶点坐标;(3)点M是⊙A上一动点(不同于O,B),过点M作⊙A的切线,交y轴于点E,交直线l于点F,设线段ME长为m,MF长为n,请猜想m•n的值,并证明你的结论;(4)若点P从O出发,以每秒一个单位的速度向点B作直线运动,点Q同时从B出发,以相同速度向点C作直线运动,经过t(0<t≤8)秒时恰好使△BPQ为等腰三角形,请求出满足条件的t值.,.,﹣)x x==5=﹣×﹣,,﹣),.4. (2014年贵州黔东南24.(14分))如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;(3)求△P AC为直角三角形时点P的坐标.考点:二次函数综合题.12999数学网分析:(1)已知B(4,m)在直线y=x+2上,可求得m的值,抛物线图象上的A、B两点坐标,可将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值.(2)要弄清PC的长,实际是直线AB与抛物线函数值的差.可设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,根据函数的性质即可求出PC的最大值.(3)根据直线AB的解析式,可求得直线AC的解析式y=﹣x+b,已知了点A的坐标,即可求得直线AC的解析式,联立抛物线的解析式,可求得C点的坐标;解答:解:(1)∵B(4,m)在直线线y=x+2上,∴m=4+2=6,∴B(4,6),∵A(,)、B(4,6)在抛物线y=ax2+bx﹣4上,∴,∵c=6,∴a=2,b=﹣8,∴y=2x2﹣8x+6.(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2﹣8n+6),∴PC=(n+2)﹣(2n2﹣8n+6),=﹣2n2+9n﹣4,=﹣2(n﹣)2+,∵PC>0,∴当n=时,线段PC最大且为.(3)设直线AC的解析式为y=﹣x+b,把A(,)代入得:=﹣+b,解得:b=3,∴直线AC解析式:y=﹣x+3,点C在抛物线上,设C(m,2m2﹣8m+6),代入y=﹣x+3得:2m2﹣8m+6=﹣m+3,整理得:2m2﹣7m+3=0,解得;m=3或m=,∴P(3,0)或P(,).点评:此题主要考查了二次函数解析式的确定、二次函数最值的应用以及直角三角形的判定、函数图象交点坐标的求法等知识;5.(2014•十堰)25.(12分)已知抛物线C1:y=a(x+1)2﹣2的顶点为A,且经过点B(﹣2,﹣1).(1)求A点的坐标和抛物线C1的解析式;(2)如图1,将抛物线C1向下平移2个单位后得到抛物线C2,且抛物线C2与直线AB相交于C,D两点,求S△OAC:S△OAD的值;(3)如图2,若过P(﹣4,0),Q(0,2)的直线为l,点E在(2)中抛物线C2对称轴右侧部分(含顶点)运动,直线m过点C和点E.问:是否存在直线m,使直线l,m与x轴围成的三角形和直线l,m与y轴围成的三角形相似?若存在,求出直线m的解析式;若不存在,说明理由.解得:解得:.=.==...解得:,解得:==≥=.=.解得:6.(2014•娄底26.(10分))如图,抛物线y=x2+mx+(m﹣1)与x轴交于点A(x1,0),B (x2,0),x1<x2,与y轴交于点C(0,c),且满足x12+x22+x1x2=7.(1)求抛物线的解析式;(2)在抛物线上能不能找到一点P,使∠POC=∠PCO?若能,请求出点P的坐标;若不能,请说明理由.7.(2014•娄底27.(10分))如图甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为1cm/s.连接PQ,设运动时间为t(s)(0<t<4),解答下列问题:(1)设△APQ的面积为S,当t为何值时,S取得最大值?S的最大值是多少?(2)如图乙,连接PC,将△PQC沿QC翻折,得到四边形PQP′C,当四边形PQP′C为菱形时,求t的值;′(3)当t为何值时,△APQ是等腰三角形?,得出==,得出,===,即=5=,=,(,最大值为cm=,=,<s==,=,,即=5=或或8. ( 2014年河南) (11分)如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B(5,0)两点,直线y=-34x+3与y轴交于点C,,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m。
中考数学试题分类动态问题
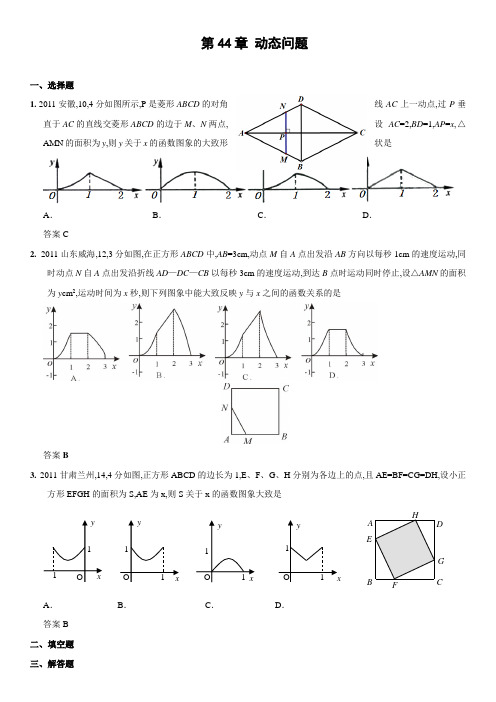
第44章 动态问题一、选择题1. 2011安徽,10,4分如图所示,P 是菱形ABCD 的对角线AC 上一动点,过P 垂直于AC 的直线交菱形ABCD 的边于M 、N 两点,设AC =2,BD =1,AP =x ,△AMN 的面积为y ,则y 关于x 的函数图象的大致形状是A .B .C .D .答案C2. 2011山东威海,12,3分如图,在正方形ABCD 中,AB =3cm,动点M 自A 点出发沿AB 方向以每秒1cm 的速度运动,同时动点N 自A 点出发沿折线AD —DC —CB 以每秒3cm 的速度运动,到达B 点时运动同时停止,设△AMN 的面积为y cm 2,运动时间为x 秒,则下列图象中能大致反映y 与x 之间的函数关系的是答案B3. 2011甘肃兰州,14,4分如图,正方形ABCD 的边长为1,E 、F 、G 、H 分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH 的面积为S,AE 为x,则S 关于x 的函数图象大致是A .B .C .D .答案B 二、填空题 三、解答题A BC DEFGHx y -1 O 1x y1 O 1 x yO 1 xy1O 1 11. 2011浙江省舟山,24,12分已知直线3+=kx y k <0分别交x 轴、y 轴于A 、B 两点,线段OA 上有一动点P 由原点O 向点A 运动,速度为每秒1个单位长度,过点P 作x 轴的垂线交直线AB 于点C ,设运动时间为t 秒.1当1-=k 时,线段OA 上另有一动点Q 由点A 向点O 运动,它与点P 以相同速度同时出发,当点P 到达点A 时两点同时停止运动如图1.① 直接写出t =1秒时C 、Q 两点的坐标;② 若以Q 、C 、A 为顶点的三角形与△AOB 相似,求t 的值. 2当43-=k 时,设以C 为顶点的抛物线n m x y ++=2)(与直线AB 的另一交点为D 如图2, ① 求CD 的长;② 设△COD 的OC 边上的高为h ,当t 为何值时,h 的值最大答案1①C 1,2,Q 2,0.②由题意得:Pt ,0,Ct ,-t+3,Q 3-t ,0, 分两种情形讨论:情形一:当△AQC ∽△AOB 时,∠AQC=∠AOB =90°,∴CQ ⊥OA , ∵CP ⊥OA ,∴点P 与点Q 重合,OQ =OP ,即3-t =t ,∴t=.情形二:当△ACQ ∽△AOB 时,∠ACQ=∠AOB =90°,∵O A=O B=3,∴△AOB 是等腰直角三角形,∴△ACQ 是等腰直角三角形,∵CQ ⊥OA ,∴AQ=2CP ,即t =2-t +3,∴t=2.∴满足条件的t 的值是秒或2秒. 2 ①由题意得:Ct ,-34t +3,∴以C 为顶点的抛物线解析式是23()34y x t t =--+, 由233()3344x t t x --+=-+,解得x 1=t ,x 2=t 34-;过点D 作DE ⊥CP 于点E ,则∠DEC=∠AOB =90°,DE ∥OA ,∴∠EDC=∠OAB ,∴△DEC ∽△AOB ,∴DE CDAO BA=, ∵AO =4,AB =5,DE =t -t-34=34.∴CD =35154416DE BA AO ⨯⨯==.②∵CD =1516,CD 边上的高=341255⨯=.∴S △COD =11512921658⨯⨯=.∴S △COD 为定值; 要使OC 边上的高h 的值最大,只要OC 最短.第24题图2第24题图1因为当OC ⊥AB 时OC 最短,此时OC 的长为125,∠BCO =90°,∵∠AOB =90°,∴∠COP =90°-∠BOC =∠OBA ,又∵CP ⊥OA ,∴Rt △PCO ∽Rt △OAB ,∴OP OC BO BA =,OP =123365525OC BO BA ⨯⨯==,即t =3625, ∴当t 为3625秒时,h 的值最大.2. 2011广东东莞,22,9分如图,抛物线2517144y x x =-++与y 轴交于点A ,过点A 的直线与抛物线交于另一点B ,过点B 作BC ⊥x 轴,垂足为点C 3,0. 1求直线AB 的函数关系式;2动点P 在线段OC 上,从原点O 出发以每钞一个单位的速度向C 移动,过点P 作⊥x 轴,交直线AB 于点M ,抛物线于点N ,设点P 移动的时间为t 秒,MN 的长为s 个单位,求s 与t 的函数关系式,并写出t 的取值范围;3设2的条件下不考虑点P 与点O ,点G 重合的情况,连接CM ,BN ,当t 为何值时,四边形BCMN 为平等四边形问对于所求的t 的值,平行四边形BCMN 是否为菱形说明理由.解1把x=0代入2517144y x x =-++,得1y = 把x=3代入2517144y x x =-++,得52y =,∴A 、B 两点的坐标分别0,1、3,52设直线AB 的解析式为y kx b =+,代入A 、B 的坐标,得1532b k b =⎧⎪⎨+=⎪⎩,解得112b k =⎧⎪⎨=⎪⎩所以,112y x =+2把x=t 分别代入到112y x =+和2517144y x x =-++ 分别得到点M 、N 的纵坐标为112t +和2517144t t -++∴MN=2517144t t -++-112t +=251544t t -+即251544s t t =-+∵点P 在线段OC 上移动, ∴0≤t ≤3.3在四边形BCMN 中,∵BC ∥MN∴当BC=MN 时,四边形BCMN 即为平行四边形 由25155442t t -+=,得121,2t t == 即当12t =或时,四边形BCMN 为平行四边形 当1t =时,PC=2,PM=32,PN=4,由勾股定理求得CM=BN=52, 此时BC=CM=MN=BN,平行四边形BCMN 为菱形; 当2t =时,PC=1,PM=2,由勾股定理求得CM=5, 此时BC ≠CM,平行四边形BCMN 不是菱形; 所以,当1t =时,平行四边形BCMN 为菱形.3. 2011江苏扬州,28,12分如图,在Rt △ABC 中,∠BAC=90o,AB<AC,M 是BC 边的中点,MN ⊥BC 交AC 于点N,动点P 从点B 出发沿射线BA 以每秒3厘米的速度运动;同时,动点Q 从点N 出发沿射线NC 运动,且始终保持MQ ⊥MP;设运动时间为t 秒t>01△PBM 与△QNM 相似吗以图1为例说明理由; 2若∠ABC=60o,AB=43厘米; ① 求动点Q 的运动速度;② 设Rt △APQ 的面积为S 平方厘米,求S 与t 的函数关系式; 3探求BP 2、PQ 2、CQ 2三者之间的数量关系,以图1为例说明理由;答案解:1△PBM 与△QNM 相似;∵MN ⊥BC MQ ⊥MP ∴ ∠NMB=∠PMQ=∠BAC =90o ∴∠PMB=∠QMN, ∠QNM=∠B =90o -∠C ∴ △PBM ∽△QNM2①∵∠ABC=60o,∠BAC =90o,AB=43,BP=3t ∴AB=BM=CM=43,MN=4 ∵ △PBM ∽△QNM ∴MN BM NQ BP = 即:3434==NQ BP ∵P 点的运动速度是每秒3厘米, ∴ Q 点运动速度是每秒1厘米; ② ∵ AC=12,CN=8∴ AQ=12-8+t=4+t, AP=43-3t∴ S=)334()4(21t t -⨯+⨯=)16(232--t 3 BP 2+ CQ 2 =PQ 2证明如下: ∵BP=3t, ∴BP 2=3t 2 ∵CQ=8-t ∴CQ 2=8-t 2=64-16t+t 2 ∵PQ 2=4+t 2+34-t 2=4t 2-16t+64 ∴BP 2+ CQ 2 =PQ 24. 2011山东德州23,12分在直角坐标系xoy 中,已知点P 是反比例函数)>0(32x xy =图象上一个动点,以P 为圆心的圆始终与y 轴相切,设切点为A .1如图1,⊙P 运动到与x 轴相切,设切点为K ,试判断四边形OKP A 的形状,并说明理由. 2如图2,⊙P 运动到与x 轴相交,设交点为B ,C .当四边形ABCP 是菱形时: ①求出点A ,B ,C 的坐标.②在过A ,B ,C 三点的抛物线上是否存在点M ,使△MBP 的面积是菱形ABCP 面积的21.若存在,试求出所有满足条件的M 点的坐标,若不存在,试说明理由.答案解:1∵⊙P分别与两坐标轴相切,∴P A⊥OA,PK⊥OK.∴∠P AO=∠OKP=90°.又∵∠AOK=90°,∴∠P AO=∠OKP=∠AOK=90°.∴四边形OKP A是矩形.又∵OA=OK,∴四边形OKP A是正方形.……………………2分2①连接PB,设点P的横坐标为x,则其纵坐标为x 32.过点P作PG⊥BC于G.∵四边形ABCP为菱形,∴BC=P A=PB=PC.∴△PBC为等边三角形.在Rt△PBG中,∠PBG=60°,PB=P A=x,PG=x 32.AP 23yx=xyKO图1OA P 23yx=xyB C图2GMsin ∠PBG =PBPG,即2x x =. 解之得:x =±2负值舍去.∴ PG,P A =B C=2.……………………4分 易知四边形OGP A 是矩形,P A =OG =2,BG =CG =1, ∴OB =OG -BG =1,OC =OG +GC =3.∴ AB 1,0C 3,0.……………………6分 设二次函数解析式为:y =ax 2+bx +c .据题意得:0930a b c a b c c ⎧++=⎪++=⎨⎪=⎩解之得:a=3, b=3-, c∴二次函数关系式为:233y x x =-9分 ②解法一:设直线BP 的解析式为:y =ux +v ,据题意得:2u v u v +=⎧⎪⎨+=⎪⎩解之得:uv=-∴直线BP的解析式为:y =-.过点A 作直线AM ∥PB ,则可得直线AM的解析式为:y =+解方程组:233y y x x ⎧=+⎪⎨=-⎪⎩得:110x y =⎧⎪⎨=⎪⎩;227x y =⎧⎪⎨=⎪⎩ 过点C 作直线CM ∥PB ,则可设直线CM的解析式为:y t =+. ∴0=t .∴t =-∴直线CM的解析式为:y =-.解方程组:2y y x x ⎧=-⎪⎨=⎪⎩得:113x y =⎧⎨=⎩ ;224x y =⎧⎪⎨=⎪⎩. 综上可知,满足条件的M 的坐标有四个,分别为:12分 解法二:∵12PAB PBC PABCS S S ∆∆==,∴AC 3,0显然满足条件.延长AP 交抛物线于点M ,由抛物线与圆的轴对称性可知,PM =P A . 又∵AM ∥BC , ∴12PBM PBA PABCS S S ∆∆==.∴点M又点M 的横坐标为AM =P A +PM =2+2=4. ∴点M点7,综上可知,满足条件的M 的坐标有四个,分别为:12分解法三:延长AP 交抛物线于点M ,由抛物线与圆的轴对称性可知,PM =P A . 又∵AM ∥BC , ∴12PBM PBA PABCS S S ∆∆==.∴点M2x x =. 解得:10x =舍,24x =. ∴点M 的坐标为点7,综上可知,满足条件的M 的坐标有四个,分别为:12分 5. 2011山东菏泽,21,9分如图,抛物线y =12x 2+bx -2与x 轴交于A ,B 两点,与y 轴交于C 点,且A -1,0. 1求抛物线的解析式及顶点D 的坐标; 2判断△ABC 的形状,证明你的结论;3点Mm ,0是x 轴上的一个动点,当MC +MD 的值最小时,求m 的值.解:1把点A -1,0的坐标代入抛物线的解析式y =12x 2+bx -2, 整理后解得32b =-, 所以抛物线的解析式为 213222y x x =--. 顶点D 325,28⎛⎫- ⎪⎝⎭.2∵AB =5,AC 2=OA 2+OC 2=5,BC 2=OC 2+OB 2=20,∴AC 2+BC 2=AB 2.∴△ABC 是直角三角形. 3作出点C 关于x 轴的对称点C′,则C′ 0,2,OC′=2. 连接C′D 交x 轴于点M ,根据轴对称性及两点之间线段最短可知,MC +MD 的值最小. 设抛物线的对称轴交x 轴于点E . △C′OM ∽△DEM . ∴OM OC EM ED '=.∴232528m m =-.∴m =2441. 6. 2011山东济宁,23,10分如图,在平面直角坐标系中,顶点为4,1-的抛物线交y 轴于A 点,交x 轴于B ,C 两点点B 在点C 的左侧. 已知A 点坐标为0,3.1求此抛物线的解析式;2过点B 作线段AB 的垂线交抛物线于点D , 如果以点C 为圆心的圆与直线BD 相切,请判断抛物线的对称轴l 与⊙C 有怎样的位置关系,并给出证明;3已知点P 是抛物线上的一个动点,且位于A ,C 两点之间,问:当点P 运动到什么位置时,PAC ∆的面积最大并求出此时P 点的坐标和PAC ∆的最大面积.答案1解:设抛物线为2(4)1y a x =--. ∵抛物线经过点A 0,3,∴23(04)1a =--.∴14a =. ∴抛物线为2211(4)12344y x x x =--=-+. ……………………………3分 2 答:l 与⊙C 相交. …………………………………………………………………4分 证明:当21(4)104x --=时,12x =,26x =. ∴B 为2,0,C 为6,0.∴AB =设⊙C 与BD 相切于点E ,连接CE ,则90BEC AOB ∠=︒=∠. ∵90ABD ∠=︒,∴90CBE ABO ∠=︒-∠.又∵90BAO ABO ∠=︒-∠,∴BAO CBE ∠=∠.∴AOB ∆∽BEC ∆. ∴CE BCOB AB =.∴2CE =.∴2CE =>.…………………………6分 ∵抛物线的对称轴l 为4x =,∴C 点到l 的距离为2.∴抛物线的对称轴l 与⊙C 相交. ……………………………………………7分 3 解:如图,过点P 作平行于y 轴的直线交AC 于点Q .可求出AC 的解析式为132y x =-+.…………………………………………8分 设P 点的坐标为m ,21234m m -+,则Q 点的坐标为m ,132m -+.∴2211133(23)2442PQ m m m m m =-+--+=-+.∵22113327()6(3)24244PAC PAQ PCQ S S S m m m ∆∆∆=+=⨯-+⨯=--+,∴当3m =时,PAC ∆的面积最大为274.x第23题此时,P 点的坐标为3,34-. ……………………………10分7. 2011山东威海,25,12分如图,抛物线2y ax bx c =++交x 轴于点(3,0)A -,点(1,0)B ,交y 轴于点(0,3)E -.点C 是点A 关于点B 的对称点,点F 是线段BC 的中点,直线l 过点F 且与y 轴平行.直线y x m =-+过点C ,交y 轴于点D .1求抛物线的函数表达式;2点K 为线段AB 上一动点,过点K 作x 轴的垂线与直线CD 交于点H ,与抛物线交于点G ,求线段HG 长度的最大值;3在直线l 上取点M ,在抛物线上取点N ,使以点A ,C ,M ,N 为顶点的四边是平行四边形,求点N 的坐标.图① 备用图答案 解:1设抛物线的函数表达式(1)(3)y a x x =-+ ∵抛物线与y 轴交于点(0,3)E -,将该点坐标代入上式,得1a =. ∴所求函数表达式(1)(3)y x x =-+,即223y x x =+-. 2∵点C 是点A 关于点B 的对称点,点(3,0)A -,点(1,0)B , ∴点C 的坐标是(5,0)C .将点C 的坐标是(5,0)C 代入y x m =-+,得5m =. ∴直线CD 的函数表达式为5y x =-+.AxyBOCD第23题EPQ设K 点的坐标为(,0)t ,则H 点的坐标为(,5)t t -+,G 点的坐标为2(,23)t t t +-. ∵点K 为线段AB 上一动点, ∴31t -≤≤.∴222341(5)(23)38()24HG t t t t t t =-+-+-=--+=-++. ∵3312-≤-≤, ∴当32t =-时,线段HG 长度有最大值414.3∵点F 是线段BC 的中点,点(1,0)B ,点 (5,0)C , ∴点F 的坐标为(3,0)F . ∵直线l 过点F 且与y 轴平行, ∴直线l 的函数表达式为3x =. ∵点M 在直线l 上,点N 在抛物线上 ,∴设点M 的坐标为(3,)M m ,点N 的坐标为2(,23)N n n n +-. ∵点(3,0)A -,点 (5,0)C ,∴8AC =. 分情况讨论: ①若线段AC 是以点A ,C ,M ,N 为顶点的四边是平行四边形的边,则须MN ∥AC ,且MN =AC =8.当点N 在点M 的左侧时,3MN n =-. ∴38n -=,解得5n =-. ∴N 点的坐标为(5,12)N -.当点N 在点M 的右侧时,3MN n =-. ∴38n -=,解得11n =. ∴N 点的坐标为(11,40)N .②若线段AC 是以点A ,C ,M ,N 为顶点的平行四边形的对角线,由“点C 与点A 关于点B 中心对称”知:点M 与点N 关于点B 中心对称.取点F 关于点B 对称点P ,则点P 的坐标为(1,0)P -.过点P 作NP ⊥x 轴,交抛物线于点N .将1x =-代入223y x x =+-,得4y =-. 过点N ,B 作直线NB 交直线l 于点M . 在△BPN 和△BFM 中,∵90NPB MBF BF BP BPN BFM ∠=∠⎧⎪=⎨⎪∠=∠=︒⎩∴△BPN ≌△BFM . ∴NB =MB .∴四边形点ANCM 为平行四边形. ∴坐标为(1,4)--的点N 符合条件.∴当点N 的坐标为(5,12)-,(11,40),(1,4)--时,以点A ,C ,M ,N 为顶点的四边是平行四边形.8. 2011山东烟台,26,14分如图,在直角坐标系中,梯形ABCD 的底边AB 在x 轴上,底边CD 的端点D 在y 轴上.直线CB 的表达式为y =-43x +163,点A 、D 的坐标分别为-4,0,0,4.动点P 自A 点出发,在AB 上匀速运行.动点Q 自点B 出发,在折线BCD 上匀速运行,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P 运动t 秒时,△OPQ 的面积为s 不能构成△OPQ 的动点除外. 1求出点B 、C 的坐标; 2求s 随t 变化的函数关系式;3当t 为何值时s 有最大值并求出最大值.答案解:1把y =4代入y =-43x +163,得x =1. ∴C 点的坐标为1,4. 当y =0时,-43x +163=0, ∴x =4.∴点B 坐标为4,0.2作CM ⊥AB 于M ,则CM =4,BM =3. ∴BC =22CM BM +=2234+=5. ∴sin ∠ABC =CM BC =45. ①当0<t <4时,作QN ⊥OB 于N , 则QN =BQ ·sin ∠ABC =45t. 备用图2O xyABCDO xyABCD备用图1 OxyABCD PQ∴S=12OP·QN=124-t×45t=-25t2+85t0<t<4.②当4<t≤5时,如备用图1, 连接QO,QP,作QN⊥OB于N.同理可得QN=4 5 t.∴S=12OP·QN=12×t-4×45t. =25t2-85t4<t≤5.③当5<t≤6时,如备用图2, 连接QO,QP.S=12×OP×OD=12t-4×4=2t-85<t≤6.3①在0<t<4时,当t=8522()5⨯-=2时,S最大=28()524()5-⨯-=85.②在4<t≤5时,对于抛物线S=25t2-85t,当t=-85225-⨯=2时,S最小=25×22-85×2=-85.∴抛物线S=25t2-85t的顶点为2,-85.∴在4<t≤5时,S随t的增大而增大.∴当t =5时,S 最大=25×52-85×5=2. ③在5<t ≤6时,在S =2t -8中,∵2>0,∴S 随t 的增大而增大. ∴当t =6时,S 最大=2×6-8=4.∴综合三种情况,当t =6时,S 取得最大值,最大值是4.说明:3中的②也可以省略,但需要说明:在2中的②与③的△OPQ ,③中的底边OP 和高CD 都大于②中的底边OP 和高.所以③中的△OPQ 面积一定大于②中的△OPQ 的面积.9. 2011四川南充市,22,8分抛物线y =ax 2+bx+c 与x 轴的交点为A m -4,0和B m ,0,与直线y =-x +p 相交于点A 和点C2m -4,m -6.1求抛物线的解析式;2若点P 在抛物线上,且以点P 和A,C 以及另一点Q 为顶点的平行四边形ACQP 面积为12,求点P,Q 的坐标; 3在2条件下,若点M 是x 轴下方抛物线上的动点,当⊿PQM 的面积最大时,请求出⊿PQM 的最大面积及点M 的坐标;答案解:1∵点Am-4,0和C2m-4,m-6在直线y =-x +p 上 ∴0(4)6(24)m p m m p =--+⎧⎨-=--+⎩解得:31m p =⎧⎨=-⎩∴A-1,0 B3,0, C2,-3 设抛物线y =ax 2+bx+c =ax-3x+1, ∵C2,-3 ∴a=1∴抛物线解析式为:y =x 2-2x-32AC=32,AC 所在直线的解析式为:y =-x -1,∠BAC=450∵平行四边形ACQP 的面积为12. ∴平行四边形ACQP 中AC 边上的高为2312=22过点D 作DK ⊥AC 与PQ 所在直线相交于点K,DK= 22,∴DN=4 ∵ACPQ,PQ 所在直线在直线ACD 的两侧,可能各有一条, ∴PQ 的解析式或为y =-x +3或y =-x -5∴2233y x x y x ⎧=--⎨=-+⎩解得:1130x y =⎧⎨=⎩或2225x y =-⎧⎨=⎩2235y x x y x ⎧=--⎨=--⎩,此方程组无解. 即P 13,0, P 2-2,5∵ACPQ 是平行四边形 ,A-1,0 C2,-3 ∴当P3,0时,Q6,-3 当P-2,5时,Q1,2∴满足条件的P,Q 点是P 13,0, Q 16,-3或 P 2-2,5,Q 21,2 (1)设M t ,t 2-2t-3,-1<t <3,过点M 作y 轴的平行线,交PQ 所在直线雨点T,则Tt,-t+3MT=-t+3- t 2-2t-3=- t 2+t+6过点M 作M S ⊥PQ 所在直线于点S, MS=22MT=22 - t 2+t+6=- 22t-212+8225∴当t=21时,M 21,-415,⊿PQM 中PQ 边上高的最大值为822510.2011 浙江杭州,24, 12图形既关于点O 中心对称,又关于直线AC ,BD 对称,AC =10,BD =6,已知点E ,M 是线段AB 上的动点不与端点重合,点O 到EF ,MN 的距离分别为1h ,2h .△OEF 与△OGH 组成的图形称为蝶形. 1求蝶形面积S 的最大值;2当以EH 为直径的圆与以MQ 为直径的圆重合时,求1h 与2h 满足的关系式,并求1h 的取值范围.答案1 如图,设EF 与AC 交于点K,由△OEF ∽△ABD,得AK EF AO BD =,1556h EF-=, O DCBAyxLK SEROABM16(5)5EF h =-,1111622(5)225S OK EF h h =⨯•=⨯•-,整理得216515()522S h =--+,当152h =时,蝶形面积S 的最大,最大值为152.2 如图,设MN 与AC 交于点L,由1得16(5)5EF h =-,则13(5)5EK h =-,23(5)5ML h =-由OK 2+EK 2=OE 2,OL 2+ML 2=OM 2,得OK 2+EK 2=OL 2+ML 2,2222112233(5)(5)55h h h h ⎡⎤⎡⎤+-=+-⎢⎥⎢⎥⎣⎦⎣⎦,整理得[]1212()17()450h h h h -+-=,当点E,M 不重合时,120h h -≠,124517h h +=.当OE ⊥AB 时,14534h =,所以145017h << 2当点,E M 重合时,则12h h =,此时1h 的取值范围为105h <<.解法二:1由题意,得四边形ABCD 是菱形. 由//EF BD ,得ABDAEF ∆∆,1565h EF -∴=,即()1655EF h =- ()2111166515255522OEFS S EF h h h h ∆⎛⎫∴==⨯=-⨯=--+ ⎪⎝⎭所以当152h =时,max 152S =. 2根据题意,得OE OM =.如图,作OR AB ⊥于R , OB 关于OR 对称线段为OS ,1当点,E M 不重合时,则,OE OM 在OR 的两侧,易知RE RM =.225334AB =+=,34OR ∴=221533434BR ⎛⎫∴=-= ⎪⎝⎭由////ML EK OB ,得,OK BE OL BMOA AB OA AB== 2OK OL BE BM BR OA OA AB AB AB ∴+=+=,即1295517h h +=124517h h ∴+=,此时1h 的取值范围为145017h <<且14534h ≠ 2当点,E M 重合时,则12h h =,此时1h 的取值范围为105h <<.11. 2011 浙江湖州,24,14如图1.已知正方形OABC 的边长为2,顶点A 、C 分别在x 、y 轴的正半轴上,M 是BC 的中点.P 0,m 是线段OC 上一动点C 点除外,直线PM 交AB 的延长线于点D . 1 求点D 的坐标用含m 的代数式表示; 2 当△APD 是等腰三角形时,求m 的值;3 设过P 、M 、B 三点的抛物线与x 轴正半轴交于点E ,过点O 作直线ME 的垂线,垂足为H 如图2.当点P 从点O 向点C 运动时,点H 也随之运动.请直接写出点H 所经过 的路径长.不必写解答过程答案解:1由题意得CM=BM ,∵∠PMC =∠DMB ,∴Rt △PMC ≌Rt △DMB ,∴DB =PC ,∴DB =2-m,AD =4-m,∴点D 的坐标为2,4-m.2分三种情况:①若AP =AD ,则224(4)m m +=-,解得32m =. ② 若PD =P A ,过P 作PF ⊥AB 于点F 如图,则AF =FD,11(4)22AF FD AD m ===-,又OP =AF ,∴1(4)2m m =-,解得43m =, ③ 若DP =DA ,∵△PMC ≌△DMB ,∴11(4)22PM PD m ==-,∵222PC CM PM +=,∴221(2)1(4)4m m -+=-, 解得122,23m m ==(舍去). 综上所述,当△APD 是等腰三角形时,过m 的值为342233或或. 3点H 5. 12. 2011宁波市,26,10分如图.平面直角坐标系xOy 中,点B 的坐标为-2,2,点B 的坐标为6,6,抛物线经过A 、O 、B 三点,线段AB 交y 轴与点E . 1求点E 的坐标; 2求抛物线的函数解析式;3点F 为线段OB 上的一个动点不与O 、B 重合,直线EF 与抛物线交与M 、N 两点点N 在y 轴右侧,连结ON 、BN ,当点F 在线段OB 上运动时,求∆BON 的面积的最大值,并求出此时点N 的坐标;4连结AN ,当∆BON 的面积的最大时,在坐标平面内使得∆BOP 与∆OAN 相似点B 、O 、N 对应的点P 的坐标.答案26.解:1设直线AB的函数解析式为y=mx+n将点A-2,2,B6,6代入得:错误!得m=错误!,n=3∴y=错误!x+3当x=0时y=3 ∴E0,3设抛物线的函数解析式为y=ax+bx将A-2,2B6,6代入得错误!解得a=错误!,b=-错误!∴抛物线的解析式为y=错误!x2-错误!x3过点N做x轴的垂线NG,垂足为G,交OB于点Q,过B作BH⊥x轴于H,设Nx, 错误!x2-错误!x 则Qx,x则S∆BON=S∆BON+S∆BON=错误!×QN×OG+错误!×QN×HG=错误!×QN×OG+HG=错误!×QN×OH=错误!〔x-错误!x2-错误!x〕×6=-错误!x2+错误!x=-错误!x-32+错误!0<x<6∴当x =3时,∆BON 面积最大,最大值为错误! 此时点N 的坐标为3, 错误! 4过点A 作AS ⊥GQ 于S ∵A -2,2,B 6,6,N 3, 错误!∴∠AOE =∠OAS =∠BOH =45°,OG =3,NG =错误!,NS =错误!,AS =5 在Rt ∆SAN 和Rt ∆NOG 中 ∴tan ∠SAN = tan ∠NOG =错误! ∴∠SAN =∠NOG∴∠OAS -∠ASN =∠BOG -∠NOG ∴∠OASN =∠BON∴ON 的延长线上存在一点P ,使∆BOP ~∆OAN ∵A -2,2, N 3, 错误! 在Rt ∆ASN 中 AN =错误!=错误!当∆BOP ~∆OAN 时 错误!=错误! ∴错误!=错误! ∴OP =错误! 过点P 作PT ⊥x 轴于点T∴∆OPT ~∆ONG ∴错误!=错误!=错误! 设P 4t ,t 在在Rt ∆POT 中,有4t 2+t 2=错误!2 ∴t 1=错误! ,t 2=-错误!舍 ∴点P 的坐标为15,错误!将∆OBP 沿直线OB 返折,可得出另一个满足条件的点P '错误!,15,由以上推理可知,当点P 的坐标为15,错误!或错误!,15时∆BOP 与∆OAN 相似.13. 2011浙江衢州,24,12分已知两直线12l l 、分别经过点()1,0A ,点()3,0B -,并且当两条直线同时相交于y 轴正半轴的点C 时,恰好有12l l ⊥,经过点A B C 、、的抛物线的对称轴于直线1l 交于点K ,如图所示. 求点C 的坐标,并求出抛物线的函数解析式.抛物线的对称轴被直线1l ,抛物线,直线2l 和x 轴依次截得三条线段,问这三条线段有何数量关系请说明理由. 当直线2l 绕点C 旋转时,与抛物线的另一个交点为M .请找出使MCK 为等腰三角形的点M .简述理由,并写出点M 的坐标.答案1解法1:由题意易知(1,.3C 0BOC COA CO AO CO BO CO COCO ∴==∴=∴即点的坐标是~由题意,可设抛物线的函数解析式为2y ax bx =++把(1,0),(3,0)A B -的坐标分别代入2y ax bx =++得{0930.a b a b +-解这个方程组,得a b ⎧⎪⎨⎪⎩∴抛物线的函数解析式为233y x x =--+ 解法2:由勾股定理,得2222222()().OC OB OC OA BC AC AB +++=+= 又314OB OA AB ===,,(.OC C ∴=∴点的坐标是由题意可设抛物线的函数解析式为()()13.y a x x =-+把(C 0代入函数解析式得a =所以抛物线的函数解析式为)()13.y x x =-+ 2解法1:截得三条线段的数量关系为.KD DE EF == 理由如下:可求得直线1l的解析式为y =+直线2l的解析式为3y x =,抛物线的对称轴为直线1x =-.由此可求得点K的坐标为(-,点D的坐标为1,3⎛⎫- ⎪ ⎪⎝⎭,点E的坐标为1,3⎛- ⎝⎭,点F 的坐标为()1,0-. ,333.KD DE EF KD DE EF ∴===∴==解法2:截得三条线段的数量关系为.KD DE EF == 理由如下:由题意可知Rt 3060ABC ABC CAB ∠=︒∠=︒中,,,则可得tan 30=tan 603EF BF KF AF =⨯︒=⨯︒. 由顶点D的坐标为1,3⎛⎫- ⎪ ⎪⎝⎭得3DF =, 3KD DE EF ∴===3解法1:i 以点K 为圆心,线段KC 长为半径画圆弧,交抛物线于点1M ,由抛物线的对称性可知点1M 为点C 关于直线1x =-的对称点.∴所以点1M的坐标为(-,此时,1M CK 为等腰三角形.ii 当以点C 为圆心,线段KC 长为半径画圆弧时,与抛物线交点为点1M 和点A ,而三点A C K 、、在同一直线上,不能构成三角形.iii 作线段KC 的中垂线l ,由点D 是KE 的中点,且12l l ⊥,可知l 经过点D ,.KD DC ∴=此时,有点2M 即点D坐标为(1,3-,使2M CK 为等腰三角形. l 与抛物线的另一交点即为1M综上所述,当点M 的坐标为(1,3--时,MCK 为等腰三角形 解法2:当点M 的坐标分别为 理由如下:i 链接BK ,交抛物线于点G ,易知点G的坐标为(- .又点C的坐标为,则//.GC AB可求得4AB BK ==,且60ABK ∠=︒,即ABK ∆为正三角形.CGK ∴∆为正三角形∴当2l 与抛物线交于点G ,即2//l AB 时,符合题意,此时点1M的坐标为(- ii 连接CD ,由230KD CK CG CKD ===∠=︒,,易知KDC ∆为等腰三角形 当2l 过抛物线顶点于点D 时,符合题意,此时点2M 的坐标为(1,)3-. iii 当点M 在抛物线对称轴右边时,只有点M 与点A 重合时,满足CM CK =,但此时,三点A C K 、、在同一直线上,不能构成三角形.综上所述,当点M的坐标分别为(1,3--时,MCK ∆为等腰三角形. 14. 2011浙江绍兴,24,14分抛物线21(1)34y x =--+与y 轴交于点A ,顶点为B ,对称轴BC 与x 轴交于点C . 1如图1,求点A 的坐标及线段OC 的长;2点P 在抛物线上,直线//PQ BC 交x 轴于点Q ,连接BQ .①若含45°角的直线三角板如图2所示放置,其中,一个顶点与C 重合,直角顶点D 在BQ 上,另一顶点E 在PQ 上,求直线BQ 的函数解析式;②若含30°角的直角三角板一个顶点与点C 重合,直角顶点D 在直线BQ 上,另一个顶点E 在PQ 上,求点P 的坐标.答案解:1把0x=代入21(1)34y x =--+得114y =, ∴点11(0,)4A , BC 为对称轴,(1,3)B ,1OC ∴=.2①如图1,过点D 作DM x ⊥轴,交x 轴于点M , 过点D 作DN PQ ⊥,交PQ 于点N ,//PQ BC90DMQ DNQ MDN ∴∠=∠=∠=︒ ∴四边形MDNQ 为矩形,90,,,,,CDE MDN CDM EDN DC DE DCM DEN DM DN ∠=∠=︒∴∠=∠=∴∆≅∆∴=∴四边形MDNQ 为正方形,45DQC ∴∠=︒,BCQ ∴∆为等腰直角三角形, 34CQ BC OQ ∴==∴=,,设直线BQ 的函数解析式为y kx b =+, 直线上两点的坐标为(1,3),(4,0)B Q , 代入求得1,4k b =-=,∴直线BQ 的函数解析式为4y x =-+.②当点P D DM x ⊥x M D DN PQ ⊥PQ N (,0)Q m 90,Rt Rt ,,,,//,,31,CDM MDE EDN MDE CDM EDN CD DMCDM EDN DE DNCD DMDN MQ DE MQ DM BCPQ BC MQ CQCD DE m ∠+∠=∠+∠=︒∴∠=∠∴∆∆∴==∴=∴=∴=-, 15. 2011浙江台州,24,14分已知抛物线n m x a y +-=2)(与y 轴交于点A,它的顶点为B,点A 、B 关于原点O 的对称点分别是点C 、D;若点A 、B 、C 、D 中任何三点都不在一直线上,则称四边形ABCD 为抛物线的伴随四边形,直线AB 为抛物线的伴随直线;1如图1,求抛物线1)2(2+-=x y 的伴随直线的解析式;2如图2,若n m x a y +-=2)(m>0的伴随直线是y=x -3,伴随四边形的面积为12,求此抛物线的解析式; 3如图3,若抛物线n m x a y +-=2)(的伴随直线是y =-2x+bb>0,且伴随四边形ABCD 是矩形; ① 用含b 的代数式表示m,n 的值;② 在抛物线的对称轴上是否存在点P,使得△PBD 是一个等腰三角形若存在,请直接写出点P 的坐标用含b 的代数式;若不存在,请说明理由;答案解:1设直线AB 的解析式为y=kx+b.由题意,得:A0,5,B2,1 ∴⎩⎨⎧=+=125b k b ∴k=-2 ,b=5∴直线AB 的解析式为y=-2x+52 由伴随直线是y=x -3,得:A0,-3,C0,3 ∴ AC=6 由伴随四边形的面积为12,得:△ABC 的面积为6=m AC ⨯⨯21∴m=±2 ∵m>0 ∴m=2当m=2时,y=-1,顶点为2,-1, 且过点C0,3 ∴抛物线的解析式为y=1)2(212---x ; 3 ① 如图,作BE ⊥x 轴,由题意,得:A0,b,C 0,-b∵抛物线的顶点Bm,n 在y=-2x+bb>0上, ∴n=-2m+b Bm, -2m+b 在矩形ABCD 中,OC=OB ∴OC 2=OB 2即:222)b -2m (++=m b ∴m5m-4b=0 ∴m 1=0舍去,m 2=b 54 ∴n=-2m+b=b 53∴ b m 54=,b n 53=; ② 存在,有4个点:b 54,b 57, b 54,b 59, b 54,b 1516, b 54,b 513-16. 2011浙江义乌,24,12分已知二次函数的图象经过A 2,0、C 0,12 两点,且对称轴为直线x =4. 设顶点为 点P ,与x 轴的另一交点为点B .1求二次函数的解析式及顶点P 的坐标;2如图1,在直线 y=2x 上是否存在点D ,使四边形OPBD 为等腰梯形若存在,求出点D 的坐标;若不存在,请说明理由;3如图2,点M 是线段OP 上的一个动点O 、P 两点除外,以每秒2个单位长度的速度由点P 向点O 运动,过点M 作直线MN ∥x 轴,交PB 于点N. 将△PMN 沿直线MN 对折,得到△P 1MN. 在动点M 的运动过程中,设△P 1MN 与梯形OMNB 的重叠部分的面积为S ,运动时间为t 秒. 求S 关于t 的函数关系式.答案1设二次函数的解析式为y =ax 2+bx +c由题意得⎪⎪⎩⎪⎪⎨⎧=++==-0241242c b a c a b 解得⎪⎩⎪⎨⎧=-==1281c b a∴二次函数的解析式为y = x 2-8x +12 点P 的坐标为4,-42存在点D ,使四边形OPBD 为等腰梯形. 理由如下:当y =0时,x 2-8x +12=0 ∴x 1=2 , x 2=6 ∴点B 的坐标为6,0设直线BP 的解析式为y =kx +m 则⎩⎨⎧-=+=+4406m k m k 解得⎩⎨⎧-==122m k∴直线BP 的解析式为y =2x -12D xA OBCPyO PC BAxy图1图2MOAxPNCBy∴直线OD ∥BP∵顶点坐标P 4, -4 ∴ OP =42 设Dx ,2x 则BD 2=2x 2+6-x 2当BD =OP 时,2x 2+6-x 2=32解得:x 1=52,x 2=2 当x 2=2时,OD =BP =52,四边形OPBD 为平行四边形,舍去∴当x =52时四边形OPBD 为等腰梯形 ∴当D 52,54时,四边形OPBD 为等腰梯形3① 当0<t ≤2时,∵运动速度为每秒2个单位长度,运动时间为t 秒, 则MP =2t ∴PH =t ,MH =t ,HN =21t ∴MN =23t ∴S =23t ·t ·21=43t 2 ② 当2<t <4时,P 1G =2t -4,P 1H =txP 1 MAO BCPNyH∵MN ∥OB ∴ EF P 1∆∽MN P 1∆∴211)(11H P G P S S MNP EF P =∆∆ ∴22)42(431t t t S EF P -=∆ ∴ EF P S 1∆=3t 2-12t +12∴S =43t 2-3t 2-12t +12= -49t 2+12t -12 ∴ 当0<t ≤2时,S=43t 2当2<t <4时,S =-49t 2+12t -12 ;17. 2011四川重庆,26,12分如图,矩形ABCD 中,AB =6,BC =2错误!,点O 是AB 的中点,点P 在AB 的延长线上,且BP =3.一动点E 从O 点出发,以每秒1个单位长度的速度沿OA 匀速动动,到达A 点后,立即以原速度沿AO 返回;另一动点F 从P 点出发,以每秒1个单位长度的速度沿射线P A 匀速动动,点E 、F 同时出发,当两点相遇时停止运动.在点E 、F 的运动过程中,以EF 为边作等边△EFG ,使△EFG 和矩形ABCD 在射线P A 的同侧,设动动的时间为t 秒t ≥0. 1当等边△EFG 的边FG 恰好经过点C 时,求运动时间t 的值;2在整个运动过程中,设等边△EFG 和矩形ABCD 重叠部分的面积为S ,请直接写出S 与t 之间的函数关系式和相应的自变量t 的取值范围;3设EG 与矩形ABCD 的对角线AC 的交点为H ,是否存在这样的t ,使△AOH 是等腰三角形若存在,求出对应的t 的值;若不存在,请说明理由.xP 1M A OB CPNG HE F y答案1当等边△EFG的边FG恰好经过点C时如图,∠CFB=60°,BF=3-t,在Rt△CBF中,BC=2错误!,∴tan∠CFB =错误!,∴tan 60°=错误!,∴BF=2,∴t=3-t =2,∴t=1.2当0≤t<1时,S= 2错误!t+4错误!;当1≤t<3时,S=错误!t 2+3错误!t+错误!;当3≤t<4时,S= -4错误! t+20错误!;当4≤t<6时,S= 错误!t2-12错误!t+36错误!.3存在,理由如下:在Rt△ABC中,tan∠CAB=错误!=错误!,∴∠CAB=30°.又∵∠HEO=60°,∴∠HAE=∠AHE=30°.∴AE=HE=3-t或t-3.ⅰ当AH=AO=3时如图②,过点E作EM⊥AH于M,则AM=错误!AH=错误!.在Rt△AME中,cos∠MAE=错误!,即cos 30°=错误!,∴AE=错误!,即3-t=错误!或t-3=错误!,t=3-错误!或3+错误!.ⅱ当HA=HO时如图③,则∠HOA=∠HAO=30°,又∵∠HEO=60°,∴∠EHO=90°.∴EO=2HE=2AE.又∵AE+EO=3,∴AE+2AE=3.∴AE=1.即3-t=1或t-3=1,t=2或4.ⅲ当OH=OA时如图④,则∠OHA=∠OAH=30°,∴∠HOB=60°=∠HEB.∴点E和O重合,∴AE=3.即3-t=3或t-3=3,t=6舍去或t=0.综上所述,存在5个这样的值,使△AOH是等腰三角形,即:t=3-错误!或t=3+错误!或t=2或t=4或t=0.18. 2011浙江省嘉兴,24,14分已知直线3+=kx y k <0分别交x 轴、y 轴于A 、B 两点,线段OA 上有一动点P 由原点O 向点A 运动,速度为每秒1个单位长度,过点P 作x 轴的垂线交直线AB 于点C ,设运动时间为t 秒.1当1-=k 时,线段OA 上另有一动点Q 由点A 向点O 运动,它与点P 以相同速度同时出发,当点P 到达点A 时两点同时停止运动如图1.① 直接写出t =1秒时C 、Q 两点的坐标;② 若以Q 、C 、A 为顶点的三角形与△AOB 相似,求t 的值. 2当43-=k 时,设以C 为顶点的抛物线n m x y ++=2)(与直线AB 的另一交点为D 如图2, ① 求CD 的长;② 设△COD 的OC 边上的高为h ,当t 为何值时,h 的值最大答案1①C 1,2,Q 2,0.②由题意得:Pt ,0,Ct ,-t+3,Q 3-t ,0, 分两种情形讨论:情形一:当△AQC ∽△AOB 时,∠AQC=∠AOB =90°,∴CQ ⊥OA , ∵CP ⊥OA ,∴点P 与点Q 重合,OQ =OP ,即3-t =t ,∴t=.情形二:当△ACQ ∽△AOB 时,∠ACQ=∠AOB =90°,∵O A=O B=3,∴△AOB 是等腰直角三角形,∴△ACQ 是等腰直角三角形,∵CQ ⊥OA ,∴AQ=2CP ,即t =2-t +3,∴t=2.∴满足条件的t 的值是秒或2秒. 2 ①由题意得:Ct ,-34t +3,∴以C 为顶点的抛物线解析式是23()34y x t t =--+, 由233()3344x t t x --+=-+,解得x 1=t ,x 2=t 34-;过点D 作DE ⊥CP 于点E ,则∠DEC=∠AOB =90°,DE ∥OA ,∴∠EDC=∠OAB ,∴△DEC ∽△AOB ,∴DE CDAO BA=, ∵AO =4,AB =5,DE =t -t-34=34.∴CD =35154416DE BA AO ⨯⨯==.②∵CD =1516,CD 边上的高=341255⨯=.∴S △COD =11512921658⨯⨯=.∴S △COD 为定值; 要使OC 边上的高h 的值最大,只要OC 最短. 因为当OC ⊥AB 时OC 最短,此时OC 的长为125,∠BCO =90°,∵∠AOB =90°,∴∠COP =90°-∠BOC =∠OBA ,第24题图2第24题图1又∵CP ⊥OA ,∴Rt △PCO ∽Rt △OAB ,∴OP OC BO BA =,OP =123365525OC BO BA ⨯⨯==,即t =3625, ∴当t 为3625秒时,h 的值最大.19. 2011福建泉州,25,12分在直角坐标系xoy 中,已知点P 是反比例函数)>0(32x xy =图象上一个动点,以P 为圆心的圆始终与y 轴相切,设切点为A .1如图1,⊙P 运动到与x 轴相切,设切点为K ,试判断四边形OKP A 的形状,并说明理由. 2如图2,⊙P 运动到与x 轴相交,设交点为B ,C .当四边形ABCP 是菱形时: ①求出点A ,B ,C 的坐标.②在过A ,B ,C 三点的抛物线上是否存在点M ,使△MBP 的面积是菱形ABCP 面积的21.若存在,试求出所有满足条件的M 点的坐标,若不存在,试说明理由.答案解:1∵⊙P 分别与两坐标轴相切, ∴ P A ⊥OA ,PK ⊥OK . ∴∠P AO =∠OKP =90°. 又∵∠AOK =90°,∴ ∠P AO =∠OKP =∠AOK =90°. ∴四边形OKP A 是矩形. 又∵OA =OK ,∴四边形OKP A 是正方形.……………………2分 2①连接PB ,设点P 的横坐标为x ,则其纵坐标为x32. 过点P 作PG ⊥BC 于G .AP23y x=xyKO第25题 图1∵四边形ABCP 为菱形, ∴BC =P A =PB =PC . ∴△PBC 为等边三角形.在Rt △PBG 中,∠PBG =60°,PB =P A =x , PG =x32. sin ∠PBG =PBPG,即2332x x =. 解之得:x =±2负值舍去.∴ PG =3,P A =B C=2.……………………4分 易知四边形OGP A 是矩形,P A =OG =2,BG =CG =1, ∴OB =OG -BG =1,OC =OG +GC =3.∴ A 0,3,B 1,0 C 3,0.……………………6分 设二次函数解析式为:y =ax 2+bx +c .据题意得:09303a b c a b c c ⎧++=⎪++=⎨⎪=⎩解之得:a =33, b =433-, c =3. ∴二次函数关系式为:2343333y x x =-+.……………………9分 ②解法一:设直线BP 的解析式为:y =ux +v ,据题意得:23u v u v +=⎧⎪⎨+=⎪⎩解之得:u =3, v =33-.∴直线BP 的解析式为:333y x =-.过点A 作直线AM ∥PB ,则可得直线AM 的解析式为:33y x =+.解方程组:233343333y x y x x ⎧=+⎪⎨=-+⎪⎩O AP 23y x=xyB C图2GM。
中考数学试题分类汇编动态问题.doc

中考数学试题分类汇编动态问题动态问题一、选择题1.(2009年长春)如图,动点P 从点A 出发,沿线段AB 运动至点B 后,立即按原路返回,点P 在运动过程中速度大小不变,则以点A 为圆心,线段AP 长为半径的圆的面积S 与点P 的运动时间t 之间的函数图象大致为( )2.(2009年江苏省)如图,在55⨯方格纸中,将图①中的三角形甲平移到图②中所示的位置,与三角形乙拼成一个矩形,那么,下面的平移方法中,正确的是( )A .先向下平移3格,再向右平移1格B .先向下平移2格,再向右平移1格C .先向下平移2格,再向右平移2格D .先向下平移3格,再向右平移2格3.(2009年新疆)下列各组图中,图形甲变成图形乙,既能用平移,又能用旋转的是( )4.(2009年天津市)在平面直角坐标系中,已知线段AB 的两个端点分别是()()41A B --,,1,1,将线段AB 平移后得到线段A B '',若点A '的坐标为()22-,,则点B '的坐标为( )A .()43,B .()34,C .()12--,D .()21--,甲 乙 甲 乙 AB CD甲乙甲乙OS tO S tO S tO S t A P B A .B .C .D .5.(2009年牡丹江市)ABC △在如图所示的平面直角坐标系中,将ABC △向右平移3个单位长度后得111A B C △,再将111A B C △绕点O 旋转180°后得到222A B C △,则下列说法正确的是( ) A .1A 的坐标为()31,B .113ABB A S =四边形C.2B C = D .245AC O ∠=°6.(2009年莆田)如图1,在矩形MNPQ 中,动点R 从点N 出发,沿N →P →Q →M 方向运动至点M 处停止.设点R 运动的路程为x ,MNR △的面积为y ,如果y 关于x 的函数图象如图2所示,则当9x =时,点R 应运动到( )A .N 处B .P 处C .Q 处D .M 处7.(2009年茂名市)如图,把抛物线2y x =与直线1y =围成的图形OABC 绕原点O 顺时针旋转90°后,再沿x 轴向右平移1个单位得到图形1111O A B C ,则下列结论错误..的是( ) A .点1O 的坐标是(10), B .点1C 的坐标是(21)-,(C .四边形111O BA B 是矩形D .若连接OC ,则梯形11OCA B 的面积是38.(2009年湖北十堰市)如图,已知Rt ΔABC 中,∠ACB =90°,AC = 4,BC=3,以AB 边所在的直线为轴,将ΔABC 旋转一周,则所得几何体的表面积是( ).A .π5168B .π24C .π584D .π129.(2009 年佛山市)将两枚同样大小的硬币放在桌上,固定其中一枚,而另一枚则沿着其边缘滚动一周,这时滚动的硬币滚动了( ) A .1圈 B .1.5圈 C .2圈 D .2.5圈二、填空题10.(2009年新疆)如图,60ACB ∠=°,半径为1cm 的O ⊙切BC 于点C ,若将O ⊙在CB 上向右滚动,则当滚动到O ⊙与CA 也相切时,圆心O 移动的水平距离是__________cm .Oy 1OB1B C1A11A -(,)11C (,)11.(2009年包头)如图,已知ACB △与DFE △是两个全等的直角三角形,量得它们的斜边长为10cm ,较小锐角为30°,将这两个三角形摆成如图(1)所示的形状,使点B C F D 、、、在同一条直线上,且点C 与点F 重合,将图(1)中的ACB △绕点C 顺时针方向旋转到图(2)的位置,点E 在AB 边上,AC 交DE 于点G ,则线段FG 的长为 cm (保留根号).12.(2009年达州)在边长为2㎝的正方形ABCD 中,点Q 为BC 边的中点,点P 为对角线AC 上一动点,连接PB 、PQ ,则△PBQ 周长的最小值为____________㎝(结果不取近似值).13.(2009年河南)如图,在Rt△ABC 中,∠ACB =90°, ∠B =60°,BC =2.点0是AC 的中点,过点0的直线l 从与AC 重合的位置开始,绕点0作逆时针旋转,交AB 边于点D .过点C 作CE ∥AB 交直线l 于点E ,设直线l 的旋转角为α. (1)①当α=________度时,四边形EDBC 是等腰梯形,此时AD 的长为_________;②当α=________度时,四边形EDBC 是直角梯形,此时AD 的长为_________;(2)当α=90°时,判断四边形EDBC 是否为菱形,并说明理由.A E C (B 图E A GBC (D图C三、解答题14. (2009年牡丹江市)已知Rt ABC △中,90AC BC C D ==︒,∠,为AB 边的中点,90EDF ∠=°,EDF ∠绕D 点旋转,它的两边分别交AC 、CB (或它们的延长线)于E 、F .当EDF ∠绕D 点旋转到DE AC ⊥于E 时(如图1),易证12DEF CEF ABC S S S +=△△△.当EDF ∠绕D 点旋转到DE AC 和不垂直时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,DEF S △、CEF S △、ABC S △又有怎样的数量关系?请写出你的猜想,不需证明.15.(2009年株洲市)已知ABC ∆为直角三角形,90ACB ∠=︒,AC BC =,点A 、C 在x 轴上,点B 坐标为(3,m )(0m >),线段AB 与y 轴相交于点D ,以P (1,0)为顶点的抛物线过点B 、D . (1)求点A 的坐标(用m 表示); (2)求抛物线的解析式;A E FB D图图ADFEC B AD BCE图F(3)设点Q 为抛物线上点P 至点B 之间的一动点,连结PQ 并延长交BC 于点E ,连结 BQ 并延长交AC 于点F ,试证明:()FC AC EC 为定值.16. (2009年北京市)在ABCD 中,过点C 作CE ⊥CD 交AD 于点E,将线段EC 绕点E 逆时针旋转90得到线段EF(如图1)(1)在图1中画图探究:①当P 为射线CD 上任意一点(P 1不与C 重合)时,连结EP 1绕点E 逆时针旋转90得到线段EC 1.判断直线FC 1与直线CD 的位置关系,并加以证明; ②当P 2为线段DC 的延长线上任意一点时,连结EP 2,将线段EP 2绕点E 逆时针旋转90得到线段EC 2.判断直线C 1C 2与直线CD 的位置关系,画出图形并直接写出你的结论.(2)若AD=6,tanB=43,AE=1,在①的条件下,设CP 1=x ,S 11P FC =y ,求y 与x之间的函数关系式,并写出自变量x 的取值范围.17. (2009年北京市)如图,在平面直角坐标系xOy 中,ABC 三个机战的坐标分别为y xQPFEDCB AO()6,0A -,()6,0B ,()0,43C ,延长AC 到点D,使CD=12AC ,过点D 作DE ∥AB 交BC 的延长线于点E. (1)求D 点的坐标;(2)作C 点关于直线DE 的对称点F,分别连结DF 、EF ,若过B 点的直线y kx b =+将四边形CDFE 分成周长相等的两个四边形,确定此直线的解析式; (3)设G 为y 轴上一点,点P 从直线y kx b =+与y 轴的交点出发,先沿y 轴到达G 点,再沿GA 到达A 点,若P 点在y 轴上运动的速度是它在直线GA 上运动速度的2倍,试确定G 点的位置,使P 点按照上述要求到达A 点所用的时间最短。
2020年全国中考数学试卷分类汇编(一)专题40 动态问题(含解析)
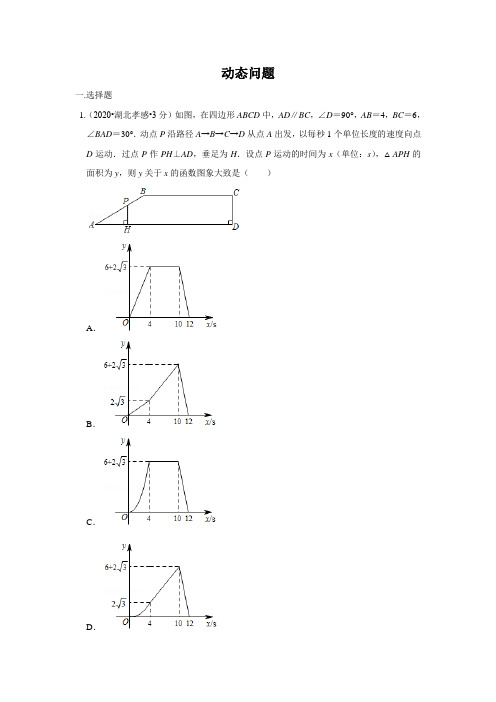
动态问题一.选择题1.(2020•湖北孝感•3分)如图,在四边形ABCD中,AD∥BC,∠D=90°,AB=4,BC=6,∠BAD=30°.动点P沿路径A→B→C→D从点A出发,以每秒1个单位长度的速度向点D运动.过点P作PH⊥AD,垂足为H.设点P运动的时间为x(单位:s),△APH的面积为y,则y关于x的函数图象大致是()A.B.C.D.【分析】分别求出点P在AB上运动、点P在BC上运动、点P在CD上运动时的函数表达式,进而求解.【解答】解:①当点P在AB上运动时,y=AH×PH=×APsinA×APcosA=×x2×=x2,图象为二次函数;②当点P在BC上运动时,如下图,由①知,BH′=ABsinA=4×=2,同理AH′=2,则y=×AH×PH=(2+x﹣4)×2=2﹣4+x,为一次函数;③当点P在CD上运动时,同理可得:y=×(2+6)×(4+6+2﹣x)=(3)(12﹣x),为一次函数;故选:D.【点评】本题是运动型综合题,考查了动点问题的函数图象、解直角三角形、图形面积等知识点.解题关键是深刻理解动点的函数图象,了解图象中关键点所代表的实际意义,理解动点的完整运动过程.二.填空题三.解答题1. (2020•江苏省常州市•10分)如图,二次函数y=x2+bx+3的图象与y轴交于点A,过点A作x轴的平行线交抛物线于另一点B,抛物线过点C(1,0),且顶点为D,连接A C.B C.B D.C D.(1)填空:b=﹣4;(2)点P是抛物线上一点,点P的横坐标大于1,直线PC交直线BD于点Q.若∠CQD =∠ACB,求点P的坐标;(3)点E在直线AC上,点E关于直线BD对称的点为F,点F关于直线BC对称的点为G,连接AG.当点F在x轴上时,直接写出AG的长.【分析】(1)将点C坐标代入解析式可求解;(2)分两种情况讨论,当点Q在点D上方时,过点C作CE⊥AB于E,设BD与x轴交于点F,可得点E(1,3),CE=BE=3,AE=1,可得∠EBC=∠ECB=45°,tan∠ACE =,∠BCF=45°,由勾股定理逆定理可得∠BCD=90°,可求∠ACE=∠DBC,可得∠ACB=∠CFD,可得点F与点Q重合,即可求点P坐标;当点Q在点D下方上,过点C作CH⊥DB于H,在线段BH的延长线上截取HF=QH,连接CQ交抛物线于点P,先求直线BD解析式,点F坐标,由中点坐标公式可求点Q 坐标,求出CQ解析式,联立方程组,可求点P坐标;(3)设直线AC与BD的交点为N,作CH⊥BD于H,过点N作MN⊥x轴,过点E作EM⊥MN,连接CG,GF,先求出∠CNH=45°,由轴对称的性质可得EN=NF,∠ENB =∠FNB=45°,由“AAS”可证△EMN≌△NKF,可得EM=NK=,MN=KF,可求CF =6,由轴对称的性质可得点G坐标,即可求解.【解答】解:(1)∵抛物线y=x2+bx+3的图象过点C(1,0),∴0=1+b+3,∴b=﹣4,故答案为:﹣4;(2)∵b=4,∴抛物线解析式为y=x2﹣4x+3∵抛物线y=x2﹣4x+3的图象与y轴交于点A,过点A作x轴的平行线交抛物线于另一点B,∴点A(0,3),3=x2﹣4x,∴x1=0(舍去),x2=4,∴点B(4,3),∵y=x2﹣4x+3=(x﹣2)2﹣1,∴顶点D坐标(2,﹣1),如图1,当点Q在点D上方时,过点C作CE⊥AB于E,设BD与x轴交于点F,∵点A(0,3),点B(4,3),点C(1,0),CE⊥AB,∴点E(1,3),CE=BE=3,AE=1,∴∠EBC=∠ECB=45°,tan∠ACE=,∴∠BCF=45°,∵点B(4,3),点C(1,0),点D(2,﹣1),∴BC==3,CD==,BD==2,∵BC2+CD2=20=BD2,∴∠BCD=90°,∴tan∠DBC====tan∠ACE,∴∠ACE=∠DBC,∴∠ACE+∠ECB=∠DBC+∠BCF,∴∠ACB=∠CFD,又∵∠CQD=∠ACB,∴点F与点Q重合,∴点P是直线CF与抛物线的交点,∴0=x2﹣4x+3,∴x1=1,x2=3,∴点P(3,0);当点Q在点D下方上,过点C作CH⊥DB于H,在线段BH的延长线上截取HF=QH,连接CQ交抛物线于点P,∵CH⊥DB,HF=QH,∴CF=CQ,∴∠CFD=∠CQD,∴∠CQD=∠ACB,∵CH⊥BD,∵点B(4,3),点D(2,﹣1),∴直线BD解析式为:y=2x﹣5,∴点F(,0),∴直线CH解析式为:y=﹣x+,∴,解得,∴点H坐标为(,﹣),∵FH=QH,∴点Q(,﹣),∴直线CQ解析式为:y=﹣x+,联立方程组,解得:或,∴点P(,﹣);综上所述:点P的坐标为(3,0)或(,﹣);(3)如图,设直线AC与BD的交点为N,作CH⊥BD于H,过点N作MN⊥x轴,过点E作EM⊥MN,连接CG,GF,∵点A(0,3),点C(1,0),∴直线AC解析式为:y=﹣3x+3,∴,∴,∴点N坐标为(,﹣),∵点H坐标为(,﹣),∴CH2=(﹣1)2+()2=,HN2=(﹣)2+(﹣+)2=,∴CH=HN,∴∠CNH=45°,∵点E关于直线BD对称的点为F,∴EN=NF,∠ENB=∠FNB=45°,∴∠ENF=90°,∴∠ENM+∠FNM=90°,又∵∠ENM+∠MEN=90°,∴∠MEN=∠FNM,∴△EMN≌△NKF(AAS)∴EM=NK=,MN=KF,∴点E的横坐标为﹣,∴点E(﹣,),∴MN==KF,∴CF=+﹣1=6,∵点F关于直线BC对称的点为G,∴FC=CG=6,∠BCF=∠GCB=45°,∴∠GCF=90°,∴点G(1,6),∴AG==.【点评】本题是二次函数综合题,考查了待定系数法求解析式,一次函数的性质,全等三角形的判定和性质,轴对称性质,等腰三角形的性质,锐角三角函数等知识,综合性强,求出∠CNH=45°是本题的关键.2. (2020•江苏省淮安市•12分)[初步尝试](1)如图①,在三角形纸片ABC中,∠ACB=90°,将△ABC折叠,使点B与点C重合,折痕为MN,则AM与BM的数量关系为AM=BM;[思考说理](2)如图②,在三角形纸片ABC中,AC=BC=6,AB=10,将△ABC折叠,使点B与。
全国中考数学真题解析120考点汇编 动态专题
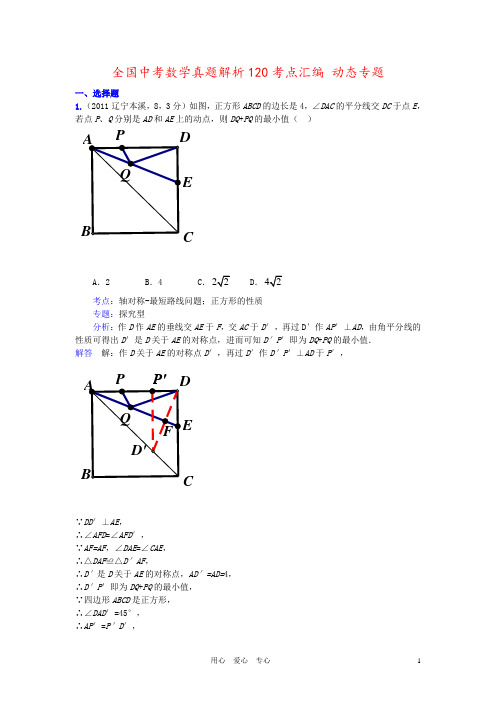
全国中考数学真题解析120考点汇编 动态专题一、选择题1.(2011辽宁本溪,8,3分)如图,正方形ABCD 的边长是4,∠DAC 的平分线交DC 于点E ,若点P 、Q 分别是AD 和AE 上的动点,则DQ +PQ 的最小值( )CEA .2B.4C .D .考点:轴对称-最短路线问题;正方形的性质 专题:探究型分析:作D 作AE 的垂线交AE 于F ,交AC 于D ′,再过D′作AP ′⊥AD ,由角平分线的性质可得出D ′是D 关于AE 的对称点,进而可知D′P ′即为DQ +PQ 的最小值. 解答 解:作D 关于AE 的对称点D ′,再过D ′作D′P ′⊥AD 于P ′,CE∵DD ′⊥AE ,∴∠AFD =∠AFD ′,∵AF=AF ,∠DAE =∠CAE , ∴△DAF ≌△D′AF ,∴D′是D 关于AE 的对称点,AD′=AD=4, ∴D′P ′即为DQ +PQ 的最小值, ∵四边形ABCD 是正方形, ∴∠DAD ′=45°, ∴AP ′=P′D ′,∴在Rt△AP′D′中,2P′D′2=AD′2,即2P′D′2=16,∴P′D′=22,即DQ+PQ的最小值为22.故选C.点评:本题考查的是轴对称﹣最短路线问题,根据题意作出辅助线是解答此题的关键.2.(2011重庆市,10,4分)如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC= 60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N 的上方),若△OMN的面积为S,直线l的运动时间为t秒(0≤t≤4),则能大致反映S与t的函数关系的图象是考点:动点问题的函数图象;正比例函数的图象;二次函数的图象;三角形的面积;含30度角的直角三角形;勾股定理;菱形的性质.分析:过A作AH⊥X轴于H,根据勾股定理和含30度角的直角三角形的性质求出AH,根据三角形的面积即可求出答案.答案:解:过A作AH⊥X轴于H,∵OA=OC=4,∠AOC=60°,∴OH=2,由勾股定理得:AH=2 ,10题图xyA BCOMNltsO242343AtsO242343BtsO242343CtsO242343D①当0≤t≤2 时,ON=t,MN= t,S= ON•MN= t2;②<t≤6时,ON=t,S= ON•2 = t.故选C.点评:本题主要考查对动点问题的函数图象,勾股定理,三角形的面积,二次函数的图象,正比例函数的图象,含30度角的直角三角形的性质,菱形的性质等知识点的理解和掌握,能根据这些性质进行计算是解此题的关键,用的数学思想是分类讨论思想.3.(2011北京,8,4分)如图在Rt△ABC中,∠ACB=90°,∠BAC=30°,AB=2,D是A B边上的一个动点(不与点A、B重合),过点D作CD的垂线交射线CA于点E.设AD=x,CE=y,则下列图象中,能表示y与x的函数关系图象大致是()A.B.C.D.考点:动点问题的函数图象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
动态问题一、选择题1. (2014•安徽省,第9题4分)如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记P A=x,点D到直线P A的距离为y,则y关于x 的函数图象大致是()A.B.C.D.考点:动点问题的函数图象.分析:①点P在AB上时,点D到AP的距离为AD的长度,②点P在BC上时,根据同角的余角相等求出∠APB=∠P AD,再利用相似三角形的列出比例式整理得到y与x的关系式,从而得解.解答:解:①点P在AB上时,0≤x≤3,点D到AP的距离为AD的长度,是定值4;②点P在BC上时,3<x≤5,∵∠APB+∠BAP=90°,∠P AD+∠BAP=90°,∴∠APB=∠P AD,又∵∠B=∠DEA=90°,∴△ABP∽△DEA,∴=,即=,∴y=,纵观各选项,只有B选项图形符合.故选B.点评:本题考查了动点问题函数图象,主要利用了相似三角形的判定与性质,难点在于根据点P的位置分两种情况讨论.2. (2014•广西玉林市、防城港市,第12题3分)如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是()A.B.C.D.考点:动点问题的函数图象.分析:根据题目提供的条件可以求出函数的解析式,根据解析式判断函数的图象的形状.解答:解:①t≤1时,两个三角形重叠面积为小三角形的面积,∴y =×1×=,②当1<x≤2时,重叠三角形的边长为2﹣x ,高为,y =(2﹣x)×=x ﹣x +,③当x≥2时两个三角形重叠面积为小三角形的面积为0,故选:B.点评:本题主要考查了本题考查了动点问题的函数图象,此类题目的图象往往是几个函数的组合体.3.(20XX年山东泰安,第14题3分)如图,△ABC中,∠ACB=90°,∠A=30°,AB=16.点P是斜边AB上一点.过点P作PQ⊥AB,垂足为P,交边AC(或边CB)于点Q,设AP=x,△APQ的面积为y,则y与x之间的函数图象大致为()A B C.D分析:分点Q在AC上和BC上两种情况进行讨论即可.解:当点Q在AC上时,∵∠A=30°,AP=x,∴PQ=xtan30°=∴y=×AP×PQ=×x×=x2;当点Q在BC上时,如图所示:∵AP=x,AB=16,∠A=30°,∴BP=16﹣x,∠B=60°,∴PQ=BP•tan60°=(16﹣x).∴==.∴该函数图象前半部分是抛物线开口向上,后半部分也为抛物线开口向下.故选:B.点评:本题考查动点问题的函数图象,有一定难度,解题关键是注意点Q在BC上这种情况.4.(2014•菏泽第8题3分)如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,C、D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是()二.填空题三.解答题1. (2014•广东,第25题9分)如图,在△ABC中,AB=AC,AD⊥AB于点D,BC=10cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t 秒(t>0).(1)当t=2时,连接DE、DF,求证:四边形AEDF为菱形;(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.考点:相似形综合题.分析:(1)如答图1所示,利用菱形的定义证明;(2)如答图2所示,首先求出△PEF的面积的表达式,然后利用二次函数的性质求解;(3)如答图3所示,分三种情形,需要分类讨论,分别求解.解答:(1)证明:当t=2时,DH=AH=2,则H为AD的中点,如答图1所示.又∵EF⊥AD,∴EF为AD的垂直平分线,∴AE=DE,AF=DF.∵AB=AC,AD⊥AB于点D,∴AD⊥BC,∠B=∠C.∴EF∥BC,∴∠AEF=∠B,∠AFE=∠C,∴∠AEF=∠AFE,∴AE=AF,∴AE=AF=DE=DF,即四边形AEDF为菱形.(2)解:如答图2所示,由(1)知EF∥BC,∴△AEF∽△ABC,∴,即,解得:EF=10﹣t.S△PEF=EF•DH=(10﹣t)•2t=﹣t2+10t=﹣(t﹣2)2+10∴当t=2秒时,S△PEF存在最大值,最大值为10,此时BP=3t=6.(3)解:存在.理由如下:①若点E为直角顶点,如答图3①所示,此时PE∥AD,PE=DH=2t,BP=3t.∵PE∥AD,∴,即,此比例式不成立,故此种情形不存在;②若点F为直角顶点,如答图3②所示,此时PE∥AD,PF=DH=2t,BP=3t,CP=10﹣3t.∵PF∥AD,∴,即,解得t=;③若点P为直角顶点,如答图3③所示.过点E作EM⊥BC于点M,过点F作FN⊥BC于点N,则EM=FN=DH=2t,EM∥FN∥A D.∵EM∥AD,∴,即,解得BM=t,∴PM=BP﹣BM=3t﹣t=t.在Rt△EMP中,由勾股定理得:PE2=EM2+PM2=(2t)2+(t)2=t2.∵FN∥AD,∴,即,解得CN=t,∴PN=BC﹣BP﹣CN=10﹣3t﹣t=10﹣t.在Rt△FNP中,由勾股定理得:PF2=FN2+PN2=(2t)2+(10﹣t)2=t2﹣85t+100.在Rt△PEF中,由勾股定理得:EF2=PE2+PF2,即:(10﹣t)2=(t2)+(t2﹣85t+100)化简得:t2﹣35t=0,解得:t=或t=0(舍去)∴t=.综上所述,当t=秒或t=秒时,△PEF为直角三角形.点评:本题是运动型综合题,涉及动点与动线两种运动类型.第(1)问考查了菱形的定义;第(2)问考查了相似三角形、图形面积及二次函数的极值;第(3)问考查了相似三角形、勾股定理、解方程等知识点,重点考查了分类讨论的数学思想.2.(2014•武汉2014•武汉,第24题10分)如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.(1)若△BPQ与△ABC相似,求t的值;(2)连接AQ,CP,若AQ⊥CP,求t的值;(3)试证明:PQ的中点在△ABC的一条中位线上.考点:相似形综合题分析:(1)分两种情况讨论:①当△BPQ∽△BAC时,∴DF==4,∵BC=8,过BC的中点R作直线平行于AC,∴RC=DF=4成立,∴D在过R的中位线上,∴PQ的中点在△ABC的一条中位线上.点评:此题考查了相似形综合,用到的知识点是相似三角形的判定与性质、中位线的性质等,关键是画出图形作出辅助线构造相似三角形,注意分两种情况讨论.点E,F,连结AF,BE相交于点P.(1)若AE=CF.①求证:AF=BE,并求∠APB的度数.的值.②若AE=2,试求AP AF(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.【答案】(1)①证明见解析,120°;②12;(2)43π.【解析】(注:没学习四点同圆和切割线定理的可由△APE∽△ACF得比例式求解)(2)如图,作△ABP外接圆满⊙O,在⊙O的优弧上取一点G,连接AG,BG,AO,BO,过点O作OH⊥AB于点H。
∵由(1)可知∠APB =120°,∴∠AGB =60°. ∴∠AOB =120°,∠AOH =60°.∵AB=6,∴AH=3. ∴AH3AO23 sin AOH sin603=︒==∠.∴1202343 APBπ⋅⋅=.∴点P 43.考点:1.动点问题;2.等边三角形的性质;3.全等三角形的判定和性质;4.圆周角定理;5. 切割线定理;6. 锐角三角函数定义;7.特殊角的三角函数值;8.垂径定理;9.弧长的计算. 4.(2014·浙江金华,第24题12分)如图,直角梯形ABCO 的两边OA ,OC 在坐标轴的正半轴上,BC ∥x 轴,OA =OC =4,以直线x =1为对称轴的抛物线过A ,B ,C 三点. (1)求该抛物线线的函数解析式.(2)已知直线l 的解析式为y x m =+,它与x 轴的交于点G ,在梯形ABCO 的一边上取点P .①当m =0时,如图1,点P 是抛物线对称轴与BC 的交点,过点P 作PH ⊥直线l 于点H ,连结OP ,试求△OPH 的面积.②当m 3=-时,过P 点分别作x 轴、直线l 的垂线,垂足为点E ,F . 是否存在这样的点P ,使以P ,E ,F 为顶点的三角形是等腰三角形?若存在,求出点P 的坐标;若不存在,请说明理由.【答案】(1)21y x x 42=-++;(2)①154;②存在,()0,3 或112,33⎛⎫⎪⎝⎭或()3,2 .【解析】试题分析:(1)由抛物线以直线x =1为对称轴,抛物线过点A ,B ,设顶点式,应用待定系数法求解.(2)①设直线x =1与x 轴交于点M ,与直线y x =交于点N ,过点H 作HD ⊥直线x =1于点D ,根据已知求出PD ,OM ,DH 的长,由OPH OPD DPH S S S ∆∆∆=+求解即可.∵MP =OC =4,OM =MN =1,∴PN =3,DH =32. ∴OPH OPD DPH 11315S S S 3132224∆∆∆=+=⨯⨯+⨯⨯=②存在.当m 3=-时,直线l 的解析式为y x 3=-,i )当点P 在OC 边上时,如图2,设点P 的坐标为()()0,p 0p 4≤≤ ,点F 的坐标为()x,x 3- ,过点F 作FI ⊥y 轴于点I .则PE PO p,PI IF === ,即()p 3p x 3x x 2+--=⇒=. ∴()22222p 3p 3p 9EF OF x x 32x 6x 9269222+++⎛⎫=+-=-+-⋅+ ⎪⎝⎭)2p 3PF 2x 2+==.()()27p p7PF2x p2p22-+⎛⎫=-=-=⎪⎝⎭.iv )当点P 在AO 边上时,以P ,E ,F 为顶点的三角形不存在.综上所述,以P ,E ,F 为顶点的三角形是等腰三角形时,点P 的坐标为()0,3 或112,33⎛⎫⎪⎝⎭或()3,2 .考点:1.动点问题;2. 待定系数法的应用;3.曲线上点的坐标与方程的关系;4.二次函数的性质;5. 等腰直角三角形的判定和性质;6.勾股定理;7. 等腰三角形存在性问题;8.转换思想和分类思想的应用.5. (2014·云南昆明,第23题9分)如图,在平面直角坐标系中,抛物线)0(32≠-+=a bx ax y 与x 轴交于点A (2-,0)、B (4,0)两点,与y 轴交于点C .(1)求抛物线的解析式;(2)点P 从A 点出发,在线段AB 上以每秒3个单位长度的速度向B 点运动,同时点Q 从B 点出发,在线段BC 上以每秒1个单位长度向C 点运动.其中一个点到达终点时,另一个点也停止运动.当△PBQ 存在时,求运动多少秒使△PBQ 的面积最大,最多面积是多少? (3)当△PBQ 的面积最大时,在BC 下方的抛物线上存在点K ,使2:5S PBQ CBK =△△:S ,求K 点坐标.考点: 二次函数综合题.分析: (1)利用待定系数法求出抛物线的解析式;(2考查动点与二次函数最值问题:先写出S 与t 的函数关系式,再确定函数最值; (3)存在所求的K 点,由(2)可求出CBK PBQ ∆∆和的面积,再把CBK ∆分成两个三角形进行面积运算.解答: 解:(1)将A (2-,0)、B (4,0)两点坐标分别代入)0(32≠-+=a bx ax y ,即⎩⎨⎧=-+=--034160324b a b a ,解得:⎪⎩⎪⎨⎧-==4383b aOxyCBAPQ∴抛物线的解析式为:343832--=x x y (2)设运动时间为t 秒,由题意可知: 20<<t过点Q 作AB QD ⊥,垂直为D , 易证OCB ∆∽DQB ∆,BQBCDQ OC =∴OC =3,OB =4,BC =5,t PB t AP 36,3-==,t BQ =t DQ 53=∴t DQ 53=∴ ∴t t t t DQ PB S PBQ 5910953)36(21212+-=⋅-=⋅=∆ 对称轴1)(210959=-⨯-=t∴当运动1秒时,△PBQ 面积最大,10959109=+-=∆PBQ S ,最大为109, (3)如图,设)34383,(2--m m m K连接CK 、BK ,作轴y KL //交BC 与L ,由(2)知:109=∆PBQ S , 2:5:=∆PBQ CBK S S ∴49=∆CBK S 设直线BC 的解析式为n kx y +=)3,0(),0,4(-C B⎩⎨⎧-==+∴34nnk,解得:⎪⎩⎪⎨⎧-==343nk∴直线BC的解析式为343-=xy∴)343,(-mmL28323mmKL-=KLBKLCCBKSSS∆∆∆+=∴)4()8323(21)8323(2122mmmmmm-⋅-⋅+⋅-⋅=)8323(4212mm-⋅⋅=即:49)8323(22=-mm解得:31==mm或∴K坐标为)827,1(-或)815,3(-点评:本题综合考查了二次函数的图象与性质、待定系数法求函数解析式、一次函数、一元二次方程、相似三角形性质、动点问题等重要知识点.6. (2014•益阳,第21题,12分)如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x.(1)求AD的长;(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;(3)设△ADP与△PCB的外接圆的面积分别为S1、S2,若S=S1+S2,求S的最小值.(第1题图)考点:相似形综合题.分析:(1)过点C作CE⊥AB于E,根据CE=BC•sin∠B求出CE,再根据AD=CE即可求出AD;(2)若以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似,则△PCB 必有一个角是直角.分两种情况讨论:①当∠PCB=90°时,求出AP,再根据在Rt△ADP 中∠DP A=60°,得出∠DP A=∠B,从而得到△ADP∽△CPB,②当∠CPB=90°时,求出AP=3,根据≠且≠,得出△PCB与△ADP不相似.(3)先求出S1=x•,再分两种情况讨论:①当2<x<10时,作BC的垂直平分线交BC于H,交AB于G;作PB的垂直平分线交PB于N,交GH于M,连结BM,在Rt△GBH中求出BG、BN、GN,在Rt△GMN中,求出MN=(x﹣1),在Rt△BMN 中,求出BM2=x2﹣x+,最后根据S1=x•BM2代入计算即可.②当0<x≤2时,S2=x(x2﹣x+),最后根据S=S1+S2=x(x﹣)2+x即可得出S的最小值.解答:解:(1)过点C作CE⊥AB于E,在Rt△BCE中,∵∠B=60°,BC=4,∴CE=BC•sin∠B=4×=2,∴AD=CE=2.(2)存在.若以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似,则△PCB必有一个角是直角.①当∠PCB=90°时,在Rt△PCB中,BC=4,∠B=60°,PB=8,∴AP=AB﹣PB=2.又由(1)知AD=2,在Rt△ADP中,tan∠DP A===,∴∠DP A=60°,∴∠DP A=∠CPB,∴△ADP∽△CPB,∴存在△ADP与△CPB相似,此时x=2.②∵当∠CPB=90°时,在Rt△PCB中,∠B=60°,BC=4,∴PB=2,PC=2,∴AP=3.则≠且≠,此时△PCB与△ADP不相似.(3)如图,因为Rt△ADP外接圆的直径为斜边PD,则S1=x•()2=x•,①当2<x<10时,作BC的垂直平分线交BC于H,交AB于G;作PB的垂直平分线交PB于N,交GH于M,连结BM.则BM为△PCB外接圆的半径.在Rt△GBH中,BH=BC=2,∠MGB=30°,∴BG=4,∵BN=PB=(10﹣x)=5﹣x,∴GN=BG﹣BN=x﹣1.在Rt△GMN中,∴MN=GN•tan∠MGN=(x﹣1).在Rt△BMN中,BM2=MN2+BN2=x2﹣x+,∴S1=x•BM2=x(x2﹣x+).②∵当0<x≤2时,S2=x(x2﹣x+)也成立,∴S=S1+S2=x•+x(x2﹣x+)=x(x﹣)2+x.∴当x=时,S=S1+S2取得最小值x.点评:此题考查了相似形综合,用到的知识点是相似三角形的性质与判定、二次函数的最值、勾股定理,关键是根据题意画出图形构造相似三角形,注意分类讨论.7. (2014•扬州,第28题,12分)已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.(第6题图)(1)如图1,已知折痕与边BC交于点O,连结AP、OP、O A.①求证:△OCP∽△PDA;②若△OCP与△PDA的面积比为1:4,求边AB的长;(2)若图1中的点P恰好是CD边的中点,求∠OAB的度数;(3)如图2,,擦去折痕AO、线段OP,连结BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;若不变,求出线段EF的长度.考点:相似形综合题;全等三角形的判定与性质;等腰三角形的判定与性质;勾股定理;矩形的性质;特殊角的三角函数值.专题:综合题;动点型;探究型.分析:(1)只需证明两对对应角分别相等即可证到两个三角形相似,然后根据相似三角形的性质求出PC长以及AP与OP的关系,然后在Rt△PCO中运用勾股定理求出OP 长,从而求出AB长.(2)由DP=DC=AB=AP及∠D=90°,利用三角函数即可求出∠DAP的度数,进而求出∠OAB的度数.(3)由边相等常常联想到全等,但BN与PM所在的三角形并不全等,且这两条线段的位置很不协调,可通过作平行线构造全等,然后运用三角形全等及等腰三角形的性质即可推出EF是PB的一半,只需求出PB长就可以求出EF长.解答:解:(1)如图1,①∵四边形ABCD是矩形,∴AD=BC,DC=AB,∠DAB=∠B=∠C=∠D=90°.由折叠可得:AP=AB,PO=BO,∠P AO=∠BAO.∠APO=∠B.∴∠APO=90°.∴∠APD=90°﹣∠CPO=∠PO C.∵∠D=∠C,∠APD=∠PO C.∴△OCP∽△PD A.②∵△OCP与△PDA的面积比为1:4,∴====.∴PD=2OC,P A=2OP,DA=2CP.∵AD=8,∴CP=4,BC=8.设OP=x,则OB=x,CO=8﹣x.在Rt△PCO中,∵∠C=90°,CP=4,OP=x,CO=8﹣x,∴x2=(8﹣x)2+42.解得:x=5.∴AB=AP=2OP=10.∴边AB的长为10.(2)如图1,∵P是CD边的中点,∴DP=D C.∵DC=AB,AB=AP,∴DP=AP.∵∠D=90°,∴sin∠DAP==.∴∠DAP=30°.∵∠DAB=90°,∠P AO=∠BAO,∠DAP=30°,∴∠OAB=30°.∴∠OAB的度数为30°.(3)作MQ∥AN,交PB于点Q,如图2.∵AP=AB,MQ∥AN,∴∠APB=∠ABP,∠ABP=∠MQP.∴∠APB=∠MQP.∴MP=MQ.∵MP=MQ,ME⊥PQ,∴PE=EQ=PQ.∵BN=PM,MP=MQ,∴BN=QM.∵MQ∥AN,∴∠QMF=∠BNF.在△MFQ和△NFB中,.∴△MFQ≌△NF B.∴QF=BF.∴QF=Q B.∴EF=EQ+QF=PQ+QB=P B.由(1)中的结论可得:PC=4,BC=8,∠C=90°.∴PB==4.∴EF=PB=2.∴在(1)的条件下,当点M、N在移动过程中,线段EF的长度不变,长度为2.点评:本题是一道运动变化类的题目,考查了相似三角形的性质和判定、全等三角形的性质和判定、矩形的性质、等腰三角形的性质和判定、勾股定理、特殊角的三角函数值等知识,综合性比较强,而添加适当的辅助线是解决最后一个问题的关键.8.(2014•滨州,第25题12分)如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,OP交AC于点Q.(1)求证:△APQ∽△CDQ;(2)P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动,移动时间为t秒.①当t为何值时,DP⊥AC?②设S△APQ+S△DCQ=y,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.考点:相似形综合题分析:(1)求证相似,证两对角相等即可,因为平行,易找,易证.(2)①当垂直时,易得三角形相似,故有相似边成比例,由题中已知矩形边长则AP长已知,故t易知.②因为S△APQ+S△DCQ=y,故求S△APQ和S△DCQ是解决问题的关键,观察无固定组合规则图象,则考虑作高分别求取.考虑两高在同一直线上,且相加恰为10,故可由(1)相似结论得,高的比等于对应边长比,设其中一高为h,即可求得,则易表示y=,注意要考虑t的取值.讨论何时y最小,y=不是我们学过的函数类型,故无法用最值性质来讨论,回观察题目问法为“探究P点运动到第几秒到第几秒之间时”,<1>并不是我们常规的在确定时间最小,<2>时间问的整数秒.故可考虑将所有可能的秒全部算出,再观察数据探究函数的变化找结论.解答:(1)证明:∵四边形ABCD是矩形,∴AB∥CD,∴∠QPA=∠QDC,∠QAP=∠QCD,∴△APQ∽△CDQ.(2)解:①当DP⊥AC时,∠QCD+∠QDC=90°,∵∠ADQ+∠QCD=90°,∴∠DCA=∠ADP,∵∠ADC=∠DAP=90°,∴△ADC∽△PAD,∴=,∴,解得PA=5,∴t=5.②设△ADP的边AP上的高h,则△QDC的边DC上的高为10﹣h.∵△APQ∽△CDQ,∴==,解得h=,∴10﹣h=,∴S△APQ==,S△DCQ==,∴y=S△APQ+S△DCQ=+=(0≤t≤20).探究:t=0,y=100;t=1,y≈95.48;t=2,y≈91.82;t=3,y≈88.91;动态问题一、选择题1. (2014•山东潍坊,第8题3分)如图,已知矩形ABCD的长AB为5,宽BC为4.E是BC边上的一个动点,AE⊥上EF,EF交CD于点F.设BE=x,FC=y,则点E从点B运动到点C 时,能表示y 关于x 的函数关系的大致图象是( )考点:动点问题的函数图象.分析:易证△ABE ∽△ECF ,根据相似比得出函数表达式,在判断图像. 解答:因为△ABE ∽△ECF ,则BE :CF =AB :EC ,即x :y =5:(4-x )y , 整理,得y =-51(x -2)2+54, 很明显函数图象是开口向下、顶点坐标是(2,54)的抛物线.对应A 选项. 故选:A .点评:此题考查了动点问题的函数图象,关键列出动点的函数关系,再判断选项.2. (2014•山东烟台,第12题3分)如图,点P 是▱ABCD 边上一动点,沿A →D →C →B 的路径移动,设P 点( )经过的路径长为x ,△BAP 的面积是y ,则下列能大致反映y 与x 的函数关系的图象是A .B .C .D .考点:平行四边形的性质,函数图象.分析:分三段来考虑点P 沿A →D 运动,△BAP 的面积逐渐变大;点P 沿D →C 移动,△BAP 的面积不变;点P 沿C →B 的路径移动,△BAP 的面积逐渐减小,据此选择即可. 解答:点P 沿A →D 运动,△BAP 的面积逐渐变大;点P 沿D →C 移动,△BAP 的面积不变;点P 沿C →B 的路径移动,△BAP 的面积逐渐减小.故选:A .点评:本题主要考查了动点问题的函数图象.注意分段考虑.3.(2014•甘肃兰州,第15题4分)如图,在平面直角坐标系中,四边形OBCD 是边长为4的正方形,平行于对角线BD 的直线l 从O 出发,沿x 轴正方向以每秒1个单位长度的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l运动的时间为t(秒),下列能反映S与t之间函数关系的图象是()A.B.C.D.考点:动点问题的函数图象.分析:根据三角形的面积即可求出S与t的函数关系式,根据函数关系式选择图象.解答:解:①当0≤t≤4时,S=×t×t=t2,即S=t2.该函数图象是开口向上的抛物线的一部分.故B、C错误;②当4<t≤8时,S=16﹣×(t﹣4)×(t﹣4)=t2,即S=﹣t2+4t+8.该函数图象是开口向下的抛物线的一部分.故A错误.故选:D.点评:本题考查了动点问题的函数图象.本题以动态的形式考查了分类讨论的思想,函数的知识和等腰直角三角形,具有很强的综合性.二、填空题1. (2014•江苏徐州,第18题3分)如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2,y与x的函数图象如图②,则线段EF所在的直线对应的函数关系式为y=﹣3x+18.考点:动点问题的函数图象.分析:根据从图②可以看出当Q点到B点时的面积为9,求出正方形的边长,再利用三角形的面积公式得出EF所在的直线对应的函数关系式.解答:解:∵点P沿边DA从点D开始向点A以1cm/s的速度移动;点Q沿边AB、BC 从点A开始向点C以2cm/s的速度移动.∴当P点到AD的中点时,Q到B点,从图②可以看出当Q点到B点时的面积为9,∴9=×(AD)•AB,∵AD=AB,∴AD=6,即正方形的边长为6,当Q点在BC上时,AP=6﹣x,△APQ的高为AB,∴y=(6﹣x)×6,即y=﹣3x+18.故答案为:y=﹣3x+18.点评:本题主要考查了动点函数的图象,解决本题的关键是求出正方形的边长.三、解答题1. (2014•四川巴中,第31题12分)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx﹣4与x轴交于点A(﹣2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.(1)求抛物线的解析式;(2)若两动点M,H分别从点A,B以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到达原点时,点H立刻掉头并以每秒个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,经过点M的直线l⊥x轴,交AC或BC 于点P,设点M的运动时间为t秒(t>0).求点M的运动时间t与△APH的面积S的函数关系式,并求出S的最大值.考点:二次函数综合题.分析:(1)根据抛物线y=ax2+bx﹣4与x轴交于点A(﹣2,0),直线x=1是该抛物线的对称轴,得到方程组,解方程组即可求出抛物线的解析式;(2)由于点M到达抛物线的对称轴时需要3秒,所以t≤3,又当点M到达原点时需要2秒,且此时点H立刻掉头,所以可分两种情况进行讨论:①当0<t≤2时,由△AMP∽△AOC,得出比例式,求出PM,AH,根据三角形的面积公式求出即可;②当2<t≤3时,过点P作PM⊥x轴于M,PF⊥y轴于点F,表示出三角形APH的面积,利用配方法求出最值即可.解答:(1)∵抛物线y=ax2+bx﹣4与x轴交于点A(﹣2,0),直线x=1是该抛物线的对称轴,∴,解得:,∴抛物线的解析式是:y=x2﹣x﹣4,(2)分两种情况:①当0<t≤2时,∵PM∥OC,∴△AMP∽△AOC,∴=,即=,∴PM=2t.解方程x2﹣x﹣4=0,得x1=﹣2,x2=4,∵A(﹣2,0),∴B(4,0),∴AB=4﹣(﹣2)=6.∵AH=AB﹣BH=6﹣t,∴S=PM•AH=×2t(6﹣t)=﹣t2+6t=﹣(t﹣3)2+9,当t=2时S的最大值为8;②当2<t≤3时,过点P作PM⊥x轴于M,作PF⊥y轴于点F,则△COB∽△CFP,又∵CO=OB,∴FP=FC=t﹣2,PM=4﹣(t﹣2)=6﹣t,AH=4+(t﹣2)=t+1,∴S=PM•AH=(6﹣t)(t+1)=﹣t2+4t+3=﹣(t﹣)2+,当t=时,S最大值为.综上所述,点M的运动时间t与△APQ面积S的函数关系式是S=,S的最大值为.点评:本题是二次函数的综合题型,其中涉及到运用待定系数法求二次函数的解析式,三角形的面积,二次函数的最值等知识,综合性较强,难度适中.运用数形结合、分类讨论及方程思想是解题的关键.2.(2014•湖南怀化,第24题,10分)如图1,在平面直角坐标系中,AB=OB=8,∠ABO=90°,∠yOC=45°,射线OC以每秒2个单位长度的速度向右平行移动,当射线OC经过点B时停止运动,设平行移动x秒后,射线OC扫过Rt△ABO的面积为y.(1)求y与x之间的函数关系式;(2)当x=3秒时,射线OC平行移动到O′C′,与OA相交于G,如图2,求经过G,O,B 三点的抛物线的解析式;(3)现有一动点P在(2)中的抛物线上,试问点P在运动过程中,是否存在三角形POB 的面积S=8的情况?若存在,求出点P的坐标,若不存在,请说明理由.考点:二次函数综合题专题:压轴题.分析:(1)判断出△ABO是等腰直角三角形,根据等腰直角三角形的性质可得∠AOB=45°,然后求出AO⊥CO,再根据平移的性质可得AO⊥C′O′,从而判断出△OO′G是等腰直角三角形,然后根据等腰直角三角形的性质列式整理即可得解;(2)求出OO′,再根据等腰直角三角形的性质求出点G的坐标,然后设抛物线解析式为y=ax2+bx,再把点B、G的坐标代入,利用待定系数法求二次函数解析式解答;(3)设点P到x轴的距离为h,利用三角形的面积公式求出h,再分点P在x轴上方和下方两种情况,利用抛物线解析式求解即可.解答:解:(1)∵AB=OB,∠ABO=90°,∴△ABO是等腰直角三角形,∴∠AOB=45°,∵∠yOC=45°,∴∠AOC=(90°﹣45°)+45°=90°,∴AO⊥CO,∵C′O′是CO平移得到,∴AO⊥C′O′,∴△OO′G是等腰直角三角形,∵射线OC的速度是每秒2个单位长度,∴OO′=2x,∴y=×(2x)2=2x2;(2)当x=3秒时,OO′=2×3=6,∵×6=3,∴点G的坐标为(3,3),设抛物线解析式为y=ax2+bx,则,解得,∴抛物线的解析式为y=﹣x2+x;(3)设点P到x轴的距离为h,则S△POB=×8h=8,解得h=2,当点P在x轴上方时,﹣x2+x=2,整理得,x2﹣8x+10=0,解得x1=4﹣,x2=4+,此时,点P的坐标为(4﹣,2)或(4+,2);当点P在x轴下方时,﹣x2+x=﹣2,整理得,x2﹣8x﹣10=0,解得x1=4﹣,x2=4+,此时,点P的坐标为(4﹣,﹣2)或(4+,﹣2),综上所述,点P的坐标为(4﹣,2)或(4+,2)或(4﹣,﹣2)或(4+,﹣2)时,△POB的面积S=8.点评:本题是二次函数综合题型,主要利用了等腰直角三角形的判定与性质,待定系数法求二次函数解析式,三角形的面积,二次函数图象上点的坐标特征,(3)要注意分情况讨论.3.(2014•湖南张家界,第25题,12分)如图,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+bx+c(a≠0)过O、B、C三点,B、C坐标分别为(10,0)和(,﹣),以OB为直径的⊙A经过C点,直线l垂直x轴于B点.(1)求直线BC的解析式;(2)求抛物线解析式及顶点坐标;(3)点M是⊙A上一动点(不同于O,B),过点M作⊙A的切线,交y轴于点E,交直线l于点F,设线段ME长为m,MF长为n,请猜想m•n的值,并证明你的结论;(4)若点P从O出发,以每秒一个单位的速度向点B作直线运动,点Q同时从B出发,以相同速度向点C作直线运动,经过t(0<t≤8)秒时恰好使△BPQ为等腰三角形,请求出满足条件的t值.考点:二次函数综合题.分析:(1)用待定系数法即可求得;(2)应用待定系数法以及顶点公式即可求得;(3)连接AE、AM、AF,则AM⊥EF,证得Rt△AOE≌RT△AME,求得∠OAE=∠MAE,同理证得∠BAF=∠MAF,进而求得∠EAF=90°,然后根据射影定理即可求得.(4)分三种情况分别讨论,①当PQ=BQ时,作QH⊥PB,根据直线BC的斜率可知HB:BQ=4:5;即可求得,②当PB=QB时,则10﹣t=t即可求得,③当PQ=PB时,作QH⊥OB,根据勾股定理即可求得.解答:解:(1)设直线BC的解析式为y=kx+b,∵直线BC经过B、C,∴,解得:,∴直线BC的解析式为;y=x﹣.(2)∵抛物线y=ax2+bx+c(a≠0)过O、B、C三点,B、C坐标分别为(10,0)和(,﹣),∴,解得,∴抛物线的解析式为:y=x2﹣x;∴x=﹣=﹣=5,y=x2﹣x=×52﹣×5=﹣,∴顶点坐标为(5,﹣);(3)m•n=25;如图2,连接AE、AM、AF,则AM⊥EF,在RT△AOE与RT△AME中∴Rt△AOE≌RT△AME(HL),∴∠OAE=∠MAE,同理可证∠BAF=∠MAF,∴∠EAF=90°,在RT△EAF中,根据射影定理得AM2=EM•FM,∵AM=OB=5,ME=m,MF=n,∴m•n=25;(4)如图3.有三种情况;①当PQ=BQ时,作QH⊥PB,∵直线BC的斜率为,∴HQ:BQ=3:5,HB:BQ=4:5;∵HB=(10﹣t)×,BQ=t,∴=,解得;t=,②当PB=QB时,则10﹣t=t,解得t=5,③当PQ=PB时,作QH⊥OB,则PQ=PB=10﹣t,BQ=t,HP=t﹣(10﹣t),QH=t;∵PQ2=PH2+QH2,∴(10﹣t)2=【t﹣(10﹣t)]2+(t)2;解得t=.点评:本题考查了待定系数法求解析式,顶点坐标的求法,圆的切线的性质,数形结合分类讨论是本题的关键.4. (20XX年贵州黔东南24.(14分))如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(,)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.(1)求抛物线的解析式;(2)是否存在这样的P点,使线段PC的长有最大值,若存在,求出这个最大值;若不存在,请说明理由;(3)求△PAC为直角三角形时点P的坐标.考点:二次函数综合题.分析:(1)已知B(4,m)在直线y=x+2上,可求得m的值,抛物线图象上的A、B两点坐标,可将其代入抛物线的解析式中,通过联立方程组即可求得待定系数的值.(2)要弄清PC的长,实际是直线AB与抛物线函数值的差.可设出P点横坐标,根据直线AB和抛物线的解析式表示出P、C的纵坐标,进而得到关于PC与P点横坐标的函数关系式,根据函数的性质即可求出PC的最大值.(3)根据直线AB的解析式,可求得直线AC的解析式y=﹣x+b,已知了点A的坐标,即可求得直线AC的解析式,联立抛物线的解析式,可求得C点的坐标;解答:解:(1)∵B(4,m)在直线线y=x+2上,∴m=4+2=6,∴B(4,6),∵A(,)、B(4,6)在抛物线y=ax2+bx﹣4上,∴,∵c=6,∴a=2,b=﹣8,∴y=2x2﹣8x+6.(2)设动点P的坐标为(n,n+2),则C点的坐标为(n,2n2﹣8n+6),∴PC=(n+2)﹣(2n2﹣8n+6),=﹣2n2+9n﹣4,=﹣2(n﹣)2+,∵PC>0,∴当n=时,线段PC最大且为.(3)设直线AC的解析式为y=﹣x+b,把A(,)代入得:=﹣+b,解得:b=3,∴直线AC解析式:y=﹣x+3,点C在抛物线上,设C(m,2m2﹣8m+6),代入y=﹣x+3得:2m2﹣8m+6=﹣m+3,整理得:2m2﹣7m+3=0,解得;m=3或m=,∴P(3,0)或P(,).点评:此题主要考查了二次函数解析式的确定、二次函数最值的应用以及直角三角形的判定、函数图象交点坐标的求法等知识;5.(2014•十堰)25.(12分)已知抛物线C1:y=a(x+1)2﹣2的顶点为A,且经过点B(﹣2,﹣1).(1)求A点的坐标和抛物线C1的解析式;(2)如图1,将抛物线C1向下平移2个单位后得到抛物线C2,且抛物线C2与直线AB相交于C,D两点,求S△OAC:S△OAD的值;(3)如图2,若过P(﹣4,0),Q(0,2)的直线为l,点E在(2)中抛物线C2对称轴右侧部分(含顶点)运动,直线m过点C和点E.问:是否存在直线m,使直线l,m与x轴围成的三角形和直线l,m与y轴围成的三角形相似?若存在,求出直线m的解析式;若不存在,说明理由.。
