垂径定理(导学案)
垂径定理 (共21张PPT)学案

3.3.2垂径定理导学案一、教材79页想一想垂径定理的逆命题是什么?已知:如图,⊙O的直径交弦AB(不是直径)于点P,AP=BP.求证:CD⊥AB,⌒AC=⌒BC师生共同归纳定理1: . 探索:平分弧的直径垂直于弧所对的弦。
已知:如图,⊙O的直径交弦AB(不是直径)于点P,⌒AC=⌒BC 求证:CD⊥AB归纳出:定理2:。
二、教材79页例题例3、赵州桥的跨径(桥拱圆弧所对的弦的长)为 37.02 m,拱高(桥拱圆弧的中点到弦的距离)为7.23m, 求赵州桥的桥拱圆弧的半径(精确到0.01m).1.下列命题中,正确的是( )A.过弦的中点的直线平分弦所对的弧B.过弦的中点的直线必过圆心C.弦所对的两条弧的中点的连线垂直平分弦,且过圆心D.弦的垂线平分弦所对的弧2.如图,⊙O的弦AB=8,M是AB的中点,且OM=3,则⊙O的半径等于( )A.8 B.2 C.10 D.53.已知⊙O的半径为2 cm,弦AB长2√3 cm,则这条弦的中点到弦所对劣弧的中点的距离为( )A. 1 cm B.2 cm C.√2cm D.√3 cm【方法宝典】利用垂径定理推论进行解答即可。
1.如图所示,在半径为13cm的圆形铁片上切下一块高为8cm的弓形铁片,则弓形弦AB 的长为().A.10cmB.16cmC.24cmD.26cm2.杭州市钱江新城,最有名的标志性建筑就是“日月同辉”,其中“日”指的是“杭州国际会议中心”,如图所示为它的主视图.已知这个球体的高度是85m,球的半径是50m,则杭州国际会议中心的占地面积是().A.1275πm2B.2550πm2C.3825πm2D.5100πm23.如图所示,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O ,另一边所在直线与半圆相交于点D ,E ,量出半径OC=5cm ,弦DE=8cm ,则直尺的宽度为( ).A.1cmB.2cmC.3cmD.4cm4.如图所示,将一个半径为5cm 的半圆O 折叠,使经过点O ,则折痕AF 的长度为( ).A.5cmB.52cmC.53cmD.103cm5.如图所示,在⊙O 中,AB ,AC 是互相垂直的两条弦,OD⊥AB 于点D ,OE⊥AC 于点E ,且AB=8cm ,AC=6cm ,那么⊙O 的半径OA 长为 .6.如图所示,有一座拱桥是圆弧形,它的跨度AB=60m ,拱高PD=18m.(1)求圆弧所在的圆的半径r 的长.(2)当洪水泛滥到跨度只有30m 时,要采取紧急措施,若拱顶离水面只有4m ,即PE=4m 时,是否要采取紧急措施?参考答案: 当堂检测:1.C 2.A 3.C 4.C5.5cm6.(1)如答图所示,连结OA.由题意得AD=21AB=30(m),OD=(r-18)(m).在Rt△ADO 中,由勾股定理得r 2=302+(r-18)2,解得r=34.∴圆弧所在的圆的半径r 的长为34m.。
圆第2课垂径定理导学案

圆第2课垂径定理导学案第2课时 24.1.2 垂直于弦的直径[学习目标]1.理解圆的轴对称性;2.掌握垂径定理及其推论,能用垂径定理及其推论进行有关的计算和证明.知识链接一、知识链接(阅读课本P81-82完成以下内容)1.圆的对称性:圆既是图形也是图形,对称轴是,有条;对称中心是2.垂径定理:垂直于弦的,并且平分弦所对的弧。
3.垂径定理推论:平分弦(非直径)的直径二、自主学习[Tip:辅助线的常用作法:连半径,过圆心向弦作垂线段。
]1.如图1,如果AB为⊙O的直径,弦CD⊥AB,垂足为E,那么下列结论中,•错误的是().A.CE=DE B.BC=BD C.∠BAC=∠BAD D.AC>AD(图1) (图2) (图3) (图4)2.如图2,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是()A.4 B.6 C.7 D.83.如图3,已知⊙O的半径为5mm,弦AB=8mm,则圆心O到AB的距离是()A.1mm B.2mm C.3mm D.4mm4.如图4,OE⊥AB、OF⊥CD,如果OE=OF,那么_______(只需写一个正确的结论)二、合作探究1.如图6,AB是O的直径,弦CD^AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为(A. 10B. 8C. 6D.4A (图6)(图7)(图8)(图9)2.如图7,在O中,若AB^MN于点C, AB为直径,试填写出三个你认为正确的结论:,, .3. P为⊙O内一点,OP=3cm,⊙O半径为5cm,则经过P点的最短弦长为;最长弦长为.4. 如图8,P为⊙O的弦AB上的点,PA=6,PB=2,⊙O的半径为5,则OP= .第 1 页共 1 页)5. 泸州市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如图9所示,污水水面宽度为60 cm,水面至管道顶部距离为10 cm,问修理人员应准备内径多大的管道?解:连接OA,过O作OE⊥AB,垂足为E,交圆于F【课堂检测】1、如图2-1,在⊙O中,点C是弧AB的中点,∠A=50°,则∠BOC等于度.图2-1 图2-22、如图2-2所示,已知AB为⊙O的直径,且AB⊥CD,垂足为M,CD=8,AM=2,则OM= .3、⊙O的半径为5,弦AB的长为6,则AB的弦心距长为 .4.如图,已知AB是⊙O的弦,P是AB上一点,若AB=10,PB=4,OP=5,求⊙O的半径的长。
导学案 垂径定理

B ACD O M )课前导学学习目标在明确圆的有关概念的基础上,学习垂径定理,并能初步应用垂径定理解决实际问题。
学习要求自己制作学具:准备一个圆形纸片,通过操作理解垂径定理,不理解的用“?”标记。
学习重点垂径定理及其运用。
学习难点探索垂径定理及利用垂径定理解决一些简单的实际问题。
学法指导 阅读法 探究法 讨论法 练习法学习用具 圆规、三角尺、圆形纸片知识回顾与准备复习:1、说出圆、弦、直径、弧(优弧、劣弧)、等圆、等弧的定义。
2、“弦是直径”这句话正确吗?为什么?。
指导自学自主学习(自学教材P 81----P 82)1.仔细阅读,完成81页探究。
2.结合81页探究,试完成讲学稿检测预习与助学.3.试归纳垂径定理。
4、试完成当堂检测。
检测预习与课堂助学一、动动手:阅读课本81页探究。
通过折叠,我发现: .我是利用 方法解决圆的对称轴问题的.因此,我可以得到:圆是 图形,其对称轴是 .二、探究进一步,还可得到:推论------平分弦(不是直径)的直径 弦,并且 弦所对的两条弧.试一试:.填空:如上图,CD 是⊙O 的直径,AB ⊥CD ,则AM= ,AC = .AD=思考:1、在上图中,已知⊙O 的半径与弦AB 的长度,且AB ⊥CD ,如何求出OM 的长度?2、根据垂径定理,利用尺规作图如何作出一个圆的圆心?如何作一条弧所在圆的圆心?三、实际应用:赵州桥主桥拱是圆弧形,他的跨度(弧所对的弦的长)为37.4米,拱高(弧的中点到弦的距离)为7.2米,你能求出赵州桥主桥拱的半径吗?助学:已知弦、拱高,所以做弦AB 的垂直平分线OC, D 为垂足,OC 与弧AB 相交于点C ,再任作一条弦的垂直平分线,两条垂直平分线的交点,即为圆心O思路导航:根据垂径定理,D 是AB 的 ,C 是 的中点,CD 就是拱高。
半径都相等,设OA=x 则OD= ,利用Rt △AOD 的三边关系求出半径。
写出解题过程:方法小结:当堂检测(1)如图是轴对称图形吗?如果是,其对称轴是 (2)写出你发现的图中相等的线段、弧和角? 相等的线段: 相等的弧: 相等的角: (3)结论 思路导航:∵直径CD 弦AB ,∴CD 平分 及 . 这样,就得到下面的定理: 垂径定理---------垂直于弦的直径 弦,并且 弦所对的两条弧.。
3.3垂径定理导学案2

课题 3.3 垂径定理2 导学案时间:课型:新授【学习目标】1、巩固垂径定理.2、熟练运用垂径定理解决有关问题.【重点难点】重点:垂径定理及应用. 难点:垂径定理的应用.【导学流程】一、知识铺垫:垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧.推论:a、垂直于弦 b、直径 c、平分弦 d、平分弦所对的优弧 e、平分弦所对的劣弧这5个,任意2个作为条件,可以推出其余3个结论.二、深入学习:例1、如图,⊙O的直径AB和弦CD相交于点E,已知AE=6cm,EB=2cm,∠CEA=30°,求CD的长.例2、如图1,AB是⊙O的直径,CD是弦,AE⊥CD,垂足为E,BF⊥CD,垂足为F,EC和DF相等吗?说明理由.如图2,若直线EF平移到与直径AB相交于点P(P不与A、B重合),在其他条件不变的情况下,原结论是否改变?为什么?如图3,当EF∥AB时,情况又怎样?如图4,CD为弦,EC⊥CD,FD⊥CD,EC、FD分别交直径AB于E、F两点,你能说明AE 和BF为什么相等吗?课海拾贝我的困惑:我们的困惑:三、迁移运用:1、如图,一条公路的转弯处是一段圆弧,点O是的圆心,E为上一点,OE⊥CD,垂足为F.已知CD = 600m,EF = 100m,求这段弯路的半径.2、已知:如图,⊙O 中, AB为弦,C 为 AB 的中点,OC交AB 于D ,AB = 6cm ,CD = 1cm. 求⊙O 的半径OA.3、如图,圆O与矩形ABCD交于E、F、G、H,EF=10,HG=6,AH=4.求BE的长.4、一工厂的厂门是由一个半圆与矩形组成的。
如图所示,AD=2.3米,CD=2米,现有一辆集装箱卡车要开进工厂,卡车高2.5米,宽1.6米,请你通过计算说明这辆卡车能否通过厂门?课后反思A BC DCODEF。
垂径定理推论 导学案

一、自学指导:1、垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧。
2、推论:平分弦(不是直径)的直径垂直于这条弦。
综合:一条直线满足:①过圆心;②垂直于弦;③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧;当中的任意两条,则可推出其它三条。
(知二得三)二、自学自测:1.已知⊙O中,弦AB的长是8cm,圆心O?到AB的距离为3cm,则⊙O的直径是_____cm.2.如图,已知⊙O的半径为5,弦AB=6,P是弦AB上任意一点,则OP?的取值范围是_______.3.如图,⊙O的直径AB垂直于弦CD,垂足为E,若∠COD=120°,OE=3厘米,则OD=?___cm.4、如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD= 22,BD=3,求AB的长。
5、如图,在⊙O中,点O是∠BAC的平分线上的一点,求证:AB=AC三、当堂达标:1、下列命题中正确的个数是()① 直径是圆中最长的弦;② 垂直于弦的直径平分弦及其所对的两弧;③ 平分弦的直径垂直于弦;④ 半圆是弧,但弧不是半圆;⑤ 等弧所对的弦相等,圆心角相等;⑥ 圆心角相等,所对的弦相等,弧也相等。
A、2个B、3个C、4个D、5个2、弦AB的长为6cm,圆心O到AB的距离为4cm,则⊙O的半径长为________。
3、如图,在半径为2cm的⊙O中有长为的弦AB,则弦AB所对的圆心角的度数为( )A. 60°B. 90°C. 120°D. 150°AB4、如图为圆弧形拱桥,半径OA=10cm ,拱高为4cm,求拱桥跨度AB的长。
四、拓展:如图,点A、B、C是⊙O上的三点,AB∥OC,(1)、求证:AC平分∠OAB。
(2)、过点O作OE⊥AB于点E,交AC于点P,若AB=2,∠AOE=30°,求PE 的长。
(完整版)新版北师大数学九年级下第三章3.垂径定理导学案
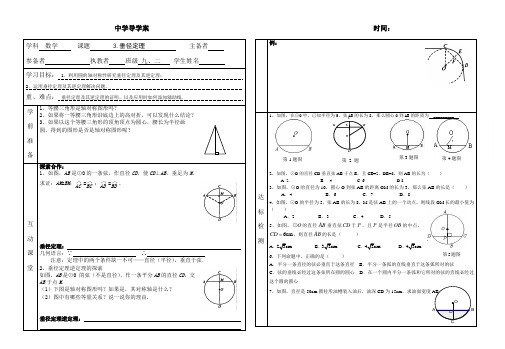
中学导学案 时间:第4题图第5题图学科 数学 课题 3.垂径定理 主备者 参备者 执教者 班级 九、二 学生姓名 学习目标: 1.利用圆的轴对称性研究垂径定理及其逆定理;2.运用垂径定理及其逆定理解决问题.重、难点: 垂径定理及其逆定理的证明,以及应用时如何添加辅助线.学前准备1、等腰三角形是轴对称图形吗?2、如果将一等腰三角形沿底边上的高对折,可以发现什么结论?3、如果以这个等腰三角形的顶角顶点为圆心,腰长为半径画 圆,得到的图形是否是轴对称图形呢?互 动 课 堂探索合作:1、如图,AB 是⊙O 的一条弦,作直径CD ,使CD ⊥AB ,垂足为M . 求证:AM =BM ;⌒AC =⌒BC ;⌒AD =⌒BD .垂径定理: 几何语言:∵ ∴注意:定理中的两个条件缺一不可——直径(半径),垂直于弦. 2、垂径定理逆定理的探索如图,AB 是⊙O 的弦(不是直径),作一条平分AB 的直径CD ,交AB 于点M .(1)下图是轴对称图形吗?如果是,其对称轴是什么? (2)图中有哪些等量关系?说一说你的理由.垂径定理逆定理:例:达 标 检 测1、如图,在⊙O 中,已知半径为5,弦AB 的长为8,那么圆心O 到AB 的距离为 _________ .2、如图,⊙O 的直径CD 垂直弦AB 于点E ,且CE=2,DE=8,则AB 的长为( )A. 2B. 4C. 6D.83、如图,⊙O 的直径为10,圆心O 到弦AB 的距离OM 的长为3,那么弦AB 的长是( )A .4B .6C .7D .8 4、如图,⊙O 的半径为5,弦AB 的长为8,M 是弦AB 上的一个动点,则线段OM 长的最小值为( )A .2B .3C .4D .5 5、如图,O ⊙的直径AB 垂直弦CD 于P ,且P 是半径OB 的中点,6cm CD ,则直径AB 的长是( )A .23cm B .32cm C .42cm D .43cm 6、下列命题中,正确的是( )A .平分一条直径的弦必垂直于这条直径B .平分一条弧的直线垂直于这条弧所对的弦C .弦的垂线必经过这条弦所在圆的圆心D .在一个圆内平分一条弧和它所对的弦的直线必经过这个圆的圆心7、如图,直径是50cm 圆柱形油槽装入油后,油深CD 为15cm ,求油面宽度ABD OBC A第3题图E BDOCA第2题第1题图。
24.1.2-垂径定理(学案1)

永宁中学九年级数学(上)导学案备课组长:教研组长:教科室:课题垂径定理第 1 课时共3 课时设计人唐伟文学习目标:1、探究垂径定理及推论; 2、会用符号语言描述垂径定理。
学习重点:探究垂径定理及推论、学习过程:一、知识点回顾(知识准备):圆的对称性:二、探究新知:如图:AB是圆形纸片的一条弦,作直径CD,使CD⊥AB,垂足为E。
沿CD对折纸片,发现:①这个图形是对称图形吗②图中有哪些相等的线段和弧请说明理由。
③你能用一句话概括这些结论吗垂直于弦的直径______________________________(垂径定理)④你能用符号语言表达这个结论吗符号语言:∵CD为⊙O的直径,且CD⊥AB于E∴_____________,__________________,________________⑤由对折以上纸片我们还进一步发现:平分弦(不是直径)的直径__________于弦,并_________弦所对的两条弧(垂径定理推论)符号语言:∵CD为⊙O的直径,且AE = BE∴_____________,__________________,_______________三、教师引导:垂径定理的题设和结论关系较复杂,从以上探究我们可进一步将其并归结为:一条直线(1)过圆心;(2)垂直于弦;(3)平分弦;(4)平分弦所对的优弧;(5)平分弦所对的劣弧。
垂径定理就是满足条件(1)、(2)而推出其他结论;推论是满足条件(1)、(3)而推出其他结论。
四、归纳小结:梳理本节所学知识点五、检测与反馈:1、判断下列图形,是否能使用垂径定理(a)AB⊥CD于E (b)E是AB中点 (c)OC⊥AB于E (d)OE⊥AB于E2、如图,AB为⊙O的直径,且AB⊥CD于E。
请用符号语言描述垂径定理及其推论。
A OBCDEO BA CEODCBAEODCBAEOBA E1。
垂径定理1导学案
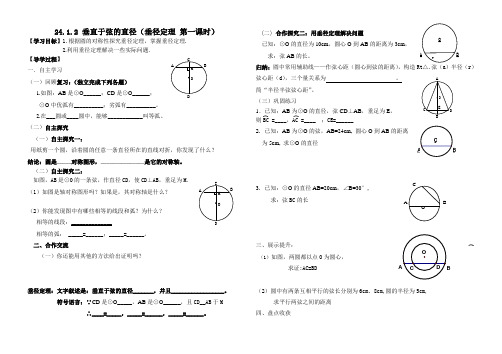
24.1.2 垂直于弦的直径(垂径定理第一课时)【学习目标】1.根据圆的对称性探究垂径定理,掌握垂径定理.2.利用垂径定理解决一些实际问题.【导学过程】一.自主学习(一)回顾复习:(独立完成下列各题)1.如图:AB是⊙O______;CD是⊙O______;⊙O中优弧有__________;劣弧有__________。
2.在___圆或____圆中,能够____________叫等弧。
(二)自主探究(一)自主探究一:用纸剪一个圆,沿着圆的任意一条直径所在的直线对折,你发现了什么?结论:圆是_____对称图形,_______________是它的对称轴。
(二)自主探究二:如图,AB是⊙O的一条弦,作直径CD,使CD⊥AB,垂足为M.(1)如图是轴对称图形吗?如果是,其对称轴是什么?(2)你能发现图中有哪些相等的线段和弧?为什么?相等的线段:______________相等的弧: _____=______;_____=______。
二、合作交流(一)你还能用其他的方法给出证明吗?垂径定理:文字叙述是:垂直于弦的直径_______,并且__________________。
符号语言:∵CD是⊙O_____,AB是⊙O______,且CD__AB于M∴____=_____,_____=______,_____=______。
(二)合作探究二:用垂径定理解决问题已知:⊙O的直径为10cm,圆心O到AB的距离为3cm,求:弦AB的长。
归纳:圆中常用辅助线——作弦心距(圆心到弦的距离),构造Rt△.弦(a)半径(r)弦心距(d),三个量关系为。
简“半径半弦弦心距”。
(三)巩固练习1.已知:AB为⊙O的直径,弦CD⊥AB,垂足为E,则BC =____,AC =____ ;CE=______2.已知:AB为⊙O的弦,AB=24cm, 圆心O到AB的距离为5cm, 求⊙O的直径3.已知:⊙O的直径AB=20cm,∠B=30°,求:弦BC的长三、展示提升:(1)如图,两圆都以点O为圆心,求证:AC=BD(2)圆中有两条互相平行的弦长分别为6cm、8cm,圆的半径为5cm, 求平行两弦之间的距离四、盘点收获OBCA。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
24.1垂径定理(导学案)
富源县后所镇中学 教师:龚达书 邮编:655505 国培中学数学班 学号:34
活动一:
动手做个圆,剪下来,研究下面的问题:
圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
活动二:
利用手中的圆做直径CD ⊥弦AB ,垂足为E .
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么? (2)你能发现图中有那些相等的线段和弧?为什么?
(3)如果直径CD ⊥弦AB ,垂足为E ,那么AE=BE ,
这个命题试着用语言叙述下来,并判断是否为真命题。
你能完成证明吗?
活动三、以下三个图,是否有 AE=BE , AC=BC , AD=BD ?
活动四 例 1: 如图,已知在⊙O 中,弦AB 的长为8厘米, 圆心O 到AB 的距离为3厘米,求⊙O 的半径
(1).在⊙O 中,直径为 10 cm,弦 AB 的长为 8 cm, 求圆心O 到AB 的距离.
(2).在⊙O 中,直径为 10 cm,圆心O 到AB 的距离为 3 cm,
D
D
D
C
D
A
B
O
求弦AB 的长.
(3)圆的半径为R ,弦长为 a ,弦心距为d ,则 R 、a 、d 满足关系式_________
活动五、课本P7例题,课本P8随堂1
活动六、在练习1图形的基础上:
变式(1) 已知:如图1,若以O 为圆心作一个⊙O 的同心圆,交大圆的弦AB 于C ,D 两点。
求证:AC =BD 。
(图1) (图2)
变式(2)再添加一个同心圆,得(图2)则AC BD 变式(3)隐去(图1)中的大圆,得(图3)连接OA ,OB ,设OA=OB , 求证:AC =BD 。
变式(4)隐去(图1)中的大圆,得(图4)连接OC ,OD ,设OC=OD , 求证:AC =BD 。
选做题、1、如图,⊙O 的半径为5,弦AB 的长为8,M 是弦AB 上的动点, 则线段OM 的长的最小值为____.最大值为____________.
2.已知⊙O 的直径是50 cm ,⊙O 的两条平行弦AB=40 cm ,CD=48cm , 求弦AB 与CD 之间的距离。
小测:AB是⊙O的直径,弦CD⊥AB,E为垂足,若AE=9,BE=1,求CD的长.
A
B
_ O
_ A
B。
