各种梁弯矩应力计算EXCEL程序

合集下载

混凝土工字形抗弯承载力 excel

混凝土工字形抗弯承载力 excel混凝土工字形梁是一种常见的结构构件，具有很好的抗弯承载能力。

在工程设计中，确定混凝土工字形梁的抗弯承载力是非常重要的一项工作。

本文将详细介绍混凝土工字形梁的抗弯承载力计算方法，并通过Excel表格的方式进行展示。

一、混凝土工字形梁的抗弯承载力计算公式混凝土工字形梁的抗弯承载力可以通过以下公式计算得出：M = f * b * h^2 / 6其中，M为混凝土工字形梁的抗弯弯矩，f为混凝土的抗弯强度，b 为梁的宽度，h为梁的高度。

二、混凝土工字形梁的抗弯承载力计算实例假设某工程需要设计一根混凝土工字形梁，其宽度为0.3米，高度为0.6米，混凝土的抗弯强度为25MPa。

我们可以通过上述公式计算该梁的抗弯承载力。

将以上数值代入公式中，可得：M = 25 * 0.3 * 0.6^2 / 6= 1.5 kNm三、混凝土工字形梁抗弯承载力计算表格为了更直观地展示混凝土工字形梁的抗弯承载力计算过程，我们可以使用Excel表格进行展示。

具体表格如下：| 宽度（m） | 高度（m） | 抗弯强度（MPa） | 抗弯承载力（kNm）||-----------|----------|-----------------|------------------|| 0.3 | 0.6 | 25 | 1.5 |通过这个表格，我们可以清晰地看到混凝土工字形梁的抗弯承载力计算结果。

四、混凝土工字形梁抗弯承载力的影响因素混凝土工字形梁的抗弯承载力受到多个因素的影响，包括混凝土的抗弯强度、梁的宽度和高度等。

其中，混凝土的抗弯强度是最重要的因素之一，其数值越大，梁的抗弯承载力也就越大。

而梁的宽度和高度则是通过几何关系来影响抗弯承载力的，宽度越大、高度越大，梁的抗弯承载力也就越大。

五、混凝土工字形梁的抗弯承载力设计要求在实际工程设计中，我们需要根据具体的使用要求和安全系数要求来确定混凝土工字形梁的抗弯承载力设计值。

后张预应力大梁计算excel表格自动计算

ρ te=(As+A p)/Ate= Ate=0.5b h+(bfb)hf=
ok
暂时不考虑 bf.hf
0.2
0.174182263
0.685277071
25.97172237
1
0.5
0.023804633
250000
σsk=(Mk ±M2-
Np0(z-
ep))/((Ap
+As)z)= e=ep+((M k± M2)/Np0) = z=[0.870.12(1r'f)*(h0 /e)^2]*h 0=
其他参数
θ
规范8.2.5
2
不出现裂
Bs=
缝选1
1
允许出现 1.24E+15 裂缝选2 截面抵抗矩塑性影响γ =(0.7+12 0/h)γm= γm值按表8.2.4=
h按表 8.2.4上方 =
ρ =(Ap+As) /(bh0)=
受拉翼缘截面面积与腹板有效截面面积的比值
1.55 600 0.01384
γf=(bf-
b)hf/(b*h
0)=
0
1.395
钢筋信息
预应力钢筋
预钢筋数n
21 fpy
1070
钢筋直径d0
单根钢筋
Ap
总面积∑Ap
13.5 fpyk
143.13882 Ep 3005.9151 受力中心ap
1860
195000 140
σ con=fpyk *(0.65~0 .75)
取σ con=fpyk *0.75=
f=f1l-f2l= 挠度判断 OK
6.706E+01
1.194E+02

弯矩应力计算xls

弯矩应力计算xls
弯矩应力计算是工程力学中的一个重要内容，尤其在结构设计和分析中。

弯矩应力是由于外力作用在结构上产生的弯曲效应而产生的内力，它会导致结构产生变形和可能的破坏。

因此，准确计算弯矩应力对于确保结构的安全性和稳定性至关重要。

在实际应用中，工程师通常使用电子表格软件（如Microsoft Excel）来辅助进行弯矩应力的计算。

通过Excel，可以方便地输入各种参数，如外力大小、力臂长度、截面尺寸等，并使用内置的数学函数和公式进行计算。

在弯矩应力计算的Excel表格中，通常包含以下几个关键部分：
参数输入区：用于输入外力、截面尺寸等相关参数。

计算区：根据输入的参数，使用力学公式计算弯矩和应力。

例如，弯矩（M）可以通过外力（F）和力臂（L）的乘积计算，即M = F × L。

应力（σ）则可以通过弯矩（M）和截面模量（W）的关系计算，即σ = M / W。

结果输出区：显示计算得到的弯矩和应力值，以及可能的安全系数或警告信息。

使用Excel进行弯矩应力计算的好处是，可以快速地进行大量计算，并且可以通过调整参数来优化设计方案。

此外，Excel还支持图表和图形化表示，使得结果更加直观易懂。

总之，利用Excel进行弯矩应力计算是一种高效、准确的方法，广泛应用于各种工程领域。

弯矩二次分配法excel

弯矩二次分配法excel弯矩二次分配法是一种结构力学中常用的计算方法，用于计算超静定梁或桁架的内力和位移。

本文将介绍如何在Excel中使用弯矩二次分配法进行计算。

首先，我们需要确定梁或桁架的几何参数和荷载条件。

假设我们要计算一个简支梁的内力和位移，其长度为L，截面形状为矩形，弹性模量为E，惯性矩为I，荷载为集中力P施加在距离左支点a处。

在Excel中，我们可以设置以下的参数：L，a，P，E，I。

可以将这些参数放在Excel的不同单元格中，并赋予相应的数值。

接下来，我们需要进行弯矩二次分配法的计算步骤。

1. 计算反力：根据力的平衡条件，可以得到右支点的反力为RA = P * (L - a)/L，左支点的反力为RB = P * a/L。

2. 计算弯矩系数：对于简支梁，弯矩系数为1。

可以将这个系数设定为Excel中的一个单元格。

3. 计算初始剪力分布：根据几何约束和力的平衡条件，当x =0到a时，剪力为V1 = RB，当x = a到L时，剪力为V2 = -RA。

4. 计算初始弯矩分布：根据剪力的分布和弯矩的定义，可以求得初始弯矩分布为M0 = 0，M1 = V1 * x，M2 = RB * x - V2 *(x - a)。

5. 计算修正剪力分布：根据弯矩的修正条件，可以得到修正剪力分布为V'1 = V1 + (M0 - M1) / L，V'2 = V2 + (M0 - M2) / L。

6. 计算修正弯矩分布：根据修正剪力分布和弯矩的定义，可以求得修正弯矩分布为M'1 = M1 + V'1 * (x - a)，M'2 = M2 + V'2 * (x - a)。

7. 计算位移：根据弯曲方程和边界条件，可以得到位移方程为y = (P * a * x * (L - x) * (L - 2a)) / (6 * E * I * L)。

通过将以上的计算公式应用到Excel中，我们可以得到弯矩分布、剪力分布和位移的数值结果。

exsel桥梁计算程序(现浇T梁)

桥梁跨径L：16000 mm 支承线距梁端：230 mm 计算跨径：15500 mm 桥梁全宽：8500 mm 护栏宽w1：464 mm 人行道宽w2：0 mm 人行道换算厚：100 mm 桥梁净宽b0：7572 mm 车道数：2主梁片数：5主梁间距：1700 mm 计算梁高h：1067 mm 取梁高h=1100 mm h1:140 mm h2:0 mm h3:0 mm h4:0 mmh5:0 mm (0.16*h-h4)*2主梁肋宽b3:200 mm b:1700 mm b1:750 mm b2:0 mmb4:0 mm 2*b3主梁肋增加宽：0 mm b1':750 mm b2':0 mm b3':200 mmb4':0 mm 2*b3横隔梁边横隔梁高：1100 mm 边横隔梁宽：180 mm 中横隔梁高：900 mm 中横隔梁宽：180 mm荷载等级：公路-2级车道集中力：168.00 KN 车道分布力：7.875 KN/m 人群荷载： 3.00 KN/m2车辆荷载：550 KN 1 前轴(1轴)：30 KN 300 mm 200 mm 2 中轴(2轴）：120 KN 600 mm 200 mm 3 后轴(2轴）：140 KN 600 mm 200 mm铺装厚H：130 mm 翼板厚t：140 mm 不等厚时为换算厚度，按跨中计算。

荷载作用长a1：460 mm 荷载作用宽b1：860 mm 板局部分布荷载：88.47 KN/m2注：仅一个车轮作用。

荷载作用位置x:850 mm 注：作用在跨中时x=1/3b~2/3b;作用在支承处x=0或x=b;作用在靠近支承处时x=0~1/3b或x=1/3b~b。

d:1400 mm 即最外两个荷载的中心距离。

板有效工作宽a：2533 mm 即荷载有效分布宽度，不得大于板全宽b。

悬臂板长度l0:750 mm 荷载作用位置b':750 mm 即悬臂板上荷载作用面外边缘至悬臂根部的距离悬臂板a:3360 mm1、每延米板上的结构自重砼容重：25.00 KN/m3桥面铺装： 3.25 KN/m 桥面板自重： 3.50 KN/m 护栏重：0.00 KN/m 合计g：6.75 KN/m2、每延米宽板条恒载内力弯矩Mmin,g= 2.44 KN.m 剪力Qg=5.74 KN 冲击系数：0.3剪力影响线竖标计算（简支梁）弯矩Mmin,q=53.34 KN.my1=0.713剪力Qq=153.40 KN y2=0.7851、极限状态跨中支点1）荷载有利设计Mud=Mg,k+1.4Mq,k=38.56 KN.m-53.98 KN.m 设计Qud=Qg,k+1.4Qq,k=220.50 KN 2）荷载不利设计Mud=1.2Mg,k+1.4Mq,k=38.80 KN.m-54.32 KN.m 设计Qud=1.2Qg,k+1.4Qq,k=221.65 KN2、正常状态1）短期组合设计Msd=Mg,k+0.7Mq,k=19.89 KN.m-27.84 KN.m 设计Qsd=Qg,k+0.7Qq,k=113.12 KN 2）长期组合设计Mld=Mg,k+0.4Mq,k=11.89 KN.m-16.64 KN.m设计Qld=Qg,k+0.4Qq,k=67.10 KN结构安全级别2重要系数γ0： 1.00板砼等级：C25砼抗拉强度ftd： 1.23 MPa 砼抗压强度fcd：11.50 MPa 钢筋种类： 2 级强度设计值：280.00 MPa界限受压高ξb：0.56设as=25 mm 则h0=115 mm 解受压区高度xfcd.b/2fcd.b.h0γ0.Md现浇整体T梁一、基础资料二、桥面板计算（三）内力组合（四）配筋设计（一）结构自重及其内力计算（二）汽车荷载内力注：考虑荷载作用在跨中，即x=b/2。

弯矩二次分配法excel表格

弯矩二次分配法excel表格
弯矩二次分配法Excel表格是一个用于计算复杂结构体系中梁的弯矩分配的工具。

该表格可以在Excel软件中使用，通过输入梁的结构参数和受力情况，自动生成梁的内力图和剪力图。

其实现原理是通过二次分配法将作用于梁上的荷载进行逐层拆解和分配，最终得出各个位置的弯矩和剪力值，从而能够准确的进行梁的设计。

使用弯矩二次分配法Excel表格可以节省设计师大量的工作时间和精力，同时还能够有效降低梁的设计难度和复杂度。

通过输入荷载和结构参数，表格能够快速的计算出梁的内力图和剪力图，为设计师提供了一个可靠的依据。

此外，该表格还具有图形化展示功能，能够直观的显示出梁的结构和内力分布情况，帮助设计师更加清晰的理解梁的设计。

总之，弯矩二次分配法Excel表格是一项非常实用的工具，能够有效的协助设计师进行梁的设计。

通过它，设计师不仅能够提高设计效率和准确度，还能够更好的满足项目的需求。

第 1 页共 1 页。

excel计算大全-钢结构计算表格-钢管结构计算程序

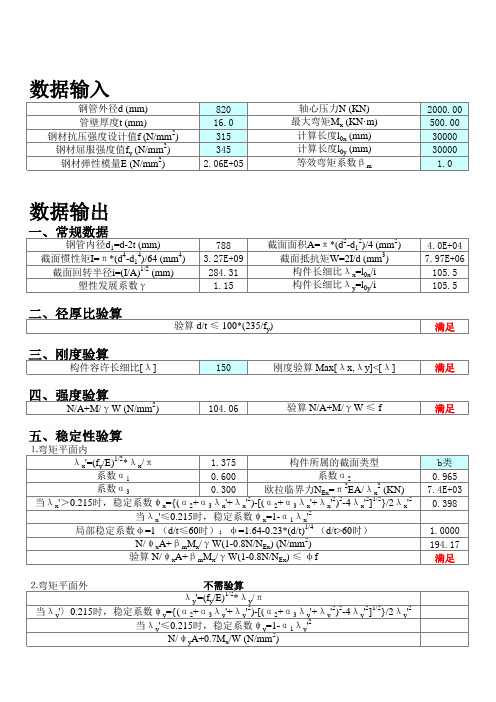
二、径厚比验算
验算 d/t ≤ 100*(235/fy) 满足
三、刚度验算
构件容许长细比[λ ] 150 刚度验算 Max[λ x,λ y]<[λ ] 满足
四、强度验算五、稳定性验算
N/A+M/γ W (N/mm )
2
104.06
验算 N/A+M/γ W ≤ f
满足
⒈弯矩平面内 1.375 构件所属的截面类型 λ x'=(fy/E)1/2*λ x/π 系数α 1 系数α 2 0.600 系数α 3 0.300 欧拉临界力NEx=π 2EA/λ x2 (KN) 当λ x'＞0.215时，稳定系数ψ x={(α 2+α 3λ x'+λ x'2)-[(α 2+α 3λ x'+λ x'2)2-4λ x'2]1/2}/2λ x'2 当λ x'≤0.215时，稳定系数ψ x=1-α 1λ x'2 局部稳定系数φ =1 （d/t≤60时）；φ =1.64-0.23*(d/t)1/4 （d/t>60时） N/ψ xA+β mMx/γ W(1-0.8N/NEx) (N/mm2) 验算 N/ψ xA+β mMx/γ W(1-0.8N/NEx) ≤ φ f ⒉弯矩平面外不需验算 λ y'=(fy/E)1/2*λ y/π 当λ y'〉0.215时，稳定系数ψ y={(α 2+α 3λ y'+λ y'2)-[(α 2+α 3λ y'+λ y'2)2-4λ y'2]1/2}/2λ y'2 当λ y'≤0.215时，稳定系数ψ y=1-α 1λ y'2 N/ψ yA+0.7Mx/W (N/mm2)

excel计算大全-钢结构计算表格-简支钢梁计算

excel计算大全-钢结构计算表格-简支钢梁计算简支钢梁计算基本数据输入:梁跨度： l=9000mm梁间距a=2400mm钢材：Q 345f =315N/mm 2fv =185N/mm 2 上翼缘：b 1=400mm t 1=14mm 下翼缘：b 2=300mm t 2=12mm 腹板：h w =574mm t w =8mm即: 断面BH 600x8x400x14x300x12截面特性计算：钢梁截面：A 0=13792mm 2 重量108.3kg/m 钢梁中和轴的位置：y 0=342mm钢梁对X轴截面惯性矩：I z =8.94E+08mm 4 钢梁上翼缘的弹性抵抗矩：W 1x = 3.46E+06mm 3 钢梁下翼缘的弹性抵抗矩：W 2x = 2.61E+06mm 3钢梁对Y轴截面惯性矩：I y = 1.02E+08mm 4i y =85.9 mm y =104.8上翼缘对Y 轴的惯性矩：I 1=7.47E+07mm 4 下翼缘对Y 轴的惯性矩：I 2= 2.70E+07mm 40.73 截面不对称影响系数：0.380.53 工字形截面简支梁的系数0.76 梁的整体稳定系数：0.74 修正后：0.672.截面验算：（1）弯矩及剪力的计算：=+=211I I I b α=-=)12(8.0b b αη=bβ==hb t l 111ξ=bφ='bφλ钢梁自重： 1.30KN/m恒载： 4.00KN/m2=10.90KN/mg1k活载：q c= 3.0KN/m2p k=18.10KN/m p=23.16KN/m 弯矩：M=234.49KN·m 剪力：V=104.22KN（2）钢梁的强度、稳定和挠度的验算：梁的整体稳定应力：σ=101.01N/mm2钢梁上翼缘应力：σ1=67.70N/mm2钢梁下翼缘应力：σ2=89.68N/mm2钢梁剪应力：τ=22.70N/mm2挠度：w=8.4mmw/l=1/1072。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

?
#VALUE! #VALUE!
#VALUE! #VALUE! #VALUE!
?
AC #VALUE! #VALUE!
#VALUE! #VALUE!
?
#VALUE! #VALUE! ?
#VALUE! #VALUE! #VALUE!
?
AC #VALUE!
#VALUE! #VALUE!
CB
#VALUE!
?
?
?
?
c L=n*C
?
?
?
q
L
q
q
L ?
c
a L ?
q
L ?
q
L/2
L/2
L
?
?
?
?
?
?
? ?
L
?
?
L/2
L/2
L
L/2
L/2
?
?
L
a L
b
?
?
?
?
a
a
?
L
?
?
a
bc
L
?
?
?
?
?
ccccc L=n*c
ccccc
L=n*c
?
?
?
c/2
cccc
c/2
L=n*c
?
?
?
q
L
?
?
q
a
a
L
?
?
?
q
a
c
a
#VALUE! #VALUE! #VALUE! #VALUE!
#VALUE! #VALUE! #VALUE! #VALUE!
?
#VALUE! #VALUE! #VALUE! #VALUE! #VALUE!
?
AC #VALUE!
#VALUE!
#VALUE! #VALUE!
CD
0 #VALUE!
?
AC #VALUE!
AB
#VALUE!
#VALUE!
0 #VALUE!
?
?
AC #VALUE!
#VALUE!
#VALUE! #VALUE!
AB
#VALUE!
#VALUE! #VALUE! #VALUE!
?
?
AC #VALUE!
#VALUE!
#VALUE!
AB
#VALUE!
#VALUE! #VALUE!
?
?
AC #VALUE!
CD
DE
?
#VALUE! #VALUE!
#VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE!
#VALUE! #VALUE! #VALUE! #VALUE!
0 #VALUE!
#VALUE! #VALUE!
?
AC #VALUE! #VALUE!
#VALUE! #VALUE!
#VALUE!
#VALUE! #VALUE!
#VALUE!
#VALUE!
#VALUE! #VALUE!
#VALUE! 2100000 ?
?
#VALUE! #VALUE! #VALUE! #VALUE! #VALUE!
#VALUE! 2100000 ?
?
#VALUE!
#VALUE! #VALUE! #VALUE!
#VALUE!
0 #VALUE!
?
?
AC #VALUE!
#VALUE!
#VALUE!
AB
#VALUE!
#VALUE! #VALUE!
?
?
AC #VALUE!
#VALUE!
AB
#VALUE!
#VALUE! #VALUE! #VALUE! #VALUE!
?
?
AC #VALUE!
#VALUE!
#VALUE! #VALUE!
#VALUE!
#VALUE! #VALUE! #VALUE!
0
0
0 #VALUE!
0 #VALUE!
?
AC #VALUE!
CB
#VALUE!
#VALUE! #VALUE! #VALUE! #VALUE!
?
AC #VALUE!
CB
#VALUE!
?
AC ?
CD
DB
?
?
AC #VALUE!
CD
DB
#VALUE!
?
?
?
?
L
q
d
c
a
b
q
d
c
?
a
b
L
b
b
?
ac
ca
L
?
?
?
?
?
?
?
?
q
L
?
?
q
L/2
L/2
L
?
?
q
a
b
L
?
?
?
?
q
a
b
L
L
?
?
L
?
?
a L
b
?
?
?
?
?
L/2
L/2
L
?
?
a
b
?
L
?
?
?
a
b
L
a
a?
L
?
?
q
L ?
d
c
?
a
b
L
?
?
?
?
?
q
q
L
?
?
L
q
q
L
?
?
L/2
L/2
L
?
?
L
?
?
a
b
L
?
?
?
?
L/2
#VALUE! 2100000 ?
?
#VALUE! #VALUE! #VALUE!
#VALUE! 2100000 ?
?
#VALUE! #VALUE! #VALUE!
#VALUE!
?
2100000 ?
?
#VALUE! #VALUE! #VALUE!
#VALUE!
反力RO （kgf）
#VALUE! #VALUE! 反力RD （kgf） #VALUE!
#VALUE! #VALUE!
最大弯矩弹性模量
Mmax E
截面惯性截面模数
（kgf· （kgf/cm 矩J
W
挠度f
cm） ^2）（cm^4）（cm^3）（cm）
转角θ （rad）
最大弯曲应力σ wmax （kgf/cm ^2）
#VALUE!
#VALUE! #VALUE!
CD
#VALUE! #VALUE!
?
?
AC #VALUE!
#VALUE!
#VALUE! #VALUE!
CD
#VALUE! #VALUE!
DB
#VALUE!
#VALUE! #VALUE! #VALUE!
?
#VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE!
#VALUE!
#VALUE! #VALUE!
AB
#VALUE!
0
反力RO （kgf）
OA #VALUE!
#VALUE!
#VALUE!
AB
#VALUE!
#VALUE!
反力RC
（kgf）
BC
#VALUE!
?
OA
AB
#VALUE!
反力RO （kgf）
#VALUE! #VALUE!
#VALUE!
#VALUE!
#VALUE! #VALUE! #VALUE! #VALUE!
?
#VALUE!
0 #VALUE!
#VALUE! #VALUE!
#VALUE! #VALUE! #VALUE! #VALUE! #VALUE! #VALUE!
#VALUE! #VALUE!
#VALUE! #VALUE!
பைடு நூலகம்
?
#VALUE! #VALUE!
?
AC #VALUE!
CD
DB
#VALUE!
?
AC #VALUE!
CD
DB
#VALUE!
#VALUE! #VALUE!
#VALUE! #VALUE! 0 #VALUE!
#VALUE! #VALUE! #VALUE! #VALUE!
?
?
AC #VALUE!
CD
DB
#VALUE!
?
AC #VALUE!
2100000 ?
?
#VALUE!
#VALUE!
#VALUE!
#VALUE!
2100000 ?
?
#VALUE!
#VALUE! #VALUE!
#VALUE!
2100000 ?
?
#VALUE!
#VALUE!
#VALUE!
#VALUE!
#VALUE! 2100000 ?
?
#VALUE! #VALUE! #VALUE!
简图
L
a
b
L
集中载荷
跨距L
P（kgf） P个数(n) （cm）
连续载荷
q
（kgf/cm
）
力偶矩M
（kgf·
cm）