正负数,数轴,绝对值,相反数复习
正数和负数、数轴、相反数、绝对值专项练习题
正数和负数、数轴、相反数、绝对值专项练习题满分100分，时间80分钟一、精心选一选，慧眼识金！（每小题3分，共24分）的相反数是（）2.下列说法正确的是（）A、正数、负数统称为有理数B、分数、整数统称为有理数C、正有理数、负有理数统称为有理数D、以上都不对3．下列都是无理数的是 ( )A.0.07,23B..0.7,π,2274、任何一个有理数的平方（）A．一定是正数 B．一定不是负数 C．一定大于它本身 D．一定不大于它的绝对值5. 有理数－22，(－2)2，|－23|，－按从小到大的顺序排列是( )A．|－23|＜－22＜－＜(－2)2 B．－22＜－＜(－2)2＜|－23|C．－＜－22＜(－2)2＜|－23| D．－＜－22＜|－23|＜(－2)26.有理数a、b在数轴上的对应的位置如图所示，则（）A．a + b＜0 B．a + b＞0 C．a－b = 0 D．a－b＞0A、6B、-6 CD、7．下列说法正确的是（）A、一个数的绝对值等于它本身，则这个数是正数B、一个数的绝对值等于它的相反数，则这个数是负数C、一个数的绝对值不可能等于零D、一个数的绝对值不可能是负数8.(0)a baba b+≠的所有可能的值有（）A.1个B.2个C.3个D.4个二、耐心填一填，一锤定音！（每小题3分，共24分）9.把下列各数填在相应的横线里：1，-4/5，8.9，-7，5/6，-3.2，+1008，-0.05，28，-9 正整数：负整数：正分数：2121212121-11a b负分数：10.有理数中，最小的正整数是 ，最大的负整数是11.有理数中，是整数而不是正数的数是 ，是负数而不是分数的数是 ，12.－（-2）的相反数是 .13.某天上午的温度是5℃，中午又上升了3℃，下午由于冷空气南下，到夜间又下降了9℃，则这天夜间的温度是 ℃。
14.a 、b 在数轴上的位置如图，化简a ＝ ，b a +＝ ，1+a ＝ 。
正负数、数轴、相反数、绝对值、倒数专题训练
有理数第一讲 正负数、数轴、相反数、绝对值、倒数一、梳理知识0⎧⎧⎪⎪⎨⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数整数负整数有理数正分数分数负分数 注意：小数和百分数可看成分数，有理数中的小数是指有限小数或无限循环小数，π不是有理数，任何分数都是有理数.最小的正整数是____，最小的自然数是 ，最大的负整数是数轴的三要素: 原点、正方向和单位长度.相反数：只有符号不同的两个数叫做互为相反数．相反数的意义：相反数是成对出现的，不能单独存在，从数轴上看，除0外，互为相反数的两个数，它们分别在原点两旁且到原点距离相等．绝对值：数轴上表示数a 的点与原点的距离叫做数a 的绝对值，记作a(0)0(0)(0)a a a a a a >⎧⎪==⎨⎪-<⎩有理数的绝对值都是非负数倒数：乘积是1的两个数互为倒数.有理数大小比较的法则：① 正数都大于0；② 负数都小于0；③ 正数大于一切负数；④两个负数，绝对值大的其值反而小．二、例题例1 把下列数分类23.14020140.3 1.2136910%3π--L ， ， ，， ， ， ， -1,正数：整数：负分数：有理数：正整数：自然数：例2 （1）有理数,a b 在数轴上的位置如图所示，化简a b a b +++的结果是（ ）20A a b B b C D a + .2 .2 . . 2（2）有理数,a b 在数轴上的对应点如图所示，则下面式子中正确的是（ ）①b ＜0＜a ； ②|b|＜|a|； ③0ab >； ④a b a b ->+A B C D .1个 . 2个 .3个 . 4个课堂练习：1、有理数a 、b 在数轴上的对应的位置如图所示： 则（ ） 0-11a bA ．a + b ＜0B ．a + b ＞0;C ．a －b = 0D ．a －b ＞02、有理数,a b 在数轴上的对应点位置如图所示，则,,,a b a b -的大小关系为（）例3 （1）在数轴上把-3对应的点移动5个单位长度后，所得到的对应点表示的数是（ ）A B C D .2 . -8 .2或-8 .不能确定（2）一个数在数轴上所对应的点向左平移6个单位后，得到它的相反数的点，则这个数为（ ）A B C D .3 . -3 .6 . -6课堂练习：1、在数轴上与-3的距离等于5个单位的点表示的数是（ ）2、绝对值大于2而小于6的所有整数的和（ ）A B C D .0 . -12 .12 . 243、下列说法正确的有（ ）①最大的负整数是1-； ②相反数是本身的数是正数； ③有理数分为正有理数和负有理数； ④在数轴上表示a -的点一定在原点的左边； ⑤ 在数轴上7与9之间的整数是8．A B C D .2个 . 3个 .4个 . 5个例4 （1）若2,1a b ==，那么a b ⋅的值有（ ）A B C D .1个 . 2个 .3个 . 4个（2）若m 为有理数，则m m -的值为（ ）A B C D .大于0 . 大于等于0 .小于0 . 小于等于0A B C D .2 . -2 .2和-2 . -8和21、若4,3a b ==，则a b -等于（ ）A B C D ± .7 . 1 .1 . 1或72、若3=2a -，则+3a 的值为（ ）A B C D .5 . 8 .5或1 . 8或4例5 （1） 用“>”连接032，，---正确的是 （ ）A 、032>-->-B 、302-->>-C 、023<-<--D 、203-<<--（2）有理数,,a b c 的大小关系为0c b a <<<，则下面的判断正确的是（ ）11000A abc a b c a c b<->-> . B. C.< D. （3）若0ab ≠，则等式a b a b +=+成立的条件是（ ）0,0000A a b B ab C a b D ab ><<+=> . . . .课堂练习：1、若a b >，则下列各式正确的为（ ）A a bB a bC a bD a b ><>> . . . .2、已知m 是正整数，则1,,m m m-的大小关系是（ ） 1111A B C D m m m m≤≤ .-m<<m . -m<m< .-m<m . -m<m 例6 （1）若a b 与互为相反数，c 的绝对值为2，,m n 互为倒数，则243a b c mn ++-的值为（ ）13A B C D .1 . .0 . 无法确定 （2）若a 、b 互为相反数，c 、d 互为倒数，则2a+3cd+2b=（3）如果 1.210a b ++-=，那么()()1 1.8a b +-+-+的值为（4）已知,a b 互为相反数，,c d 互为倒数，x 且的绝对值是5， 试求：()3x a b cd a b cd -+++++-1、若a b 与互为倒数，当3a =时，代数式2()b ab a -的值为（ ） 23983289A B C D . . . . 2、若a b 与互为倒数，,x y 互为相反数，则()()a b x y ab ++-的值为（ ）A B C D .0 . 1 .-1 . 无法确定3、若320x y -++=，则x y +的值为4、绝对值不小于1而小于3的整数的和为5、如果0ab ≠，则a ba b +的值不可能为（ ）2A B C D -、0 、1 、2 、作业1、3-的倒数为（ ）1133A B C D . . - .3 . -32、如图所示，根据有理数a 、b 、c 在数轴上的位置，下列关系正确的是（）3、有理数123,,555---的大小顺序是（）4、已知,a b 为有理数，且a ＞0，b ＜0，a ＜|b|，则,,,a b a b --的大小顺序是（ ）.A b a a b <-<<- .a a b b -<<-<B .a b a b -<<<-C .b a a b -<<-<D 5、6、如果5x+3与－2x+9是互为相反数，则x －2的值是7、数轴上表示互为相反数的两个点之间的距离是243，则这两个数是 8、绝对值大于2且小于5的所有整数的和是（ ）A ．0B ．7C ．14D ．289、已知a 、b 互为相反数，m 、n 互为倒数，求mn m n b a -+)(的值。
数轴、相反数、绝对值
数轴、相反数、绝对值数学是研究数量、结构、变化及空间等概念的学科。
在数学中，数轴、相反数和绝对值是非常重要的概念，它们在解决各种实际问题中发挥着关键作用。
一、数轴数轴是数学中的一个基本概念，它是一个有序的直线，用来表示实数和有理数。
数轴上的点表示实数，原点表示零，正半轴表示正数，负半轴表示负数。
通过数轴，我们可以直观地比较两个实数的大小，也可以找出任何实数的相反数和绝对值。
二、相反数相反数是数学中的另一个重要概念。
如果一个数x的相反数是-x，那么它们在数轴上位于原点的两边，并且它们的距离相等。
例如，3的相反数是-3，5的相反数是-5。
在数学中，相反数经常被用于抵消或中和，以解决各种问题。
三、绝对值绝对值是数学中的一个非常有用的概念。
在数轴上，任何一个实数x的绝对值就是从原点到点x的距离。
例如，3的绝对值是3，-5的绝对值也是5。
绝对值的计算公式是|x| = x(x > 0)或 0(x = 0)或 -x(x < 0)。
绝对值的概念可以帮助我们确定一个数的符号和它的大小。
四、总结数轴、相反数和绝对值是数学中的基本概念，它们在解决各种实际问题中发挥着关键作用。
通过了解这些概念，我们可以更好地理解数学的本质，并解决各种复杂的问题。
因此，对于每一个学习数学的人来说，理解这些基本概念都是非常重要的。
《相反数、绝对值复习》课件一、教学目标1、复习相反数和绝对值的概念和性质，掌握它们的计算方法。
2、提高学生对于相反数和绝对值的理解和应用能力。
3、培养学生的思维能力和自主学习能力。
二、教学内容1、相反数的概念及性质。
2、绝对值的概念及性质。
3、相反数和绝对值的计算方法。
三、教学重点与难点重点：掌握相反数和绝对值的计算方法。
难点：理解相反数和绝对值的概念及性质，并应用到实际问题中。
四、教学方法与手段1、通过PPT展示相反数和绝对值的概念和性质，让学生自主思考和讨论。
2、通过例题讲解和练习，让学生掌握计算方法。
相反数、绝对值及比较大小复习知识点
绝对值及有理数大小比较和相反数知识点一：数轴上表示数a 的点与原点的 叫数a 的绝对值，记作 。
如－2到原点的距离是 ，所以－2的绝对值是 ，即｜－2｜＝ 。
知识点二：一个正数的绝对值是 ；一个负数的绝对值是 ；0的绝对值是 。
即：如果a > 0，那么｜a ｜＝ ；如果a ＝0，那么｜a ｜＝ ；如果a < 0，那么｜a ｜＝ 。
（注意：由于0的绝对值是0，既可以看作是0本身，也可以看作是0的相反数，所以绝对值是这个数本身的数包括 和 （即非负数）；绝对值是这个数的相反数的数包括 和 （即非正数））例题1：｜－6｜＝ ；｜7｜＝ ；｜0｜＝ ．任意有理数的绝对值一定是 数，即｜a ｜ 0（即非负性）。
例题2：｜－5｜＝ ；｜5｜＝ 。
互为相反数的两个数的绝对值 ；一个数的绝对值等于正数，这样的数应该有两个，它们互为相反数。
例题3：已知｜a ｜＝4，｜b ｜＝2，且a>b ，求a 、b 的值。
解：因为｜a ｜=4,｜b ｜＝2，所以a =±4,b=±2,但a > b,所以a=4, b=±2.《绝对值的非负性、双值性都是保证做题全面的关键》知识点三：有理数比较大小：方法一：数轴直观法——数轴左边的数小于数轴右边的数。
方法二：法则——两个负数相比较，绝对值大的反而小。
正数大于0，0大于负数，正数大于负数。
例题6：比较－65和－76的大小： 解：因为｜－65｜＝65＝4235，｜－76｜＝76＝4236，而4235＜4236，所以－65＞－76。
（依据“两个负数相比较，绝对值大的反而小”法则）知识点四：只有符号不同的两个数叫互为相反数，它们位于原点 ，且到原点的距离 。
求相反数的方法是在数（正负数均可）前面加个“－”号即可。
多重符号化简的方法：只看“－”号的个数，偶数个结果为正，奇数个结果为负。
正号可以省略。
例题7：化简：－⎥⎦⎤⎢⎣⎡+-)31( 解：原式＝+（+31）＝31 例题8：－（－3）的相反数是 。
有理数正负数_数轴_相反数_绝对值复习课教案
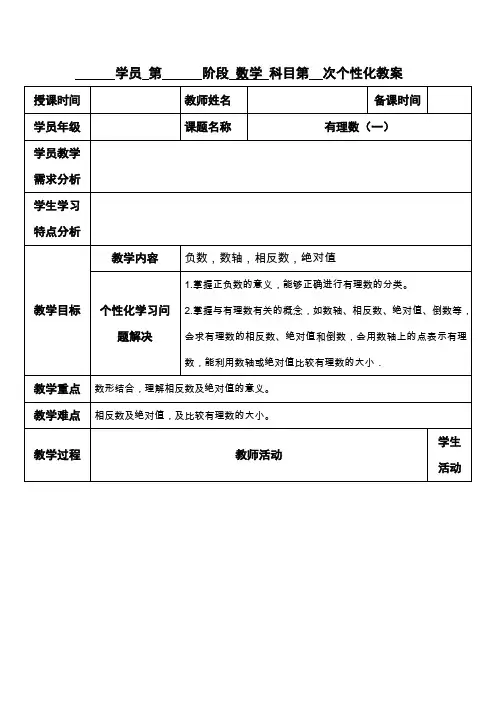
学员第阶段数学科目第次个性化教案授课时间教师姓名备课时间学员年级课题名称有理数（一）学员教学需求分析学生学习特点分析教学目标教学内容负数，数轴，相反数，绝对值个性化学习问题解决1.掌握正负数的意义，能够正确进行有理数的分类。
2.掌握与有理数有关的概念，如数轴、相反数、绝对值、倒数等，会求有理数的相反数、绝对值和倒数，会用数轴上的点表示有理数，能利用数轴或绝对值比较有理数的大小．教学重点数形结合，理解相反数及绝对值的意义。
教学难点相反数及绝对值，及比较有理数的大小。
教学过程教师活动学生活动教学过程：一、基础知识1）、【正负数】_____________统称整数，试举例说明。
_____________统称分数，试举例说明。
____________统称有理数。
正确理解非负和非正。
有理数的分类：[基础练习]1、把下列各数填在相应额大括号内：1，－0.1，-789，25，0，-20，-3.14，-590，6/7正整数集｛ …｝；正有理数集｛ …｝； 负有理数集｛ …｝负整数集｛ …｝； 自然数集｛ …｝；正分数集｛ …｝ 负分数集｛ …｝2、某种食用油的价格随着市场经济的变化涨落，规定上涨记为正，则-5.8元的意义是 ；如果这种油的原价是76元，那么现在的卖价是 。
2）、【数轴】规定了 、 、 的直线，叫数轴 数轴上两点A(a)、B(b)的距离公式： ，中点公式： 。
[基础练习]1、如图所示的图形为四位同学画的数轴，其中正确的是（ ）2、在数轴上画出表示下列各数的点，并按从大到小的顺序排列，用“>”有理数有理数号连接起来。
4，-|-2|， -4.5， 1， 03、下列语句中正确的是（ ） Ａ数轴上的点只能表示整数 Ｂ数轴上的点只能表示分数 Ｃ数轴上的点只能表示有理数Ｄ所有有理数都可以用数轴上的点表示出来4、①比－3大的负整数是_______； ②已知ｍ是整数且-4<m<3，则ｍ为_______________。
专题 有理数的分类、数轴、相反数及绝对值(知识大串讲)(解析版)
专题01 有理数的分类、数轴、相反数及绝对值（知识大串讲）【知识点梳理】考点1 正数和负数1.概念正数：大于0的数叫做正数。
负数：在正数前面加上负号“—”的数叫做负数。
2.意义：在同一个问题上，用正数和负数表示具有相反意义的量。
考点2 有理数1.概念整数：正整数、0、负整数统称为整数。
分数：正分数、负分数统称分数。
（有限小数与无限循环小数都是有理数。
）注：正数和零统称为非负数，负数和零统称为非正数，正整数和零统称为非负整数，负整数和零统称为非正整数。
2.分类：两种⑴按正、负性质分类：⑵按整数、分数分类：正有理数正整数正整数有理数正分数整数0零有理数负整数负有理数负整数分数正分数负分数负分数考点3 数轴1.概念：规定了原点、正方向、单位长度的直线叫做数轴。
三要素：原点、正方向、单位长度2.对应关系：数轴上的点和有理数是一一对应的。
比较大小：在数轴上，右边的数总比左边的数大。
3.应用求两点之间的距离：两点在原点的同侧作减法，在原点的两侧作加法。
（注意不带“+”“—”号）考点4 相反数1.概念代数：只有符号不同的两个数叫做相反数。
（0的相反数是0）几何：在数轴上，离原点的距离相等的两个点所表示的数叫做相反数。
2.性质：若a与b互为相反数，则a＋b=0，即a=-b；反之，若a＋b=0，则a与b互为相反数。
两个符号：符号相同是正数，符号不同是负数。
3.多重符号的化简多个符号：三个或三个以上的符号的化简，看负号的个数（：当“—”号的个数是偶数个时，结果取正号当“—”号的个数是奇数个时，结果取负号）考点5 绝对值1.几何意义：一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值。
一个正数的绝对值是它的本身（若|a|＝|b|，则a＝b或a＝﹣b）2.代数意义一个负数的绝对值是它的相反数0的绝对值是03.代数符号意义：a ＞0，|a|=a 反之，|a|＝a，则a≥0，|a|＝﹣a，则a≦0a = 0，|a|=0a＜0，|a|=‐a注：非负数的绝对值是它本身，非正数的绝对值是它的相反数。
有理数复习提纲
《有理数》复习提纲基本概念一、正数和负数1. 大于 0 的数叫做正数，若a>0，则 a 表示的是任一正数。
在正数前面加上负号“-”的数叫做负数。
若 a<0，则 a 表示的是任一负数2、既不是正数，也不是负数。
3、现实生问题中，常用正数与负数表示的量。
4、非负数指；非正数指。
二．数轴1.定义：规定了、、的直线叫数轴。
2．数轴上表示的两个数，的总比的大。
3.正数0，0 大于，大于。
4.两个负数，大的反而小。
三．相反数1.定义：不同的两个数叫做互为相反数。
2、一般地， a 和 -a 互为，特别地，0的相反数仍是。
3、相反数等于本身的数是。
4、一对相反数的相等。
5、一对相反数的和为。
6、除 0 外，一对相反数的商为。
7、数轴上表示相反数的两个点（0 除外）位于原点的左、右两侧，到原点的距离。
8、在任意一个数前面添上“-”号，新的数就表示原数的。
四．绝对值1、定义：数轴上表示数 a 的点与距离叫做数 a 的绝对值。
2、一个正数的绝对值是；一个负数的绝对值是；0的绝对值。
3、绝对值等于的数为非负数，绝对值等于它的相反数的数为，绝对值最小的有理数是。
4、绝对值等于a（ a>0) 的数为。
5、任何数的绝对值都是。
五．倒数1、为1的两个数互为倒数。
2、0 没有倒数。
3、倒数等于本身的数为。
六．科学记数法是指把一个大于的数写成a×10n的形式，其中,且 n 为。
七．近似数和有效数字一般地，一个近似数，四舍五入到哪一位，就说这个近似数精确到哪一位。
这时，从左边的数字起，到为止，所有的数字都叫做这个数的有效数字。
八．有理数的分类1、与统称为有理数。
2、有理数还可以分为正有理数、、。
3、整数包括、、，有最小的正整数为，有最大的负整数为；分数包括正分数、负分数。
基本运算一．加法1、同号两数相加，符号，并把2、绝对值不相等的异号两数相加，3、两个数相加得0。
4、一个数同0 相加，仍得这个数。
相加。
北师大版七年级数学上册 把握数轴、相反数和绝对值的考点
把握数轴、相反数和绝对值的考点一、知识回顾：1、数轴：规定了原点、正方向和单位长度的直线叫数轴．2、相反数：只有只有符号不同的两个数，称为相反数；零的相反数是零．在数轴上看，表示互为相反数的两个点，分别在原点的两侧且到原点的距离相等．（1）a 的相反数通常表示为-a ；（2）若a 、b 互为相反数，则 a+b=0；3、绝对值：一个正数的绝对值是它本身，一个负数的绝对值是它的相反数，0的绝对值是0．在数轴上，一个数的绝对值就是表示这个数的点到原点的距离．a(a ＞0)a = 0(a=0)－a (a ＜0)二、考点考点1：数轴方法导引：画一条水平的直线，在这条直线上任取一点作为原点，用这个点表示0，规定这条直线上从原点向右的方向（以箭头表示）为正方向，相反的方向为负方向，选取某一长度作单位长度，就得到数轴．数轴上两个点表示的数，右边的数总比左边的数大．考点2：相反数方法导引：求一个数的相反数，要准确掌握相反数的概念：只有符号不同的两个数叫做互为相反数，零的相反数是零．若a 、b 互为相反数，则a+b=0,反之也成立；利用这些性质来解决某些实际问题更为方便．在数轴上表示相反数的两个点分别在原点两侧．并且到原点的距离相等． 考点3：绝对值：数轴上表示数a 的点到原点的距离叫做数a 的绝对值．记做：a ．注意：－a -=a ±，－（－a ）=a考点4：相反数与绝对值的性质a(a 为非负数) ＞a （a 为负数）（1）a = （2）－a= = a （a 为0）－a (a 为正数) ＜a （a 为正数）注意：a 不一定大于－a ．考点5：有理数的大小比较①正数＞0＞负数；②绝对值较大的负数＜绝对值较小的负数三、考题1、数轴例1（南宁市）a b ，在数轴上的位置如图1所示，则下列各式正确的是（ ）A ．a b >B ．a b >-C ．a b <D ．a b -<-分析：从a b ，在数轴上的位置可以看出，对应的数a ＜0，b ＞0故选C ． 点评：数轴上两个点表示的数，右边的数总比左边的数大．例2（安顺市）数轴上点A 表示3-，点B 表示1，则表示A B ，两点间的距离的算式是（ ）A ．31-+B ．31--C ．1(3)--D ．13-分析：数轴上两点间的距离可以用表示这两个数的点坐标之差来表示，并且这个距离是一个正数，因此，可以选择C ．点评：数轴上两点间的距离用表示这两点的坐标表示就是AB=A B x x -．2、相反数例3（河北省）7-的相反数是（ ）A ．7B ．7-C ．17 D ．71- 分析：互为相反数是指只有符号不同的两个数，因此，可以知道选项A 正确，故选择A ．点评：求一个数的相反数只须改变这个数的符号即可．3、绝对值例4（厦门市）|－3| ．分析:本题考查的是绝对值的概念，正数的绝对值还是正数，负数的绝对值是其相反数，0的绝对值还是0． 3-=－（－3）=3，故填3．点评：准确掌握概念是解答问题的关键．绝对值的化简关键是去掉绝对值符号，当绝对值号内是具体数时，可按绝对值定义去掉觉得绘制符号而的出非负数．4、相反数与绝对值的综合例5（山东聊城市）如果x 与2互为相反数，那么1x -等于（ ）A ．1B ．2-C ．3D ．3-分析：本题先根据“如果x 与2互为相反数”，求出x=－2，再把x=－2代入1x -，得：3312=-=--，故选择C ．点评：本题综合考查了相反数与绝对值的基本概念，只有基础扎实，灵活应用，才能准确解答．5、绝对值的性质例6（娄底市）若11a a -=-，则a 的取值范围为（ ）A ．1a ≥B ．1a ≤C ．1a >D ．1a <分析：本题主要是考查绝对值的性质：绝对值等于其相反数的数是非正数．故11a a -=-可以知道，1－a ≤0，得1a ≤，故选择B ．点评：当绝对值号内为含有字母的代数式时，应根据题目中所给字母的范围及绝对值定义去化简．本题先把1-a 化简，得到：)1(11--=-=-a a a ，由“如果一个数的绝对值等于其相反数，那么这个数是非正数”．此时不要忘记“等号”，只取“＜”，这是同学们最容易出现错误的地方．6、非负数的性质例7（北京市）若22(1)0m n ++-=，则2m n +的值为（ ）A ．4-B ．1-C ．0D ．4 分析：在现阶段，一个数是非负数的表示形式有a ≥0，2a ≥0．由22(1)0m n ++-=，得02=+m ，01=-n ，则2-=m ，1=n ，再把2-=m ，1=n 代入2m n +得：0．故选择C ．点评：若干个非负数的和为零，则必有每个非负数同时为零，这是非负数性质之一，大家必须掌握，利用其可以解答一些问题．7、有理数的大小比较例8（山西省太原市）比较大小：3- 2-．（用“>”，“=”或“<”填空） 分析：这是两个负数大小的比较，由“绝对值较大的负数＜绝对值较小的负数”可以知道，应该填“<”．点评：两个负数比较一定要注意：绝对值大的反而小，这是同学们最容易忽视的地方．四、课外考场1、（山东省青岛市）12-的绝对值等于（ ）． A ．2- B ．2 C ．12- D ．12 2、（湖北省宜昌市）若2-的绝对值是a ，则下列结论正确的是（ ）A ．2a =B ．12a =C ．2a =-D ．12a =- 3、（长沙市）请写出一对互为相反数的数： 和 ．4、（河南省）52的相反数是 ． 5、（长沙市）如图，点A B ，在数轴上对应的实数分别为m n ，，则A B ，间的距离是 ．（用含m n ，的式子表示）6、（贵阳市）比较大小：2- 3（填“>，<或=”符号）参考答案：1、D ；2、A ；3、答案不唯一，如2与2-等；4、52-； 5、m n -；6、<．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
0.2
（3） ，-3.14 5、到原点距离为2的点____ 到原点距离小于2的点____ 到原点距离不大于2的点____
6、绝对值等于4的数____ 绝对值小于4的数____ 绝对值不大于4的数____ 7、零件尺寸为 10 0.05 mm，最大____，最 小____ 8.已知a<0,b>0, a > b , 在数轴上表示出a，b，-a，-b，并用<连接 9绝对值大于3不大于6的数____
11、若一个数的绝对值等于本身，它是____ 若一个数的绝对值等于它的相反数，它 是____ 12、若 a =a，则a____0 若 a =-a，则a____0
1、____是最小的正整数， ____ 是最大的负整数 2、绝对值是3的数是____ 3、绝对值小于2.1的数____ 4、比较大小 7 5 （1） 6 ， 8 （2） 0.01
1、比较大小 1 （1） ，
2
1 3
1 (2) ,-0.621 8
2、绝对值不大于2.5的数____ 3、若a>0,b<0, a > b 在数轴上表示出a，b，-a，-b，并用>连结
作业
• 学习指导
5、有理数的大小比较：
几何方法（数形结合）：在数轴上 ____________________________ ① ② 代数方法(利用法则) ③ ④ ⑤ 6、数a的倒数：____（a 0） 相反数：____ 绝对值：____
7、相反数大于本身的数是____ 相反数小于本身的数是____ 相反数等于于本身的数是____ 8、数a的绝对值是指数轴上表示a的点与____ 的距离，记作____ 9、正数的绝对值是____ 0的绝对值是____ 负数的绝对值是____ 10、当a>0, a ____ 0 当a=0, a ____0 当a<0, a ____0
正负数，数轴，绝对值，相反 数复习
张淅
学习目标
• 1、巩固正负数，数轴，绝对值，相反数的 相关知识 • 2、规范做题格式
知识要点
1、__有理数
3、规定了____、____、____的____叫数轴。 4、数轴上原点表示____，原点左边的数表示 ____，原点右边的数表示____。