高一数学映射与函数
高一数学 函数映射、单调性

高一数学函数及函数的性质1、映射的概念(1)映射是特殊的对应,即是“一对一”的对应和“多对一”的对应,而“一对多”的对应不是映射.(2)给定一个映射f:A→B,则A中的每一个元素都有唯一的象,B的某些元素可以没有原象,如果有原象,也可以不唯一的.2、函数的概念(1)函数是特殊的映射,即集合A、B均为非空数集的映射.(2)构成函数的三要素;对应关系f、定义域A、值域{f(x)|x∈A},其中值域{f(x)|x∈A} B.正确理解函数符号y=f(x):①它表示y是x的函数,绝非f与x的积;②f(a)仅表示函数f(x)在x=a时的函数值,是一常数.(3)确定函数的条件:当对应关系f和定义域A已确定,则函数已确定,判定两个函数是否相同时,就要看定义域和对应法则是否完全一致.(4)函数的定义域,一般是使函数解析式有意义的x值的集合,在具体问题中则应考虑x的实际意义,如时间t,距离d均应为非负数等.求函数定义域的基本方法:①分式中分母不为零;②偶次根式中的被开方式不小于零;③ [f(x)]0中的底f(x)不为零;④如果f(x)是由几个部分的数学式子构成的,那么函数的定义域是使每个部分式子都有意义的实数集合.根据对应法则的性质求定义域,如已知f(x)的定义域为[a,b],则f[ψ(x)]的定义域应为ψ(x)的定义域与a≤ψ(x)≤b的解集的交集.3、函数的表示法:解析法、列表法、图象法.4、函数的值域是全体函数值所组成的集合,有观察法,换元法、配方法、图象法、反求法、判别式法等求值域的基本方法.函数的值域是函数的“三要素”之一,在一个给定的函数中,函数的值域随对应法则和定义域而确定.几个基本初等函数的值域:一次函数y=kx+b(k≠0)的值域:{y|y∈R};二次函数y=ax2+bx+c(a≠0)的值域:当a>0时,;当a<0时,;反比例函数(k≠0)的值域:(-∞,0)∪(0,+∞).求函数值域的基本方法(1)直接法:从自变量x的范围出发,推出y=f(x)的取值范围;例如:的值域为[1,+∞).这是因为x≤3,所以≥0,∴ y≥1.(2)二次函数法:利用换元法将函数转化为二次函数求值域(或最值);(3)反函数法:将求函数值域转化为求反函数的定义域;4)判别式法:运用方程的思想,将函数变形成关于x的二次方程,依据二次方程有实根,求出y 的取值范围;(5)利用函数的单调性求值域;(6)图象法:作出函数的图象,由图象来确定函数的值域.1、判断下列对应是否是从集合A到集合B的映射;(1)A=R,B={x|x>0且x∈R},x∈A,f:x→|x|;(2)A=N,B=N*,x∈A,f:x→|x-1|;(3)A={x|x>0且x∈R},B=R,x∈A,f:x→x2.2、求函数的定义域.1、已知映射f:A→B,则下列说法正确的是()A.A中某一元素的象可能不止一个 B.A中两个不同元素的象必不相同C.B中某一元素的原象可能不止一个 D.B中两个不同元素的原象可能相同2、若A={2,4,6,8},B={-1,-3,-5,-7},下列对应法则:①f:x→9-2x;②f:x→1-x;③f:x→7-x;④f:x→x-9中,能确定A到B的映射的是()A.①②B.②③ C.③④D.②④3、下面四组函数f(x)与g(t)中,表示同一函数的是()A.B.C.D.4、函数的定义域是()A.(4,+∞) B.(2,3)C.(-∞,2)∪(3,+∞) D .(-∞,2)∪(2,3)∪(3,+∞)5、已知f(x)是一次函数,且满足2f(2)-3f(1)=5,2f(0)-f(-1)=1,则f(x)的解析式为()A.3x-2 B.3x+2 C.2x-3 D.2x+36、设函数y=f(x)的定义域为[-],则函数y=f(-2)的定义域是()A.[-,2] B.[2-,2+] C.[6-4,6+4] D.[0,6+4]7、若函数的定义域为A,y=的定义域为B,的定义域为C,则集合A、B、C之间的关系是()A.A∩B=C B.A∩B C C.A∩B C D.A∪B C8、若函数y=f(x)的定义域为[0,1],则函数y=f(x+a)+f(2x+a)(0<a<1)的定义域是()A.B.C.[-a,1-a] D.9.下列图中,画在同一坐标系中,函数与的图象只可能是()A. B.C. D.10、给出四个命题:(1)函数是其定义域到值域的映射;2)是函数;(3)函数y=2x(x∈N)是一次函数;4)与g(x)=x是同一个函数.其中正确的有()A.1个B.2个 C.3个 D.4个11、设(x,y)在映射f:A→B的作用下的象是(),则在f的作用下,元素(-1,1)象是_____________,元素(3,-2)的原象是_____________.12、若f(x+1)=2x2+1,则f(x-1)= _____________.13、(1)f(x)是二次函数,且f(2)=-3,f(-2)=-7,f(0)=-3,求f(x)的表达式;(2)已知:f(2x-1)=4x2-2x,求f(x)的表达式.14、已知函数y=f(x)的定义域为[0,1],设函数F(x)=f(x+a)+f(x-a),求正实数a的取值范围,并求函数F(x)的定义域.15、已知f(x)是二次函数,且f(x+1)+f(x-1)=2x2-4x,求f(1-)的值.6、求下列函数的值域.1、函数的单调性(1)定义: 设函数y=f(x)的定义域为 A :区间,如果对于区间I上的任意两个自变量的值,当时,都有,那么就说f(x)在区间I上是增函数. 区间I称为y=f(x)的单调增区间;如果对于区间I上的任意两个自变量的值,当时,都有,那么就说f(x)在这个区间上是减函数。
映射和函数的关系

映射和函数的关系在数学中,映射和函数是两个非常重要的概念,它们之间存在着密切的关系。
本文将从不同的角度介绍映射和函数,并探讨它们之间的联系和特点。
一、映射的定义和特点映射是数学中一个基本的概念,它描述了两个集合之间的元素之间的对应关系。
具体来说,设A和B是两个非空集合,如果对于A中的每个元素a,都有一个元素b与之对应,那么就称这种对应关系为映射。
映射具有以下特点:1. 一对一映射:如果对于A中的不同元素a1和a2,其对应的b1和b2也是不同的,那么称这种映射为一对一映射。
2. 多对一映射:如果对于A中的不同元素a1和a2,其对应的b1和b2是相同的,那么称这种映射为多对一映射。
3. 映射的定义域和值域:对于映射f:A→B,A称为定义域,B称为值域。
4. 映射的像和逆像:对于映射f:A→B,对于B中的任意元素b,称在A中所有与b对应的元素的集合为b的逆像,称在B中与A的所有元素对应的元素的集合为A的像。
二、函数的定义和性质函数是一种特殊的映射,它具有以下性质:1. 定义域和值域:函数f:A→B的定义域为A,值域为B。
2. 唯一性:对于定义域A中的每个元素a,函数f只能有一个值b 与之对应。
3. 图像和原像:对于函数f:A→B,对于B中的任意元素b,称在A 中与b对应的元素为b的原像,称在B中与A的所有元素对应的元素的集合为A的图像。
4. 单调性:函数可以是单调递增的,也可以是单调递减的,或者不具备单调性。
三、映射与函数的关系映射是一个更加一般的概念,而函数是映射的一种特殊情况。
具体来说,函数是一种满足每个元素只有一个唯一值与之对应的映射。
在映射中,元素之间的对应关系可以是一对一的或多对一的,但在函数中,元素之间的对应关系必须是一对一的。
因此,函数是映射的一种特殊情况。
映射和函数都具有定义域和值域的概念,用来描述元素的取值范围。
只不过在函数中,定义域中的每个元素只能有一个对应的值域元素,而在映射中可以有多个。
【高一函数培优班】12 映射和函数的定义
D. 4,2 2,4
12.为确保信息安全,信息需加密传输,发送方由明文 密文(加密),接收方由密文 明文(解密),已
知加密规则为:明文 a,b, c, d 对应密文 a 2b, 2b c, 2c 3d , 4d. 例如,明文1, 2,3, 4 对应密文 5, 7,18,16. 当
接收方收到密文14, 9, 23, 28 时,则解密得到的明文为(B )
2
3
3
8
2.给定映射 f : (a,b) (a 2b, 2a b) ,则在映射 f 下, (3,1) 的原象是( B )
A. (5,5)
B. (1,1)
C. (3,1)
D. (1 , 1)
22
3 已知映射 f : A B ,期中 A 3,2,1,1,2,3,4,集合 B 中的元素都是 A 中元素在 f 下的象且对于任
2A:定义域,原象的集合 B:值域,象的集合(C)其中 C B f:对应法则 xA yB
3函数符号:y=f(x) —— y 是 x 的函数,简记 f(x)
4.关于函数值 f(a)
例:f(x)=x2+3x+1 则 f(2)=22+3×2+1=11
注意:1在 y=f(x)中 f 表示对应法则,不同的函数其含义不一样。
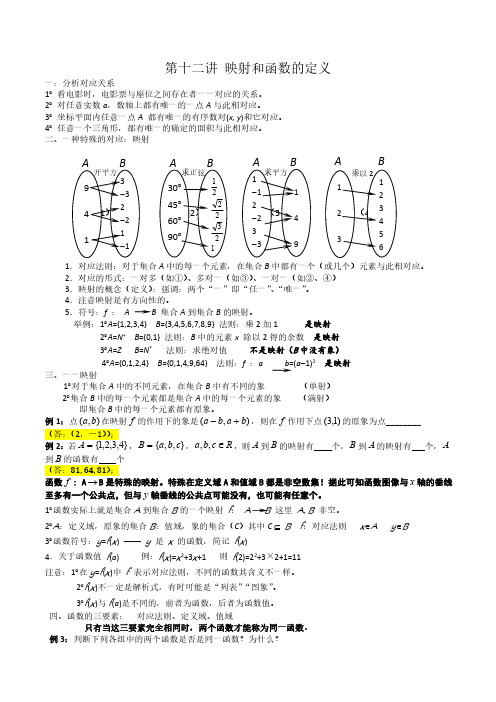
第十二讲 映射和函数的定义
一:分析对应关系
1 看电影时,电影票与座位之间存在者一一对应的关系。 2 对任意实数 a,数轴上都有唯一的一点 A 与此相对应。 3 坐标平面内任意一点 A 都有唯一的有序数对(x, y)和它对应。 4 任意一个三角形,都有唯一的确定的面积与此相对应。 二、一种特殊的对应:映射
意的 a A , f (a) a ,则集合 B 中元素的个数是( A )
大一高数知识点映射与函数

大一高数知识点映射与函数高等数学是大多数理工科专业大一必修的一门课程,其中包含了许多重要的数学知识点。
在这篇文章中,我们将重点讨论高数中的映射与函数。
一、映射的概念与性质映射是数学上非常重要的概念,它描述了元素之间的对应关系。
在集合论中,我们将一个元素从一个集合映射到另一个集合,这两个集合可以是相同的,也可以是不同的。
映射一般用函数符号f(x) 表示,其中 x 是原集合的元素,f(x) 是它在目标集合中的对应元素。
映射具有以下性质:1. 单射:若 f(x1) = f(x2),则 x1 = x2。
即不同的元素在映射中有不同的对应元素。
2. 满射:若对于任意的 y ∈目标集合,都存在 x ∈原集合,使得 f(x) = y。
即每一个元素都有对应的映射元素。
3. 一一映射:即又是单射又是满射的映射。
二、函数的定义与性质函数是映射的一种特殊形式,它在数学和其他学科中都有着广泛的应用。
函数的定义比较简洁,它是一种特殊的映射,其中原集合只能有一个元素对应到目标集合中的一个元素。
函数具有以下性质:1. 定义域和值域:函数的定义域是指输入变量的取值范围,值域是指函数输出的取值范围。
2. 奇偶性:函数 f(x) 的奇偶性取决于 f(-x) = f(x) 或 f(-x) = -f(x) 是否成立。
3. 单调性:函数在定义域上的增减状况,可以分为递增、递减或保持不变。
4. 极值与最值:函数在定义域的某一点或某一区间上取得的最大值或最小值。
5. 对称性:函数是否具有关于某个轴的对称性。
三、常见的函数类型在高数课程中,我们学习了许多常见的函数类型。
下面是其中一些重要的函数:1. 幂函数:y = x^n,其中 n 是正整数。
2. 指数函数:y = a^x,其中 a 是正实数且不等于 1。
3. 对数函数:y = log_a(x),其中 a 是正实数且不等于 1。
4. 三角函数:包括正弦函数、余弦函数和正切函数等。
5. 反三角函数:包括反正弦函数、反余弦函数和反正切函数等。
高一数学映射及函数的表示方法知识精讲

高一数学映射及函数的表示方法【本讲主要内容】一. 本周教学内容:映射及函数的表示方法映射的概念、函数的概念、函数的表示方法【知识掌握】 【知识点精析】1. 函数的定义:设A 、B 是两个非空数集,如果按照某个确定的对应关系f ,使对于集合A 中的任一个数x ,在集合B 中都有唯一确定的数y 和它对应,那么就称f :A →B 为从集合A 到集合B 的一个函数,记作y=f(x),x ∈A ,其中x 叫自变量,x 的取值X 围A 叫做函数的定义域;与x 的值相对应的y 值叫函数值,函数值的集合})(|{A x x f y y ∈=,叫函数的值域。
2. 两个函数的相等:当且仅当两个函数的定义域和对应法则都分别相同时,这两个函数才是同一函数,例如:x y =与33x y =。
3. 映射的定义:一般地,A 、B 是两个集合,如果按照某个对应法则f 对于集合A 中的任一个元素,在集合B 中都有唯一的元素和它对应,那么这样的对应(包括集合A 和B ,及集合A 到集合B 的对应法则f )叫做集合A 到集合B 的映射,记做f :A →B 。
4. 函数的实质:函数是特殊的映射,即要求A 、B 都是非空数集。
5. 函数的表示方法:解析式(分段函数法、图像法、列表法)【解题方法指导】例1. (1)设}8621021{}4210{,,,,,=,,,B A =下列对应法则能构成A 到B 的映射的是( ) A. 1:2-→x x f B. 2)1(:-→x x f C. x x f 2:→D. 12:-→x x f点拨:根据映射定义,检验集合A 中每一元素依照对应法则在B 中是否都有唯一元素与之对应。
解析:选C 。
在集合A 中,\10B ∈-→ 在集合B 中,\94B ∈→ 在集合D 中,\42B ∈→(2)下图中可表示函数)(x f y =图象的只可能是( )与图像相交,如果只有唯一的交点,则是函数图象,否则不是。
解析:根据函数定义,对任意一个x ,都要有唯一的y 与之对应,故选D 。
高一数学第5讲:映射、函数的概念(教师版)

第5讲映射、函数的概念1.函数的定义(1)传统定义:在某一个变化过程中有两个变量x和y,如果对于在某一个范围内的任一个x的值,都有唯一的y值与它对应,则称y是x的函数,x叫做自变量,y叫做因变量。
(2)近代定义:给定两个非空数集A和B,如果按照某个对应关系f,对于A中任何一个数x,在集合B中都存在唯一确定的数f(x)与之对应,那么就把对应关系f叫做定义在A 上的函数,记作A→B,或y=f(x),x∈A,此时,x叫做自变量,集合A叫做函数的定义域,集合{f(x)|x∈A}叫做函数的值域,习惯上我们称y是x的函数。
(3)两个定义间的联系:函数的两个定义本质是一致的,只是叙述概念的出发点不同,传统定义是从运动变化的观点出发,而近代定义是从集合的观点出发。
这样,就不难得知函数的实质是从非空数集A到非空数集B的一个特殊对应。
2.函数的定义域函数的定义域是自变量x的取值范围,但要注意,在实际问题中,定义域要受到实际意义的制约。
如函数y {x|x≥0},圆半径r与圆面积S的函数关系为S=πr2的定义域为{r|r>0}。
求函数定义域的一般原则是:①如果f(x)为整式,其定义域为实数集R;②如果f(x)为分式,其定义域是使分母不为0的实数集合;③如果f(x)是二次根式(偶次根式),其定义域是使根号内的式子不小于0的实数集合;④如果f(x)是由以上几个部分的数学式子构成的,其定义域是使各部分式子都有意义的实数集合;⑤f(x)=x0的定义域是{x∈R|x≠0}。
求函数定义域除上述所列外,还应注意以下几点:①如果是实际问题,除应考虑解析式本身有意义外,还应考虑使实际问题有意义;②如果不给出解析式:已知f(x)的定义域为x∈A,则f[g(x)]的定义域是求使g(x)∈A 的x的取值范围;已知f[g(x)]的定义域为A,则f(x)的定义域是求g(x)在A上的值域。
3.函数的对应法则对应关系f是函数关系的本质特征,y=f(x)的意义是:y就是x在关系f下的对应值,而f是“对应”得以实现的方法和途径。
第一节 映射与函数课件

第一节 映射与函数
两点说明
(1) 函数两要素:定义域、对应法则 例如:函数 f (x) = x2 ,自然定义域为 (- , + ),
若它表示正方形的面积 则其定义域为(0 , + ).
表达式有意义的全体实数的集合,称之为自然定义域.
y
1 (x , y)
-1 O x 1 x -1 (x , -y)
第一节 映射与函数
例3
设
f
:
π 2
,
π 2
[1
,
1]
,
定义域
Df
π 2
,
π 2
,
值域 Rf = [ -1 , 1 ] . y
1
π 2
f (x) = sin x
O
πx
2
-1
第一节 映射与函数
2、常见映射类型
(1)若 f ( X ) Y , 则称 f 为满射.
映射 g 为 f 的逆映射,记作 f -1 , 其定义域 D f 1 R f ,
值域 R f 1 X .
Rf
只有单射才存在逆映射
第一节 映射与函数
(2)定义 设有两个映射 g : X Y 1 , f : Y 2 Z ,
其中 Y1 Y2 , 则由映射 g 和 f 可以定义一个从 X 到 Z 的对应法则,它将每个 x X 映成 f [g(x)] Z . 这个法 则确定了一个从 X 到 Z 的映射,称之为映射 g 和 f 构成
X
Rg Df
Z
第一节 映射与函数
例4.
第一节 映射与函数
二、函数
高数课件映射与函数

3
图像和原像的关系
图像和原像之间存在一对多或多对一的关系,取决于映射的特性。
函数的定义和性质
什么是函数?
函数是一种特殊的映射,它 将定义域中的每个元素映射 到值域中唯一的元素。
函数的性质
函数具有单调性、有界性和 奇偶性等重要性质,可应用 于各个领域。
示例
举例说明具体函数的定义和 性质,在实际问题中的应用。
映射与函数的关系
1 映射与函数的相同点
映射和函数都是描述元素之间的对应关系,具有相似的数学概念和性质。
2 映射与函数的不同点
映射是一个更普遍的概念,而函数是一种特殊的映射。
3 映射与函数的交叉应用
通过具体案例来展示映射和函数在高等数学中的应用。
映射与函数在高数中的应用
微积分
映射和函数是微积分中研究函数 极限、导数和积分等重要工具。
高数课件映射与函数
欢迎来到高数课件映射与函数的世界!本课程将带你深入了解映射和函数的 定义、性质以及它们在高等数学中的应用。准备好开始探索吧!
映射的定义和性质
1 什么是映射?
映射是一个将一个集合中的每个元素映射到另一个集合中的元素的规则。
2 映射的性质
映射可以是单射、满射或双射,具有重要的代数和几何意义。
图论
映射和函数被广泛应用于图论中 的图的表示和性质研究。
最优化问题
映射和函数为解决最优化问题提 供了数学建模的基础。
ห้องสมุดไป่ตู้
什么是复合函数?
复合函数是将两个函数结合在 一起形成一个新的函数。
复合函数的性质
复合函数的定义域和值域取决 于两个函数的定义域和值域。
示例
通过具体的数学表达式和图形 展示复合函数的概念和性质。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复 习:
1.集合与元素简单关系:
2.集合与集合之间的关系:
符号的哪边是元素? 问题1: a A a B A B,A 问题2: B,A B 分别表示什么?
新课: 初中我们学过一些“对应”的例子:
(2)对于坐标平面内的任何一个点,都有唯一的有序 实数对(x,y)和它对应; (3)对于任意一个三角形,都有唯一的确定的面积 和它对应;
象与原象的概念 一一映射的定义 单射+满射 = 一一映射
*注意:
1.映射是一种特殊的对应:多对一、一对一 2.一一映射是一种特殊的映射:A到B是映射, B到A也是映射。
; https:/// 日本不动产
jor593fhl
涡,嘭的一声,水面炸开了五六个大水柱,五条青龙冲出水面,龙爪抓住面具男撕成了碎片,江水一片血红,山神在空中俯视着他们,没有哀 嚎声只有龙的咆哮,面具人开始逐渐减少,山神飞到一棵树顶上看着江面,面具男已经基本被处理完了。在茫茫的江面上一只黑色的水龙飞到 山神面前,这只黑龙通体黑色,只有爪子和尾巴是青色比起那五只青龙不知强壮了多少倍,看它的鳞片锋利坚硬,犹如铠甲一般。黑龙开口: “你也被盯上了,最近不太平啊”山神望着江面缓缓开口道:“妫族的渡劫者出现了”。“几万年了,烛龙,九尾他们还不死心吗”黑龙叹了 口气说继续说:妫族究竟有什么灵力和秘密值得他们追寻几万年,难道就是不用历劫吗?山神摇摇头说:“我也不知道”一阵沉默,山神看着 黑龙说:“我突然想起了一件事,十二年前,就是暮笙还在古宅的时候,有一个女孩,看年纪应该是二十岁左右,依我看,她是人类,可她居 然闯过了重重关卡毫发无伤的走进了古宅,要知道当时整座山都被我布下了结节,别说是人类,就是法力高强的妖怪也不可能闯的进古宅,而 她却能轻而易举的进来,这些结节似乎对她都没有什么用,暮笙问她怎么找到这里来的,我记得当时他也是挺纳闷的说她在北方的一个城市里 上学,她去市中心买东西,过马路的时候看到一辆大卡车疾驰而过,那辆卡车速度很快根本不像是卡车应有的速度,而前面有一位老奶奶在过 马路,当时她几乎是下意识地就把老奶奶推开,自己眼看着车子就要撞过来了,只是短短的一瞬间她就感觉到了死亡,不知过了多久身边没有 任何急刹车的声音,也没有人的惊恐声,她睁开眼睛发现自己还站在人行道里,根本没有过斑马线,难道刚才都是幻觉,正觉得奇怪,那个老 奶奶站在她身后说,谢谢姑娘,要不是你,自己早就被车撞死了,她惊讶的啊了一声,老奶奶说,姑娘,要不是你及时把我从斑马线上拉回来, 我早就被卡车撞死了。她心里感到疑惑,这么说自己是救了认了,可自己清楚地看到卡车向自己撞过来了啊。老奶奶说:“姑娘,你可以送我 回家吗?”她想想自己也没什么事,自己也对这一带还算熟悉就答应了。那位老奶奶带着她七拐八拐来到了一处老城区进入里面,恍若迷宫, 她心里想自己居然不知道还有这么一个地方自己怎么从未听说过,来到一栋古宅面前,就是和山里那栋古宅一模一样,老奶奶手捂住脸,这时 她看到老奶奶带着一个龙型手镯,因为样子奇特,所以她记得非常清楚,老奶奶说:我到了,这就是我住的地方,你救了我,作为报答,我可 以告诉你一个秘密。听到这句话她心里觉得毛毛的忙说不用了,不用了。话说完,一顶红色的轿子踏云而来,她看着眼前的以前使劲掐了自己 的脸一下,这是真的。觉得自己一定是见鬼
答:不是映射。
(3)A=Z,B=N*,对应法则 f:求绝对值
答:不是映射。
(4)A={11,16,20,21},B={6,2,4,0}, 对应法则 f:求被7除的余数
答:是映射,且是一一映射。 练习:课本49页1---4
课时小结:
映射的定义(映射三要素:两个集合,一种对应法则)
映射的表示方法 f:A→B
(2)
A
300
求正弦
B
½
450
600 900
1
(3)
A
1 -1 2 -2 3 -3
求平方
B
1 4 9 前进
(4)
A
1 2 3
乘与2
B
1 2 3 4 5 6
总结:
对于集合A中的任何一个元素,按照某种法则f, 在集合B中都有确定的(一个或多个)元素和它对应。 问题4:前面是各张图中,A中元素和B中分别 是怎样的对应?
问题4:根据映射定义,指出哪些对应是A到B的映射?
(1)
A
9
开平方
B
3 -3 2 -2 1 -1
(2)
A
300
450 600 900
求正弦
B
½
4
1
(3)
√
1 乘与2
A
1 -1 2 -2 3 -3
求平方
B
1
(4)
A
1
B
1 2 3 4 5 6
4
9
√
2
3
√
例1:判断下面的对应是否为映射 :
(1)设A={1,2,3,4},B={3,4,5,6,7,8,9}。 集合A中的元素x按照对应法则“乘2加1”和集合B中的 元素2x+1对应,这个对应是否为集合A到集合B的映射? 为什么?
例2:判断下面的对应是否为映射 ,是否为一一映射?
(1)A={0,1,2,4,9},B={0,1,4,9,64}, 对应法则 f:a →b = (a-1)2 A
0 1 2
B
0
1
4
9 64
4
9
答:是映射,不是一一映射。
(2)A={0,1,4,9,16},B={-1,0,1,2,3,4}, 对应法则 f:求平方根
引出
定义3:
前进
定义3:一般地,设A、B是两个集合。f:A→B
是集合A到集合B的映射,如果在这个映射 下,对于集合A的不同元素,在集合B中 有不同的象,且B中每一个元素都有原象, 那么这个映射叫做A到B上的一一映射。
单射
充要条件
满射 注意:
(1)一一映射是一种特殊的映射。
(2)映射和一一映射之间的充要关系 一一映射 映射是一一映射的必要而不充分条件 返回 (3)一一映射: A和B中元素个数相等
√
给定一个集合A到集合B的映射,且a∈A, 定义2:
b∈B。如果元素a和元素b对应,那么我 们把元素b叫做元素a的象,元素a叫做元 素b的原象。
A B
a
f
b
a的象
b的原象
(1)
A
9 4 1
开平方
B
3 -3 2 -2 1 -1
(2)
A
300 450
求正弦
B
½
的原象
600
900
1
450的象
(3)
回上图
发现规律:上图(2)(3)(4)中,A中任何一个 元素在B中都有唯一的元素和它对应
引出
定义:
一般地,设A、B是两个集合。如果按照 定义1:
某种对应法则ƒ,对于集合A中的任何一 个元素,在集合B中都有唯一的元素和它 对应,那么这样的对应(包括集合A、B 及A到B的对应法则f)叫做集合A到集合B 的映射。记作:f:A→B
求平方
B
1 4 9
4
( 1) A
a b c d
f
B
m n p q
( 2) A
1
f
B
3 5 7 9
√
2 3 4
√
( 3) A
1 2 3 4
f
B
1
3
5
7
9
√
问题5:图中所示的三个对应 是不是映射?
( 1) A
a b c d
f
B
m n p q
( 2) A
1 2 3 4
f
B
3 5 7 9
问题6:图中的(1)(2)所示的映射有什么特点? 发现规律: (1)对于集合A中的不同元素,在集合B中有不同的象, 我们把这样的映射称为单射。 (2)集合B中的每一个元素都有原象,我们把这样 的映射称为满射。 问题7:单射+满射=?
(1)对于任何一个实数,数轴上都有唯一的点和它对应;
(4)对于任意一个二次函数,相应坐标平面内都有 唯一的抛物线和它对应。
问题3:你还能找出生活中的一些 “对应”的例子吗?
*从集合的角度来讲,这些对应是集合之间根据 一定的法则进行的对应
A
对应
法则fΒιβλιοθήκη B回到前面(1)对于任何一个实数,数轴上都有唯一的点和它对应; A=R,B={数轴上的点} 法则f:在数轴上画点 (2)对于坐标平面内的任何一个点,都有唯一的有序 实数对(x,y)和它对应; A={坐标平面内的点},B={(x,y)| x , y ∈ R }
(1)映射是一种特殊的对应; 注意:
(2)符号“f:A→B”表示A到B的映射; (3)映射有三个要素:两个集合,一种对应法则; (4)集合的顺序性:f:A→B 与 f:B→A是不同的: (5)箭尾集合中元素的任意性(少一个也不行)。 箭头集合中元素的唯一性(多一个也不行)。 即只能多对一、一对一,不能开花!
法则f:在坐标平面内画点 (3)对于任意一个三角形,都有唯一的确定的面积 和它对应; A={三角形},B={三角形的面积} 法则f:求面积 (4)对于任意一个二次函数,相应坐标平面内都有 唯一的抛物线和它对应。 A={二次函数},B={坐标平面内的抛物线}
法则f:画图像
(1)
A
9 4 1
开平方
B
3 -3 2 -2 1 -1
√
(2)设A=N+,B={0,1}。集合A中的元素x按照对应 法则“x除以2得的余数和集合B中的元素对应”,这个对 应是否为集合A到集合B的映射?为什么?
√
(3)设A={x | x是直角三角形},B={y | y>0},集合A 中的元素x按照对应法则“计算面积”和集合B中的元素对 应,这个对应是否为集合A到集合B的映射?为什么?
