Secure Network Coding on a Wiretap
network is unreachable的解决方法

network is unreachable的解决方法全文共四篇示例,供读者参考第一篇示例:“network is unreachable”是一种常见的网络连接问题,通常意味着您的设备无法访问互联网或局域网。
这种问题可能会导致您无法浏览网页、收发邮件或与其他设备进行通信。
出现这种问题时,不要惊慌,可以尝试一些简单的解决方法来解决这个问题。
1. 检查网络连接您需要确保您的设备已正确连接到网络。
您可以检查一下网络连接是否正确连接并且运作正常,确保网络线没有损坏,并且路由器已正常工作。
有时候只需重新插拔网络线或者重启路由器就可以解决问题。
2. 检查IP地址设置如果网络连接没有问题,您可以检查一下设备的IP地址设置。
确保您的设备获取到了正确的IP地址,并且网络配置正确。
您可以尝试切换到静态IP地址或者使用自动获取IP地址的方式来解决问题。
3. 检查防火墙设置防火墙可能会阻碍您与网络的连接,导致“network isu nreachable”的问题。
您可以检查一下设备的防火墙设置,确保没有阻止网络连接的规则。
如果有必要,您可以尝试关闭防火墙来测试一下是否可以解决问题。
4. 检查DNS设置DNS是将域名解析为IP地址的服务,如果DNS设置不正确,可能会导致“network is unreachable”的问题。
您可以尝试更改DNS 设置,或者使用其他公共DNS服务,比如Google的8.8.8.8和8.8.4.4来解决问题。
5. 检查网络设备有时候是网络设备出现了问题,比如路由器、交换机或者调制解调器。
您可以尝试重新启动网络设备,或者升级固件来解决问题。
确保您的网络设备运行正常,并且没有硬件故障。
“network is unreachable”是一个比较普遍的网络连接问题,可能由多种原因引起。
不过,大多数情况下可以通过上面提到的解决方法来解决问题。
如果您尝试了以上方法仍然无法解决问题,可能需要联系网络管理员或者网络服务提供商来获取进一步的帮助。
broadcast-probe reply disable

broadcast-probe reply disablebroadcast-probe reply disable是一种网络设置的功能,它可以禁用网络广播探测的回复。
广播探测是广播一条消息,然后等待网络上所有的设备回复,以确定网络上的设备数量和类型。
这可以帮助管理员识别网络中的设备并进行故障排查。
然而,在某些情况下,禁用广播探测的回复可能是有用的。
一种常见的情况是在网络中存在大量的设备,这样会导致广播探测的回复产生大量的网络流量。
在某些情况下,网络流量可能会造成网络拥塞,并影响正常的网络通信。
此时,禁用广播探测的回复可以有效减少网络流量,提高网络的性能和稳定性。
另一种情况是在网络中存在安全隐患的情况下,禁用广播探测的回复可以增加网络的安全性。
广播探测的回复可以泄露网络上存在的设备,包括类型、版本等信息,这可能会被黑客用来进行网络攻击和入侵。
通过禁用广播探测的回复,可以减少黑客获取有关网络设备的信息的机会,从而提高网络的安全性。
为了禁用广播探测的回复,可以按照以下步骤进行操作:1. 登录到网络设备的管理界面。
这通常需要管理员账户和密码。
2. 寻找关于广播探测的配置选项。
这在不同的设备上可能有所不同,可以参考设备的用户手册或询问设备制造商的技术支持。
3. 在广播探测的配置选项中,找到相关的设置项。
可能会有一个名为"broadcast-probe reply"的选项。
4. 将该选项的值设置为"disable"。
有些设备可能使用其他关键字或选项来实现相同的功能,可以根据设备的文档或技术支持找到正确的设置。
5. 保存更改并重新启动网络设备。
在重新启动后,网络设备将禁止回复广播探测。
需要注意的是,禁用广播探测的回复可能会影响一些网络的功能和管理任务。
例如,一些网络管理工具可能依赖广播探测来识别设备并进行管理操作。
在禁用广播探测的回复之前,应该对网络进行细致的分析和评估,以确保禁用这个功能不会对网络的正常运行造成不利影响。
CISCO无线配置非法AP进行压制
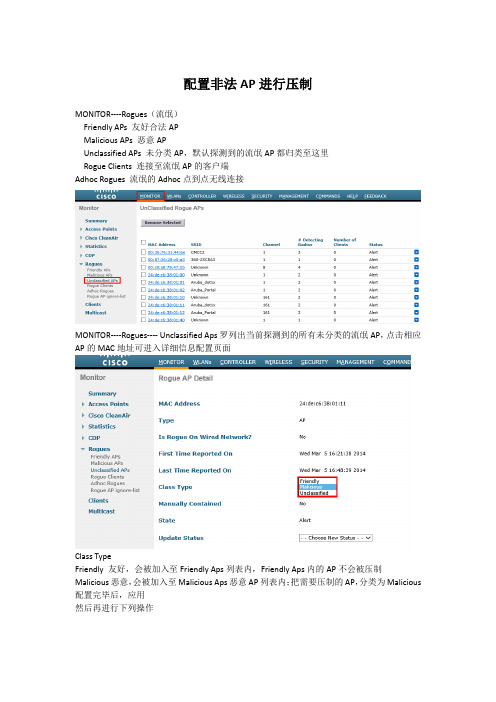
配置非法AP进行压制
MONITOR----Rogues(流氓)
Friendly APs 友好合法AP
Malicious APs 恶意AP
Unclassified APs 未分类AP,默认探测到的流氓AP都归类至这里
Rogue Clients 连接至流氓AP的客户端
Adhoc Rogues 流氓的Adhoc点到点无线连接
MONITOR----Rogues---- Unclassified Aps罗列出当前探测到的所有未分类的流氓AP,点击相应AP的MAC地址可进入详细信息配置页面
Class Type
Friendly 友好,会被加入至Friendly Aps列表内,Friendly Aps内的AP不会被压制Malicious恶意,会被加入至Malicious Aps恶意AP列表内;把需要压制的AP,分类为Malicious 配置完毕后,应用
然后再进行下列操作
Update Status 内选择Contain(压制),压制恶意AP的最大AP数(Maximum number of APs to contain the rogue)选择相应数量的AP后应用。
压制配置完毕后效果:
管理帧保护
在SECURITY----Wireless Protection Policies----AP Authentication Policy,此处可以配置管理帧保护Management Frame Protection,管理帧保护可以对Malicious APs分类下的恶意AP进行攻击。
宁盾Windows电脑无客户端AD域准入方案

受移动化影响,每时每刻,不同终端在企业内网与外网之间进进出出,这些终端是否是企业授权的?安全是否合规?由谁在使用?大部分企业仍采用以防火墙为中心的内外网安全防护,对终端身份及安全合规性处于模糊状态。
宁盾新一代终端准入(NAC)基于Forrest 的“Zero Trust Model”,不信任访问企业业务的任何终端,直到终端完成身份与终端合规性校验。
Windows终端作为企业最常用办公工具,宁盾提供Windows 无客户端AD域检测及Windows客户端检测两种检测方式。
常用方案如下:∙终端资产可视化;∙终端身份认证(网络身份认证或终端AD域无感知校验);∙Windows客户端合规性安全检测;∙终端准入控制示例:以“是否安装杀毒软件”为Windows电脑终端准入条件;∙第三方联动及软件推送;∙U盘管控;∙防私接;∙网络拓扑可视化;1、终端入网可视化宁盾新一代终端准入主动探测访问企业业务的一切IP终端的终端类型、操作系统、终端身份、终端合规性状态等,并通过直接或折叠的方式将终端展示于NAC控制中台,实现终端可视化管理。
更多折叠信息终端网络信息:MAC地址、IP地址、认证账号、域账号、终端类型、数据包、流量、首次入网时间、最后离网时间、网络来源;Linux电脑基础信息:终端类型、操作系统、功能及作用、CPU 占用率、剩余内存、总内存;终端安全信息:是否安装客户端、补丁版本是否更新、是否安装杀毒软件、病毒库是否过期、安装了那些应用、运行着那些应用等。
2、Windows终端AD域身份认证•设置AD域身份作为终端准入条件;•自动化检测入网终端是否加入AD域;•对合规终端执行Vlan116操作,同时非合规终端调控到其他Vlan网段;通过AD域终端检测,解决网络身份认证不能区分BYOD及企业派发设备的困惑,快速将BYOD隔离于企业外网。
3、Windows客户端合规性安全检测宁盾客户端(User Connector)提供32/64位客户端,用于检测是否安装客户端、补丁版本是否更新、是否安装杀毒软件、病毒库是否过期、安装了那些应用、运行着那些应用、CPU占用率、终端剩余内存等。
NAP_802.1X_StepByStep

微软公司 发布时间:2008.2
摘要
网络访问保护 (NAP) 是 Windows Vista、Windows Server 2008 和 Windows XP SP3 操作系统中 一项新的策略强制技术。NAP 提供了组件和应用程序接口(API)帮助管理员强制网络访问和通讯顺 从健康要求 。这篇文章包含介绍 NAP 和搭建一个测试环境部属 802.1x 强制模式 NAP。 实验要求 两台Байду номын сангаас务器和两个客户端,一台支持使用 RADIUS tunnel 属性指定 802.1x 客户端 VLAN 的 802.1x 交换机。在这个测试网络,你可以使用 NAP 和交换机 802.1x 特性创建和强制客户端健康要求。
版权信息
This document supports a preliminary release of a software product that may be changed substantially prior to final commercial release, and is the confidential and proprietary information of Microsoft Corporation. It is disclosed pursuant to a non-disclosure agreement between the recipient and Microsoft. This document is provided for informational purposes only and Microsoft makes no warranties, either express or implied, in this document. Information in this document, including URL and other Internet Web site references, is subject to change without notice. The entire risk of the use or the results from the use of this document remains with the user. Unless otherwise noted, the example companies, organizations, products, domain names, e-mail addresses, logos, people, places, and events depicted herein are fictitious, and no association with any real company, organization, product, domain name, e-mail address, logo, person, place, or event is intended or should be inferred. Complying with all applicable copyright laws is the responsibility of the user. Without limiting the rights under copyright, no part of this document may be reproduced, stored in or introduced into a retrieval system, or transmitted in any form or by any means (electronic, mechanical, photocopying, recording, or otherwise), or for any purpose, without the express written permission of Microsoft Corporation. Microsoft may have patents, patent applications, trademarks, copyrights, or other intellectual property rights covering subject matter in this document. Except as expressly provided in any written license agreement from Microsoft, the furnishing of this document does not give you any license to these patents, trademarks, copyrights, or other intellectual property. © 2008 Microsoft Corporation. All rights reserved. Microsoft, MS-DOS, Windows, Windows NT, and Windows Server are either registered trademarks or trademarks of Microsoft Corporation in the United States and/or other countries. All other trademarks are property of their respective owners.
Polar码在保密通信中的应用研究

Polar码在保密通信中的应用研究万丹丹【摘要】Polar码是一种能够达到香农限且编译码复杂度低的基于信道极化理论的信道编码方法.本文简单介绍了极化码在窃听信道中的构造方法.同时为非退化窃听模型,提出利用多次反馈来扩大等效主信道和窃听信道之间的差距,通过反馈实现非退化向退化的等效转变.仿真结果表明在二进制对称窃听信道下,所提出的基于多次反馈的传输方案误码率性能明显优于一次反馈,保证了信息可以更好地进行安全可靠地传输.【期刊名称】《微型机与应用》【年(卷),期】2016(035)005【总页数】4页(P8-11)【关键词】Polar码;窃听信道;误码率;多次反馈【作者】万丹丹【作者单位】浙江工业大学信息工程学院,浙江杭州310013【正文语种】中文【中图分类】TN198随着无线通信的广泛应用,其安全性能也受到人们越来越多的关注。
由于无线网络的多样性和太复杂的算法的出现使得加密技术很难实现。
目前,物理层安全性成为信息安全的一个重要分支,其一般以窃听信道为基础进行分析。
保密容量为其一个重要参数,被定义为当窃听者具有有关消息的最大不确定性时的最大系统传输速率。
信道编码技术是一种很好的确保窃听信道安全的方法。
Turbo码[1]和低密度奇偶校验码(Low Density Parity Check Codes,LDPC)[2]被相继提出,这两种码字性能接近香农限,但并没有达到香农限,而且复杂度较差。
2007 年,Erdal Arikan提出了一种新的编译码复杂度较低的线性分组码——Polar 码,并证明其性能在理论上能达到香农信道容量限[3]。
2010 年,E. Hof等人将Polar码应用在Wyner窃听信道中,从安全通信[4]的角度分析了Polar码。
1.1 polar码定义1:对于一个给定的二进制离散无记忆信道(Binary Discrete Memoryless Channel,BDMC),必然存在一组陪集码(N,K,A,uAc)满足不等式,其中N是码长,K是信息位的长度,A是一个序列集合,是[1,2,…,N]的子集,称为信息位集合,Ac是A的补集,称为固定位集合。
rfc2661.Layer Two Tunneling Protocol L2TP

Network Working Group W. Townsley Request for Comments: 2661 A. Valencia Category: Standards Track cisco Systems A. Rubens Ascend Communications G. Pall G. Zorn Microsoft Corporation B. Palter Redback Networks August 1999 Layer Two Tunneling Protocol "L2TP"Status of this MemoThis document specifies an Internet standards track protocol for the Internet community, and requests discussion and suggestions forimprovements. Please refer to the current edition of the "InternetOfficial Protocol Standards" (STD 1) for the standardization stateand status of this protocol. Distribution of this memo is unlimited.Copyright NoticeCopyright (C) The Internet Society (1999). All Rights Reserved.AbstractThis document describes the Layer Two Tunneling Protocol (L2TP). STD 51, RFC 1661 specifies multi-protocol access via PPP [RFC1661]. L2TP facilitates the tunneling of PPP packets across an interveningnetwork in a way that is as transparent as possible to both end-users and applications.Table of Contents1.0 Introduction (3)1.1 Specification of Requirements (4)1.2 Terminology (4)2.0 Topology (8)3.0 Protocol Overview (9)3.1 L2TP Header Format (9)3.2 Control Message Types (11)4.0 Control Message Attribute Value Pairs (12)4.1 AVP Format (13)4.2 Mandatory AVPs (14)4.3 Hiding of AVP Attribute Values (14)Townsley, et al. Standards Track [Page 1]4.4.1 AVPs Applicable To All Control Messages (17)4.4.2 Result and Error Codes (18)4.4.3 Control Connection Management AVPs (20)4.4.4 Call Management AVPs (27)4.4.5 Proxy LCP and Authentication AVPs (34)4.4.6 Call Status AVPs (39)5.0 Protocol Operation (41)5.1 Control Connection Establishment (41)5.1.1 Tunnel Authentication (42)5.2 Session Establishment (42)5.2.1 Incoming Call Establishment (42)5.2.2 Outgoing Call Establishment (43)5.3 Forwarding PPP Frames (43)5.4 Using Sequence Numbers on the Data Channel (44)5.5 Keepalive (Hello) (44)5.6 Session Teardown (45)5.7 Control Connection Teardown (45)5.8 Reliable Delivery of Control Messages (46)6.0 Control Connection Protocol Specification (48)6.1 Start-Control-Connection-Request (SCCRQ) (48)6.2 Start-Control-Connection-Reply (SCCRP) (48)6.3 Start-Control-Connection-Connected (SCCCN) (49)6.4 Stop-Control-Connection-Notification (StopCCN) (49)6.5 Hello (HELLO) (49)6.6 Incoming-Call-Request (ICRQ) (50)6.7 Incoming-Call-Reply (ICRP) (51)6.8 Incoming-Call-Connected (ICCN) (51)6.9 Outgoing-Call-Request (OCRQ) (52)6.10 Outgoing-Call-Reply (OCRP) (53)6.11 Outgoing-Call-Connected (OCCN) (53)6.12 Call-Disconnect-Notify (CDN) (53)6.13 WAN-Error-Notify (WEN) (54)6.14 Set-Link-Info (SLI) (54)7.0 Control Connection State Machines (54)7.1 Control Connection Protocol Operation (55)7.2 Control Connection States (56)7.2.1 Control Connection Establishment (56)7.3 Timing considerations (58)7.4 Incoming calls (58)7.4.1 LAC Incoming Call States (60)7.4.2 LNS Incoming Call States (62)7.5 Outgoing calls (63)7.5.1 LAC Outgoing Call States (64)7.5.2 LNS Outgoing Call States (66)7.6 Tunnel Disconnection (67)8.0 L2TP Over Specific Media (67)8.1 L2TP over UDP/IP (68)Townsley, et al. Standards Track [Page 2]9.0 Security Considerations (69)9.1 Tunnel Endpoint Security (70)9.2 Packet Level Security (70)9.3 End to End Security (70)9.4 L2TP and IPsec (71)9.5 Proxy PPP Authentication (71)10.0 IANA Considerations (71)10.1 AVP Attributes (71)10.2 Message Type AVP Values (72)10.3 Result Code AVP Values (72)10.3.1 Result Code Field Values (72)10.3.2 Error Code Field Values (72)10.4 Framing Capabilities & Bearer Capabilities (72)10.5 Proxy Authen Type AVP Values (72)10.6 AVP Header Bits (73)11.0 References (73)12.0 Acknowledgments (74)13.0 Authors’ Addresses (75)Appendix A: Control Channel Slow Start and CongestionAvoidance (76)Appendix B: Control Message Examples (77)Appendix C: Intellectual Property Notice (79)Full Copyright Statement (80)1.0 IntroductionPPP [RFC1661] defines an encapsulation mechanism for transportingmultiprotocol packets across layer 2 (L2) point-to-point links.Typically, a user obtains a L2 connection to a Network Access Server (NAS) using one of a number of techniques (e.g., dialup POTS, ISDN,ADSL, etc.) and then runs PPP over that connection. In such aconfiguration, the L2 termination point and PPP session endpointreside on the same physical device (i.e., the NAS).L2TP extends the PPP model by allowing the L2 and PPP endpoints toreside on different devices interconnected by a packet-switchednetwork. With L2TP, a user has an L2 connection to an accessconcentrator (e.g., modem bank, ADSL DSLAM, etc.), and theconcentrator then tunnels individual PPP frames to the NAS. Thisallows the actual processing of PPP packets to be divorced from thetermination of the L2 circuit.One obvious benefit of such a separation is that instead of requiring the L2 connection terminate at the NAS (which may require along-distance toll charge), the connection may terminate at a (local) circuit concentrator, which then extends the logical PPP session over Townsley, et al. Standards Track [Page 3]a shared infrastructure such as frame relay circuit or the Internet.From the user’s perspective, there is no functional difference between having the L2 circuit terminate in a NAS directly or using L2TP.L2TP may also solve the multilink hunt-group splitting problem.Multilink PPP [RFC1990] requires that all channels composing amultilink bundle be grouped at a single Network Access Server (NAS).Due to its ability to project a PPP session to a location other thanthe point at which it was physically received, L2TP can be used tomake all channels terminate at a single NAS. This allows multilinkoperation even when the calls are spread across distinct physicalNASs.This document defines the necessary control protocol for on-demandcreation of tunnels between two nodes and the accompanyingencapsulation for multiplexing multiple, tunneled PPP sessions.1.1 Specification of RequirementsThe key words "MUST", "MUST NOT", "REQUIRED", "SHALL", "SHALL NOT","SHOULD", "SHOULD NOT", "RECOMMENDED", "MAY", and "OPTIONAL" in thisdocument are to be interpreted as described in [RFC2119].1.2 TerminologyAnalog ChannelA circuit-switched communication path which is intended to carry3.1 kHz audio in each direction.Attribute Value Pair (AVP)The variable length concatenation of a unique Attribute(represented by an integer) and a Value containing the actualvalue identified by the attribute. Multiple AVPs make up ControlMessages which are used in the establishment, maintenance, andteardown of tunnels.CallA connection (or attempted connection) between a Remote System and LAC. For example, a telephone call through the PSTN. A Call(Incoming or Outgoing) which is successfully established between a Remote System and LAC results in a corresponding L2TP Sessionwithin a previously established Tunnel between the LAC and LNS.(See also: Session, Incoming Call, Outgoing Call).Townsley, et al. Standards Track [Page 4]Called NumberAn indication to the receiver of a call as to what telephonenumber the caller used to reach it.Calling NumberAn indication to the receiver of a call as to the telephone number of the caller.CHAPChallenge Handshake Authentication Protocol [RFC1994], a PPPcryptographic challenge/response authentication protocol in which the cleartext password is not passed over the line.Control ConnectionA control connection operates in-band over a tunnel to control the establishment, release, and maintenance of sessions and of thetunnel itself.Control MessagesControl messages are exchanged between LAC and LNS pairs,operating in-band within the tunnel protocol. Control messagesgovern aspects of the tunnel and sessions within the tunnel.Digital ChannelA circuit-switched communication path which is intended to carrydigital information in each direction.DSLAMDigital Subscriber Line (DSL) Access Module. A network device used in the deployment of DSL service. This is typically a concentrator of individual DSL lines located in a central office (CO) or local exchange.Incoming CallA Call received at an LAC to be tunneled to an LNS (see Call,Outgoing Call).Townsley, et al. Standards Track [Page 5]L2TP Access Concentrator (LAC)A node that acts as one side of an L2TP tunnel endpoint and is apeer to the L2TP Network Server (LNS). The LAC sits between anLNS and a remote system and forwards packets to and from each.Packets sent from the LAC to the LNS requires tunneling with theL2TP protocol as defined in this document. The connection fromthe LAC to the remote system is either local (see: Client LAC) or a PPP link.L2TP Network Server (LNS)A node that acts as one side of an L2TP tunnel endpoint and is apeer to the L2TP Access Concentrator (LAC). The LNS is thelogical termination point of a PPP session that is being tunneled from the remote system by the LAC.Management Domain (MD)A network or networks under the control of a singleadministration, policy or system. For example, an LNS’s Management Domain might be the corporate network it serves. An LAC’sManagement Domain might be the Internet Service Provider that owns and manages it.Network Access Server (NAS)A device providing local network access to users across a remoteaccess network such as the PSTN. An NAS may also serve as an LAC, LNS or both.Outgoing CallA Call placed by an LAC on behalf of an LNS (see Call, IncomingCall).PeerWhen used in context with L2TP, peer refers to either the LAC orLNS. An LAC’s Peer is an LNS and vice versa. When used in context with PPP, a peer is either side of the PPP connection.POTSPlain Old Telephone Service.Townsley, et al. Standards Track [Page 6]Remote SystemAn end-system or router attached to a remote access network (i.e.a PSTN), which is either the initiator or recipient of a call.Also referred to as a dial-up or virtual dial-up client.SessionL2TP is connection-oriented. The LNS and LAC maintain state foreach Call that is initiated or answered by an LAC. An L2TP Session is created between the LAC and LNS when an end-to-end PPPconnection is established between a Remote System and the LNS.Datagrams related to the PPP connection are sent over the Tunnelbetween the LAC and LNS. There is a one to one relationshipbetween established L2TP Sessions and their associated Calls. (See also: Call).TunnelA Tunnel exists between a LAC-LNS pair. The Tunnel consists of aControl Connection and zero or more L2TP Sessions. The Tunnelcarries encapsulated PPP datagrams and Control Messages betweenthe LAC and the LNS.Zero-Length Body (ZLB) MessageA control packet with only an L2TP header. ZLB messages are usedfor explicitly acknowledging packets on the reliable controlchannel.Townsley, et al. Standards Track [Page 7]2.0 TopologyThe following diagram depicts a typical L2TP scenario. The goal is to tunnel PPP frames between the Remote System or LAC Client and an LNS located at a Home LAN.[Home LAN][LAC Client]----------+ |____|_____ +--[Host]| | |[LAC]---------| Internet |-----[LNS]-----+| |__________| |_____|_____ :| || PSTN |[Remote]--| Cloud |[System] | | [Home LAN]|___________| || ______________ +---[Host]| | | |[LAC]-------| Frame Relay |---[LNS]-----+| or ATM Cloud | ||______________| :The Remote System initiates a PPP connection across the PSTN Cloud to an LAC. The LAC then tunnels the PPP connection across the Internet, Frame Relay, or ATM Cloud to an LNS whereby access to a Home LAN isobtained. The Remote System is provided addresses from the HOME LANvia PPP NCP negotiation. Authentication, Authorization and Accounting may be provided by the Home LAN’s Management Domain as if the userwere connected to a Network Access Server directly.A LAC Client (a Host which runs L2TP natively) may also participatein tunneling to the Home LAN without use of a separate LAC. In thiscase, the Host containing the LAC Client software already has aconnection to the public Internet. A "virtual" PPP connection is then created and the local L2TP LAC Client software creates a tunnel tothe LNS. As in the above case, Addressing, Authentication,Authorization and Accounting will be provided by the Home LAN’sManagement Domain.Townsley, et al. Standards Track [Page 8]3.0 Protocol OverviewL2TP utilizes two types of messages, control messages and datamessages. Control messages are used in the establishment, maintenance and clearing of tunnels and calls. Data messages are used toencapsulate PPP frames being carried over the tunnel. Controlmessages utilize a reliable Control Channel within L2TP to guarantee delivery (see section 5.1 for details). Data messages are notretransmitted when packet loss occurs.+-------------------+| PPP Frames |+-------------------+ +-----------------------+| L2TP Data Messages| | L2TP Control Messages |+-------------------+ +-----------------------+| L2TP Data Channel | | L2TP Control Channel || (unreliable) | | (reliable) |+------------------------------------------------+| Packet Transport (UDP, FR, ATM, etc.) |+------------------------------------------------+Figure 3.0 L2TP Protocol StructureFigure 3.0 depicts the relationship of PPP frames and ControlMessages over the L2TP Control and Data Channels. PPP Frames arepassed over an unreliable Data Channel encapsulated first by an L2TP header and then a Packet Transport such as UDP, Frame Relay, ATM,etc. Control messages are sent over a reliable L2TP Control Channelwhich transmits packets in-band over the same Packet Transport.Sequence numbers are required to be present in all control messagesand are used to provide reliable delivery on the Control Channel.Data Messages may use sequence numbers to reorder packets and detect lost packets.All values are placed into their respective fields and sent innetwork order (high order octets first).3.1 L2TP Header FormatL2TP packets for the control channel and data channel share a common header format. In each case where a field is optional, its space does not exist in the message if the field is marked not present. Notethat while optional on data messages, the Length, Ns, and Nr fieldsmarked as optional below, are required to be present on all controlmessages.Townsley, et al. Standards Track [Page 9]This header is formatted:0 1 2 30 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+|T|L|x|x|S|x|O|P|x|x|x|x| Ver | Length (opt) |+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+| Tunnel ID | Session ID |+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+| Ns (opt) | Nr (opt) |+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+| Offset Size (opt) | Offset pad... (opt)+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+Figure 3.1 L2TP Message HeaderThe Type (T) bit indicates the type of message. It is set to 0 for a data message and 1 for a control message.If the Length (L) bit is 1, the Length field is present. This bitMUST be set to 1 for control messages.The x bits are reserved for future extensions. All reserved bits MUST be set to 0 on outgoing messages and ignored on incoming messages.If the Sequence (S) bit is set to 1 the Ns and Nr fields are present. The S bit MUST be set to 1 for control messages.If the Offset (O) bit is 1, the Offset Size field is present. The Obit MUST be set to 0 (zero) for control messages.If the Priority (P) bit is 1, this data message should receivepreferential treatment in its local queuing and transmission. LCPecho requests used as a keepalive for the link, for instance, should generally be sent with this bit set to 1. Without it, a temporaryinterval of local congestion could result in interference withkeepalive messages and unnecessary loss of the link. This feature is only for use with data messages. The P bit MUST be set to 0 for allcontrol messages.Ver MUST be 2, indicating the version of the L2TP data message header described in this document. The value 1 is reserved to permitdetection of L2F [RFC2341] packets should they arrive intermixed with L2TP packets. Packets received with an unknown Ver field MUST bediscarded.The Length field indicates the total length of the message in octets. Townsley, et al. Standards Track [Page 10]Tunnel ID indicates the identifier for the control connection. L2TPtunnels are named by identifiers that have local significance only.That is, the same tunnel will be given different Tunnel IDs by eachend of the tunnel. Tunnel ID in each message is that of the intended recipient, not the sender. Tunnel IDs are selected and exchanged asAssigned Tunnel ID AVPs during the creation of a tunnel.Session ID indicates the identifier for a session within a tunnel.L2TP sessions are named by identifiers that have local significanceonly. That is, the same session will be given different Session IDsby each end of the session. Session ID in each message is that of the intended recipient, not the sender. Session IDs are selected andexchanged as Assigned Session ID AVPs during the creation of asession.Ns indicates the sequence number for this data or control message,beginning at zero and incrementing by one (modulo 2**16) for eachmessage sent. See Section 5.8 and 5.4 for more information on usingthis field.Nr indicates the sequence number expected in the next control message to be received. Thus, Nr is set to the Ns of the last in-ordermessage received plus one (modulo 2**16). In data messages, Nr isreserved and, if present (as indicated by the S-bit), MUST be ignored upon receipt. See section 5.8 for more information on using thisfield in control messages.The Offset Size field, if present, specifies the number of octetspast the L2TP header at which the payload data is expected to start. Actual data within the offset padding is undefined. If the offsetfield is present, the L2TP header ends after the last octet of theoffset padding.3.2 Control Message TypesThe Message Type AVP (see section 4.4.1) defines the specific type of control message being sent. Recall from section 3.1 that this is only for control messages, that is, messages with the T-bit set to 1. Townsley, et al. Standards Track [Page 11]This document defines the following control message types (seeSection 6.1 through 6.14 for details on the construction and use ofeach message):Control Connection Management0 (reserved)1 (SCCRQ) Start-Control-Connection-Request2 (SCCRP) Start-Control-Connection-Reply3 (SCCCN) Start-Control-Connection-Connected4 (StopCCN) Stop-Control-Connection-Notification5 (reserved)6 (HELLO) HelloCall Management7 (OCRQ) Outgoing-Call-Request8 (OCRP) Outgoing-Call-Reply9 (OCCN) Outgoing-Call-Connected10 (ICRQ) Incoming-Call-Request11 (ICRP) Incoming-Call-Reply12 (ICCN) Incoming-Call-Connected13 (reserved)14 (CDN) Call-Disconnect-NotifyError Reporting15 (WEN) WAN-Error-NotifyPPP Session Control16 (SLI) Set-Link-Info4.0 Control Message Attribute Value PairsTo maximize extensibility while still permitting interoperability, a uniform method for encoding message types and bodies is usedthroughout L2TP. This encoding will be termed AVP (Attribute-ValuePair) in the remainder of this document.Townsley, et al. Standards Track [Page 12]4.1 AVP FormatEach AVP is encoded as:0 1 2 30 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+|M|H| rsvd | Length | Vendor ID |+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+| Attribute Type | Attribute Value...+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+[until Length is reached]... |+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+The first six bits are a bit mask, describing the general attributes of the AVP.Two bits are defined in this document, the remaining are reserved for future extensions. Reserved bits MUST be set to 0. An AVP receivedwith a reserved bit set to 1 MUST be treated as an unrecognized AVP. Mandatory (M) bit: Controls the behavior required of animplementation which receives an AVP which it does not recognize. If the M bit is set on an unrecognized AVP within a message associatedwith a particular session, the session associated with this messageMUST be terminated. If the M bit is set on an unrecognized AVP within a message associated with the overall tunnel, the entire tunnel (and all sessions within) MUST be terminated. If the M bit is not set, an unrecognized AVP MUST be ignored. The control message must thencontinue to be processed as if the AVP had not been present.Hidden (H) bit: Identifies the hiding of data in the Attribute Value field of an AVP. This capability can be used to avoid the passing of sensitive data, such as user passwords, as cleartext in an AVP.Section 4.3 describes the procedure for performing AVP hiding.Length: Encodes the number of octets (including the Overall Lengthand bitmask fields) contained in this AVP. The Length may becalculated as 6 + the length of the Attribute Value field in octets. The field itself is 10 bits, permitting a maximum of 1023 octets ofdata in a single AVP. The minimum Length of an AVP is 6. If thelength is 6, then the Attribute Value field is absent.Vendor ID: The IANA assigned "SMI Network Management PrivateEnterprise Codes" [RFC1700] value. The value 0, corresponding toIETF adopted attribute values, is used for all AVPs defined withinthis document. Any vendor wishing to implement their own L2TPextensions can use their own Vendor ID along with private Attribute Townsley, et al. Standards Track [Page 13]values, guaranteeing that they will not collide with any othervendor’s extensions, nor with future IETF extensions. Note that there are 16 bits allocated for the Vendor ID, thus limiting this featureto the first 65,535 enterprises.Attribute Type: A 2 octet value with a unique interpretation acrossall AVPs defined under a given Vendor ID.Attribute Value: This is the actual value as indicated by the Vendor ID and Attribute Type. It follows immediately after the AttributeType field, and runs for the remaining octets indicated in the Length (i.e., Length minus 6 octets of header). This field is absent if the Length is 6.4.2 Mandatory AVPsReceipt of an unknown AVP that has the M-bit set is catastrophic tothe session or tunnel it is associated with. Thus, the M bit shouldonly be defined for AVPs which are absolutely crucial to properoperation of the session or tunnel. Further, in the case where theLAC or LNS receives an unknown AVP with the M-bit set and shuts down the session or tunnel accordingly, it is the full responsibility ofthe peer sending the Mandatory AVP to accept fault for causing annon-interoperable situation. Before defining an AVP with the M-bitset, particularly a vendor-specific AVP, be sure that this is theintended consequence.When an adequate alternative exists to use of the M-bit, it should be utilized. For example, rather than simply sending an AVP with the M- bit set to determine if a specific extension exists, availability may be identified by sending an AVP in a request message and expecting a corresponding AVP in a reply message.Use of the M-bit with new AVPs (those not defined in this document)MUST provide the ability to configure the associated feature off,such that the AVP is either not sent, or sent with the M-bit not set.4.3 Hiding of AVP Attribute ValuesThe H bit in the header of each AVP provides a mechanism to indicate to the receiving peer whether the contents of the AVP are hidden orpresent in cleartext. This feature can be used to hide sensitivecontrol message data such as user passwords or user IDs.The H bit MUST only be set if a shared secret exists between the LAC and LNS. The shared secret is the same secret that is used for tunnel authentication (see Section 5.1.1). If the H bit is set in any Townsley, et al. Standards Track [Page 14]AVP(s) in a given control message, a Random Vector AVP must also bepresent in the message and MUST precede the first AVP having an H bit of 1.Hiding an AVP value is done in several steps. The first step is totake the length and value fields of the original (cleartext) AVP and encode them into a Hidden AVP Subformat as follows:0 1 2 30 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+| Length of Original Value | Original Attribute Value ...+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+... | Padding ...+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+-+Length of Original Attribute Value: This is length of the OriginalAttribute Value to be obscured in octets. This is necessary todetermine the original length of the Attribute Value which is lostwhen the additional Padding is added.Original Attribute Value: Attribute Value that is to be obscured.Padding: Random additional octets used to obscure length of theAttribute Value that is being hidden.To mask the size of the data being hidden, the resulting subformatMAY be padded as shown above. Padding does NOT alter the value placed in the Length of Original Attribute Value field, but does alter thelength of the resultant AVP that is being created. For example, If an Attribute Value to be hidden is 4 octets in length, the unhidden AVP length would be 10 octets (6 + Attribute Value length). After hiding, the length of the AVP will become 6 + Attribute Value length + sizeof the Length of Original Attribute Value field + Padding. Thus, ifPadding is 12 octets, the AVP length will be 6 + 4 + 2 + 12 = 24octets.Next, An MD5 hash is performed on the concatenation of:+ the 2 octet Attribute number of the AVP+ the shared secret+ an arbitrary length random vectorThe value of the random vector used in this hash is passed in thevalue field of a Random Vector AVP. This Random Vector AVP must beplaced in the message by the sender before any hidden AVPs. The same random vector may be used for more than one hidden AVP in the same Townsley, et al. Standards Track [Page 15]message. If a different random vector is used for the hiding ofsubsequent AVPs then a new Random Vector AVP must be placed in thecommand message before the first AVP to which it applies.The MD5 hash value is then XORed with the first 16 octet (or less)segment of the Hidden AVP Subformat and placed in the Attribute Value field of the Hidden AVP. If the Hidden AVP Subformat is less than 16 octets, the Subformat is transformed as if the Attribute Value field had been padded to 16 octets before the XOR, but only the actualoctets present in the Subformat are modified, and the length of theAVP is not altered.If the Subformat is longer than 16 octets, a second one-way MD5 hash is calculated over a stream of octets consisting of the shared secret followed by the result of the first XOR. That hash is XORed with the second 16 octet (or less) segment of the Subformat and placed in the corresponding octets of the Value field of the Hidden AVP.If necessary, this operation is repeated, with the shared secret used along with each XOR result to generate the next hash to XOR the next segment of the value with.The hiding method was adapted from RFC 2138 [RFC2138] which was taken from the "Mixing in the Plaintext" section in the book "NetworkSecurity" by Kaufman, Perlman and Speciner [KPS]. A detailedexplanation of the method follows:Call the shared secret S, the Random Vector RV, and the AttributeValue AV. Break the value field into 16-octet chunks p1, p2, etc.with the last one padded at the end with random data to a 16-octetboundary. Call the ciphertext blocks c(1), c(2), etc. We will also define intermediate values b1, b2, etc.b1 = MD5(AV + S + RV) c(1) = p1 xor b1b2 = MD5(S + c(1)) c(2) = p2 xor b2. .. .. .bi = MD5(S + c(i-1)) c(i) = pi xor biThe String will contain c(1)+c(2)+...+c(i) where + denotesconcatenation.On receipt, the random vector is taken from the last Random VectorAVP encountered in the message prior to the AVP to be unhidden. The above process is then reversed to yield the original value.Townsley, et al. Standards Track [Page 16]。
netconf message framing error

netconf message framing error
“netconf message framing error”的意思是“网络配置消息帧错误”。
这种错误可能是由多种原因导致的,例如:
- 网络设备故障:设备可能存在硬件或软件问题,导致无法正确处理网络配置消息。
- 配置错误:网络配置可能存在语法错误或不符合网络设备的要求。
- 网络连接问题:网络连接可能由于网络拥塞、干扰或其他原因而不可靠,导致消息丢失或损坏。
为了解决这个问题,可以尝试以下方法:
- 检查网络设备的配置:确保配置正确且符合设备的要求。
- 检查网络连接:确保网络连接可靠,没有干扰或其他问题。
- 重启网络设备:有时重启设备可以解决临时性问题。
- 联系网络设备供应商:如果问题仍然存在,请联系设备供应商寻求技术支持。
如果你对“netconf message framing error”的解决方法还有其他疑问,可以继续向我提问。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Secure Network Coding on a WiretapNetworkNing Cai,Senior Member,IEEE,and Raymond W.Yeung,Fellow,IEEEAbstract—In the paradigm of network coding,the nodes in a network are allowed to encode the infor-mation received from the input links.With network coding,the full capacity of the network can be utilized. In this paper,we propose a model,call the wiretap network,that incorporates information security with network coding.In this model,a collection of subsets of the channels in the network is given,and a wiretapper is allowed to access any one(but not more than one) of these subsets without being able to obtain any information about the message transmitted.Our model includes secret sharing in classical cryptography as a special case.We present a construction of secure linear network codes that can be used provided a certain graph-theoretic condition is satisfied.We also prove the necessity of this condition for the special case that the wiretapper may choose to access any subset of channels of afixed size.The optimality of our code construction is established for this special case.Finally,we extend our results to the scenario when the wiretapper is allowed to obtain a controlled amount of information about the message.Index Terms—Algebraic coding,cryptography,mul-ticast,network coding,secret sharing,wiretap channel.I.I NTRODUCTIONThefirst information-theoretically secure commu-nication system,the so-called Shannon cipher sys-tem studied by Shannon in his celebrated paper[25], The work of N.Cai was partially supported by grants from the National Natural Science Foundation of China(Ref.No. 60832001and No.60672119).The work of R.W.Yeung was partially supported by a grant from the Research Grant Commit-tee(RGC Ref.No.CUHK2/06C)and a grant from the University Grants Committee(Project No.AoE/E-02/08)of the Hong Kong Special Administrative Region,China.N.Cai is with The State Key Lab.of ISN,Xidian Univer-sity,Xi’an,Shaanxi,710071,China.He was with Department of Information Engineering,The Chinese University of Hong Kong,N.T.,Hong Kong when this work was done.Email: caining@R.W.Yeung is with the Institute of Network Coding and De-partment of Information Engineering,The Chinese University of Hong Kong,N.T.,Hong Kong.Email:whyeung@.hk is formulated as follows.Suppose a sender wants to send the output of a random source message M with alphabet M={0,1,...,p−1}to a receiver.The sender can send information via a“public”channel, whose output can be accessed by the receiver as well as a wiretapper who tries to obtain some information about M,or the sender can send information via a“secure”channel,whose output can be accessed only by the receiver.The usual way to protect M from the wiretapper is that the sender generates a “secret key”K independent of the source message M according to the uniform distribution over M. Let m be the outcome of M,and let k be the outcome of K.Then the sender sends the key k to the receiver via the secure channel,and sends m+k (mod p)via the public channel.Upon receiving both k and m+k,the receiver as the legal user can recover m because m=(m+k)−k.On the other hand,the wiretapper cannot obtain any information about m by knowing m+k alone because what he/she knows is a total randomization of the message m.In other words,M and K are statistically independent.This notion of security is often referred to as information-theoretic security in the literature.In this work,we will refer to it as perfect security so as to distinguish from a few other notions of security to be discussed.The main idea in the above scheme is that the sender has to randomize the message in order to protect it from the wiretapper,where in this case the alphabets of the random key and of the information source have the same size(the two alphabets are the same).Shannon showed in[25]that this protocol is optimal in the sense of minimizing the size of the random key.This result,known as the perfect se-crecy theorem,has been generalized to the imperfect secrecy theorem by Yeung[27](p.116).In the above scheme,if another wiretapper ob-serves k but cannot observe m+k,he/she againcannot obtain any information about M.Thus the only thing we have to do for security is to ensure that an illegal user cannot obtain the outputs of both the public and the secure channels.This observation tells us that there is logically no difference between the public channel and the secure channel.The Shannon cipher system can be regarded as a secure code defined for the simple network in Fig.1with two nodes,a source and a sink nodes,connected by two channels,such that a wiretapper can obtain no information about the“secure message”M by accessing any single channel.Based on this obser-vation,in the conference version of the current paper [5],we proposed a model for secure network coding called the wiretap network.A wiretap network con-sists of a communication network and a collection of subsets of wiretap channels in the network.A network code is secure for a wiretap network if a wiretapper can obtain no information about the secure message by accessing any wiretap subset, while all the sink nodes in the network as legal users can decode the secure message with zero error. In particular,a wiretap network is called an r-WN (WN stands for“wiretap network”)if the collection of wiretap subsets are all subsets of channels with cardinalities not larger than r.A network code is r-secure if it is secure for an r-WN.That is,for an r-secure network code,a wiretapper can obtain no information about the secure message by accessing any r channels.The Shannon cipher system is the simplest1-secure network code.Obviously,for the existence of r-secure network codes,it is necessary that r is strictly smaller than the value of maximumflow from the source node to every sink node,because otherwise a wiretapper accessing all the channels at a minimum cut be-tween the source node and a sink node would have all the information received by the sink node and therefore can correctly decode the secure message. This reveals the fact that for security,a legal user must know more than an illegal one.Another well-known model of a cipher system is the secret sharing model proposed independently by Blakley[3]and Shamir[24](see also Ozarow and Wyner’s wire-tap channel II[22],a special case of secret sharing).This model subsumes the Shannon cipher system.We will show in Section II that our model subsumes secret sharing and in fact,the threshold secret sharing scheme is a special r-secure network code.One of the main results in[5]was a construc-tion of linear secure network codes,which will be presented in Section III.In the construction,we use a special matrix to transform a non-secure linear network code into a secure network code.The opti-mality of this construction(discussed in Section IV) was presented in[30].Subsequent to[5],Feldman et al.[11]pointed out that the condition required for the special matrix is equivalent to a Hamming distance property of a certain type of codes.They also derived a tradeoff between the size of the message set M and the size of the transmission alphabet F.In[10],El Rouayheb and Soljanin presented a construction of secure network codes by using secure codes for wiretap channel II[22]. Theyfirst encode the source message by a secure code based on an MDS code for a wiretap channel II and then send the resulting codeword by a linear network code through the network.They derived a secure condition for the described coding schemes and accordingly proposed a code construction.Their bound on the alphabet size for the construction is smaller than ours.Moreover,they showed that their construction is actually equivalent to ours. Bhattad and Narayanan[2]introduced weakly secure network coding,where security is defined as wiretappers not being able to decode any part of source messages correctly.They showed that one can use a weakly secure network code without trading off the throughput.The r-secure linear network code was strength-ened to the strongly r-secure linear network code by Harada and Yamamoto[14].For a strongly r-secure network code,a wiretapper can obtain no information about any s components of the source message by accessing n−s channels provided that the maximumflows to all the sink nodes are at least n,where s≤n−r.They presented a polynomial-time algorithm to construct strongly secure linear network codes.They pointed out that strong security in fact contains weak security in[2] as a special case.In[4],Cai showed that a random linear network code[15]is strongly secure with high probablity,provided that the order of codingfield is sufficiently large.In a recent paper by Ngai et al.[20],the gener-alized Hamming weight for linear error correction codes,introduced by Wei[26],was generalized to linear network codes.They called it the network generalized Hamming weight and studied its basic ing these properties,they obtained a complete a characterization of the security perfor-mance of a linear block code when it is used in conjunction with a given linear network code.The model of wiretap network was extended to multiple sources by the authors[6],where the randomness for protecting the source messages can be generated at a set of nodes instead of one node.A necessary and sufficient condition for the security of a linear network code was derived by the authors in this work for the case that all the source messages have positive probability and then by Zhang and Yeung[32]for the general case.Perhaps the most general model of multi-source secure network coding was due to Chan and Grant [8].They considered the case of multiple sources and multiple wiretappers.Each wiretapper is inter-ested in a particular subset of the source messages and can access an arbitrary subset of channels in his/her own collection of wiretap subsets.Again the security they considered is perfect security,i.e., a wiretapper can obtain no information about the messages he/she is interested in.They obtained a lower bound and an upper bound on the capacity region in term ofΓ∗,the region of all entropy functions[28].In the sequel,we will refer to the model as the general wiretap network.There have been several alternative models for secure network coding.Among them,Jain[17]fo-cused on the relation between security and network topology.In their model,there is a single source node and a single sink node in the network,and all the nodes may generate randomness to help the secure transmission.They asked when messages can be transmitted with perfect security and did not consider the cost incurred.A necessary and suffi-ciently condition was derived.The tradeoff between security and the cost of network coding was studied by Tan and M´e dard[23].In their model,with certain probability,each channel may be accessed by a wiretapper and the wiretapper is interested in the messages from a subset of sources.Their criterion of security is the probability for the wiretapper to be able to decode the message of interest correctly.They proposed two heuristic solutions and com-pared their performances with traditional routing by simulation.Their results showed that coding may be more effective for both reducing the cost and increasing the security.In the above literature, security is measured by information quantities(mu-tual information or entropy)or decoding probability, whereas Lima et al.[19]proposed an algebraic secure criterion.They considered the security of random linear network codes and assume that all intermediate nodes are potentially wiretappers who completely comply with the communication proto-cols in random coding but want to decode the source message transmitted over the network.To measure security they used the number of symbols that an intermediate node has to guess in order to be able to decode one of the transmitted symbols in terms of the rank of the partial global encoding matrix.With this security measure,they analyzed the security of random linear network codes over complete directed acyclic graphs.Network coding for error correction was studied by[29],[7],where the fundamental coding bounds were obtained.Secure network coding with error correction was studied by Ngai and Yeung[21].In this work,they presented a construction of secure error-correcting(SEC)network codes that can pro-tect the source message from wiretapping,random errors,and errors injected by the wiretapper.They also proved the optimality of their construction.In the next section,we present our model of a wiretap network and define a secure network code, which in our terminology is called an admissible code.The difference between our model and some other models are explained in two examples.In Section3,wefirst construct a class of linear codes based on the work of Li et al.[18]on linear net-work coding.Then we present a sufficient condition for the construction to be admissible.The proof of the sufficiency of this condition is deferred to Section5.In Section4,we prove the optimality of our construction in Section3for r-secure network codes.In Section6,we extend our results to the scenario when the wiretapper is allowed to obtain a controlled amount of information about the message. The paper is concluded in Section7.II.C OMMUNICATION S YSTEM ON A W IRETAPN ETWORKIn this section,wefirst present our model of the wiretap network.Then we define secure or admissible network codes for a wiretap network.A wiretap network consists of the following com-ponents:1)Directed multigraph G:The pair G=(V,E) is called a directed multigraph1,where V and E are the node set and the edge set of G,respectively.In our model,we assume that G is acyclic,i.e.,it does not contain a directed cycle.2)Source node s:The node set V contains a node s,called the source node,where a random message M taking values in an alphabet M is generated. 3)Set of user nodes U:A user node is a node in V which is fully accessed by a legal user who is required to receive the random message M with zero error.There is generally more than one user node in a network.The set of user nodes is denoted by U.4)Collection of sets of wiretap edges A:A is a collection of subsets of the edge set E.Each member of A may be fully accessed by a wiretapper,but no wiretapper may access more than one member of A. We refer to the quadruple(G,s,U,A)as a wiretap network.We also refer to the multigraph G as a network and the edges in E as channels.The random message M is generated at the source node s according to an arbitrary distribution on an alphabet M,called the message set.On each channel in E,an index taken from an alphabet F called the transmission alphabet can be transmitted.We are interested in the maximum value of|M|for which the message M can be multicast from the source node s to the set of user nodes U while being protected from a wiretapper who can access any set of channels in A.The system has been extended to multiple sources and multiple wiretapper in[8],where each wire-tapper is interested in the messages from a subset of the multiple sources and has his/her own col-lection of wiretap subsets.In other words,different wiretappers may be interested in different subsets 1In a multigraph,there can be more than one edge from one node to another node.of the sources and may have different collections of wiretap subsets.The current work is a generalization of the work by Ahlswede et al.[1]and Li et al.[18]on network coding.In the paradigm of network coding,the nodes in a communication network are allowed to encode the information received from the input links before it is transmitted on the output links. The advantage of network coding is that it can utilize the full capacity of a network for multicasting information.In the model we study in the current paper,in the absence of a wiretapper,i.e.,A=∅,the wiretap network is reduced to the model studied in[1]and [18].It was proved in[1]that information can be multicast from the source node s to all the user nodes in U at rateτif and only if the value of a maximumflow from s to each user node is at leastτin the graph G.In general,information can be multicast from the source node to the user nodes at a higher rate with network coding than without network coding when there are at least two user nodes(see the example in[1],called the butterfly network).Subsequently,it was proved in[18]by an explicit construction that this can be achieved by linear network codes.For a comprehensive treatment of network coding,we refer the reader to[28].As we have discussed earlier,it is necessary to randomize the message in order to protect it from the wiretapper.This can be explained as follows.If there is no randomness in the network,the index transmitted on any channel is a function of the message M and hence is not independent of M unless the index takes a constant value.If this is the case,the channel becomes degenerate as it transmits no useful information.Thus for a wiretap network, without randomness,a wiretapper would be able to obtain some knowledge about the source message by accessing any single“non-degenerate”channel. Introducing randomness in the network to protect the source message inevitably reduces the through-put because additional bandwidth is needed to trans-mit different randomized versions of the source message.Note that our secure criterion is that the wiretappers may obtain absolutely no information about the whole source message.In the case of the general wiretap network in[8]where there are multiple sources and multiple wiretappers interestedin different subsets of the sources,or in the case that the secure criterion is relaxed,it is not always necessary to reduce the throughput for security.This will be shown in Example2at end of the section. Butfirst let us define an admissible code for a wiretap network.Let K be an independent random variable,called the key,that takes values in an alphabet K according to the uniform distribution.To facilitate our discus-sion,we denote the sets of input and output channels of a given node a∈V by In(a)and Out(a), respectively.A code for a wiretap network consists of a set of local encoding mappings{φe:e∈E} such that for all e,φe is a function from M×K to F if e∈Out(s),and is a function from F|In(t)| to F if e∈Out(t)for t=s.For e∈E,let Y e be the random symbol in F transmitted on channel e, i.e.,the value ofφe.For a subset B of E,denote (Y e:e∈B)by Y B.To complete the description of a code,we have to specify the order in which the channels send the indices,called the encoding order.Since the graph G is acyclic,it defines a partial order on the node set V.Then the nodes in V can be indexed in a way such that for two nodes t and t ,if there is a channel from node t to node t ,then t<t .According to this indexing,node t sends indices in its output channels before node t if and only if t<t .The order in which the channels within the set of output channels of a node send the indices is immaterial.The important point here is that whenever a channel sends an index,all the indices necessary for encoding have already been received.A code defined as such induces a function Φu from M×K to F|In(u)|for all user nodes u∈U, where the value ofΦu denotes the indices received by the user node u in its input channels.A code{φe:e∈E}is admissible for a wiretap network(G,s,U,A)if the following conditions are satisfied:1)For all user nodes u∈U and all m,m ∈M with m=m ,Φu(m,k)=Φu(m ,k )for all k,k ∈K,where k,and k may or may not be the same.This guarantees that any two messages are distinguishable at every user node because the formula ensures that for every user node u∈U,there exist no k,k ∈K,be they the same or different,that can produce from two different messages m and m the same set of indices at the input channels of the user node u.This is referred to as the decodable condition.2)For all A∈AH(M|Y A)=H(M).Here H(·|·)and H(·)denote conditional entropy and entropy,respectively.In other words,M and Y A are independent.This is referred to as the secure condition.We call a wiretap network an r-WN if A is the collection of all subsets of channels with cardinal-ities not exceeding r.An admissible code for an r-WN is called an r-secure network code.For an r-secure network code,a wiretapper can obtain abso-lutely no information about the source messages by accessing any r channels in the network.Obviously, the Shannon cipher system is a1-secure network code for the network with a source node s and a user u and two parallel channels from s to u.In a secret sharing scheme,a random secret message M taken from afinite set M is shared among n participants in[n]:={1,2,...,n}in such a way that only the so-called qualified subsets of[n] are able to reconstruct M,whereas any other subsets of[n]should know absolutely nothing about M.To share the secret M,a dealer with full access to the secret source sends a random“share”Y i to every participant i∈[n]according to the value m of the secret message M.A basic problem in secret sharing is(*)at most how many bits of secret can be shared if each participant i receives at mostr i bits of share,where the non-negativereal vector(r1,r2,...,r n)is given.We can easily see that this is equivalent to asking whether there exists an admissible code for the wire-tap network to be described in the next paragraph, and an admissible code for this particular wiretap network is exactly a secret sharing scheme.In this sense,secure network coding contains secret sharing as a special case.Let a secret sharing scheme be given.Denote by Q the collection of qualified subsets in[n]and let Q0be its minimal sets(i.e.,Q∈Q0if andonly if Q∈Q and no other subset of Q is in Q).We now construct a wiretap network which has three layers of nodes:top,middle,and bottom. The only node on the top layer is the source node s and it corresponds to the dealer in the secret sharing scheme.There are n intermediate nodes on the middle layer,each of them corresponding to a participant in the secret sharing scheme.For every i∈[n],the source node s is connected to the intermediate node i by a channel(s,i)with capacity r i.There are|Q0|user nodes labelled by Q0on the bottom layer.An intermediate node i is connected to a user node Q∈Q0if and only if i∈Q. Finally,the collection of wiretap subsets is defined as A={{(s,i),i∈A}:A∈2[n]\Q},where 2[n]is the power set of[n].Obviously,for the given secret sharing scheme,the network code sending the random share Y i to the intermediate node i for all i∈[n]is admissible,because each user node on the bottom layer can decode the secret message by virtue of the secret sharing scheme.On the other hand,an admissible code for the network defines a secret sharing scheme.An(r,n)-threshold secret sharing scheme[3][24], where r≤n,is a secret sharing scheme such that any r of the n participants can correctly recover the secret message but any r−1or less participants can have no information about the secret message.Then obviously an(r,n)-threshold secret sharing scheme is equivalent to an(r−1)-secure network code for the network described in the last paragraph.As in general the problem(*)is extremely hard,tofind optimal admissible codes for an arbitrary wiretap network is a very difficult problem.Example1(Secret Sharing):Consider the wire-tap network shown in Fig.1withU={u1,u2,u3}andA={{(s,a1)},{(s,a2)},{(s,a3)}}.This wiretap network represents the(2,3)-threshold secret sharing scheme.In the definition of our admissible code,we use perfect security as the secure condition.To achieve this level of security,however,a relatively high price needs to be paid in terms of the throughput as well as the amount of randomness used in theFig.1.A wiretap network representing the(2,3)-threshold secret sharing scheme.Fig.2.An example of an admissible code for a wiretap network. scheme.As such,some weaker secure conditions have been proposed.The following example gives a comparison between perfect secrecy and these secure conditions.Example2:Consider the wiretap network shown in the Fig.2withU={u1,u2}andA={{e}:e∈E}.That is,the wiretap network is obtained by addinga collection A of subsets of wiretap channels to the well-known butterfly network in[1],where the wiretapper can access any single channel in the network.To simplify our discussion,we assume that the source message M is generated according to the uniform distribution on M.In the wiretap network, there are exactly two disjoint paths from the source node s to each of the user nodes u1and u2.For each A∈A,which contains exactly one channel,there is one path that starts at the source node s and has that channel in A as the last channel on the path. Such a path will be called a path from the source node s to A.For example,(s,a1),(a1,a0),(a0,b)is a path from the source node s to A={(a0,b)}. We now describe a linear network code for this wiretap network over GF(3).Let M be a ternary source taking values in GF(3).At the source node s,an independent random key K is also generated according to the uniform distribution on GF(3). Denote the values taken by M and K by m1and k1, respectively.Then Figure2shows a linear network code on the wiretap network.It is easy to check that such a code satisfies the decodable condition and the secure condition,and is therefore admissible.In fact, as we will see,the existence of such an admissible code is guaranteed by Theorem3.Weak security introduced by Bhattad and Narayanan[2]is defined as that a wiretapper can-not decode any component of the source message correctly.It was shown that there is no extra cost for weak security provided that the codingfield is sufficiently large and that the wiretapper is not allowed to obtain all the information received by any single user.This can be done over GF(q)with q≥4in the butterfly network as follows.Let M=(M1,M2)be generated at the source node s,where M1and M2are two independent random symbols taking values in GF(q)according to the uniform distribution.Denote by m i the value of M i,i=1,2.Letα0,α1,andα2be three distinct non-zero elements in GF(q).The source node s sends m1+α1m2to u1and a0through a1,and sends m2+α2m2to u2and a0through a2.Upon receiving m1+α1m2and m1+α2m2,a0then sends m1+α0m2to u1and u2through b.Obviously, the code is weakly secure if the wiretapper cannot access any two channels transmitting linearly inde-pendent information simultaneously.In this scheme, the number of symbols that can be sent to the users is equal to the maximumflow from the source node to the each of the user node,so that there is no sacrifice in throughput.Also,no randomness is needed for protecting the message.Let us again assume that a wiretapper can assess at most one channel in the butterfly network.Then the same code is also secure for the following general wiretap network[8].In this general wiretap network,we assume that M1and M2are generated from different sources,and two wiretappers,who are able to access any single channel,are interested in M1and M2,respectively.Then the code in last para-graph is secure for this general wiretap network.To see this,we note that H(M1|Y)=H(M1)=log q for the random output Y of any single channel. Thus for this general wiretap network,the required security can be achieved at no extra cost.The reason is quite clear,because M2serves as the “randomness”to protect M1,and vice versa.The same phenomenon can also be found in the analysis of the strongly r-secure code in[4].However,for this network code,we have I(M1;M2|Y)=log q>0.This yields that a wire-tapper interested in the whole message(M1,M2) can gain log q bits of information upon accessing any single channel if we use mutual information as the security measure.Following[27,Example 6.15],we call this imperfect secrecy.We will see in Section VI that this is indeed the best possible security that can be achieved if one does not pay extra for security.Recall that the original linear code on the but-terfly network in[1]is over GF(2).Here we let M=(M1,M2)be two independent random bits taking values in GF(2)according to the uniform distribution.In their coding scheme,the source node s sends m1to u1and a0through a1,and sends m2to u2and a0through a2.Upon receiving m1 and m2,a0sends m1+m2to u1and u2through b.Lima et al.in[19]partitioned V\{s,u1,u2} into three subsets,V0={b},V1={a1,a2},and V2={a0},and observed that a node in V i is able to decode exactly i bit(s)in m=(m1,m2).Thus from the wiretapper’s point of view,node a0is the best node and node b is the worst node to access in。
