波动(4)-网上
网络波动的概念

网络波动的概念网络波动是指网络延迟和带宽的变化,即网络连接的不稳定性和不一致性。
在一个稳定的网络环境中,网络的延迟和带宽都是相对固定和可预测的。
但是,在现实生活中,网络波动是普遍存在的,它可能受到多种因素的影响,包括网络拥塞、网络故障、网络设备性能等。
网络波动主要表现为网络延迟的变化。
网络延迟是指从数据包发送端发送数据到数据包到达接收端之间所需的时间。
网络延迟越低,数据传输的速度越快,网络的响应时间也较短。
当网络延迟发生波动时,意味着数据包的传输时间不一致,可能会导致当数据包到达接收端时出现延迟,从而影响到网络的稳定性和性能。
网络波动还包括带宽的波动。
带宽是指单位时间内从网络中传输的数据量。
当网络带宽较高时,网络可以同时传输更多的数据,数据传输的速度也更快。
而当网络带宽波动时,网络的数据传输能力会随之变化,传输速度也会发生变化。
这种带宽波动可能是由于网络拥塞、带宽限制等原因引起的,影响到数据的传输效率和网络的可靠性。
网络波动对网络连接的影响是多方面的。
首先,网络波动会导致网络的稳定性下降。
当网络延迟发生波动时,用户在访问网页、发送消息等操作时可能会遇到卡顿现象,用户体验也会受到影响。
其次,网络波动还会影响到实时应用的性能,如在线游戏、视频通话等。
如果网络延迟和带宽发生波动,会导致游戏画面卡顿、语音和视频传输出现延迟等问题,严重影响到用户体验。
此外,对于一些对网络连接有较高要求的应用,如金融交易、医疗影像传输等,如果网络波动发生,可能会导致数据传输的错误和不完整,从而对数据的安全和完整性产生风险。
造成网络波动的原因有很多。
首先,网络拥塞是导致网络波动的常见原因之一。
当网络中的数据量过大,超过网络的处理能力时,会导致网络的拥塞,从而引起网络延迟和带宽波动。
其次,网络故障也是网络波动的原因之一。
例如,网络设备的硬件故障、网络线路的故障等都可能导致网络的不稳定性和波动。
此外,网络设备的运行性能也会对网络波动产生影响。
高中物理奥林匹克竞赛专题---波动

一、波动中的几个概念
波面
1.波线
波的传播方向为波线。 波线
波 前
2.波面
振动相位相同的各点 组成的曲面。
平面波 波面
3.波前
波线
波
前
某一时刻波动所达到最前
方的各点所连成的曲面。
球面波
二、惠更斯原理
1.介质中波动到的各点,都可看成发射子 波的子波源(点波源)。
2.任意时刻这些子波的包络面就是新的波 前。
三.相干波条件
1.两列波振动方向相同; 2.两列波频率相同; 3.两列波有稳定的相位差。
加 强
减 弱
四.加强减弱条件 两列波
为同方向同频率振动合成。合成后振幅为
1.加强条件
当
时,波程差为
当波程差为波长的整数倍时加强。
2.减弱条件
当
时,波程差为
当波程差为半波长的奇数倍时减弱。
例:两相干波源 A、B 位置如图所示,频率
②.该点与波源的相位差; ③.该波的振幅、频率、波长。 解: ①.由波函数
单位:焦耳/秒,瓦,J•s-1, 与功率相同
2.平均能流密度----波强 单位时间内通过垂直于波的传播方向
的单位面积上的平均能量。
单位:J•s-1•m-2 , W •m-2
例:一球面波源的功率为 100W,则距波 源 10m 处,波的平均能流密度 I 是多少? 解:
(W •m-2 )
§5 惠更斯原理
第2章 波 动 §1 机械波的产生与传播 §2波动周期、频率、波长、波速 §3平面简谐波的波函数 §4波的能量 §5惠更斯原理 §6波的干涉 §7 驻波 §8 多普勒效应
§1 机械波的产生与传播
一、机械波 机械振动在弹性介质中传播形成机械波。
《波动》答案

第5章 波动一、选择题1(C),2(A),3(A),4(D),5(C),6(D),7(D),8(D),9(D),10(A) 二、填空题 (1).(2). ]/2cos[1φ+π=T t A y ,2cos[2(//)]y A t T x λφ=++π (3). 11cos[(/)/4]y A t L u ω=-+π,12()L L uω+(4). 4 (5). 2122/R R (6).2Sw ωλπ(7). 相同,2/3(8). cos[2(/)]A t x νλ++ππ,112cos(2/)cos(2)22A x t λν++ππππ (9). 5 J (10). Hz , Hz 三、计算题1. 如图,一平面波在介质中以波速u = 20 m/s 沿x 轴负方向传播,已知A 点的振动方程为 t y π⨯=-4cos 1032 (SI).(1) 以A 点为坐标原点写出波的表达式;(2) 以距A 点5 m 处的B 点为坐标原点,写出波的表达式.解:(1) 坐标为x 点的振动相位为 )]/([4u x t t +π=+φω)]/([4u x t +π=)]20/([4x t +π= 波的表达式为 )]20/([4cos 1032x t y +π⨯=- (SI)(2) 以B 点为坐标原点,则坐标为x 点的振动相位为 ]205[4-+π='+x t t φω (SI) ABxu波的表达式为 ])20(4cos[1032π-+π⨯=-xt y (SI)2. 如图所示,一平面简谐波沿Ox 轴的负方向传播,波速大小为u ,若P 处介质质点的振动方程为 )cos(φω+=t A y P ,求 (1) O 处质点的振动方程; (2) 该波的波动表达式;(3) 与P 处质点振动状态相同的那些点的位置.解:(1) O 处质点的振动方程为 ])(cos[0φω++=u Lt A y (2) 波动表达式为 ])(cos[φω+++=u Lx t A y(3) x = -L kωuπ2 ( k = 1,2,3,…)3. 如图所示,一简谐波向x 轴正向传播,波速u = 500 m/s ,x 0 = 1 m, P 点的振动方程为 )21500cos(03.0π-π=t y (SI).(1) 按图所示坐标系,写出相应的波的表达式; (2) 在图上画出t = 0时刻的波形曲线.解:(1) 2m )250/500(/===νλu m波的表达式 ]/2)1(21500cos[03.0),(λπ--π-π=x t t x y]2/2)1(21500cos[03.0π--π-π=x t)21500cos(03.0x t π-π+π= (SI)(2) t = 0时刻的波形曲线 x x x y π=π-π=sin 03.0)21cos(03.0)0,( (SI)OL ux (m)u x 0Py (m)Ox (m)uP O-2-112-0.030.034. 一微波探测器位于湖岸水面以上 m 处,一发射波长21 cm 的单色微波的射电星从地平线上缓慢升起,探测器将相继指出信号强度的极大值和极小值.当接收到第一个极大值时,射电星位于湖面以上什么角度解:如图,P 为探测器,射电星直接发射到P 点的波①与经过湖面反射有相位突变的波②在P 点相干叠加,波程差为 λ∆21+-'=DP P O 22cos sin sin λθθθ+-=h h = k = (取k = 1)θλθsin 21)2cos 1(=-h∵ θθ2sin 212cos -= ∴ λθ21sin 2=h==)4/(sin h λθ = 6°5. 设入射波的表达式为 )(2cos 1TtxA y +π=λ,在x = 0处发生反射,反射点为一固定端.设反射时无能量损失,求(1) 反射波的表达式;(2) 合成的驻波的表达式; (3) 波腹和波节的位置.解:(1) 反射点是固定端,所以反射有相位突变,且反射波振幅为A ,因此反 射波的表达式为 ])//(2cos[2π+-π=T t x A y λ(2) 驻波的表达式是 21y y y += )21/2cos()21/2cos(2π-ππ+π=T t x A λ (3) 波腹位置: π=π+πn x 21/2λ, P D hO ′θθ2θ①②λ)21(21-=n x , n = 1, 2, 3, 4,… 波节位置: π+π=π+π2121/2n x λ λn x 21=, n = 1, 2, 3, 4,…6. 一弦上的驻波表达式为 t x y ππ⨯=-550cos )6.1(cos 1000.32(SI).(1) 若将此驻波看作传播方向相反的两列波叠加而成,求两波的振幅及波速; (2) 求相邻波节之间的距离; (3) 求t = t 0 = ×10-3s 时,位于x = x 0 = m 处质点的振动速度.解:(1) 将 t x y ππ⨯=-550cos 6.1cos 1000.32与驻波表达式 )2cos()/2cos(2t x A y νλππ= 相对比可知: A = ×10-2m, = m , = 275 Hz 波速 u == m/s(2) 相邻波节点之间距离 λ21=∆x = m (3) 2.4600,-=∂∂=t yt x v m/s7. 如图7所示,一平面简谐波沿x 轴正方向传播,BC 为波密媒质的反射面.波由P 点反射,OP = 3 /4,DP = 6.在t = 0时,O 处质点的合振动是经过平衡位置向负方向运动.求D 点处入射波与反射波的合振动方程.(设入射波和反射波的振幅皆为A ,频率为.)解:选O 点为坐标原点,设入射波表达式为 ])/(2cos[1φλν+-π=x t A y 则反射波的表达式是 ])(2cos[2π++-+-π=φλνxDP OP t A y合成波表达式(驻波)为 )2cos()/2cos(2φνλ+ππ=t x A yOP B Cx入射反射D 图7在t = 0时,x = 0处的质点y 0 = 0, 0)/(0<∂∂t y , 故得 π=21φ 因此,D 点处的合成振动方程是)22cos()6/4/32cos(2π+π-π=t A y νλλλt A νπ=2sin 38. 一弦线的左端系于音叉的一臂的A 点上,右端固定在B 点,并用T = N 的水平拉力将弦线拉直,音叉在垂直于弦线长度的方向上作每秒50次的简谐振动(如图).这样,在弦线上产生了入射波和反射波,并形成了驻波.弦的线密度 = g/m ,弦线上的质点离开其平衡位置的最大位移为4 cm .在t = 0时,O 点处的质点经过其平衡位置向下运动,O 、B 之间的距离为L = m .试求: (1) 入射波和反射波的表达式; (2) 驻波的表达式.解:按题意,弦线上行波的频率= 50 Hz ,波速u = (T/)1/2= 60 m/s ,波长= u /= m. 取O 点为x 轴和y 轴的原点.x 轴向右,y 轴向上.令入射波在B 点的初相为π-21B φ,则其表达式为 ]2)(22cos[1π-+-π-π=B L x t A y φλν ① B 点为固定点,则反射波的表达式为 ]2)(22cos[2π++-π+π=B L x t A y φλν ② 弦线上驻波表式为 21y y y +=]2cos[]2)(2cos[2B t L x A φνλ+ππ+-π= ③ 据此,O 点振动方程为 ]2cos[]22cos[20B t L A y φνλ+ππ+π-= 由4/7/=λL 有 )2cos(20B vt A y φ+π-=)2cos(2π-+π=B vt A φ ④由③式可知弦线上质点的最大位移为2A ,即 2A = 4 cmBAO L再由题给条件可得④式中 π=π-21B φ, 即 π=23B φ 由此可得:入射波: ]26.0100cos[100.221π+π-π⨯=-x t y (SI) 反射波: ]26.0100cos[100.222π+π+π⨯=-x t y (SI) 驻波: )2100cos(6.0cos100.42π+ππ⨯=-t x y (SI)9.一声源S 的振动频率为S= 1000 Hz ,相对于空气以v S = 30 m/s的速度向右运动,如图.在其运动方向的前方有一反射面M ,它相对于空气以v = 60 m/s 的速度向左运动.假设声波在空气中的传播速度为u = 330 m/s ,求:(1) 在声源S 右方空气中S 发射的声波的波长; (2) 每秒钟到达反射面的波的数目; (3) 反射波的波长.解:(1) 设一接收器R 静止于空气中,声源S 以v S 速率接近接收器R ,则由多普勒效应公式可知,R 接收到的声波频率 1100100030330330=⨯-=-=S S u u ννv Hz 则 ==νλ/u 330/1100 = 0.30 m(2) 每秒钟到达反射面处波的数目在数值上等于反射面处接收到的波的频率ν'.由多普勒效应公式有: 130010003033060330=⨯-+=-+='S S u u ννv v Hz (3) 接收器接收到反射面的反射波的频率νν'-=vu uR 反射波的波长 21.0130060330=-='-==ννλv u u R R mS v SvM四研讨题1. 波传播时,介质的质元并不随波迁移。
连续介质中的波动现象

连续介质中的波动现象波动现象是自然界中普遍存在的一种物理现象,它在连续介质中表现出多样化的形式和特征。
无论是声波、水波还是光波,它们都是通过介质的振动传播而产生的。
本文将从连续介质中波动的性质、波动的传播速度以及波动的应用等方面进行探讨。
一、连续介质中波动的性质连续介质中的波动具有一些共同的性质。
首先,波动是通过介质的振动传播的,介质中的粒子在波动作用下做周期性的振动。
其次,波动具有传播的性质,波动能够沿着介质传播并传递能量。
此外,波动还具有波长、频率、振幅等基本特征。
波长是波动的周期性重复单位,频率是单位时间内波动的周期数,振幅则表示波动的最大偏离程度。
二、波动的传播速度波动的传播速度是波动现象的一个重要特征,它与介质的性质有关。
在同一介质中,不同类型的波动具有不同的传播速度。
以声波为例,声波在空气中的传播速度约为343米/秒,而在水中的传播速度则约为1482米/秒。
这是因为不同介质中的分子间相互作用力不同,导致波动传播速度的差异。
三、波动的应用波动现象在生活中有着广泛的应用。
首先,声波的传播使我们能够进行语言交流。
人们通过声波的传播,借助声音进行交流和沟通。
其次,水波的波动现象被广泛应用于水上运动和海洋工程等领域。
水波的起伏和波动性质使得冲浪、帆船比赛等运动成为可能。
此外,光波的波动性质被广泛应用于光学领域。
光波的折射、反射等现象使得我们能够使用镜子、眼镜等光学器件。
四、波动现象的研究与发展波动现象的研究对于物理学的发展具有重要意义。
通过对波动现象的研究,人们能够更好地理解自然界的规律,并将其应用于实际生活中。
例如,声波的研究使得医学中的超声波成像技术得以发展,为医生提供了更准确的诊断手段。
此外,波动现象的研究还为科学家们提供了探索宇宙的工具。
例如,天文学家利用电磁波的特性来观测远离地球的天体,探索宇宙的奥秘。
总结起来,连续介质中的波动现象是一种普遍存在且具有多样性的物理现象。
波动的性质、传播速度以及应用都是人们研究和探索的重要方向。
大学物理(第四版)课后习题及答案-波动
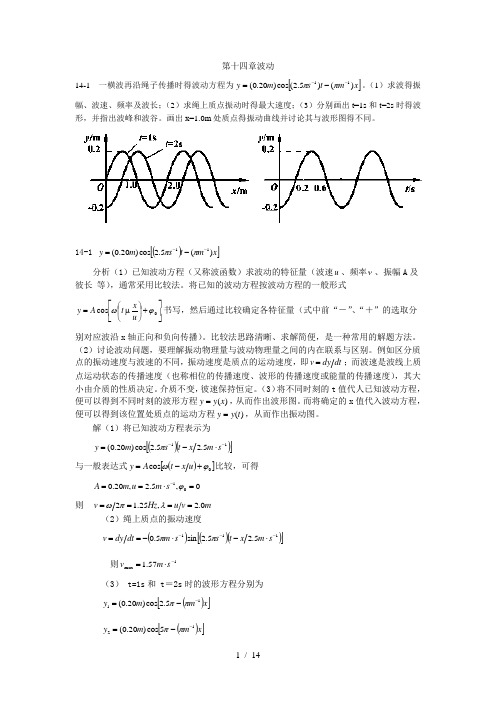
第十四章波动14-1 一横波再沿绳子传播时得波动方程为[]x m t s m y )()5.2(cos )20.0(11---=ππ。
(1)求波得振幅、波速、频率及波长;(2)求绳上质点振动时得最大速度;(3)分别画出t=1s 和t=2s 时得波形,并指出波峰和波谷。
画出x=1.0m 处质点得振动曲线并讨论其与波形图得不同。
14-1 ()[]x m t s m y )(5.2cos )20.0(11---=ππ分析(1)已知波动方程(又称波函数)求波动的特征量(波速u 、频率ν、振幅A 及彼长 等),通常采用比较法。
将已知的波动方程按波动方程的一般形式⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛=0cos ϕωu x t A y μ书写,然后通过比较确定各特征量(式中前“-”、“+”的选取分别对应波沿x 轴正向和负向传播)。
比较法思路清晰、求解简便,是一种常用的解题方法。
(2)讨论波动问题,要理解振动物理量与波动物理量之间的内在联系与区别。
例如区分质点的振动速度与波速的不同,振动速度是质点的运动速度,即dt dy v =;而波速是波线上质点运动状态的传播速度(也称相位的传播速度、波形的传播速度或能量的传播速度),其大小由介质的性质决定。
介质不变,彼速保持恒定。
(3)将不同时刻的t 值代人已知波动方程,便可以得到不同时刻的波形方程)(x y y =,从而作出波形图。
而将确定的x 值代入波动方程,便可以得到该位置处质点的运动方程)(t y y =,从而作出振动图。
解(1)将已知波动方程表示为()()[]115.25.2cos )20.0(--⋅-=s m x t s m y π 与一般表达式()[]0cos ϕω+-=u x t A y 比较,可得0,5.2,20.001=⋅==-ϕs m u m A则 m v u Hz v 0.2,25.12====λπω(2)绳上质点的振动速度()()()[]1115.25.2sin 5.0---⋅-⋅-==s m x t s s m dt dy v ππ 则1max 57.1-⋅=s m v(3) t=1s 和 t =2s 时的波形方程分别为()[]x m m y 115.2cos )20.0(--=ππ()[]x m m y 125cos )20.0(--=ππ波形图如图14-1(a )所示。
资本魔方—《波动四法》讲座图例节选(共7页)

波动四法?讲座图例节选节选?金股博弈?第二章第二小节的局部内容二、“道理〞与“是非〞的思维突破道理在证券公司门口约是非一会儿到他那里去,因此是非回到自己的大户室简单地浏览了一遍当天?证券报?中比拟重要的消息之后,就向道理那里走去。
推开门,看到道理居然没在。
“这小子,约了我自己却不在。
〞是非一边发着牢骚,一遍做到道理的电脑前,想看看行情。
没有想到电脑正在进行数据计算。
是非刚想走,道理急冲冲地抱着两本书回来了。
是非看到道理回来了,成心拉下脸来,没有搭理道理。
道理知道是非误会了,赶忙解释:“对不起,对不起,刚刚不是说要给你讲一讲我参加的个函授培训吗?我想让你也看看函授资料,这不,急忙回了趟家拿回来了。
〞“原来是给我拿资料去了。
〞是非明白了道理不在的原因,不满的情绪也就烟消云散了。
“你说说,到底是什么函授技术资料让你这么着迷。
〞道理指着那两本书说道:“这里面讲的也是怎么看K线,与我的研究方向一致,但这是我第一次知道还有这么看K线,这么理解K线的技术方法,或者说这种方法已经超越了技术的范畴,它不但是技术与心理的结合体,还是与多种学科的结合体。
〞是非:“瞧你说的,简直神了。
〞道理:“不是神,是这些方法不由得你不信服啊。
〞道理利用整整一个上午的时间,将?五域论湛?函授培训班所讲到的内容给是非讲述了一遍。
由此道理和是非对股市操作又有了一番新的认识。
是非:“?五域论湛?中的方法是以大盘为参照物,寻找强势股票的方法,这个方法结合了?心理学?、?统计学?、?哲学?、?历史?、?政治?等方面的内容,可以说是我所见到的技术方法中涉及面最全面的。
〞道理:“都说炒股要成为杂家,就是政治、经济、逻辑等等都要精通,一时间可是难坏了股民,一个人怎么可能什么都精通呢?不过通过培训班的方法,可是将这些方面都结合在了一起。
〞是非:“是啊!我看到?五域论湛?培训主要讲到的是怎样在弱势中找到强势股票,然后在大盘强势以后怎样介入这些股票的系统方法,现在大盘从今年4月见顶,已经跌了半年多了,我们看看有那些股票符合?五域论湛?的标准,也好找到几只大牛股及时介入赚它一笔。
波动热的名词解释

波动热的名词解释在现代社会中,一个词汇的诞生往往意味着一种新兴事物的存在。
而波动热(Flaming Hot)就是其中之一。
作为一个相对较新的词汇,波动热在互联网和社交媒体上广泛流行,并迅速成为各种话题、趋势和营销策略的重要元素。
波动热通常用来形容一种热度或盛行程度迅速上升的状态,像火焰一样燃烧、蔓延。
它由“波动”和“热”两个词汇组成,波动表示变化、起伏或流动,而热则暗示着一种热情、热烈或火爆的意象。
将两者结合在一起,波动热给人以充满活力和热情的感觉。
波动热一词最初源于社交媒体平台,通过迅速蔓延的社交分享和互联网用户之间的相互关联,形成了话题、事件或事物的关注热潮。
这种热潮可以涵盖各个领域,从流行文化到时尚、体育、科技乃至政治,几乎无所不包。
波动热的特点之一就是具有迅速兴起和短暂持续的特征,一段时间之后人们的关注往往会逐渐转移至其他新的热点。
波动热的产生和传播通常离不开互联网和社交媒体的推动。
当一个事件或话题在社交媒体上迅速引起人们的关注和讨论时,信息会迅速扩散,吸引更多的用户参与其中,从而形成热潮。
这种现象往往是由人们的好奇心、社交需求和信息获取的渴望所驱动的。
波动热的兴起对于品牌营销和产品推广来说具有重要的意义。
众多品牌和公司都意识到,通过抓住波动热的机会,可以在短时间内获得大规模的曝光和传播,从而提升品牌影响力和销售量。
因此,许多品牌经常与波动热相关的话题进行联动,通过制作相关的广告、活动或创意内容来吸引消费者的关注。
然而,波动热的持久效应并不总是可靠的。
当一个话题或事件的热度过去后,注意力往往会转向其他新的事物。
这对于那些只专注于追逐潮流的品牌来说是一个挑战,因为他们需要不断创新和跟进,以保持与消费者的互动。
然而,尽管波动热的热潮往往是短暂的,它们在一段时间内提供了一个独特的社交背景和文化共鸣。
波动热可以促进人们之间的交流和讨论,加强社区感和归属感。
它们还能激发人们的创造力和想象力,推动创新和变革。
复习振动第四节波动的基本规律第五节波的能量和波的衰减.ppt
2 ( 2 ) T
u
波动方程的物理意义:
给定x=x0时,
给定t=t0时,
m V 给定点振动方程
给定时刻波形曲线
* 当t 、x 都变化时,
描写任意时刻波线上任意点位移情况。
第五节
一、波的能量
波的能量与波的衰减
介质中各质点在各自平 衡位置附近振动动能 介质间相互作用产生弹性 形变势能
1 2 1 22 2 x E V E VA sin [ ( t )] p 2 2 u
二
能量密度
(energy density)
单位体积介质中的波动能量——能量密度w : 22
I
1
能量密度的平均值: ——平均能量密度
dx
能流密度(波的强度):垂直通过单位截面积的平均能流。
( W·m –2 ) 单位:瓦·米2
三 波的衰减 波的衰减:机械波在介质中传播时,强度(或振幅) 随传播距离的增加而减弱(小)。 导致波衰减的主要原因:
①扩散衰减:
②散射衰减:
由于波面扩大造成单位截面积通过的 波的能量减少。
由于散射使沿原方向传播的波的强度减弱。
③介质对波的吸收: 由于介质的粘滞性(内摩擦)等原 因,波的能量随传播距离的增加逐渐转化 为其他形式的能量。
平面简谐波在各个向同性的介质中传播的 衰减规律 平面简谐波沿x 轴正向传播,经厚度为dx 一层介质后, 强度衰减了-dI :
I0(x 0处的强度 )
两边积分得:
I
μ——介质的吸收系数
(由波的频率与介质性 质决定)。
I0
dIIdx
o
dI
I I0ex
扩散衰减 Variation of intensity of a spherical wave with distance: r2 * Sound from a point source A2 spreads out in all directions.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
与波源的频率 ν s 间的关系 R
17
一、相对地面,媒质、波源和观察者都不动的情况 US = 0,UR = 0
νR =ν =
u
λ
=ν
s
18
二、相对于地面,媒质和波源不动,接受器靠近/ 媒质和 远离波源运动
ν = νS
US= 0
νs
uR uR uR
R向S靠近时 (uR > 0)
接受器: 波在媒质中的速度 增加”,波长不变:
反
0
x
入射波方程 y 入 ( x , t ) = A cos[( ω t + 2π
x
λ
)±π]
12
练习 在固定端x = 0处,反射波方程: 反 = A cos 2π (νt − y
无能量损失,求入射波波动方 程、驻波方程、腹点、节点 x y 解: ( x , t ) = A cos( ω t − 2π λ )
−2
练习 在固定端x = 0处,反射波方程: 反 = A cos 2π (νt − ) y λ ψ 无能量损失,求入射波波动方程 入 Φ x 1 解: o x 反 y ( x , t ) = A cos( ω t − 2π ) λ 方 法 入射简谐波 y 入 ( x , t ) = A cos( ω t + 2π x + c ] c < 2π λ 1 Φ2 x ∆Φ = Φ 2 − Φ 1 = 4 π +c λ 在x=0处为一波节,即相干相消: ∆Φ = c = ( 2 k + 1)π
1 1
1 2
1
2
2
2
y 1 ( r1 , t ) = A1 cos( ω t −
2 2 2
2 π r1
方 y ( r , t ) = A cos(ω t − +ϕ ) 法 λ 2 S 1 <=> S 2 驻波 r1 = r r2 = l − r
20
λ 2πr2
+ ϕ 10 )
y1
S1 r
r 1
P
l
y2
λ = 12m; A = 0.2m; T = 2S → ω = π
解:
ϕ = π/2
0.2 0 1 2
u= λ/T=6m/s A点的振动方程
t
y (t)=0.2cos(π t+π/2) (SI) 入射波的波动方程 y(x,t)=0.2cos[π (t - x/6) + π/2]
A
m
8
沿x正方向传播
练习
*三个频率的定义: 波源的频率 ν s 是单位时间内波源振动的次数或 或发出的‘完整波’的个数; 观察者接受到的频率 νR 是观察者在单位时间内 接收到的振动次数或完整的波数; 波的频率ν是媒质质元在单位时间内振动的次数 或单位时间内通过媒质质元的完整波的个数。
媒质 ν =
u
波的频率ν 是桥梁
λ
寻找观察者接收到的频率ν
1
1
y 1 ( r , t ) = A1 cos( ω t −
2 2
2π r
+ ϕ 10 )
20
y1
y2
S2
2
1
S1 P
1
1
1
10
2
S2 P
2
2
2
20
y(t) = y1 + y2 = A cos( ω t + ϕ )
0
由P点任意性 略去角标 P
r1 = r
; r2 = l − r
2π
y( x, t ) = (
入
驻波 方程
y( x, t ) = y入 + y反 = 2 A cos( 2π x + π ) cos(ωt + π )
λ
2 2 13
腹点:2π
x
λ
x
+
π
2
= kπBiblioteka x=λ2k−
λ
4
k = 1,2,3 ⋅ ⋅ ⋅
节点: 2π
λ
+
π
2
= ( 2k + 1)
π
2
x=
λ
2
k
k = 0,1,2 ⋅ ⋅ ⋅
0,
P OP 1 1 1
波动 方程
y + (t ) = A1 cos(ωt − 2π
x
+ ϕ1 )
S1
Pl
S2
x
yP (t) = y1 + y2 = A cos( ω t + ϕ )
0
由P点任意性 略去角标 P
0≤ x≤l
4π
y( x, t ) = (
A1 + A1 + 2 A1 A1 cos(ϕ2 − ϕ1 +
如果波源和观察者的运动不是沿它们连线方向(纵 向),则以上公式中US,UR 应理解为波源和观察者 21 在它们连线方向上的速度分量(即纵向分量)。
一、驻波的特点
上次课教学内容复习
1. 振幅 合成各点振动周期相同,但各点振幅不同。
波幅振幅最大,波节振幅最小. 相邻两个波腹和波节之间的距离都是λ/2。
2.振幅 相邻的波节之间相位相同;波节的两侧相位相反。 相位: 3. 能量: 能量在波腹和波节之间转换。驻波进行中没有
能量的定向传播,总能流密度为零。
四、相对于地面,媒质不动, 观察者和波源同 时相对于媒质运动 此情况下, νS ≠ ν ≠ νR
由于波源相对于媒质运动,媒质中波的频率为
u ν = νs u − us
由于观察者相对于媒质运动,观察者接收到的频率与媒 质中波的频率关系为
注意:
u + uR νR = ν u
u + uR νR = νs u − us
0
a d
u
b c (b) 行波 d
c (a) 驻波
x
x
6
ψ
解:
a b c (a) 驻波 d
ψ
a b c (b)
u
d 行波
0
x
0
x
(1) 对于驻波a,b,c,d 点 此时的运动速度为零.
a b
对于行波a,b,c,d 点此 时的运动方向如图。
(2) 对于驻波 Φ − Φ = 0 相邻的两波节之间 x 对于行波 Φ( x, t ) = (ωt − 2π + ϕ ) λ
节
λ
4
腹
,
λ
2
节
,
3λ , 4
腹
λ ⋅⋅⋅
节
14
本次课教学重点和难点 重点
掌握多普勒效应 *了解电磁波的多普勒效应 *了解电磁波的多普勒效应 难点
多普勒公式的应用
u + uR νR = νs u − us
15
多普勒效应
到的频率与波源的频率不同,这种现象称为多普勒效应。 一.机械波的(纵向)多普勒效应 参照系:媒质( 如:相对地面静止的媒质-空气)
多普勒效应: 当波源,接收者相对于媒质运动时,接收者接收
*三个对象:波源,接收者,媒质
设S和R的运动沿二者连线上
S
*三个速度的定义:
·
υS
·
υR
R
u为波在相对地面静止的媒质中传播的速度
us ; u R
分别为波源S和接收者R相对地面/媒质的运动速度
速度符 u始终为正; 号规定 S 和R 相互靠近时,us ; uR 皆为正;反之为负 16
反
x
ψ
λ
)
入
o
反
x
反射波引起o点的振动方程:y 0 ( t ) = A cos ω t 入射波引起o点的振动方程: ( t ) = A cos( ω t + π ) y
0
入射波 y ( x , t ) = A cos[ ω (t + x ) + π ] = A cos[( ω t + 2π x ) + π ] λ u 方程
y
0
u
u
√ x
y
0
u x u
5
练习
已知一驻波在t时刻各点振动到最大位移处其 波形图如(a)所示;有一平面简谐行波,沿x正方 向传播,图(b)所示为该行波t 时刻的波形图. (1) 试分别在两图上注明a,b,c,d 四点此时的运动 速度方向(设横波). (2) 求两种情况下ϕa-- ϕb.
ψ
a
0
ψ
b
在弦线上有一简谐波,其表达式 Φ1 4π x −2 y1 ( x, t ) = 2 × 10 cos[100π (t + ) − ] 20 3
为了在此弦线上形成驻波,并且在x=0处为一波节, 求此弦线上另一简谐波的其表达式。
解: 弦线上另一简谐波的表达式 x 4π −2 y 2 ( x , t ) = 2 × 10 cos[ 100 π ( t − ± π ] 错! )− 3 20 x −2 y 2 ( x , t ) = 2 × 10 cos[ 100 π ( t − ) + c ] c < 2π 20 Φ2 4 ∆Φ = Φ 2 − Φ 1 = c + π − 10 π x 3 在x=0处 为一波节,即相干相消: 4π π 5π 9 = ( 2 k + 1)π → c = − ; ∆Φ = c+ 3 3 3
“频率增加了”
u + uR
接收者接收到的频率与源发出的频率关系:
λ=
u + uR = u + uR ν = ν s u u
u
ν
νR =
u + uR
λ
当观察者(接收者)远离波源运动时: uR为负值
19
