五年级奥数精品讲义 第8讲逻辑推理(有精讲,有分层精炼)
苏教版小学五年级奥数— 逻辑推理图文百度文库

苏教版小学五年级奥数—逻辑推理图文百度文库一、拓展提优试题1.(7分)爱尔兰作家刘易斯曾写过一篇反讽寓言,文中描述了一个名为尼亚特泊的野蛮国家.在这个国家里使用西巴巴数字.西巴巴数字的形状与通用的阿拉伯数字相同,但含义相反.如“0”表示“9”,“1”表示“8”,以次类推.他们写数字是从左到右,使用的运算符号也与我们使用的一样.例如,他们用62代表我们所写的37.按照尼亚特泊人的习惯,应怎样写837+742的和是419.【分析】“0”表示“9”,0+9=9,“1”表示“8”,1+8=9,由此可知西巴巴数字,表示的数字与正常数字的和都是9;由此找出837、742表示的数字,然后相加即可.2.(7分)后羿朝三个箭靶分别射了三支箭,如图:他在第一个箭靶上得了29分,第二个箭靶上得了43分.请问他在第三个箭靶上得了分.3.如图,从A到B,有条不同的路线.(不能重复经过同一个点)4.用长是5厘米、宽是4厘米、高是3厘米的长方体木块叠成一个正方体,至少需要这种长方体木块块.5.已知一个五位回文数等于45与一个四位回文数的乘积(即=45×),那么这个五位回文数最大的可能值是59895.6.甲、乙两人进行射击比赛,约定每中一发得20分,脱靶一发扣12分,两人各打10分,共得208分,最后甲比乙多得64分,乙打中发.7.(8分)有四个人甲、乙、丙、丁,乙欠甲1元,丙欠乙2元,丁欠丙3元,甲欠丁4元.要想把他们之间的欠款结清,只因要甲拿出元.8.三位偶数A、B、C、D、E满足A<B<C<D<E,若A+B+C+D+E=4306,则A最小.9.两个数的最大公约数和最小公倍数分别是3和135,求这两个数的差最小是.10.如图,魔术师在一个转盘上的16个位置写下来了1﹣16共16个数,四名观众甲、乙、丙、丁参与魔术表演.魔术师闭上眼,然后甲从转盘中选一个数,乙、丙、丁按照顺时针方向依次选取下一个数,图示是一种可能的选取方式,魔术师睁开眼,说:“选到偶数的观众请举手.”,这时候,只有甲和丁举手,这时候魔术师就大喝一声:“我知道你们选的数了!”.你认为甲和丁选的数的乘积是.11.大于0的自然数n是3的倍数,3n是5的倍数,则n的最小值是.12.定义新运算:θa=,则(θ3)+(θ5)+(θ7)(+θ9)+(θ11)的计算结果化成最简真分数后,分子与分母的和是.13.如图六角星的6个顶点恰好是一个正六边形的6个顶点,那么阴影部分面积是空白部分面积的倍.14.如图是一个正方体的平面展开图,若该正方体相对的两个面上的数值相等,则a﹣b×c的值是.15.(7分)对于a、b,定义运算“@”为:a@b=(a+5)×b,若x@1.3=11.05,则x=.【参考答案】一、拓展提优试题1.解:西巴巴数字8表示阿拉伯数字9﹣8=1,西巴巴数字3表示阿拉伯数字9﹣3=6,西巴巴数字7表示阿拉伯数字9﹣7=2,西巴巴数字4表示阿拉伯数字9﹣4=5,西巴巴数字2表示阿拉伯数字9﹣2=7,所以837+742表示的正常算式为:162+257=419.故答案为:419.2.【分析】这个箭靶共三个环,设最小的环为a分,中间环为b分,最外环为c分,得:第一个靶得分为:2b+c=29①第二个靶得分为:2a+c=43②第三个靶得分为:a+b+c③通过等量代换,解决问题.解:设最小的环为a分,中间环为b分,最外环为c分,得:第一个靶得分为:2b+c=29①第二个靶得分为:2a+c=43②第三个靶得分为:a+b+c③由①+②得:2a+2b+2c=29+43=72即a+b+c=36即第三个靶的得分为36分.答:他在第三个箭靶上得了36分故答案为:36.3.解:如图,因为,从A到B有5条直连线路,每条直连线路均有5种不同的路线可以到达B点,所以,共有不同线路:5×5=25(条),答:从A到B,有25条不同的路线,故答案为:25.4.解:正方体的棱长应是5,4,3的最小公倍数,5,4,3的最小公倍数是60;所以,至少需要这种长方体木块:(60×60×60)÷(5×4×3),=216000÷60,=3600(块);答:至少需要这种长方体木3600块.故答案为:3600.5.解:根据分析,得知,=45=5×9既能被5整除,又能被9整除,故a的最大值为5,b=9,45被59□95整除,则□=8,五位数最大为59895故答案为:598956.解:假设全打中,乙得了:(208﹣64)÷2=72(分),乙脱靶:(20×10﹣72)÷(20+12),=128÷32,=4(发);打中:10﹣4=6(发);答:乙打中6发.故答案为:6.7.解:根据分析,从甲开始,乙欠甲1元,故甲应得1元,甲欠丁4元,故甲应还4元;清算时,甲还应拿出4﹣1=3元,此时甲的账就结清了;再看看丁的账,丁得到甲的4元后,还给丙3元,即可结清;再看看丙的账,丙得到丁的3元后,还给乙2元,丙的账也清了;再看看乙的账,乙得到丙的2元后,还给甲1元,乙的账也结清;综上,甲只须先拿出4元还给丁,后得到乙的1元,故而甲总共只须拿出3元.故答案是:3.8.解:最大的三位偶数是998,要满足A最小且A<B<C<D<E,则E最大是998,D最大是996,C最大是994,B最大是992,4306﹣(998+996+994+992)=4306﹣3980=326,所以此时A最小是326.故答案为:326.9.解:因为135÷3=45,45分解成两个互质的数有两种情况即1和45、9与5,所以差最小的是:9和5,所以这两个数分别是:9×3=275×3=1527﹣15=12答:这两个数的差最小是12.故答案为:12.10.解:依题意可知:2个偶数中间间隔是2个奇数.发现只有数字10,11,9,12是符合条件的数字.乘积为10×12=120.故答案为:12011.解:3n是5的倍数,3n的个数一定是0或5又因为大于0的自然数n是3的倍数,所以3n最小是453n=45n=15所以n最小取15时,n是3的倍数,3n是5的倍数.答:n的最小值是15.故答案为:15.12.解:原式=++++=++++=×(﹣+﹣+…+﹣)=×()=5+24=29故答案为:2913.解:根据分析,如图所示,将图进行分割成面积相等的三角形,阴影部分由18个小三角形组成,而空白部分有6个小三角形,故阴影部分面积是空白部分面积的18÷6=3倍.故答案是:3.14.解:依题意可知:3a+2与17是对立面,3a+2=17,所以a=5;7b﹣4与10是对立面,7b﹣4=10,所以b=2;a+3b﹣2c与11的对立面,5+3×2﹣2c=11,所以c=0;所以a﹣b×c=5故答案为:515.解:由定义可知:x@1.3=11.05,(x+5)1.3=11.05,x+5=8.5,x=8.5﹣5=3.5故答案为:3.5。
小学奥数微课 逻辑推理8.22

例1
典例精析
周一清晨,梅子老师走进
教室,发现坏桌凳全修好了。 门卫告诉她:这是她班的四个 住校学生中的某一人所做。
审查揭秘
审查 结果
许兵:桌凳不是我修的. 李平:桌凳是张明修的. 刘成:桌凳是李平修的. 张明:我没有修过桌凳.
四个人中,只有一个 人说的是真话,我想 知道这桌凳究竟是谁 修的?
据“两个互相否定的思想不能同真” 假设李说的是真话,则张是假话 又根据条件:只有1人说的是真话 这样,由许说的可推出:
练习2
“我肯定考得 最好”
“我没有A考 得好,但也不是 最差的”
“我不会是最差 某次考试考完后, 的” A,B,C,D四
个同学猜测他们
的考试成绩.
D说:“可能我
考得最差”
成绩公布,只有一个人说错了,请你按照 考试分数由高到低排出他们的顺序.
聪明的你,
做对了吗?
归纳总结
逻辑推理问题的解决,需要我们
深入地理解条件和结论,分析关键 所在,找到突破口,进行合情合理 的推理,最后作出正确的判断。
谢谢!
这样,许和张都修过,与要求相矛盾
李平说的为假话。
李和张不能同真,必有一假。 这样说,即张修过桌凳。 许和刘都是假话。 桌凳是许兵修的。 因此,开头假设不成立!
张说了真话,则许、刘假话。
例2
逻辑推理典型例题
A说“不是我偷的” ;B说“是A偷的; C说”不是我“ ;D说”是B偷的“ 。 他们4人中只有一人说的是真话,你知00人聚会,其中至少有一人说 假话,这500人里任意两个人总有 一个说真话。说真话的有多少人? 说假话的有多少人?
则说假话b人
∴b<2 ∴ a≥1
∴ a=499
∴ b=1
五年级奥数逻辑推理题讲座及练习答案 (优选.)

wo最新文件---------------- 仅供参考--------------------已改成-----------word文本--------------------- 方便更改rd五年级奥数集训专题讲座——逻辑推理解答推理问题常用的方法有:排除法、假设法、反证法。
一般可以从以下几方面考虑: 1 、选准突破口,分析时综合几个条件进行判断。
2、根据题中条件,在推理过程中,不断排除不可能的情况,从而得出要求的结论。
3、对可能出现的情况作出假设,然后再根据条件推理,如果得到的结论和条件不矛盾,说明假设是正确的。
4、遇到比较复杂的推理问题,可以借助图表进行分析。
例1:有三个小朋友在谈论谁做的好事多。
冬冬说:“兰兰做的比静静多。
”兰兰说:“冬冬做的比静静多”静静说:“兰兰做的比冬冬少。
”这三位小朋友中,谁做的好事最多?准做的好事最少?【思路导航】我们用“ > ”来表示每个小朋友之间做好事多少的关系。
兰兰>静静冬冬>静静冬冬>兰兰所以,冬冬>兰兰>静静,冬冬做的好事最多,静静做的最少答:冬冬做的最多,静静做的最少。
【疯狂操练】( l )卢刚,丁飞和陈瑜一位是工程师,一位是医生,一位是飞行员。
现在只知道:卢刚和医生不同岁;医生比丁飞年龄小;陈瑜比飞行员年龄大。
请问,谁是工程师,谁是医生,谁是飞行员?解:卢刚和医生不同岁,那么卢刚是工程师或者飞行员。
医生比丁飞年龄小;那么医生只能是卢刚或者陈瑜。
这里可以知道,医生就是陈琦。
(卢刚和陈瑜不同岁;陈瑜比丁飞年龄小)陈琦比飞行员年龄大。
那么飞行员是卢刚,工程师就是丁飞了。
〔 2 )小李、小徐和小张是同学,大学毕业后分别当了教师,数学家和工程师。
小张年龄比工程师大;小李和数学家不同岁;数学家比小徐年龄小。
想一想,谁是教师,谁是数学家,谁是工程师。
解:(1)此题解答的关键在于抓住“小张年龄比工程师大;小李和数学家不同岁;数学家比小徐年龄小”这一条件来推理.①小张年龄比工程师大→小张不是工程师,②②小李和数学家不同岁→小李不是数学家,③③数学家比小徐年龄小→小徐也不是数学家.④由②③→小张是数学家.进一步推出小徐是教师,小李是工程师.解:(2)小张比工程师年龄大,说明小张不是工程师,小李和数学家不同岁,说明小李不是数学家,数学家比小徐年龄小,说明小徐也不是数学家,而小李和小徐都不是数学家,那只有小张是数学家了.然而从小张比工程师年龄大,又比小徐年龄小这两句话可以看出小徐不是工程师,那只有小徐是教师,小李是工程师了.因此,小徐是教师,小张是数学家,小李是工程师.( 3 )江波、刘晓、吴萌三位老师,其中一位教语文,一位教数学,一位教英语。
五年级奥数逻辑推理题讲座及练习答案

五年级奥数集训专题讲座——逻辑推理解答推理问题常用的方法有:排除法、假设法、反证法。
一般可以从以下几方面考虑:1 、选准突破口,分析时综合几个条件进行判断。
2、根据题中条件,在推理过程中,不断排除不可能的情况,从而得出要求的结论。
3、对可能出现的情况作出假设,然后再根据条件推理,如果得到的结论和条件不矛盾,说明假设是正确的。
4、遇到比较复杂的推理问题,可以借助图表进行分析。
例1:有三个小朋友在谈论谁做的好事多。
冬冬说:“兰兰做的比静静多。
”兰兰说:“冬冬做的比静静多”静静说:“兰兰做的比冬冬少。
”这三位小朋友中,谁做的好事最多?准做的好事最少?【思路导航】我们用“ > ”来表示每个小朋友之间做好事多少的关系。
兰兰>静静冬冬>静静冬冬>兰兰所以,冬冬>兰兰>静静,冬冬做的好事最多,静静做的最少答:冬冬做的最多,静静做的最少。
【疯狂操练】( l )卢刚,丁飞和陈瑜一位是工程师,一位是医生,一位是飞行员。
现在只知道:卢刚和医生不同岁;医生比丁飞年龄小;陈瑜比飞行员年龄大。
请问,谁是工程师,谁是医生,谁是飞行员?解:卢刚和医生不同岁,那么卢刚是工程师或者飞行员。
医生比丁飞年龄小;那么医生只能是卢刚或者陈瑜。
这里可以知道,医生就是陈琦。
(卢刚和陈瑜不同岁;陈瑜比丁飞年龄小)陈琦比飞行员年龄大。
那么飞行员是卢刚,工程师就是丁飞了。
〔 2 )小李、小徐和小张是同学,大学毕业后分别当了教师,数学家和工程师。
小张年龄比工程师大;小李和数学家不同岁;数学家比小徐年龄小。
想一想,谁是教师,谁是数学家,谁是工程师。
解:(1)此题解答的关键在于抓住“小张年龄比工程师大;小李和数学家不同岁;数学家比小徐年龄小”这一条件来推理.①小张年龄比工程师大→小张不是工程师,②②小李和数学家不同岁→小李不是数学家,③③数学家比小徐年龄小→小徐也不是数学家.④由②③→小张是数学家.进一步推出小徐是教师,小李是工程师.解:(2)小张比工程师年龄大,说明小张不是工程师,小李和数学家不同岁,说明小李不是数学家,数学家比小徐年龄小,说明小徐也不是数学家,而小李和小徐都不是数学家,那只有小张是数学家了.然而从小张比工程师年龄大,又比小徐年龄小这两句话可以看出小徐不是工程师,那只有小徐是教师,小李是工程师了.因此,小徐是教师,小张是数学家,小李是工程师.( 3 )江波、刘晓、吴萌三位老师,其中一位教语文,一位教数学,一位教英语。
【精品奥数】五年级上册数学思维训练讲义-第八讲 倍数问题(一) 人教版(含答案)

第八讲 倍数问题(一)第一部分:趣味数学将军饮马古希腊亚里山大里亚城有一位久负盛名的学者,名叫海伦。
一天,有位将军不远千里专程前来向海伦求教一个百思不得其解的问题:如图,将军从A 地出发到河边饮马,然后再到B 地军营视察,显然有许多走法.问走什么样的路线最短呢?精通数理的海伦稍加思索,便作了完善的回答.这个问题后来被人们称作“将军饮马”问题.分析:下面我们来看看数学家是怎样解决的.海伦发现这是一个求折线和最短的数学问题.同学们知道,连接两点的所有线中,直线段最短.只要知道两点间直线段最短,那么显然要把折线变成直线再解。
如果直接连AB ,与直线不会相交,怎么办呢?当A 、B 位于直线的异侧时,就有交点了.于是我们就希望在直线的另一侧找到一点A ′,使得连A ′B 与直线相交于P 点后(这时A ′P +PB 最短)线段A ′P 与AP 一样长.由对称的知识可知道,点A 关于直线的对称点A ′就有资格扮演A 的角色.解答:如图1先作A 关于直线的对称点A ′,连接A ′B 与直线相交于P 点,则AP +PB 就最小。
那么这样作出的AP +PB 是否真的最小呢?有兴趣的同学可以自己试着证明一下。
原来海伦本解决本问题时,是利用作对称点把折线问题转化成直线问题求解的。
后来这一方法已形成了思想,它在解决许多问题中都在起作用。
现在人们把凡是用对称点来实现解题的思想方法叫对称原理。
事实上,不仅是将军有这样的烦恼,运动着的车、船、飞机,包括人们每天走路都要遇到这样的问题.古今中外的任何旅行者总希望寻求最佳的旅行路线,尽量走近道,少走冤枉路。
我们把这类求近道的问题统称最短线路问题。
第二部分:奥数小练【例题1】 两根同样长的铁丝,第一根剪去18厘米,第二根剪去26厘米,余下的铁丝第一根是第二根的3倍。
原来两根铁丝各长多少厘米? lP A'l B A 图1。
五年级奥数逻辑推理题讲座及练习答案

五年级奥数集训专题讲座——逻辑推理解答推理问题常用的方法有:排除法、假设法、反证法。
一般可以从以下几方面考虑:1 、选准突破口,分析时综合几个条件进行判断。
2、根据题中条件,在推理过程中,不断排除不可能的情况,从而得出要求的结论。
3、对可能出现的情况作出假设,然后再根据条件推理,如果得到的结论和条件不矛盾,说明假设是正确的。
4、遇到比较复杂的推理问题,可以借助图表进行分析。
例1:有三个小朋友在谈论谁做的好事多。
冬冬说:“兰兰做的比静静多。
”兰兰说:“冬冬做的比静静多”静静说:“兰兰做的比冬冬少。
”这三位小朋友中,谁做的好事最多?准做的好事最少?【思路导航】我们用“ > ”来表示每个小朋友之间做好事多少的关系。
兰兰>静静冬冬>静静冬冬>兰兰所以,冬冬>兰兰>静静,冬冬做的好事最多,静静做的最少答:冬冬做的最多,静静做的最少。
【疯狂操练】( l )卢刚,丁飞和陈瑜一位是工程师,一位是医生,一位是飞行员。
现在只知道:卢刚和医生不同岁;医生比丁飞年龄小;陈瑜比飞行员年龄大。
请问,谁是工程师,谁是医生,谁是飞行员?解:卢刚和医生不同岁,那么卢刚是工程师或者飞行员。
医生比丁飞年龄小;那么医生只能是卢刚或者陈瑜。
这里可以知道,医生就是陈琦。
(卢刚和陈瑜不同岁;陈瑜比丁飞年龄小)陈琦比飞行员年龄大。
那么飞行员是卢刚,工程师就是丁飞了。
〔 2 )小李、小徐和小张是同学,大学毕业后分别当了教师,数学家和工程师。
小张年龄比工程师大;小李和数学家不同岁;数学家比小徐年龄小。
想一想,谁是教师,谁是数学家,谁是工程师。
解:(1)此题解答的关键在于抓住“小张年龄比工程师大;小李和数学家不同岁;数学家比小徐年龄小”这一条件来推理.①小张年龄比工程师大→小张不是工程师,②②小李和数学家不同岁→小李不是数学家,③③数学家比小徐年龄小→小徐也不是数学家.④由②③→小张是数学家.进一步推出小徐是教师,小李是工程师.解:(2)小张比工程师年龄大,说明小张不是工程师,小李和数学家不同岁,说明小李不是数学家,数学家比小徐年龄小,说明小徐也不是数学家,而小李和小徐都不是数学家,那只有小张是数学家了.然而从小张比工程师年龄大,又比小徐年龄小这两句话可以看出小徐不是工程师,那只有小徐是教师,小李是工程师了.因此,小徐是教师,小张是数学家,小李是工程师.( 3 )江波、刘晓、吴萌三位老师,其中一位教语文,一位教数学,一位教英语。
最新小学五年级奥数全册讲义(1-30讲)(含详解)【值得拥有】

小学五年级奥数全册讲义第1讲数字迷(一)第2讲数字谜(二)第3讲定义新运算(一)第4讲定义新运算(二)第5讲数的整除性(一)第6讲数的整除性(二)第7讲奇偶性(一)第8讲奇偶性(二)第9讲奇偶性(三)第10讲质数与合数第11讲分解质因数第12讲最大公约数与最小公倍数(一)第13讲最大公约数与最小公倍数(二)第14讲余数问题第15讲孙子问题与逐步约束法第16讲巧算24第17讲位置原则第18讲最大最小第19讲图形的分割与拼接第20讲多边形的面积第21讲用等量代换求面积第22 用割补法求面积第23讲列方程解应用题第24讲行程问题(一)第25讲行程问题(二)第26讲行程问题(三)第27讲逻辑问题(一)第28讲逻辑问题(二)第29讲抽屉原理(一)第30讲抽屉原理(二)第1讲数字谜(一)数字谜的内容在三年级和四年级都讲过,同学们已经掌握了不少方法。
例如用猜想、拼凑、排除、枚举等方法解题。
数字谜涉及的知识多,思考性强,所以很能锻炼我们的思维。
这两讲除了复习巩固学过的知识外,还要讲述数字谜的代数解法及小数的除法竖式问题。
例1 把+,-,×,÷四个运算符号,分别填入下面等式的○内,使等式成立(每个运算符号只准使用一次):(5○13○7)○(17○9)=12。
分析与解:因为运算结果是整数,在四则运算中只有除法运算可能出现分数,所以应首先确定“÷”的位置。
当“÷”在第一个○内时,因为除数是13,要想得到整数,只有第二个括号内是13的倍数,此时只有下面一种填法,不合题意。
(5÷13-7)×(17+9)。
当“÷”在第二或第四个○内时,运算结果不可能是整数。
当“÷”在第三个○内时,可得下面的填法:(5+13×7)÷(17-9)=12。
例2 将1~9这九个数字分别填入下式中的□中,使等式成立:□□□×□□=□□×□□=5568。
五年级奥数热点专题讲义8
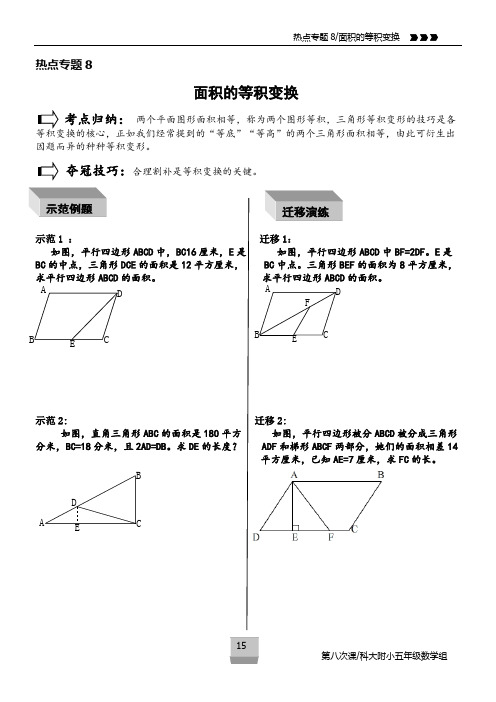
第八次课/科大附小五年级数学组 热点专题8面积的等积变换考点归纳: 两个平面图形面积相等,称为两个图形等积,三角形等积变形的技巧是各因题而异的种种等积变形。
夺冠技巧:合理割补是等积变换的关键。
示范1 : 迁移1:如图,平行四边形ABCD 中,BC16厘米,E 是 如图,平行四边形ABCD 中BF=2DF 。
E 是 BC 的中点,三角形DCE 的面积是12平方厘米, BC 中点。
三角形BEF 的面积为8平方厘米, 求平行四边形ABCD 的面积。
求平行四边形ABCD 的面积。
示范2: 迁移2:如图,直角三角形ABC 的面积是180平方 如图,平行四边形被分ABCD 被分成三角形 分米,BC=18分米,且2AD=DB 。
求DE 的长度? ADF 和梯形ABCF 两部分,她们的面积相差14平方厘米,已知AE=7厘米,求FC 的长。
A B C EA B C D E F AB C D E第八次课/科大附小五年级数学组热身1: 拓展1:如图,梯形ABCD 中,△ABE 和△ADE 的 如图,在梯形ABCD 中,三角形ABE 的面 面积分别是2平方厘米,3平方厘米,求三角 积为30平方厘米,EC=2AE ,求梯形ABCD 的 形CDE 的面积是多少? 面积。
热身2: 拓展2:在长方形ABCD 中,AD=15厘米, 如图,长方形ABCD 中,AD 长20厘米, AB=8厘米,阴影部分的面积为68平方厘米, DC 长10厘米,对角线交于O ,F 是BC 上任意 四边形EFGO 的面积是多少? 一点(不是B 、C 点),四边形OEFG 的面积为25平方厘米。
求阴影部分的面积。
A B C D E32A B C D E。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年级奥数讲义
第八讲逻辑推理
一、学法指导
数学不仅要计算,而且要讲道理,要善于分析,善于判断,善于论证,更要根据已经知道的一些事实,推断出某些结果,这就是推理。
逻辑推理问题中的条件错综复杂,解题时必须根据事情的逻辑关系进行合情推理,仔细分析,寻找突破口。
在解题时常用的方法有:
1.如果要判断正方体六个面上写的数字之间的对应关系,可以从出现最多的那个数字着手先进行考虑;
2.如果是给出几句判断,要辨别对错,这时可以从其中一句话先着手进行假设,要是出现了矛盾就再换过来;
3.如果涉及到几个对象的不同方面特点,可以采用图表来帮助分析,找出相互之间的关系,从给出的条件最多的那个对象着手先进行分析。
当然,逻辑推理题形式很多,遇到具体的问题还是要进行具体的分析,灵活运用所学的方法进行解答。
二、例题:
例1、小明、小华和小刚三位同学中,有一位同学做了件好事。
老师向他们三人了解情况。
小明说:“是小华做的。
”
小华说:“不是我做的。
”
小刚说:“不是我做的。
”
他们三人中只有一人说的是真话。
那么到底谁说的是真话,又是谁做的好事呢?
例2、甲、乙、丙三个人分别是学校足球队、乒乓球队和篮球队的。
下面的说法只有一种是对的:
(1)甲是足球队;
(2)乙不是足球队;
(3)丙不是篮球队的。
请你判断他们三个人各是哪一对的?
例3、同住一间寝室的甲、乙、丙、丁四个人分别来自上海、南京、北京和沈阳。
已知:
(1)甲不是来自上海,也不是来自北京;
(2)乙的家乡不是南京,也不是上海;
(3)如果甲不是来自南京,那么丙就不是来自上海;
(4)丁的家乡不是北京和上海。
那么他们四个人分别来自哪儿?
例4、小杨、小陈、小张三人在今年的高考中,分别考取了北大、清华、北师大三所学校的数学系、物理系、化学系,现在已经知道下列情况:(1)小杨不在北大;
(2)小陈不在清华;
(3)在北大的不在数学系;
(4)在清华的在物理系;
(5)小陈不在化学系。
请根据这些条件,请你判断小杨、小陈、小张三人
在什么学校?什么系?
例5、有五块小正方体,每个正方体的六个面都按一定的顺序写着1,2,3,4,5,6.把它们重叠成如图所示的形状,
则2的反面是几?4的反面是几?5的反面
是几?
例6、如左图所示小方格中数字表示此格的面积,试根据图中条件求阴影部分的周长?
例7、现有人民币一角的1张,二角的1张,五角的1张,一元的4张,五元的2张。
用这些人民币任意组合,则可以组成不同数额的币值共有多少种?
三、练习
A卷、基本能力训练
1.一天,老师发现教室里原有一张坏的凳子被修好了,
老师找到四个住校的学生:A,B,C,D向他们了解
A:凳子不是我修的
B:凳子是D修的
C:凳子是B修的
D:凳子不是我修的
他们四个中只有一个说了真话。
问:凳子是谁修的?
2.这是一个正方体的三种不同摆法,判断每个数字和谁相对
3.有四个人参加数学竞赛,他们猜测成绩是:
A 说:我可能成绩最差。
B 说:我不会是成绩最差。
C说:我肯定是成绩最好。
D说:我没有C考的好,但也不是最差。
成绩公布后,只有一人猜错了,那么四人成绩从高到低顺序是_______ 。
4.老师让四个学生分辨四张分别是白、回、苗、壮族的画像。
A 说:2号是白族,3号是苗族。
B 说:1号是壮族,2号是回族。
C说:2号是白族,4号是壮族。
D说:4号是壮族,1号是苗族。
老师说:你们每个人只说对了一个,请问这几个画像分别是几号?
5.有人民币一角的1张,二角的1张,五角的1张,一元的4张,五元的2张,用这些人民币任意组合,可以组成不同数额的币值共多少种?
6.A.B.C 三位老师分别上语文,数学和英语课。
已知:
(1)A上课全用汉语
(2)英语老师是一个学生的哥哥
(3)C是一位女教师,她比数学老师活泼
A.B.C 三位老师各上什么课?
7.甲、乙、丙、丁四位同学的运动衫上印有不同的号码。
赵说:“甲是2号,乙是3号.”
钱说:“丙是4号,乙是2号.”
孙说:“丁是2号,丙是3号.”
李说:“丁是4号,甲是1号.”
又知道赵、钱、孙、李每人都只说对了一半,那么丙的号码是几?
8.某校办数学竞赛,A、B、C、D.E五位同学得了前五名,发奖前,老师让他们猜一猜各人的名次排列情况。
A说:B第三名,C第五名。
B说:E第四名,D第五名。
C说:A第一名,E第四名。
D说:C第一名,B第二名。
E说:A第三名,B第四名。
老师说:每个名次都有人猜对.那么,这五名同学的名次是怎样排列的?
9. A、B、C、D四人同住一间寝室,其中一人在修指甲,一人在洗头,一人在画画,另一人在看书,已知:
①A不在修指甲,也不在看书;
②B不在画画,也不在修指甲;
③若A不在画画,则D不在修指甲;
④C既不在看书,也不在修指甲;
⑤D不在看书,也不在画画。
请问:他们各自在干什么?
10、甲、乙、丙、丁与小强五人一起比赛象棋,每两个人都要比赛一盘,到现在
为止,甲赛了4盘,乙赛了3盘,丙赛了2盘,丁赛了1盘,问小强赛了几盘?
B卷、重点中学试题集锦
1、警察抓住4名盗窃犯A、B、C、D,下面是他们的答话:
A说:是B干的; B说:是D干的;
C说:不是我干的; D说: B在说谎。
后来证实,这四个人中只有一人说的是真话,你知道罪犯是谁吗?
2、一个数,它比45小,不是4的倍数,是6的倍数;这个数的2倍大于60.求这个数。
3、将八个数从左到右排成一行,从第三个数开始,每个数都恰好等于它前面两个数之和。
如果第七个数和第八个数分别是81、131.那么第一个数是多少?
4、有1000人,其中至少有1人说假话。
而且这1000人里,任意两人至少有1人说真话,问说真话的有多少人?说假话的有多少人?
5、某气象站观测天气,记录了x天,记录结果是:
(1)下了8次雨,时间是上午或者下午;
(2)当下午下雨时,当天上午恰好是晴天;
(3)有9个下午是晴天;
(4)有13个上午是晴天。
这份记录中的x天至少是_______天。
