c语言计算平面桁架内力计算程序
桁架计算(TRUSS)

桁架内力计算程序(TRUSS)一、程序功能及编制方法桁架内力计算程序(TRUSS),能计算任意平面和空间桁架(包括网架)在结点荷载作用下各结点的位移和各杆的轴力。
程序采用变带宽一维数组存储总刚度矩阵,先处理法引进支座条件。
计算结果输出各结点的位移和各杆的轴力。
二、程序使用方法使用方法与“APF”程序相同。
用文件编辑编辑器建立数据文件后即可运行。
计算结果将写在结果文件中。
三、数据文件填写格式数据文件填写格式大致与APF程序相似。
1.总信息:T,NJ,NE,NR,NB,NP,EO,DS其中:T——桁架类型,平面桁架 T=2,空间桁架 T=3。
NR——支座约束数。
其他变量与APF程序相同。
2.结点坐标数组XYZ(NJ, 3)每个结点填一行,每行三个数分别填写结点的x,y,z三个坐标数值,平面桁架只填x,y 值(单位:m)。
3.单元信息数组G(NE)采用紧缩存储方式,每个单元填一个数。
把单元的左端、右端结点号和杆的类型号三个数紧缩为一个数。
例如某单元左端结点号为15,在端结点号为8,类型号为3,则写成0.15083,一般格式为0.×××××。
4.单元截面信息数组AI(NB)填写各类单元的杆截面面积(m2)。
5.约束信息数组R(NR)采用紧缩存储方式,每个约束(支座链杆)填一个数。
把约束作用的作用点写在该数的整数部分,约束的方向写在小数部分。
x方向的约束为“l”,y方向的约束为“2”。
例如某支座链杆作用在 17号结点上,方向沿整体坐标 y方向,则写为 17.2,一般格式为××.×。
6.结点荷载信息数组F(NP,2)每个结点荷载填一行,每行两个数。
前一个数用紧缩方式填写荷载作用的结点号和作用方向,格式与约束信息的格式相同。
后一个数为荷载的数值。
单位为kN,与整体坐标方向一致者为正值,相反者为负值。
例如,作用在16号结点上,数值为183.5 kN,方向向下的力,则写成:16.2,-183.5(这里,假定坐标轴y轴向上)。
第二章 第四节 平面静定桁架内力的计算标准版文档

桁架静力分析 简化计算模型
节点
杆件
节点
杆件
节点
杆件
节点
杆件
桁架静力分析 静力分析的基本方法
节
以节点为平衡对象;
点
节点力的作用线已知, 指向可以假设;
法
不仅可以确定各杆受
力,还可以确定连接
件的受力。
桁架静力分析 静力分析的基本方法
指向可以假设;
节点法 用假想截面将桁架截开;
桁架静力分析 静力分析的基本方法
节点法
例 题
以节点为平衡对象,画出受力图:
FA B FA D
FC y
FB A
F BC FB D
FC B FC D
FC x
FD B FD C
FD A
指向节者点为压力;
FD y 背向节者点为拉力。
桁架静力分析 静力分析的基本方法
FC x = 0 , FC y = - 800 N , FD y = 2600 N 。
指向可以假设; 工程中由杆件通过焊接、铆接 直接求得杆件的内力,进
节点力的作用线已知, 工程中由杆件通过焊接、铆接
不仅可以确定各杆受
例 直接求得杆件的内力,进
平面简单桁架的内力计算 工程中由杆件通过焊接、铆接
用假想截面将桁架截开; 用假想截面将桁架截开; 力,还可以确定连接
题 指向可以假设;
桁架静力分析 静力分析的基本方法
用假想截面将桁架截开;
不仅可以确定各杆受
节点力的作用线已知,
截 工程中由杆件通过焊接、铆接
工程中由杆件通过焊接、铆接
以节点为平衡对象,画出受力图:
以节点为平衡对象,画出受力图:
用假想截面将桁架截开;
弹性力学与有限元分析第二章-平面桁架有限元分析及程序设计

x
由单元①的刚度方程:
Fj
①
k
① ji
i
①
k
① jj
j
①
k
① ji
2
k
① jj
1
由单元③的刚度方程:
Fj
③
k
③ ji
i
③
k
③ jj
j
③
k
③ ji
3
k
③ jj
1
§2.3 结点平衡与整体刚度矩阵的集成
代入结点1的平衡条件:
k
l
xi
)
(dx j
dxi
)
(
yj
l
yi )
(dy j
dyi )
(dx j dxi ) (dy j dyi )
cos sin
由于杆件的变形产生位移:
ui dxi vi dyi
u j dxj v j dy j
因此,杆件应变为:
dl l
l
(ui
uj)
l
(vi
vj)
杆件轴力为:
(2k1 k2 )v4 P
结构的整体刚度系数
v4
P 2k1
k2
12 3
l2 l1 l1
4 P
N1
N1y
cos
k1v4
cos
k1P
(2k1 k2 ) cos
N2
k2v4
k2P 2k1 k2
位移法求解超静定结构。
§2.1 平面桁架单元的离散
结构的离散化:尽量将结构离散成数量最少的等截面直 杆单元
kki③ ③jii
ki③j
k
③ jj
3 3 3 3
§2.3 结点平衡与整体刚度矩阵的集成
2桁架杆件内力的求解方法

求解桁架内力的方法
将每个节点视为平面汇交力系平衡对象,逐个节点求解。
例1:平面桁架如图示,已知:F=2kN,
试求:各杆的内力与支座约束力。
F
y
A
B
C
解: F
FAB
A
4m
x
D
E
333 3
FAD
[A]
Fiy = 0 : − F − FAD
4 =0 32 + 42
FAD
=
−
25 4
=
−2.5kN
Fix
= 0:
FAB
+ FAD
3 5
=0
FAB = 1.5kN
FDA D
FDB
[D]
Fiy
= 0:
FDA
4 5
+
FDB
4 5
=0
FDE
Fix
= 0:
FDB
3 5
−
FDA
3 5
+
FDE
=0
FDB = 2.5kN
FDE = −3kN
F
[B]
FBA B
FBC
A
B
C
FBD
FBE
4m
D
E
Fiy = 0 : Fix = 0
FC
a
a
n B
F [节点H]
FEH
=
4 3
F
D
F =0 ix
a FEH + FGH a2 + b2 − FHK = 0
F FCF C
n
A
Fy = 0,
F
− FGH
b a2 + b2
桁架结构内力计算方法

桁架结构内力计算方法
在计算桁架结构内力时,可以采用以下步骤:
1.给定载荷:首先确定桁架结构所受到的外部载荷,包括竖向荷载、
水平荷载和斜向荷载等。
这些载荷可以通过静力学分析或者实际测量得到。
2.确定支座反力:根据结构平衡条件,计算出桁架结构支座的反力。
支座反力是由桁架结构与支座之间的约束关系决定的。
3.确定节点平衡条件:桁架结构中的每个节点都应满足平衡条件,即
节点受力平衡。
根据节点的受力平衡条件,可以得到每个节点处的力平衡
方程。
4.建立杆件的受力方程:根据构件材料的力学性质和几何形状,建立
每根杆件的受力方程。
通常使用杆件受力平衡和伸缩力平衡方程。
5.解方程求解内力:将节点平衡条件和杆件受力方程组合起来,得到
一个线性方程组。
通过求解这个方程组,可以求解出各个构件的内力大小
和方向。
在具体计算过程中,可以采用不同的计算方法来求解桁架结构的内力。
以下是几种常用的计算方法:
1.切线法:切线法是一种基于几何形状的方法,通过假设桁架结构各
个构件处于弧形变形状态,利用切线关系计算出内力。
该方法适用于相对
简单的桁架结构。
2.牛顿-拉夫逊法:牛顿-拉夫逊法是一种基于力的平衡条件的方法,
通过迭代计算桁架结构内力。
该方法适用于复杂的桁架结构。
3.力法:力法是一种基于力平衡方程和几何条件的方法,通过逐个构件计算内力。
该方法适用于任意形状的桁架结构。
以上是桁架结构内力计算的基本方法和一些常用的计算方法。
在实际应用中,还可以根据具体情况选择适合的方法进行计算。
静力学-平面简单桁架的内力计算

3. 取左(右)部分分析, 列平面任意力系的平衡方程。
2. 截面法 求某几根杆件内力常用的方法 —平面任意力系问题
例: 求:1、2、3杆件内力
3. 取左(右)部分分析,假设 “拉”
C ①D
FAy
②
A
③
F FB 列平面任C意力①系的平F衡1方程。
B
FAy
② F2
FAx E
G
F1
F2
解:1. 求支座约束力
A
(2)
F
f f
A
如果作用于物块的全部主动力合力 F
的作用线落在摩擦角之外( ≥ f ),则
无论此合力多小,物块必滑动。
FRA
2. 自锁现象
(phenomena of self-locking)
FRA
FRA
0 f 物体静止平衡时,全约束力必在摩擦角内
Fmax FS
FN f
A
(1)
F
f f
(2)
A
FAx
③ E
F3
P1
MA0
FB
ME 0
F1
MB 0
FAy
Fy 0
F2
Fx 0
FAx
Fx 0
F3
2. 把桁架截开 不要截在节点处
赛 车 起 跑
为什么赛车运动员起跑前要将车轮与 地面摩擦生烟?
第四章 摩擦 Friction
摩擦(friction): 一种极其复杂的物理-力学现象。
涉及:
“滚动摩阻定律”
—滚动摩阻系数 ,长度量纲
r
P A
FS FN
Q
r
临界平衡 P
A
Mf
FS
FN
6-3-2平面静定桁架的内力计算(精)

1. 内力计算的方法
平面静定桁架的内计算
平面静定桁架的内力计算的方法通常有结点法和截面法。 结点法是截取桁架的一个结点为隔离体,利用该结点的静力 平衡方程来计算截断杆的轴力。 截面法是用一截面(平面或曲面)截取桁架的某一部分(两个结 点以上)为隔离体,利用该部分的静力平衡方程来计算截断杆 的轴力。
FNADy=10kN-40kN=-30kN FNADy FNAD 3.35m 67KN 1.5m FNADy FNADx 3m 60kN 1.5m
国家共享型教学资源库
四川建筑职业技术学院
取结点C为隔离体 (图 c),由∑Fx=0得
FNCF= FNAC=60kN 取结点D为隔离体(图d),列出平衡方程
M
D
0
得
FNdx=-15kN
利用比例关系,得
FNd= -18.05KN
国家共享型教学资源库
四川建筑职业技术学院
国家共享型教学资源库
四川建筑职业技术学院
3. 比例关系的应用
F N F Nx FNy l lx ly
例6-5 求图a所示桁架各杆的轴力。
国家共享型教学资源库
四川建筑职业技术学院
解 (1)求支座反力。
FAx 0
FAy 40KN
FB 40KN
(2)求各杆的内力。
取结点A为隔离体(图b)
利用比例关系,得
FNb
FNbx 3.61m 18.05KN 3m
四川建筑职业技术学院
国家共享型教学资源库
(3)求杆d的内力。联合应用结点法和截面法计算杆d的内力较
为方便。先取结点E为隔离体(图c),由平衡方程∑Fx=0 ,得
FNCE= FNc=52.5kN 再用截面Ⅱ-Ⅱ截取桁架左半部分为隔离体(图d),列平衡方程 由
习题课3.静定平面桁架的内力计算
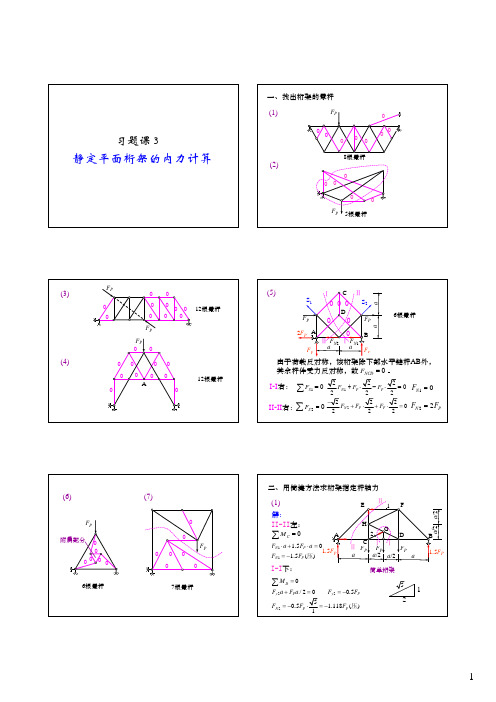
习题课3静定平面桁架的内力计算一、找出桁架的零杆(1)F P000000(2)8根零杆5根零杆F P000(3)12根零杆F PF P 00000000000F P 12根零杆(4)A 000000000006根零杆(5)a aaaS 1S 2F P 2F P F P F N 2F N 1AB C DⅡⅡⅠⅠ00000由于荷载反对称,该桁架除下部水平链杆AB 外,其余杆件受力反对称,故。
0=NCD F 1S F=∑I-I 右:20S F =∑II-II 右:12220222N P P F F F +⋅−⋅=10N F =22220222N P P F F F −+⋅+⋅=22N P F F =F PF P(7)(6)F P0附属部分6根零杆7根零杆F P0000000二、用简捷方法求桁架指定杆轴力150+II-II 左:(1)ABC DE FGHa /2a /2ⅡⅡⅠⅠ12解:CM=∑11 1.51.5()N P N P F a F a F F ⋅⋅==−压220/200.5Dy P y PMF a F a F F =+==−∑I-I 下:250.5 1.118()1N P P F F F =−⋅=−压简单桁架1.5F PF P F P F Pa a /2aa /2 1.5F P125(2)F NF yB =2F P dd dd F PAC DB dⅡⅡⅠⅠ1F yC =F PF yA =F PF xA =2F P 323F P2F P331)020()2)0()3)0()C N P P N P x N P y yC P M F d F d F d F F F F F F F F =+−======↑∑∑∑拉拉I-I 右:联合桁架解:F NF yB =2F P dd ddF PAC DB dⅡⅡⅠⅠ1F yC =F PF yA =F PF xA =2F P 323F P2F P1210()()032()D N P P yN P P P M F F d F dF F F F F ==−⋅=−==−=−∑∑压压II-II 左:整体平衡:10(322)()2ByA P P P P P MF F d F d F d F d F d==+⋅−−=↑∑(3)F P0A -F P-F P-F PF DEC 12F PF PPF 2F N F Pa /2aⅠⅠ00B 0EN MF ==∑1)I-I 右:02=N F 2)结点C :1102()yy PN P FF F F F ===∑拉3)结点F :aa /2aa /2联合桁架解:(4)F P 4m4mF P F P F P 4F P6.67F P6.67F P AB FC F N 2134ⅡⅠEⅡD GH 4m4m3m3mⅠ解:1220()0()33DN P xN P MF F FF F ====−∑∑拉压1) I-I 右:2) 结点E :2222550()346xx PN x P FF F F F F ====∑拉简单桁架F PF N 2E 23PF F P 4m4mF P F P F P 4F P6.67F P6.67F P AB FC F N 2134ⅡⅠEⅡD G H4m4m3m3mⅠ553434343x Py P PN F F F F F F ==⋅==4) 结点D :F PFN 3F N 5D2F P2F P /3410(48)2()6F N P P P M F F F F −==+=−∑压3) II-II 右:xF=∑(5)F PCA B dⅠ1 1.5F P 1.5F P02F P F Pd 0复杂桁架1)结点C:结构与荷载均对称,两斜杆轴力为零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
#include<stdio.h>#include<math.h>#include<stdlib.h>#define M 5int n,nc,nn,m,e,f;//节点总数,固定节点数,自由度数,杆件数int io,jo;//单根杆对号指示数int ihl[M],ihr[M];//杆件左右节点号double a[M];//各杆截面积double mm[M];//杆件质量double ea[M];//杆件EA的值double x[M],y[M];//节点坐标double dp[M];//总体系下的节点载荷double t[2];//0,1分别为坐标转换矩阵的cos(),sin()double c[2][2];//总体系下的单刚double clxy[3];//0,1,2分别为杆长,正弦,余弦double h[M];//杆件轴力double r[M][M];//总刚度阵double rd;//桁架轴力杆局部系单刚double u[M];//桁架节点位移double v[2];//存放节点位移差double d[M];//LDLT分解时的D矩阵的对角线元素double l[M][M];////LDLT分解时的D矩阵的对角线元素double fdp[M];//总体系下支座反力void iojo(int k)//计算对号指示数io,jo{int i,j;i=ihl[k-1];//k号杆左节点号进入ij=ihr[k-1];//k号杆节点右号进入iio=2*(i-nc-1);//uxi前未知位移的个数jo=2*(j-nc-1);//uyi前未知位移的个数}void ch(int k)//计算杆长与方向余弦函数{int i,j;i=ihl[k-1];//k号杆左节点进入ij=ihr[k-1];//k号杆右节点进入jclxy[1]=x[j-1]-x[i-1];//k号杆x坐标差clxy[2]=y[j-1]-y[i-1];//k号杆y坐标差clxy[0]=sqrt(clxy[1]*clxy[1]+clxy[2]*clxy[2]);//k号杆长clxy[1]=clxy[1]/clxy[0];//k号杆件x轴余弦clxy[2]=clxy[2]/clxy[0];//k号杆件y轴余弦void stif(int k)//计算k号杆件总体系下的单元刚度阵{int i,j;ch(k);//调用ch(),计算k号杆件杆长与余弦t[0]=clxy[1];t[1]=clxy[2];rd=ea[k-1]/clxy[0];for(i=0;i<2;i++){for(j=0;j<2;j++){c[i][j]=t[i]*t[j]*rd;}}}void dor()//总体系下的总刚度阵的组集{int i,j,k;for(i=0;i<nn;i++){for(j=0;j<nn;j++){r[i][j]=0.0;//总刚度阵清0}}for(k=1;k<=m;k++){iojo(k);//调用k的对号指示函数,从而确定组集位置stif(k);//第k号杆件的总体系下的单刚if(io>=0){for(i=io+1;i<=io+2;i++){for(j=io+1;j<=io+2;j++){r[i-1][j-1]+=c[i-io-1][j-io-1];//在r中io+1,io+2行以及io+1,io+2列位置累加k的单刚}for(j=jo+1;j<=jo+2;j++){r[i-1][j-1]-=c[i-io-1][j-jo-1];//在r中io+1,io+2行以及jo+1,jo+2列位置累加k的负单刚r[j-1][i-1]=r[i-1][j-1];}}for(i=jo+1;i<=jo+2;i++){for(j=jo+1;j<=jo+2;j++){r[i-1][j-1]+=c[i-jo-1][j-jo-1];//在r中jo+1,jo+2行以及jo+1,jo+2列位置累加k的单刚}}}else if(jo>=0)//如果io<0,即左节点为固定节点,jo>=0,右端为可动节点,则只在jo+1,jo+2对角分块位置累加{for(i=jo+1;i<=jo+2;i++){for(j=jo+1;j<=jo+2;j++){r[i-1][j-1]+=c[i-jo-1][j-jo-1];//在r中jo+1,jo+2行以及jo+1,jo+2列位置累加k的单刚}}}}}void choldlt()//总刚度阵的LDLT分解{int i,j,k;double m,t[M][M];for(i=0;i<nn;i++){l[i][i]=1.0;}d[0]=r[0][0];//d[0]=r[0][0]for(i=1;i<nn;i++){for(j=0;j<i;j++){m=0.0;for(k=0;k<j;k++){m+=t[i][k]*l[j][k];}t[i][j]=r[i][j]-m;l[i][j]=t[i][j]/d[j]; //计算l[i][j]m=0.0;for(k=0;k<i;k++){m+=t[i][k]*l[i][k];d[i]=r[i][i]-m; //计算d[i]}l[j][i]=l[i][j];}}}void trildlt()//回代求节点位移{int i,k;double m,y[M];y[0]=dp[0];for(i=1;i<nn;i++){m=0.0;for(k=0;k<i;k++){m+=l[i][k]*y[k];y[i]=dp[i]-m; //计算y[i] }}u[nn-1]=y[nn-1]/d[nn-1];for(i=nn-1;i>=0;i--){m=0.0;for(k=i+1;k<nn;k++){m+=l[k][i]*u[k];u[i]=y[i]/d[i]-m; //计算u[i]}}}void doh()//计算杆件的轴力{int i,k;for(k=1;k<=m;k++){iojo(k);//调用第k号杆件的左右端点的位移指示数for(i=0;i<2;i++)//计算每个节点2个自由度循环{if(io<0)//把右节点的2个位移存入v[0],v[1]{v[i]=u[jo+i];}else//把右节点的2个位移存入v[0],v[1]{v[i]=u[jo+i]-u[io+i];}}stif(k);//计算第k号杆件总体系单刚,存入[2]h[k-1]=0.0;//数组h[k-1]清零for(i=1;i<=2;i++)//对两个位移循环{h[k-1]=h[k-1]+t[i-1]*v[i-1]*rd;//轴力存入h[k-1]}}}void dowt() //考虑自重,且规定y轴竖直向上{int k,ko,i;double g; //g为重力printf("请输入杆件质量:\n");for(i=0;i<m;i++) //各杆件质量值输入{printf("mm[%d]=",i+1);scanf("%lf",&mm[i]);}for(k=1;k<=m;k++) //对桁架杆件循环{iojo(k); //调用函数ch(k);g=mm[k-1]*9.80665; //重力计算公式if(io>=0) //左节点为自由节点{dp[io+1]=dp[io+1]-(g/2); //左节点的y轴荷载减少二分之一重力dp[jo+1]=dp[jo+1]-(g/2); //右节点的y轴荷载减少二分之一重力}else if(jo>=0) //若右节点为自由节点,则仅有右节点做如下处理{ko=io+2*nc; //定义反力指示数ko 等于2*(固定节点号-1)dp[jo+1]=dp[jo+1]-(g/2);fdp[ko+1]=fdp[ko+1]-(g/2); //支座反力叠加重力的一半}}}void dofanli() //计算反力{int k,ko;for(k=1;k<=m;k++) //对杆件循环{iojo(k); //引用函数ch(k);ko=io+2*nc; //记录左节点if(io<0) //左节点为固定节点{fdp[ko]=fdp[ko]-h[k-1]*clxy[1]; //为第i个节点x轴向力加杆件轴力反力fdp[ko+1]=fdp[ko+1]-h[k-1]*clxy[2]; //为第i个节点y轴向力加杆件轴力反力}}}void verify() //强度校核函数{int k,i;double sigema,sigema0,sigema1; //定义应力,拉伸许用应力,压缩许用应力printf("请输入各杆截面积:\n"); //截面面积输入for(i=0;i<m;i++){printf("a[%d]=",i+1);scanf("%lf",&a[i]);}printf("请输入杆件拉伸许用应力:\n"); //杆件拉伸许用应力输入scanf("%lf",&sigema0);printf("请输入杆件压缩许用应力(输入正数):\n"); //杆件压缩许用应力输入scanf("%lf",&sigema1);for(k=1;k<=m;k++) //对杆件循环{sigema=h[k-1]/a[k-1]; //计算公式轴力与面积之商if(sigema>sigema0||sigema<-1*sigema1) //对应力,许用应力进行比较(注:压应力为负值,所以不小于压缩许用应力){printf("第%d根杆件超过许用应力,为危险杆件,请增加横截面积或更换其他材料\n",k);}}}void assemble() //装配应力计算{int k,ko;double l; //定义杆件被拉长l printf("请输入存在装配应力的杆件号:\n");scanf("%d",&k);printf("请输入杆件装配时的拉长长度:\n");scanf("%lf",&l);iojo(k); //引用函数ch(k);h[k-1]=h[k-1]+ea[k-1]*l/clxy[0]; //储存装配杆件的应力值if(io>=0){dp[io]=dp[io]+ea[k-1]*l*clxy[1]/clxy[0]; //左节点x轴方向附加载荷增加P=△l*EA/l乘其方向余弦dp[io+1]=dp[io+1]+ea[k-1]*l*clxy[2]/clxy[0]; //y轴方向同上操作dp[jo]=dp[jo]-ea[k-1]*l*clxy[1]/clxy[0]; //注:右节点与左节点附加装配应力相反dp[jo+1]=dp[jo+1]-ea[k-1]*l*clxy[2]/clxy[0];}else{ko=io+2*nc;dp[jo]=dp[jo]-ea[k-1]*l*clxy[1]/clxy[0]; //注:右节点与左节点附加装配应力相反dp[jo+1]=dp[jo+1]-ea[k-1]*l*clxy[2]/clxy[0];printf("%f,%f\n",dp[jo],dp[jo+1]);fdp[ko]=fdp[ko]+ea[k-1]*l*clxy[1]/clxy[0]; //固定节点ihl反力叠加装配应力fdp[ko+1]=fdp[ko+1]+ea[k-1]*l*clxy[1]/clxy[0];}}void tem() //计算温度应力{int k,ko;double t0,arf,t1,t2,detal; //定义变量,温差,热膨胀系数,初始温度,最终温度,温变引起的长度变化printf("请输入初始温度\n"); //变量输入scanf("%lf",&t1);printf("请输入最终温度\n");scanf("%lf",&t2);printf("请输入杆件的热膨胀系数\n");scanf("%lf",&arf);t0=t2-t1;for(k=1;k<=m;k++){iojo(k); //引用函数ch(k);detal=-1*arf*t0*clxy[0]; //等效为装配应力杆件受压h[k-1]=h[k-1]+ea[k-1]*detal/clxy[0];if(io>=0){dp[io]=dp[io]+ea[k-1]*detal*clxy[1]/clxy[0];//左节点x轴方向附加载荷增加P=△l*EA/l乘其方向余弦dp[io+1]=dp[io+1]+ea[k-1]*detal*clxy[2]/clxy[0]; //y轴方向同上操作dp[jo]=dp[jo]-ea[k-1]*detal*clxy[1]/clxy[0]; //注:右节点与左节点附加温度应力相反dp[jo+1]=dp[jo+1]-ea[k-1]*detal*clxy[2]/clxy[0];}else{ko=io+2*nc;dp[jo]=dp[jo]-ea[k-1]*detal*clxy[1]/clxy[0]; //注:右节点与左节点附加温度应力相反dp[jo+1]=dp[jo+1]-ea[k-1]*detal*clxy[2]/clxy[0];fdp[ko]=fdp[ko]+ea[k-1]*detal*clxy[1]/clxy[0]; //固定节点ihl反力叠加温度应力fdp[ko+1]=fdp[ko+1]+ea[k-1]*detal*clxy[1]/clxy[0];}}}int main(){int i;printf(" *****************求解平面桁架节点位移与杆端力程序*****************\n\n");printf("\n ------------------输入数据时请用空格或回车符间隔------------------\n");printf("\n\n请输入桁架节点总数n,固定节点数nc,杆件数m:\n");scanf("%d,%d,%d",&n,&nc,&m);nn=2*(n-nc);printf("请输入节点坐标:\n");for(i=0;i<n;i++){printf("x[%d]=",i+1);scanf("%lf",&x[i]);printf("y[%d]=",i+1);scanf("%lf",&y[i]);}printf("输入杆件左右节点号:\n");for(i=0;i<m;i++){printf("ihl[%d]=",i+1);scanf("%d",&ihl[i]);printf("ihr[%d]=",i+1);scanf("%d",&ihr[i]);}printf("请输入杆件的EA值[ea]:\n");for(i=0;i<m;i++){printf("ea[%d]=",i+1);scanf("%lf",&ea[i]);}printf("请输入节点载荷[dp]:\n");for(i=0;i<nn;i++){printf("dp[%d]=",i+1);scanf("%lf",&dp[i]);}dor();choldlt();printf("是否需要考虑自重,需要请输入‘1’,不需要请输入‘0’。
