中考数学复习第2章方程(组)与不等式(组)第9课时不等式
合集下载
2025年中考数学总复习第一部分考点精讲第二章方程(组)与不等式(组)第一节一次方程(组)及其应用
2025版
第二章
第一节
数学
甘肃专版
方程(组)与不等式(组)
一次方程(组)及其应用
2025版
数学
甘肃专版
2025版
等
式
一次 的
方程 性
（组）质
及其 及
应用 其
应
用
数学
甘肃专版
2025版
一
一次 元
方程 一
（组）次
及其 方
应用 程
数学
甘肃专版
2025版
一
一次 元
方程 一
（组）次
及其 方
应用 程
数学
海．今凫雁俱起，问何日相逢？”大意：今有野鸭从南海起飞，7天到北
海；大雁从北海起飞，9天到南海．现野鸭从南海，大雁从北海同时起飞，
问经过多少天相遇？设经过x天相遇，根据题意可列方程为( D )
A.(9＋7)x＝1
B．(9－7)x＝1
1
C.(
7
1
D．(
7
−
1
)x＝1
9
+
1
)x＝1
9
2025版
数学
甘肃专版
8＝x，由0.
8ሶ
＝0.888 8…可知，10x＝8.888
8
8…，所以10x＝8＋x，解方程，得x＝ ，于是
9
8
ሶ
ሶ
得0.8＝ .则0.2ሶ 7写成分数形式为
9
3
11
.
2025版
数学
甘肃专版
2025版பைடு நூலகம்
数学
甘肃专版
命题点：一次方程(组)的应用(省卷近5年考查4次，兰州近5年考查3次)
1.(2024·兰州第10题3分)数学家朱世杰所著的《四元玉鉴》是中国元代重要的数学著作之
第二章
第一节
数学
甘肃专版
方程(组)与不等式(组)
一次方程(组)及其应用
2025版
数学
甘肃专版
2025版
等
式
一次 的
方程 性
（组）质
及其 及
应用 其
应
用
数学
甘肃专版
2025版
一
一次 元
方程 一
（组）次
及其 方
应用 程
数学
甘肃专版
2025版
一
一次 元
方程 一
（组）次
及其 方
应用 程
数学
海．今凫雁俱起，问何日相逢？”大意：今有野鸭从南海起飞，7天到北
海；大雁从北海起飞，9天到南海．现野鸭从南海，大雁从北海同时起飞，
问经过多少天相遇？设经过x天相遇，根据题意可列方程为( D )
A.(9＋7)x＝1
B．(9－7)x＝1
1
C.(
7
1
D．(
7
−
1
)x＝1
9
+
1
)x＝1
9
2025版
数学
甘肃专版
8＝x，由0.
8ሶ
＝0.888 8…可知，10x＝8.888
8
8…，所以10x＝8＋x，解方程，得x＝ ，于是
9
8
ሶ
ሶ
得0.8＝ .则0.2ሶ 7写成分数形式为
9
3
11
.
2025版
数学
甘肃专版
2025版பைடு நூலகம்
数学
甘肃专版
命题点：一次方程(组)的应用(省卷近5年考查4次，兰州近5年考查3次)
1.(2024·兰州第10题3分)数学家朱世杰所著的《四元玉鉴》是中国元代重要的数学著作之
中考数学复习《二元一次方程组》
中考考点精讲精练
考点1 解二元一次方程组［5年1考：2013年(解答题)］
典型例题
1. 解方程组： x+y=5, 2x+3y=11.
解： x+y=5, ① 2x+3y=11. ②
①×3-②,得x=4. 把x=4代入①，得y=1. 则方程组的解为 x=4,
y=1.
2x+3y=12, 2. 解方程组：
y= -1.
4. 解方程组： x+3y=-1, 3x-2y=8.
解： x+3y=-1, ①
3x-2y=8. ②
由①得x=-1-3y. ③
把③代入②,得3(-1-3y)-2y=8.
解得y=-1.
则x=-1-3×(-1)=2. 故二元一次方程组的解为
x=2, y=-1.
考点点拨： 本考点是广东中考的高频考点，题型一般为计算题，难度简 单. 解答本考点的有关题目，关键在于熟练掌握消元法和代入法 解二元一次方程组. 注意以下要点： (1)用代入消元法解二元一次方程组的步骤； (2)用加减消元法解二元一次方程组的步骤.
பைடு நூலகம்
方法规律
1. 用代入消元法解二元一次方程组的一般步骤(概括为“变， 代，解，回代，联”五步) (1)从方程组中选出一个系数比较简单的方程，将这个方程中
的一个未知数(例如y)用含另一个未知数(例如x)的代数式表示 出来，即写成y=ax+b的形式，即“变”. (2)将y=ax+b代入到另一个方程中，消去y，得到一个关于x的
3. 列二元一次方程组解应用题的一般步骤(概括为“审，找， 列，解，答”五步) (1)审：通过审题，把实际问题抽象成数学问题，分析已知数 和未知数，并用字母表示其中的两个未知数. (2)找：找出能够表示题意的两个相等关系. (3)列：根据这两个相等关系列出必需的代数式，从而列出方 程组. (4)解：解这个方程组，求出两个未知数的值. (5)答：在对求出的方程组的解做出是否合理的判断的基础上， 写出答案.
2025年四川省成都市九年级中考数学大单元复习课件-第二单元__第2节__不等式(组)及其应用
(1)数学书和语文书共90本恰好摆满该书架，求书架上数学书和语文书
各多少本；
解：设书架上数学书有x本，语文书有y 本，
+ =
由题意，得
. + . =
=
，解得
，
=
答：书架上数学书有60本，语文书有30本；
7.(2024江西)如图，书架宽84 cm，在该书架上按图示方式摆放数学书和
语文书，已知每本数学书厚0.8 cm，每本语文书厚1.2 cm.
(2)如果书架上已摆放10本语文书，那么数学书最多还可以摆多少本？
解：设数学书还可以摆m本，
由题意，得10×1.2＋0.8m≤84，
解得m≤90.
答：数学书最多还可以摆90本．
实际问题
设未知数，根据不等
关系列不等式
数学问题
抽象为数学模型
一元一次不等式
一元一次不等式组
解不等式
应用
不等式的性质
实际问题的解
检验
数学问题的解
解不等式组
公共解
数形
结合
口
诀
解决不等式的实际应用问题时,常见的关键词与不等号的对应表：
常见关键词
不等号
大于，多于，超过，高于
>
小于，少于，不足，低于
<
至少，不低于，不小于，不小于
________
≥
至多，不高于，不大于，不超过
________
≤
1. (2024上海)如果x＞y，那么下列正确的是( C )
A. x＋5＜y＋5
B. x－5＜y－5
性质 1
不等式两边加(或减)同一个数(或式子)，不等号的方向不变，
即如果a＞b，那么a±c>b±c
各多少本；
解：设书架上数学书有x本，语文书有y 本，
+ =
由题意，得
. + . =
=
，解得
，
=
答：书架上数学书有60本，语文书有30本；
7.(2024江西)如图，书架宽84 cm，在该书架上按图示方式摆放数学书和
语文书，已知每本数学书厚0.8 cm，每本语文书厚1.2 cm.
(2)如果书架上已摆放10本语文书，那么数学书最多还可以摆多少本？
解：设数学书还可以摆m本，
由题意，得10×1.2＋0.8m≤84，
解得m≤90.
答：数学书最多还可以摆90本．
实际问题
设未知数，根据不等
关系列不等式
数学问题
抽象为数学模型
一元一次不等式
一元一次不等式组
解不等式
应用
不等式的性质
实际问题的解
检验
数学问题的解
解不等式组
公共解
数形
结合
口
诀
解决不等式的实际应用问题时,常见的关键词与不等号的对应表：
常见关键词
不等号
大于，多于，超过，高于
>
小于，少于，不足，低于
<
至少，不低于，不小于，不小于
________
≥
至多，不高于，不大于，不超过
________
≤
1. (2024上海)如果x＞y，那么下列正确的是( C )
A. x＋5＜y＋5
B. x－5＜y－5
性质 1
不等式两边加(或减)同一个数(或式子)，不等号的方向不变，
即如果a＞b，那么a±c>b±c
人教版九年级数学第二单元《方程(组)与不等式(组)》中考知识点梳理
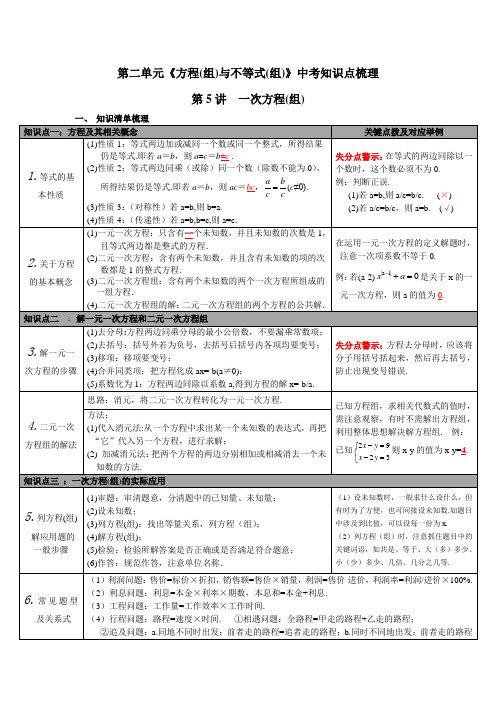
第二单元《方程(组)与不等式(组)》中考知识点梳理第5讲一次方程(组)第6讲一元二次方程第7讲分式方程三、知识清单梳理第8讲一元一次不等式(组)知识点一：不等式及其基本性质关键点拨及对应举例1.不等式的相关概念（1）不等式：用不等号(＞，≥，＜，≤或≠)表示不等关系的式子.（2）不等式的解：使不等式成立的未知数的值.（3）不等式的解集：使不等式成立的未知数的取值范围.例：“a与b的差不大于1”用不等式表示为a－b≤1.2.不等式的基本性质性质1：若a＞b,则a±c>b±c；性质2：若a＞b,c>0，则ac>bc，ac>bc；性质3：若a＞b,c<0，则ac<bc，ac<bc.牢记不等式性质3，注意变号.如：在不等式－2x＞4中，若将不等式两边同时除以－2，可得x＜2.知识点二：一元一次不等式3.定义用不等号连接，含有一个未知数，并且含有未知数项的次数都是1的，左右两边为整式的式子叫做一元一次不等式. 例：若230mmx++>是关于x的一元一次不等式，则m的值为-1.4.解法（1）步骤：去分母；去括号；移项；合并同类项；系数化为1.失分点警示系数化为1时，注意系数的正负性，若系数是负数，则不等式改变方向.（2）解集在数轴上表示:x≥a x＞a x≤a x＜a知识点三：一元一次不等式组的定义及其解法5.定义由几个含有同一个未知数的一元一次不等式合在一起，就组成一个一元一次不等式组．（1）在表示解集时“≥”，“≤”表示含有，要用实心圆点表示；“＜”，“＞”表示不包含要用空心圆点表示．（2）已知不等式（组）的解集情况，求字母系数时，一般先视字母系数为常数，再逆用不等式（组）解集的定义，反推出含字母的方程，最后求出字母的值.如：已知不等式（a-1）x＜1-a 的解集是x＞-1，则a的取值范围是a＜1.6.解法先分别求出各个不等式的解集，再求出各个解集的公共部分7.不等式组解集的类型假设a＜b解集数轴表示口诀x ax b≥⎧⎨≥⎩x≥b大大取大x ax b≤⎧⎨≤⎩x≤a小小取小x ax b≥⎧⎨≤⎩a≤x≤b大小，小大中间找x ax b≤⎧⎨≥⎩无解大大，小小取不了知识点四：列不等式解决简单的实际问题8.列不等式解应用题（1）一般步骤：审题；设未知数；找出不等式关系；列不等式；解不等式；验检是否有意义.（2）应用不等式解决问题的情况：a.关键词：含有“至少（≥）”、“最多（≤）”、“不低于（≥）”、“不高于（≤）”、“不大（小）于”、“超过（＞）”、“不足（＜）”等；注意：列不等式解决实际问题中，设未知数时，不应带“至少”、“最多”等字眼，与方程中设未知数一致.。
陕西专版中考数学新突破复习第一部分教材同步复习第二章方程(组)与不等式(组)2.2一元二次方程课件
答：应将销售单价定位56元．
易 错 辨析
易错点 解一元二次方程“丢根”现象 【例4】 方程x(x＋1)＝3(x＋1)2的根为____________． 【错解】 x(x＋1)＝3(x＋1)2，两边同时除以(x＋1)
得， x＝3(x＋1) x＝3x＋3 －2x＝3 x＝－32.
【错解分析】 观察方程可知方程两边有公因式(x＋ 1)，所以方程两边同时除以(x＋1)，得x＝3(x＋1)，解得x＝ －32，没有按正确的步骤来解方程．
2．列一元二次方程解应用题的步骤 (1)审：弄清题意． (2)设：设未知数． (3)列：根据题中的等量关系列出方程． (4)解：解方程． (5)验：检验根的合理性． (6)答：写出答案．
3．列一元二次方程解应用题时需掌握以下两个关系 (1)增长率等量关系：
增量 ①增长率＝基础量×100%. ②设a为原来量，m为平均增长(下降)率，n为增长(下降) 次数，b为增长(下降)后的量，则a(1＋m)n＝b[或a(1－m)n＝ b]． (2)利润等量关系： ①利润＝售价－成本．
【注意】选择四种解法的使用顺序：直接开平方法，因 式分解法，配方法，公式法．
►知识点三 一元二次方程根的判别式
一元二次方程ax2＋bx＋c＝0(a≠0)的根的判别式是Δ＝ ___b_2－__4_a_c______.
1．Δ＞0⇔__方__程__有__两__个__不__相__等__的__实__数__根__． 2．Δ＝0⇔__方__程__有__两__个__相__等__的__实__数__根_． 3．Δ＜0⇔__方__程__没__有__实__数__根_________．
第一部分 教材同步复习
第二章 方程(组)与不等式(组)
2.2 一元二次方程
知识要点 ·归纳
易 错 辨析
易错点 解一元二次方程“丢根”现象 【例4】 方程x(x＋1)＝3(x＋1)2的根为____________． 【错解】 x(x＋1)＝3(x＋1)2，两边同时除以(x＋1)
得， x＝3(x＋1) x＝3x＋3 －2x＝3 x＝－32.
【错解分析】 观察方程可知方程两边有公因式(x＋ 1)，所以方程两边同时除以(x＋1)，得x＝3(x＋1)，解得x＝ －32，没有按正确的步骤来解方程．
2．列一元二次方程解应用题的步骤 (1)审：弄清题意． (2)设：设未知数． (3)列：根据题中的等量关系列出方程． (4)解：解方程． (5)验：检验根的合理性． (6)答：写出答案．
3．列一元二次方程解应用题时需掌握以下两个关系 (1)增长率等量关系：
增量 ①增长率＝基础量×100%. ②设a为原来量，m为平均增长(下降)率，n为增长(下降) 次数，b为增长(下降)后的量，则a(1＋m)n＝b[或a(1－m)n＝ b]． (2)利润等量关系： ①利润＝售价－成本．
【注意】选择四种解法的使用顺序：直接开平方法，因 式分解法，配方法，公式法．
►知识点三 一元二次方程根的判别式
一元二次方程ax2＋bx＋c＝0(a≠0)的根的判别式是Δ＝ ___b_2－__4_a_c______.
1．Δ＞0⇔__方__程__有__两__个__不__相__等__的__实__数__根__． 2．Δ＝0⇔__方__程__有__两__个__相__等__的__实__数__根_． 3．Δ＜0⇔__方__程__没__有__实__数__根_________．
第一部分 教材同步复习
第二章 方程(组)与不等式(组)
2.2 一元二次方程
知识要点 ·归纳
陕西专版中考数学新突破复习第一部分教材同步复习第二章方程(组)与不等式(组)2.3分式方程课件202
方程x－a 1＋1x＝0 可能产生的增根是_x_＝__1_或__0___.
►知识点二 分式方程的应用
列分式方程解应用题的步骤跟其他方法解应用题有一 点 不 一 样 的 是 要 检 验 两 次 ， 既 要 检 验 求 出 来 的 解 是原否方为程 ______的根，又要检验符是合否题__意________．
第一部分 教材同步复习
第二章 方程(组)与不等式(组)
2.3 分式方程
知识要点 ·归纳
►知识点一 分式方程
1．分式方程的概念 __分__母____中含有未知数的方程叫分式方程． 2．解分式方程 (1)基本思想：分式方程去―分 ―→母整式方程
将方程x－1 2＋x＋4 2＝0 化为整式方程为_x_＋__2_＋___4_(x_－__2_)_ __＝___0_______.
易 错 辨析
易错点 解分式方程步骤错误 【例 3】 解分式方程：x－1 2＝x2－ －1x－1. 【错解】 方程两边同乘以(x－2)，得1＝1－x－1， x＝－1. 【错解分析】 去分母过程中常数项没有乘公分母，
且没有验根．
【正解】 x－1 2＝x2－ －1x－1 1＝1－x－(x－2) x＝1. 检验：当 x＝1 时，x－2≠0，∴x＝1 是原分式方程的解．
•
15、一个人炫耀什么，说明他内心缺 少什么 。。2022年3月 2022/3/22022/3/22022/3/23/2/2022
•
16、业余生活要有意义，不要越轨。2022/3/22022/3/2Marc h 2, 2022
•
17、一个人即使已登上顶峰，也仍要 自强不 息。2022/3/22022/3/22022/3/22022/3/2
•
12、人乱于心，不宽余请。2022/3/22022/3/22022/3/2Wednesday, March 02, 2022
►知识点二 分式方程的应用
列分式方程解应用题的步骤跟其他方法解应用题有一 点 不 一 样 的 是 要 检 验 两 次 ， 既 要 检 验 求 出 来 的 解 是原否方为程 ______的根，又要检验符是合否题__意________．
第一部分 教材同步复习
第二章 方程(组)与不等式(组)
2.3 分式方程
知识要点 ·归纳
►知识点一 分式方程
1．分式方程的概念 __分__母____中含有未知数的方程叫分式方程． 2．解分式方程 (1)基本思想：分式方程去―分 ―→母整式方程
将方程x－1 2＋x＋4 2＝0 化为整式方程为_x_＋__2_＋___4_(x_－__2_)_ __＝___0_______.
易 错 辨析
易错点 解分式方程步骤错误 【例 3】 解分式方程：x－1 2＝x2－ －1x－1. 【错解】 方程两边同乘以(x－2)，得1＝1－x－1， x＝－1. 【错解分析】 去分母过程中常数项没有乘公分母，
且没有验根．
【正解】 x－1 2＝x2－ －1x－1 1＝1－x－(x－2) x＝1. 检验：当 x＝1 时，x－2≠0，∴x＝1 是原分式方程的解．
•
15、一个人炫耀什么，说明他内心缺 少什么 。。2022年3月 2022/3/22022/3/22022/3/23/2/2022
•
16、业余生活要有意义，不要越轨。2022/3/22022/3/2Marc h 2, 2022
•
17、一个人即使已登上顶峰，也仍要 自强不 息。2022/3/22022/3/22022/3/22022/3/2
•
12、人乱于心，不宽余请。2022/3/22022/3/22022/3/2Wednesday, March 02, 2022
陕西专版中考数学新突破复习第一部分教材同步复习第二章方程(组)与不等式(组)2.2一元二次方程课件201902213
A．6
B．8
C．10
D．12
【思路点拨】 本题考查根与系数的关系．根据根与系
数的关系，得到x1＋x2＝2，x1·x2＝－3，再变形x
2 1
＋x
2 2
得到
(x1＋x2)2－2x1·x2，然后代入计算即可．
【解答】 ∵一元二次方程x2－2x－3＝0的两根是x1、
x2，∴x1＋x2＝2，x1·x2＝－3，∴x
【错解】 x(x＋1)＝3(x＋1)2，两边同时除以(x＋1) 得，
x＝3(x＋1) x＝3x＋3 －2x＝3 x＝－32.
【错解分析】 观察方程可知方程两边有公因式(x＋ 1)，所以方程两边同时除以(x＋1)，得x＝3(x＋1)，解得x＝ －32，没有按正确的步骤来解方程．
【正解】 x(x＋1)＝3(x＋1)2 x(x＋1)－3(x＋1)2＝0 (x＋1)[x－3(x＋1)]＝0 (x＋1)(－2x－3)＝0 x1＝－1，x2＝－32.
三年中考 ·讲练
典 例 精析
一元二次方程及其解法 (热频考点)
【例1】 (2014·陕西)若x＝－2是关于x的一元二次方程
x2－52ax＋a2＝0的一个根，则a的值为(
)
A．1或4
B．－1或－4
C．－1或4
D．1或－4
【思路点拨】 本题考查解一元二次方程．先将x＝－2
代入x2－
5 2
ax＋a2＝0中，即可得到关于a的一元二次方程，再
＝0或a＋1＝0，
解得：a＝－4或a＝－1.
十字相乘法，就是把一个二次三项式化为两个因式相乘的形式.用十字相乘法把形如＋＋的二次三项式分解因式，如下：
＋＋＝＋(＋)＋＝(＋)(＋)
⇑
⇑
(广西专用)2019年中考数学复习第二章方程(组)与不等式(组)2.3分式方程(讲解部分)素材(pdf)
３． 一般地，解分式方程时， 去分母后所得整式方程的解有可
ң②㊀ 整式方程㊀ ．
������������������������������������������������������
（２） 将方程两边同乘最简公分母，约去分母，得到一个整式方程； （３） 解这个整式方程；（４） 验根．
（１） 适当变形， 通常是对分母分解因式， 找到最简公分母；
１２ ㊀
５ 年中考 ３ 年模拟
ɦ ２． ３㊀ 分式方程
３１
考点一㊀ 分式方程及其解法
㊀ ㊀ １． ①㊀ 分母㊀ 中含有未知数的方程叫做分式方程． ２． 解分式方程的基本思路：分式方程
去分母 ㊀
４． 去分母解分式方程的一般步骤：
能使原方程中分母为零，因此应进行如下检验： 将整式方程的解 代入③㊀ 最简公分母 ㊀ ， 若最简公分母的值不为零， 则整式方程的 解是原分式 方 程 的 解； 否 则， 这 个 解 不 是 原 分 式 方 程 的 解， 是 增根．
考点二㊀ 分式方程的应用
㊀ ㊀ １． 常见题型有行程问题和工程问题．
是④㊀ 原方程㊀ 的根，再检验方程的根是否符合⑤㊀ 题意㊀，缺一不可．
２． 用分式方程解应用题时，检验分为两步，先检验所求根是不
第二章㊀ 方程（ 组） 与不等式（ 组）
１３ ㊀
３１
方法㊀ 分式方程的应用
㊀ ㊀ 在列方程之前，应先弄清问题中的已知量与未知量， 以及它 们之间的数量关系，用含未知数的式子表示相关量， 再用题中的 主要相等关系列出方程． 求出解后，必须进行检验，既要检验是不 是所列分式方程的解，又要检验是否符合题意． 需求，要求购买排球和足球若干个． 已知足球的单价比排球的单 价多 ３０ 元，用 ５００ 元购得的排球数量与用 ８００ 元购得的足球数 量相等． （１） 排球和足球的单价各是多少元？ （２） 若恰好用去 １ ２００ 元，有哪几种购买方案？ ＋３０） 元，根据题意可得方程，再求解即可； 例㊀ （ ２０１７ 河池，２４， ８ 分 ） 某班为满足同学们课外活动的
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做
毕节中考考点梳理
中考典题精讲精练
毕节中考考情及预测
毕节中考真题试做