结构动力学作业答案(roy r.craig)
结构动力学_克拉夫(第二版)课后习题

例题E2-1 如图E2-1所示,一个单层建筑理想化为刚性大梁支承在无重的柱子上。
为了计算此结构的动力特性,对这个体系进行了自由振动试验。
试验中用液压千斤顶在体系的顶部(也即刚性大梁处)使其产生侧向位移,然后突然释放使结构产生振动。
在千斤顶工作时观察到,为了使大梁产生0.20in[0.508cm]位移需要施加20 kips[9 072 kgf]。
在产生初位移后突然释放,第一个往复摆动的最大位移仅为0.16 in[0. 406 cm],而位移循环的周期为1.4 s。
从这些数据可以确定以下一些动力特性:(1)大梁的有效重量;(2)无阻尼振动频率;(3)阻尼特性;(4)六周后的振幅。
2- 1图E2-1所示建筑物的重量W为200 kips,从位移为1.2 in(t=0时)处突然释放,使其产生自由振动。
如果t=0. 64 s时往复摆动的最大位移为0.86 in,试求(a)侧移刚度k;(b)阻尼比ξ;(c)阻尼系数c。
2-2 假设图2- la 所示结构的质量和刚度为:m= kips ·s 2/in ,k=40 kips/in 。
如果体系在初始条件in 7.0)0(=υ、in/s 6.5)0(=υ&时产生自由振动,试求t=1.0s 时的位移及速度。
假设:(a) c=0(无阻尼体系); (b) c=2.8 kips ·s/in 。
2-3 假设图2- 1a 所示结构的质量和刚度为:m=5 kips ·s 2/in ,k= 20 kips/in ,且不考虑阻尼。
如果初始条件in 8.1)0(=υ,而t=1.2 s 时的位移仍然为1.8 in ,试求:(a) t=2.4 s 时的位移; (b)自由振动的振幅ρ。
例题E3-1 一种便携式谐振荷载激振器,为在现场测量结构的动力特性提供了一种有效的手段。
用此激振器对结构施以两种不同频率的荷载,并分别测出每种情况下结构反应的幅值与相位。
由此可以确定单自由度体系的质量、刚度和阻尼比。
结构力学课后答案第10章结构动力学

解:
若 为静力荷载,弹簧中反力为 。
已知图示体系为静定结构,具有一个自由度。设为B点处顺时针方向转角 为坐标。建立动力方程:
则弹簧支座的最大动反力为 。
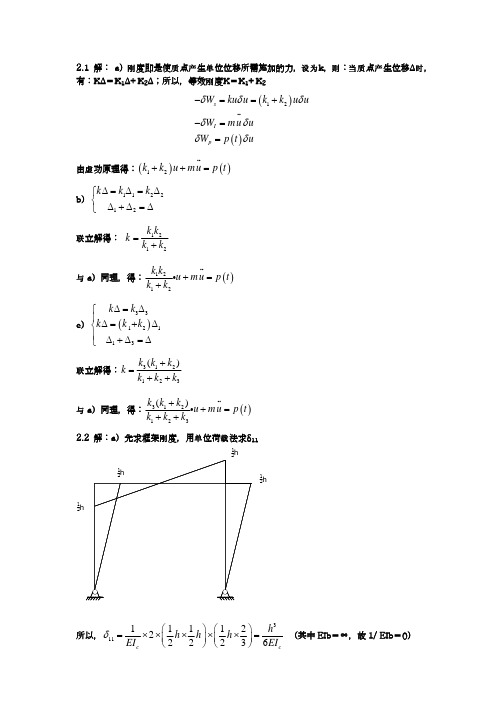
10-21设图a所示排架在横梁处受图b所示水平脉冲荷载作用,试求各柱所受的最大动剪力。已知EI=6×106Nm2,t1=,FP0=8×104N。
(a)
则同样有: 。
10-9图示结构AD和DF杆具有无限刚性和均布质量 ,A处转动弹簧铰的刚度系数为kθ,C、E处弹簧的刚度系数为k,B处阻尼器的阻尼系数为c,试建立体系自由振动时的运动方程。
*
解:
取DF隔离体, :
取AE隔离体:
将R代入,整理得:
/
10-10试建立图示各体系的运动方程。
(a)
解:(1)以支座B处转角作为坐标,绘出梁的位移和受力图如下所示。图中惯性力为三角形分布,方向与运动方向相反。
图 图
(1)求结构运动方程
如所示弯矩图,图乘后,
其中 ,稳态解:
所示结构的运动方程为 ,C点最大动位移幅值为
(2)求B点的动位移反应
,
!
B点的动位移幅值为
(3)绘制最大动力弯矩图
图 图
最大动力弯矩图
10-20试求图示集中质量体系在均布简谐荷载作用下弹簧支座的最大动反力。设杆件为无限刚性,弹簧的刚度系数为k。
(2)画出 和 图(在B点处作用一附加约束)
…
(3)列出刚度法方程
, ,
代入 、 的值,整理得:
(b)
解:
图 图
】
试用柔度法解题
此体系自由度为1 。设质量集中处的竖向位移y为坐标。
y是由动力荷载 和惯性力矩 共同引起的。
结构动力学习题解答一二章

2、 动量距定理法
适用范围:绕定轴转动的单自由度系统的振动。
解题步骤:(1) 对系统进行受力分析与动量距分析;
(2) 利用动量距定理J ,得到系统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
3、 拉格朗日方程法:
;
1、7求图1-36所示齿轮系统的固有频率。已知齿轮A的质量为mA,半径为rA,齿轮B的质量为mB,半径为rB,杆AC的扭转刚度为KA,,杆BD的扭转刚度为KB,
解:由齿轮转速之间的关系 得角速度 ;转角 ;
系统的动能为:
CA
;B D
图1-36
系统的势能为:
;
系统的机械能为
;
由 得系统运动微分方程
;
适用范围:所有的单自由度系统的振动。
解题步骤:(1)设系统的广义坐标为 ,写出系统对于坐标 的动能T与势能U的表达式;进一步写求出拉格朗日函数的表达式:L=T-U;
(2)由格朗日方程 =0,得到系统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
4、 能量守恒定理法
1、2叙述用衰减法求单自由度系统阻尼比的方法与步骤。
用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法与共振法。
方法一:衰减曲线法。
求解步骤:(1)利用试验测得单自由度系统的衰减振动曲线,并测得周期与相邻波峰与波谷的幅值 、 。
(2)由对数衰减率定义 , 进一步推导有
,
因为 较小,所以有
。
方法二:共振法求单自由度系统的阻尼比。
;L/2L/2
则固有频率为:
图1-33(b)
结构动力学习题解答

然后积分求初始速度
̇̇ d t = θ̇0 = θ 0
0+ 0+ 0+
∫
0
∫ hδ ( t ) d t = h ∫ δ ( t ) d t = h
0 0 0+
;
再积分求初位移
̇̇ d t == h )d t = 0 ; θ0 = θ 0
0+
∫
0
∫
0
̇̇ 、 θ̇ 和 θ 的瞬态响应 这样方程(6)的解就是系统对于初始条件 θ 0 0 0
1.6 求图 1-35 所示系统的固有频率。图中磙子半径为 R,质量为 M,作纯滚动。弹簧刚度 为K 。 解:磙子作平面运动, 其动能 T=T 平动 +T 转动 。
K R M 图 1-35 x
T平动 = T转动
1 ̇2; Mx 2 2 2 ̇ ⎞ 1 ⎛ MR 2 ⎞ ⎛ x ̇⎞ 1 ⎛x = I⎜ ⎟ = ⎜ ⎟⎜ ⎟ ; 2 ⎝R⎠ 2 ⎝ 2 ⎠⎝ R ⎠
U= r 2 1 1 1 1⎛ K A ϕ A 2 + K B ϕ B 2 = K Aϕ A 2 + K B ϕ B 2 = ⎜ K A + K B A 2 2 2 2 2⎜ rB ⎝
(
)
⎞ 2 ⎟ϕ ; ⎟ A ⎠
系统的机械能为
T +U = r 2 1 1⎛ ̇ A2 + ⎜ K A + K B A (m A + m B )rA 2ϕ 4 2⎜ rB 2 ⎝
d (T + U ) = 0 ,进一步得到系 dt
统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。 用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法和共振法。 方法一:衰减曲线法。 求解步骤: (1)利用试验测得单自由度系统的衰减振动曲线,并测得周期和相邻波峰和波谷 的幅值 Ai 、 Ai +1 。 (2)由对数衰减率定义 δ = ln(
结构动力学习题答案

结构动力学习题答案在结构动力学中,习题答案通常涉及对结构在动态载荷下的行为进行分析和计算。
这些习题可能包括自由振动分析、受迫振动分析、随机振动分析、模态分析、响应谱分析等。
以下是一些典型的结构动力学习题答案示例。
习题一:单自由度系统的自由振动问题:一个单自由度系统具有质量m=2kg,阻尼系数c=0.5N·s/m,弹簧刚度k=800N/m。
初始条件为位移x(0)=0.1m,速度v(0)=0。
求该系统自由振动的位移时间历程。
答案:首先,确定系统的自然频率ωn:\[ \omega_n = \sqrt{\frac{k}{m}} = \sqrt{\frac{800}{2}}\text{ rad/s} \]然后,计算阻尼比ζ:\[ \zeta = \frac{c}{2\sqrt{mk}} = \frac{0.5}{2\sqrt{2 \cdot 800}} \]由于ζ < 1,系统将进行衰减振动。
可以使用以下公式计算位移时间历程:\[ x(t) = A e^{-\zeta \omega_n t} \cos(\omega_d t + \phi) \] 其中,\( \omega_d = \sqrt{\omega_n^2 - \zeta^2 \omega_n^2} \) 是阻尼频率,A是振幅,\( \phi \)是相位角。
初始条件给出x(0)=0.1m,v(0)=0,可以解出A和\( \phi \)。
最终位移时间历程的表达式为:\[ x(t) = 0.1 e^{-\zeta \omega_n t} \cos(\omega_d t) \]习题二:单自由度系统的受迫振动问题:考虑上述单自由度系统,现在施加一个简谐力F(t)=F_0sin(ωt),其中F_0=100N,ω=10 ra d/s。
求系统的稳态响应。
答案:稳态响应可以通过傅里叶级数或直接应用受迫振动的公式来求解。
对于简谐力,系统的稳态响应为:\[ x_{ss}(t) = \frac{F_0}{k - m\omega^2} \sin(\omega t + \phi) \]其中,\( \phi \) 是相位差,可以通过以下公式计算:\[ \phi = \arctan\left(\frac{2\zeta\omega}{\omega_n^2 -\omega^2}\right) \]习题三:多自由度系统的模态分析问题:考虑一个二自由度系统,其质量矩阵M和刚度矩阵K如下:\[ M = \begin{bmatrix} m_1 & 0 \\ 0 & m_2 \end{bmatrix},\quad K = \begin{bmatrix} k_1 & -k_c \\ -k_c & k_2\end{bmatrix} \]其中,\( m_1 = 2kg \),\( m_2 = 1kg \),\( k_1 = 800N/m \),\( k_2 = 1600N/m \),\( k_c = 200N/m \)。
[美]R.克里夫《结构动力学》补充详解及习题解
![[美]R.克里夫《结构动力学》补充详解及习题解](https://img.taocdn.com/s3/m/198055225627a5e9856a561252d380eb629423b8.png)
前言结构动力学是比较难学的一门课程,但是你一旦学会并且融会贯通,你就会为成为结构院士、大师和总工垫定坚实的基础。
结构动力学学习的难点主要有以下两个方面。
1 概念难理解,主要表现在两个方面,一是表达清楚难,如果你对概念理解的很透彻,那么你写的书对概念的表述也会言简意赅,切中要害(克里夫的书就是这个特点),有的书会对一个概念用了很多文字进行解释,但是还是没有说清楚,也有的书受水平限制,本身表述就不清楚。
二是理解难,有点只可意会不可言传的味道,老师讲的头头是道,自己听得云山雾绕。
2 公式推导过程难,一是力学知识点密集,推导过程需要力学概念清析,并且需要每一步的力学公式熟悉;二是需要一定的数学基础,而且有的是在本科阶段并没有学习的数学知识。
克里夫《结构动力学》被称为经典的结构动力学教材,但是也很难看懂。
之所以被称为经典,主要就是对力学的概念表达的语言准确,概念清楚。
为什么难懂呢?是因为公式的推导过程比较简单,省略过多。
本来公式的推导过程既需要力学概念清楚也需要数学公式熟悉,但是一般人不是力学概念不清楚,就是数学公式不熟悉,更有两者都不熟悉者。
所以在学习过程中感觉很难,本学习详解是在该书概念清楚的基础上,对力学公式推导过程进行详细推导,并且有的加以解释,帮助你在学习过程中加深理解和记忆。
达到融会贯通,为你成为结构院士、大师和总工垫定坚实的基础。
以下黑体字是注释,其它为原书文字。
[美] R∙克里夫《结构动力学》辅导学习详解第1章结构动力学概述… …第Ⅰ篇单自由度体系第2章基本动力体系的组成… …§2-5 无阻尼自由振动分析如上一节所述,有阻尼的弹簧-质量体系的运动方程可表示为mv̈(t)+cv̇(t)+kν(t)=p(t)(2-19)其中ν(t)是相对于静力平衡位置的动力反应;p(t)是作用于体系的等效荷载,它可以是直接作用的或是支撑运动的结构。
为了获得方程(2-19)的解,首先考虑方程右边等于零的齐次方程,即mv̈(t)+cv̇(t)+kν(t)=0(2-20)mv(t)+kν(t)=0(2-20a)此处公式应该为mv(t)+kν(t)=0,因为该节是无阻尼自由振,而且(2-20)的解,式(2-21)也是公式mv(t)+kν(t)=0的解在作用力等于零时产生的运动称为自由振动,现在要研究的即为体系的自由振动反应。
结构动力学习题答案
k 3500 ×10 3 = = 2rad / s m 875 ×10 3
设 u (t ) = A cos wn t + B sin wn t 将 u (0 ) = 4.6 及 u (1.2) = 4.6 代入解得:
A = 4.6
B = 11.8
⇒ u (t ) = 4.6 cos 2t + 11.8 sin 2t ⇒ u (2.4) = −11.4cm
−δ Ws = kuδ u −δ WD = C u δ u
ii ii ⎛ ii ⎞ −δ WI = m1 u δ u + m2 ⎜ u + L θ ⎟ δ ( u + Lθ ) ⎝ ⎠ i
= m1 u δ u + m2 u δ u + m2 L θ δ u + m2 L u δθ + m2 L2 θ δθ
i i ⎤ 1 ⎤ ⎧ ii ⎫ ⎡ ⎧ ⎫ 0 ⎥ ⎪ q1 ⎪ ⎢ 0 2m2 q1 q2 ⎥ ⎧ q1 ⎫ ⎪− m2 g sin q 1 iq2 − m1 gL sin q1 ⎪ 2 ⎨ ii ⎬ + ⎢ ⎨ ⎬=⎨ ⎬ i 2⎥ q ⎥⎪ ⎩ ⎭ 2 ⎪ ⎪ ⎪ q + m g cos q kb m2 ⎦ ⎥⎩ 2⎭ ⎣ ⎢ 0 k − m2 q1 ⎦ ⎥ ⎩ ⎭ 2 1
1 3 2 ii i 2 ii ii i i
δ W p = m2 g cos q1δ q2 − m2 g sin q1 iq2δ q1 − m1 gL sin q1δ q1
由 δ Ws + δ WI + δ W p = 0 得:
1 2
⎡1 2 2 ⎢ 3 m1 L + m2 q2 ⎢ 0 ⎢ ⎣
结构动力学1~15

《结构动力学》习题答案1~151. 1简述求多自由度体系时程反应的振型叠加法的主要步骤 答1)建立多自由度体系的运动方程)()()()(t p t kv t v c t vm =++ 2)进行振型和频率分析对无阻尼自由振动,这个矩阵方程能归结为特征问题)(ˆ2t p vm k =-ω 由此确定振型矩阵φ和频率向量ω 3)求广义质量和荷载依次取每一个振型向量n φ,计算每一个振型的广义质量和广义荷载n T n nm Mφφ= )()(t p t p Tn n φ=4)求非耦合运动方程用每个振型的广义质量、广义力、振型频率n ω和给定的振型阻尼比n ξ就能写出每一个振型的运动方程2)(2)(ωωξ++t Y t Y n n n n nn nMt P t Y )()(=5)求对荷载的振型反应根据荷载类型,用适当的方法解这些单自由度方程,每一个振型的一般动力反应表达式用Duhamel 积分给出ττωτωξτωd t t P M t Y Dn n n tn nn n )(sin )](exp[)(1)(0---=⎰写出标准积分形式τττd t h P t Y n tn n )()()(0-=⎰式中)](exp[)(sin 1)(τωξτωωτ---=-t t M t h n n Dn nn n 10<<n ξ6)振型自由振动每一个振型有阻尼自由振动反应的通式为)exp[]sin )0()0(cos )0([)(t t Y Y t Y t Y n n Dn Dnnn n n Dn n n ωξωωωξω-++=7)求在几何坐标中的位移反应通过正规坐标变换求几何坐标表示的位移式)()()()(2211t Y t Y t Y t V n n φφφ+++=显然,它反映了各个振型贡献的叠加。
因此命名为振型叠加法。
8)弹性力反应抵抗结构变形的弹性力)()()(t Y k t kv t f s φ==当频率、振型从柔度形式的特征方程中求出时,可以采用另一种弹性力的表达式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
P2.3 解答2.3 如图所示,刚性梁AB 受到弹簧BC 的激励。
C 点的运动方程为z (t )。
试用B 点的位移u 为变量来推导系统的运动方程。
假设为小运动,采用牛顿定律来求解。
解:1. 画自由体受力图2. 列力矩平衡方程∑=0AM根据受力分析,可知:022211=+---L f Lf L f M c I3. 力与位移关系弹簧力2/11u k f =; 阻尼力2/11uc f c =; 弹簧力)(22u z k f -= 惯性力矩ML u dl Ll M u l uL l dl L M l a dm M L LLI 31)()(02200==⋅⋅=⋅⋅=⎰⎰⎰4. 将力与位移关系代入到力矩平衡方程,并化简:z k u k k u c u M 2211)41(4131=+++P2.13 解答2.13 一根均匀的杆的质量密度为ρ,其杆端有一集中质量M 。
应用假定振型法(L x x /)(=ψ)推导如下系统的轴向自由振动的运动方程。
解:1. 形函数及几何边界条件0),0(=t U )()(),(t u x t x U ψ=2. 建立虚功方程0'=+-=inertia nc W V W W δδδδ因为没有外力,所以0=nc W δu LAEudx L u L u AE Udx AEU V LL δδδδ===⎰⎰0)'( 对于惯性力而言,其虚功包括杆本身的虚功1inertia W δ和杆端集中质量的虚功2inertia W δ。
u uALdx x Lu u A Udx UA W LLinertia δρδρδρδ 3)(0221-=-=-=⎰⎰ u u M t L U t L UM W inertia δδδ -=-=),(),(2 3. 化简0)3(=⎥⎦⎤⎢⎣⎡++-u u L AE u M ALδρ因为u δ为虚位移,即0≠u δ,所以运动方程为0)3(=++u L AEu M AL ρP3.7 解答3.7 一台机器的质量为70kg ,安装在弹簧上,弹簧的总刚度为15kN/m ,总阻尼为1.2kN.s/m 。
试求如下初始条件的运动u(t)。
解:1. 运动方程及其相关参数由图可知,其运动方程为0=++ku u c um 其中kg m 70=,m N k /1054⨯=,m s N c /1200⋅=。
所以sc c ms N m c s m k n d cr n cr n /rad 32.2532.0173.26132.02.37421200/2.374273.267022/rad 73.26705000022=-⨯=-====⋅=⨯⨯=====ζωωζωω2. 系统的自由振动解⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫⎝⎛++=-t u ut u e t u d d n d t n ωωζωωζωsin cos )(000 3. 不同初始条件下的自由运动(a )0,1000==umm u ()t t et ut u e t u td d n d t n 32.25sin 34.032.25cos 1001sin cos )(55.800+=⎥⎦⎤⎢⎣⎡+=--ωωζωωζω(b )s mm uu /100,000== t e t ue t u t d dtn 32.25sin 2.2531sin )(55.80--===ωωζωP4.8 解答4.8 转动机械中的不平衡是很普遍的激励源。
下图正是这样一个例子。
(M -m )是机械的质量,m 是转动不平衡块的质量,其转动圆频率为Ω。
a. 推导机械垂向运动方程;b. 推导系统稳态响应表达式并绘制频响曲线。
解:1. 向心力及其垂向分量向心力的大小2Ω=me F ,垂向分量为t me t F F u ΩΩ=Ω=sin sin 2。
2. 系统的运动方程t me ku u c uM ΩΩ=++sin 2 化简后可得:t Mme u u u n n ΩΩ=++sin 222ωζω 3. 系统的稳态响应[]22/1222212tan )sin()2()1(r rt r r k me u -=-Ω+-Ω=ζααζ现在考虑其频率响应幅值[][][]2/1222222/1222222/12222)2()1()2()1()2()1(r r r k me r r kme r r k me u nn nζωζωωζ+-⋅=+-⎪⎪⎭⎫ ⎝⎛Ω⋅=+-Ω=定义静位移为kme U n20ω=,因此,[]22/122220)2()1()(r D r r r U U H s ⋅=+-==ΩζP5.1 解答5.1 用一个非常简单的模型来研究着陆的一架轻型飞机的冲击。
如图所示,以一个线性弹簧的集中质量表示着陆的装置。
当弹簧触到地面时,质量m 具有一垂直下降速度V 。
接触时t=0,并令u(0)=0。
(a)确定弹簧保持在接触地面时间内,质量的垂向位置u (t )的表达式; (b)确定弹簧回弹脱离地面接触的时间。
解:1. 受力分析根据初始条件:V uu t ===)0(,0)0(,0 ,及上图可知,物体的受力图如右所示。
2. 运动微分方程所以,根据受力图,其运动微分方程为:mg ku um =+3. 垂向位置)(t u 的解t A t A kmgt u n n ωωsin cos )(21++=根据初始条件,可得mkVA kmg A n n==-=221,,ωω 所以,t Vt k mg t u n nn ωωωsin )cos 1()(+-=。
4. 弹簧回弹脱离地面的时间当弹簧再次脱离地面时,其运动状态为:g t u V t ut u =-==)(,)(,0)(111 。
因此,可以任意选取一个运动量来求解脱离时间1t 。
这里,我们取速度量,则有V t V t kmgt un n n -=+=111cos sin )(ωωω 11cos 1sin t t V g n n nωωω+=-nn V g t ωπω=-2tan1⎥⎦⎤⎢⎣⎡+=-πωωn n V g t 11tan 21 ku um mg9.2 一均匀薄刚杆BC 的质量m ,长度L 附在一均匀弹性梁AB 上,设侧向位移很小。
应用恰当的自由体图,确定A 与B 点的边界条件。
解:1. A 点的边界条件为固支,即0),0(=t v00=∂∂=x xv2. B 点的边界条件刚体的受力图如上所示。
对于端部剪力边界条件,3232223222B x Lx L x Lvv mL v S EI m xt x t ===∂∂∂==+∂∂∂∂(注:2322222x L x LvL v tx t ==∂∂+∂∂∂为刚杆BC 的质心加速度)对于端部弯距边界条件,Lx Lx B xv t I xvEI M 222222)(==∂∂∂∂=∂∂=其中231mL I =解:1. 特征方程现拟采用如下通解形式x C x C x C x C x V λλλλcos sin cosh sinh )(4321+++=两端边界条件为自由端,所以L x x dx V d dx V d ==⎪⎪⎭⎪⎪⎬⎫,03322将边界条件代入通解表达式,可得0sin cos sinh cosh cos sin cosh sinh 00004321333322223322=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-----C C C C L L L L L L L L λλλλλλλλλλλλλλλλλλλλ 如果上面方程有非零解,则其系数行列式为零。
化简后得特征方程:0)cos cosh 1(10=-L L λλλ由此可见,本系统有零固有频率,而其非零频的特征方程为:00cos cosh 1≠=-λλλL L2. 现确定零频率的个数。
当0=λ时,根据自由运动微分方程(10.12),可得:044=dx Vd 。
因此,我们可以假定解的形式为342321)(x a x a x a a x V +++=。
考虑边界条件,可知043==a a 。
因此,零频率的振型为x a a x V 21)(+=。
考察得到的振型函数可知,只可能存在2个相互正交的组合。
相对应的,存在两个零频率。
3. 求零频率的刚体模态(利用正交性)。
设x a a V 210+=,x b b V 211+=,则有:0010=⎰Ldx V AV ρ032)(222122111=+++L b a L b a b a b a由于L 具有任意性,所以022=b a 。
因此可以设0,022≠=b a 。
因此,上式变为:Lb b Lb b 1221202-=⇒=+ 所以,两个刚体模态为:10a V =,)21(11Lxb V -=。
可进一步,采用102=⎰L dx AV ρ正规化方法,求解1a 、1b 。
通过计算得到:ALa ρ11=,ALb ρ31=所以,正规化的刚体模态为ALρφ10=,)21(31Lx AL -=ρφ 4. 非零频率对于非零频的特征方程,只能采用数值的方法求解。
结果是:421)731.4(ALEIρω=,422)854.7(ALEIρω=。
5. 振型通过线性方程组,4个方程中的三个,我们可以得到弯曲模态的振型表达式(0≠ω)()()()()[]x x L L x x L L A x V n n n n n n n n n n λλλλλλλλsin sinh cos cosh cos cosh sin sinh )(+--+-=P11.26 解答11.26 运用假定振型法求解悬臂梁的2-DOF 模型。
其中,自由端的变形)(t v 和转角)(t θ被定义为模型的广义坐标。
相应的振型函数如下图所示。
解:(a )推导基于如下一般多项式的形函数)(1x ψ和)(2x ψ。
32)(⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+=L x d L x c L x b a x ψ (b )推导此2-DOF 模型的运动微分方程。
解:(a )由图可知,对于)(1x ψ而言,有:.0)(;1)(;0)0(;0)0('11'11====L L ψψψψ⎪⎪⎩⎪⎪⎨⎧=+=+==⇒032100L d Lc d c b a.2;3;0;0-====⇒d c b a所以, 32123)(⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛=L x L x x ψ 对于)(2x ψ而言,有: .1)(;0)(;0)0(;0)0('22'22====L L ψψψψ⎪⎪⎩⎪⎪⎨⎧=+=+==⇒132000L d Lc d c b a.;;0;0L d L c b a =-===⇒所以, 322)(⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=L x L L x L x ψ(b )1.首先求形函数的二阶导数。
