第五章:异方差性(作业)教学文案
第五章 异方差性

Qt
ALt
K
t
eut
• U为随机误差项,它包含了资本K和劳动力L
以外的因素对产出Q的影响,比如能源、环境、
政策等。由于不同的地区这些因素不同造ui 成了 对产出的影响出现差异,使得模型中的 具有
异方差,并且这种异方差的表现是随资本和劳 动力的增加而有规律变化的。
(二)样本数据的观测误差
• 一方面,样本数据的观测误差常随着时间的 推移而逐步积累,引起随机误差项的方差增 加。另一方面,随着时间的推移,样本观测 技术会随之提高,也可能使得样本的观测误 差减少,引起随机误差项的方差减小。因此, 随着时间的推移,样本数据的观测误差会发 生变化,从而引起随机误差项的变化。
Yt 1 2 X 2i 3 X 3i ui (1)
Y 1 2 X 2 3 X 3
(2)
Yt 1' 2 X 2i ui'
(3)
Y 1' 2 X 2
(4)
由(2)、(4)得:1' 1 3 X3 (5)
由(1)、(3)、(5)得:
Var(ui )
2 i
f
(X
ji )
i 1, 2, , n
则称随机误差项存在异方差.
( 即回归模型中随机误差项的方差不是常数 )
例2:使用截面数据研究储蓄函数
假设 储蓄函数模型Y i 0 1X i ui
式中:Y i第i个家庭的储蓄额,X i第i个家庭的可支配收入,ui 代表除可支配收入以外影响储蓄额的其它因素,如利率、家庭 人口、文化背景等等。这里,同方差假设显然与事实不符。
ui' 1 3 X 3i ui 1'
5异方差性

钱还很多,这些余钱可用于购买奢侈消费品,也可用于储蓄或投资,其消费支出的方差 将会很大。显然,这里存在异方差现象。
又例如,使用截面资料建立储蓄模型(可能存在异方差)
Yi 1 2 X i ui
Yi : 第i个家庭的储蓄额; X i : 第i个家庭的可支配收入 ui : 除可支配收入之外的其它因素(如 : 利息、家庭人口、文化背景等)
销售收入 利润总额
商店名称
X
Y
回归值
残差
1、百货大楼 2、城乡贸易中心
… 19.新街口百货商场 20.星座商厦
160.0
12.8
10.2
2.634705
151.8
8.9
9.6
-0.717881
…
…
…
…
22.2
1.0
1.0
0.033928
20.7
0.5
0.9
-0.365935
资料来源:《北京统计年鉴》1997年卷 利润总额对销售收入的线性回归, Kt增大),观测误差降低, 引起ui偏离均值的程度不同,会产生异方差。
又例如,边学边改学习模型(人们在学习过程中,其行为误差随时间而减少)。
在给定的一段时间内,打字出错个数与用于打字练习的小时数的关系。随着打字练 习时间的增加,平均打错个数及打错个数的方差都有所下降。
E(2
xi u i xi2
2)2
E(
xi u i xi2
)2
xi2
u
2 i
E(
2
i j
xi x juiu j
)
E(
xi2
u
2 i
)
(xi2 ) 2
(xi2 ) 2
xi2
庞浩 计量经济学5第五章 异方差性

同方差
递增型异方差
递减型异方差
复杂型异方差
18
2.借助X-e2散点图进行判断 观察散点的纵坐标是否随解释变量Xi的变化而 变化。
~2 e2e i ei e2 ~2
X 同方差 递增异方差
X
e2
~2 e i
~2 e 2 e i
X 递减异方差 复杂型异方差
X
19
二、戈德菲尔德—夸特 (Goldfeld-Quanadt)检验
3
说明1
矩阵表示: Y X u 随机扰动项向量 其方差—协 u1 u 方差矩阵不 2 u 再是: un n1 而是:
2 2 Var Cov ( ui ) 2 nn
ei X i v i
ei
1 vi Xi
ei X i v i 1 ei vi Xi
③利用上述回归的R2、t统计量、F统计量等判断,R2 好、t统计量和F统计量显著,即可判定存在异方差。 28
说明: 1.也可以用 e i 与可能产生异方差的多个解释变 量进行回归模拟; 2.戈里瑟检验的优点在于不仅检验了异方差是否 存在,同时也给出了异方差存在时的具体表现 形式,为克服异方差提供了方便。 3.试验模型选得不好,也可能导致检验不出是否 存在异方差性。
12 2 2 Var Cov ( ui ) 2 n nn
4
说明2
随机扰动项 ui具有异方差性,可理解释为被解释变量 的条件分散程度随解释变量的变化而变化,如下图所 示:var( ui ) i2 2 f ( X i)(i 1,2,, n)
10
第二节 异方差性的后果
第五章-异方差性(作业任务)
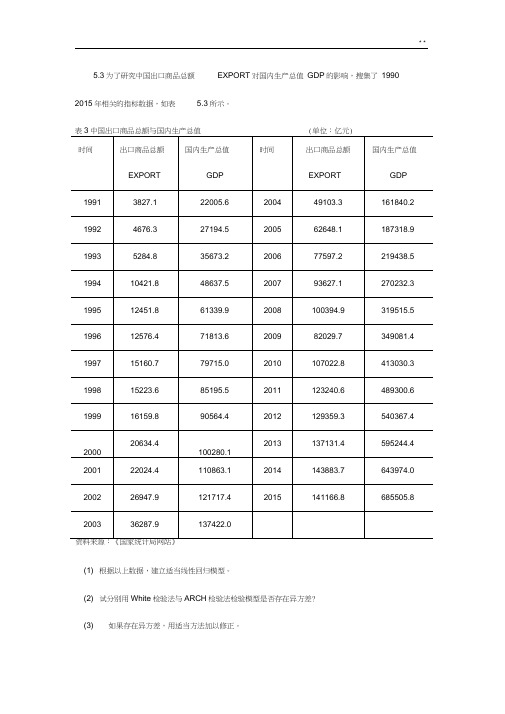
5.3为了研究中国出口商品总额EXPORT对国内生产总值GDP的影响,搜集了1990 2015年相关的指标数据,如表 5.3所示。
(1) 根据以上数据,建立适当线性回归模型。
(2) 试分别用White检验法与ARCH检验法检验模型是否存在异方差?(3) 如果存在异方差,用适当方法加以修正。
解:(1)Dependent Variable: YMethod: Least SquaresDate: 04/18/20 Time: 15:38Sample: 1991 2015Included observations: 25Variable Coefficient Std. Error t-Statistic Prob.C -673.0863 15354.24 -0.0438370.965 4X 4.061131 0.201677 20.136840.000 0R-squared 0.946323 Mean dependent var234690. 8Adjusted R-squared 0.943990 S.D. dependent var210356. 7S.E. of regression 49784.06 Akaike info criterion 24.5454Sum squared resid 5.70E+10 Schwarz criterion 24.64291 Log likelihood -304.8174 Hannan-Quinn criter. 24.57244F-statistic 405.4924 Durbin-Watson stat 0.366228Prob(F-statistic) 0.000000模型回归的结果:AY 673.0863 4.0611X it ( 0.0438 )(20.1368)R20.9463, n 25(2) white:该模型存在异方差Heteroskedasticity Test: WhiteF-statistic 4.493068 Prob. F(2,22) 0.0231Obs*R-squared 7.250127 Prob. Chi-Square(2) 0.0266 Scaled explained SS 8.361541 Prob. Chi-Square(2) 0.0153Test Equation:Dependent Variable: RESIDEMethod: Least SquaresDate: 04/18/20 Time: 17:45Sample: 1991 2015Included observations: 25Variable Coefficient Std. Error t-Statistic Prob.C -1.00E+09 1.43E+09 -0.7003780.491 0XA2 -0.455420 0.420966 -1.081847 0.2910 X 102226.2 60664.19 1.685117 0.1061R-squared 0.290005 Mean dependent var2.28E+0 9Adjusted R-squared 0.225460 S.D. dependent var 3.84E+09S.E. of regression 3.38E+09 Akaike info criterion 46.83295Sum squared resid 2.51E+20 Schwarz criterion 46.97922 Log likelihood -582.4119 Hannan-Quinn criter. 46.87352F-statistic 4.493068 Durbin-Watson stat 0.749886Prob(F-statistic) 0.023110ARCH检验:该模型存在异方差Test Equation:Dependent Variable: RESID A2Method: Least SquaresDate: 04/18/20 Time: 19:55Sample (adjusted): 1992 2015Included observations: 24 after adjustmentsVariableCoefficient Std. Error t-Statistic Prob. C8.66E+08 6.92E+08 1.251684 0.2238RESID A 2(-1) 0.817146 0.1889444.3248020.0003 R-squared0.459511 Mean dependent var 2.37E+09 Adjusted R-squared 0.434944 S.D. dependent var 3.90E+09S.E. of regression 2.93E+09 Akaike info criterion 46.51293 Sum squared resid 1.89E+20 Schwarz criterion 46.61110 Log likelihood -556.1552 Hannan-Quinn criter. 46.53898 F-statistic 18.70391Durbin-Watson stat0.888067Prob(F-statistic)0.000273(3)修正:加权最小二乘法修正却 WF Woricflil-ri UTLECi id tl e^cJ\ i « T t"l t-|<p-r f T 护i ■"i-i ■「■ H 1 < ~HV Prbll 1 T ffM r« 11 BHR 7 F r F -K * J *■ J —厂ilTHL 日芦£臼电*电引 OdiJ 1 0*左(■ 20 3>5r^lucilifl -MI^I TGR 1 Z7Q I S w= — T ,皿”=E Ba^-oa 山口 fE=-UH a P -OE = -口曰 3.2 1 且-口9 I B 之与尸-口口 ti .3-Z2E-DO 出q,峙尸・C 旦( 4.3-1 E-O^3 0 3IE 09 N.HMU O-QI 立o 右匚> - nO4 TDE--W Z.&15^=- DC1 hi-tiE - "IIIJ i. um r ci Q SJ ^F -iii i 旦日二-①口Dependent Variable: Y Method: Least Squares Date: 04/18/20 Time: 20:46 Sample: 1991 2015Included observations: 25 Weighting series: W2Weight type: Inverse variance (average scaling)VariableCoefficientStd. Errort-StatisticProb.C 10781.17 2188.706 4.925821 0.0001 X3.9316060.19200420.476670.0000Weighted StatisticsR-squared0.947998 Mean dependent var 51703.40 Adjusted R-squared 0.945737 S.D. dependent var 11816.72 S.E. of regression 8420.515 Akaike info criterion 20.99135 Sum squared resid1.63E+09Schwarz criterion21.08886「工 P U 『匕 7 日nQ r U J-4m y Q M-n!R-0 Kc D 」a 口 9m 日0: B 吝口 oaooom 口 「1 ;「m =2 Q 工H rKLog likelihood -260.3919 Hannan-Quinn criter. 21.01839F-statistic 419.2938 Durbin-Watson stat 0.539863 Prob(F-statistic) 0.000000 Weighted mean dep. 39406.30 Unweighted StatisticsR-squared 0.944994 Mean dependent var234690. 8Adjusted R-squared 0.942602 S.D. dependent var 210356.7S.E. of regression 50396.82 Sum squared resid 5.84E+1修正后进行white检验:Heteroskedasticity Test: WhiteF-statistic 0.261901 Prob. F(2,22) 0.7720 Obs*R-squared 0.581387 Prob. Chi-Square(2) 0.7477 Scaled explained SS 0.211737 Prob. Chi-Square(2) 0.8995Test Equation:Dependent Variable: WGT_RESID A2Method: Least SquaresDate: 04/18/20 Time: 20:41Sample: 1991 2015Included observations: 25Collinear test regressors dropped from specificationVariable Coefficient Std. Error t-Statistic Prob.C 71441488 22046212 3.2405340.003 8X*WGTA2 -2711.961 5055.773 -0.536409 0.5971 WGTA2 13536351 20714871 0.653461 0.5202R-squared 0.023255 Mean dependent var 65232673 Adjusted R-squared -0.065539 S.D. dependent var 61762160 S.E. of regression 63753972 Akaike info criterion 38.89113Sum squared resid 8.94E+16 Schwarz criterion 39.03739 Log likelihood -483.1391 Hannan-Quinn criter. 38.9317F-statistic 0.261901 Durbin-Watson stat 0.898907Prob(F-statistic) 0.771953修正后的模型为AY 10781.17 3.931606X it (4.925821)(20.47667)R20.9480, n 255.4 表5.4的数据是2011年各地区建筑业总产值(X)和建筑业企业利润总额(Y)。
计量经济学课件:第五章-异方差性汇总
第五章异方差性本章教学要求:根据类型,异方差性是违背古典假定情况下线性回归模型建立的另一问题。
通过本章的学习应达到,掌握异方差的基本概念包括经济学解释,异方差的出现对模型的不良影响,诊断异方差的方法和修正异方差的方法。
经过学习能够处理模型中出现的异方差问题。
第一节异方差性的概念一、例子例1,研究我国制造业利润函数,选取销售收入作为解释变量,数据为1998年的食品年制造业、饮料制造业等28个截面数据(即n=28)。
数据如下表,其中y表示制造业利润函数,x表示销售收入(单位为亿元)。
Y对X的散点图为从散点图可以看出,在线性的基础上,有的点分散幅度较小,有的点分散幅度较大。
因此,这种分散幅度的大小不一致,可以认为是由于销售收入的影响,使得制造业利润偏离均值的程度发生了变化,而这种偏离均值的程度大小不同是一种什么现象?如何定义?如果非线性,则属于哪类非线性,从图形所反映的特征看并不明显。
下面给出制造业利润对销售收入的回归估计。
模型的书写格式为2ˆ12.03350.1044(0.6165)(12.3666)0.8547,..84191.34,152.9322213.4639,146.4905Y YX R S E FY s =+=====通过变量的散点图、参数估计、残差图,可以看到模型中(随机误差)很有可能存在一种系统性的表现。
例2,改革开放以来,各地区的医疗机构都有了较快发展,不仅政府建立了一批医疗机构,还建立了不少民营医疗机构。
各地医疗机构的发展状况,除了其他因素外主要决定于对医疗服务的需求量,而医疗服务需求与人口数量有关。
为了给制定医疗机构的规划提供依据,分析比较医疗机构与人口数量的关系,建立卫生医疗机构数与人口数的回归模型。
根据四川省2000年21个地市州医疗机构数与人口数资料对模型估计的结果如下:i iX Y 3735.50548.563ˆ+-= (291.5778) (0.644284) t =(-1.931062) (8.340265)785456.02=R 774146.02=R 56003.69=F式中Y 表示卫生医疗机构数(个),X 表示人口数量(万人)。
05 异方差性学习辅导

05 异方差性学习辅导一、本章的基本内容(一)基本内容图5.1 第五章基本内容(二)本章的教学目标本章的教学目标是:深刻理解异方差性的实质、异方差出现的原因、异方差的出现对模型的不良影响(即异方差的后果),掌握估计和检验异方差性的基本思想和修正异方差的若干方法;能够运用所学的知识处理模型中出现的异方差问题,并要求初步掌握用EViews处理异方差的基本操作方法。
二、重点与难点分析1、对异方差性的基本认识由于2()()i i i i i Var u X Var Y X σ==,这里的方差度量的是被解释变量Y 的观测值围绕其条件期望的分散程度。
因此对于同方差假定来说,指的是Y 的观测值围绕回归线的分散程度相同,而异方差性指的是被解释变量观测值的分散程度是随着解释变量的变化而变化的。
从设定误差角度看,模型中的随机扰动项主要代表两方面的影响:(1)被模型忽略的其他变量对被解释变量的影响 ;(2)测量误差的影响。
实际上随机扰动主要代表的两方面因素都有可能随纳入模型的解释变量i X 的变化而变化,导致随机扰动的方差也随i X 的变化而变化,这种情况即称为存在异方差性。
所以进一步可以把异方差性看成随机扰动项的方差是某个解释变量的函数,22()()i i i Var u f X σσ== (1,2,)i n =L 。
2.为什么存在异方差时OLS 估计仍然是无偏估计?参数OLS 估计的无偏性仅依赖于基本假定中随机误差项的零均值假定(即0)(=i u E ),以及解释变量的非随机性。
事实上在第二章和第三章关于OLS 估计式无偏性的证明中并未涉及同方差性,所以异方差的存在并不影响参数估计式的无偏性。
3. 为什么存在异方差时OLS 估计式不再具有有效性?为了便于理解出现异方差或自相关时对OLS 估计式方差的影响,以一元回归12i i i Y X u ββ=++为例来说明。
22222212222()ˆ()i iii i i iiiiiii iii i i i i x y x Y Y x Y Y x Y xx xxx x X x x u x u x ββββ-===-==++=+∑∑∑∑∑∑∑∑∑∑∑∑∑∑2222222222ˆˆ()()[()][]i i i i i i x u x u Var E E E x x βββββ=-=+-=∑∑∑∑ 2222222()2[]()()2()()i ii i j ji jii i i j i j i jix u x u x u E x x E u x x E u u x ≠≠+=+=∑∑∑∑∑∑1)在异方差且自相关时,22(),()0i i i j E u E u u σ=≠,则有22222()2()ˆ()()iii j i j i j ix E ux x E u V x a u r β≠+=∑∑∑2)在异方差但无自相关时,22(),()0i i i j E u E u u σ==,则有222222222()ˆ()()()ii ii iix E u x Var x x σβ==∑∑∑∑3)在同方差且无自相关时,22(),()0i i j E u E u u σ==,则有2222222()ˆ()()ii iix E u Var x xσβ==∑∑∑4)在同方差但自相关时,22(),()0i i j E u E u u σ=≠,则有222222()ˆ()()i j i j i jiix x E u u Var xx σβ≠=+∑∑∑设存在异方差时的参数为*2β,估计式为*2ˆβ。
第五章-异方差性-答案说课讲解

第五章-异方差性-答案第五章 异方差性一、判断题1. 在异方差的情况下,通常预测失效。
( T )2. 当模型存在异方差时,普通最小二乘法是有偏的。
( F )3. 存在异方差时,可以用广义差分法进行补救。
(F )4. 存在异方差时,普通最小二乘法会低估参数估计量的方差。
(F )5. 如果回归模型遗漏一个重要变量,则OLS 残差必定表现出明显的趋势。
( T )二、单项选择题1.Goldfeld-Quandt 方法用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性2.在异方差性情况下,常用的估计方法是( D )A.一阶差分法B.广义差分法C.工具变量法D.加权最小二乘法3.White 检验方法主要用于检验( A )A.异方差性B.自相关性C.随机解释变量D.多重共线性4.下列哪种方法不是检验异方差的方法( D )A.戈德菲尔特——匡特检验B.怀特检验C.戈里瑟检验D.方差膨胀因子检验5.加权最小二乘法克服异方差的主要原理是通过赋予不同观测点以不同的权数,从而提高估计精度,即( B )A.重视大误差的作用,轻视小误差的作用B.重视小误差的作用,轻视大误差的作用C.重视小误差和大误差的作用D.轻视小误差和大误差的作用6.如果戈里瑟检验表明,普通最小二乘估计结果的残差与有显著的形式的相关关系(满足线性模型的全部经典假设),则用加权最小二乘法估计模型参数时,权数应为( B )A. B. C. D. 7.设回归模型为,其中()2i2i x u Var σ=,则b 的最有效估计量为( D )i e i x i i i v x e +=28715.0i v i x 21i x i x 1ix 1i i i u bx y +=A. B. C. D. ∑=i i x y n 1b ˆ 8.容易产生异方差的数据是( C )A. 时间序列数据B.平均数据C.横截面数据D.年度数据9.假设回归模型为i i i u X Y ++=βα,其中()2i 2i X u Var σ=,则使用加权最小二乘法估计模型时,应将模型变换为( C )。
第五章异方差性

∑
2
ˆ σ 2 = ∑ ei2 n − k 是有偏的,在此基础上的区间估 是有偏的,
计和假设检验都将不可靠。 计和假设检验都将不可靠。
第三节 异方差性的检验
一. 图形分析法
基本思想: 基本思想: 异方差性的表现是 u i 的方差随某个解释变量的变 化而变化, 的分散程度随X的变化而变化 化而变化 , 或 Y的分散程度随 的变化而变化 。 因此可 的分散程度随 的变化而变化。 与某解释变量的散布图, 利用 u i 的代表 ei 与某解释变量的散布图,观察是否存 在异方差及其异方差的形式。 在异方差及其异方差的形式。 具体方法: 具体方法: ●假定不存在异方差,进行回归,并计算剩余平方 e 2,描绘 假定不存在异方差,进行回归, 假定不存在异方差
⋅ ⋅⋅ ⋅⋅ ⋅
Yi
⋅⋅ ⋅ ⋅ ⋅ ⋅⋅ ⋅
⋅
C个
Xi
●将前后两部分分别作回归,分别计算出各部 将前后两部分分别作回归, 分剩余 ei , 2 ● 比较前后两个回归的剩余平方和 ∑ ei : ei2 之比接近于 ,为同方差; 如果两个 ∑ 之比接近于1,为同方差; ei2 之比不同于 ,为异方差 如果两个 ∑ 之比不同于1, 前提条件: 前提条件: ●样本容量较大 服从正态分布, ● ui 服从正态分布,并除异方差外满足其他 基本假定
具体步骤: 具体步骤:
●排序 将观测值按解释变量 大小顺序排列 排序:将观测值按解释变量 排序 将观测值按解释变量X大小顺序排列 数据分组:去掉中间的 去掉中间的C个 ●数据分组 去掉中间的 个(约1/4)观测值,分别 )观测值, 进行前后两部分 (n − c) 2 个观测值的回归 ●提出假设:分别进行前后两部分回归的基础上,提出 提出假设 分别进行前后两部分回归的基础上, 分别进行前后两部分回归的基础上 检验假设: 检验假设: o : ui H 即
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章:异方差性(作业)5.3 为了研究中国出口商品总额EXPORT对国内生产总值GDP的影响,搜集了1990~2015年相关的指标数据,如表5.3所示。
表3 中国出口商品总额与国内生产总值(单位:亿元)资料来源:《国家统计局网站》(1) 根据以上数据,建立适当线性回归模型。
(2) 试分别用White检验法与ARCH检验法检验模型是否存在异方差?(3) 如果存在异方差,用适当方法加以修正。
解:(1)100,000200,000300,000400,000500,000600,000700,000XYDependent Variable: Y Method: Least Squares Date: 04/18/20 Time: 15:38 Sample: 1991 2015 Included observations: 25Variable Coefficient Std. Error t-StatisticProb. C -673.0863 15354.24 -0.043837 0.9654 X 4.061131 0.201677 20.13684 0.0000 R-squared 0.946323 Mean dependent var 234690.8 Adjusted R-squared 0.943990 S.D. dependent var 210356.7 S.E. of regression 49784.06 Akaike info criterion 24.54540 Sum squared resid 5.70E+10 Schwarz criterion 24.64291 Log likelihood -304.8174 Hannan-Quinn criter. 24.57244 F-statistic 405.4924 Durbin-Watson stat 0.366228 Prob(F-statistic) 0.000000模型回归的结果:^673.0863 4.0611iX i Y =-+()(0.043820.1368)t =-20.9463,25R n ==(2)white: 该模型存在异方差Heteroskedasticity Test: WhiteF-statistic 4.493068 Prob. F(2,22)0.0231Obs*R-squared 7.250127 Prob. Chi-Square(2) 0.0266 Scaled explained SS 8.361541 Prob. Chi-Square(2) 0.0153 Test Equation:Dependent Variable: RESID^2Method: Least SquaresDate: 04/18/20 Time: 17:45Sample: 1991 2015Included observations: 25Variable Coefficient Std. Error t-Statistic Prob.C -1.00E+09 1.43E+09 -0.700378 0.4910X^2 -0.455420 0.420966 -1.081847 0.2910X 102226.2 60664.19 1.685117 0.1061 R-squared 0.290005 Mean dependent var 2.28E+09 Adjusted R-squared 0.225460 S.D. dependent var 3.84E+09 S.E. of regression 3.38E+09 Akaike info criterion 46.83295 Sum squared resid 2.51E+20 Schwarz criterion 46.97922 Log likelihood -582.4119 Hannan-Quinn criter. 46.87352 F-statistic 4.493068 Durbin-Watson stat 0.749886 Prob(F-statistic) 0.023110ARCH检验:该模型存在异方差Heteroskedasticity Test: ARCHF-statistic 18.70391 Prob. F(1,22) 0.0003 Obs*R-squared 11.02827 Prob. Chi-Square(1) 0.0009 Test Equation:Dependent Variable: RESID^2Method: Least SquaresDate: 04/18/20 Time: 19:55Sample (adjusted): 1992 2015Included observations: 24 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.C 8.66E+08 6.92E+08 1.251684 0.2238RESID^2(-1) 0.817146 0.188944 4.324802 0.0003 R-squared 0.459511 Mean dependent var 2.37E+09 Adjusted R-squared 0.434944 S.D. dependent var 3.90E+09 S.E. of regression 2.93E+09 Akaike info criterion 46.51293 Sum squared resid 1.89E+20 Schwarz criterion 46.61110 Log likelihood -556.1552 Hannan-Quinn criter. 46.53898 F-statistic 18.70391 Durbin-Watson stat 0.888067 Prob(F-statistic) 0.000273(3)修正:加权最小二乘法修正Dependent Variable: YMethod: Least SquaresDate: 04/18/20 Time: 20:46Sample: 1991 2015Included observations: 25Weighting series: W2Weight type: Inverse variance (average scaling)Variable Coefficient Std. Error t-Statistic Prob.C 10781.17 2188.706 4.925821 0.0001X 3.931606 0.192004 20.47667 0.0000Weighted StatisticsR-squared 0.947998 Mean dependent var 51703.40 Adjusted R-squared 0.945737 S.D. dependent var 11816.72 S.E. of regression 8420.515 Akaike info criterion 20.99135 Sum squared resid 1.63E+09 Schwarz criterion 21.08886 Log likelihood -260.3919 Hannan-Quinn criter. 21.01839 F-statistic 419.2938 Durbin-Watson stat 0.539863 Prob(F-statistic) 0.000000 Weighted mean dep. 39406.30Unweighted StatisticsR-squared 0.944994 Mean dependent var 234690.8 Adjusted R-squared 0.942602 S.D. dependent var 210356.7 S.E. of regression 50396.82 Sum squared resid 5.84E+10 修正后进行white检验:Heteroskedasticity Test: WhiteF-statistic 0.261901 Prob. F(2,22) 0.7720 Obs*R-squared 0.581387 Prob. Chi-Square(2) 0.7477 Scaled explained SS 0.211737 Prob. Chi-Square(2) 0.8995 Test Equation:Dependent Variable: WGT_RESID^2Method: Least SquaresDate: 04/18/20 Time: 20:41Sample: 1991 2015Included observations: 25Collinear test regressors dropped from specificationVariable Coefficient Std. Error t-Statistic Prob.C 71441488 22046212 3.240534 0.0038 X*WGT^2 -2711.961 5055.773 -0.536409 0.5971 WGT^213536351 20714871 0.653461 0.5202 R-squared0.023255 Mean dependent var 65232673 Adjusted R-squared -0.065539 S.D. dependent var 61762160 S.E. of regression 63753972 Akaike info criterion 38.89113 Sum squared resid 8.94E+16 Schwarz criterion 39.03739 Log likelihood -483.1391 Hannan-Quinn criter. 38.93170 F-statistic0.261901 Durbin-Watson stat 0.898907 Prob(F-statistic)0.771953 修正后的模型为^10781.17 3.931606iX i Y =+(4.925821)(20.47667)t =20.9480,25R n ==5.4 表5.4的数据是2011年各地区建筑业总产值(X )和建筑业企业利润总额(Y )。
表5.4 各地区建筑业总产值(X )和建筑业企业利润总额(Y ) (单位:亿元)数据来源:国家统计局网站根据样本资料建立回归模型,分析建筑业企业利润总额与建筑业总产值的关系,并判断模型是否存在异方差,如果有异方差,选用最简单的方法加以修正。
