青岛版六年级上册前四单元回顾整理1
最新六年级数学上册 第四单元 比(回顾整理)教学 青岛版优选教学课件

男孩冷静的和鱼进行拉锯战,但是强大的水流加上大鱼有力地挣扎,孩子渐渐地被拉到布满漩涡的下游深水去的边缘。我知道一但鲑鱼到达深水区就可以轻而易举地逃脱了。孩子的父亲虽然早把自己的钓竿他在一旁,但一言不发,只是站在原地关注着儿子的一举一动。
二 暗恋会导致的奇怪行迹
那是第一次见到叶少天。后来的许多天里,蕊敏都拖着亚宁一起去护城河边溜达。她知道自己是想遇上他,一想到这里,她的心就慌成一团,堵得很。 亚宁在满是野姜花的傍晚枕着胳膊大声地宣布,蕊敏,我暗恋了!我暗恋播音室的广播员,他的声音像糖。那姿态,好像暗恋是一件漂亮的新衣裳,拿出来炫耀一下。
17.有人背后称赞你,被你无意听到或者有人转告你。 18.有一个可以回去的故乡,那里有老父母、老房子,小时候爬过的那颗树以及和自己爬过树的伙伴。
19.有几个朋友,无论空间距离远近,你们之间的感觉是那样的:相见亦无事,别来常思君。 20.和老朋友信物挂碍地度过一个怀旧的下午。
21.闹些小矛盾之后与老朋友和解,丢失不起的最后并没有失去。 22.无论你是什么年龄,你有一个忘年交,是那种在你觉得幼稚的时候,有一个比你大的忘年交;在你觉得你自己老气的时候,有一个比你小的忘年交。
7 3+7
=
28(人)
答:男队员有12人,女队员有28人。
繁华的城市,川流不息的车流和人群,让人无顾及四季的美景.有人说,在这座城市中很难看到星星,因为它太渺小了.其实不然,只是你没有这份心情,身边的灯红酒绿让你视他而不见。 我常常站在阳台上望着满天的星星,想着我们曾经有过的那一幕幕。这个城市见有多少人和我一样在望着那些星星。默默地看着星星在流泪?是不是寂寞的人都喜欢看星星?
青岛版六年级上册科学全册知识点整理

第一单元遗传和变异第1课细胞1.房屋是用一块块砖建成的,蜂巢是由一个个巢房构成的。
那么,构成生物体的基本单位是细胞。
2.草履虫是由一个细胞构成的。
3.17世纪,英国科学家罗伯特·胡克用自制的显微镜观察一片软木薄片的结构,发现并命名了细胞。
4.显微镜5.植物细胞是植物生命活动的结构与功能的基本单位,由原生质体和细胞壁两部分组成。
此外还有细胞液等。
6.绝大多数生物体是由细胞构成的。
细胞是生物体的基本组成单位。
7.不同生物细胞结构不同,生物体生长发育的过程中细胞不断生长、繁殖、衰老、死亡第2课我像谁1.生物将自身的形态特征或生理特性传给后代的现象称为遗传。
2.同种生物世代之间或同代生物不同个体之间在形态特征、生理特征等方面的差异称为变异。
3.遗传和变异是生物界普遍存在的现象。
第3课灭绝的生物1.古代生物的遗体、遗物或遗迹埋藏在地下变成的跟石头一样的东西叫化石。
2.化石可以告诉我们关于地球的历史以及生物进化的许多信息,对于科学研究具有重要的作用。
3.科学家通过对恐龙粪化石的研究,可以知道恐龙的食性;通过对恐龙足迹化石的研究,可以了解恐龙的体重、长度、行进速度、生活习性等。
4.猛犸象比较耐寒,而大象没有像猛犸象一样耐寒。
猛犸象主要是生存在亚寒带和寒带的地区生活的地方,主要是以草和灌木为主。
猛犸象和大象的形态特征也是有着非常大的差别,猛犸象的象牙非常的大,而大象就没有像猛犸象一样有那么大的象牙,还有猛犸象的象毛也要比大象的象毛长很多。
5.了解恐龙等生物灭绝的原因原因一:气候变迁说6500万年前,地球气候陡然变化,气温大幅下降,造成大气含氧量下降,令恐龙无法生存。
原因二:火山爆发说因为火山的爆发,二氧化碳大量喷出,造成地球急激的温室效应,使得植物死亡。
进而造成恐龙灭亡。
原因三:大陆漂移说由于地壳变化,这块大陆在侏罗纪发生的较大的分裂和漂移现象,最终导致环境和气候的变化,恐龙因此而灭绝。
原因四:陨石坠落说约六千多万年前有一颗庞然大物坠落在地球!这一撞击使地球的地形大气层发生了翻天覆地的变化,它们没办法呼吸,吃不到食物,喝不到水……久而久之,使恐龙及其他生物灭绝。
青岛版-数学-六年级上册-【精品】《回顾整理》课件 (2)

先求男女队员各占舞蹈队 先求一份有多少人。 总人数的几分之几。
三、典型训练题
1.计算。
2 3
∶÷ 4 =
1 6
26×
12 13
=
24
1∶÷
5 7
=
1
2 5
5 8
×
2 15
= 112
三、典型训练题
2.在2008年北京奥运会上,中国获得51枚金牌,美国获得 的金牌数是中国的 121。美国获得多少枚金牌?
区别比:表示两个数的关系;分数是一个数;
返回
除法是一种运算。
二、系统梳理
用分数乘除法知识解决问题:
1. 一只大杯的容积是
1 10
升,
中杯是大杯的 1 。中杯
2
2.
一只中杯的容积是
1 20
升,
是大杯的
1 2
。大杯可以
可以盛水多少升?
盛水多少升?
1 1
×
1 2
= 210(升)
0
求一个数的几分之几是多少。
8∶10=(8×3)∶(10×3)
=(8÷2)∶(10÷2)
化简比
数
8∶10=(8÷2)∶(10÷2) = 4∶5
比
与分数、除法的关系
联系比:的前项相当于分数的分子、除法的被
除数;比的后项相当于分数的分母、除法的
除数,比值相当于分数值、除法的商。 8∶10=180= 8÷10=0.8
比的基本性质─分数的基本性质─商不变的规律
=
2 7
1
6 7
÷
5 14
=
6 7
×
124 5
=
12 5
1
计算方法
青岛版(6年制)数学六年级上册《4 回顾整理》教案

4 回顾整理⏹教学内容教材第70~72页,回顾整理⏹教学提示圆的周长,圆的面积公式的灵活应用⏹教学目标知识与能力通过引导学生回顾整理,加深学生对圆形的特征和周长面积公式的理解,进一步将知识系统化,形成知识网络。
过程与方法让学生主动参与数学知识的整理过程,经历系统整理和复习所学数学知识的过程。
情感、态度与价值观进一步经历数学知识的应用过程,提高应用所学数学知识解决简单实际问题的能力培养创新意识,在应用数学解决问题的过程中进一步体会数学的价值。
⏹重点、难点重点:学会圆的特征、会计算圆的周长、圆的面积难点:会用周长、面积公式解决实际问题。
教学准备教师准备:实物投影仪。
学生准备:练习本。
⏹教学过程一、新课导入师:同学们,想一想通过本单元的学习,你都学到了哪些知识?有什么收获?咱们交流一下吧!(学生自由发言,学生的回答可能有以下几种情况)生1:我认识了圆,我还知道圆的特征。
生2:我知道了直径与半径的相互关系,并知道圆周率是怎样来的。
生3:我学会了求圆的周长和面积。
……设计意图:通过回顾,为整理梳理知识结构做铺垫。
(二)探究新知:师:同学们能不能自己整理出本单元的知识网络?要不讨论一下,然后尝试整理。
看看那组同学做的比较好。
(1)讨论知识联系。
学生分小组进行尝试构建知识网络,教师巡视指导,了解信息。
(2)小组内说想法。
(3)交流展示。
指名到展示台前进行汇报。
生:展示知识网络师:同学们整理的非常好,下面我们应用我们整理的知识解决实际问题。
设计意图:通过构造知识网络,使知识之间的内在联系更条理,思路更清晰,有利于学生掌握。
(三)巩固新知:1、综合练习第1题(动手操作)师:同学们,既然我们对圆有了深刻的了解,那我们就先来画一个圆,要按要求来画:①画一个半径昰1.5厘米的圆。
②用字母标出圆心、半径和直径。
③画出一条它的对称轴。
(让学生独立动手画圆,并且互相比较交流在同一个圆里所有的半径怎样?所有的直径怎样?)2、综合练习第2题。
青岛版六年级数学上册知识点整理归纳

六年级上册数学知识点第一单元 分数乘法〔一〕分数乘法意义:1、分数乘整数的意义及整数乘法的意义一样,就是求几个一样加数的和的简便运算。
注:“分数乘整数〞指的是第二个因数必须是整数,不能是分数。
例如:53×7表示: 求7个53的和是多少? 或表示:53的7倍是多少? 2、一个数乘分数的意义就是求一个数的几分之几是多少。
注:“一个数乘分数〞指的是第二个因数必须是分数,不能是整数。
〔第一个因数是什么都可以〕例如:53×61表示: 求53的61是多少?9 ×61表示: 求9的61是多少? A×61表示: 求a 的61是多少?〔二〕分数乘法计算法则:1、分数乘整数的运算法则是:分子及整数相乘,分母不变。
注:〔1〕为了计算简便能约分的可先约分再计算。
〔整数和分母约分〕〔2〕约分是用整数和下面的分母约掉最大公因数。
〔整数千万不能及分母相乘,计算结果必须是最简分数〕2、分数乘分数的运算法则是:用分子相乘的积做分子,分母相乘的积做分母。
〔分子乘分子,分母乘分母〕注:〔1〕如果分数乘法算式中含有带分数,要先把带分数化成假分数再计算。
〔2〕分数化简的方法是:分子、分母同时除以它们的最大公因数。
〔3〕在乘的过程中约分,是把分子、分母中,两个可以约分的数先划去,再分别在它们的上、下方写出约分后的数。
〔约分后分子和分母必须不再含有公因数,这样计算后的结果才是最简单分数〕〔4〕分数的根本性质:分子、分母同时乘或者除以一个一样的数〔0除外〕,分数的大小不变。
〔三〕积及因数的关系:一个数〔0除外〕乘大于1的数,积大于这个数。
a×,当b >1时,c>a.一个数〔0除外〕乘小于1的数,积小于这个数。
a×,当b <1时,c<a(b≠0).一个数〔0除外〕乘等于1的数,积等于这个数。
a×,当b=1时,.注:在进展因数及积的大小比拟时,要注意因数为0时的特殊情况。
小学数学青岛版六年级上册回顾与整理教案

小学数学青岛版六年级上册回顾与整理——总复习单元备课单元教学内容青岛版小学数学六年级下册84-118页 ,包括“数与代数”.“空间与图形”.“统计与可能性”.“策略与方法”部分。
单元教材分析本单元是对小学阶段所学的数学知识进行系统地回顾整理,不仅是本册教材的一个重点,也是小学生全套教材的一个重要组成部分。
本单元教学质量的高低关系到小学阶段数学教学目标能否圆满地完成。
为了更好地实现预定的教学目标,便于教师引导学生进行系统地整理和复习,本单元把整个小学阶段所学数学知识划分为“知识与技能”.“策略与方法”两大部分,依次进行整理和复习。
本复习不仅回顾与整理小学阶段所学的知识,还对渗透的数学思想方法加以梳理,使之与所学知识融为一体,以提高学生的思维品质与数学能力,形成良好的数学素养,为后继学习打好坚实的基础。
本单元在内容编排及结构安排上打破了传统的教材总复习的框架结构,从整体上将总复习分为“知识与技能”.“策略与方法”两大部分;“知识与技能”部分又分为“数与代数”.“空间与图形”.“统计与可能性”三大领域,每个领域又细化为几个板块,如“空间与图形”领域分为“图形的认识与测量”.“图形的位置与变换”两个板块;在每个板块里又设置了“回顾与整理”.“讨论与交流”.“应用与反思”三个部分。
这样将分散的知识点连成线.织成网.组成块,较好地揭示了知识间的内在联系,有利于学生形成完整的知识结构。
单元教学目标1.复习巩固第一.二学期所学的数学知识,获得适应进一步学习所必需的数学基础和知识(包括数学事实.数学活动经验)以及必要的应用技能。
2.在对知识回顾与整理的过程中,掌握整理知识的方法,并使所学知识系统化.网络化,形成完整的认知结构。
3.在回顾整理的过程中,加深对数学思想方法的认识,能综合运用所学的知识与技能解决实际问题,形成一些解决问题的基本策略,发展应用意识。
4.学会与人合作,初步形成评价与反思意识。
5.体会数学与自然及人类社会的密切联系,感受数学的应用价值,能在数学学习活动中获得成功体验,锻炼克服困难的意志,加深对数学的理解,增强学好数学的信心,从而实现《课程标准》中所制订的各项教学指标。
青岛版(六年制)六年级数学上册第四单元 比 教案5 回顾整理

5 回顾整理⏹教学内容教材第48~51页,回顾整理⏹教学提示甲数是乙数的几分之几的灵活应用。
⏹教学目标知识与能力通过引导学生回顾整理,加深学生对分数乘除法意义的理解,会把比的问题转化成分数问题;使学生进一步掌握用算术法或方程解答已知一个数的几分之几,求这个数的生活问题和稍复杂的分数乘除法问题。
过程与方法让学生主动参与数学知识的整理过程,经历系统整理和复习所学数学知识的过程。
情感、态度与价值观进一步经历数学知识的应用过程,提高应用所学数学知识解决简单实际问题的能力培养创新意识,在应用数学解决问题的过程中进一步体会数学的价值。
⏹重点、难点重点:弄清单位“1”,会分析题中的数量关系。
难点:正确解答分数乘除法问题。
教学准备教师准备:实物投影仪。
学生准备:练习本。
⏹教学过程一、新课导入师:同学们,想一想通过分数乘除法和比的学习,你都学到了哪些知识?有什么收获?咱们交流一下吧!(学生自由发言,学生的回答可能有以下几种情况)生1:我学会了计算分数的乘除法。
生2:我能用分数的乘除法解决一些实际问题。
生3:我可以把比的问题转化成分数问题进行解决。
……设计意图:通过回顾,为整理梳理知识结构做铺垫。
(二)探究新知:师:同学们能不能自己整理出这部分的知识网络?要不讨论一下,然后尝试整理。
看看那组同学做的比较好。
(1)讨论知识联系。
学生分小组进行尝试构建知识网络,教师巡视指导,了解信息。
(2)小组内说想法。
(3)交流展示。
指名到展示台前进行汇报。
生:展示知识网络(实物投影)学生可能整理的很细但比较凌乱。
师:同学们整理的非常好。
师:出示知识网络对比。
师:下面我们应用我们整理的知识解决实际问题。
设计意图:通过构造知识网络,使知识之间的内在联系更条理,思路更清晰,有利于学生掌握。
(三)巩固新知:1、综合练习第1、2、3、5题 学生独立完成。
2、综合练习第4题。
第一个分率句的单位“1”是全校240名学生,第二个分率句的单位“1”是送鲜花的学生。
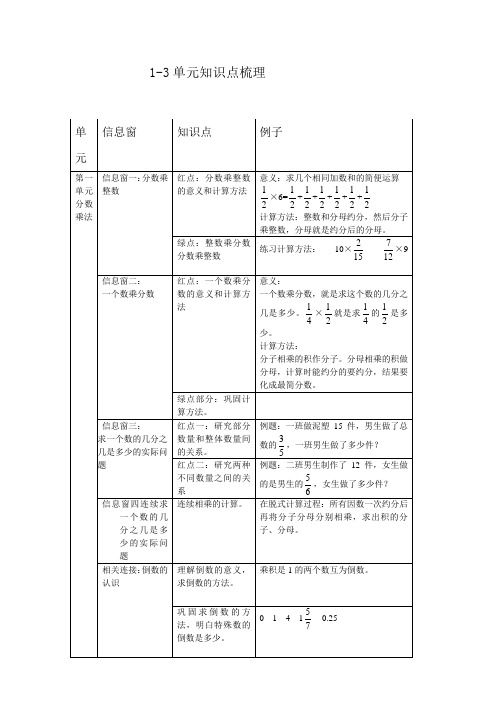
青岛版六年级数学上册1-3单元知识点梳理
分数乘法混合运算的方法和整数、小数的混合运算顺序相同。
第三单元比
比
学习比的意义、比的各部分的名称及求比值的方法。
两个数相除又叫做两个数的比。
比的前项除以后项所得的商叫做比值。
学习比的基本性质
比的前项和后项同时乘或除以相同的数(0除外),比值不变。这叫做比的基本性质。
1-3单元知识点梳理
单元
信息窗
知识点
例子
第一单元分数乘法
信息窗一:分数乘整数
红点:分数乘整数的意义和计算方法
意义:求几个相同加数和的简便运算
×6= + + + + +
计算方法:整数和分母约分,然后分子乘整数,分母就是约分后的分母。
绿点:整数乘分数分数乘整数
练习计算方法:10× ×9
信息窗二:
一个数乘分数
红点一:一个量中的“已知一个数的几分之几是多少,求这个数”的实际问题
第一布艺兴趣小组做了8个蝴蝶结,完成了本组计划的 ,第一小组机会做了多少个蝴蝶结?
红点二:两个数量间“已知一个数的几分之几是多少,求这个数”
第二小组有6人,是第一小组人数的 。第一小组有多少人?
信息窗四:学习分数乘除混合运算。
红点:
学习化简比
14:21=(14÷7):(21÷7)=2:3
14:21=( )=
约分
按比例分配
学习按比例分配的问题
科学研究表明,儿童体内水分与其他物质的比是4:1,明明体内含的水分及其他物质各有多少千克?
红点:一个数乘分数的意义和计算方法
意义:
一个数乘分数,就是求这个数的几分之几是多少。 × 就是求 的 是多少。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
40×
3
3+7 7 3+7
= 12(人)
3+7=10
40×
= 28(人)
40÷10×3 = 12 (人) 40÷10×7 = 28(人)
先求一份有多少人。
先求男女队员各占舞蹈队 总人数的几分之几。
三、综合应用
1.计算。
2 1 ∶4 = ÷ 6 3 12 26× = 24 13
5 ∶ 1÷ 7
2 = 1 5
5 2 1 × = 8 15 12
三、综合应用
2.在2008年北京奥运会上,中国获得51枚金牌,美国获得 的金牌数是中国的 12 。美国获得多少枚金牌? 17
12 51× = 36(枚) 17
答:美国获得36枚金牌。
三、综合应用
3.计算。 4 5 1 ― ×― × ― 5 12 8 1 1 4 5 1 = ― ×― × ― 5 12 8 1 3 1 = ― 24 23 23 3 ―÷―× ― 33 24 8 1 3 1 23 24 3 = ―×―× ― 33 23 8 11 1 1 3 = ― 11 9 3 1 ―÷―÷ ― 10 5 4 3 1 9 5 2 = ―×― × 4 10 3 1 2 1 = 6
返回
除法是一种运算。
二、系统梳理
用分数乘除法知识解决问题:
1 升, 1 一只中杯的容积是 升, 2. 1. 一只大杯的容积是 20 10 1 。大杯可以 1 是大杯的 中杯是大杯的 。中杯 2 2
可以盛水多少升?
盛水多少升?
1×1 = 1 (升) 10 2 20
求一个数的几分之几是多少。
解:设大杯可以盛水x升。 1 x 1 = 2 20 x= 1 ÷ 1 20 2 1 x= 10 已知一个数的几分之几是 多少,求这个数。
1 4 4 4 ×3 = × 3 = 9 3 9 3
一个数乘分 数
求一个数的几分
之几是多少。
可先约分再 1 1 3 4 1 计算。 3 4 × × = = 8 9 6 积化成最简分 8 9 数。 3 2
二、系统梳理
分数除法的计算方法:
举例 分数除以整数 计算方法
一个数除以分数
2 2 6 1 6 ÷3 = × = 7 7 3 7 1 2 6 6 14 5 12 ÷ × = = 5 5 7 7 14 1
回顾整理
整体回顾 系统梳理 综合应用 评价反思
一、整体回顾
意义 分数乘除法 计算方法
混合运算
比
意义 求比值 比与分数、 除法间的关系
比的基本性质 化简比 分数乘除法问题 按比例分配问题
解决问题
二、系统梳理
分数乘法的意义和计算方法:
意义 求几个相同加数 分数乘整数 和的简便运算。 举例 计算方法 分子与分子相 乘的积作分子, 分母与分母相 乘的积作分母。
三、综合应用
1 4.母亲节期间全校有240名同学给母亲送礼物。其中 的 3 同学送鲜花,送贺卡的人数相当于送鲜花的 1 。送贺 2 卡的同学有多少人?
1 1 × 240 × = 40(人) 3 2
答:送贺卡的同学有40人。
三、综合应用
5.为给教室消毒,需要配制5010毫升的消毒液。如果原液 与水的比是1∶500,需要原液多少毫升?
8∶10=(8÷2)∶(10÷2) = 4∶ 5
比
比的前项相当于分数的分子、除法的 联系: 被除数;比的后项相当于分数的分母、除法 的除数,比值相当于分数值、除法的商。 8 8∶10= = 8÷10=0.8 10
比的基本性质─分数的基本性质─商不变的规律
与分数、除法的关系
比表示两个数的关系;分数是一个数; 区别:
1 5010× = 10(毫升) 500+1
答:需要原液10毫升。
三、综合应用
6.一个长方形的周长是64分米,长和宽的比是5∶3,这个 长方形的面积是多少平方分米?
64÷2=32(分米) 5 32× =20(分米) 5+3 3 32× =12(分米) 5+3 20×12=240(平方分米)
答:这个长方形的面积是240平方分米。
甲数除以乙数(0除外),
等于甲数乘乙数的倒数。
返回
二、系统梳理
意义:两个数相除又叫两个数的比。
8÷10=8∶10 求比值:前项除以后项 8∶10=8÷10=0.8 化简比
数
基本性质: 比的前项和后项
比
同时乘或除以一个相同的数 (0除外),比值不变。 8∶10=(8×3)∶(10×3) =(8÷2)∶(10÷2)
二、系统梳理
用分数乘除法知识解决问题: 1 1 升,一只中杯的容积是 升, 3. 一只大杯的容积是 10 20 中杯的容积是大杯的几分之几?
1 ÷ 1 1 = 2 10 20
求一个数是另一道题之间有什么联系和区别?
二、系统梳理
按比例分配问题: 学校舞蹈队共有40人,其中男、女队员的人数比是3∶7。 男、女队员各有多少人?
