2005年浙江宁波市中考数学试题及答案
盘点出现在中考数学填空_选择_题_省略_照射下利用影长求物体高度问题为例_徐骏
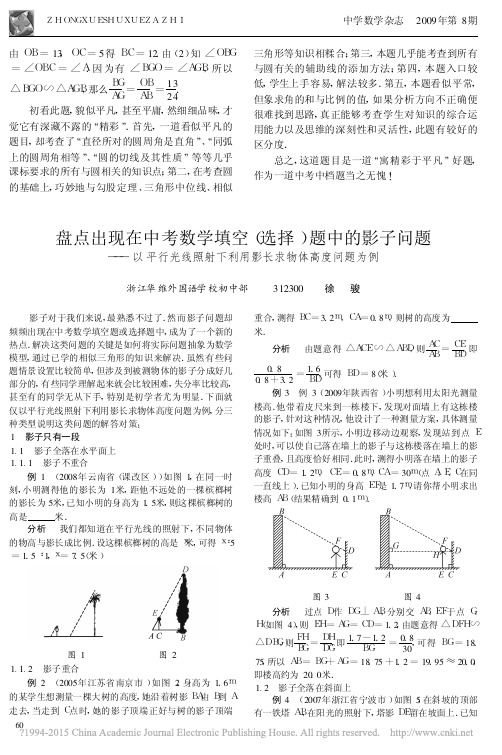
18), 则
EF=DE+DF =4.4
+0.2
=4.6,
由
AF EF
=01.4,
即
AB-0.3 4.6
=01.4, 可得
AB=11.8(米 ).
作者简介 徐骏 , 男 , 1978年 12月生 , 浙江上虞人 , 中学 一级教师 , 主要从事 课堂有效 教学研究和 解题教 学研究 .有 多篇论文 (案例 )获市一 等奖 , 在省 级以上 专业 期刊 发表论 文 30余篇 .
量树的高度 .在阳光下 , 一名同学测得一根长为 1米的竹
竿的影长为 0.4米 , 同时另一名同学测量树的高度时 , 发
现树的影子不全落在地面上 , 有一部分落在教学楼的第一
图 17 图 18
分析 影子既有在地上部分 , 又有在台阶踢面上的 ,
还有在台阶踏面上的 .过点 D作 DF⊥ AB于点 F(如图
华站在沿 DE方向的坡脚下 , 影子在平地上 , 两人的影长
分别为 4m与 2m,那么 , 塔高 AB =
m.
杆的影长为 2米 ,则电线杆的高度为
米.
图 5 图 6 图 7
分析 可用两种方法解答此题 : 法 1 过点 D作 DF⊥ CD交 AE于点 F, 过点 F作 FG
⊥ AB于点
初看此题 , 貌似平凡 , 甚至平庸 , 然细细品味 , 才
觉它有深藏不露的 “精彩 ”.首先 , 一道看似平凡的
题目 , 却考查了 “直径所对的圆周角是直角 ” 、“同弧
上的圆周角相等 ”、“圆的切线及其性质 ” 等等几乎
课标要求的所有与圆相关的知识点 ;第二 , 在考查圆
的基础上 , 巧妙地与勾股定理 、三角形中位线 、相似
2005年浙江省绍兴市中考数学试题及参考答案
益阳市2010年普通初中毕业学业考试试卷数 学注意事项:1. 本学科试卷分试题卷和答题卡两部分;2. 请将姓名、准考证号等相关信息按要求填写在答题卡上;3. 请按答题卡上的注意事项在答题卡上作答,答在试题卷上无效;4. 本学科为闭卷考试,考试时量为90分钟,卷面满分为120分;5. 考试结束后,请将试题卷和答题卡一并交回。
试 题 卷一、选择题:本大题共8小题,每小题4分,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.数轴上的点A 到原点的距离是6,则点A 表示的数为A . 6或6-B . 6C . 6-D . 3或3- 2.某班体育委员记录了第一小组七位同学定点投篮(每人投10个)的情况,投进篮框的个数为6,10,5,3,4,8,4,这组数据的中位数和极差分别是 A .4,7B .7,5C .5,7D .3,73.下列计算正确的是A.030= B.33-=-- C.331-=- D.39±=4.小军将一个直角三角板(如图1)绕它的一条直角边所在的直线旋转一周形成一个几何体,将这个几何体的侧面展开得到的大致图形是B .C .5.如图2,火车匀速通过隧道(隧道长大于火车长)时,火车进入隧道的时间x与火车在隧道内的长度y 之间的关系用图象描述大致是A. B . C . D .1图2图AB CD6.一元二次方程)0(02≠=++a c bx ax 有两个不相等...的实数根,则ac b 42-满足的条件是A.ac b 42-=0 B.ac b 42->0C.ac b 42-<0 D.ac b 42-≥07. 货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x 千米/小时,依题意列方程正确的是A.203525-=x x B.x x 352025=- C.203525+=x x D.xx 352025=+ 8.如图3,已知△ABC ,求作一点P ,使P 到∠A 的两边的距离相等,且P A =PB .下列A.P 为∠A 、∠B 两角平分线的交点B.P 为∠A 的角平分线与AB 的垂直平分线的交点 C.P 为AC 、AB 两边上的高的交点 D.P 为AC 、AB 两边的垂直平分线的交点二、填空题:本大题共5小题,每小题4分,共20分.把答案填在答题卡...中对应题号后的横线上.9.若622=-n m ,且3=-n m ,则=+n m .10. 有三张大小、形状完全相同的卡片,卡片上分别写有数字1、2、3,从这三张卡片中随机同时抽取两张,用抽出的卡片上的数字组成两位数,这个两位数是偶数的概率是 .11.如图4,在△ABC 中,AB =AC =8,AD 是底边上的高,E 为AC 中点,则DE = .12.如图5,分别以A 、B 为圆心,线段AB 的长为半径的两个圆相交于C 、D 两点,则∠CAD的度数为 . 13.如图6,反比例函数xky =的图象位于第一、三象限,其中第一象限内的图象经过点A yo x2A4图5图6图AB3图(1,2),请在第三象限内的图象上找一个你喜欢的点P ,你选择的P 点坐标为 .三、解答题:本大题共3小题,每小题8分,共24分. 14.解不等式1315>--x x ,并将解集在数轴上表示出来.15.已知31=-x ,求代数式4)1(4)1(2++-+x x 的值.16.如图7,在菱形ABCD 中,∠A =60°,AB =4,O 为对角线BD 的中点,过O 点作OE ⊥AB ,垂足为E . (1) 求∠ABD 的度数; (2)求线段BE 的长.四、解答题:本大题共2小题,每小题10分,共20分.17.南县农民一直保持着冬种油菜的习惯,利用农闲冬种一季油菜.南县农业部门对2009年的油菜籽生产成本、市场价格、种植面积和产量等进行了调查统计,并绘制了如下统计表与统计图: 请根据以上信息解答下列问题⑴ 种植油菜每亩的种子成本是多少元? ⑵农民冬种油菜每亩获利多少元?⑶2009年南县全县农民冬种油菜的总获利多少元?(结果用科学记数法表示)18.我们知道,海拔高度每上升1千米,温度下降6℃.某时刻,益阳地面温度为20℃,设高出地面x 千米处的温度为y ℃. (1)写出y 与x 之间的函数关系式;(2)已知益阳碧云峰高出地面约500米,求这时山顶的温度大约是多少℃?(3)此刻,有一架飞机飞过益阳上空,若机舱内仪表显示飞机外面的温度为-34℃,求飞机离地面的高度为多少千米?油菜每亩生产成本统计图D A BO607图五、解答题:本题满分12分.19. 我们把对称中心重合,四边分别平行的两个正方形之间的部分叫“方形环”,易知方形环四周的宽度相等..... 一条直线l 与方形环的边线有四个交点M 、'M 、'N 、N .小明在探究线段'MM 与N N ' 的数量关系时,从点'M 、'N 向对边作垂线段E M '、F N ',利用三角形全等、相似及锐角三角函数等相关知识解决了问题.请你参考小明的思路解答下列问题: ⑴当直线l 与方形环的对边相交时(如图18-),直线l 分别交AD 、D A ''、C B ''、BC 于M 、'M 、'N 、N ,小明发现'MM 与N N '相等,请你帮他说明理由; ⑵当直线l 与方形环的邻边相交时(如图28-),l 分别交AD 、D A ''、C D ''、DC于M 、'M 、'N 、N ,l 与DC 的夹角为α,你认为'MM 与N N '还相等吗?若 相等,说明理由;若不相等,求出NN MM ''的值(用含α的三角函数表示).六、解答题:本题满分12分.20.如图9,在平面直角坐标系中,已知A 、B 、C 三点的坐标分别为A (-2,0),B (6,0),C (0,3).(1)求经过A 、B 、C 三点的抛物线的解析式;(2)过C点作CD 平行于x 轴交抛物线于点D ,写出D 点的坐标,并求AD 、BC 的交点E 的坐标;(3)若抛物线的顶点为P,连结PC 、PD ,判断四边形CEDP 的形状,并说明理由.MA D 'NB 'C E 'B 'M 'A 'D N F (αPACD E Boy 1-11'N A C D E B MN 'A 'D F'M 'C 'B l 18-图28-图益阳市2010年普通初中毕业学业考试试卷数学参考答案及评分标准二.填空题:本大题共5小题,每小题4分,共20分. 9.2 10.31 11.4 12. 120 13.答案不唯一,x 、y 满足2=xy 且0,0<<y x 即可 三.解答题:本大题共3小题,每小题8分,共24分.14.解:3315>--x x ……………………………2分 42>x ……………………………4分2>x ……………………………6分……………………………8分15.解法一:原式=2)21(-+x ……………………………2分 =2)1(-x ……………………………4分 当31=-x 时原式= 2)3( ……………………………6分 =3 ……………………………8分 解法二:由31=-x 得13+=x ……………………………1分化简原式=444122+--++x x x ……………………………3分=122+-x x ……………………………4分 =1)13(2)13(2++-+ …………………………5分=12321323+--++ …………………………7分 =3 ……………………………8分16.解:⑴ 在菱形ABCD 中,AD AB =,︒=∠60A∴ABD ∆为等边三角形∴︒=∠60ABD ……………………………4分⑵由(1)可知4==AB BD9图212- 1-又∵O 为BD 的中点∴2=OB ……………………………6分 又∵AB OE ⊥,及︒=∠60ABD ∴︒=∠30BOE∴1=BE ……………………………8分四、解答题:本大题共2小题,每小题10分,共20分.17.解:⑴ %10%45%35%101=--- ……………………………1分 11%10110=⨯(元) ……………………………3分⑵ 2801103130=-⨯(元) ……………………………6分⑶ 140000000500000280=⨯ ……………………………8分 =8104.1⨯(元) ………………………10分 答:略.18.解:⑴ x y 620-= (0>x ) ……………………………4分⑵ 500米=5.0千米 …………………………5分 1750620=⋅⨯-=y (℃) ……………………………7分 ⑶ x 62034-=- ……………………………8分 9=x ……………………………10分答:略.五、解答题:本题满分12分. 19.⑴解: 在方形环中,∵AD BC F N AD E M ,',⊥⊥'∥BC ∴NF N M EM FN N EM M F N E M ',90','∠='∠=∠='∠='︒∴△E MM '≌△F NN '∴N N M M '=' ……………………………5分⑵解法一:∵α='∠='∠︒='∠='∠M M E N FN M ME N NF ,90 ∴N NF '∆∽EM M '∆ ……………………………8分 ∴NF E M N N M M '='' ∵F N E M '='∴αtan ''='=NF F N N N MM (或ααcos sin )……………………………10分 ①当︒=45α时,tan α=1,则N N M M '=' ②当︒≠45α时,N N M M '≠'则αtan =''N N M M (或ααcos sin ) ……………………………12分解法二:在方形环中,︒=∠90D又∵CD F N AD E M ⊥⊥'', ∴E M '∥E M F N DC '=',∴α=∠='∠NF N E M M ' 在F N N Rt '∆与E M M Rt '∆中, MM EM N N F N ''='=ααcos ,'sin N N M M E M M M N N F N ''=''⋅'=='cos sin tan ααα 即 αtan =''N N M M (或ααcos sin ) ……………………………10分①当︒=45α时,N N M M '=' ②当︒≠45α时,N N M M '≠'则αtan =''NN M M (或ααcos sin ) ……………………………12分 六、解答题:本题满分12分.20.解:⑴ 由于抛物线经过点)3,0(C ,可设抛物线的解析式为)0(32≠++=a bx ax y ,则⎩⎨⎧=++=+-036360324b a b a ,解得⎪⎩⎪⎨⎧=-=141b a∴抛物线的解析式为3412++-=x x y ……………………………4分 ⑵ D 的坐标为)3,4(D ……………………………5分直线AD 的解析式为121+=x y 直线BC 的解析式为321+-=x y由⎪⎪⎩⎪⎪⎨⎧+-=+=321121x y x y求得交点E 的坐标为)2,2( ……………………………8分 ⑶ 连结PE 交CD 于F ,P 的坐标为)4,2(又∵E )2,2(,)3,4(),3,0(D C∴,1==EF PF 2==FD CF ,且PE CD ⊥∴四边形CEDP 是菱形 ……………………………12分。
2005年宁波市数学中考试题-中考数学试题、初中数学中考试卷、模拟题-初中数学试卷

2005年宁波市数学中考试题-中考数学试题、初中数学中考试卷、模拟题、复习资料-初中数学试卷-试卷下载宁波市2005年高中招生数学试题一.选择题(每小题3分,共30分)1. –3的相反数是()A.B.3C. -D.-32.“天上星星有几颗,7后跟上22个0”这是国际天文学联合会上宣布的消息,用科学记数法表示宇宙空间星星颗数为()A.700×1020B.7×1023C.0.7×1023D.7×10223.如图,圆和圆的位置关系是()BAA.相交B.外离C.相切D.内含E4.不等式2-x<1的解是()A. x>1B.x>-1C.x<1D.x<-1DC5.如图,AB∥CD,∥B=230, ∥D=420,则∥E=()A.230B.420C.650D.1906.一元二次次方程x2+2x-5=0的两个根的倒数和等于()A.B.-C.D.-7.若四边形的两条对角线相等,则顺次连结该四边形各边中点所得的四边形是()A.梯形B.矩形C.菱形D.正方形YA8.正比例函数y=x与反比例函数y=的图象相交于A、C两点.AB∥x轴于B,CD∥y轴于D(如图),则四边形ABCD的面积为()OXBDA.1B.C.2D.C9.边长分别为3,4,5的三角形的内切圆半径与外接圆半径的比为()A.1∥5B.2∥5C.3∥5D.4∥5BEA10.一个袋中有4个珠子,其中2个红色,2个蓝色,除颜色外其余特征均相同,若从这个袋中任取2个珠子,都是蓝色的概率是()FDCAB.C. D.二.O填空;(每小题3分,共24分)C1BC11.分解因式2x2-18 = .ao12.实数a在数轴上的位置如图所示,化简= .13.如图,∥ABC内接于∥O, ∥B=300,AC=2cm则∥O半径长为cm.14.已知抛物线解析式为y=x2-3,则此抛物线的顶点坐标为.15.已知一个底面直径为10cm,母线长为8cm的圆锥形漏斗,它的侧面积是cm.16.在航天知识竞赛中包括甲同学在内的6名同学的平均分为74分,其中甲同学考了89分,则除甲以外的5名同学的平均分为分.17.矩形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE=cm.18.已知a-b=b-c=,a2+b2+c2=1则ab+bc+ca的值等于.三.解答题(第19、20题各5分,21~23题各6分,24~25题各8分,26题10分,27题12分,共66分)19.计算:20.已知关于x的方程的解是x=2,其中a≠0且b≠0,求代数式的值。
2005年宁波市中考数学模拟试题

2005年宁波市中考数学模拟试题学校 姓名 准考证号一. 选择题:(每小题 3 分,满分 30 分) 1. 下列计算正确的是( )A .a 3·a 2 = a 5 B. a 3÷a =a 3 C. (a 2)3 = a 5 D. (3a )3 = 3a 3 2.一元二次方程x 2-5x +2=0的两个根为x 1 , x 2 ,则x 1·x 2等于( )A. –2B. 2C. –5D. 53. 如果两个圆只有两条公切线,那么这两个圆的位置关系是( )A. 外离B. 外切C. 相交D. 内切4.用配方法将二次三项式a 2+ 4a +5变形,结果是( )A.(a –2)2+1B.(a +2)2+1C.(a –2)2-1D.(a +2)2-15.计算x xx -÷-2122(),所得正确结果是( ) A. x B. -1x C.1xD.--x x 26. 若实数x 、y 满足(x 2+y 2+2)( x 2+y 2-1)=O,则x 2+y 2的值为 A .1 B .-2 C .2或-1 D .-2或1 7.. 下列四个命题中错误的是( )A. 两条对角线互相垂直且相等的四边形是正方形B. 菱形的一条对角线平分一组对角C. 顺次连结四边形的各边中点所得的四边形是平行四边形D. 等腰梯形的两条对角线相等8.. 随着计算机技术的迅猛发展,电脑价格不断降低。
某品牌电脑按原售价降低m 元后,又降价20%,现售价为n 元,那么该电脑的原售价为( )A. ()45n m +元B. ()54n m +元 C. ()5m n +元 D. ()5n m +元9. 二次函数y ax bx c a =++≠20()的图象如图所示,下列结论:( ) (1)c <0 ()20b >(3)420a b c ++>(4)()a c b +<22其中正确的有A. 1个 B. 2个 C. 3个 D. 4个10.如图,正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从M 点沿正方体的表面爬到D 1点,蚂蚁爬行的最短距离是()(A (B )3 (C )5 (D )2B 1二. 填空题:(每小题3分,满分36分) 11. 分解因式:2a 2 —a —4 =_________.12母线长为3cm 底面半径为1cm 的圆锥的表面展开图的面积__________. 13函数y x =-+21,与两轴交于A 、B 点, 则AB=____________.14. sinB=1/2,tanB= .15. 将一张矩形纸片纸对折(如图),然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是 形 16. 观察下列各式:111222233334222+=⨯+=⨯+=⨯…………请你将猜想到的规律用自然数n n ()≥1表示出来__________________。
浙江省宁波市中考数学试题分类解析 专题12 押轴题

宁波市2002-2013年中考数学试题分类解析专题12 押轴题一、选择题1. (2002年浙江宁波3分)如图,有一住宅小区呈四边形ABCD,周长为2000 m,现规划沿小区周围铺上宽为3m的草坪,则草坪的面积是(精确至lm2)【】2. (2003年浙江宁波3分)如图,八边形ABCDEFGH中,∠A=∠B=∠C=∠D=∠E=∠F=∠G=∠H=135°,AB=CD=EF=GH=1cm,BC=DE=FG=HA=2cm,则这个八边形的面积等于【】【分析】如图,延长AB、DC交于M点,延长CD、FE交于N点,延长EF、HG交于P点,延长GH、BA交于Q点,则MNPQ是正方形,△BCM、△DEN、△FGP、△AHQ均为等腰直角三角形∴这个八边形的面积等于=矩形面积-4个小三角形的面积13341172=⨯-⨯⨯⨯=。
故选A。
3. (2003年浙江宁波3分)如图,八边形ABCDEFGH中,∠A=∠B=∠C=∠D=∠E=∠F=∠G=∠H=135°,AB=CD=EF=GH=1cm,BC=DE=FG=HA=2cm,则这个八边形的面积等于【】4. (2005年浙江宁波3分)一个袋中有4个珠子,其中2个红色,2个蓝色,除颜色外其余特征均相同,若从这个袋中任取2个珠子,都是蓝色的概率是【】A. 12B.13C.14D.16【答案】D。
【考点】概率。
【分析】根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率。
因此,设4个珠子分别为红1,红2,蓝1,蓝2,从这个袋中任取2个珠子的所有情况有(红1,红2),(红1,蓝1),(红1,蓝2),(红2,蓝1),(红2,蓝2),(蓝1,蓝2)6种,都是蓝色的情况为1种,∴从这个袋中任取2个珠子,都是蓝色的概率是16。
故选D。
5. (2006年浙江宁波大纲卷3分)已知∠BAC=45°,一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为1的⊙O与射线AC有公共点,那么x的取值范围是【】6. (2006年浙江宁波课标卷3分)如图,直角梯形ABCD中,AD∥BC,AB⊥BC,AD=3,BC=5,将腰DC绕点D逆时针方向旋转90°至DE,连接AE,则△ADE的面积是【】A.1 B.2 C.3 D.47. (2007年浙江宁波3分)如图,在斜坡的顶部有一铁塔AB ,B 是CD 的中点,CD 是水平的,在阳光 的照射下,塔影DE 留在坡面上.已知铁塔底座宽CD=12 m ,塔影长DE=18 m ,小明和小华的身高都是1.6m ,同一时刻,小明站在点E 处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别 为2m 和1m ,那么塔高AB 为【 】【答案】A 。
浙江省2005年初中毕业生学业考试试卷数学

浙江省2005年初中毕业生学业考试试卷数 学考生须知:1.全卷满分为150分,考试时间120分钟.试卷共4页,有三大题,24小题. 2.本卷答案必须做在答题卷Ⅰ、Ⅱ的相应位置上,做在试卷上无效.答卷Ⅰ共1页、答卷Ⅱ共4页.3.请用钢笔或圆珠笔将姓名、准考证号分别填写在答题卷Ⅰ、Ⅱ的相应位置上. 温馨提示:请仔细审题,细心答题,相信你一定会有出色的表现! 参考公式:二次函数y =ax 2+bx +c 的顶点坐标是)44,2(2ab ac a b --. 试 卷 Ⅰ请用铅笔将答卷Ⅰ上的准考证号和学科名称所对应的括号或方框内涂黑,然后开始答题.一、选择题(本题有10小题,每小题4分,共40分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分) 1. 计算12--的结果是( ▲ )A 、3-B 、2-C 、1-D 、3 2. 如右图,由三个小立方体搭成的几何体的俯视图是( ▲ )3. 二次函数y =x 2的图象向上平移2个单位,得到新的图象的二次函数表达式是( ▲ )A 、22-=x yB 、2)2(-=x yC 、22+=x yD 、2)2(+=x y4. 在ABC ∆中,︒=∠90C ,AB =15,sin A =31,则BC 等于( ▲ )A 、45B 、5C 、51 D 、451 5. 下列图形中,既是轴对称图形,又是中心对称图形的是 ( ▲ )6. 某住宅小区六月份中1日至6日每天用水量变化情况如图所示,那么这6天的平均用水量是 ( ▲ )A 、30吨B 、31吨C 、32吨 D、33吨7. 一个扇形的圆心角是120°,它的面积为3πcm 2,那么这个扇形的半径是( ▲ )A 、3cm B、3cm C、6cm D、9cm 8. 如图,⊙O 的直径为10,圆心O 到弦AB 的距离OM 的长为3,则弦AB 的长 是( ▲ )A 、4B 、6C 、7D 、89. 根据下列表格的对应值:判断方程02=++c bx ax (a ≠0,a ,b ,c 为常数)一个解x 的范围是( ▲ ) A 、3<x <3.23 B 、3.23<x <3.24 C 、3.24<x <3.25 D 、3.25 <x <3.2610. 一个均匀的立方体六个面上分别标有数1,2,3,4,5,6.右图是这个立方体表面的展开图.抛掷这个立方体,则朝上一面上的数恰好等于朝下一面上的数的21的概率是( ▲ ) A 、61 B 、31C 、21D 、32 试 卷 Ⅱ请将本卷的答案或解答过程用钢笔或圆珠笔写在答卷Ⅱ上. 二、填空题(本题有6小题,每小题5分,共30分) 11. 点P (1,2)关于y 轴对称的点的坐标是 ▲ . 12. 如图所示,直线a ∥b ,则∠A = ▲ 度.13. 已知⊙O 的半径为8, 圆心O 到直线l 的距离是6, 则直线l 与⊙O 的位置关系是 ▲ .14. 如果直角三角形的斜边与一条直角边的长分别是13cm 和5cm ,那么这个直角三角形的面积是 ▲ cm 2.15. 在日常生活中如取款、上网等都需要密码.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式44y x -,因式分解的结果是))()((22y x y x y x ++-,若取x =9,y =9时,则各个因式的值是:(x -y )=0,(x +y )=18,(x 2+y 2)=162,于是就可以把“018162”作为一个六位数的密码.对于多项式234xy x -,取x =10,y =10时,用上述方法产生的密码是: ▲ (写出一个即可).16. 两个反比例函数xy 3=,x y 6=在第一象限内的图象如图所示, 点P 1,P 2,P 3,…,P 2 005在反比例函数xy 6=图象上,它们的横坐标分别是x 1,x 2,x 3,…,x 2 005,纵坐标分别是1,3,5,…,共2 005个连续奇数,过点P 1, P 2,P 3,…,P 2 005分别作y 轴的平行线,与xy 3=的图象交点依次是Q 1(x 1,y 1),Q 2(x 2,y 2),Q 3(x 3,y 3),…,Q 2 005(x 2 005,y 2 005),则y 2 005= ▲ .三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)17. (1) 计算:12-0)25(60sin 2+-︒; (2) 解方程:1315+=-x x .18. 如图,在□ABCD 中,E ,F 是对角线AC 上的两点,且AE=CF .求证:BE=DF .19. 我国政府在农村扶贫工作中取得了显著成效.据国家统计局公布的数据表明,2004年末我国农村绝对贫困人口为2 610万人(比上年末减少290万人),其中东部地区为374万人,中部地区为931万人,西部地区为1 305万人.请用扇形统计图表示出2004年末这三个地区农村绝对贫困人口分布的比例(要在图中注明各部分所占的比例).20. 请将四个全等直角梯形(如图),拼成一个平行四边形,并画出两种不同的拼法示意图(拼出的两个图形只要不全等就认为是不同的拼法).21. 一个矩形,两边长分别为x cm 和10cm ,如果它的周长小于80cm ,面积大于100cm 2.求x 的取值范围.22. 某电脑公司现有A ,B ,C 三种型号的甲品牌电脑和D ,E 两种型号的乙品牌电脑.希望中学要从甲、乙两种品牌电脑中各选购一种型号的电脑. (1) 写出所有选购方案(利用树状图或列表方法表示);(2) 如果(1)中各种选购方案被选中的可能性相同,那么A 型号电脑被选中的概率是多少?(3) 现知希望中学购买甲、乙两种品牌电脑共36台(价格如图所示),恰好用了10万元人民币,其中甲品牌电脑为A 型号电脑,求购买的A 型号电脑有几台.23. 据了解,火车票价按“总里程数实际乘车里程数全程参考价⨯”的方法来确定.已知A 站至H 站总里程数为1 500千米,全程参考价为180元.下表是沿途各站至H 站的里程数:例如,要确定从B 站至E 站火车票价,其票价为()8736.8715004021130180≈=-⨯(元).(1) 求A 站至F 站的火车票价(结果精确到1元);(2) 旅客王大妈乘火车去女儿家,上车过两站后拿着火车票问乘务员:我快到站了吗?乘务员看到王大妈手中票价是66元,马上说下一站就到了.请问王大妈是在哪一站下车的?(要求写出解答过程).24. 如图,边长为1的正方形OABC 的顶点O 为坐标原点,点A 在x 轴的正半轴上,点C在y 轴的正半轴上.动点D 在线段BC 上移动(不与B ,C 重合),连接OD ,过点D 作DE ⊥OD ,交边AB 于点E ,连接OE .记CD 的长为t .(1) 当t =31时,求直线DE 的函数表达式;(2) 如果记梯形COEB 的面积为S ,那么是否存在S 的最大值?若存在,请求出这个最大值及此时t 的值;若不存在,请说明理由; (3) 当OD 2+DE 2的算术平方根取最小值时,求点E 的坐标.浙江省2005年初中毕业生学业考试数学参考答案和评分细则一、选择题(本题有10小题,每小题4分,共40分)二、填空题(本题有6小题,每小题5分,共30分)11. (-1,2) 12. 22 13. 相交 14. 30 15. 101030,或103010,或301010 16. 2004.5三、解答题(本题有8小题,第17~20题每题8分,第21题10分,第22、23题每题12分,第24题14分,共80分)17. 解:(1) 12-0)25(60sin 2+-︒=1332--……………………(每项算对,各给1分)…………3分=13-.…………………………………………………………… 1分(注:用计算器求解正确或只写答案13-均给3分)(2) 去分母,得5(x +1)=3(x -1),…………………………………………………1分去括号,得5x +5=3x -3,………………………………………………………1分 移项、合并同类项,得2x =8-. ∴x =4-.……………………………1分 经检验,x =4-是原方程的根,所以,x =4-是原方程的根.………………1分18. 证法一: ∵ 四边形ABCD 是平行四边形,∴AB CD AB CD =∥,……………………………2分 ∴BAE DCF ∠=∠.…………………………………2分 ∵AE CF =,∴ ABE CDF △≌△.……………………………2分 ∴BE DF =.……………………………………2分证法二:∵ 四边形ABCD 是平行四边形,∴AD BC AD BC =∥,.…………2分 ∴ DAF BCE ∠=∠.……………………………………………………2分 ∵ AE CF =,∴AF AE EF CF EF CE =+=+=.……………………………………1分 ∴ △ADF ≌△CBE .…………………………………………………1分DF BE ∴=∴BE DF =.……………………………………………………………2分(第18题)19. 解:东部、中部和西部三个地区农村绝对贫困人口分布的比例依次为14.3%、35.7%和50.0%,扇形统计图的圆心角依次为51.6º、128.4º和180º. 如图所示.(注:画图比例基本正确得6分,图中正确标注比例 得2分)20. 拼对一个4分,共8分,不同的拼法例举如下:21. 解:矩形的周长是2(x +10)cm ,面积是10x cm 2………………………………2分根据题意,得⎩⎨⎧><+.10010,80)10(2x x ………………………………………………4分解这个不等式组,得⎩⎨⎧><.10,30x x ………………………………………………………2分所以x 的取值范围是10<x <30.……………………………………………2分 22. 解:(1) 树状图如下(3分): 列表如下(3分):有6种可能结果:(A ,D ),(A ,E ),(B ,D ),(B ,E ),(C ,D ),(C ,E ).(注:用其它方式表达选购方案且正确给1分)(2) 因为选中A 型号电脑有2种方案,即(A ,D )(A ,E ),所以A 型号电脑被选中的概率是2163=………………………………4分 (3) 由(2)可知,当选用方案(A ,D )时,设购买A 型号、D 型号电脑分别为x ,y 台,根据题意,得3660005000100000.x y x y +=⎧⎨+=⎩,…………………………………1分解得80116.x y =-⎧⎨=⎩,经检验不符合题意,舍去;……………………………1分(第19题)(注:如考生不列方程,直接判断(A ,D )不合题意,舍去,也给2分) 当选用方案(A ,E )时,设购买A 型号、E 型号电脑分别为x ,x 台,根据题意,得3660002000100000.x y x y +=⎧⎨+=⎩,……………………………………………1分解得729.x y =⎧⎨=⎩,………………………………………………………1分所以希望中学购买了7台A 型号电脑.………………………………1分23.(1) 解法一:由已知可得=总里程数全程参考价12.01500180=.……………………………………2分A 站至F 站实际里程数为1500-219=1281.………………………2分所以A 站至F 站的火车票价为 0.12⨯1281=153.72≈154(元)……………2分解法二:由已知可得A 站至F 站的火车票价为15472.1531500)2191500(180≈=-⨯(元). …………………………………6分(2)设王大妈实际乘车里程数为x 千米,根据題意,得:661500180=x.………2分 解得 x =550(千米).…………………………………………………2分对照表格可知,D 站与G 站距离为550千米,所以王大妈是D 站或G 站下的车.……………………………………………………………………………2分 (注:解答(2)没有过程,直接给出答案,给4分;只答一个也给2分).24. 解:(1)易知△CDO ∽△BED ,所以BDCO BE CD =,即311131-=BE ,得BE =92,则点E的坐标为E 719⎛⎫⎪⎝⎭,.……………………………(2分)设直线DE 的一次函数表达式为y kx b =+,直线经过两点D 13⎛⎫ ⎪⎝⎭,1和E 719⎛⎫ ⎪⎝⎭,,代入y k x b =+得31-=k ,910=b ,故所求直线DE 的函数表达式为y =91031+-x . (2))(注:用其它三角形相似的方法求函数表达式,参照上述解法给分)(2) 存在S 的最大值.………………………………………………1分求最大值:易知△COD ∽△BDE ,所以DB CO BE CD =,即tBE t -=11, 2BE t t =-;……………………………2分2211151(1).2228S t t t ⎛⎫=⨯⨯+-=-+ ⎪⎝⎭……………………………1分故当t =21时,S 有最大值85.………………………………2分 (3) 在Rt △OED 中,22222OD DE OE OD DE +=+,的算术平方根取最小值,也就是斜边OE 取最小值.……………………………………………………1分 当斜边OE 取最小值且一直角边OA 为定值时,另一直角边AE 达到最小值, …………………………………………………………………………………1分 于是△OEA 的面积达到最小值,………………………………1分 此时,梯形COEB 的面积达到最大值.……………………………1分 由(2)知,当t =21时,梯形COEB 的面积达到最大值,故所求点E 的坐标是 314⎛⎫⎪⎝⎭,.…………………………………1分注:(3)t =2154⎛⎫ ⎪⎝⎭其值为.…………………………1分运用计算器可以验证猜想是正确的,…………………3分 此时点E 的坐标是31 4⎛⎫ ⎪⎝⎭,.…………………………………1分。
2005-2011年浙江省宁波市数学中考试卷及答案(7套)

新世纪教育网 精品资料版权所有@新世纪教育网2005年浙江省衢州市中考数学试卷一、选择题(共12小题,每小题4分,满分48分)1、(2009•随州)3的相反数是()A、﹣3B、3C、D、﹣考点:相反数。
分析:根据相反数的性质,互为相反数的两个数和为0,采用逐一检验法求解即可.解答:解:根据概念,(3的相反数)+(3)=0,则3的相反数是﹣3.故选A.点评:本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“﹣”号:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.2、(2005•衢州)设x1,x2是方程2x2+3x﹣2=0的两个根,则x1+x2的值是()A、﹣3B、3C、﹣D、考点:根与系数的关系。
分析:根据一元二次方程根与系数的关系求则可.设x1,x2是关于x的一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数)的两个实数根,则x1+x2=,x1x2=.题目所求x1+x2的结果正好为两根之和的形式,根据原方程列式计算即可求出x1+x2的值.解答:解:这里a=2,b=3,则x1+x2=.故选C点评:本题考查了一元二次方程根与系数的关系,比较简单.3、(2005•衢州)抛物线y=x2+2x﹣3与x轴的交点的个数有()A、O个B、1个C、2个D、3个考点:抛物线与x轴的交点。
分析:利用△判定二次函数图象与x轴的交点的情况即可解答.解答:解:△=22﹣4×(﹣3)>0,抛物线y=x2+2x﹣3与x轴有两个交点.故选C.点评:主要考查了二次函数的性质与一元二次方程之间的关系.4、(2005•衢州)如图,点D,E,F分别为△ABC三边的中点,且S△DEF=2,则△ABC的面积为()A、4B、6C、8D、12考点:三角形中位线定理;相似三角形的判定与性质。
分析:根据中位线定理可证△DEF∽△CBA,相似比为,所以S△BAC=4S△DEF=4×2=8.解答:解:∵D,E,F分别为△ABC三边的中点,∴DE=BC,EF=AB,DF=AC,∴△DEF∽△CBA,相似比为,∴S△DEF:S△BAC=1:4,即S△BAC=4S△DEF=4×2=8.故选C.点评:本题考查的是三角形中位线定理及相似三角形的性质.5、(2005•衢州)已知⊙O1和⊙O2的半径分别为2cm和5cm,且O1O2=6cm,则⊙O1和⊙O2的位置关系是()A、相离B、相交C、内切D、外切考点:圆与圆的位置关系。
【中考12年】浙江省宁波市2002-中考数学试题分类解析 专题11 圆

宁波市2002-2013年中考数学试题分类解析专题11 圆一、选择题1. (2003年浙江宁波3分)如图,PA切⊙O于点A,割线PBC交⊙O于点B、C,已知PB=BC=3,则PA的长是【】2. (2004年浙江宁波3分)如图,PA切⊙O于A,割线PBC经过圆心O,交⊙O于B、C两点,若PA=4,PB=2,则tan∠P的值为【】【答案】B。
【考点】切线的性质,切割线定理,锐角三角函数定义。
【分析】∵PA,PB分别是⊙O的切线和割线,∴PA2=PB•PC。
∵PA=4,PB=2,∴PC=8,BC=6。
∴OB=3。
连接OA,则∠OAP=90°。
∴OA3tan PPA4∠==。
故选B。
3. (2005年浙江宁波3分)如图,圆和圆的位置关系是【】4. (2005年浙江宁波3分)边长分别为3,4,5的三角形的内切圆半径与外接圆半径的比为【】A.1∶5B.2∶5C.3∶5D.4∶55. (2006年浙江宁波大纲卷3分)已知∠BAC=45°,一动点O在射线AB上运动(点O与点A不重合),设OA=x,如果半径为1的⊙O与射线AC有公共点,那么x的取值范围是【】6. (2007年浙江宁波3分)已知两圆的半径分别为3和5,圆心距为4,则这两圆的位置关系是【】(A)内切 (B)外切 (C)相交 (D)相离7. (2008年浙江宁波3分)已知半径分别为5cm和8cm的两圆相交,则它们的圆心距可能是【】A.1cm B.3cm C.10cm D.15cm8. (2010年浙江宁波3分)两圆的半径分别为3和5,圆心距为7,则两圆的位置关系是【】A、内切B、相交C、外切D、外离9. (2011年浙江宁波3分)如图,⊙O1 的半径为1,正方形ABCD的边长为6,点O2为正方形ABCD 的中心,O1O2垂直AB于P点,O1O2 =8.若将⊙O1绕点P按顺时针方向旋转360°,在旋转过程中,⊙O1 与正方形ABCD的边只有一个公共点的情况一共出现【】【答案】B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宁波市2005年高中招生数学试题一. 选择题(每小题3分,共30分) 1. –3的相反数是( ) A.13 B.3 C. - 13D.-3 2.“天上星星有几颗,7后跟上22个0”这是国际天文学联合会上宣布的消息,用科学记数法表示宇宙空间星星颗数为( )A.700³1020B.7³1023C.0.7³1023D.7³1022 3.如图,圆和圆的位置关系是( )A.相交B.外离C.相切D.内含 4.不等式2-x<1的解是( )A. x>1B.x>-1C.x<1D.x<-15.如图,AB ∥CD,∠B=230, ∠D=420,则∠E=( ) A.230 B.420 C.650 D.196.一元二次次方程x 2+2x -5=0的两个根的倒数和等于( ) A.25B.-25 C.52D.- 527.若四边形的两条对角线相等,则顺次连结该四边形各边中点所得的四边形是( )A.梯形B.矩形C.菱形D.正方形8.正比例函数y=x 与反比例函数y=1x 的图象相交于A 、CD(如图),则四边形ABCD 的面积为( )A.1B.32 C.2 D.52 9.边长分别为3,4,5A.1∶5B.2∶5C.3∶5D.4∶510.一个袋中有4个珠子,其中2个红色,2个蓝色,除颜色外其余特征均相同,若从这个袋中任取2个珠子,都是蓝色的概率是( ) A.12 B.13 C.14 D.16二. 填空;(每小题3分,共24分)11.分解因式2x 2-18 = .12.实数a 在数轴上的位置如图所示, = .13.如图,△ABC 内接于⊙O, ∠B=300,AC=2cm 则⊙O 半径长为 cm. 14.已知抛物线解析式为y=x 2-3,则此抛物线的顶点坐标为 .15.已知一个底面直径为10cm,母线长为8cm 的圆锥形漏斗,它的侧面积是 cm.16.在航天知识竞赛中包括甲同学在内的6名同学的平均分为74分,其中甲同学考了89分,则除甲以外的5名同学的平均分为 分.17.矩形纸片ABCD 中,AD=4cm ,AB=10cm,按如图方式折叠,使点B 与点D 重合,折痕为EF,则DE= cm.A B C E DA OBC A EB CDF C 118.已知a-b=b-c=35,a2+b2+c2=1则ab+bc+ca的值等于.三.解答题(第19、20题各5分,21~23题各6分,24~25题各8分,26题10分,27题12分,共66分)19.计算:2022223-⎛⎫⎛⎛⎫-+--⎪ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭20.已知关于x的方程323a x bx--=的解是x=2,其中a≠0且b≠0,求代数式a bb a-的值。
21(1)画出1B1C1D1使1B1C1D1与关于直线MN对称;(2)画出A2B2C2D2,A2B2C2D2与ABCD关于点O中心对称;(3) A1B1C1D1与A2B2C2D2是对称图形吗?若是,请在图上画出对称轴或对称中心22.已知一次函数物图象经过A(-2,-3),B(1,3)两点.(1)求这个一次函数的解析式;(2)试判断点P(-1,1)是否在这个一次函数的图象上?BN23.如图,△ABC 中,AB=AC,过点A 作GE ∥BC,角平分线BD 、CF 相交于点H,它们的延长线分别交GE 于点E 、G.试在图中找出3对全等三角形,并对其中一对全等三角形给出证明.24.已知关于x 的方程x 2-2(m+1)x+m=0 (1) 当m 取何值时,方程有两个实数根;(2) 为m 选取一个合适的整数,使方程有两个不相等的实数根,并求出这两个实数根.25.泸杭甬高速公路拓宽宁波段工程进入全面施工阶段,在现有双向四车道的高速公路两侧经加宽形成双向八车道.如图,路基原横断面为等腰梯形ABCD,AD ∥BC,斜坡DC 的坡度为i 1,在其一侧加宽DF=7.75米,点E 、F 分别在BC 、AD 的延长线上,斜坡FE 的坡度为i 2(i 1<i 2).设路基的高DM=h 米,拓宽后横断面一侧增加的四边形DCEF 的面积为s 米2. (1)已知i 2=1:1.7,h=3米,求ME 的长. (3) 不同路段的i 1、i 2、、、h 是不同的,请你设计一个求面积S 的公式(用含i 1、i 2的代数式表示).(通常把坡面的铅直高度与水平宽度的比叫做坡度.坡度常用字母i 表示,即i=hl,通常写成1:m 的形式)26.宁波港是一个多功能、综合性的现代化大港,年货物吞吐量位于中国大陆第二,世界排名第五,成功跻身于国际大港行列。
如图是宁波港1994年~2004年货物吞吐量统计图。
(1)统计图中你能发现哪些信息,请说出两个;(2)有人断定宁波港贷物吞吐量每年的平均增长率不超过15%,你认为他的说法正确吗?A B CD HF EG AB C M DEF请说明理由。
27.已知抛物线y=-x 2-2kx+3k 2(k>0)交x 轴于A 、B 两点,交y 轴于点C,以AB 为直径的⊙E 交y 轴于点D 、F(如图),且DF=4,G 是劣弧A D 上的动点(不与点A 、D 重合),直线CG 交x 轴于点P.(1) 求抛物线的解析式;(2) 当直线 CG 是⊙E 的切线时,求tan ∠PCO 的值.(3) 当直线CG 是⊙E 的割线时,作GM ⊥AB,垂足为H,交PF 于点M,交⊙E 于另一点N,设MN=t,GM=u,求u 关于t 的函数关系式.年份货物吞吐量(万吨)宁波市2005年高中段招生考试数学试题参考答案及评分标准三、解答题(共66分)注:1.阅卷时应按步计分,每步只设整分;2.如有其它解法,只要正确,都可参照评分标准,各步相应给分.19.解:原式=49121-+ -----------------------------------------------------------(3分) =43- -----------------------------------------------------------(5分)20.解:把x=2代入方程得33222-=-b a , -----------------------------------------(1分) 化简得322b a =, -----------------------------------------------------------(2分)∴34=b a ,43=a b . -----------------------------------------------------------(4分) ∴1274334=-=-a b b a . ------------------------------------------------------------(5分) 21.解:(1)如图,平行四边形A 1B 1C 1D 1,就是所求的平行四边形. -----------------------(2分)(2)如图,平行四边形A 2B 2C 2D 2,就是所求的平行四边形. ----------------------(4分) (3)是轴对称图形,对称轴是直线EF. -----------------------(6分)22.解:(1)设所求的一次函数的解析式为y = kx + b. ----------------------------------------(1分)E N 2B 1B 2由题意得⎩⎨⎧=+-=+-.3,32b k b k解得⎩⎨⎧==.1,2b k ----------------------------------------------------------------------------------------(2分)∴所求的解析式为y = 2x + 1. -----------------------------------------(4分) (2)点P(-1,1)不在这个一次函数的图象上. -----------------------------------------(6分) ∵当x =-1时,y = 2³(-1) + 1=-1, ∴点P(-1,1)不在直线y = 2x + 1上.23.解:△BCF ≌△CBD. ---------------------------------------(注意答案不唯一) (1分)△BHF ≌△CHD. ---------------------------------------------------------------(2分) △BDA ≌△CFA. ---------------------------------------------------------------(3分) 证明△BCF ≌△CBD. ∵AB=AC.∴∠ABC=∠ACB. ---------------------------------------------------------------(4分) ∵BD 、CF 是角平分线. ∴∠BCF=21∠ACB ,∠CBD=21∠ABC. ∴∠BCF=∠CBD. ---------------------------------------------------------------(5分)又BC=CB.∴△BCF ≌△CBD. ---------------------------------------------------------------(6分) 还有答案供参考:△BAE ≌△CAG ,△AGF ≌△AED. 24.解:(1)⊿=[-2(m + 1)]2-4m 2.=8m + 4. -------------------------------------------------------------------------(1分) 由题意知:8m + 4≥0. ------------------------------------------------------------------------(2分)解得m ≥21-. ------------------------------------------------------------------------(3分) ∴当m ≥21-时,方程有两个实数根. -------------------------------------------------(4分)(2)选取m = 0. ----------------------------------------------(答案不唯一,注意开放性) (5分) 方程为x 2-2x = 0 ------------------------------------------------------(6分) 解答x 1 = 0,x 2 = 2. ------------------------------------------------------(8分) 25.解:(1)过F 作FN ⊥CE 于N -------------------------------------------------------(1分) 则MN=DF=7.75(米),FN=DM=3(米) ∵NEFNi =2, ∴NE = 5.1(米) -------------------------------------------------------(2分) ∴ME=MN+NE=7.75 + 5.1=12.85(米) -------------------------------------------------------(4分) (2) ∵MCDMi =1,∴1i hMC =. -------------------------------------------------------(5分) 同理得2i h NE =. CE = ME -MC = MN+NE -MC. -------------------------------------------------------(6分) =7.7521i h i h -+. ∴DM CE DF S )(21+=-------------------------------------------------------(7分) h i h i h )75.775.7(2112-++=. 即h i hi h S )5.15(2112-+=. -------------------------------------------------------(8分)26.解:(1)①从统计图中可知货物吞吐量每年都在增长;---------(答案不唯一,合理即正确)(1分)②2004年货物吞吐量为22000万吨; -------------------------------(2分) (2)不正确. -------------------------------(3分) 举一反例说明这个判断不正确,例如2002年—2004年:设从2002年—2004年平均每年的增长率为x ,则--(说理方案不唯一,经估算也可以)(4分) 15398(1+x)2 = 22000 -----------------------(可选用1998—2002的数据说明)(7分) 解得x 1≈0.195,x 2≈-2.195(舍去). -----------------------(9分) ∵0.195 = 19.5%>15%. -------------------------------------------------------(10分) ∴他的说法不正确.27.解:(1)解方程 -x 2 -2kx + 3k 2 = 0.得x 1=-3k ,x 2=k..由题意知OA = |-3k | = 3k ,OB = |k| = k. ------------------------------------------(1分) ∵直径AB ⊥DF.∴OD=OF=21DF= 2 . ------------------------------------------(2分) ∵OF OD OB OA ⋅=⋅,∴3k ²k = 2³2. ----------------------------------------------------------------(3分) 得k = ±332(负的舍去). A D F 第25题N则所求的抛物线的解析式为43342+--=x x y . ---------------------------------------(4分) (2)由(1)可知AO=32,AB=338,EG=334,OC=3k 2 = 4. 连结EG ,∵CG 切⊙E 于G ,∴∠PGE=∠POC=90°, ∴Rt △PGE ∽Rt △POC. ∴33==CO EG PO PG .(﹡) ----------------------------------------------------------------(5分) 由切割线定理得)338(2+=⋅=PA PA PB PA PG . --------------------------------(6分) PO = PA+AO = PA +32.代入(﹡)式整理得PA 2 + 32PA -6 = 0.解得PA = 3-3(∵PA >0). --------------------------------(7分)∴tan ∠PCO=433+=+OC AO PA .-------------------------------------------------------------(8分) (3) ∵GN ⊥AB ,CF ⊥AB ,∴GN ∥CF ,∴△PGH ∽△PCO ,∴PO PHCO GH=. -------------------------------------------------------------(9分) 同理PO PH OF HM =. ∴OFHMCOGH=. -------------------------------------------------------------(10分) ∵CO = 4,OF = 2,∴HM =21GH =21HN = MN , -------------------------------------------------------------(11分) ∴GM=3MN , 即u = 3t(0<t ≤332)------------------------------------------------(不写出t 的取值范围不扣分)(12分)第27题。
