spss思考与练习解析
spss练习题及简 答解读

SPSS练习题1、现有两个SPSS数据文件,分别为“学生成绩一”和“学生成绩二”,请将这两份数据文件以学号为关键变量进行横向合并,形成一个完整的数据文件。
先排序data---sort cases再合并data---merge files2、有一份关于居民储蓄调查的数据存储在EXCEL中,请将该数据转换成SPSS数据文件,并在SPSS中指定其变量名标签和变量值标签。
转换Data---transpose,输题目3、利用第2题的数据,将数据分成两份文件,其中第一份文件存储常住地是“沿海或中心繁华城市”且本次存款金额在1000-2000之间的调查数据,第二份数据文件是按照简单随机抽样所选取的70%的样本数据。
选取数据data---select cases4、利用第2题数据,将其按常住地(升序)、收入水平(升序)存款金额(降序)进行多重排序。
排序data---sort cases一个一个选,加5、根据第1题的完整数据,对每个学生计算得优课程数和得良课程数,并按得优课程数的降序排序。
计算transform---count按个输,把所有课程选取,define设区间,再排序6、根据第1题的完整数据,计算每个学生课程的平均分和标准差,同时计算男生和女生各科成绩的平均分。
描述性统计,先转换Data---transpose学号放下面,全部课程(poli到his)放上面,ok,analyze---descriptive statistics---descriptives,全选,options。
先拆分data---split file 按性别拆分,analyze---descriptive statistics---descriptives全选所有课程options---mean7、利用第2题数据,大致浏览存款金额的数据分布状况,并选择恰当的组限和组距进行组距分组。
数据分组Transform---recode---下面一个,输名字,change,old,range,new value---add 挨个输,从小加到大,等距8、在第2题的数据中,如果认为调查“今年的收入比去年增加”且“预计未来一两年收入仍会会增加”的人是对自己收入比较满意和乐观的人,请利用SPSS的计数和数据筛选功能找到这些人。
统计学spss课后题答案解析

实操训练答案目录第一章 (1)第二章 (2)第三章 (3)第四章 (4)第五章 (7)第六章 (10)第七章 (17)第八章 (21)第九章 (26)第十章 (31)第一章(一)思考题略(二)练习题1.(1)定类变量(2)定类变量(3)定序变量(4)数值型变量(5)数值型变量2. A3. B4. A B C D5. D A6. A B(三)操作题略1第二章(一)思考题略(二)练习题1. BD AC2. C3. D4. D5. A(三)操作题1. 见SPSS文件2.1.sav。
2. 略。
3. 略。
4. 略。
第三章1. 2011年人均国内生产总值(agdp2011),排在前五位的是天津、上海、北京、江苏、浙江;排在后五位的是广西、西藏、甘肃、云南、贵州。
. 2011年国内生产总值(gdp2011),在东部各省市里,排在第1位的是广东,排在最后1位的分别是海南;在中部各省市里,排在第1位的是河南,排在最后1位的分别是吉林;在西部各省市里,排在第1位的是四川,排在最后1位的分别是西藏。
2. 见SPSS文件3.2.sav。
3. 见SPSS文件3.3.sav。
4. A老师提供的管理学成绩见SPSS文件3.4-1.sav,B老师提供的经济学成绩见SPSS文件3.4-2.sav,合并后的文件见SPSS文件3.4.sav。
5. 见SPSS文件3.5.sav。
6. 见SPSS文件3.6.sav。
7. 见SPSS文件3.7.sav。
8. 见SPSS文件3.8.sav。
9. 两门课程都在80分以上的共4人,见SPSS文件3.5.sav。
10. 管理学成绩在80-89,经济学成绩在90分以上的只有1人,见SPSS文件3.6.sav。
第四章1. 由于变量品牌(brand)是定类变量,所以分别用众数和异众比来描述其集中趋势和离散趋势。
由分析结果可知,众数是B,异众比是(800-279)/800=65.1%。
统计量品牌N 有效800缺失0众数 2品牌频率百分比有效百分比累积百分比有效 A 164 20.5 20.5 20.5B 279 34.9 34.9 55.4C 110 13.8 13.8 69.1D 55 6.9 6.9 76.0E 192 24.0 24.0 100.0合计800 100.0 100.02.由于变量《统计学》这门课程难吗(v2.4)是定序变量,所以用众数,中位数,四分位数来描述其集中趋势,用四分位差来描述其离散趋势。
SPSS思路和答案

一、1)对数据集居民储蓄调查数据(存款).sav按照户口类型和年龄对存款金额进行分类汇总,计算其均值和标准差。
(方法一:打开数据-分类汇总-“年龄和户口”移入分组变量、将“存款金额”两次移动到变量摘要里-分别点击下方函数——得到变量摘要里“a5 mean 和a5sd”---再点击下方“创建只包含汇总变量。
”)(方法二:利用拆分-比较组点进“年龄和户口”-分析-描述统计-描述-点进“存款金额”)得到如下:2)分组、频数分析(对数据集居民储蓄调查数据(存款).sav进行分析)(原理与上题方法二一样利用拆分--只是最后将“描述统计”中的“描述”换成“频率”)得到:(也可以加上直方图)3)分析储户的户口和职业的基本情况(听老师说可以直接做饼状图:去掉拆分——图形-——旧对话框——饼图——个案组摘要、定义——职业移入“定义区分”,户口移入“行”)得出:4)分析储户一次存款金额的分布,并对城镇储户和农村储户进行比较。
存款金额分为500元以下(包括500元)、500~2000元,2000~3500元、3500-5000元,5000以上。
(将存款金额重新编码为不同变量,定义新值,做拆分—描述——频率:转换——重新编码不同变量——。
这个应该都熟悉具体不赘述,重新定义完后要返回到变量视图给“金额等级”赋值1代表500一下,2代表500-2000.。
然后做拆分(选入户口)——分析——频率——选入“金额等级”)得到:然后可以利用“复式条形图”做出下面:(去掉拆分——图形——旧对话框——条形图——复式条形图、定义——“金额等级”到类别轴,户口到定义类聚。
两个颠倒无所谓)二. 打开数据Employee data.sav,进行如下操作:1)计算薪水增加额(saladd = salary- salbegin)(简单不说了)2)将薪水增加额分为四组(1:<=10000;2:10000-20000;3:20000-30000;4:>30000)并将分组结果保存在为变量saladd_g,定义变量saladd_g的Label (变量名标签)为薪水增加等级。
《统计分析和SPSS的应用(第五版)》课后练习答案与解析(第9章)

《统计分析与SPSS的应用〔第五版〕》〔薛薇〕课后练习答案第9章SPSS的线性回归分析1、利用第2章第9题的数据,任意选择两门课程成绩作为解释变量和被解释变量,利用SPSS 提供的绘制散点图功能进行一元线性回归分析。
请绘制全部样本以与不同性别下两门课程成绩的散点图,并在图上绘制三条回归直线,其中,第一条针对全体样本,第二和第三条分别针对男生样本和女生样本,并对各回归直线的拟和效果进行评价。
选择fore和phy两门成绩体系散点图步骤:图形→旧对话框→散点图→简单散点图→定义→将fore导入Y轴,将phy导入X轴,将sex 导入设置标记→确定。
接下来在SPSS输出查看器中,双击上图,打开图表编辑在图表编辑器中,选择"元素"菜单→选择总计拟合线→选择线性→应用→再选择元素菜单→点击子组拟合线→选择线性→应用。
分析:如上图所示,通过散点图,被解释变量y<即:fore>与解释变量phy有一定的线性关系。
但回归直线的拟合效果都不是很好。
2、请说明线性回归分析与相关分析的关系是怎样的?相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度。
只有当变量之间存在高度相关时,进行回归分析寻求其相关的具体形式才有意义。
如果在没有对变量之间是否相关以与相关方向和程度做出正确判断之前,就进行回归分析,很容易造成"虚假回归"。
与此同时,相关分析只研究变量之间相关的方向和程度,不能推断变量之间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况,因此,在具体应用过程中,只有把相关分析和回归分析结合起来,才能达到研究和分析的目的。
线性回归分析是相关性回归分析的一种,研究的是一个变量的增加或减少会不会引起另一个变量的增加或减少。
3、请说明为什么需要对线性回归方程进行统计检验?一般需要对哪些方面进行检验?检验其可信程度并找出哪些变量的影响显著、哪些不显著。
spss思考与练习解析

1、 (1)操作:分析-回归-线性,因变量y,自变量x1,x2-确定。
得方程y=+。
(2)对回归方程的显著性检验:采用P 值法做检验,提出原假设H 0:β1=β2=0,构造统计量F=1)-p -SSE/(n SSR/p,p 是自变量个数此时是2,n 是样本个数14。
F 服从分布:F~F (2,11)。
从上图最后两列看出,在显著性水平α=的条件下,p 值=sig<α,从而拒绝原假设,即在显著性水平α=的条件下,认为y 与x1,x2有显著的线性关系。
对回归系数的显著性检验:采用P 值法做检验,提出原假设H 0:βi =0(i=1,2),构造统计量)1(t ~iii--=∧∧p n i c t σβ,其中1--=∧p n SSEσ。
p值=sig<α),从而拒绝原假设,即在显著性水平α=的条件下,认为xi(i=1,2)对因变量y的线性效果显著。
(3)操作:分析-回归-线性,因变量y,自变量x1,x2-统计量-回归系数-置信区间、估计。
得到βi 的1-α的置信区间为()β1的置信水平为的置信区间是(,);β2的置信水平为的置信区间是(,);(4)回归方程的复相关系数SST SSRR2=,比较接近1,说明回归方程拟合效果较好。
模型汇总模型RR 方 调整 R 方 标准 估计的误差1 .941a.885 .864a. 预测变量: (常量), x2, x1。
(5)操作:先把待预测的数据输入表格,分析-回归-线性,因变量y,自变量x1,x2,保存-预测值、残差项选择“未标准化”-预测区间(“均值”)。
得到E (y )的点估计值是,置信水平为的置信区间是(,)3、(1)操作:分析-回归-线性,因变量y,自变量x,确定。
得方程y=。
系数a模型 非标准化系数标准系数tSig. B标准 误差试用版 1(常量).442.065 x.004 .000.839.000a. 因变量: y(2)诊断该问题是否存在异方差性,两种方法等级相关系数法残差图e y ~∧。
《统计分析和SPSS的应用(第五版)》课后练习答案与解析(第9章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第9章SPSS的线性回归分析1、利用第2章第9题的数据,任意选择两门课程成绩作为解释变量和被解释变量,利用SPSS 提供的绘制散点图功能进行一元线性回归分析。
请绘制全部样本以及不同性别下两门课程成绩的散点图,并在图上绘制三条回归直线,其中,第一条针对全体样本,第二和第三条分别针对男生样本和女生样本,并对各回归直线的拟和效果进行评价。
选择fore和phy两门成绩体系散点图步骤:图形→旧对话框→散点图→简单散点图→定义→将fore导入Y轴,将phy导入X轴,将sex导入设置标记→确定。
接下来在SPSS输出查看器中,双击上图,打开图表编辑→点击子组拟合线→选择线性→应用。
分析:如上图所示,通过散点图,被解释变量y(即:fore)与解释变量phy有一定的线性关系。
但回归直线的拟合效果都不是很好。
2、请说明线性回归分析与相关分析的关系是怎样的?相关分析是回归分析的基础和前提,回归分析则是相关分析的深入和继续。
相关分析需要依靠回归分析来表现变量之间数量相关的具体形式,而回归分析则需要依靠相关分析来表现变量之间数量变化的相关程度。
只有当变量之间存在高度相关时,进行回归分析寻求其相关的具体形式才有意义。
如果在没有对变量之间是否相关以及相关方向和程度做出正确判断之前,就进行回归分析,很容易造成“虚假回归”。
与此同时,相关分析只研究变量之间相关的方向和程度,不能推断变量之间相互关系的具体形式,也无法从一个变量的变化来推测另一个变量的变化情况,因此,在具体应用过程中,只有把相关分析和回归分析结合起来,才能达到研究和分析的目的。
线性回归分析是相关性回归分析的一种,研究的是一个变量的增加或减少会不会引起另一个变量的增加或减少。
3、请说明为什么需要对线性回归方程进行统计检验?一般需要对哪些方面进行检验?检验其可信程度并找出哪些变量的影响显著、哪些不显著。
主要包括回归方程的拟合优度检验、显著性检验、回归系数的显著性检验、残差分析等。
SPSS思路和标准答案
一、
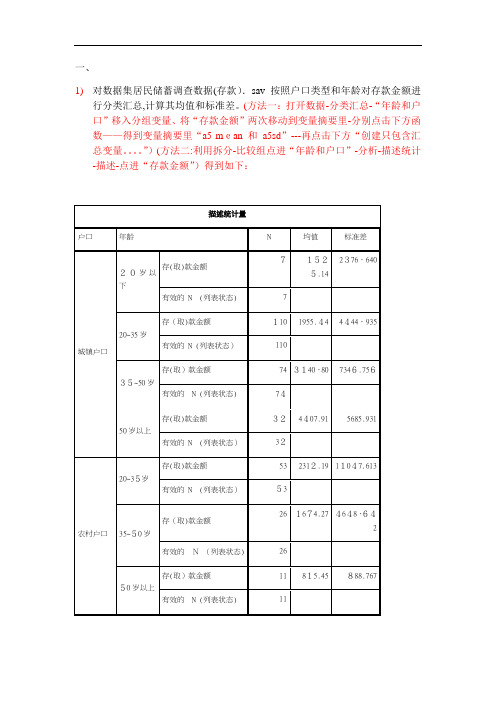
1)对数据集居民储蓄调查数据(存款).sav按照户口类型和年龄对存款金额进
行分类汇总,计算其均值和标准差。
(方法一:打开数据-分类汇总-“年龄和户口”移入分组变量、将“存款金额”两次移动到变量摘要里-分别点击下方函数——得到变量摘要里“a5 mean 和a5sd”---再点击下方“创建只包含汇总变量。
”)(方法二:利用拆分-比较组点进“年龄和户口”-分析-描述统计-描述-点进“存款金额”)得到如下:
2)分组、频数分析(对数据集居民储蓄调查数据(存款).sav进行分析)
(原理与上题方法二一样利用拆分--只是最后将“描述统计”中的“描述”换成“频率”)得到:(也可以加上直方图)
3)分析储户的户口和职业的基本情况(听老师说可以直接做饼状图:去掉拆分—
—图形-——旧对话框——饼图——个案组摘要、定义——职业移入“定义区分”,户口移入“行”)得出:。
spss习题及其答案

spss习题及其答案
SPSS习题及其答案
SPSS(Statistical Package for the Social Sciences)是一种统计分析软件,广泛应用于社会科学和商业研究。
它可以帮助研究人员对数据进行分析、建模和预测。
在学习和使用SPSS的过程中,习题和答案是非常重要的,可以帮助我们更好地理解和掌握SPSS的使用方法和技巧。
下面是一些常见的SPSS习题及其答案,供大家参考:
1. 问题:如何在SPSS中导入数据?
答案:在SPSS中,可以通过“文件”菜单中的“打开”选项来导入数据,也可以直接拖拽数据文件到SPSS的工作区。
2. 问题:如何计算变量的描述性统计量?
答案:在SPSS中,可以使用“分析”菜单中的“描述统计”选项来计算变量的描述性统计量,包括均值、标准差、最大值、最小值等。
3. 问题:如何进行相关性分析?
答案:在SPSS中,可以使用“分析”菜单中的“相关”选项来进行相关性分析,可以计算变量之间的皮尔逊相关系数或斯皮尔曼相关系数。
4. 问题:如何进行回归分析?
答案:在SPSS中,可以使用“回归”选项来进行回归分析,可以进行简单线性回归、多元线性回归等不同类型的回归分析。
5. 问题:如何进行因子分析?
答案:在SPSS中,可以使用“因子”选项来进行因子分析,可以帮助研究人员发现变量之间的潜在结构和关联。
通过以上习题及其答案的学习和实践,我们可以更好地掌握SPSS的使用方法,提高数据分析的效率和准确性。
希望大家在学习SPSS的过程中能够多多练习,不断提升自己的数据分析能力。
SPSS习题及其答案是我们学习的好帮手,也是我们进步的动力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、 (1)操作:分析-回归-线性,因变量y,自变量x1,x2-确定。
得方程y=209.875+0.292x1-87.647x2。
(2)对回归方程的显著性检验:采用P 值法做检验,提出原假设H 0:β1=β2=0,构造统计量F=1)-p-SSE/(n SSR/p,p 是自变量个数此时是2,n 是样本个数14。
F 服从分布:F~F (2,11)。
从上图最后两列看出,在显著性水平α=0.05的条件下,p 值=sig<α,从而拒绝原假设,即在显著性水平α=0.05的条件下,认为y 与x1,x2有显著的线性关系。
对回归系数的显著性检验:采用P 值法做检验,提出原假设H 0:βi=0(i=1,2),构造统计量)1(t ~iii--=∧∧p n i c t σβ,其中1--=∧p n SSEσ。
p 值=sig<α),从而拒绝原假设,即在显著性水平α=0.05的条件下,认为xi (i=1,2)对因变量y 的线性效果显著。
(3)操作:分析-回归-线性,因变量y,自变量x1,x2-统计量-回归系数-置信区间、估计。
得到βi 的1-α的置信区间为()β1的置信水平为0.95的置信区间是(0.096,0.488);β2的置信水平为0.95的置信区间是(-115.034,-60.261);(4)回归方程的复相关系数SST SSRR2=0.885,比较接近1,说明回归方程拟合效果较好。
模型汇总模型 R R 方调整 R 方标准 估计的误差 1.941a.885.86423.55766模型汇总模型R R 方调整R 方标准估计的误差1.941a.885.86423.55766a. 预测变量: (常量), x2, x1。
(5)操作:先把待预测的数据输入表格,分析-回归-线性,因变量y,自变量x1,x2,保存-预测值、残差项选择“未标准化”-预测区间(“均值”)。
得到E(y)的点估计值是165.9985,置信水平为0.95的置信区间是(150.61813,181.37887)3、(1)操作:分析-回归-线性,因变量y,自变量x,确定。
得方程y=0.004x-0.831。
模型汇总模型R R 方调整R 方标准估计的误差1.839a.705.699 1.57720a. 预测变量: (常量), x。
Anova b模型 平方和 df均方 F Sig. 1回归 302.633 1 302.633 121.658.000a残差 126.866 51 2.488总计429.49952a. 预测变量: (常量), x 。
b. 因变量: y系数a模型 非标准化系数标准系数 t Sig. B 标准 误差试用版1(常量) -.831 .442-1.882.065 x.004.000.83911.030.000a. 因变量: y(2)诊断该问题是否存在异方差性,两种方法等级相关系数法残差图e y ~∧。
残差图法:分析-回归-线性,因变量y,自变量x 。
保存-残差、预测值-未标准化。
得到残差值:图形-旧对话框-散点-简单分布-定义-y 轴是e (RES_1),x 轴是∧y (PRE_1)-确定:从残差图看出误差项具有明显的异方差性,因为误差随x轴增加呈现明显的增加态势。
第二种方法:等级相关系数法操作:分析-回归-线性,因变量y,自变量x。
保存-残差-未标准化。
求|ei|:转换-计算变量-如图-确定:然后,分析-相关-双变量-操作如图:得到结果:相关系数e绝对值xSpearman 的rho e绝对值相关系数 1.000.318*Sig.(双侧)..021N5353x相关系数.318* 1.000Sig.(双侧).021.N5353*. 在置信度(双测)为0.05 时,相关性是显著的。
,p值=0.021<0.05,认为|ei|与自变量xi显著相关,存在异方差。
(3)如果存在异方差性,用幂指数型的权函数建立加权最小二乘回归方程。
分析-回归-权重估计-设置权重变量:得到结果:对数似然值b幂-2.000-121.068-1.500-114.545-1.000-108.466-.500-102.983.000-98.353.500-94.8371.000-92.5811.500-91.588a2.000-91.756a. 选择对应幂以用于进一步分析,因为它可以使对数似然函数最大化。
b. 因变量: y,源变量: x模型摘要复相关系数.812 R 方.659调整R 方.652估计的标准误.008对数似然函数值-91.588说明m=1.5时,对数似然函数达到极大,所以幂指数函数的最佳幂指数取1.5,得到回归方程为y=-0.683+0.004xPS:这种方法得到的方程的复相关系数0.812>普通二乘法方程的复相关系数R方(0.705),说明用加权法得到的回归方程更好。
另:此题属于一元加权最小二乘估计建立回归方程的方法,若为多元的(比如多一个x2),其操作的区别在于分析-相关-双变量时,变量一栏里是x1,x2,e绝对值,得出等级相关系数,再进行权重估计操作时,用等级相关系数最大的那个自变量(比如是x2)作为“权重变量”。
4、(1)用普通最小二乘法建立y关于x的回归方程。
操作:分析-回归-线性,因变量y,自变量x,确定。
得方程y=0.176x-1.427(2)用残差图及DW检验诊断序列相关性。
(误差项独立性的检验,目的是消除自相关)残差图(e t~e t-1):首先计算残差e:分析-回归-线性-保存-残差(未标准化),计算出残差RES_1(e t-1)。
从第二行复制该列粘贴到下一列,作为e t。
图形-旧对话框-散点-简单分布-定义-y轴是RES_1,x轴是res_2-确定:这些点落在一(三)象限,说明存在正自相关性。
DW检验:分析-回归-线性-统计量-DW:模型汇总b模型R R 方调整R 方标准估计的误差Durbin-Watson1.999a.998.998.09813.683a. 预测变量: (常量), x。
b. 因变量: y(3)分别用迭代法和一阶差分法建立回归方程;迭代法:借助上一小题,求得一元线性回归方程并求得残差间的一阶自相关系数ρ=0.683。
转换-计算变量,令y*i =y i+1—ρyi,x*i=x i+1—ρxi。
分析-回归-线性—自变量x*,因变量y*—统计量-DW-得到回归方程:y*=0.172x*-0.274,即系数a模型非标准化系数标准系数t Sig. B标准误差试用版1(常量)-.274.179-1.528.145 x星.172.004.99647.051.000 a. 因变量: y星模型汇总b模型R R 方调整R 方标准估计的误差Durbin-Watson1.996a.992.992.07432 1.430a. 预测变量: (常量), x星。
b. 因变量: y星Anova b模型平方和df均方F Sig.1回归12.226112.2262213.750.000a 残差.09417.006总计12.32018a. 预测变量: (常量), x星。
b. 因变量: y星此时DW=1.430,表明y*之间不相关,从而迭代结束。
可用下列方程做预测:y*=0.172x*-0.274,即yi+1=0.683*yi-0.274+0.172*(x i+1—0.683xi)一阶差分法(p47):先分别从第二行复制x,y作为x i+1,y i+1。
转换-计算变量,求Δy=y i+1-yi,Δx=x i+1-xi:分析-回归-线性—自变量Δx,因变量Δy—得到回归方程:Δy=0.161Δx+0.032,即y i+1=yi+0.161(x i+1-xi)+0.032,以下三表说明该方程通过了各种检验。
系数a模型非标准化系数标准系数t Sig. B标准误差试用版1(常量).032.027 1.199.247Δx.161.009.97718.915.000 a. 因变量: Δy模型汇总模型R R 方调整R 方标准估计的误差1.977a.955.952.07687a. 预测变量: (常量), Δx。
(4)比较上述几种不同方法所得的回归方程的优良性。
普通最小二乘法建立的方程:y=0.176x-1.427,R方=0.998,残差平方和SSE=0.173。
迭代法建立的方程:y*=0.172x*-0.274,即yi+1=0.683*yi-0.274+0.172*(x i+1—0.683xi),R方=0.992,残差平方和SSE=0.094一阶差分法建立的方程:Δy=0.161Δx+0.032,即y i+1=yi+0.161(x i+1-xi)+0.032。
R方=0.955,残差平方和SSE=0.100。
