2015-2016学年北京市顺义区初三二模数学试题

合集下载

2015北京各区中考数学二模26、27、28题汇编(带答案)

OC
（用含 x 的式子表示），
【问题解决】
2015 北京模拟 2 / 18
已知，如图 2，点 M、N、P 为圆 O 上的三点，且∠P=β，tanβ = 1 ，求 sin2β 的值. 2
y
C B
2α
M
β
P
A
D
D
O
α
A
N
O
B
O C
x
图1
图2
26．如图，在平面直角坐标系 xOy 中，矩形 ABCD 各边都平行于坐标轴，且 A（-2，2），C（3，-2）．对矩形 ABCD 及其内部的点进行如下操作：把每个点的横坐标乘以 a，纵坐标乘以 b，将得到的点再向右平移 k （k 0）个单位，得到矩形 A ' B ' C ' D ' 及其内部的点（ A ' B ' C ' D ' 分别与 ABCD 对应）．E（2，1）经过上述操作后的对应点记为 E ' ．（1）若 a=2，b=-3，k=2，则点 D 的坐标为，点 D ' 的坐标为；（2）若 A ' （1，4）， C ' （6，-4），求点 E ' 的坐标． 26．阅读下面的材料：小明遇到一个问题：如图 1，在□ABCD 中，点 E 是边 BC 的中点，点 F 是线段 AE 上一点，BF 的延长线交射线 CD 于点 G. 如果 AF 3 ，求 CD 的值． CG EF 他的做法是：过点 E 作 EH∥AB 交 BG 于点 H，那么可以得到△BAF∽△HEF．请回答：（1）AB 和 EH 之间的数量关系是，CG 和 EH 之间的数量关系是， CD 的值为．
5 4 3 2 1 –5 –4 –3 –2 –1 o –1 –2 –3 –4 –5 1 2 3 4 5

北京市顺义区初三数学二模试卷 (1)

顺义区房二摸2008届初三第二次统一练习一、选择题1．13-的绝对值是（）A ．3- B ．3 C ．13 D ．13- 2．若分式11x x +-的值为0，则x 的值是（）A ．-1 B ．1 C ．0 D ．1± 3．若反比例函数的图象经过点)1,2(--M ，则反比例函数的解析式为（）A ．x y 2=B . x y 2-=C . x y 21=D .xy 21-= 4．算式44442222+++的结果是（）A ．162 B ．48 C ．82 D ．625．刘强同学为了调查全市初中生人数，他对自己所在城区人口和城区初中生人数作了调查：城区人口约3万，初中生人数约1200．全市实际人口约300万，为此他推断全市初中生人数约为12万．但市教委提供的全市初中生人数约为8万，与估计数据有很大偏差．请你用所学的统计知识，找出其中错误的原因是（）A ．样本不能估计总体 B ．样本不具代表性、广泛性、随机性C ．市教委提供的数据有误D ．推断时计算错误6．如图，AB 是⊙O 的直径，AC 是弦，若AB=2， 3则∠AOC 的度数是（）A ．120°B ．130°C ．140°D ．150°7．下面三张卡片上分别写有一个整式，把它们背面朝上洗匀，小明从中随机抽取一张卡片，再从剩下的卡片中随机抽取一张．第一次抽取的卡片上的整式做分子，第二次抽取的卡片上的整式做分母，则能组成分式的概率是（）A ．13 B ．12 C ．23 D ．568．如图是一个经过改造的台球桌面的示意图，图中4个角上的阴影部分分别表示4个入球孔．如果1个球按图中所示的方向被击中（球可以经过多次反射，并且不会在台球桌中间停止），那么该球最后将落入的球袋是（） A ．1号袋B ．2号袋 C ．3号袋 D ．4号袋二、填空题（共4个小题，每小题4分，共16分）9．已知：如图，AB ∥CD ，CE 平分∠ACD ，交AB 于点E ，若∠A=110°，则∠BEC 的度数是．10．如图，在△ABC 中，∠A=90，分别以B 、C 为圆心的两个等圆外切，两圆的半径都为2cm ，则图中阴影部分的面积为 cm 2．11．如图，图①，图②，图③，图④……是用围棋棋子摆成的一列具有一定规律的“山”字．则第n 个“山”字中的棋子个数是．a2a - 43号袋2号袋1…图①图②图③图④DEBCA12．线段AB 、CD 在平面直角坐标系中的位置如图所示，O 为坐标原点．若线段AB 上一点P 的坐标为(a ，b )，则直线OP 与线段CD 的交点的坐标为________________． 13．分解因式：322224a ab a b +-．14．解2151132x x -+-≤，并将解集在数轴上表示出来．15．设25111x x A B x x -==---，，当x 为何值时，A 与B 的值相等？16．先化简，再求值：2224524422a a a a a a⎛⎫--÷ ⎪-+--⎝⎭，其中，a 是方程2310xx -+=的根．四、解答题（共2个小题，17小题5分，18小题6分，共11分） 17．如图，E 、F 是菱形ABCD 的对角线BD 所在直线上两点，且DE=BF ．请你以F 为一个端点，和图中已标有字母的某一点连成一条新的线段，猜想并证明它和已有的某一条线段相等．（1）连结；（2）猜想：；（3）证明：18．为了保护野生动物，某中学在全校所有学生中，对四种国家一级保护动物的喜爱情况进行问卷调查．要求每位学生只选一种自己最喜爱的动物，调查结果绘制成如下未完整的统计表和统计图，请你根据图表中提供的信息，解答以下问题：动物名称频数（学生人数）频率金丝猴 0.20 大熊猫 1000 0.50 藏羚羊 500 丹顶鹤 100 0.05 合计1FEDCBA5%丹顶鹤（1）请把表格和统计图分别补充完整；（2）为了更好地保护野生动物，请你提出一条合理的建议． 19．已知关于x 的方程22(1)10kxk x k +++-=有两个不相等的实数根．（1）求k 的取值范围；（2）请选取一个你喜欢的k 值，代入方程并求出方程的根．20．一座建于若干年前的水库大坝的横断面为梯形ABCD ，如图所示，其中背水面为AB ，现准备对大坝背水面进行整修，将坡角由45°改为30°，若测量得AB=20米，求整修后需占用地面的宽度BE 的长．（精确到0.12 1.414,3 1.732,6 2.449≈≈≈）21．如图，在平面直角坐标系xOy 中，以点(3,0)A 为圆心的圆与x 轴交于原点O 和点B ，直线l 与x轴、y 轴分别交于点C （-2，0）、D （0，3）．（1）求出直线l 的解析式；（2）若直线l 绕点C 顺时针旋转，设旋转后的直线与y 轴交于点E （0，b ），且03b <<，在旋转的过程中，直线CE 与⊙A 有几种位置关系？试求出每种位置关系时，b 的取值范围．频数（学生人数） 1000 800 600 400 200金丝猴大熊猫藏羚羊丹顶鹤动物名称30°45°E DCB AlyxDC BA O22．已知：如图，平行四边形ABCD 中， AE 、BE 、CF 、DF 分别平分∠BAD 、∠ABC 、∠BCD 、∠CDA ，BE 、DF 的延长线分别交AD 、BC 于点M 、N ，连结EF ，若AD=7，AB=4，求EF 的长．23．已知：如图，在正方形ABCD 中，点G 是BC 延长线一点，连结AG ，分别交BD 、CD 于点E 、F ．（1）求证：DCE DAE ∠=∠；（2）当CG=CE 时，试判断CF 与EG 之间有怎样的数量关系？并证明你的结论．（3）在（2）的条件下，求DF FC的值．24．某校开展“迎2008年北京奥运会”的主题校会活动，老师派小明同学去学校附近的超市购买笔记本作为奖品．小明选择了该超市单价为8元和4.8元的两种笔记本，他要购买这两种笔记本共40本．（1）如果他一共带了240元，全部用于购买奖品，那么能买这两种笔记本各多少本？（2）小明根据主题校会活动的设奖情况，决定所购买单价为8元笔记本的数量要少于单价为4.8元笔记本数量的12，但又不少于单价为4.8元笔记本数量的14．如果他买了单价为8元的笔记本x 本，买这两种笔记本共花了y 元．①请写出y （元）关于x （本）的函数关系式，并求出自变量x 的取值范围；②请帮小明计算一下，这两种笔记本各购买多少本时，所花的钱最少，此时花了多少元钱？25．在平面直角坐标系xOy 中，抛物线2y ax bx c =++经过A （3，0）、B （5，0）、C （0，5）三点．（1）求此抛物线的解析式；（2）设抛物线的顶点为D ，求△BCD 的面积；（3）若在抛物线的对称轴上有一个动点P ，当△OCP 是腰长为5的等腰三角形时，求点P 的坐标．NMFEDCBA GFEDC BA顺义区2008届初三第二次统一练习一、选择题题号 1 2 3 4 5 6 7 8 答案CBADBACD二、填空题9．145︒； 10．π； 11． 52n +； 12．(2,2)a b ．三、解答题（共4个小题，13小题4分，其余每小题5分，共19分） 13．解：原式222(2)a a b ab =+- 22()a a b =-14．解：去分母，得 2(21)3(51)6x x --+≤去括号，得 421536x x ---≤移项，合并同类项，得 1111x -≤ 系数化1，得 1x ≥- 将解集在数轴上表示为：15．依题意，得25111x x x x -=--- 去分母，得 2(1)1(5)x x x x +=---去括号，得 2215x x x x +=--+移项，合并同类项，得 24x = 系数化1，得 2x =经检验，2x =是原方程的根∴当2x =时，A 与B 的值相等．16．解：原式2(2)(2)5(2)(2)22a a a a a a ⎡⎤+--=-⨯⎢⎥--⎣⎦25(2)222a a a a a +-⎛⎫=-⨯ ⎪--⎝⎭ (3)2a a -=21(3)2a a =-a 是方程2310x x -+=的根，∴2310a a -+= ，∴231a a -=- ∴原式12=-．四、解答题（共2个小题，17小题5分，18小题6分，共11分）17．（1）连结 CF ；（2）猜想： CF=AE ；（3）证明：∵四边形ABCD 是菱形， ∴AD=BC ，AD ∥BC ．∴∠1=∠2．∵∠1+∠3=180°，∠2+∠4=180°， ∴∠3=∠4∵DE=BF ，∴△ADE ≌△CBF （SAS ）∴CF = AE ．或连结 AF ；猜想： AF=AE ；证明略． 18．解：（1）金丝猴 400 藏羚羊 0.25 合计2000（填表每空1分，共3分，两个统计图正确各1分）（2）答案如：①禁止乱捕滥杀野生动物．②禁止人为破坏野生动物的生存环境．（答案只要合理都得1分）五、解答题（共3个小题，每小题5分，共15分）19．解：（1）△24(21)4(1)k k k k =++--2248444k k k k =++-+ 124k =+ ∵方程22(1)10kx k x k +++-=有两个不相等的实数F 30°45°EDCB A EFlyxDC BA O3MDA根，∴01240k k ≠⎧⎨+>⎩ ∴013k k ≠⎧⎪⎨>-⎪⎩∴k 的取值范围是13k >-且0k ≠（2）取K=1，方程为240x x +=，解得 120,4x x ==-．20．解：过点A 作AF ⊥BC ，垂足为F ．在Rt △ABF 中，∵∠ABF=45°，AB=20，∴2sin 4520102AF AB =⋅︒==102BF AF ==．在Rt △AEF 中，∠EAF=90°-∠E=90°-30°=60°．∴tan 601023106EFAF =⋅︒==10610210(62)10(2.449 1.414)10.4BE EF BF =-==≈-≈（米）．答：整修后需占用地面的宽度BE 的长约为10.4米．21．解：（1）设直线l 的解析式为y kx b =+，依题意，得203k b b -+=⎧⎨=⎩ ∴323k b ⎧=⎪⎨⎪=⎩ ∴直线l 的解析式为332y x =+．（2）在旋转的过程中，直线CE 与⊙A 有三种位置关系：相离、相切、相交．当直线CE 与⊙A 相切时，如图所示，设切点为F ，连结AF ，有∠AFC=90°． ∵A 点坐标为（3，0），C 点坐标为（-2，0），∴OA=3，AF=3，OC=2，∴AC=5，CF=4．∵∠COE=∠CF A=90°，∠OCE=∠FCA ，∴△COE ∽△CF A ．∴OC CF OE AF =，即 243OE =．∴32OE =．∴当332b <<时，直线CE 与⊙A 相离；当32b =时，直线CE 与⊙A 相切；当302b <<时，直线CE 与⊙A 相交．六、解答题（共2个小题，22小题5分，23小题7分，共12分） 22．解：∵四边形ABCD 是平行四边形，∴AD ∥BC ，AD=BC ，AB=CD ．∴∠2=∠3．∵BE 平分∠ABC ，∴∠1=∠2． ∴∠1=∠3．∴AM=AB=4．∵AE 平分∠BAD ，∴12EM BM =．同理，CN=CD ，12DF DN =．∴AM=CN ．∴AD - AM=BC DA- CN ，即 DM=BN ．∴四边形BNDM 是平行四边形．∴BM=DN ，BM∥DN ．∴EM=DF ，EM ∥DF ．∴四边形MEFD 是平行四边形． ∴EF=MD ．∵D=AD -AM=AD -AB=7-4=3， ∴EF=3．23．（1）证明：∵四边形ABCD 是正方形，∴AD=CD ，∠ADE=∠CDE ．∵DE=DE ，∴△ADE ≌△CDE ．∴∠DAE=∠DCE ．（2）13CFEG =．证明：∵四边形ABCD 是正方形， ∴AD ∥BC ，∠DCB=90° ∴∠DAE=∠G ．∴∠DCE=∠G ． ∵CG=CE ，∴∠1=∠G ． ∴∠DCE=∠1． ∴CF=EF ．∵∠2=∠1+∠DCE=2∠1=2∠G ，又∵∠DCG=180°-∠DCB=90°，∴∠G=30°∴12CFFG =． ∴13CF EG =．（3）设CF x =，则EF CF x ==，22FG CF x ==．在Rt △CFG 中，223CG FG CF x =-=． ∵△ADE ≌△CDE ，∴AE=CE=CG 3x =．∴AF=AE +EF=31)x ．∵AD ∥BC ，∴△ADF ∽△GCF ∴(31)3122DF AF x FC FG x +===．七、解答题（本题满分7分）24．解：（1）设能买单价为8元的笔记本x 本，则能买单价为4.8元的笔记本(40)x -本．依题意，得8 4.8(40)240x x +-=．解得15x =．40401525x -=-=∴．答：能买单价8元的笔记本1 5本，单价为4.8元的笔记本25本．（2）①依题意，得8 4.8(40) 3.2192y x x x =+-=+．又由题意，有1(40)21(40)4x x x x ⎧<-⎪⎪⎨⎪-⎪⎩，．≥ 解得4083x <≤．y ∴关于x 的函数关系式为 3.2192y x =+，自变量x 的取值范围是4083x <≤且x 为整数．②对一次函数3.2192y x =+， 3.20k =>∵， y ∴随x 的增大而增大．∴对于4083x <≤，当8x =时，y 值最小．此时4040832x -=-=， 3.28192217.6y =⨯+=最小（元）．答：当买单价为8元的笔记本8本，单价为4.8元的笔记本32本时，所花的钱最少为217.6元八、解答题（本题满分8分）25．解：（1）根据题意，5c =． ∴935025550a b a b ++=⎧⎨++=⎩解得1,383a b ⎧=⎪⎪⎨⎪=-⎪⎩∴抛物线解析式为 218533y x x =-+．（2）22218116115(816)5(4)333333y x x x x x =-+=-+-+=--∴抛物线顶点D 的坐标为1(4,)3-设直线CD 的解析式为y kx b =+，则5,14.3b k b =⎧⎪⎨+=-⎪⎩∴4,35.k b ⎧=-⎪⎨⎪=⎩∴直线CD 的解析式为453y x =-+．设直线CD 与x 轴交于点F ，则F 点坐标为15(,0)4． ∴155544BF =-=．∴15115105243243BCD BFD BFC S S S ∆∆∆=+=⨯⨯+⨯⨯=．（3）分四种情况：设对称轴与x 轴交于点E ．①当OP=OC=5，且∠COP 为锐角时，如图1，则有2222543PEOP OE =-=-=，∴P 点坐标为（4，3）．②当OP=OC=5，且∠COP 为钝角时，如图2，则有2222543PEOP OE =-=-=，∴P 点坐标为（4，-3）．③当OC =CP =5，且∠OCP 为锐角时，如图3，作PQ ⊥y 轴，垂足为Q ，则有2222543CQ PC PQ =-=-=，∴532OQ OC CQ =-=-=．∴P 点坐标为（4，2）．④当OC =CP =5，且∠OCP 为钝角时，如图4，作PQ ⊥y 轴，垂足为Q ，则有2222543CQ PC PQ =-=-=，∴538OQ OC CQ =+=+=．∴P 点坐标为（4，8）．综上所述，点P 的坐标为（4，3）、（4，-3）、（4，2）或（4，8）．以上各题答案若有其他解法，请老师们参照评分参考酌情给分．。

2016北京中考数学各区二模28题汇编(含答案)

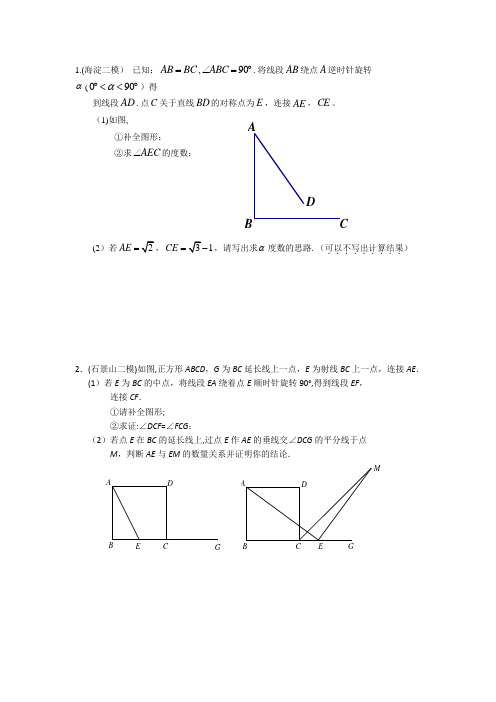
1.(海淀二模）已知：AB BC =,90ABC ∠=︒.将线段AB 绕点A 逆时针旋转α(090α︒<<︒）得到线段AD .点C 关于直线BD 的对称点为E ，连接AE ，CE 。

（1)如图, ①补全图形；②求AEC ∠的度数；(2）若AE =1CE =，请写出求α度数的思路.（可以不写出计算结果．．．．．．．．．）2．(石景山二模)如图,正方形ABCD ，G 为BC 延长线上一点，E 为射线BC 上一点，连接AE ． (1）若E 为BC 的中点，将线段EA 绕着点E 顺时针旋转90°,得到线段EF ，连接CF ． ①请补全图形; ②求证:∠DCF =∠FCG ；（2）若点E 在BC 的延长线上,过点E 作AE 的垂线交∠DCG 的平分线于点M ，判断AE 与EM 的数量关系并证明你的结论．EGD CBAMABCDGE3.（顺义二模）已知:如图，90ACD ∠=︒，MN 是过点A 的直线,AC DC =，DB MN ⊥于点B ．图2图3图1ABCDNMABCDNMNMABCD（1）在图1中，过点C 作CE CB ⊥，与直线MN 于点E ，①依题意补全图形；②求证:BCE ∆是等腰直角三角形；③图1中,线段BD 、AB 、CB 满足的数量关系是； (2）当MN 绕A 旋转到如图（2）和图（3）两个位置时，其它条件不变. 在图2中，线段BD 、AB 、CB 满足的数量关系是；在图3中，线段BD 、AB 、CB 满足的数量关系是；（3）MN 在绕点A 旋转过程中,当30BCD ∠=︒，BD =则CB = ．4.（通州二模）已知，在菱形ABCD 中,∠ADC=60°，点F 为CD 上任意一点（不与C 、D 重合）,过点F 作CD 的垂线，交BD 于点E ，连接AE 。

（1）①依愿意补全图1；②线段EF 、CF 、AE 之间的等量关系是 . （2）在图1中将ΔDEF 绕点D 逆时针旋转，当点F 、E 、C 在一条直线上(如图2）. 线段EF 、CE 、AE 之间的等量关系是。

2015北京各区中考数学二模25题全面总结及答案

2015北京各区中考数学25题汇编及答案25．如图，Rt △ABC 中，∠A =90°，以AB 为直径的⊙O 交BC 于点D ，点E 在⊙O 上， CE =CA ， AB ，CE 的延长线交于点F ．（1）求证：CE 与⊙O 相切；（2）若⊙O 的半径为3，EF =4，求BD 的长．25．如图1，AB 为⊙O 的直径，弦CD ⊥AB 于点E ，点F 在线段ED 上．连接AF 并延长交 ⊙O 于点G ，在CD 的延长线上取一点P ，使PF=PG ．（1）依题意补全图形，判断PG 与⊙O 的位置关系，并证明你的结论；（2）如图2，当E 为半径OA 的中点，DG ∥AB，且OA PG 的长．25．如图，已知AB 是⊙O 的直径，C 是⊙O 上一点，∠BAC 的平分线交⊙O 于点D ，交⊙O 的切线BE 于点E ，过点D 作DF ⊥AC ，交AC 的延长线于点F ．（1）求证：DF 是⊙O 的切线；F（2）若DF =3，DE =2．①求值；②求FAB ∠的度数．25．如图，点A B C D E 、、、、在⊙O 上，AB CB ⊥于点B ，tan 3D =，2BC=，H为CE 延长线上一点，且AH =CH =（1）求证：AH 是⊙O 的切线；（2）若点D 是弧CE 的中点，且AD 交CE 于点F ，求EF 的长．25．如图，⊙O 是△ABC 的外接圆，AB= AC ，BD 是⊙O的直径，P A ∥BC ，与DB 的延长线交于点P ，连接AD ．（1）求证：P A 是⊙O 的切线；（2）若BC =4 ，求AD 的长．25．如图，△ABC 中，AB =AC ，点D 为BC 上一点，且AD =DC ，过A ，B ，D 三点作⊙O ，AE是⊙O 的直径，连结DE ．（1）求证：AC 是⊙O 的切线；BEADCC（2）若4sin 5C =，AC =6，求⊙O 的直径．25．如图，AB 是⊙O 的直径．半径OD 垂直弦AC 于点E ．F 是BA 延长线上一点，CDB BFD ∠=∠．（1）判断DF 与⊙O 的位置关系，并证明；（2）若AB =10，AC =8，求DF 的长．25．如图，AB 是⊙O 的直径，以AB 为边作△ABC ，使得AC = AB ，BC 交⊙O 于点D ，联结OD ，过点D 作⊙O 的切线，交AB 延长线于点E ，交AC 于点F ．25．如图，⊙O 为△ABC 的外接圆，BC 为⊙O 的直径，AE 为⊙O 的切线，过点B 作BD ⊥AE 于D ．（1）求证：∠DBA =∠ABC ；（2）如果BD =1，tan ∠BAD =12，求⊙O 的半径．25.如图，AB 是⊙O 的直径，点C 是⊙O 上一点， AD ⊥ DC 于D , 且AC 平分∠DAB ，延长DC 交AB 的延长线于点P ，弦CE 平分∠ACB ，交AB 于点F ，连接BE ．（1）求证：PD 是⊙O 的切线；（2）若tan ABC =43∠，BE =PC 的长．25．如图，△ABC 内接于⊙O ，OC ⊥AB 于点E ，点D 在OC 的延长线上，且∠B =∠D =30°.（1）求证：AD 是⊙O 的切线；（2）若AB =求⊙O 的半径．25．如图，已知，⊙O 为△ABC 的外接圆，BC 为直径，点E 在AB 边上，过点E 作EF ⊥BC ，延长FE 交⊙O 的切线AG 于点G ．（1）求证：GA =GE ．PE（2）若AC =6，AB =8，BE =3，求线段OE 的长．答案25．(本小题满分5分) 证明：连接OE ，OC ．在△OEC 与△OAC 中， ,,,OE OA OC OC CE CA =⎧⎪=⎨⎪=⎩F∴△OEC ≌△OAC ． (1)分∴∠OEC =∠OAC ．∵∠OAC =90°，∴∠OEC =90°． ∴OE ⊥CF 于E ． ∴CF与⊙O相切．………………………………………………………………………………...2分（2）解：连接AD ．∵∠OEC =90°， ∴∠OEF =90°． ∵⊙O 的半径为3， ∴OE =OA=3．在Rt △OEF 中，∠OEF =90°，OE = 3，EF = 4，∴5OF ，………………………………………………………………………3分3tan 4OE F EF ==．在Rt △F AC 中，∠F AC =90°，8AF AO OF =+=， ∴tan 6AC AF F =⋅=．…………………………………………………………………………4分∵AB 为直径，∴AB =6=AC ，∠ADB =90°． ∴BD =2BC．在Rt △ABC 中，∠BAC =90°，∴BC =F∴BD=．…………………………………………………………………………………….5分25. 解：（1）补全图形如图5所示. ………………………………………………………… 1分答：PG 与⊙O 相切. 证明：如图6，连接OG .∵ PF =PG ， ∴ ∠1=∠2.又∵OG =OA ， ∴ ∠3=∠A .∵ CD ⊥AB 于点E ， ∴ ∠A +∠AFE =90°. 又∵∠2 =∠AFE ，∴ ∠3+∠1=90°. ……………………… 2分即 OG ⊥PG . ∵ OG 为⊙O 的半径，∴ PG 与⊙O 相切. …………………… 3分（2）解：如图7，连接CG . ∵ CD ⊥AB 于点E ，∴ ∠OEC =90°. ∵ DG ∥AB ，∴∠GDC =∠OEC =90°. ∵∠GDC 是⊙O 的圆周角， ∴ CG 为⊙O 的直径. ∵ E 为半径OA 的中点， ∴ 22OA OCOE ==. ∴ ∠OCE =30°即∠GCP =30°.又∵∠CGP =90°，2CG OA ==A∴tan 4PG CG GCP =⋅∠==. …………………………… 5分25. （1）连结OD ， ∵AD 平分∠BAC ∴∠DAF ＝∠DAO ∵OA =OD ∴∠OAD ＝∠ODA ∴∠ DAF ＝∠ODA ∴AF ∥OD ．┉┉1分 ∵DF ⊥AC ∴OD ⊥DF ∴DF 是⊙O 的切线┉┉2分（2）①连接BD ∵直径AB ， ∴∠ADB =90° ∵圆O 与BE 相切 ∴∠ABE =90°∵∠DAB +∠DBA =∠DBA +∠DBE =90° ∴∠DAB =∠DBE ∴∠DBE =∠F AD ∵∠BDE=∠AFD =90° ∴△BDE ∽△AFD ∴32==DF DE AD BE ┉┉3分 ②连接OC ，交AD 于G 由①，设BE =2x ，则AD =3x ∵△BDE ∽△ABE ∴BE DE AE BE =∴xx x 22232=+∵AB BC ⊥于点B∴AC 是⊙O 的直径…………………………………1分 ∵D ACB ∠=∠，∴tan tan 3D ACB =∠= 在Rt ABC ∆中，2BC =，∴36AB BC == 由勾股定理AC =在CAH ∆中，由勾股定理逆定理：22250AC AH CH +==∴90CAH ∠=°即CA AH ⊥∴AH 是⊙O 的切线…………………………………2分（2）解：∵点D 是弧CE 的中点∴EAD DAC ∠=∠…………………………………3分 ∵AC 是⊙O 的直径 ∴AE CH ⊥∴90H EAH H HCA ∠+∠=∠+∠=° ∴EAH HCA ∠=∠∴EAD EAH DAC HCA ∠+∠=∠+∠ 即AFH HAF ∠=∠∴HF HA =∵CA AH ⊥AE CH ⊥∴2AH EH CH =⨯可得EH = ∴EF =5分25.（1）证明：连接OA 交BC 于点E ，由AB =AC 可得OA ⊥BC ．………………………1分C B∵PA ∥BC ， ∴∠PAO =∠BEO =90°. ∵OA 为⊙O 的半径，∴PA 为⊙O 的切线. …………………………… 2分（2）解：根据（1）可得CE =21BC=2． Rt △ACE 中，122=-=CE AC AE . ………………………………3分∴tan C =21=CE AE ． ∵BD 是直径，∴∠BAD =90°．…………………………………………………………4分又∵∠D =∠C ， ∴AD =52tan =DAB.………………………………………………………5分25．（1）证明：∵AB =AC ，AD =DC ，∴∠1=∠C =∠B ，..................................................1分又∵∠E =∠B ，∴∠1=∠E ， ∵AE 是⊙O 的直径，∴∠ADE =90°， ∴∠E +∠EAD =90°， ∴∠1+∠EAD =90°，∴AC 是⊙O 的切线．...........................................2分（2）解：过点D 作DF ⊥AC 于点F ， ∵DA =DC ，AC =6， ∴CF =12AC =3，..................................... ............3分 ∵4sin 5E =，∴4sin 5C =， ∴在Rt △DFC 中，DF =4，DC =5， ∴AD =5，∵∠ADE =∠DFC =90°，∠E =∠C ，∴△ADE ∽△DFC ，.............................................4分C∴AD DFAE DC =， ∴545AE =， ∴AE =254，∴⊙O 的直径为254．....................5分25．解：（1）DF 与⊙O 相切． ∵CAB CDB ∠=∠，又∵CDB BFD ∠=∠，∴BFD CAB ∠=∠． ∴AC ∥DF ． ………………………………… 2分∵半径OD 垂直于弦AC 于点E ，∴DF OD ⊥． ∴DF 与⊙O 相切． ………………………………… 3分（2）∵半径OD 垂直于弦AC 于点E ，AC =8，∴482121=⨯==AC AE ． ∵AB 是⊙O 的直径， ∴5102121=⨯===AB OD OA ．在AEORt ∆中，3452222=-=-=AE OA OE ． ……………………………………… 4分∵AC ∥DF ， ∴OAE ∆∽OFD ∆． ∴DF AEOD OE = ． ∴DF453=． ∴321DF CEB A O320=DF ． ………………………………………………… 5分25．（1）证明：联结AD ．∵AB 是⊙O 的直径，∴∠ADB =90°，AD ⊥BC .∵AC = AB ，∴12∠=∠．…….1分 ∵OA OD =，∴13∠=∠． ∴23∠=∠，∴OD ∥AC ．…….2分（2）∵AC = AB =10，∴B C ∠=∠．∴cos C=cos 5ABC ∠=．在Rt △ABD 中，∠ADB =90°，cos 5BD ABC AB ∠==， ∴BDCD = BD….3分∵EF 为⊙O 的切线，∴OD ⊥EF ，由∵OD ∥AC ，∴∠DFC =90°. …….4分在Rt △CDF 中，cos C=5CF CD =，∴CF =2．∴AF =8． ∵OD ∥AC ，∴ODE ∆∽AFE ∆．∴OE OD AE AF =．∴OB BE ODAB BE AF+=+． ∵152OB OA OD AB ====,∴103BE =．…….5分 25．（本小题满分5分）（1）证明：连接OA .（如图）∵ AE 为⊙O 的切线，BD ⊥AE ， ∴ ∠DAO =∠EDB =90°. ∴ DB ∥AO .∴ ∠DBA =∠BAO . …………1分又 ∵OA =OB ， ∴ ∠ABC =∠BAO .∴ ∠D B A =∠A B C . ………………………………………………2分（2）在Rt △ADB 中，∠ADB =90°，C∵ BD =1，tan ∠BAD =12， ∴ AD =2，……………………………………………………………………3分由勾股定理得AB .∴ cos ∠DBA 又∵ BC 为⊙O 的直径， ∴ ∠BAC =90°. 又∵∠DBA =∠ABC .∴ cos ∠ABC = cos ∠DBA∴ 5.cos ABBC ABC===∠…………………………………………4分 ∴ ⊙O 的半径为5.2…………………………………………………………5分25.解：（1）∵ OC =OA∴ ∠CAO =∠OCA ∵ AC 平分∠DAB ∴ ∠DAC =∠CAO ， ∴ ∠ACO =∠DAC ． ∴ OC ∥AD ．…………………………………………………………………….1分 ∵ AD ⊥PD ， ∴OC ⊥PD ． ∴ PD 是⊙O 的切线……………………………………………………………...2分（2）连接AE ．∵CE 平分∠ACB ，∴AE BE =，∴AE BE == ∵AB 为⊙O 的直径， ∴∠AEB =90°．在Rt △ABE 中，14AB =………………………………………3分 ∵ ∠P AC =∠PCB ，∠P =∠P ， ∴ △P AC ∽△PCB ， ∴ PC AC PB BC =．…………………………………………………………………..4分又∵4tan 3ABC =∠，∴43AC PCBC PB==，设PC =4k ，PB =3k ，则在Rt △POC 中，PO =3k +7，OC =7，∵ PC 2+OC 2=OP 2， ∴()()2224737k k +=+， ∴ 126,0k k ==(舍去)．∴ PC =4k =4×6=24． …………………………………………………………..5分25证明：（1）连接OA .∵∠B =∠D =30°，∴∠AOC =2∠B =60°，……………………….(1分) ∴∠OAD =180°-∠AOD -∠D =90°，…………….(2分) 即OA ⊥AD ,∴AD 是⊙O 的切线.……………….(3分)（2）∵OA =OC ,∠AOC =60°，∴△ACO 是等边三角形， ∵CO ⊥AB ∴ ……………………….(4分)在Rt △ABC 中∴⊙O 的半径为6.……………………………….(5分)1122AE AB ==⨯=sin sin60AEACE AC∠==︒6AC ===。

初三数学二模题答案-顺义

顺义区2015届初三第二次统一练习数学答案一、选择题（本题共30分，每小题3分）下面各题均有四个选项，其中只有一个是符合题意的．二、填空题（本题共18分，每小题3分）11．4a ； 12．()221m -； 13．14.3； 14．3； 15．12，8；（第一空1分第二空2分）16． 1A （1，1），3A （4，4），11nn n A --（2,2）．（每空1分）三、解答题（本题共30分，每小题5分）17．解：2113tan30+3-⎛⎫- ⎪⎝⎭19=-+…………...4分（其中第一、三项化简各1分，第二项化简2分）8=…………………………………………………………………………………....5分18．证明：∵AB ∥CD ，∴∠C =∠ABC ．…………………………....1分又∵AB =BC ，∠A =∠1，……………………..3分 ∴△ABE ≌△BCD ，………………..……...4分 ∴BE =CD ．………………………………....5分 19．解：2(2)(32)x x x +-+224432x x x x =++--…………………………………………......2分（每项1分） 24x x =-+……………………………………………………………….……......3分∵25x x -=，∴原式24x x =-+54=-+1=-．………………………......5分20．解：()2214x x x +-=-…………………………………………………....2分22214x x x +-=-23x =-32x =-………………………………………………………………..…….....3分经检验可知32x =-是原方程的根，…………………………….…...……...4分∴原方程的根是32x =-．…………………………………………….…..……....5分1EACD21．解：（1）∵点A 的坐标是（-1，a ），在直线22y x =-+上，∴a =4，…………………………………………………………………………………........1分 ∴点A 的坐标是（-1，4），代入反比例函数my x=， ∴m =-4．…………………………………………………………………………………......2分（2）∵OP 与直线22y x =-+平行，∴OP 的解析式为2y x =-， …………………………………………………………......3分∵点P 是双曲线4y x =-上一点， ∴设点P 坐标为（x , 4x-），代入到2y x =-中， ∴4=2x x--，.......................................................................................................................4分∴x = ∴点P的坐标为-或(．………………………………..………......5分22．解：设2012年到2014年烟花爆竹销售量的年平均下降率为x ．…………….....1分依题意可列：()2200011280x -=…………………………………………………......3分解得0.2x =……………………………………………………………………………......4分答：2012年到2014年烟花爆竹销售量的年平均下降率为20%．…………………......5分四、解答题（本题共20分，每小题5分）23．画图………………………………………………………………………1分（1）证明：∵四边形ABCD 是矩形， ∴∠ADC =90º，CD =AB ， ∵EF ⊥AD ， ∴∠EHD =90º， ∴∠EHD =∠ADC ， ∴EF ∥CD ，又∵DE ∥AC ，∴四边形EFCD 是平行四边形，……………......2分又∵DE =AB ， ∴DE =CD ，∴四边形EFCD 是菱形．……………………......3分HEDC BAF（2）解：过点D作DG⊥AC于G．在Rt△ABC中，AB=3，BC=∴tan3ACB∠==，CD=3，∴∠ACB=30º，……………………………………......4分∴∠1=60º，∴在Rt△DCG中，CD=3，sin1322DG CD=⋅∠=⨯=∴平行线DE与AC…………......5分24．解：（1）5200；………………………….…......1分补图……………………………………..3分（2）0.40，0.35，0.30．………………………........4分说明恩格尔系数越小消费水平越高．.................5分25．（1）证明：∵AB=AC，AD=DC，∴∠1=∠C=∠B，..................................................1分又∵∠E=∠B，∴∠1=∠E，∵AE是⊙O的直径，∴∠ADE=90°，∴∠E+∠EAD=90°，∴∠1+∠EAD=90°，∴AC是⊙O的切线．...........................................2分（2）解：过点D作DF⊥AC于点F，∵DA=DC，AC=6，∴CF=12AC=3，..................................... ............3分∵4sin5E=，∴4sin5C=，∴在Rt△DFC中，DF=4，DC=5，∴AD=5，∵∠ADE =∠DFC=90°，∠E =∠C，∴△ADE∽△DFC，.............................................4分∴AD DFAE DC=，∴545AE=，∴AE=254，∴⊙O的直径为254．....................5分CH1GFAB CDE26．解：（1）D （3，2），'D （8，-6），..................................................................................2分（2）依题可列：21,3 6.a k a k -+=⎧⎨+=⎩则a =1，k =3，2b =4，b =2，.........................................................4分（a ，b ，k 求出一个给1分） ∵点E （2，1），∴'E （5，2）．.....................................................................................................5分五、解答题（本题共22分，第27题7分，第28题7分，第29题8分） 27．解：（1）24b ac -=()()2243m m ---........................................................1分 =244412m m m -+-+ =2816m m -+ =()24m - ∵()240m -≥，∴方程()2230x m x m +-+-=总有两个实数根．..............................................2分（2）1,2x =()242m m -±-．...............................................3分∴11x =-，23x m =-+，∴抛物线()223y x m x m =+-+-总过x 轴上的一个定点（-1,0）．................4分（3）∵抛物线()223y x m x m =+-+-与x 轴的另一个交点为B ，与y 轴交于点C ， ∴B （3-m ,0），C （0, m -3），...................................................................................5分 ∴△OBC 为等腰直角三角形， ∵△OBC 的面积小于或等于8， ∴OB ，OC 小于或等于4， 30m -≠，∴3m -≤4且3m ≠， ...........................................................................................6分又∵A ，B 不重合，∴4m ≠，∴-1≤m ≤7且3m ≠，4m ≠．................................................................................7分（1）∵边BA绕点B顺时针旋转α角得到线段BP，∴BA= BP，∵α=60°，∴△ABP是等边三角形，..................................1分∴∠BAP=60º，AP= AC，又∵∠BAC=90°，∴∠P AC=30º，∠ACP=75º，∵PD⊥AC于点D，∴∠DPC=15º．....................................................................2分（2）结论：∠DPC=75º．..................................................3分（3）画图.............................................................................4分过点A作AE⊥BP于E．∴∠AEB=90º，∵∠ABP=150°，∴∠1=30º，∠BAE=60º，又∵BA= BP，∴∠2=∠3=15º，∴∠P AE=75º，∵∠BAC=90°，∴∠4=75º，∴∠P AE=∠4，∵PD⊥AC于点D，∴∠AEP=∠ADP =90º，∴△APE≌△APD，..............................................................5分∴AE= AD，在Rt△ABE中，∠1=30º，∴12AE AB=，又∵AB=AC，∴1122AE AD AB AC ===，∴AD=CD，又∵∠ADP=∠CDP=90º，∴△ADP≌△CDP，.............................................................6分∴∠DCP=∠4=75º，∴∠DPC=15º．.......................................................................7分4123EDBAC PEBP321EAPCBD（1）∵点C （0，8）在抛物线223y x bx c =-++上， ∴8c =，................................................................................................................................1分又∵B （6，0）在抛物线2283y x bx =-++上， ∴02468b =-++， ∴83b =， ∴抛物线的表达式为228833y x x =-++．......................................................................2分（2）结论：以P ，C ，E ，'E 为顶点的四边形为菱形．..............................................3分证明：∵E 和'E 关于直线PC 对称，∴∠'E CP =∠ECP ，'EP E P =，'EC E C =，又∵PE ∥y 轴，∴∠EPC =∠'E CP =∠ECP ，∴EP =EC ，..........................................................................................................................5分 ∴''EC E C EP E P ===，∴四边形'E CEP 为菱形．................................................................................................6分（3）∵B （6，0），C （0，8）， ∴BC 的表达式为483y x =-+．设228,833P x x x ⎛⎫-++ ⎪⎝⎭，则4,83E x x ⎛⎫-+ ⎪⎝⎭， ∴PE 的长为228488333x x x ⎛⎫⎛⎫-++--+ ⎪ ⎪⎝⎭⎝⎭=2243x +x -，过点E 作EF ⊥y 轴于点F ， ∴△CFE ∽△COB ，∴35EF CE =，∴53CE EF =，即53CE x =．由PE =EC 得225433x +x x -=，解得72x =，∴点P 的坐标为755,26⎛⎫ ⎪⎝⎭．................................................8分（不需要过程，结论正确给2分）。

2016北京市各区初三数学二模分类汇编几何综合题汇编无答案

2016年各区二模几何综合题汇编1.(顺义)28.已知：如图，90ACD ∠=︒，MN 是过点A 的直线，AC DC =，DB MN ⊥于点B ．图2图3图1ABCDNMABCDNMNMABCD（1）在图1中，过点C 作CE CB ⊥，与直线MN 于点E ，①依题意补全图形；②求证：BCE ∆是等腰直角三角形；③图1中，线段BD 、AB 、CB 满足的数量关系是；（2）当MN 绕A 旋转到如图（2）和图（3）两个位置时，其它条件不变. 在图2中，线段BD 、AB 、CB 满足的数量关系是；在图3中，线段BD 、AB 、CB 满足的数量关系是；（3）MN 在绕点A 旋转过程中，当30BCD ∠=︒，BD =则CB = ．2.(昌平)28. 在等边△ABC 中，AB =2，点E 是BC 边上一点，∠DEF =60°，且∠DEF 的两边分别与△ABC 的边AB ，AC 交于点P ，Q （点P 不与点A ，B 重合）.（1）若点E 为BC 中点．①当点Q 与点A 重合，请在图1中补全图形；②在图2中，将∠DEF 绕着点E 旋转，设BP 的长为x ，CQ 的长为y ，求y 与x 的函数关系式，并写出自变量x 的取值范围；（2）如图3，当点P 为AB 的中点时，点M ，N 分别为BC ，AC 的中点，在EF 上截取EP '=EP ，连接NP '. 请你判断线段NP '与ME 的数量关系，并说明理由.图3图1A BE C图2DPQF3.(东城)28.【问题】在△ABC 中，AC =BC ，∠ACB =90°，点E 在直线BC 上（B ,C 除外），分别经过点E 和点B 做AE 和AB 的垂线，两条垂线交于点F ，研究AE 和EF 的数量关系.【探究发现】某数学兴趣小组在探究AE ，EF 的关系时，运用“从特殊到一般”的数学思想，他们发现当点E 是BC 的中点时，只需要取AC 边的中点G （如图1），通过推理证明就可以得到AE 和EF 的数量关系，请你按照这种思路直接写出AE 和EF 的数量关系；图1【数学思考】那么当点E 是直线BC 上（B ，C 除外）（其它条件不变），上面得到的结论是否仍然成立呢？请你从“点E 在线段BC 上”；“点E 在线段BC 的延长线”；“点E 在线段BC 的反向延长线上”三种情况中，任选一种情况，在图2中画出图形，并证明你的结论；图2【拓展应用】当点E 在线段CB 的延长线上时，若BE =nBC （01n ＜＜），请直接写出ABC S △：AEFS △的值．4.(海淀)28. 已知：AB BC =，90ABC ∠=︒.将线段AB 绕点A 逆时针旋转α（090α︒<<︒）得到线段AD .点C 关于直线BD 的对称点为E ，连接AE ，CE . （1）如图， ①补全图形； ②求AEC ∠的度数；（2）若AE1CE =，请写出求α度数的思路.（可．以不写出计算结果．．．．．．．．） 5.(西城)28．在等腰直角三角形ABC 中，AB =AC ，∠BAC =90°．点P为直线AB 上一个动点（点P 不与点A ，B 重合），连接PC ，点D 在直线BC 上，且PD =PC ．过点P 作EP ⊥PC 于点P ，点D ，E 在直线AC 的同侧，且PE =PC ，连接BE ．（1）情况一：当点P 在线段AB 上时，图形如图1所示；情况二：如图2，当点P 在BA 的延长线上，且AP <AB 时，请依题意补全图．．．．．．2．；（2）请从问题（1）的两种情况中，任选．．一种情况．．．．，完成下列问题： ①求证：∠ACP =∠DPB ；②用等式表示线段BC ，BP ，BE 之间的数量关系，并证明．图1 图26.(朝阳)28．在ABC ∆中，点D 、E 分别在AB 、AC 上，BE 、CD 相交于点O ，且A EBC DCB ∠=∠=∠21．（1）如图1，若AB =AC ，则BD 与CE 的数量关系是______________；（2）如图2，若AC AB ≠，请你补全图2，思考BD 与CE 是否仍然具有（1）中的数量关系，并说明理由；（3）如图3，︒=∠105BDC ，BD =3，且BE 平分∠ABC ，请写出求BE 长的思路．（不用写出计算结果）7.(房山)28.在△ABC中，BD平分∠ABC（∠ABC＜60°）（1）如图28-1，当点D在AC边上时，若∠ABC=42°，∠ACB=32°，请直接写出AB，DC和BC之间的数量关系．（2）如图28-2，当点D在△ABC内部，且∠ACD=30°时，①若∠BDC=150°，直接写出AB，AD和BC之间的数量关系，并写出结论成立的思路．②若∠ABC=2α，∠ACB=60°-α，请直接写出∠ADB的度数（用含α的式子表示）．8.(丰台) 28.在△ABC中，AC=BC，∠ACB=90°. 点D为AC的中点．将线段DE绕点D逆时针旋转90°得到线段DF，连接EF，CF．过点F作FH FC，交直线AB于点H．（1）若点E在线段DC上，如图1，①依题意补全图1；②判断FH与FC的数量关系并加以证明．（2）若E为线段DC的延长线上一点，如图2，且CE=的面积请求出∠FCHCFEΔ,15=,20∠CFE=12°，请写出求△FCH的面积的思路.（可以不写．．．．出计算．．．结果．．）EDADAABAB9.(石景山)28．如图，正方形ABCD ，G 为BC 延长线上一点，E 为射线BC 上一点，连接AE ．（1）若E 为BC 的中点，将线段EA 绕着点E 顺时针旋转90°，得到线段EF ，连接CF ．①请补全图形； ②求证：∠DCF =∠FCG ；（2）若点E 在BC 的延长线上，过点E 作AE 的垂线交∠DCG 的平分线于点M ，判断AE 与EM 的数量关系并证明你的结论．10.(怀柔)28.在△ABC 中，∠ABC=90°，D 为△ABC 内一动点，BD=a,CD=b(其中a ，b 为常数，且a<b).将△CDB 沿CB 翻折，得到△CEB. 连接AE. (1)请在图1中补全图形;(2)若∠ACB=α，AE ⊥CE ，则∠AEB=；(3)在(2)的条件下，用含a,b,α的式子表示AE 的长.图1 备用图11.(通州)28. 已知，在菱形ABCD 中，∠ADC=60°，点F 为CD 上任意一点（不与C 、D 重合），过点F 作CD 的垂线，交BD 于点E ，连接AE.（1）①依愿意补全图1； ②线段EF 、CF 、AE 之间的等量关系是。

北京市顺义区2016届九年级上学期期末考试数学试题

顺义区2015——2016学年度第一学期期末九年级教学质量检测数学试卷一、选择题（共10道小题，每小题3分，共30分）下面各题均有四个选项，其中只有一个．．是符合题意的． 1． 13-的倒数是 A ．3B ．13 C．13- D ．3- 2AB C ． D ．3．不等式321x +>-的解集是A ．13x >- B ．13x <- C ．1x >- D ．1x <- 4．下列银行标志中，既不是中心对称图形也不是轴对称图形的是5．若)0(43≠=xy y x ,则下列比例式成立的是 A ．34yx = B ．yx 43= C ．43=y x D ．43y x =6．在Rt △ABC 中，∠C =90º，35BC AB ==，，则cos A 的值为A ．35B ．45C ． 34D ． 437．如图，在平行四边形ABCD 中，点E 在AD 上，连接CE 并延长与BA 的延长线交于点F ，若2AE ED =，则FAFB的值是A ．13 B ．25 C ．12 D ． 238．如图，⊙O 的直径AB=2，弦AC=1，点D 在⊙O 上，则∠D 的度数为A ．30°B ．45°C ．60°D ． 75°9．若正方形的边长为6，则其外接圆半径与内切圆半径的大小分别为 A ．6， B． 3 C ．6，3 D．，10．如图所示，扇形AOB 的圆心角为120°，半径为2，则图中阴影部分的面积为A．43π-B．43π-C ．43π-D ．43π二、填空题（共6道小题，每小题3分，共18分）11．分解因式：269mn mn m ++= ． 12．一名射击爱好者5次射击的中靶环数如下：6，7，9，8，9，这5个数据的中位数是．13．如图，身高是1.6m 的某同学直立于旗杆影子的顶端处，测得同一时刻该同学和旗杆的影子长分别为1.2m 和9m ，则旗杆的高度为________m ． 14．若反比例函数1m y x-=的图象在同一象限内，y 随x 的增大而减小，则m 的取值范围是．15．将抛物线y ＝2x 2向下平移3个单位, 再向左平移1个单位，所得抛物线的解析式为 . 16．如图，在平面直角坐标系xOy 中，ABC ∆外接圆的圆心坐标是，半径是．三、解答题（共13道小题，第17—26小题，每小题5分，第27题7分，第28题7分，第29题8分，共72分）17．计算： 0)245(cos 60sin 30tan 60cos -︒-︒⋅︒+︒ 18．已知023a b=≠，求代数式2252(2)4a b a b a b -⋅--的值． 19．求二次函数342+-=x x y 的顶点坐标及对称轴，并在所给坐标系中画出该二次函数的图象．20．如图，已知在平面直角坐标系xOy 中，O 是坐标原点，点(2,5)A ，在反比例函数ky x=的图象上，过点A 的直线y x b =+交x 轴于点B ．（1）求k 和b 的值；（2）求AOB ∆的面积．21．张大叔想用篱笆围成一个周长为80米的矩形场地，矩形面积S （单位：平方米）随矩形一边长x （单位：米）的变化而变化．（1）求S 与x 之间的函数关系式，并写出自变量x 的取值范围；（2）当x 是多少时，矩形场地面积S 最大？最大面积是多少？22．已知: 如图，AB 是⊙O的直径，弦AC =B =60°，OD ⊥AC ，垂足为D ．（1）求OD 的长；（2）求劣弧AC 的长．23．已知：如图，在四边形ABCD 中，8AB AD ==，60A ∠=︒°，150D ∠=︒,四边形的周长为32，求BC 和DC 的长.24．在一次数学实践活动课上，老师带领学生去测一条南北流向的河宽，如图所示，某学生在河东岸点A 处观测到河对岸水边有一点C ，测得C 在A 北偏西31°的方向上，沿河岸向北前行40米到达B 处，测得C 在B 北偏西45°的方向上，请你根据以上数据，求这条河的宽度．（参考数值：3tan315︒≈）yxO 11j'DBA25．已知抛物线1)2()1(2--+-=x m x m y 与x 轴相交于A 、B 两点，且2AB =，求m 的值.26．在ABC ∆中，6AB =cm ，12AC =cm ，动点D 以1cm/s 的速度从点A 出发到点B 止，动点E 以2cm/s 的速度从点C 出发到点A 止，且两点同时运动，当以点A 、D 、E 为顶点的三角形与ABC ∆相似时，求运动的时间t .27．如图，AB 是O ⊙的直径，点C 在O ⊙上，CAB ∠的平分线交O ⊙于点D ，过点D 作AC 的垂线交AC 的延长线于点E ，连接BC 交AD 于点F .（1）猜想ED 与O ⊙的位置关系，并证明你的猜想；（2）若65AB AD ==，，求AF 的长.28．如图，在平行四边形ABCD 中，过点A 作AE BC ⊥，垂足为E ，连接DE ，F 为线段DE 上一点，且AFE B ∠=∠（1）求证：ADF ∆∽DEC ∆；（2）若8AB =，AD = AFAE 的长．29．已知：如图，直线33y x =+与x 轴交于C 点，与y 轴交于A 点，B 点在x 轴上，OAB △是等腰直角三角形．（1）求过A B C 、、三点的抛物线的解析式；（2）若直线CD AB ∥交抛物线于D 点，求D 点的坐标；（3）若P 点是抛物线上的动点，且在第一象限，那么PAB △是否有最大面积？若有，求出此时P点的坐标和PAB △的最大面积；若没有，请说明理由．BA参考答案一、选择题1、D2、B3、C4、D5、A6、B7、D8、C9、B 10、A 解析：二、填空题11、2(3)m n + 12、8 13、12 14、m ＞115、y ＝2（x ＋1）2－3 16、（5,2），三、解答题 17、原式＝112+＝0 18、原式＝1061(26)4362-⨯-=- 19、顶点坐标（2,3），对称轴x ＝2，图象略。

中考试题北京市顺义区二模试卷.docx

2016年北京市顺义区中考二模数学试卷一、单选题（共10小题）1．实数4的算术平方根是（）A．B．C．D．考点：平方根、算术平方根、立方根答案：B试题解析：4的算术平方根是22．2015年“十一”黄金周的第二天，北京故宫景点，接待游客超过了最大接待容量，当天接待92 800人次．将92 800用科学记数法表示应为（）A．B．C．D．考点：科学记数法和近似数、有效数字答案：C试题解析：92 800=3．如图，数轴上有A，B，C，D四个点，其中表示互为相反数的点是（）A．点A与点B B．点B与点CC．点B与点D D．点A与点D考点：实数的相关概念答案：D试题解析：A表示的点为-2，D表示的点为2，-2和2是相反数，所以选D4．函数中，自变量的取值范围是（）A．B．C．D．考点：二次根式及其性质答案：C试题解析：x-3≥0，x≥35．在下列调查中，适宜采用全面调查的是（）A．了解七（1）班学生校服的尺码情况B．了解我市中学生视力情况C．检测一批电灯泡的使用寿命D．调查顺义电视台《师说》栏目的收视率考点：数据的收集与整理答案：A试题解析：适合全面调查的必须有2点，数量不是很多不能是损耗品,所以选A6．下图是顺义区地图的一部分，小明家在怡馨家园小区，小宇家在小明家的北偏东约15°方向上，则小宇家可能住在（）A．裕龙花园三区B．双兴南区C．石园北区D．万科四季花城考点：平面直角坐标系及点的坐标答案：B试题解析：以小明家为坐标原点，建立平面直角坐标系，然后就可以得到答案，选B7．四张质地、大小相同的卡片上，分别画上如下图所示的四个图形，在看不到图形的情况下从中任意抽出一张卡片，则抽出的卡片上的图形是轴对称图形的概率为（）A．B．C．D．1考点：概率及计算答案：A试题解析：概率及计算8．如图，四边形内接于⊙，，则的度数是（）A ．B．C．D．考点：圆周角定理及推论答案：D试题解析：∠A+∠C=180°，∠A=110°∴∠C=70°∵∠BOD=2∠C∴∠BOD=140° .9．如图是一个正方体的展开图，把展开图折叠成正方体后，“你”字一面相对的面上的字是（）A．梦B．我C．中D．国考点：立体图形的展开与折叠答案：A试题解析：做一个正方体，然后展开，写上字，就可以得到答案，选A10．已知点M为某封闭图形边界上一定点，动点P从点M出发，沿其边界逆时针运动一周，设点P走过的路程为x，线段MP的长为y，表示y与x的函数关系的图象大致如图所示，则该封闭图形可能是（）A．B．C．D．考点：函数的表示方法及其图像答案：D试题解析：MP是先增大，到达最大值后减小，只有圆的运动轨迹符合要求，故选D二、填空题（共6小题）11.若，则．考点：实数的相关概念答案：3试题解析：根据题意得：m-2=0，n-1=0，解得：m=2，n=1，所以m+n=312.甲、乙两地某月上旬的日平均气温如图所示，则甲、乙两地这10天日平均气温方差大小关系为S甲2 S乙2（填＞或＜）．考点：极差、方差、标准差答案：>试题解析：方差表示的数据变化情况，方差大，说明数据变化大，根据图形，发现甲地的气温变化大，所以甲地气温的数据的方差大．13.小林、小芳和小亮三人玩飞镖游戏，各投5支飞镖，规定在同一圆环内得分相同，中靶和得分情况如图，则小亮的得分是．考点：二元一次方程（组）及其解法答案：21试题解析：设内圈得分为x分，外圈得分为y分，根据题意得：解得：x=5，y=3，3x+2y=15+6=2114.如图，在中，．按以下步骤作图：①以点为圆心，小于的长为半径画弧，分别交、于点、；②分别以点、为圆心，大于的长为半径画弧，两弧相交于点；③作射线交边于点．则的度数为__________．考点：尺规作图答案：70°试题解析：根据尺规作图，AD是∠CAB的角平分线，∵∠CAB=40°，∴∠CAD=20°，∴∠CDA=70°15.某函数符合如下条件：①图象经过点（1，3）；②随的增大而减小．请写出一个符合上述条件的函数表达式．考点：一次函数解析式的确定答案：y=-x+4试题解析：设解析式为y=kx+b，把x=1，y=3代入得：3=k+b，b=3-k，因为y随x的增大而减小，所以k<0，设k=-1，b=4，y=-x+416.如图，为了使电线杆稳固的垂直于地面，两侧常用拉紧的钢丝绳索固定，由于钢丝绳的交点E在电线杆的上三分之一处，所以知道BE的高度就可以知道电线杆AB的高度了．要想得到BE的高度，需要测量出一些数据，然后通过计算得出．请你设计出要测量的对象：；请你写出计算AB高度的思路：．考点：解直角三角形答案：和线段；思路：在Rt中，由，求出试题解析：和线段；思路：在Rt中，由，求出三、计算题（共1小题）17.计算：．考点：实数运算答案：见解析试题解析：四、解答题（共11小题）18.解不等式组：，并写出它的所有整数解．考点：一次不等式（组）的解法及其解集的表示答案：见解析试题解析：解不等式，得．解不等式，得，∴原不等式组的解集为，∴原不等式组的所有整数解为、、019.已知，求代数式的值．考点：代数式及其求值答案：见解析试题解析：原式====，∵，∴，∴原式=20.某地为了打造风景带，将一段长为360m的河道整治任务由甲、乙两个工程队先后接力完成，共用时20天，已知甲工程队每天整治24m，乙工程队每天整治16m，求甲、乙两个工程队分别整治了多长的河道．考点：一次方程（组）的应用答案：见解析试题解析：设甲工程队整治了米的河道，则乙工程队整治了米的河道根据题意得：，解得：，∴。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

6.下图是顺义区地图的一部分，小明家在怡馨家园小区，小宇家在小明家的北偏东约15°方向上，则小宇家可能住在 A .裕龙花园三区 B .双兴南区 C .石园北区D .万科四季花城顺义区2016届初三第二次统一练习数学试卷考生须知1. 本试卷共8页，共三道大题，29道小题，满分120分.考试时间120分钟。

2. 在试卷和答题卡上准确填写学校名称、姓名和准考证号。

3 .试题答案一律填涂或书写在答题卡上，在试卷上作答无效。

4.在答题卡上，选择题、作图题用 2B 铅笔作答，其他试题用黑色字迹签字笔作答。

5 .考试结束，将本试卷、答题卡和草稿纸一并交回。

一、选择题（本题共 30分，每小题3分）下面各题均有四个选项，其中只有一个是符合题意的.[来™]1 •实数4的算术平方根是A . -2B . 2c . -2D . 42.2015年“ ^一”黄金周的第二天，北京故宫景点，接待游客超过了最大接待容量，当天接待92 800人次.将92 800用科学记数法表示应为2345A . 928 10B . 92.8 10C . 9.28 10D . 9.28 10A ,B ,C ,D 四个点，其中表示互为相反数的点是4. 函数y=、、x-3中，自变量x 的取值范围是5. 在下列调查中，适宜采用全面调查的是 A. 了解七（1）班学生校服的尺码情况B. 了解我市中学生视力情况C.检测一批电灯泡的使用寿命D.调查顺义电视台《师说》栏目的收视率3.如图，数轴上有 A .点A 与点B C .点B 与点DB .点B 与点CD .点A 与点DABC-4 ------ -------------- u-2 -1 0 1B . x > 3C . x > 3D . x ::: 3I 的呼曰4■'号-APBM尊I 可・呼心 KStE >«■7•四张质地、大小相同的卡片上，分别画上如下图所示的四个图形，在看不到图形的情况下从中任意抽出一张卡片，则抽出的卡片上的图形是轴对称图形的概率为直角三角形平行四边形矩形圆1 1 3 A. B. C. D.1244&如图，四边形 ABCD 内接于O O , ■ A =110，则• BOD 的度数是A. 70B. 110C. 120D. 1409•如图是一个正方体的展开图，把展开图折叠成正方体后, 一面相对的面上的字是 A .梦B.我C.中 D .国10.已知点M 为某封闭图形边界上一定点，动点 P 从点M 出发，沿其边界逆时针运动一周，设点P走过的路程为x ,线段MP 的长为y ，表示y 与x 的函数关系的图象大致如图所示，则该封闭图形可能是你我的中国梦A DOCAB C D件的函数表达式16•如图，为了使电线杆稳固的垂直于地面，两侧常用拉紧的钢丝绳索固定，由于钢丝绳的交点 E 在电线杆的上三分之一处，所以知道 BE 的高度就可以知道电线杆 AB 的高度了 .要想得到 BE 的高度，需要测量出一些数据，然后通过计算得出•请你设计出要测量的对象：；请你写出计算AB 高度的思路：13.小林、小芳和小亮三人玩飞镖游戏，各投情况如图，则小亮的得分是 •5支飞镖，规定在同一圆环内得分相同，中靶和得分14•如图，在 △ ABC 中，N C =90°忆CAB =40° .按以下步骤作图：①以点 A 为圆心，小于 AC 的长为半径画弧，分别1 交AB 、AC 于点E 、F ；②分别以点E 、F 为圆心，大于丄EF2的长为半径画弧，两弧相交于点 G :③作射线AG 交BC 边于点D •则N ADC 的度数为 _____________ 15 •某函数符合如下条件：①图象经过点（ 1, 3）；②y 随x 的增大而减小.请写出一个符合上述条、填空题（本题共 18分，每小题3 分）10天日平均气温方差大小关系为小林19分小方23分小亮FD三、解答题（本题共72分，第17-26题，每小题5分，第27题7分，第28题7分，第29题8 分）解答应写出文字说明，演算步骤或证明过程17•计算：f1p1- 1+ 1-72 + 78-2cos45= •13丿15x - 3 ::: 2x,7x 33x.218 •解不等式组: 并写出它的所有整数解219•已知x • x -3 =0，求代数式2x -2x 120•已知：如图，在. ABC , AB=AC , AD是BC边上的中线，E是AC的中点，BF _ CA延长线于点F .求证：/CBF = ADE .21 •某地为了打造风景带，将一段长为360m的河道整治任务由甲、乙两个工程队先后接力完成，共用时20天，已知甲工程队每天整治24m,乙工程队每天整治16m求甲、乙两个工程队分别整治了多长的河道.AC — BD，垂足为M ,过点A作AE — AC , 22. 已知：如图，在四边形ABCD中，AB // DC , 交CD的延长线于点E .(1)求证：四边形ABDE是平行四边形；4(2)若AC =8 , sin ABD ，求BD 的长.423. 在平面直角坐标系xOy中，一次函数y - -x • k的图象与反比例函数y 的图象交于点A (x4, n)和点B .(1 )求k的值和点B的坐标；(2)若P是x轴上一点，且AP = AB，直接写出点P的坐标.24.已知：如图，在ABC中，以AB为直径的O O分别交AC、BC于点D、E，且AD二DC(1)求证：AB =BC ;(2)过点B作O O的切线，交AC的延长线于点F，且CF二DC，求si n N CAE的值.25. 为了传承中华优秀传统文化，某校组织了一次八年级350名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况，随机抽取了其中若干名学生的成绩（成绩X取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：频数（人数）请根据所给信息，解答下列问题：（1）a= ___________ ，b = ___________ ；（2）请补全频数分布直方图；（3 ）这次比赛成绩的中位数会落在_____________ 分数段；（4）若成绩在90分以上（包括90分）的为“优”等，则该年级参加这次比赛的350名学生中成绩“优”等的约有多少人？26. 阅读理解：如图1,在四边形ABCD的边AB上任取一点E （点E不与点A、点B重合），分别连接ED, EC , 可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把点E叫做四边形ABCD在边AB上的相似点；如果这三个三角形都相似，我们就把点E叫做四边形ABCD在边AB 上的强相似点•解决问题：（1）如图1,在四边形ABCD中，.A = /B=/DEC=50，试判断点E是否是四边形ABCD在边AB上的相似点，并说明理由；（2）如图2,在矩形ABCD中，AB=5, BC =2，且A，B，C，D四边均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图2中画出矩形ABCD在边AB上的一个强相似点E.成绩X/分频数频率50W X v 6020.04 60< X v 7060.12 70W x v 809b 80W x v 90a0.36 90 w x w100150.30图1 72.已知关于x的一元二次方程x -(2m • 1)x • 2m = 0.(1)求证：不论m为任何实数时，该方程总有两个实数根；2(2)若抛物线y =x -(2m 1)x 2m与x轴交于A、B两点(点A与点B在y轴异侧)，且AB = 4,求此抛物线的表达式；2(3)在(2)的条件下，若抛物线y = x -(2m - 1)x 2m向上平移b个单位长度后，所得到的图象与直线y = x没有交点，请直接写出b的取值范围28.已知：如图，.ACD =90 , MN 是过点A 的直线，AC 二DC , DB _ MN 于点B .（1）在图1中，过点C 作CE — CB ，与直线MN 于点E ,① 依题意补全图形；② 求证：：BCE 是等腰直角三角形；③ 图1中，线段BD 、AB 、CB 满足的数量关系是；（2）当MN 绕A 旋转到如图（2）和图（3）两个位置时，其它条件不变 . 在图2中，线段BD 、AB 、CB 满足的数量关系是；在图3中，线段BD 、AB 、CB 满足的数量关系是；（3） MN 在绕点A 旋转过程中，当一 BCD = 30 ， BD = 2时，贝U CB 二.图229.在平面直角坐标系xOy中，对于点P和O C给出如下定义：若O O上存在两个点A , B，使得.APB =60，则称P为O C的关联点.1 i已知点M(2,2)，N(-2,0) , E(0, -4) , F(2、,3,0)(1 )当0 O的半径为1时，①在点M , N , E , F中，O O的关联点是；②过点F作直线I交y轴正半轴于点G，使.GFO =30，若直线I上的点P(m, n)是O O的关联点，求m的取值范围;(2)若线段EF上的所有点都是半径为r的O O的关联点，求半径r的取值范围来源:Z*xx*]顺义区2016届初三第二次统一练习数学答案及评分参考、填空题（本题共 18分，每小题3 分） 11. 3; 12.. ; 13. 21; 14. 70 ；16. • BCE 和线段 BC ；BE思路：①在 RtA BCE 中，由 tanNBCE =—— 求出 BE = BC tanZBCE BC ，，1 2 3 3②由 AE AB ，可求 BE AB ，求得 AB BE BC tan. BCE .3 3 2 2三、解答题（本题共 72分，第17-26题，每小题5分，第27题7分，第28题7分，第29题8 分）17•解:/X.-1由"砂J"。

沖也 .........2=2 - 2 2 …… .. ......................................18.解：解不等式 5x -3 ：：：2x ，得x < 1.…… . ........ …… . .... .…1分7x +3解不等式3x ，得x-3 . ................... ...... ..... .. ........ ... …2分2原不等式组的解集为-3 ：：： X ：：： 1............ .... ................ .…4分•••原不等式组的所有整数解为 -2、-1、0 .1X 1 x —1 x 215.-X 4 （不唯一）；.... ....5 分 19. 解: 原式=(x 1)(x-1)(x-1)21 + x+1.…1分.(x-1)(x 1) ..........................(x-1)(x 2) (x_1)(x 2)........3 分2x x 1=~2 ..................................................................x 2 x-2J 来源 :]二 x 2 x =320. 证明：•/ AB 二AC , AD 是BC 边上的中线,••• . ADC =90 ... ................................................................................... .….1 分又E 是AC 的中点，•- AE = DE , ................................ ...... ...................................................................... .….2 分 • . ADE =/EAD=90 _ . C . ................................................................... ..…..3 分•/ BF _ CA 延长线于点F ,• . CBF=90 - . C . ................................................................................................................. .4 分_ CBF - ADE . .................................................................................................. ..….5 分21•解：设甲工程队整治了 x 米的河道，则乙工程队整治了 (360 - x)米的河道.…… ...................... 1分根据题意得： △•型 x=20 .............................................................. .…...…3分24 16解得：x =120 ................................................. .….….…4分••• 360-X =240答：甲工程队整治了 120米的河道，乙工程队整治了 240米的河道 … ...... ..5分22.(1) 证明：•/ AC _ BD , AE _ AC ,• AE // BD , ............................................................................................. ............. ............ .1 分 •/ AB // DC , • AB // DE .•四边形ABDE 为平行四边形. .................................... .. ....... ..….2分 (2) 解：•••四边形ABDE 为平行四边形，x 2 x 1 3 1x^TRT 4 ............................................ ....5 分••• BD =AE , E =/ABD .•「si n . ABD =4 ,5•- sin E E在 RT △ EAC 中，AC =8,4 23.解：(1 )把A (— 4, n )代入y 中，得n=1 , .......................... .…….1分x把A (— 4, 1)代入y = -X k 中，得k = -3 .................................. .….…….2分.…...…3分(2)点P 的是坐标(3,0)或(-11,0) .............................................. .………5分24. (1)证明：•/ AB 为O O 的直径，• • ADB =90 ................................................................................. ..……1 分又••• AD = DC ,• AB 二 BC . .......................................................................................................................... 2 分 (2)解：•/ BF 切O O 于点B ,/ ABF =90【 .......................................................... .... 3-分 ....• BAF F =90 .又••• BAF ABD =90 ,• ABD = F , • △ ABD BFD , • AD _ BD "BD DF ，• BD 2 二 AD DF ....….3分• CE =10, AE =6 ,[来源:]••• BD =6 ..................................................................................• • • • • • ~~・・・・・丿」解方程组y 一x_3,4y「7y =1.x = 1, y一4.又••• CF = DC ,••• CF 二DC = AD ,设CF 二DC 二AD=k，贝V BD^ AD DF 二k 2k =2k2 ,• BD=、,2k .snCAE拐25.解：(1) 18, 0.18; ............................ ... .................... .……2 分(2) 频数(人数)20181612840 50 60 70 80 90 100 成绩/分 .......................................... 3分(3) 80-90; ............................................................. 4 分(4) 350 0.30 =105 (人) .............................. ... .......... ..……5 分答：约有105人.26.解：( 1)结论：点E是四边形ABCD在边AB上的相似点.......... •…1分证明：••• A=/B=/DEC =50 ,•1+ 2=130 , 1+ 3=130 ,•2= 3, ..................................................................... ..……2分•△ AED BCE ,•••点E是四边形ABCD在边AB上的相似点........ .. …3分(2)A E BC A E在RT^ BCD 中, BC=、、3k ,。